
Прежде чем изучать готовые решения задач, нужно знать теорию, поэтому для вас я подготовила сначала очень краткую теорию по предмету «химия», после которого, чуть ниже размещены подробные решения задач.
Эта страница подготовлена для школьников и студентов любых специальностей.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Аналитическая химия
Аналитическая химия — наука, развивающая теоретические основы химического анализа веществ и материалов и разрабатывающая методы идентификации, обнаружения, разделения и определения химических элементов и их соединений, а также методы установления химического состава веществ. Проведение химического анализа в настоящее время заключается в получении информации о составе и природе вещества. wikipedia.org/wiki/Аналитическая_химия
В зависимости от задач, аналитическая химия подразделяется на качественный анализ, нацеленный на определение того, что (или какие вещества), в какой форме находится в образце, и количественный анализ, нацеленный на определение сколько данного вещества (элементов, ионов, молекулярных форм и др.) находится в образце.
В задачи качественного анализа входит:
- установление присутствия (обнаружение, открытие) в пробе тех или иных компонентов (молекул, атомов, ионов);
- идентификация веществ и компонентов в пробе неизвестного состава (установление их аналогии соответствующим эталонам).
Задачи количественного анализа — определение содержания или концентрации компонентов в пробе.
Титриметрический метод анализа ионная сила, активность, коэффициент активности
Произведение активностей гидроксильных ионов и ионов водорода в водных растворах при данной температуре — величина постоянная:
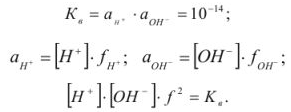
При проведении расчетов следует различать действительную (или истинную), обозначаемую обычно буквой с, и эффективную (или активную) концентрацию, обозначаемую буквой а. Обе концентрации имеют размерность моль/л и связь между ними осуществляется посредством коэффициента активности
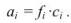
Коэффициент активности характеризует степень отклонения системы от идеальной из-за электростатических взаимодействий ионов, участвующих в реакции, с посторонними (или собственными, если их концентрация очень высока) ионами. В идеальной системе (в разбавленных растворах сильных электролитов, когда 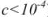 )
) 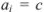 и коэффициент активности равен единице.
и коэффициент активности равен единице.
Это означает, что электростатическое взаимодействие отсутствует.
В растворах с большей концентрацией 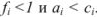 . Величина коэффициента активности, а значит и активности, зависит от заряда и ионной силы, создаваемой всеми ионами в растворе. Ионная сила
. Величина коэффициента активности, а значит и активности, зависит от заряда и ионной силы, создаваемой всеми ионами в растворе. Ионная сила 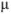 равна полусумме произведения концентрации всех ионов в растворе на квадрат их заряда:
равна полусумме произведения концентрации всех ионов в растворе на квадрат их заряда:
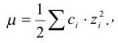
где 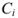 — концентрация (в молях на литр);
— концентрация (в молях на литр); 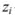 — заряд иона.
— заряд иона.
В растворах слабых электролитов 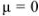 . Зная
. Зная 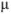 , можно рассчитать коэффициент активности по формулам Дебая-Хюкксля:
, можно рассчитать коэффициент активности по формулам Дебая-Хюкксля:
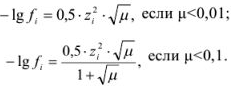
Но чаще всего для определения коэффициента активности 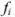 пользуются справочными таблицами (см. приложение). Зная коэффициент активности, можно оценить активность иона или электролита в растворе.
пользуются справочными таблицами (см. приложение). Зная коэффициент активности, можно оценить активность иона или электролита в растворе.
Возможно эта страница вам будет полезна:
Для облегчения расчетов можно пользоваться следующими допущениями.
- Коэффициенты активности ионов одинакового заряда независимо от радиуса иона примерно равны. Поэтому в справочниках часто приводятся усредненные величины коэффициентов активности для одно-, двух-, трех- и четырехзарядных ионов.
- Коэффициенты активности нейтральных частиц в разбавленных растворах электролитов принимают равными единице.
- Очень разбавленные или насыщенные растворы малорастворимого электролита можно считать идеальными.
Задача №1
Рассчитайте активность иона натрия и сульфат-иона в растворе, в одном литре которого содержится 0,005 моль 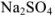 и 0,02 моль
и 0,02 моль 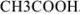
Решение:
Записываем процесс ионизации сильного электролита:
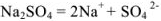
и определяем концентрацию каждого иона:
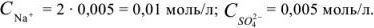
Ионизацией молекул 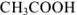 пренебрегаем, так как
пренебрегаем, так как 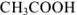 является слабым электролитом и не участвует в создании ионной силы. Рассчитываем ионную силу раствора:
является слабым электролитом и не участвует в создании ионной силы. Рассчитываем ионную силу раствора:
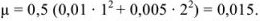
По табл. 1 приложения определяем приближенные значения 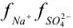 и вычисляем активности ионов:
и вычисляем активности ионов:
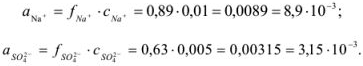
Задача №2
Рассчитайте коэффициент активности для 0,1 М раствора гидроксида натрия и сравните его с экспериментально найденной величиной 0,764.
Решение:
Рассчитаем ионную силу раствора:
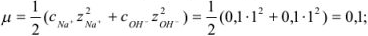
По формуле Дсбая-Хюккеля находим 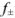 :
:
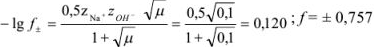
Как видно, в данном случае рассчитанное и экспериментально найденное значения коэффициента активности близки; различие составляет 0,8 %.
Часто при расчетах сложных равновесий коэффициенты активности принимают равными единице. В этих случаях рассчитанные величины коэффициентов активности могут быть далекими от истинных; влияние химических факторов гораздо больше, чем электростатических сил, поэтому пренебрежение последними при расчетах сложных равновесий не вносит ощутимой погрешности в результаты.
Расчет эквивалентных масс
В основе объемного анализа лежит закон эквивалентов, согласно которому вещества реагируют друг с другом в строго определенных (эквивалентных) соотношениях.
Химический эквивалент — реальная или условная частица вещества в кислотно-основной реакции химически равноценна одному иону 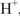 , а в окислительно-восстановительной реакции — одному электрону.
, а в окислительно-восстановительной реакции — одному электрону.
Реальная частица — ион, атом или молекула, условная частица — определенная часть (половина, треть и т.д.) иона, атома или молекулы.
В общем случае эквивалент любого вещества X обозначают следующим образом: 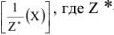 — число эквивалентности.
— число эквивалентности.
Число эквивалентности 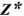 — число ионов Н+ в кислотноосновной реакции или число электронов в окислительно-восстановительной реакции, которое химически равноценно одной частице вещества X.
— число ионов Н+ в кислотноосновной реакции или число электронов в окислительно-восстановительной реакции, которое химически равноценно одной частице вещества X.
Фактор эквивалентности 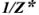 — число, которое показывает, какая доля реальной частицы X эквивалентна одному иону Н+ в кислотно-основной реакции или одному электрону в окислительно-восстановительной реакции.
— число, которое показывает, какая доля реальной частицы X эквивалентна одному иону Н+ в кислотно-основной реакции или одному электрону в окислительно-восстановительной реакции.
Химическое количество эквивалента вещества X — 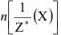 — величина, численно равная отношению массы вещества X к молярной массе его эквивалента. Единица измерения — моль.
— величина, численно равная отношению массы вещества X к молярной массе его эквивалента. Единица измерения — моль.
Расчет эквивалентов при использовании различных методов объемного анализа производится на основании конкретных химических реакций.
Так, в случае метода нейтрализации число эквивалентов рассчитывается по числу 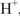 или
или 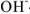 -ионов, вступающих во взаимодействие.
-ионов, вступающих во взаимодействие.
Задача №3
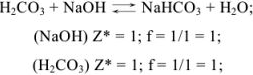
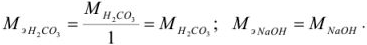
Задача №4
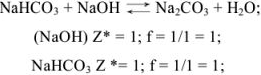
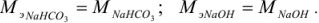
Задача №5
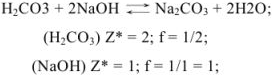
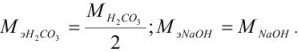
Если применяют метод осаждения, молекулярную массу делят на число зарядов иона, участвующего в образовании осадка, и получают массу, эквивалентную (Мэ).
Задача №6
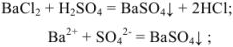
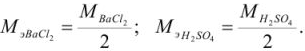
Задача №7
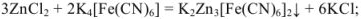
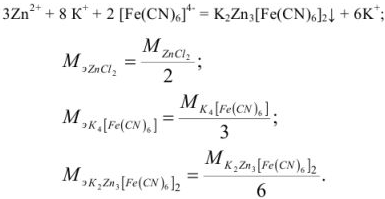
В случае методов окисления-восстановления величина эквивалента окислителя равна молекулярной (ионной) массе окислителя, деленной на число приобретенных электронов. Эквивалент восстановителя равен молекулярной (ионной) массе восстановителя, деленной на число отданных электронов.
Задача №8
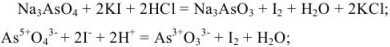
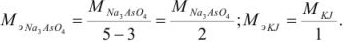
В косвенных определениях эквивалент определяемого вещества равен эквиваленту титруемого заместителя.
Задача №9
Для определения кальция методом перманганатометрии кальций осаждают в виде 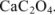 . Осадок отделяют от раствора, растворяют в соляной кислоте и титруют выделившуюся щавелевую кислоту перманганатом калия в кислой среде:
. Осадок отделяют от раствора, растворяют в соляной кислоте и титруют выделившуюся щавелевую кислоту перманганатом калия в кислой среде:
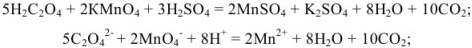
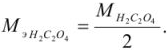
Так как в осадке количество эквивалентов кальция равно количеству эквивалентов щавелевой кислоты, то
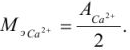
Способы выражения концентрации
Способ выражения концентрации в объемном анализе зависит от назначения раствора и характера компонентов, образующих раствор.
Концентрация растворов неорганических веществ в воде, которые используются в качестве рабочих для титрования, выражается в грамм-эквивалентах на 1 л раствора (молярная концентрация эквивалента, н.), в молях на 1 л раствора (молярные растворы, М), в молях на 1 кг растворителя (молярьные растворы, 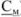 ), через титр рабочего раствора (
), через титр рабочего раствора (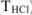 ) и титр рабочего раствора по определяемому веществу (
) и титр рабочего раствора по определяемому веществу (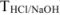 ).
).
Концентрация растворов, использующихся для вспомогательных операций (создания определенной среды, сдвига равновесия реакции в нужную сторону, подавления гидролиза и пр.), выражается в граммах на 100 г или 100 мл раствора (процентные растворы — массовая или объемная доля растворенного вещества). Концентрацию растворов двух неограниченно смешивающихся компонентов выражают в мольных долях.
Концентрация, выраженная в процентах, показывает, какое весовое (объемное) количество вещества содержится в 100 г раствора.
Массовая доля растворенного вещества 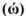 выражается в долях единицы, процентах (%), миллионных долях (млн
выражается в долях единицы, процентах (%), миллионных долях (млн ). Массовая доля численно равна отношению массы растворенного вещества
). Массовая доля численно равна отношению массы растворенного вещества 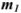 к общей массе раствора:
к общей массе раствора:
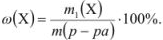
Объемная доля растворенного вещества 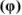 выражается в долях единицы, процентах (%) и численно равна отношению объема жидкого или газообразного вещества
выражается в долях единицы, процентах (%) и численно равна отношению объема жидкого или газообразного вещества 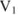 к общему объему раствора V:
к общему объему раствора V:
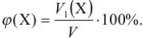
Задача №10
Вычислить концентрацию раствора хлорида натрия, приготовленного растворением 12,8 г соли в 250 мл воды.
Решение:
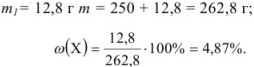
Для перехода от массы к его объему используют зависимость 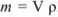 .
.
Тогда
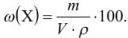
Концентрация, выраженная в молях, показывает, какое количество молей вещества растворено в 1 л раствора, и называется молярной концентрацией вещества 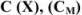
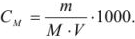
Задача №11
В 300 мл раствора содержится 40 г сульфата натрия. Определите молярную концентрацию раствора.
Решение:
1 способ
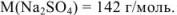
Найдем количество соли:
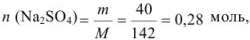
Рассчитаем молярную концентрацию раствора: в 300 г раствора — 0,28 моль вещества, в 1000 г раствора — х моль вещества.
Решив пропорцию, получим х = 0,93 моль.
См = 0,93 моль/л.
Решение:
II способ
Молярную концентрацию раствора также можно рассчитать по формуле, подставив соответствующие значения:
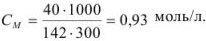
Концентрация раствора, выраженная через моляльность 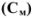 , рассчитывается по аналогичной формуле, только вместо объема раствора берется масса растворителя (1 кг):
, рассчитывается по аналогичной формуле, только вместо объема раствора берется масса растворителя (1 кг):
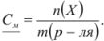
Разница между молярностью и моляльностью разбавленных растворов незначительна. Однако в тех случаях, когда измерения проводят при различных температурах, рекомендуется концентрацию выражать в моляльностях, так как моляльность раствора нс изменяется при изменении температуры.
Молярная концентрация эквивалента вещества (эквивалентная концентрация 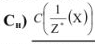 показывает, какое количество грамм-эквивалентов вещества растворено в 1 л раствора:
показывает, какое количество грамм-эквивалентов вещества растворено в 1 л раствора:
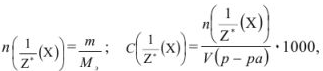
где 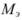 — масса эквивалентная:
— масса эквивалентная:
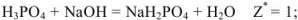
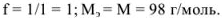
Грамм-эквивалент 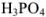 в данном случае равен значению молярной массы вещества, выраженной в граммах (1 моль).
в данном случае равен значению молярной массы вещества, выраженной в граммах (1 моль).
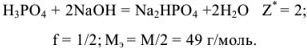
Грамм-эквивалент 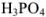 здесь равен половине значения молярной массы вещества (1/2 моль).
здесь равен половине значения молярной массы вещества (1/2 моль).
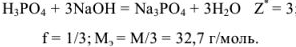
Грамм-эквивалент 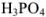 в этом случае равен 1/3 значения молярной массы вещества (1/3 моль).
в этом случае равен 1/3 значения молярной массы вещества (1/3 моль).
Задача №12
Рассчитать эквивалентную концентрацию раствора гидроксида калия, приготовленного растворением 11,2 г препарата в 200 мл воды. Плотность полученного раствора равна 1,04 г/мл.
Решение:
I способ
Эквивалентная масса КОН в реакциях нейтрализации равна его молекулярной массе. Поэтому концентрацию раствора можно рассчитать по формуле
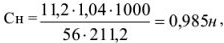
где масса раствора равна 200 + 11,2 = 211,2 г.
Решение:
II способ
Рассчитаем массу полученного раствора:
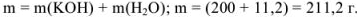
Объем полученного раствора составляет
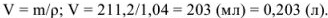
Определяем количество гидроксида калия, растворенного в воде. Эквивалентная масса 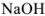 в реакциях нейтрализации равна молекулярной массе. Поэтому
в реакциях нейтрализации равна молекулярной массе. Поэтому 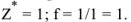
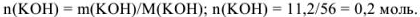
Эквивалентная концентрация раствора гидроксида калия равна
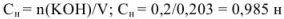
Задача №13
Рассчитать эквивалентную концентрацию раствора перманганата калия, приготовленного растворением 18 г препарата, предназначенного для титрования в кислой среде, в 250 мл воды.
Решение:
В кислой среде ион марганца восстанавливается из семи — до двухзарядного, т.е. в реакции окисления-восстановления участвуют 5 электронов. Поэтому 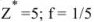
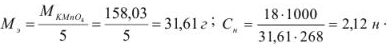
Концентрация, выраженная через титр, показывает, какое количество растворенного вещества в граммах содержится в 1 мл рабочего раствора. Титр рассчитывается по формуле
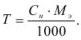
Задача №14
Рассчитайте титр 0,08 н раствора соляной кислоты.
Решение:
Эквивалентная масса соляной кислоты равна молекулярной массе 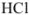 , поэтому
, поэтому
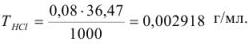
Титр по определяемому веществу показывает, какое количество определяемого вещества (в граммах) эквивалентно одному миллилитру рабочего раствора данной концентрации:
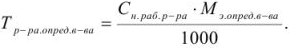
Задача №15
Рассчитать титр 0,1 н раствора едкого натрия по уксусной кислоте.
Решение:
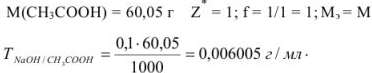
Молярная доля растворенного вещества 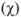 — выражается в долях единицы или процентах (%) и численно равна отношению химического количества растворенного вещества
— выражается в долях единицы или процентах (%) и численно равна отношению химического количества растворенного вещества 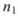 к суммарному числу моль всех компонентов раствора
к суммарному числу моль всех компонентов раствора 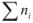 :
:
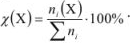
Число молей каждого компонента равно 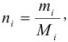
где 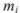 — масса компонентов;
— масса компонентов; 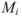 — молекулярная масса.
— молекулярная масса.

Возможно эта страница вам будет полезна:
Задача №16
К 200 мл воды добавлено 350 мл этилового спирта. Рассчитать количество мольных долей каждого компонента смеси.
Решение:
Мольная доля воды
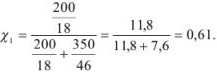
Мольная доля спирта
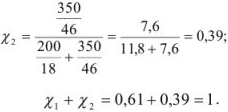
Перевод значений концентрации раствора из одних единиц в другие
Если концентрация выражена в весовых процентах 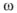 (%), то для перехода к концентрации, выраженной через молярную концентрацию эквивалентов, можно использовать формулу
(%), то для перехода к концентрации, выраженной через молярную концентрацию эквивалентов, можно использовать формулу
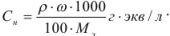
Задача №17
Рассчитать молярную концентрацию эквивалентов 12 %-ного раствора серной кислоты 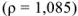
Решение:
Масса, эквивалентная серной кислоте, равна 49, так как 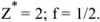
Масса раствора равна 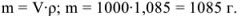
Рассчитаем, сколько 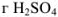 содержится в 1085 г раствора:
содержится в 1085 г раствора:
12 г 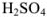 содержится в 100 г раствора;
содержится в 100 г раствора;
х г 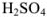 содержится в 1085 г раствора.
содержится в 1085 г раствора.
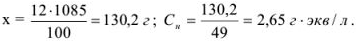
Молярную формуле концентрацию эквивалентов можно рассчитать по формуле
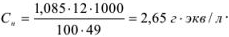
Для перехода от процентной концентрации к молярной используют аналогичную формулу, в которую вместо эквивалентной массы подставляют молекулярную массу растворенного вещества.
Задача №18
Рассчитать молярность 13,7 %-ного раствора углекислого натрия, плотность которого 1,145.
Решение:
Масса раствора равна
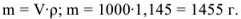
Рассчитаем, сколько г 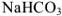 содержится в 1145 г раствора:
содержится в 1145 г раствора:
13,7 г 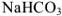 содержится в 100 г раствора;
содержится в 100 г раствора;
х г 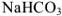 содержится в 1145 г раствора.
содержится в 1145 г раствора.
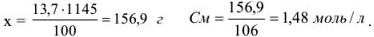
Молярную концентрацию можно рассчитать по формуле, подставив соответствующие значения:
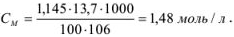
Для вычисления моляльности раствора, содержащего 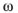 вещества, используем формулу
вещества, используем формулу
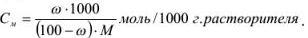
Задача №19
Рассчитать моляльность 8 %-ного раствора азотной кислоты.
Решение:
8 г азотной кислоты находится в (100-8) г растворителя; х г азотной кислоты находится в 1000 г растворителя.
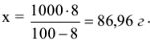
Найдем количество моль азотной кислоты, растворенной в 1000 г растворителя:
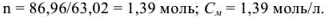
Моляльную концентрацию можно рассчитать по формуле, подставив соответствующие значения:
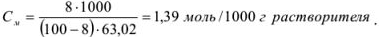
Растворы готовят из навесок, если исходное вещество твердое, или методом разбавления, если вещество находится в виде раствора. Основная расчетная формула, применяющаяся при приготовлении растворов методом разбавления:
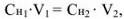
где 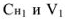 — молярная концентрация эквивалентов и объем исходного раствора;
— молярная концентрация эквивалентов и объем исходного раствора; 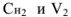 — молярная концентрация эквивалентов и объем приготовленного раствора.
— молярная концентрация эквивалентов и объем приготовленного раствора.
Задача №20
Рассчитать, какое количество 2,0 н серной кислоты необходимо взять для приготовления 300 мл 0,07 н раствора.
Решение:
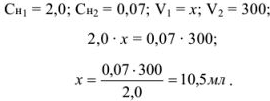
Массу навески (в г) для приготовления определенного объема V раствора с заданной молярной концентрацией эквивалентов рассчитывают по формуле.
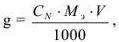
где 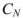 — нормальная концентрация рабочего раствора;
— нормальная концентрация рабочего раствора; 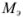 — масса эквивалентная определяемого вещества; V — объем раствора определяемого вещества.
— масса эквивалентная определяемого вещества; V — объем раствора определяемого вещества.
Расчет значений ph в растворах электролитов
Для сильной кислоты
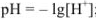
для сильного основания
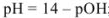
для слабой кислоты
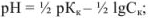
для слабого основания
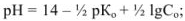
для буферной смеси (кислой)
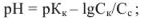
для буферной смеси (щелочной)
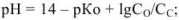
для соли сильного основания и слабой кислоты
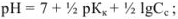
для соли слабого основания и сильной кислоты
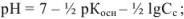
для соли слабого основания и слабой кислоты
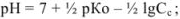
для смеси двух слабых кислот, если 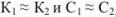 ,
,
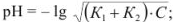
для смеси двух слабых кислот, если 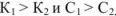
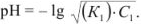
Сильные кислоты и основания
Задача №21
Рассчитать 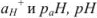 0,01 н, раствора соляной кислоты.
0,01 н, раствора соляной кислоты.
Решение:
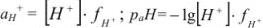
Ионная сила 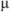 0,01 н раствора соляной кислоты равна
0,01 н раствора соляной кислоты равна
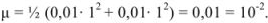
Поэтому коэффициент активности можно рассчитать по расширенному уравнению Дсбая-Хюккеля или найти в соответствующей справочной литературе.
Для
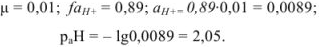
Если рассчитать значение pH без учета коэффициента активности, получаем 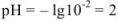 ; Разница составляет
; Разница составляет 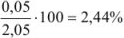 .
.
Задача №22
Рассчитать pH в 0,02 М растворе NaOH.
Решение:
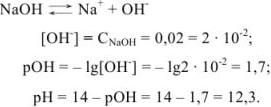
Слабые кислоты и основания
В водном растворе слабая кислота диссоциирует согласно уравнению
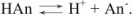
Применим закон действующих масс:
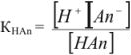 , так как
, так как 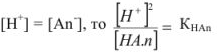
или
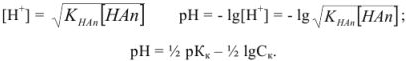
Аналогично выводится уравнение для расчета 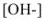 в слабых основаниях:
в слабых основаниях:
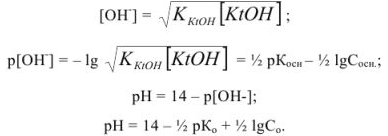
Задача №23
Рассчитать pH в 0,1 М растворе уксусной кислоты.
Решение:
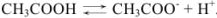
Уксусная кислота — слабый электролит, 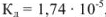 ,
,
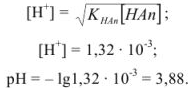
Задача №24
Рассчитать pH в 0,02 М растворе 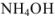 .
.
Решение:
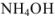 — слабый электролит,
— слабый электролит, 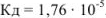 .
.
В формулу подставляем значения и получаем
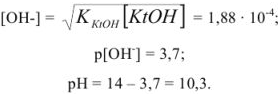
Гидролиз катионов и анионов
Помимо кислот и оснований, растворы которых отличаются соответственно кислой и щелочной реакцией, растворы многих солей также имеют кислую или щелочную реакцию.
Водные (и неводные) растворы солей подвергаются гидролизу.
Кислая среда характерна для растворов солей, образованных катионами слабых оснований и анионами сильных кислот (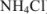 ):
):
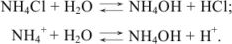
Применим закон действующих масс:
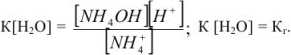
Умножим и разделим левую часть уравнения на [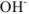 ], получим
], получим
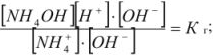
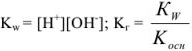
Из уравнения следует, что
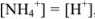
тогда
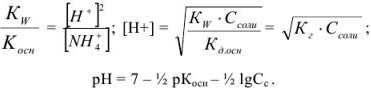
Щелочная среда характерна для растворов солей, образованных катионами сильных оснований и анионами слабых кислот (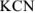 ):
):

Аналогично выводится уравнение для расчета [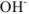 ]. В результате получим
]. В результате получим
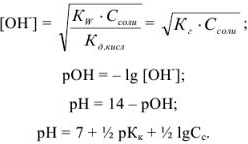
Буферные растворы
Растворы, содержащие одновременно какую-либо слабую кислоту и ее соль и оказывающие буферное действие (способность поддерживать постоянное значение pH), называются кислыми буферными растворами (pH < 7).
Например:
- ацетатный буфер
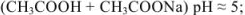
- формиатный буфер
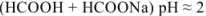
Растворы, содержащие одновременно какое-либо слабое основание и его соль и оказывающие буферное действие, называются основными буферными растворами (pH > 7).
Например:
аммиачно-аммонийный буфер 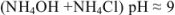
В буферном растворе содержится слабая кислота 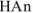 и ее соль МсАп. Запишем выражение для константы ионизации:
и ее соль МсАп. Запишем выражение для константы ионизации:
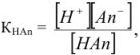
где 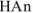 — слабая кислота. Она присутствует в растворе почти исключительно в виде неионизированных молекул, так как одноименные ионы (
— слабая кислота. Она присутствует в растворе почти исключительно в виде неионизированных молекул, так как одноименные ионы (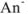 ) практически полностью подавляют ее ионизацию, т. е. [
) практически полностью подавляют ее ионизацию, т. е. [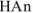 ] =
] = 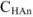 .
.
С другой стороны, поскольку соль 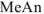 диссоциирована полностью, а кислота ионизирована очень слабо, почти все имеющиеся в растворе
диссоциирована полностью, а кислота ионизирована очень слабо, почти все имеющиеся в растворе 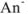 — анионы получены в результате ионизации соли, причем каждая молекула соли дает один анион
— анионы получены в результате ионизации соли, причем каждая молекула соли дает один анион 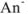 .
.
Отсюда следует, что 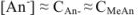
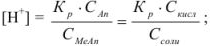
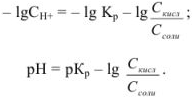
Аналогично выводится уравнение для расчета pH в щелочном буферном растворе:
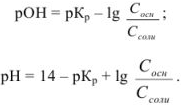
Задача №25
Рассчитать pH раствора, полученного при титровании 100 мл 0,08 н раствора уксусной кислоты 15 мл 0,1 н раствора едкого натра.
Решение:
При титровании до точки эквивалентности образуется буферная смесь, состоящая из неоттитрованной 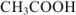 и образовавшегося
и образовавшегося 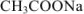

Построение кривых титрования
При использовании метода нейтрализации кривые титрования строятся в координатах pH — количество прибавленного рабочего раствора (мл).
Задача №26
Построить кривую титрования 100 см 0,1 н раствора
0,1 н раствора 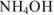 0,1 н раствором
0,1 н раствором 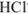 .
.
Решение:
Определяем pH в точках кривой титрования.
1. До начала титрования. В растворе находится слабое основание 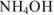 . Для вычисления pH используем формулу для слабых оснований:
. Для вычисления pH используем формулу для слабых оснований:
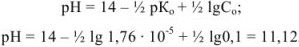
2. При титровании до точки эквивалентности. В титриметрической смеси присутствуют неоттитрованный 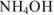 и образовавшаяся при титровании соль
и образовавшаяся при титровании соль 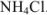 . Кислотно-основная пара
. Кислотно-основная пара 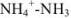 обладает буферными свойствами, pH в таких растворах вычисляют по формуле
обладает буферными свойствами, pH в таких растворах вычисляют по формуле
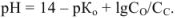
Оттитрованная часть основания превратилась в соль, поэтому отношение 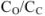 равно отношению числа миллилитров оттитрованного основания (или к равному ему числу миллилитров прибавленной кислоты).
равно отношению числа миллилитров оттитрованного основания (или к равному ему числу миллилитров прибавленной кислоты).
В момент, когда оттитровано 50 % основания:
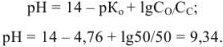
Прибавлено 90 % кислоты: 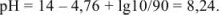
Прибавлено 99 % кислоты: 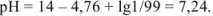
Прибавлено 99,9 % кислоты: 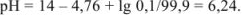
3. В точке эквивалентности 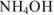 полностью оттитрован и переведен в соль
полностью оттитрован и переведен в соль 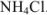 , которая подвергается гидролизу по катиону. pH в растворе этой соли можно вычислить с использованием формулы
, которая подвергается гидролизу по катиону. pH в растворе этой соли можно вычислить с использованием формулы 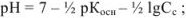
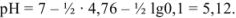
4. После точки эквивалентности в растворе появляется избыток 0,1 мл сильной кислоты 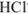 :
:
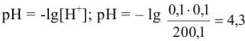
Избыток соляной кислоты 1 мл:
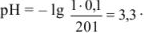
Избыток соляной кислоты 10 мл:
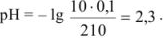
Избыток соляной кислоты 100 мл:
Область скачка титрования лежит в пределах значений pH от момента, когда осталось 0,1 мл неоттитрованного свободного основания, до момента, когда прибавлено 0,1 мл сильной кислоты (в интервале pH 6,24-4,3).
Точка эквивалентности не совпадает с точкой нейтрализации, из-за гидролиза соли она сдвинута в слабо-кислую область (pH = 5,12).
Для определения точки эквивалентности в процессе титрования нужно применить индикатор метиловый красный (pH = 4,2 — 6,2) или метиловый оранжевый (pH = 3,1 — 4,0). При использовании метилового оранжевого погрешность будет больше.
Ошибки титрования
Задача №27
Рассчитаем, чему равна индикаторная ошибка титрования 0,1 н раствора 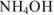 0,1 и раствором
0,1 и раствором 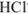 с различными индикаторами:
с различными индикаторами:
а) метиловым красным;
б) фенолфталеином;
в) метиловым оранжевым.
Решение:
Величина pH в точке эквивалентности равна 5,12.
а) При титровании 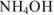 с метиловым красным титрование заканчивается при pH = 6,2 вместо 5,12, поэтому возникает
с метиловым красным титрование заканчивается при pH = 6,2 вместо 5,12, поэтому возникает 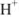 — ошибка:
— ошибка:
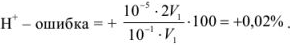
б) С фенолфталеином — при pH = 9. В растворе находится некоторое количество неоттитрованного 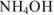 , т. е. необходимо рассчитать основную ошибку:
, т. е. необходимо рассчитать основную ошибку:
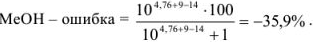
Из расчетов видно, что недотитрованного 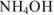 останется в растворе 35,9 %.
останется в растворе 35,9 %.
в) При титровании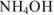 с метиловым оранжевым титрование заканчивается при pH = 4 вместо 5,12, поэтому возникает
с метиловым оранжевым титрование заканчивается при pH = 4 вместо 5,12, поэтому возникает 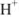 — ошибка:
— ошибка:
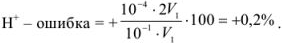
Как видно из расчетов, наименьшую погрешность мы получим при титровании в присутствии метилового красного, наибольшую — с фенолфталеином. Индикатор метиловый оранжевый тоже пригоден, погрешность лежит в пределах допустимой нормы.
Расчет результатов анализа проводят на основании закона эквивалентности.
В точке эквивалентности объемы исследуемого и рабочего растворов пропорциональны их нормальностям:
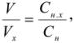
где 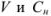 — объем и молярная концентрация эквивалентов рабочего раствора;
— объем и молярная концентрация эквивалентов рабочего раствора; 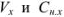 — объем и молярная концентрация эквивалентов исследуемого раствора.
— объем и молярная концентрация эквивалентов исследуемого раствора.
Поэтому по количеству эквивалентов рабочего раствора, затраченного на титрование, можно рассчитать количество эквивалентов исследуемого вещества.
Результаты прямого титрования в граммах рассчитываются по формуле
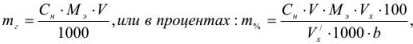
где 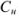 — молярная концентрация эквивалентов рабочего раствора;
— молярная концентрация эквивалентов рабочего раствора; 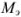 -масса эквивалентная определяемого вещества;
-масса эквивалентная определяемого вещества; 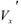 аликвотная часть исследуемого раствора, взятая для титрования;
аликвотная часть исследуемого раствора, взятая для титрования; 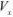 — исходный объем раствора определяемого вещества;
— исходный объем раствора определяемого вещества; 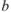 — навеска определяемого вещества.
— навеска определяемого вещества.
Задача №28
На титрование раствора КОН до точки эквивалентности ушло 12 мл 0,08 н раствора соляной кислоты. Сколько граммов едкого кали содержится в растворе?
Решение:
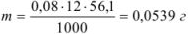
Задача №29
Рассчитать процентное содержание 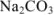 в препарате, если на титрование 10 мл раствора соды, приготовленного растворением 2,0202 г навески ее в 250 мл воды, ушло 12 мл 0,1 и раствора соляной кислоты.
в препарате, если на титрование 10 мл раствора соды, приготовленного растворением 2,0202 г навески ее в 250 мл воды, ушло 12 мл 0,1 и раствора соляной кислоты.
Решение:

Окислительно — восстановительные реакции
Уравнение Нернста
В редоксометрии используются реакции окисления — восстановления, связанные с переходом электронов от одного иона (молекулы) к другому.
Окислитель — вещество, атомы которого принимают электроны, превращается в ионы с более низкой степенью окисления (процесс восстановления).
Восстановитель — вещество, атомы которого отдают электроны, превращается в ионы с более высокой степенью окисления (процесс окисления). Следует говорить не об отдельном окислителе или восстановителе, а об окислительно-восстановительных системах:
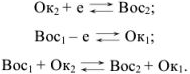
Для того чтобы в приведенных схемах реакция протекала слева направо, необходимо, чтобы 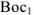 был более сильным восстановителем, чем образованная из
был более сильным восстановителем, чем образованная из 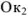 его сопряженная форма
его сопряженная форма 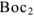 . Согласно всему сказанному
. Согласно всему сказанному 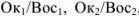 , являются соответственно окислительно-восстановительными системами.
, являются соответственно окислительно-восстановительными системами.
Представить направление окислительно-восстановительной реакции можно, только зная количественную характеристику относительной силы окислительно-восстановительной системы. Такой характеристикой является величина окислительно-восстановительного потенциала.
Значение окислительно-восстановительного потенциала зависит от величины стандартного окислительно-восстановительного потенциала Е° концентрации и реакции среды. Эта зависимость выражается уравнением Нернста:
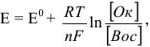
где 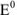 — стандартный окислительно-восстановительный потенциал; R -газовая постоянная (8,313 дж/(моль- град); Т — абсолютная температура, К; F — число Фарадея (96 500 кулон/г-экв); n — число электронов (теряемых или получаемых).
— стандартный окислительно-восстановительный потенциал; R -газовая постоянная (8,313 дж/(моль- град); Т — абсолютная температура, К; F — число Фарадея (96 500 кулон/г-экв); n — число электронов (теряемых или получаемых).
Если подставить числовые значения констант и от натурального перейти к десятичному, то для комнатной температуры (20 °C) получим:
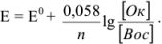
Очень часто превращение окисленной формы анионов кислородосодержащих кислот в восстановленную сопровождается глубоким изменением их состава и происходит при участии 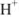 -ионов:
-ионов:
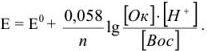
Константа равновесия
Возможность изменения направления реакций окисления — восстановления на прямо противоположное является, очевидно, следствием обратимости этих реакций. Обратимые реакции, как известно, приводят к установлению химического равновесия. Константу равновесия нетрудно рассчитать, зная стандартные потенциалы обеих окислительно-восстановительных пар.
Сделаем такой расчет для реакции:

константа равновесия которой равна
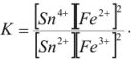
Напишем прежде всего выражения для окислительно-восстановительных потенциалов пар 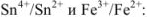
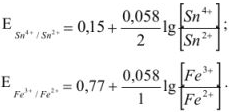
В результате течения реакции эти потенциалы сравняются и устанавливается равновесие:
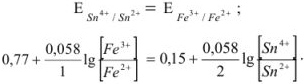
Решив это уравнение, получим
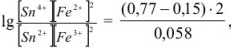
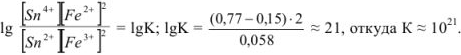
Найденный результат показывает, что в состоянии равновесия произведение концентраций 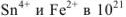 раз превышает произведение концентраций
раз превышает произведение концентраций 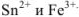
Другими словами, большое числовое значение константы равновесия свидетельствует о том, что соответствующая реакция протекает практически до конца.
Используя приведенное вычисление константы равновесия К, получим для любого обратимого окислительно-восстановительного процесса (при 20 °C) следующее уравнение:
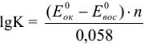
где 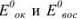 — стандартные потенциалы пар, соответствующих взятым окислителю
— стандартные потенциалы пар, соответствующих взятым окислителю 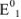 и восстановителю
и восстановителю 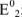 ; n — число электронов.
; n — число электронов.
Из формулы видно, что константа равновесия должна быть тем больше, чем больше разность стандартных потенциалов обеих пар.
Если разность велика, реакция идет практически до конца. Наоборот, при малой разности потенциалов химическое превращение взятых веществ до конца не дойдет. Для использования подобной реакции необходимо подобрать концентрации участвующих в ней веществ или ионов так, чтобы реакция протекала более полно до конца.
Построение кривых титрования
При редоксиметрическом титровании концентрации участвующих в реакции веществ или ионов все время изменяются.
Должен, следовательно, изменяться и окислительно-восстановительный потенциал раствора (Е) подобно тому, как при титровании по методу кислотноосновного титрования все время изменяется pH раствора.
Если величины окислительно-восстановительных потенциалов, соответствующие различным моментам титрования, наносить на график, то получаются кривые титрования, аналогичные кривым, получаемым по методу кислотно-основного титрования.
Комплексонометрия
Циклические комплексные соединения с полидентантными лигандами называются хелатами. Хелаты, в которых замыкание цикла сопровождается вытеснением из кислотных групп лиганда одного или нескольких протонов ионом металла, называют внутрикомплексными соединениями.
Органические реагенты, которые образуют с ионами металлов устойчивые и растворимые в воде внутрикомплексные (клешневидные, хелатные) соединения, называются комплексонами. Образующиеся при этом соединения называются комплексонатами.
В молекуле комплексонов должны присутствовать группы:
основные: 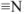 :
:
кислотные: 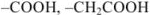
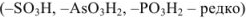
Хорошо известными комплексонами являются производные аминокарбоновых кислот. Простейший из них — комплексон I.
Комплексон I — это трехосновная нитрилотриуксусная кислота (НТА):
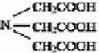
Наибольшее значение имеет этилендиаминтетрауксусная кислота (ЭДТА) — комплексон II:
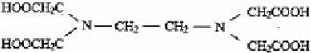
На практике применяют ее двунатрисвую соль, комплексон III или трилон Б (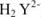 ):
):
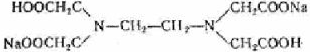
Образующиеся при этом соединения очень прочны, отличаются достаточно малыми величинами 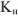 , (например, для
, (например, для 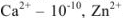 —
—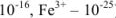 ):
):
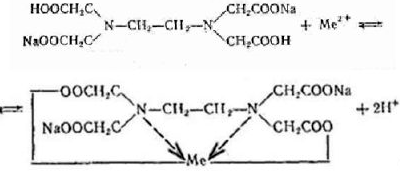
Очень важно для анализа то, что почти со всеми ионами металлов в различных условиях образуются комплексные соединения строго определенного состава, а именно такие, в которых отношение ионов металла к лиганду равно 1:1.
При комплексонометрических титрованиях нужно иметь в виду, что ЭДТА- четырехосновная кислота. Ступенчатые константы ее ионизации отвечают значениям рК = 2,0; 2,7; 6,2; 10,3. В образующихся комплексах ионы металла замещают водородные ионы двух или более карбоксильных групп реагента. Поэтому pH раствора имеет большое значение при титровании комплексоном III.
В качестве индикаторов в комплексонометрии применяют так называемые металлиндикаторы, которые позволяют визуально определять точку конца титрования. Металлиндикаторы — органические красители, образующие окрашенные комплексные соединения с ионами металла, менее прочные, чем комплекс металла с комплексоном (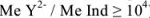 ).
).
В качестве примера металлиндикатора можно рассмотреть эрио-хром черный Т (сокращенно ЭХЧ-Т), который очень широко применяется в комплексонометрии. Анион индикатора, который можно обозначить как 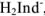 , имеет формулу
, имеет формулу
Этот ион проявляет себя как кислотно-основной индикатор:
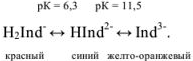
При pH = 7-11, когда индикатор имеет синий цвет, многие ионы металлов образуют комплексы красного цвета, например такие ионы, как 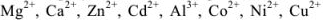 и др. Реакции
и др. Реакции 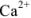 и
и 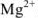 с индикатором можно представить уравнением
с индикатором можно представить уравнением
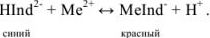
Следовательно, если в раствор, например, соли кальция, при pH = 7-11 ввести эриохром черный Т, то раствор окрасится в красный цвет; если этот раствор титровать раствором комплексона Ш, который с 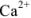 дает бесцветный, более прочный комплекс
дает бесцветный, более прочный комплекс 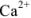 с индикатором, то в конечной точке титрования раствор примет синий цвет.
с индикатором, то в конечной точке титрования раствор примет синий цвет.
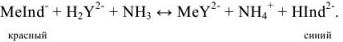
Гравиметрический метод анализа
Весовой анализ основан на законе сохранения веса веществ при химических превращениях. Анализ включает несколько стадий, основные из которых следующие:
- превращение определяемого компонента в труднорастворимое соединение;
- количественное отделение осадка от маточного раствора;
- отмывание его от соосаждаемых примесей;
- термическая обработка осадка;
- взвешивание полученной весовой формы.
Одним из важнейших теоретических вопросов весового анализа является равновесие между осадком и его насыщенным раствором.
Равновесие в насыщенных растворах описывают исходя из правила растворимости. Если осадок переходит в раствор по схеме
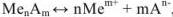
Правило произведения растворимости выражается следующим образом:
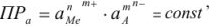
а так как
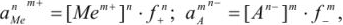
то
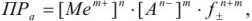
где 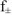 — средний коэффициент активности, который согласно предельному закону Дебая и Хюккеля учитывается в вычислениях, если ионная сила раствора больше
— средний коэффициент активности, который согласно предельному закону Дебая и Хюккеля учитывается в вычислениях, если ионная сила раствора больше 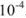 . Если произведение растворимости мало и в насыщенном растворе нет постороннего электролита,
. Если произведение растворимости мало и в насыщенном растворе нет постороннего электролита, 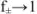 , а активность приравнивается к концентрации.
, а активность приравнивается к концентрации.
В этом случае правило произведения растворимости записывается так:
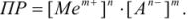
Зная растворимость осадка в воде, можно рассчитать его произведение растворимости.
Возможно эта страница вам будет полезна:
Вычисление произведения растворимости
Задача №30
Вычислить произведение растворимости сульфита кальция, если его растворимость при температуре 20 «С равна 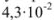 г в литре раствора.
г в литре раствора.
Решение:
Для вычисления произведения растворимости необходимо выразить растворимость вещества в молях на литр. Молекулярная масса 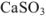 равна 120,2. Следовательно,
равна 120,2. Следовательно,
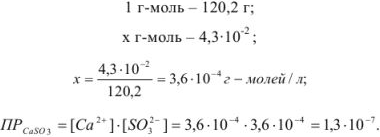
Вычисление растворимости осадка по величине произведения растворимости
Растворимость осадка может быть определена из произведения растворимости.
Расчет по формуле
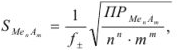
где S — растворимость осадка (в молях на литр); n, m — заряды ионов осадка.
Задача №31
Вычислить растворимость сульфата бария в воде, если 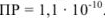
Решение:
Ионы 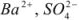 переходят в раствор согласно уравнению
переходят в раствор согласно уравнению
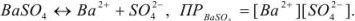
Следовательно, растворимость
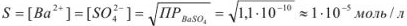
(поскольку растворимость менее 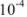 г-ион/л, нет необходимости учитывать коэффициент активности).
г-ион/л, нет необходимости учитывать коэффициент активности).
Возможно эта страница вам будет полезна:
Влияние различных факторов на растворимость осадка
Влияние одноименных ионов
Согласно правилу произведение концентраций ионов какого-либо малорастворимого электролита в насыщенном растворе представляет собой величину постоянную при данной температуре и равную произведению растворимости. Если понижаем один из множителей, то необходимо повысить второй путем ввода избытка реагента.
Задача №32
Рассчитать растворимость сульфата бария в растворе, в 1 л которого содержится 0,01 моля сульфата натрия.
Решение:
Одноименным к иону осадка является сульфат-ион. Поэтому растворимость 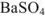 вычисляется исходя из концентрации ионов бария:
вычисляется исходя из концентрации ионов бария:
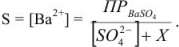
где X — избыточная концентрация одноименного иона. Значит,
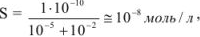
где
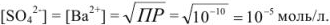
Растворимость сульфата бария в присутствии сульфата натрия уменьшается по сравнению с растворимостью его в воде в 10‘5/10’8 = 1000 раз.
Влияние посторонних электролитов (солевой эффект)
Присутствие в растворе различных сильных электролитов и слишком большое количество осадителя обычно повышают растворимость осадка.
Растворимость осадка в растворе электролита вычисляется с учетом коэффициентов активности. В этом случае оценивают ионную силу раствора 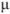 , которая определяется общей солевой концентрацией по уравнению
, которая определяется общей солевой концентрацией по уравнению
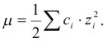
Затем по закону Дебая и Хюккеля или по таблицам справочной литературы находят коэффициенты активности ионов осадка при данной ионной силе раствора. Найденный коэффициент активности используют для вычисления растворимости по формуле
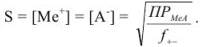
Задача №33
Вычислить растворимость оксалата кальция в 0,1 М растворе хлорида калия 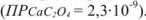 .
.
Решение:
Находим концентрацию ионов 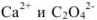 из величины ПР оксалата кальция:
из величины ПР оксалата кальция:
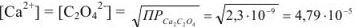
Ионная сила раствора
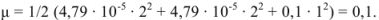
Коэффициенты активности ионов 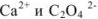 в растворе с ионной силой 0,1 равны
в растворе с ионной силой 0,1 равны
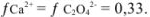
Следовательно, 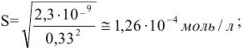
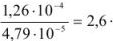
Таким образом, растворимость осадка в 0,1 М растворе хлористого калия в 2,6 раза больше, чем в воде.
Условия выпадения осадка
Образование осадков происходит лишь при условии, что произведение концентраций (точнее, активностей) соответствующих ионов превысит величину произведения растворимости осаждаемого соединения при данной температуре.
В насыщенном растворе 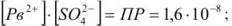
- в ненасыщенном —
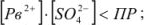
- в пересыщенном —
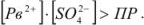
Из пересыщенных растворов выпадает осадок. При выпадении осадка постепенно уменьшается концентрация 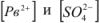 , т.е. раствор перестает быть пересыщенным, с течением времени устанавливается динамическое равновесие насыщенный раствор
, т.е. раствор перестает быть пересыщенным, с течением времени устанавливается динамическое равновесие насыщенный раствор 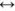 осадок.
осадок.
Абсолютно нерастворимых веществ не существует, ПР > 0. Следовательно, ни одно осаждение не бывает совершенно полным.
Задача №34
Смешали равные объемы 0,0001 М растворов 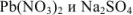 . Выпадет ли осадок?
. Выпадет ли осадок?
Решение:
При смешивании равных объемов растворов концентрации каждого из указанных веществ уменьшаются вдвое и станут равными 0,00005 М или 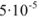 М. Поскольку соли как сильные электролиты в водных растворах диссоциированы практически нацело, а каждая молекула указанных солей, диссоциируя, образует по одному иону
М. Поскольку соли как сильные электролиты в водных растворах диссоциированы практически нацело, а каждая молекула указанных солей, диссоциируя, образует по одному иону 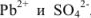 , концентрации этих ионов после смешения будут равны:
, концентрации этих ионов после смешения будут равны:
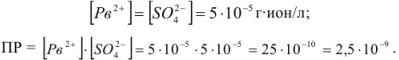
Так как 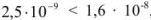 , т.е. величины
, т.е. величины 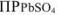 при данной температуре, раствор получается ненасыщенным относительно
при данной температуре, раствор получается ненасыщенным относительно 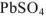 и осадок этой соли нс образуется.
и осадок этой соли нс образуется.
Растворимость солей, образованных анионами слабых кислот, зависит от pH раствора, так как изменение содержания ионов водорода оказывает влияние на диссоциацию слабых кислот и, следовательно, на концентрацию иона осадителя.
В этом случае для определения произведения растворимости используют выражение
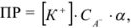
где СА — общая концентрация аниона 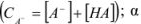 — доля аниона осадителя, равная
— доля аниона осадителя, равная 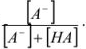
Если выразить концентрацию НА через константу диссоциации слабой кислоты и подставить значение в приведенную формулу, получим
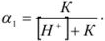
Зная 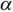 , можно рассчитать растворимость (при любом значении pH) по формуле
, можно рассчитать растворимость (при любом значении pH) по формуле
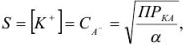
которая применима для осадков, содержащих равнозарядные ионы: осадок
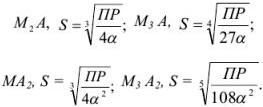
В общем случае для осадка 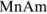 , когда
, когда
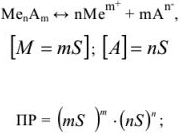
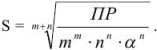
Возможно эта страница вам будет полезна:
Задача №35
Рассчитать растворимость йодада серебра при
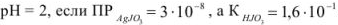
Решение:
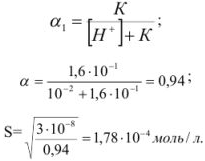
Ошибки в количественном анализе систематические и случайные ошибки
К систематическим относятся методические и индивидуальные ошибки. Систематические ошибки сравнительно велики по абсолютному значению, характеризуются знаком, имеют размерность той величины, погрешность которой определяют, и при оценке результатов анализа могут быть учтены тем или иным способом.
Случайные ошибки малы по абсолютной величине, нс определяются знаком, безразмерны, могут быть сведены к минимальному значению путем увеличения числа измерений и учтены с помощью методов математической статистики.
Способ выражения ошибок зависит от характера определения. Погрешность прямых определений может быть выражена в виде абсолютной или относительной ошибки. Для оценки погрешности косвенных методов измерения, где результат получается из сочетания нескольких значений, целесообразно рассчитывать относительную ошибку определения.
Абсолютная ошибка определяется разностью между полученным и истинным значением определяемой величины.
Задача №36
В навеске стандартного образца стали содержится 0,0424 г марганца. Какова абсолютная ошибка определения (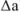 ), если найдено 0,0396 г марганца?
), если найдено 0,0396 г марганца?
Решение:
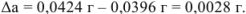
Если значение определяемой величины неизвестно, абсолютную ошибку рассчитывают исходя из среднего арифметического ряда определений 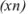 как наиболее достоверного значения.
как наиболее достоверного значения.
Задача №37
На титрование четырех одинаковых объемов кислоты израсходовано 12,50; 12,52; 12,48; 12,46 мл щелочи. Вычислите абсолютную ошибку определения.
Решение:
Наиболее достоверным значением определяемой величины является среднее арифметическое измерений:
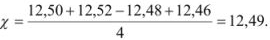
Абсолютные ошибки (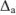 ) каждого определения равны:
) каждого определения равны:
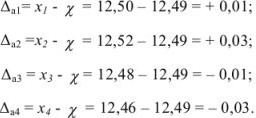
Полученные величины отклонений отдельных измерений от среднего арифметического называются остаточными погрешностями. Алгебраическая сумма остаточных погрешностей равна нулю.
Относительная ошибка измерения (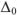 ) определяется отношением абсолютной ошибки к истинному значению определяемой величины или к среднему арифметическому измерений, выраженному в процентах.
) определяется отношением абсолютной ошибки к истинному значению определяемой величины или к среднему арифметическому измерений, выраженному в процентах.
Для примера 1 относительная ошибка:
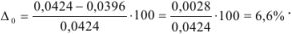
Для примера 2 относительные ошибки вычисляются для каждого определения:
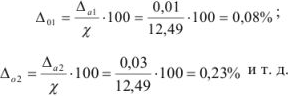
Индикаторные ошибки титрования
Метод нейтрализации
Индикаторные ошибки относятся к систематическим ошибкам и возникают тогда, когда изменение окраски индикатора не соответствует точке эквивалентности реагирующих веществ.
При титровании по методу нейтрализации индикаторные ошибки обусловлены несовпадением pH в точке эквивалентности с показателем титрования (рТ) применяющегося индикатора. Различают водородную, гидроксильную, кислотную, щелочную и солевую ошибки титрования.
Водородная ошибка (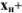 ) определяется наличием в системе в момент изменения окраски индикатора неоттитрованной сильной кислоты и рассчитывается по уравнению
) определяется наличием в системе в момент изменения окраски индикатора неоттитрованной сильной кислоты и рассчитывается по уравнению
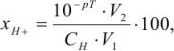
где 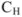 — молярная концентрация эквивалентов титруемой кислоты;
— молярная концентрация эквивалентов титруемой кислоты; 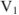 — объем титруемой кислоты;
— объем титруемой кислоты; 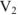 — объем раствора в конце титрования.
— объем раствора в конце титрования.
Задача №38
Рассчитать индикаторную ошибку титрования 0,1 н раствора соляной кислоты раствором едкого натра той же концентрации в присутствии метилового оранжевого, рТ которого равен 4.
Решение:
При титровании сильной кислоты сильным основанием pH в точке эквивалентности должно быть равно 7, но так как показатель титрования метилового оранжевого 4, титрование заканчивается в кислой среде (pH = 4) в присутствии некоторого количества неоттитрованной сильной кислоты. Поэтому
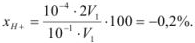
Минус поставлен потому, что исследуемый раствор соляной кислоты недотитрован.
Гидроксильная ошибка (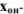 ) определяется наличием в системе в момент изменения окраски индикатора неоттитрованного сильного основания, которое полностью диссоциирует на ионы. Ошибка рассчитывается по уравнению
) определяется наличием в системе в момент изменения окраски индикатора неоттитрованного сильного основания, которое полностью диссоциирует на ионы. Ошибка рассчитывается по уравнению
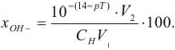
Задача №39
Рассчитать индикаторную ошибку титрования 0,1 н раствора соляной кислоты раствором едкого натра той же концентрации в присутствии фенолфталеина, рТ которого равен 9.
Решение:
В присутствии фенолфталеина титрование заканчивается при pH = 9, т. е. в щелочной среде. Следовательно, в момент изменения окраски индикатора в растворе находится избыток гидроксильных ионов. Поэтому ошибка вычисляется по уравнению
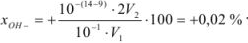
Ошибка имеет положительное значение, так как раствор перетитрован.
Кислотная ошибка определяется наличием в системе в момент изменения окраски индикатора неоттитрованной слабой кислоты и рассчитывается по уравнению
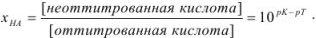
Возможно эта страница вам будет полезна:
Задача №40
Вычислить ошибку титрования 0,1 н раствора уксусной кислоты раствором едкого натра той же концентрации в присутствии метилового оранжевого (рТ = 4).
Решение:
При титровании слабой кислоты сильным основанием в точке эквивалентности
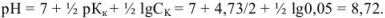
Так как титрование заканчивается при pH = рТ = 4, в системе остается некоторое количество неоттитрованной слабой кислоты и
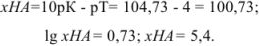
С другой стороны,
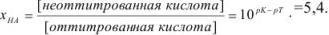
Если всего было (5,4 + 1) частей кислоты, а осталось неоттитрованной 5,4 части, то
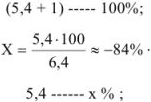
Щелочная ошибка имеет тот же смысл, что и кислотная, и рассчитывается по уравнению
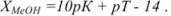
Задача №41
Вычислить ошибку титрования 0,1 н раствора гидроксида аммония раствором соляной кислоты той же концентрации в присутствии фенолфталеина, рТ которого 9.
Решение:
В точке эквивалентности должно быть
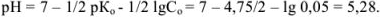
Так как титрование в присутствии фенолфталеина заканчивается при pH = 9, раствор недотитрован и
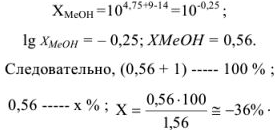
При титровании многоосновных кислот и их солей в зависимости от рТ применяемого индикатора возможны так называемые солевые ошибки титрования, которые учитываются аналогичным образом по схеме:
- рассчитывают pH в точке эквивалентности;
- сопоставляют значение pH в точке эквивалентности с рТ применяемого индикатора;
- выражают ошибку в виде отношения соответствующих концентраций ионов, находящихся в системе до конца титрования, и вычисляют ошибку.
Задача №42
Рассчитать ошибку титрования карбоната натрия до гидрокарбоната в присутствии фенолфталеина (рТ = 9).
Решение:
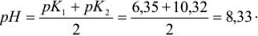
рТ фенолфталеина больше значения pH в точке эквивалентности, следовательно, карбонат полностью не оттитрован до гидрокарбоната и
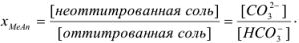
Исходя из констант диссоциации угольной кислоты находим концентрации 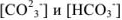 :
:
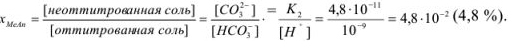
Метод окисления — восстановления
При использовании метода окисления — восстановления индикаторные ошибки обусловлены несовпадением величины нормального окислительно-восстановительного потенциала индикатора с потенциалом системы в точке эквивалентности. Если в качестве рабочего раствора применяется раствор окислителя, до точки эквивалентности ошибка 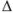 рассчитывается из уравнения
рассчитывается из уравнения
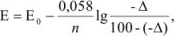
где Е — потенциал системы в конечной точке титрования; 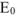 — нормальный потенциал титруемого восстановителя.
— нормальный потенциал титруемого восстановителя.
После достижения точки эквивалентности для вычисления ошибки применяется уравнение
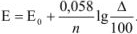
Для выяснения вопроса о том, перетитрован или недотитрован раствор, вычисляется потенциал системы в точке эквивалентности по уравнению
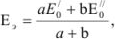
где а и b — количество электронов окислителя и восстановителя соответственно, принимающих участие в реакции; 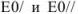 — значения нормальных окислительно-восстановительных потенциалов.
— значения нормальных окислительно-восстановительных потенциалов.
Полученное значение потенциала сравнивается с потенциалом системы в момент окончания титрования.
Задача №43
Рассчитать ошибку титрования двухвалентного железа перманганатом калия до потенциала 910 мВ.
Решение:
В точке эквивалентности
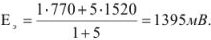
Поскольку 1395 мВ >910 мВ, при Е = 910 мВ раствор двухвалентного железа недотитрован и ошибку нужно рассчитывать из уравнения
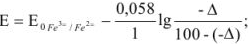
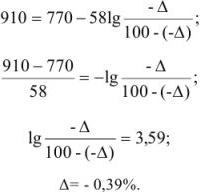
Методы осаждения и комплексонометрического титрования
При титровании по методу осаждения в качестве индикаторов используют вещества, которые с рабочим раствором образуют труднорастворимые осадки.
Если индикатор выбран правильно, осадок выпадет после достижения точки эквивалентности, поэтому ошибка титрования имеет положительное значение.
Абсолютная ошибка определяется разностью между концентрацией металл-иона в конце титрования 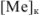 и его концентрацией в точке эквивалентности
и его концентрацией в точке эквивалентности 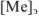 . Концентрации
. Концентрации 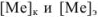 рассчитываются из величин произведений растворимости соответствующих труднорастворимых осадков.
рассчитываются из величин произведений растворимости соответствующих труднорастворимых осадков.
Задача №44
Вычислить индикаторную ошибку титрования 25 мл раствора хлорида натрия в присутствии 2 мл 0,01 М раствора хромата калия 0,05 М раствором азотнокислого серебра 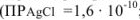 ;
; 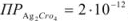
Решение:
Концентрация хромата калия в титруемом растворе
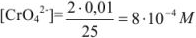
Осадок хромата серебра из 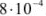 М раствора начинает выпадать при
М раствора начинает выпадать при
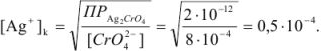
В точке эквивалентности
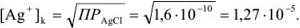
Тогда относительная ошибка титрования
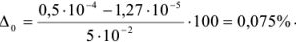
Для вычисления индикаторных ошибок в комплексонометрии Рингбом предложил уравнение*
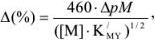
где 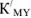 — эффективная константа устойчивости трилоната; [М] — общая концентрация металлического иона в растворе;
— эффективная константа устойчивости трилоната; [М] — общая концентрация металлического иона в растворе; 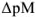 — разность между концентрациями Me-иона в конечной точке титрования (
— разность между концентрациями Me-иона в конечной точке титрования (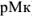 ) и в точке эквивалентности (
) и в точке эквивалентности (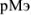 ). (Опытным путем установлено, что при визуальном способе установлении точки эквивалентности
). (Опытным путем установлено, что при визуальном способе установлении точки эквивалентности 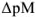 = 0,5.)
= 0,5.)
Эффективная константа устойчивости 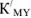 вычисляется по уравнению
вычисляется по уравнению
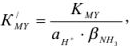
где 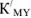 константа устойчивости трилоната;
константа устойчивости трилоната; 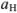 — доля ЭДТА-иона, не связанного с водородом, при определении pH;
— доля ЭДТА-иона, не связанного с водородом, при определении pH; 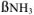 — доля Ме-иона, нс связанного в комплекс с аммиаком.
— доля Ме-иона, нс связанного в комплекс с аммиаком.
Значения 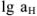 для этилендиаминтетрауксусной кислоты при различных pH приведены ниже:
для этилендиаминтетрауксусной кислоты при различных pH приведены ниже:
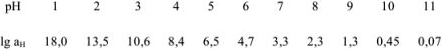
Величина 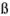 рассчитывается по уравнению
рассчитывается по уравнению
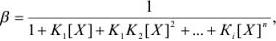
где [X] — концентрация иона комплексообразователя.
Кстати готовые задачи на продажу и теория из учебников тут.
Приложение
Таблица 1
Приближенные значения средних коэффициентов активности ионов при различной силе раствора
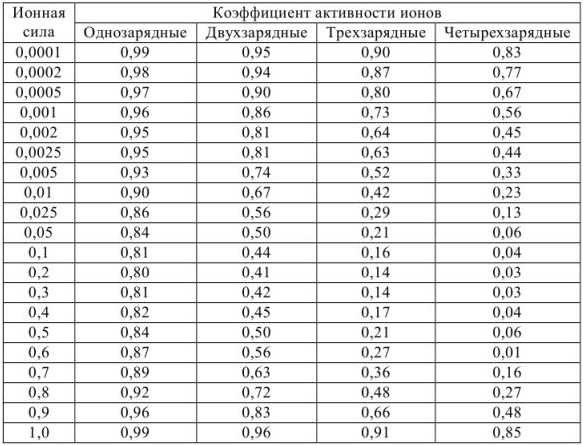
Таблица 2
Произведения растворимости некоторых малорастворимых веществ
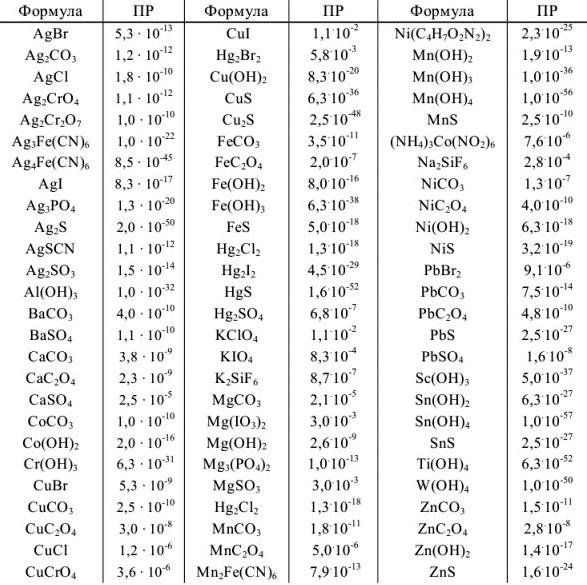
Таблица 3
Плотности и концентрации растворов в воде при 20 °C
а) растворы гидроксида натрия
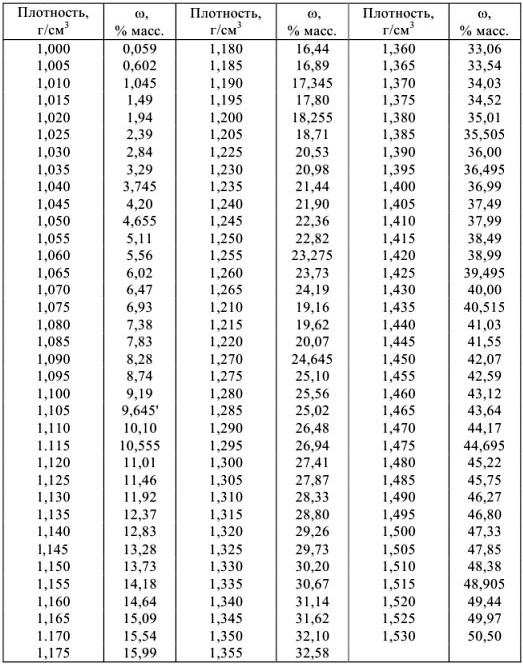
б) растворы соляной кислоты
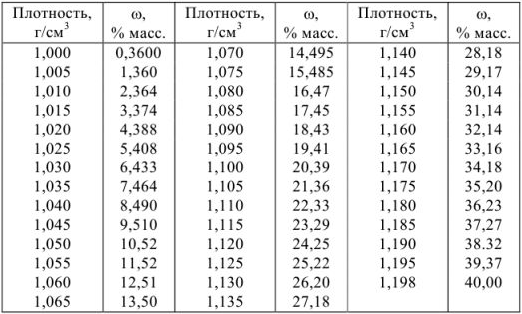
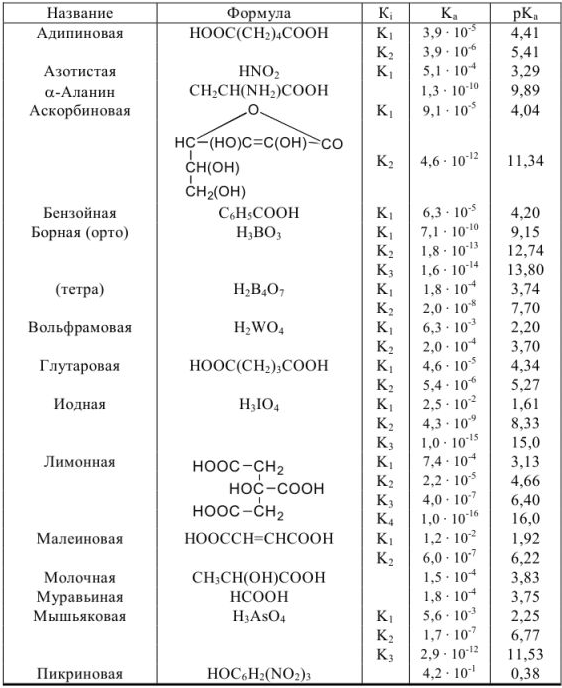
Таблица 4
Константы ионизации некоторых кислот и оснований
а) кислоты
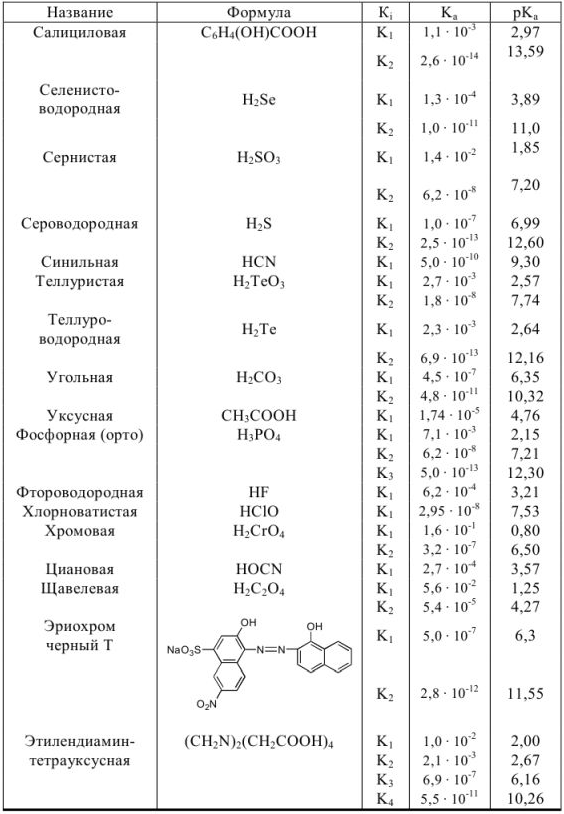
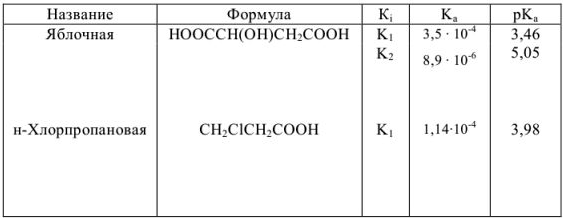
б) основания
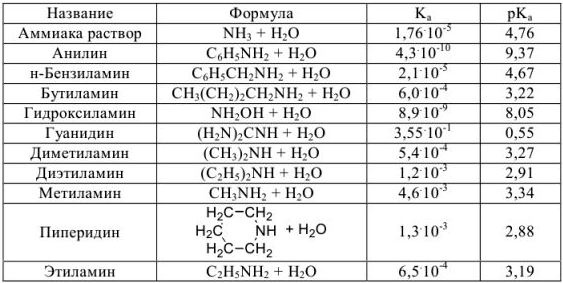
Таблица 5
Некоторые кислотно-основные индикаторы
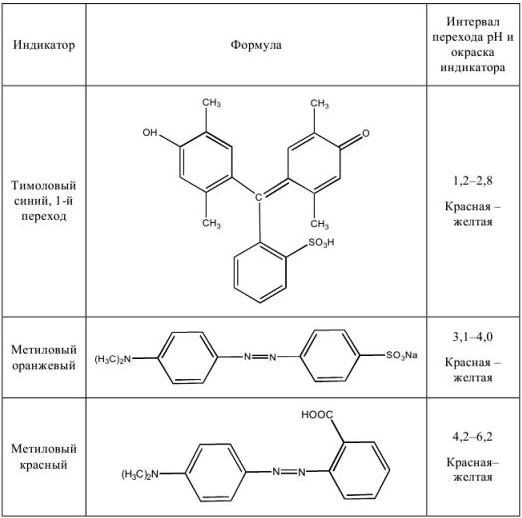
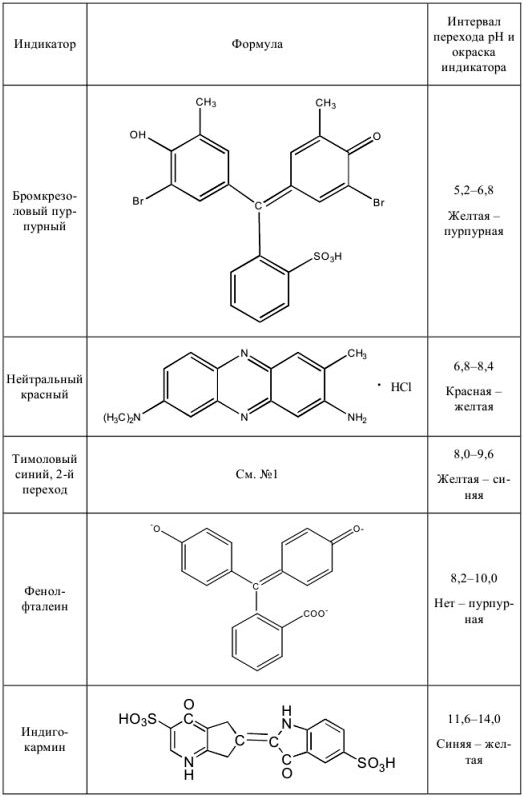
Таблица 6
Нормальные окислительно-восстановительные потенциалы
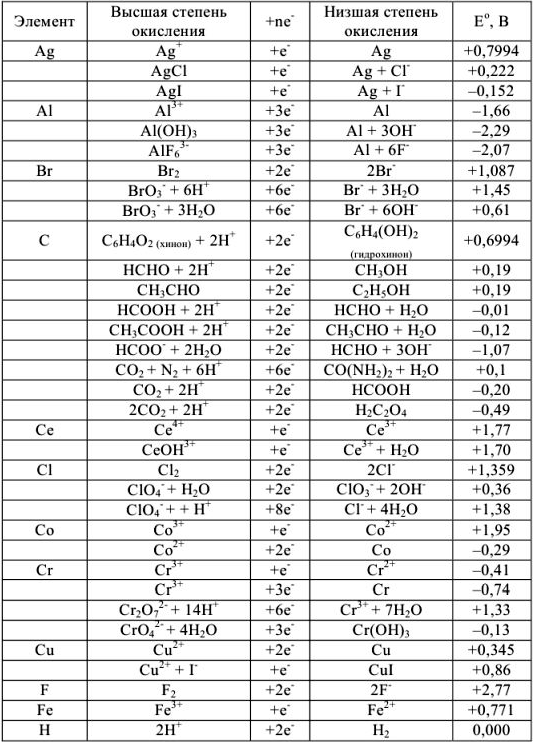
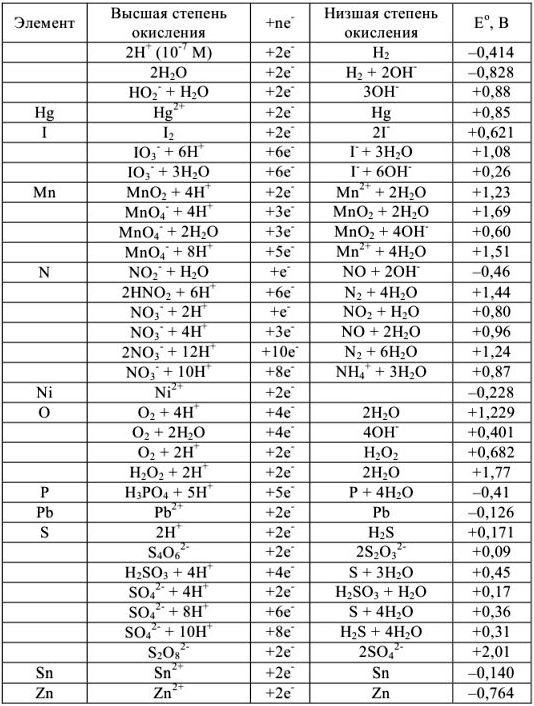
Таблица 7
Важнейшие окислительно-восстановительные индикаторы
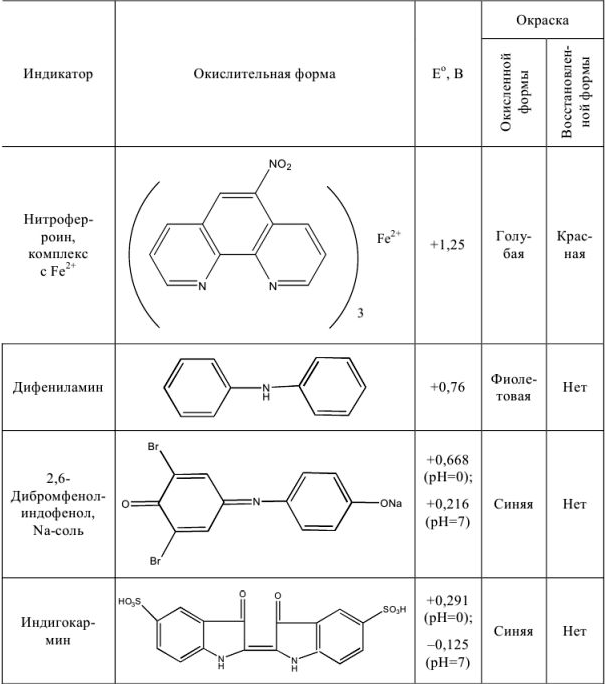
Таблица 8
Константы устойчивости комплексных ионов
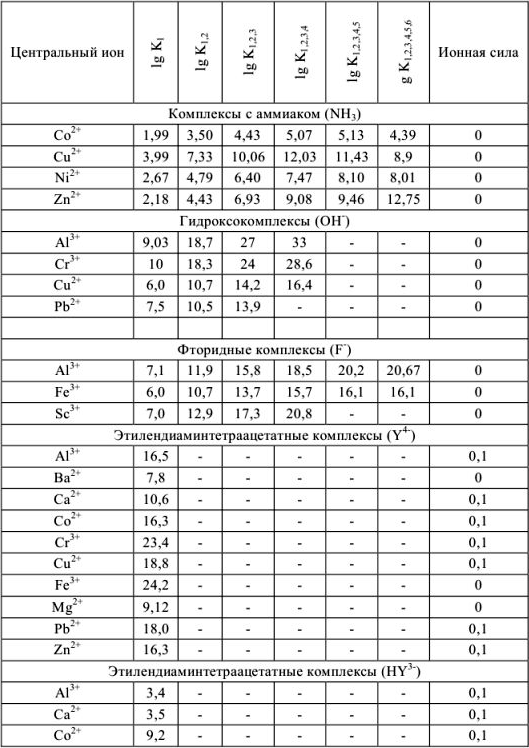
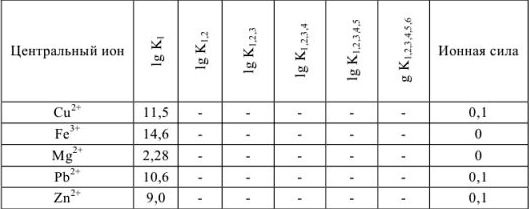
Примечание. Две и более цифр индекса поставлены у констант полной диссоциации комплексов с соответствующим числом групп лиганда, например для комплекса 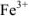 с хлорид-ионами
с хлорид-ионами
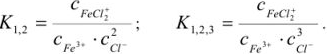
Таблица 9
Наиболее распространенные индикаторы в комплексонометрии

Готовые примеры и задачи по аналитической химии по всем темам
В зависимости от задач аналитическая химия делится на качественный анализ, направленный на определение того, что (или какие вещества), в какой форме, и количественный анализ, направленный на определение количества данного вещества (элементов, ионов, молекулярных форм и т.д.) в образце.
В задачи качественного анализа входит:
- установление присутствия (обнаружение, открытие) в пробе тех или иных компонентов (молекул, атомов, ионов);
- идентификация веществ и компонентов в пробе неизвестного состава (установление их аналогии соответствующим эталонам).
Задачи количественного анализа — определение содержания или концентрации компонентов в пробе.
Общие сведения и рекомендации
Условные обозначения и размерности величин
X — формула частицы вещества (например, 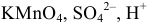 и др.);
и др.);
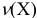 — количество вещества, моль;
— количество вещества, моль;
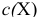 — молярная концентрация, моль/л;
— молярная концентрация, моль/л;
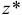 — число эквивалентности;
— число эквивалентности; 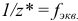 — фактор эквивалентности;
— фактор эквивалентности;
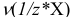 или
или 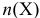 в титриметрии — число молей эквивалентов вещества X;
в титриметрии — число молей эквивалентов вещества X;
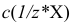 или
или 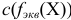 — молярная концентрация эквивалента вещества X, моль/л (ранее — г-экв/л);
— молярная концентрация эквивалента вещества X, моль/л (ранее — г-экв/л);
[X] — равновесная молярная концентрация вещества X, моль/л;
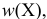 % — массовая доля вещества X, %;
% — массовая доля вещества X, %;
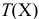 — титр вещества X, г/мл;
— титр вещества X, г/мл;
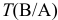 — титр рабочего раствора вещества В по определяемому веществу А, г/мл;
— титр рабочего раствора вещества В по определяемому веществу А, г/мл;
S(X) — растворимость вещества X, моль/л;
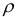 — плотность раствора, кг/
— плотность раствора, кг/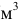 или г/
или г/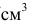 (г/мл);
(г/мл);
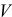 — объем раствора, мл, л;
— объем раствора, мл, л;
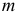 — масса, г;
— масса, г;
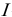 — ионная сила раствора;
— ионная сила раствора;
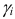 — коэффициент активности i-того иона;
— коэффициент активности i-того иона;
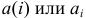 — активность иона, моль/л;
— активность иона, моль/л;
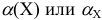 — доля частиц вещества X или самого вещества X в растворе, степень диссоциации, доля свободных ионов и др.;
— доля частиц вещества X или самого вещества X в растворе, степень диссоциации, доля свободных ионов и др.;
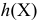 — степень гидролиза вещества X;
— степень гидролиза вещества X;
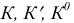 — реальная, условная и термодинамическая константы равновесия;
— реальная, условная и термодинамическая константы равновесия;
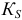 (ранее — ПP) — константа растворимости малорастворимого электролита;
(ранее — ПP) — константа растворимости малорастворимого электролита;
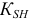 — константа автопротолиза растворителя (для воды —
— константа автопротолиза растворителя (для воды — 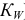 );
);
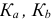 — константы кислотности и основности (константы диссоциации кислоты и основания); для многоосновных кислот —
— константы кислотности и основности (константы диссоциации кислоты и основания); для многоосновных кислот — 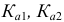 и т. д..
и т. д..
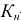 — общая константа нестойкости комплексного соединения;
— общая константа нестойкости комплексного соединения;
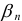 — общая константа образования (устойчивости) комплексного соединения;
— общая константа образования (устойчивости) комплексного соединения;
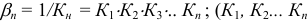 — ступенчатые константы образования);
— ступенчатые константы образования);
 и т.д.
и т.д.
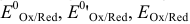
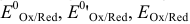 ~ Стандартный, формальный, равновесный окислительно-восстановительные (электродные) потенциалы.
~ Стандартный, формальный, равновесный окислительно-восстановительные (электродные) потенциалы.
Правила вычисления в химии
Примеры с решением:
- Правила вычисления в химии с примерами решения
- Чувствительность аналитических реакций с примерами решения
Химическое равновесие в реальных системах
Химические реакции, используемые в аналитической химии, проводятся в растворах и являются в той или иной степени обратимыми. В связи с этим теория химического анализа базируется на законах химического равновесия. Для понимания химической реакции необходимо знание её стехиометрии, термодинамики и кинетики.
Термодинамика касается направления и глубины протекания реакции и через свободную энергию Гиббса отражается в термодинамических константах равновесия 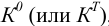 , которые для разных видов простых равновесий приведены в справочной литературе, в том числе, в таблицах 2-4 приложения. Кинетика дает представление о механизме и скорости реакции.
, которые для разных видов простых равновесий приведены в справочной литературе, в том числе, в таблицах 2-4 приложения. Кинетика дает представление о механизме и скорости реакции.
При рассмотрении законов химического равновесия следует различать идеальные и реальные системы. В идеальных системах ионы и молекулы свободны от влияния других частиц и способны полностью проявить свою химическую природу. К таким системам приближаются бесконечно разбавленные растворы. В реальной системе частицы испытывают влияние со стороны окружающих ионов и молекул. Вследствие этого при участии в химических реакциях даже в разбавленных растворах они проявляют себя как бы в меньшей концентрации, чем она есть в действительности. Поэтому для описания поведения ионов в реальных системах вместо концентрации используют величину, называемую активностью 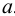 . В идеальной системе активность частицы равна её концентрации, а в реальной опа обычно меньше концентрации.
. В идеальной системе активность частицы равна её концентрации, а в реальной опа обычно меньше концентрации.
Отклонение поведения ионов в растворе от идеального может быть связано с их электростатическими и химическими взаимодействиями. Именно они учитываются при расчетах химических равновесий в растворах электролитов. Химические реакции могут протекать между ионами, а также при специфических сольватационных взаимодействиях ионов с молекулами растворителя (например при гидролизе). При этом следует помнить, что влияние химических взаимодействий на химическое равновесие во много раз сильнее, чем действие электростатических сил. Поэтому в практических расчетах влиянием электростатических взаимодействий пренебрегают при протекании в растворах побочных химических реакций: ионную силу раствора считают равной нулю, 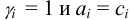 .
.
Примеры с решением:
- Влияние электростатических взаимодействий на поведение ионов в растворе. Ионная сила раствора. Коэффициент активности с примерами решения
- Влияние химических факторов на равновесие. Молярная доля компонента в растворе с примерами решения
- Направление химических реакций. Способы выражения констант равновесия. Ступенчатые и общие константы равновесия с примерами решения
Кислотно-основное (протолитическое) равновесие
Примеры с решением:
- Расчет [H+], [OH-], pH, pOH в растворах сильных и слабых кислот и оснований с примерами решения
- Буферные растворы с примерами решения
- Расчеты при приготовлении растворов протолитов с заданным значением pH с примерами решения
- Равновесие в растворах комплексных соединений с примерами решения
Окислительно-восстановительное равновесие
Примеры с решением:
- Оценка окислительно-восстановительной способности веществ с примером решения
- Расчет стандартного потенциала полуреакции, являющейся сочетанием двух полуреакций с примерами решения
- Вычисление потенциала в реальных условиях. Уравнение Нернста с примером решения
Влияние электростатических и химических взаимодействий на величину потенциала. Формальный потенциал
В тех случаях, когда на величину равновесного потенциала влияют электростатические и химические факторы (см. главу 2), удобно пользоваться общими концентрациями окисленной и восстановленной форм 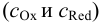 .
.
Поскольку, 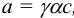 , то уравнение Нернста приобретает вид:
, то уравнение Нернста приобретает вид:
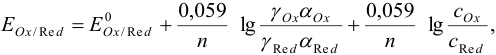
где сумма первых двух членов представляет собой формальный потенциал 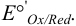 . Он равен равновесному потенциалу при общих концентрациях окисленной и восстановленной форм, равных 1, и заданных концентрациях всех других веществ, присутствующих в системе, но не меняющих степень окисления.
. Он равен равновесному потенциалу при общих концентрациях окисленной и восстановленной форм, равных 1, и заданных концентрациях всех других веществ, присутствующих в системе, но не меняющих степень окисления.
Как видно из уравнения (5.4), формальный потенциал 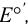 , в отличие от стандартного
, в отличие от стандартного 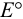 , зависит от ионной силы, глубины протекания конкурирующих реакций и концентрации частиц, не являющихся окисленной и восстановленной формами, но принимающих участие в полуреакции. Именно формальный, а не стандартный потенциал следует использовать для оценки направления окислительно-восстановительной реакции в реальных условиях.
, зависит от ионной силы, глубины протекания конкурирующих реакций и концентрации частиц, не являющихся окисленной и восстановленной формами, но принимающих участие в полуреакции. Именно формальный, а не стандартный потенциал следует использовать для оценки направления окислительно-восстановительной реакции в реальных условиях.
Например, для полуреакции:
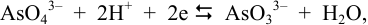
согласно (5.4), уравнение Нернста для равновесного потенциала можно представить, помня о том, что 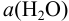 = 1 (стандартное состояние), в виде:
= 1 (стандартное состояние), в виде:
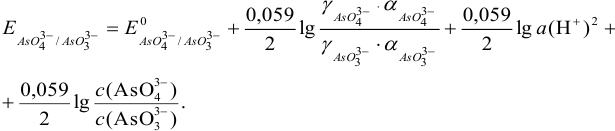
Формальный потенциал 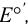 при этом можно представить как:
при этом можно представить как:
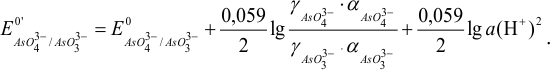
Примеры с решением:
- Влияние ионной силы на потенциал с примером решения
- Влияние pH раствора на величину потенциала с примерами решения
- Влияние комплексообразования на величину потенциала с примерами решения
- Влияние образования малорастворимых соединений на потенциал с примерами решения
Расчеты с использованием константы равновесия окислительно-восстановительной реакции
Примеры с решением:
- Расчет константы равновесия по стандартным и формальным потенциалам с примерами решения
- Вычисление равновесных концентраций по величине константы с примерами решения
- Вычисление растворимости веществ в окислительно-восстановительной реакции с примерами решения
- Расчеты с использованием ЭДС гальванического элемента с примерами решения
Гетерогенное равновесие в системе осадок — раствор
Реакции осаждения и растворения представляют один из наиболее важных для аналитической химии видов гетерогенного равновесия. Они широко используются для обнаружения, разделения и количественного определения катионов и анионов.
В системе осадок — раствор, т. е. в насыщенном растворе малорастворимого электролита типа 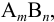 устанавливаются равновесия, которые можно представить в виде (заряды ионов упущены для упрощения записи):
устанавливаются равновесия, которые можно представить в виде (заряды ионов упущены для упрощения записи):
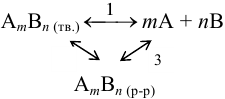
Для соединений с ионной решеткой (большая часть сильных электролитов) преобладает равновесие 1 (ионная растворимость). Для соединений с молекулярной решеткой (очень слабые электролиты) — равновесие 2 (молекулярная растворимость).
Термодинамическую константу равновесия 1 — равновесия между малорастворимым соединением и его ионами в растворе -называют термодинами ческим произведением растворимости (табл. 6 приложения). Эту константу можно выразить следующим образом 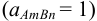 :
:
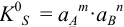
(устаревшее обозначение — 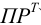 ).
).
Эта константа связана с реальным (концентрационным) 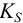 и условным
и условным 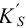 произведением растворимости (см. также раздел 2.3, выражение (2.1)) через коэффициенты активности
произведением растворимости (см. также раздел 2.3, выражение (2.1)) через коэффициенты активности 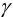 и молярные доли а соответствующих ионов. Учитывая, что для иона А, например, активность
и молярные доли а соответствующих ионов. Учитывая, что для иона А, например, активность 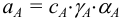 , причем
, причем 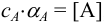 , получаем выражение:
, получаем выражение:
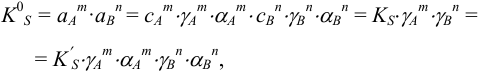
где 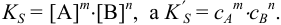
При невысоких значениях ионной силы раствора 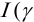 близки к 1), а также в отсутствие конкурирующих реакций
близки к 1), а также в отсутствие конкурирующих реакций 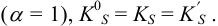 Тогда в расчетах можно по табличному значению
Тогда в расчетах можно по табличному значению 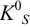 найти в насыщенном растворе общие концентрации ионов А и В, которые только в этом случае равны равновесным. В тех случаях, когда ионы, образующие осадок, участвуют в побочных реакциях (пример 2.5), или существенны электростатические взаимодействия, при расчетах следует пользоваться соотношением (6.1).
найти в насыщенном растворе общие концентрации ионов А и В, которые только в этом случае равны равновесным. В тех случаях, когда ионы, образующие осадок, участвуют в побочных реакциях (пример 2.5), или существенны электростатические взаимодействия, при расчетах следует пользоваться соотношением (6.1).
Произведение растворимости позволяет провести расчеты условий образования или оценить растворимость осадков в данном растворителе, в том числе и при протекании химических реакций.
Примеры с решением:
- Определение условий выпадения осадка и разделения ионов с примерами решения
- Вычисление растворимости малорастворимого электролита с примерами решения
- Влияние ионной силы раствора на растворимость с примерами решения
- Влияние одноименного иона на растворимость осадка с примерами решения
- Влияние конкурирующих реакций на растворимость с примерами решения
- Вклад молекулярной растворимости в общую растворимость с примерами решения
Расчеты в гравиметрии
Гравиметрический анализ или гравиметрия — это метод количественного анализа, основанный на измерении массы вещества известного состава, химически связанного с определяемым компонентом. Он основан на законе сохранения массы вещества при химических превращениях. Существует три типа гравиметрических определений:
- Определяемую составную часть выделяют из вещества и взвешивают. Это может быть минеральная часть пробы после удаления при сгорании органической части.
- Определяемую составную часть удаляют и взвешивают остаток. Так чаще всего определяют летучие соединения, влагу в пробах разного происхождения (методы отгонки).
- Определяемую составную часть превращают в соответствующее химическое соединение, которое выделяют и взвешивают.
Аналитические определения чаще ведут по третьему типу, используя реакции осаждения (методы осаждения). Основные этапы анализа включают:
- а) растворение навески та анализируемого вещества;
- б) осаждение путем добавления некоторого избытка реагента — осадителя для превращения компонента А в осаждаемую форму;
- в) фильтрование полученной смеси для отделения осадка;
- г) промывание осадка для удаления адсорбированных примесей;
- д) высушивание или прокаливание для превращения осадка в гравиметрическую (весовую) форму);
- е) взвешивание гравиметрической формы
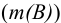 и проведение вычислений. Общую схему гравиметрического анализа можно представить в виде:
и проведение вычислений. Общую схему гравиметрического анализа можно представить в виде:

Некоторые примеры гравиметрических определений приведены в табл. 7.1. Из примеров видно, что осаждаемая и гравиметрическая формы могут быть представлены разными химическими соединениями.
Массу определяемого компонента 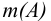 и его массовую долю
и его массовую долю
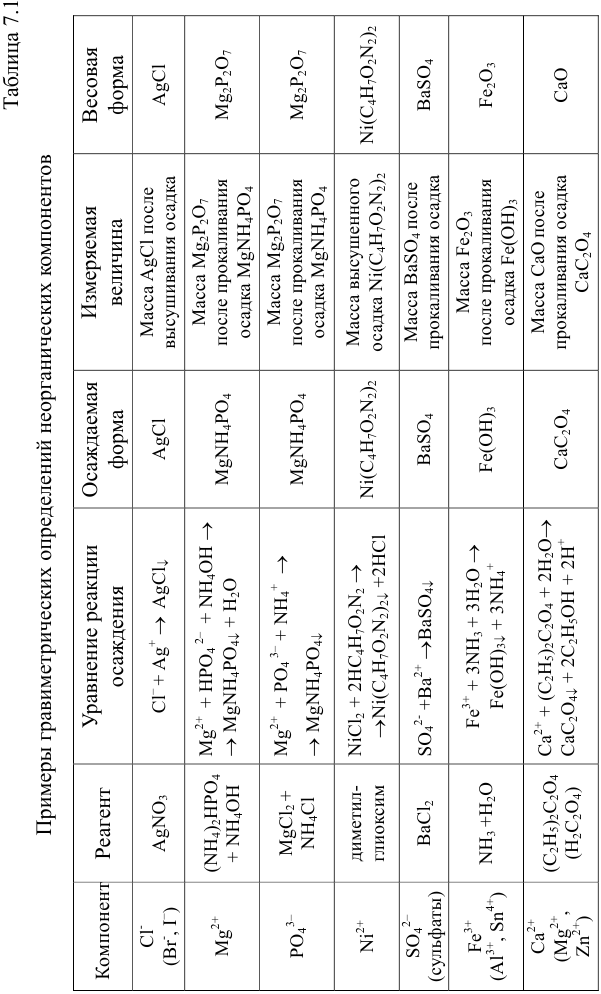
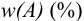 рассчитывают по формулам:
рассчитывают по формулам:
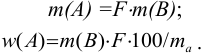
В приведенных формулах F — гравиметрический фактор (называемый также аналитическим множителем, фактором пересчета). Он показывает, массу определяемого компонента (г), соответствующую 1 г гравиметрической формы.
Гравиметрический анализ является абсолютным методом — не требует образцов сравнения (эталонов). На основании данных гравиметрического элементного анализа может быть также установлена формула анализируемого соединения. Погрешность метода обычно составляет 0,05 — 0,2 %.
Примеры с решением:
- Гравиметрический фактор и его значение с примерами решения
- Расчет величины навески анализируемой пробы с примерами решения
- Расчет количества осадителя с примерами решения
- Расчет потерь при промывании осадка с примерами решения
- Расчет результатов анализа в гравиметрии с примерами решения
Расчеты в титриметрии
Сущность титриметрии
Титриметрия или титриметрические методы количественного анализа основаны на измерении объема раствора реактива В, израсходованного на реакцию с определяемым веществом А. Раствор реактива (титрант, рабочий раствор) должен при этом иметь известную концентрацию. Различают рабочий раствор с «приготовленным титром», установленным титром (по другому раствору с известной концентрацией) и полученный растворением вещества «фиксанала» или «стандарт-титра» (ампулы с точной навеской) в мерной колбе соответствующего объема.
Титр — способ выражения концентрации раствора, определивший название метода и показывающий массу растворенного вещества в граммах в 1 миллилитре раствора (г/мл). Процесс постепенного добавления титранта к раствору определяемого вещества называют титрованием. При титровании наступает момент, когда рабочий раствор В и определяемое вещество А прореагируют между собой в эквивалентных количествах, т. е. в строгом соответствии со стехиометрией реакции. В таком случае справедлив закон эквивалентов, составляющий основу расчетов в титриметрии:
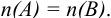
При титровании важно зафиксировать конец реакции, называемый точкой стехиометричности или точкой эквивалентности (ТЭ). Для экспериментального установления конечной точки титрования КТТ, по возможности наиболее близкой к ТЭ, используют изменение окраски индикатора или какого-либо физического свойства раствора.
К химической реакции титрования предъявляются следующие требования: 1) строгая стехиометричность, отсутствие побочных реакций; 2) высокая скорость; 3) практическая необратимость 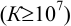 , обеспечивающая количественное превращение реагирующих веществ в продукты реакции; 4) наличие подходящего индикатора или другого способа фиксирования ТЭ.
, обеспечивающая количественное превращение реагирующих веществ в продукты реакции; 4) наличие подходящего индикатора или другого способа фиксирования ТЭ.
В титриметрии используют мерную посуду: мерные колбы -для приготовления растворов; пипетки — для отмеривания определенного объема раствора и бюретки — для измерения объема титранта.
Титриметрические методы характеризуются быстротой анализа, простотой оборудования, возможностью автоматизации. Чувствительность методов не превышает 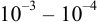 моль/л, относительная погрешность
моль/л, относительная погрешность 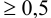 %.
%.
Примеры с решением:
- Методы, приемы и способы титрования с примерами решения
Способы выражения концентрации растворов в титриметрии
Все расчеты в титриметрии связаны с законом эквивалентов и понятием «эквивалент». Эквивалентом называют реальную или условную частицу вещества, которая в данной реакции равноценна (эквивалентна) одному иону водорода или одному электрону. Например, эквивалент 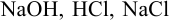 — реальная частица, соответствующая молекуле этих веществ. Эквивалент
— реальная частица, соответствующая молекуле этих веществ. Эквивалент 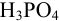 , в зависимости от числа участвующих в реакции протонов, может представлять реальную молекулу
, в зависимости от числа участвующих в реакции протонов, может представлять реальную молекулу 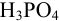 или условную часть молекулы: 1/2
или условную часть молекулы: 1/2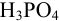 или 1/З
или 1/З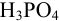 . Дробь, показывающую, какая часть молекулы или иона является эквивалентом, называют фактором эквивалентности
. Дробь, показывающую, какая часть молекулы или иона является эквивалентом, называют фактором эквивалентности 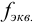 . Фактор эквивалентности рассчитывают на основе стехиометрии реакции. Число, показывающее, сколько эквивалентов содержится в молекуле, называют числом эквивалентности и обозначают
. Фактор эквивалентности рассчитывают на основе стехиометрии реакции. Число, показывающее, сколько эквивалентов содержится в молекуле, называют числом эквивалентности и обозначают 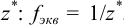 . Молярная масса эквивалента вещества — это масса одного моля эквивалента этого вещества, равная произведению фактора эквивалентности на молярную массу вещества.
. Молярная масса эквивалента вещества — это масса одного моля эквивалента этого вещества, равная произведению фактора эквивалентности на молярную массу вещества.
Например, для вещества В:
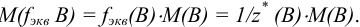
Примеры с решением:
- Примеры решения вычисления молярной массы эквивалента
Способы выражения концентрации растворов
При приготовлении рабочих растворов и вычислениях результатов в титриметрии обычно используют следующие способы выражения концентрации:
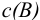 — молярная концентрация вещества В, моль/л;
— молярная концентрация вещества В, моль/л;
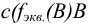 — молярная концентрация эквивалента вещества В, моль/л.
— молярная концентрация эквивалента вещества В, моль/л.
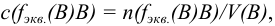
где 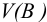 — объем раствора (л), содержащего п моль эквивалентов В; соответствует старому названию — нормальная концентрация.
— объем раствора (л), содержащего п моль эквивалентов В; соответствует старому названию — нормальная концентрация.
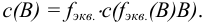
В методиках анализа, установленных стандартами, разрешены только единицы системы СИ. В частности, размерность объема при выражении молярной концентрации — 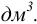 Такие внесистемные размерности объема, как литр (л), миллилитр (мл) являются разрешенными в химии и используются в учебной и научной литературе, в том числе на страницах пособия.
Такие внесистемные размерности объема, как литр (л), миллилитр (мл) являются разрешенными в химии и используются в учебной и научной литературе, в том числе на страницах пособия.
Не рекомендуется использовать термины ‘’молярность” и “нормальность” раствора, но эти понятия применяются в контекстах после величины концентрации, например: …0,1 молярный раствор, …0,1 нормальный раствор. Разрешаются сокращенные обозначения, например 0,025М 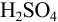 — 0,025 молярный раствор
— 0,025 молярный раствор 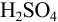 , т. е. в одном литре раствора содержится 0,025 моль вещества
, т. е. в одном литре раствора содержится 0,025 моль вещества 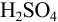 ; 0,050 н.
; 0,050 н. 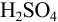 -0,050 нормальный раствор
-0,050 нормальный раствор 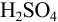 , т. е. в одном литре раствора содержится 0,050 моль эквивалента вещества
, т. е. в одном литре раствора содержится 0,050 моль эквивалента вещества 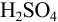 .
.
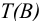 — mump раствора вещества В, г/мл. Он показывает массу вещества В в одном миллилитре раствора:
— mump раствора вещества В, г/мл. Он показывает массу вещества В в одном миллилитре раствора:
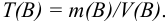
С использованием 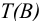 возможен простой расчет навески вещества, необходимой для приготовления определенного объема рабочего раствора с заданным титром.
возможен простой расчет навески вещества, необходимой для приготовления определенного объема рабочего раствора с заданным титром.
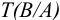 — mump рабочего раствора В по определяемому веществу г/мл (условный титр). Он показывает, какая масса вещества А эквивалентна или оттитровывается одним миллилитром рабочего раствора В. Например, выражение
— mump рабочего раствора В по определяемому веществу г/мл (условный титр). Он показывает, какая масса вещества А эквивалентна или оттитровывается одним миллилитром рабочего раствора В. Например, выражение 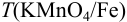 = 0,001396 г/мл означает, что 1 мл такого раствора
= 0,001396 г/мл означает, что 1 мл такого раствора 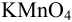 эквивалентен (оттитровывает) 0,001396 г Fe. Такой способ выражения концентрации удобен при серийных анализах, т. к.
эквивалентен (оттитровывает) 0,001396 г Fe. Такой способ выражения концентрации удобен при серийных анализах, т. к.
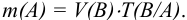
Между указанными способами выражения концентрации существует простая связь:
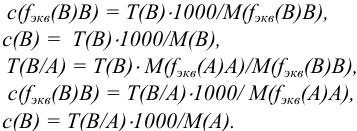
В анализе чаще всего пользуются растворами с концентрациями -0,002 или 0,1 моль/л. Не применяются 1 М растворы, так как в этом случае велика капельная ошибка титрования, т. е. ошибка при добавлении одной лишней капли титранта с высокой концентрацией.
Использование в титриметрии концентрации 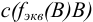 (моль эквивалента В в одном литре раствора) связано с удобством расчетов, т. к. при одинаковых концентрациях растворов веществ А и В реакции идут между равными объемами этих веществ (согласно закону эквивалентов):
(моль эквивалента В в одном литре раствора) связано с удобством расчетов, т. к. при одинаковых концентрациях растворов веществ А и В реакции идут между равными объемами этих веществ (согласно закону эквивалентов):
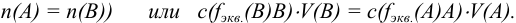
Выражение закона в обозначениях, встречающихся в ранее изданной литературе: 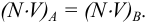
В практике титриметрии часто пользуются так называемым поправочным коэффициентом к, который показывает степень отклонения практической концентрации полученного раствора от его теоретического (расчетного) значения:
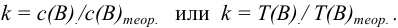
Например, если при приготовлении 0,1000 М раствора  практическое значение концентрации полученного раствора оказалось равным 0,09983 моль/л, то на этикетке можно записать:
практическое значение концентрации полученного раствора оказалось равным 0,09983 моль/л, то на этикетке можно записать: 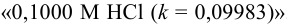 . И, наоборот, если в условиях задачи (эксперимента) используется, например, «0,2000 и. раствор
. И, наоборот, если в условиях задачи (эксперимента) используется, например, «0,2000 и. раствор 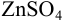
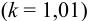 », то в расчетные формулы следует подставить:
», то в расчетные формулы следует подставить:
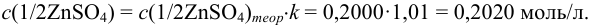
Примеры с решением:
- Примеры решения расчета при приготовлении рабочих растворов и установлении их концентрации
- Расчеты результатов анализа в титриметрии с примерами решения
Построение кривых титрования
В процессе титрования изменяются равновесные концентрации титруемого вещества А, титранта В, продуктов реакции и соответственно свойства раствора. Свойствами, связанными с концентрацией А, являются равновесный потенциал Е в окислительно-восстановительном титровании, величина pH — в кислотно-основном, рМ — в осадительном и комплексометрии. Ход реакции титрования можно изобразить графической моделью или кривой титрования.
Кривой титрования называют график зависимости параметра системы, связанного с концентрацией титруемого вещества, титранта или продукта реакции от состава раствора в процессе титрования (например от объема титранта 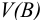 или степени оттитрованности
или степени оттитрованности 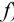 ). По оси ординат в химических методах титриметрии, как правило, откладывают логарифм концентрации или логарифмически связанную с ней величину (например Е). В таком случае получаются полулогарифмические (монологарифмические) кривые титрования.
). По оси ординат в химических методах титриметрии, как правило, откладывают логарифм концентрации или логарифмически связанную с ней величину (например Е). В таком случае получаются полулогарифмические (монологарифмические) кривые титрования.
Кривые титрования помогают выбрать индикатор, оценить погрешность, наглядно проследить за ходом титрования.
При расчете кривых титрования прибегают к некоторым допущениям, не оказывающим заметного влияния на конечный результат. К таким допущениям относится:
1) пренебрежение изменением объема раствора в ходе титрования (более справедливо при использовании титранта В с более высокой концентрацией, чем А);
2) пренебрежение малыми концентрациями выводимых из сферы реакции ионов при образовании прочных продуктов (вода, осадки, комплексы). Погрешность при этом пренебрежении тем меньше, чем выше константы равновесия реакции титрования, т. е. когда 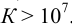
Если принимаемые допущения несправедливы, происходит нарушение плавного хода кривой титрования. Тогда следует пользоваться более точными формулами расчета равновесий в соответствии с рекомендациями, приведенными в главах 3-6. См. также примеры 3.2, 3.4, 8.22.
Пусть исходное количество А: 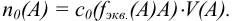
Согласно закону эквивалентов (8.1), в каждый момент титрования справедливо соотношение:
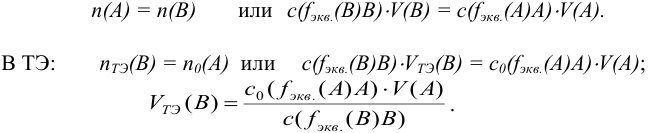
Отношение количества оттитрованного в данный момент вещества А к исходному количеству А называют степенью оттитрованности 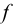 :
:
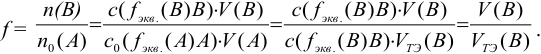
При равных концентрациях Л и В справедливо: 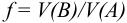 .
.
Степень оттитрованности может быть выражена в %. Очевидно, что до ТЭ 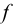 < 1 или
< 1 или 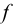 < 100 %, после ТЭ
< 100 %, после ТЭ 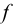 > 1 или
> 1 или 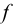 > 100 %, в ТЭ
> 100 %, в ТЭ 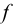 = 1 или
= 1 или 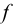 = 100 %.
= 100 %.
При построении кривых титрования задаются молярными концентрациями эквивалентов 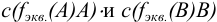 — и начальным объемом раствора определяемого вещества
— и начальным объемом раствора определяемого вещества 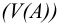 . Затем по закону эквивалентов рассчитывают
. Затем по закону эквивалентов рассчитывают 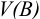 в ТЭ. Принимают его за 100% и рассчитывают объемы
в ТЭ. Принимают его за 100% и рассчитывают объемы 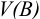 в промежуточных точках, соответствующих, например: 10 %; 50 %; 90 %; 99 %; 99,9 %; 101,1 %; 101 % и 110 % добавленного титранта или задаются
в промежуточных точках, соответствующих, например: 10 %; 50 %; 90 %; 99 %; 99,9 %; 101,1 %; 101 % и 110 % добавленного титранта или задаются 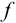 (см. табл. 8.4 — 8.12). Такой выбор значений объемов обусловлен плавным изменением кривой вдали от ТЭ и резким вблизи (рис. 8.1 — 8.3). Резкое изменение рассчитываемого параметра (pH, рМ или E) вблизи ТЭ называется скачком титрования и связано с крутизной кривой. Границы скачка расширяются при снижении требований к точности титрования.
(см. табл. 8.4 — 8.12). Такой выбор значений объемов обусловлен плавным изменением кривой вдали от ТЭ и резким вблизи (рис. 8.1 — 8.3). Резкое изменение рассчитываемого параметра (pH, рМ или E) вблизи ТЭ называется скачком титрования и связано с крутизной кривой. Границы скачка расширяются при снижении требований к точности титрования.
В кислотно-основном титровании рассчитываемым параметром состава раствора является pH, осадительном и комплексонометрическом — рМ , окислительно-восстановительном — равновесный потенциал Е.
Для реакции титрования: А + В = продукты
целесообразно рассчитывать параметр состава раствора до ТЭ по концентрации титруемого раствора вещества А и, если необходимо, продукта его превращения, пренебрегая концентрацией В. После ТЭ — по избытку добавленного титранта В, пренебрегая концентрацией А.
В ТЭ в растворе преобладают продукты реакции. Концентрации А и В малы и расчет параметра системы, связанного с концентрацией А, проводится через константу соответствующего равновесия: в кислотно-основном через 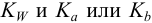 ; в осадительном -через
; в осадительном -через 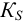 в комплексонометрическом — через константу устойчивости комплексного соединения
в комплексонометрическом — через константу устойчивости комплексного соединения 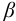 ; в окислительно-восстановительном — через соответствующие значения
; в окислительно-восстановительном — через соответствующие значения 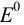 редокс-пар А и В (см. табл. 8.4-8.11).
редокс-пар А и В (см. табл. 8.4-8.11).
Величина скачка титрования определяется константой равновесия, концентрацией реагирующих веществ, температурой, природой титруемого вещества и титранта, наличием посторонних веществ и др. При правильном выборе индикатора для визуального обнаружения ТЭ интервал перехода его окраски должен полностью или частично укладываться в пределы скачка титрования (рис. 8.1).
При несовпадении рТ индикатора (или среднего значения интервала перехода индикатора) с точкой эквивалентности (ТЭ) титрование заканчивается при так называемой конечной точке титрования — КТТ. Это является причиной индикаторных ошибок. Пояснения к расчету индикаторных ошибок титрования и необходимые формулы приведены в разделе 8.6.
Расчетные формулы в табл. 8.6 и других даны без вывода и предполагают усвоение теоретических разделов и расчетов химических равновесий, в том числе, приведенных в разделах 2-6 глав. С выводами сделан расчет кривой титрования многоосновного основания 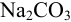 (пример 8.22).
(пример 8.22).
Примеры с решением:
- Расчет кривых кислотно-основного титрования с примерами решения
- Расчет кривых окислительно-восстановительного титрования с примерами решения
- Расчет кривых титрования в методах осаждения с примерами решения
- Расчет кривых титрования в методе комплексонометрии с примерами решения
Индикаторные погрешности титрования
Как было сказано выше, при несоответствии интервала перехода индикатора и ТЭ, титрование заканчивается при так называемой конечной точке титрования — КТТ, что является причиной индикаторных погрешностей титрования (ПТ). Титрование может быть закончено до ТЭ или после ТЭ, в результате чего возникают отрицательные (недотитровывания) и положительные (перетитровывания) систематические ПТ. Их можно оценить по кривым титрования или расчетным способом (графический способ — в рекомендованной учебной литературе).
Примеры с решением:
- Расчет индикаторных погрешностей кислотно-основного титрования с примерами решения
Математическая обработка результатов количественного анализа
При получении результатов количественного анализа, как правило, проводят несколько аналитических операций, начиная с отбора и подготовки проб, используют несколько последовательно измеренных величин. Каждое измерение физической величины, каждая операция вносят свой вклад в общую погрешность результата анализа. Например, любое титриметрическое определение включает в себя: 1) погрешность определения титра рабочего раствора, которая зависит от точности взвешивания и правильности измерения объема; 2) погрешность титрования анализируемого вещества, зависящую от правильности измерения объемов и правильности установления точки эквивалентности с помощью индикаторов (индикаторные ошибки титрования). Погрешности необходимо уметь выявлять, оценивать, знать и использовать способы их уменьшения. Например, в титриметрических методах анализа стремятся к относительной погрешности, не превышающей 0,1 %, в гравиметрических — 0,05 %.
Оценка погрешностей (ошибок) результата связана с требованиями к точности химического анализа, являющейся одной из его метрологических характеристик.
Примеры с решением:
- Классификация и оценка погрешностей количественного анализа с примерами решения
- Сравнение результатов двух методов количественного анализа с примерами решения
- Суммирование погрешностей в химических методах количественного химического анализа с примерами решения
Приложение
Таблица 1
Коэффициенты активности ионов при различных значениях ионной силы раствора
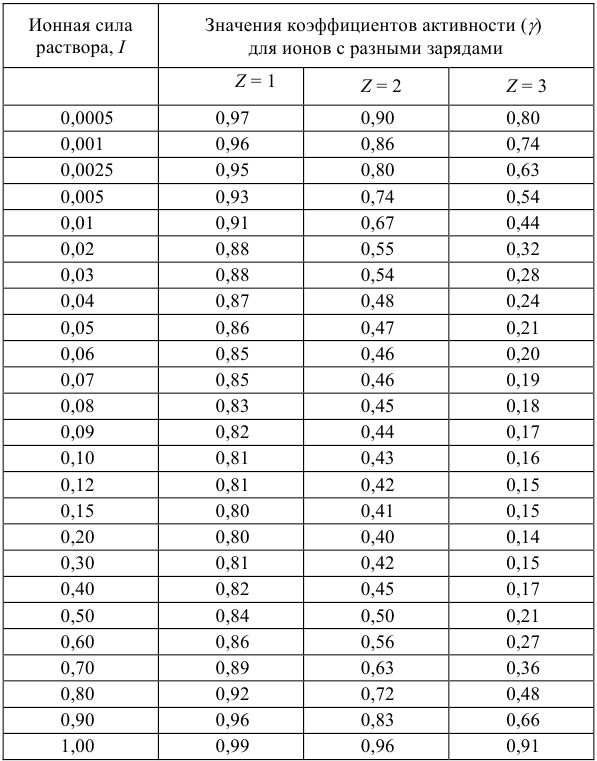
Таблица 2
Термодинамические константы кислотности некоторых кислот в водном растворе
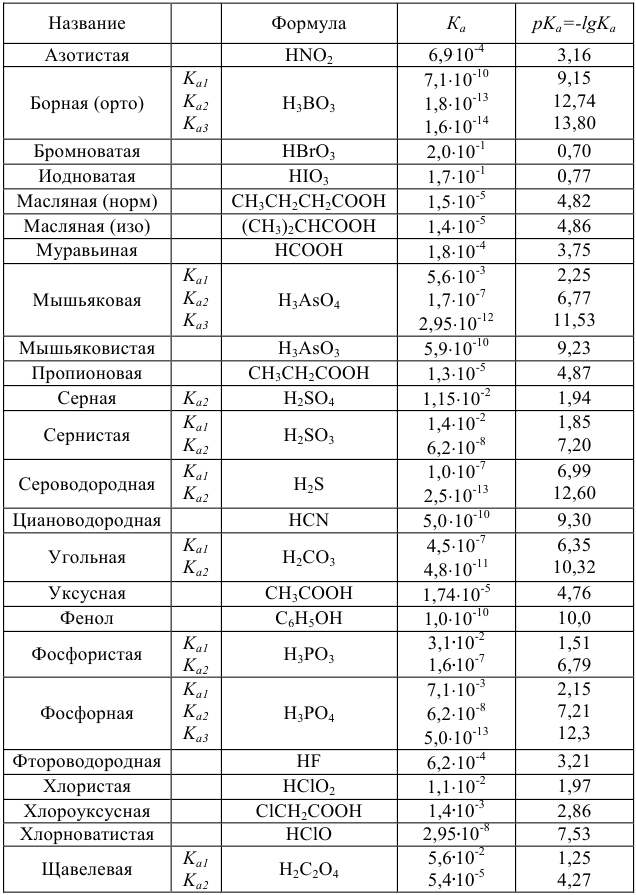
Таблица 3
Термодинамические константы основности некоторых оснований в водном растворе
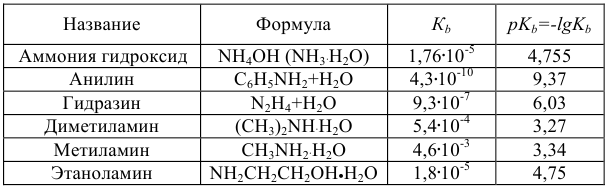
Таблица 4
Константы устойчивости комплексных ионов Комплексы с аммиаком 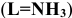
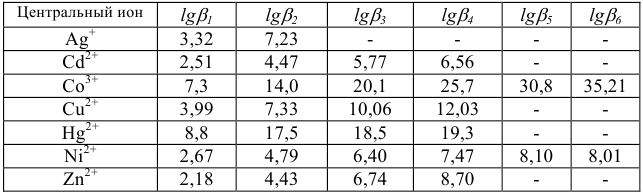
Гидроксокомплексы 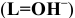
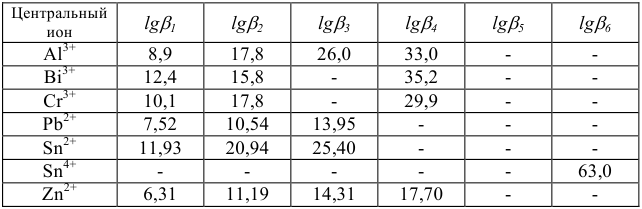
Иодидные комплексы 
Продолжение табл. 4
Фторидные комплексы 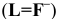

Роданидные (тиоцианатные) комплексы 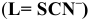
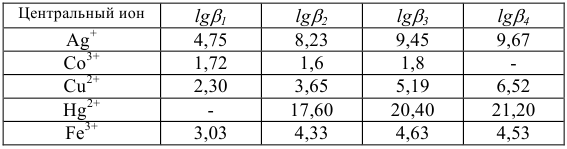
Хлоридные комплексы 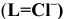

Цианидные комплексы 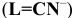
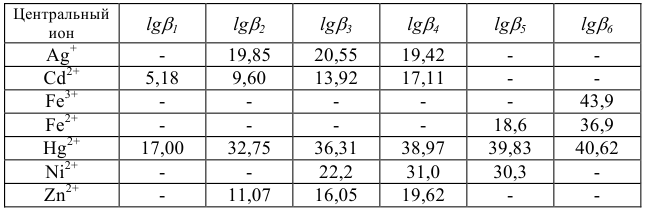
Комплексы с ЭДТА 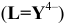
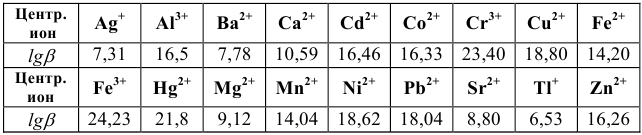
Таблица 5
Стандартные окислительно-восстановительные потенциалы 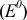 при 25°C
при 25°C
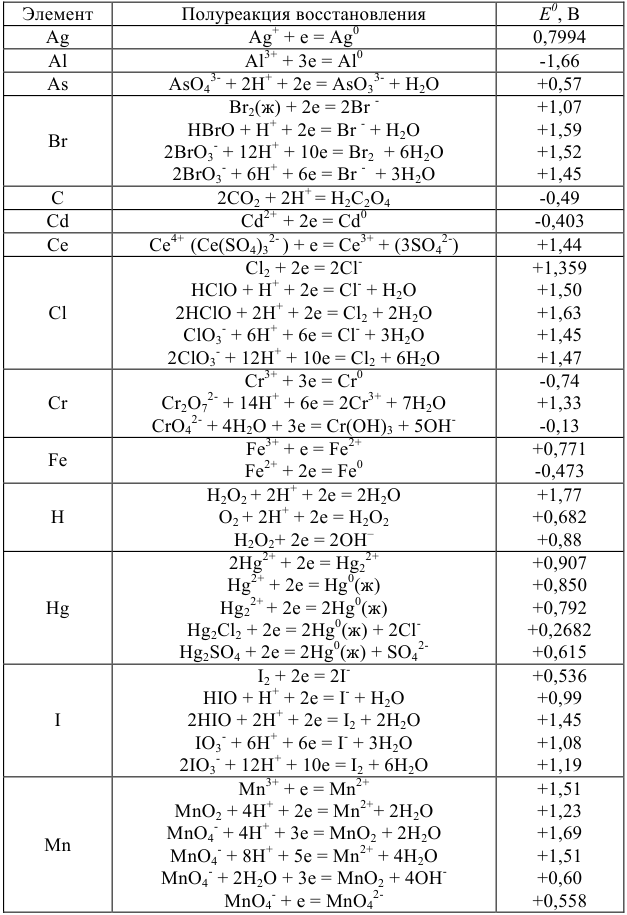
Продолжение табл. 5
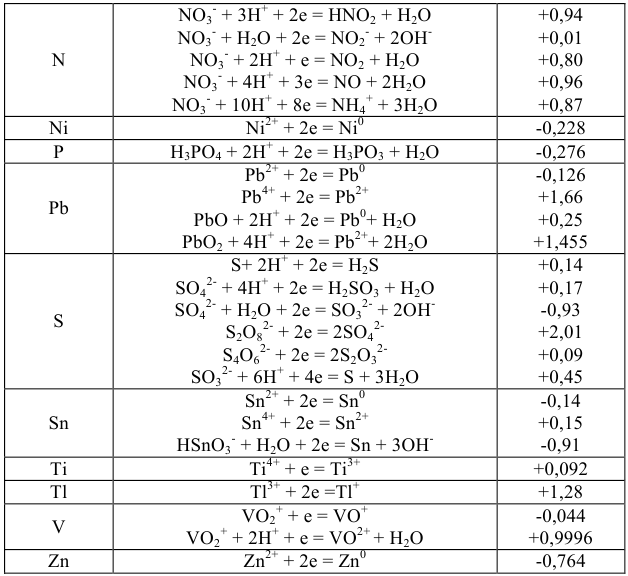
Таблица 6
Константы растворимости важнейших малорастворимых веществ
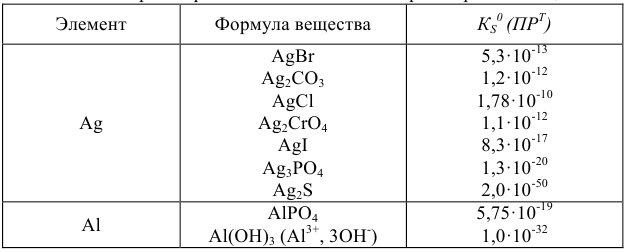
Продолжение табл. 6
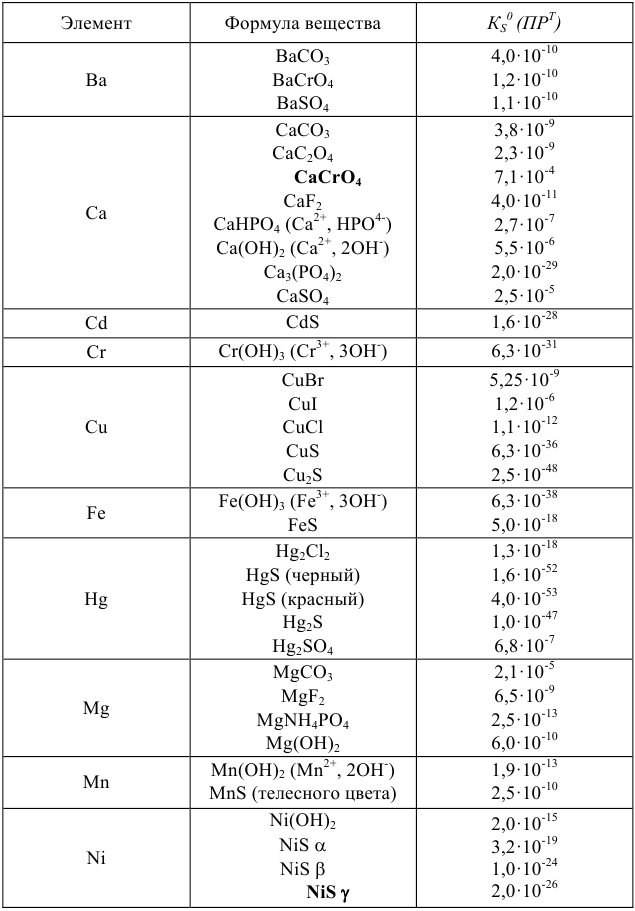
Продолжение табл. 6
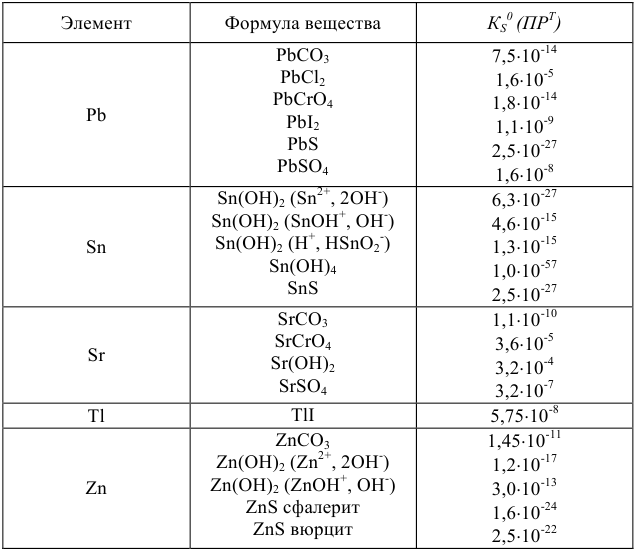
Таблица 7
Молярные доли свободных ионов 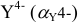 для этилендиаминтетрауксусной кислоты в растворах с различными значениями pH
для этилендиаминтетрауксусной кислоты в растворах с различными значениями pH
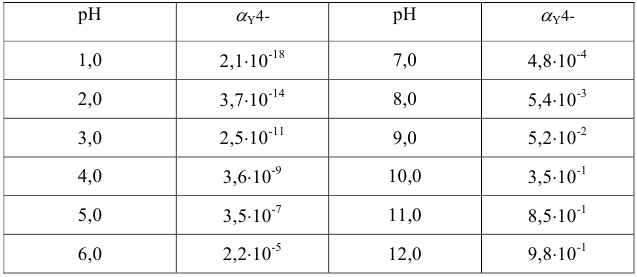
Таблица 8
Коэффициенты Стьюдента 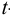 для различной доверительной вероятности
для различной доверительной вероятности
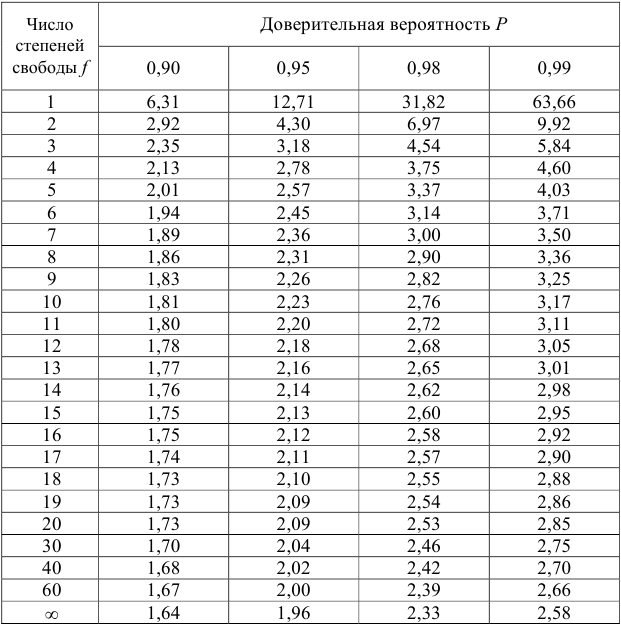
Таблица 9
Значения Q — критерия
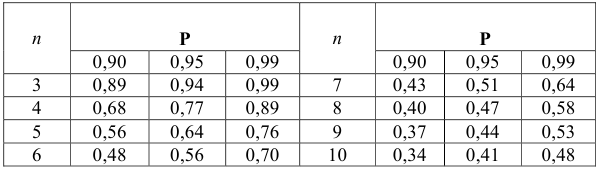
Таблица 10
Численные значения критерия Фишера F при доверительной вероятности Р = 0,95
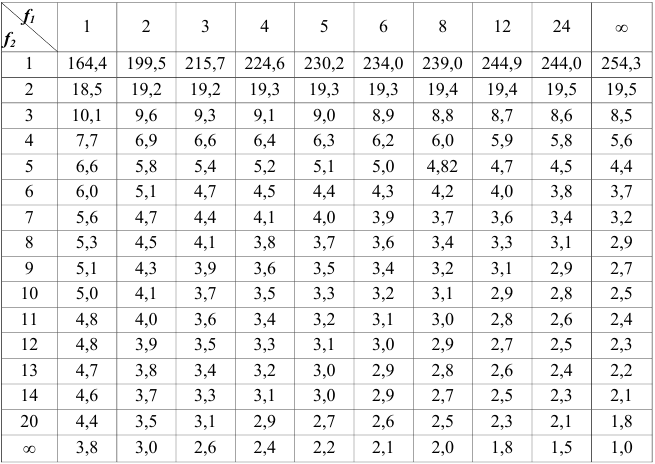
Таблица 11
Максимально допустимые абсолютные погрешности (мл) мерной посуды 2 класса (мл)
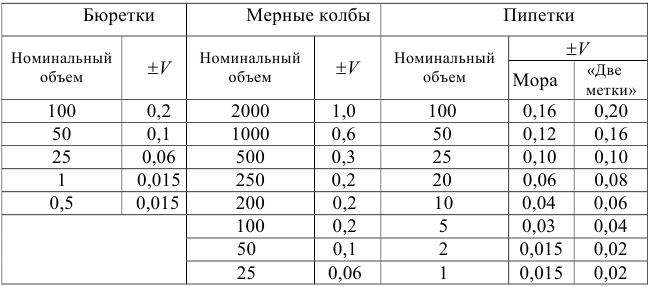

ИЗ ОПЫТА РАБОТЫ
Решение задач на смеси и сплавы
с помощью схем и таблиц
Задачи на смеси и сплавы вызывают наибольшие
затруднения у школьников. В процессе решения
каждой такой задачи целесообразно действовать
по следующей схеме.
1. Изучение условия задачи. Выбор неизвестных
величин (их обозначаем буквами х, у и т.д.),
относительно которых составляем пропорции.
Выбирая неизвестные параметры, мы создаем
математическую модель ситуации, описанной в
условии задачи.
2. Поиск плана решения. Используя условия
задачи, определяем все взаимосвязи между данными
величинами.
3. Осуществление плана, т.е. оформление
найденного решения – переход от словесной
формулировки к составлению математической
модели.
4. Изучение полученного решения, критический
анализ результата.
При решении задач на смеси часто путают
проценты и доли, раствор и растворенное вещество.
Необходимо помнить, что массовая доля ![]() находится делением
находится делением
значения процентной концентрации на 100%, а масса
растворенного вещества m(в-ва) равна
произведению массы раствора m(р-ра) на
массовую долю:
m(в-ва) = m(р-ра)•![]() .
.
В большинстве случаев задачи на смеси и сплавы
становятся нагляднее, если при их решении
использовать схемы, иллюстративные рисунки или
вспомогательные таблицы.
Задача 1. В каких пропорциях нужно смешать а%-й
и b%-й растворы кислоты (a < b), чтобы
получить с%-й раствор?
Возьмем х г а%-го раствора и у г b%-го
раствора кислоты. Составим таблицу:
| Kонцентрация раствора, % |
Масса раствора, г |
Масса кислоты, г |
|---|---|---|
| a | х | 0,01ax |
| b | у | 0,01by |
| c (смесь) | x + y | 0,01c(x + y) |
Составим и решим уравнение:
0,01ах + 0,01by = 0,01c(x + y),
(b – с)у = (с – а)х,
x : у = (b – с) : (с – а).
Воспользуемся диагональной схемой*:
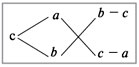
В этой схеме а и b – концентрации
исходных растворов, с – требуемая
концентрация кислоты в процентах, а
«крест-накрест» – записаны их разности (b – с)
и (с – а), соответствующие отношению масс
растворов а и b.
Задача 2. Сколько по массе 90%-го и 60%-го
растворов фосфорной кислоты надо взять, чтобы
получить 5,4 кг 80%-го раствора фосфорной кислоты?
Решение
Составим диагональную схему:
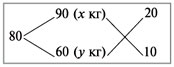
Получаем:
х : у = 20 : 10 = 2 : 1.
Значит, 90%-го раствора фосфорной кислоты надо
взять в 2 раза больше, чем 60%-го, т.е. х = 2y.
Составим уравнение: 2y + y = 5,4.
Отсюда y = 1,8 кг.
Ответ. 3,6 кг 90%-го и 1,8 кг 60%-го
растворов фосфорной кислоты.
Задача 3. Сплавили два слитка серебра: 75 г
600-й и 150 г 864-й пробы. Определить пробу сплава.
Решение
Пусть проба сплава равна х.
Составим диагональную схему:
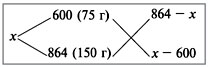
Получаем:
(864 – х) : (х – 600) = 75 : 150 = 1 : 2;
1728 – 2х = х – 600; х = 776.
Ответ. Получили сплав 776-й пробы.
Задача 4. Смешали некоторые количества 72%-го
и 58%-го растворов кислоты, в результате получили
62%-й раствор той же кислоты. Если бы каждого
раствора было взято на 15 л больше, то получился бы
63,25%-й раствор. Сколько литров каждого раствора
было взято первоначально для составления первой
смеси?
Решение
Дважды используем диагональную схему:
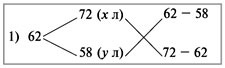
Получаем:
х : у = 4 : 10 = 2 : 5.
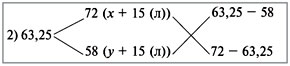
Получаем:
(х + 15) : (y + 15) = 5,25 : 8,75 = 3 : 5.
Составим систему уравнений и решим ее:
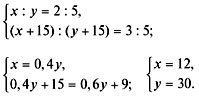
Ответ. В первой смеси было 12 л 72%-го
раствора
и 30 л 58%-го раствора.
Задача 5. Сколько граммов 9%-го раствора
спирта можно получить из 200 г 70%-го раствора
спирта?
Решение
9%-й раствор спирта получают из 70%-го, разбавляя
его водой. В воде 0% спирта. Применим диагональную
схему:
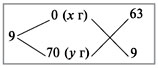
Получаем:
х : у = 63 : 9 = 7 : 1.
Значит, 1 часть 70%-го раствора спирта надо
разбавить 7 частями воды. Поэтому 200 г 70%-го
раствора спирта надо разбавить 200•7 = 1400 г воды.
Всего получим: 200 + 1400 = 1600 г 9%-го раствора спирта.
Ответ. Из 200 г 70%-го раствора спирта
можно
получить 1 кг 600 г 9%-го раствора спирта.
Задача 6. Имеются три смеси (I–III),
составленные из трех элементов А, В и С. В первую
смесь входят только элементы А и В в массовом
отношении 1 : 2, во вторую смесь входят только
элементы В и С в массовом отношении 1 : 3, в третью
смесь входят только элементы А и С в массовом
отношении 2 : 1. В каком соотношении нужно взять
эти смеси, чтобы во вновь полученной смеси
элементы А, В и С содержались в массовом
отношении 11 : 3 : 8?
Решение
Для решения задачи составим схему 1:
Схема 1
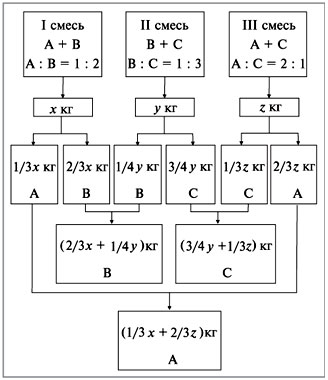
По условию задачи в полученной смеси
соотношение масс А : В : С = 11 : 3 : 8. Поэтому
![]()
Составим систему уравнений и решим ее:
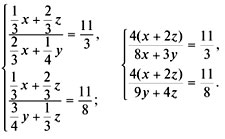
Пусть ![]() = а,
= а, ![]() = b, тогда
= b, тогда
система примет вид:
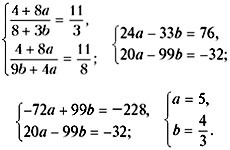
Значит,
х : z = 1 : 5 = 3 : 15, х : у = 3 : 4,
поэтому
х : у : z = 3 : 4 : 15.
Ответ. Чтобы элементы А, В и С
содержались
в массовом отношении 11 : 3 : 8, смеси I, II, III
надо взять в соотношении 3 : 4 : 15 по массе.
Задача 7. Имеется два сплава меди, никеля и
железа, причем первый из них содержит 4% меди. Если
сплавить их в равных количествах, получится
сплав, содержащий 66% железа, а если взять 3 кг
первого сплава и 7 кг второго, получится сплав,
содержащий 0,4 кг меди. Определить процентное
содержание никеля во втором сплаве, если
известно, что оно в 2 раза выше, чем в первом
сплаве.
Решение
Пусть во втором сплаве массовая доля никеля
равна x, а железа – у. Для решения задачи
составим схему 2.
Исходя из схемы 2, составим и решим систему
уравнений:
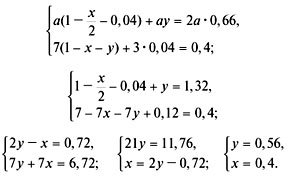
Схема 2
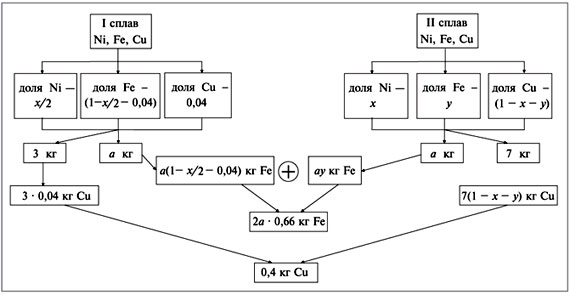
Во втором сплаве массовая доля никеля равна 0,4,
т.е. 40%.
Ответ. 40%.
Задача 8. Значения процентного содержания
(по объему) спирта в трех растворах образуют
геометрическую прогрессию. Если смешать первый,
второй и третий растворы в объемном отношении 2 : 3
: 4, то получится 32%-й раствор спирта. Если смешать
их в объемном отношении
3 : 2 : 1, то получится раствор, содержащий 22% спирта.
Сколько процентов спирта содержит каждый
раствор?
Решение
Пусть в первом растворе х% спирта, во втором
– у%, в третьем – z%. Согласно условию
задачи процентное содержание спирта в трех
растворах образует геометрическую прогрессию,
потому справедливо уравнение:
у2 = xz. (1)
На основании данных задачи составим таблицы и
математические выражения.
Таблица 1
Смешивание трех растворов в объемном
отношении 2 : 3 : 4
| Вид раствора | Объем раствора, л | Содержание спирта, % | Объем спирта, л |
|---|---|---|---|
| 1-й раствор | 2 | х | 2х/100 |
| 2-й раствор | 3 | y | 3y/100 |
| 3-й раствор | 4 | z | 4z/100 |
| Cмесь | 9 | 32 | 9•32/100 |
2х/100 + 3y/100 + 4z/100 = 288/100,
2х + 3y + 4z = 288.
(2)
Таблица 2
Смешивание трех растворов в объемном
отношении 3 : 2 : 1
| Вид раствора | Объем раствора, л | Содержание спирта, % | Объем спирта, л |
|---|---|---|---|
| 1-й раствор | 3 | х | 3х/100 |
| 2-й раствор | 2 | y | 2y/100 |
| 3-й раствор | 1 | z | z/100 |
| Cмесь | 6 | 22 | 6•22/100 |
3х/100 + 2y/100 + z/100 = 132/100,
3х + 2y + z = 132.
(3)
Составим и решим систему из трех уравнений (1–3):
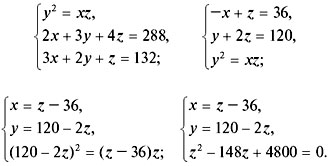
При z1 = 48, x = 12, y = 24;
при z2 = 100, x = 64, y = –80, решение не
имеет смысла.
Ответ. В первом растворе 12% спирта,
во втором – 24%, в третьем – 48%.
* При решении задач на смешивание
растворов разных концентраций автор использует
диагональные схемы («правило креста»). На
диагональной схеме в точке пересечения двух
прямых обозначают концентрацию смеси. Например,
далее в задаче 2 – это 80%. У концов этих прямых
слева от точки пересечения указывают
концентрации составных частей смеси, а справа –
разности концентраций смеси и ее составных
частей:
Из этой схемы следует, что, например, для
приготовления 30 г 80%-го раствора H3PO4
требуется взять 20 г 90%-го и 10 г 60%-го растворов
кислоты. (Прим. ред.)
Т.Н.Епифанова,
учитель химии
школы № 1954 (Москва)
Задача
1.
Пробу объемом 5,00 мл смеси хлороводородной
и фосфорной кислот разбавили до 200,0 мл.
На титрование 20,00 мл полученного раствора
с метиловым оранжевым, израсходовали
18,20 мл 0,1012 М раствора гидроксида натрия;
при титровании такой же пробы раствора
с фенолфталеином израсходовали 34,70 мл
раствора NaOH. Какая масса НСl и H3PO4
содержится в 100,0 мл смеси?
Решение.
HCl
+ NaOH
↔ NaCl
+ H2O
HCl
титруется полностью и с индикатором
м.о., и с индикатором ф.ф. (f
= 1).
Н3РО4
+ NaOH
↔ NaН2РО4
+
H2O
Ка1
= 7,1 ∙ 10-3;
рКа1
= 2,15;
NaН2РО4
+
NaOH
↔ Na2НРО4
+
Н2О
Ка2
= 6,2 ∙ 10-8;
рКа2
= 7,21;
Na2НРО4
+
NaOH
↔ Na3РО4
+ Н2О
Ка3
= 5,0 ∙ 10-13;
рКа3
= 12,30.
Фосфорная
кислота может титроваться только по
двум ступеням, так как Ка3
<
10-8.
По
I
ступени Н3РО4
титруется с индикатором м.о. (f
= 1);
рНТЭ1
= (рКа1
+ рКа2)
: 2 = 2,15 + 7,21 = 4,68.
По
II
ступени Н3РО4
титруется
с индикатором ф.ф. (f
= ½);
рНТЭ2
= (рКа2
+ рКа3)
: 2 = 7,21 + 12,30 = 9,76.
Т.о.,
согласно условию задачи, с м.о. будет
титроваться вся HCl
и Н3РО4
по
I
ступени; с
ф.ф. будет титроваться вся HCl
и Н3РО4
по
двум (I
и II)
ступеням.
Находим
объемы раствора NaOH,
пошедшие на титрование каждого компонента
смеси:
Vна
Н3РО4
по
одной ступени
= Vф.ф.
– Vм.о.
= 34,70 – 18,20 = 16,50 мл
(fэ(Н3РО4)
= 1).
Vна
НCl
= Vм.о.
– Vна
Н3РО4
по
одной ступени
= 18,20 – 16,50 = 1,70 мл
(fэ(Н3РО4)
= 1).
М(Н3РО4)
= 98,00 г/моль;
fэ(Н3РО4)
= 1;
Мэ(Н3РО4)
= М(Н3РО4)
∙ fэ(Н3РО4)
= 98,00 г/моль;
М(НCl)
= 36,46 г/моль;
fэ(НCl)
= 1;
Мэ(НCl)
= М(НCl)
∙ fэ(НCl)
= 36,46 г/моль.
Рассчитываем,
сколько граммов HCl
и H3PO4
содержится в 100,0 мл смеси по формуле:
![]() ;
;
![]() г;
г;
![]() г.
г.
Ответ:
1,26 г HCl
и 32,73 г H3PO4
содержится в 100,0 мл смеси.
Задача
2. Ряд
растворов, в которых могут содержаться
гидроксид натрия, карбонат натрия и
гидрокарбонат натрия (один или несколько
компонентов), оттитровали 0,1200 М раствором
хлороводородной кислоты. В приведенной
ниже таблице указаны объемы стандартного
раствора хлороводородной кислоты,
необходимые для титрования 25,00 мл
каждого анализируемого раствора до
перехода окраски фенолфталеина V1
и метилового оранжевого V2.
На основании этих данных установите
состав анализируемых растворов и
рассчитайте содержание каждого компонента
смеси в мг/мл.
|
№ раствора |
V1 с инд. ф.ф. |
V2 с |
|
1 |
22,42 |
22,44 |
|
2 |
15,67 |
42,13 |
|
3 |
29,64 |
36,42 |
|
4 |
16,12 |
32,23 |
|
5 |
0,00 |
33,33 |
Решение.
Для
решения задачи надо определить, как
титруется гидроксид натрия, карбонат
натрия и гидрокарбонат натрия раствором
хлороводородной кислоты в присутствии
метилового оранжевого и фенолфталеина.
а).
NaOH
+ HCl
↔ NaCl
+ H2O
Точку
конца титрования в этом случае можно
зафиксировать и при помощи метилового
оранжевого и при помощи фенолфталеина,
так как вблизи точки эквивалентности
происходит резкое изменение рН среды
и оба эти индикатора в этот момент
изменяют свою окраску. Объемы кислоты,
идущие на титрование гидроксида натрия
с метиловым оранжевым и фенолфталеином
практически одинаковы. Поэтому в растворе
№ 1 может содержаться только гидроксид
натрия.
М(NaOH)
= 40,00 г/моль;
fэ(NaOH)
= 1;
Мэ(NaOH)
= М(NaOH)
∙ fэ(NaOH)
= 40,00 г/моль.
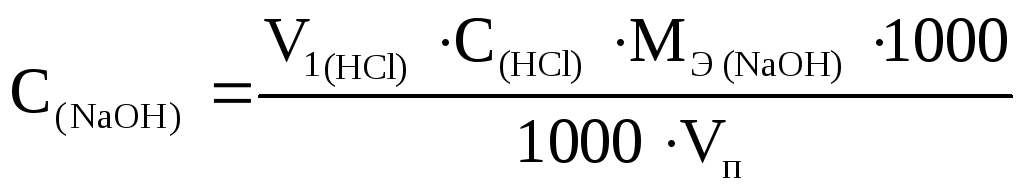 ;
;
![]() мг/мл.
мг/мл.
б).
Na2СO3
+ HCl ↔ NaНСO3
+ NaCl
NaНСO3
+ HCl
↔ Н2СO3
+ NaCl
Карбонат
натрия титруется хлороводородной
кислотой по ступеням. С фенолфталеином
– как однокислотное основание до
гидрокарбоната (fэ
= 1). Тогда:
М(Na2СO3)
= 106,0 г/моль;
fэ(Na2СO3)
= 1;
Мэ(Na2СO3)
= М(Na2СO3)
∙ fэ(Na2СO3)
= 106,0 г/моль.
С
метиловым оранжевым гидрокарбонат
дотитровывается до угольной кислоты,
т.е. с этим индикатором карбонат натрия
титруется как двухкислотное основание
сразу по двум ступеням (fэ
= ½).
М(Na2СO3)
= 106,0 г/моль;
fэ(Na2СO3)
= ½;
Мэ(Na2СO3)
= М(Na2СO3)
∙ fэ(Na2СO3)
= 53,00 г/моль.
Следовательно,
объем кислоты, идущий на титрование с
метиловым оранжевым V1
в два раза
больше объема кислоты, идущей на
титрование с фенолфталеином V2.
Значит, в растворе №4 содержится только
карбонат натрия.
![]() ;
;
![]() мг/мл.
мг/мл.
в).
NaНСO3
+ HCl
↔ Н2СO3
+ NaCl
Гидрокарбонат
натрия титруется хлороводородной
кислотой как однокислотное основание
(fэ
= 1) с
индикатором метиловым оранжевым. С
фенолфталеином гидрокарбонат натрия
не титруется V1
= 0,00.
Следовательно, в
растворе № 5 содержится только
гидрокарбонат натрия.
М(NaНСO3)
= 84,01 г/моль;
fэ(NaНСO3)
= 1;
Мэ(NaНСO3)
= М(NaНСO3)
∙ fэ(NaНСO3)
= 84,01 г/моль.
![]() ;
;
![]() мг/мл.
мг/мл.
г).
При титровании
раствора № 2 V2
больше V1
более, чем в два раза. Это значит, что
раствор содержит два компонента, один
из которых титруется с фенолфталеином
и с метиловым оранжевым, причем V2
= 2V1;
второй компонент титруется только с
метиловым оранжевым. Это соответствует
раствору, содержащему смесь карбоната
натрия и гидрокарбоната натрия.
Объем
кислоты, идущей на титрование карбоната
натрия по первой ступени равен V1.
Разность объемов (V2
– 2V1)
представляет собой объем кислоты, идущей
на титрование гидрокарбоната натрия.
Рассчитываем
содержание карбоната натрия:
М(Na2СO3)
= 106,0 г/моль;
fэ(Na2СO3)
= 1;
Мэ(Na2СO3)
= М(Na2СO3)
∙ fэ(Na2СO3)
= 106,0 г/моль.
![]() ;
;
![]() мг/мл.
мг/мл.
Рассчитываем
содержание гидрокарбоната натрия:
М(NaНСO3)
= 84,01 г/моль;
fэ(NaНСO3)
= 1;
Мэ(NaНСO3)
= М(NaНСO3)
∙ fэ(NaНСO3)
= 84,01 г/моль.
![]() ;
;
![]() мг/мл.
мг/мл.
д).
При титровании раствора № 3 V2
больше V1
менее, чем в два раза. Следовательно,
раствор содержит два компонента, один
из которых титруется с фенолфталеином
и с метиловым оранжевым, причем V2
= 2V1;
второй компонент титруется также с
двумя индикаторами, но для него V2
= V1.
Это соответствует раствору, содержащему
смесь карбоната натрия и гидроксида
натрия.
Разность
объемов (V2
– 2V1)
представляет собой объем кислоты, идущей
на титрование карбоната натрия по второй
ступени. Значит, на титрование всего
карбоната натрия расходуется 2(V2
– V1).
Так как с метиловым оранжевым полностью
оттитровывается и гидроксид натрия и
карбонат натрия, то объем раствора
хлороводородной кислоты, идущей на
титрование гидроксида натрия равен
разности (V2
– 2(V2
– V1)).
М(NaOH)
= 40,00 г/моль;
fэ(NaOH)
= 1;
Мэ(NaOH)
= М(NaOH)
∙ fэ(NaOH)
= 40,00 г/моль.
 ;
;
![]() мг/мл.
мг/мл.
М(Na2СO3)
= 106,0 г/моль;
fэ(Na2СO3)
= ½;
Мэ(Na2СO3)
= М(Na2СO3)
∙ fэ(Na2СO3)
= 53,00 г/моль.
![]() ;
;
![]() мг/мл.
мг/мл.
Ответ:
1. 4,309 мг/мл NaOH.
2.
7,973 мг/мл Na2СO3;
4,350 мг/мл NaНСO3.
3.
4,389 мг/мл NaOH;
3,451 мг/мл Na2СO3.
4.
8,202 мг/мл Na2СO3.
5.
13,44 мг/мл NaНСO3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изучение и использование алгоритма Л. Ф. Магницкого. При построении математической модели алгоритма Л. Ф. Магницкого возможно быстрое решение практических задач на смешивание веществ.
Ключевые слова:
алгоритм, арифметика Магницкого, смеси, модель.
Studying and using L. F. Magnitsky’s algorithm. By constructing a mathematical model of L. F. Magnitsky’s algorithm it is possible to quickly solve practical problems on mixing substances.
Keywords:
algorithm, Magnitsky’s arithmetic, mixtures, model.
При решении практических задач из разных предметных областей появляется возможность не только лучше понять учебный материал других дисциплин, а также развить мышление и провести исследование в соответствии с поставленной целью. При этом первостепенное значение должно отводиться моделированию, так как модели могут имитировать существенные черты объектов-оригиналов и достаточно точно воспроизводить их поведение.
Создание математических моделей реальных процессов и явлений, а затем проведение эксперимента на математических моделях — одно из перспективнейших направлений использования прикладного математического аппарата при проведении исследовательской деятельности.
Технология математического моделирования лучше всего осваивается на задачах из разных предметных областей: математики, физики, химии, биологии, экономики и др. Предлагаем вашему вниманию задачу из области химии.
Как следует смешивать различные вещества, чтобы получать смеси определенной пробы, концентрации или цены?
С подобным вопросом люди сталкивались не только в старину — и в современном мире человеку зачастую приходится искать ответы на поставленный вопрос. Попытаемся ответить на него с помощью старинного алгоритма Л. Ф. Магницкого, работая по следующему плану:
1) изучить старинный алгоритм на смешивание веществ, предложенный Л. Ф. Магницким;
2) изобразить алгоритм в виде схемы;
3) решить задачи на смешивание двух веществ с помощью алгоритма Л. Ф. Магницкого;
4) провести анализ полученных результатов, найти практически значимые способы применения полученной «полезной модели».
Рассмотрим следующую задачу:
Пусть имеется серебро двух разных проб: одно — 11-й, а другое — 14-й пробы. Сколько какого серебра надо взять, чтобы получить 1 фунт серебра 12-й пробы?
Примечание. В России существовала золотниковая система обозначения пробы на основе русского фунта, содержащего 96 золотников. Проба выражалась весовым количеством благородного металла в 96 единицах сплава. Например, фраза «серебро 11-й пробы» означает, что в 96 единицах некоторого сплава содержится 11 частей серебра. В настоящее время проба означает число частей благородного металла в 1000 частях — по массе — сплава.
Решим данную задачу по алгоритму Л. Ф. Магницкого, предложенному им в его знаменитой книге «Арифметика» (1703 г) [1].
Алгоритм.
Для того, чтобы алгоритм Л. Ф. Магницкого был более понятен на современном языке, изобразим его в виде схемы:
1. Запишите друг под другом две исходные пробы имеющегося вещества (11; 14).
2. Слева от них и примерно посредине запишите пробу смеси (12).
3. Соедините написанные числа черточками. Получится такая схема (рис. 1):
Рис. 1. Исходная математическая схема смесей
4.Меньшую пробу (11) вычтите из пробы смеси (12); полученный результат (1) запишите справа от большей пробы.
5. Из большей пробы (14) вычтите пробу смеси (12); результат (2) запишите справа от меньшей пробы. Схема примет следующий вид (рис. 2):
Рис. 2. Результирующая математическая схема смесей
Ответ. Таким образом исходя из алгоритма Л. Ф. Магницкого получаем: для получения 1 фунта серебра 12-й пробы нужно взять 2 части (0,67 фунта) серебра 11-й пробы и 1 часть (0,33 фунта) серебра 14-й пробы.
Построение математической модели на смешивание двух любых веществ
Обычно сначала строят математическую модель, а затем алгоритм. В данном случае алгоритм нам известен. По заданному алгоритму построим математическую модель. Однако прежде определим, что «дано» и что необходимо «найти» в нашей задаче [2] [3].
Дано: а— проба (или концентрация, или цена) 1-го вещества;
b — проба (или концентрация, или цена) 2-го вещества;
c — проба (или концентрация, или цена) смеси;
Ko l— вес (или объем) смеси в г (л, мл или фунтах и т. д.);
Sm — единицы измерения смеси (фунт, мл, л, г, кг и т. д.).
Найти:
rа — количество частей 1-го вещества для смешивания;
rb — количество частей 2-го вещества для смешивания;
rr — вес (или объем) 1-го вещества в смеси.
Связь:
rr =kol · ra/(ra + rb);
kol — rr — объем 2-го вещества в смеси.
При построении математической модели на смешивание двух любых веществ по алгоритму Л. Ф. Магницкого рассмотрим три случая:
а) при а < с
б) при а > с > b:
в) при а, b, с < 0 или (с > а и с > b): нет решений.
Два первых варианта а), б) имеют решение; изобразили его двумя схемами (при а < с
с > b) и там же записали формулы для вычислений rа, rb. Для варианта в) нет решений (при а, b, с < 0 или (с > а и с > b)).
Представим решение данной задачи математическим методом:
Пусть х частей первого сплава нужно взять, а (1-x) частей — второго сплава. Тогда получим уравнение 11х+14(1-x) =12. Решим его:
11x+14–14x=12
—3x=-2
х=
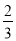
— получено в частях количество первого сплава, тогда второго будет
1-
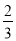
=
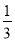
Отсюда следует, что первого сплава потребуется 2 части, а второго — 1 часть. Нетрудно подсчитать массы сплавов по их частям: 0,67 фунта первого сплава и 0,33 фунта второго.
Данный алгоритм обладает свойством массовости, то есть применим для определенного типа задач [4] [5] [6].
Проверим справедливость расчетов с помощью алгоритма при решении другой задачи:
На фабрике два сорта чая — по 40 и 60 рублей за кг. По сколько килограммов чая каждого сорта надо взять для получения 400 кг смеси по 55 руб. за 1 кг?
Решим эту задачу двумя способами: формально выполним расчеты с помощью алгоритма Магницкого (рис. 3).

Рис. 3. Математическая модель алгоритма Магницкого для решения задачи
Получили следующий результат: первого сорта чая потребуется 5 частей или по массе это 100 кг, а второго сорта — 15 частей, то есть по массе 300 кг.
Решим задачу математически:
Пусть х кг чая первого сорта надо взять, тогда (400-х) кг — чая второго сорта. 40х руб. — стоимость взятого чая первого сорта, 60(400-х) руб. — стоимость чая второго сорта. Смесь стоит 55*400 рублей. Получаем уравнение: 40х+60(400-х) =55*400. Решив его, получим х=100 — т. е. столько килограммов чая первого сорта взяли, 400–100=300 кг чая второго сорта взяли.
Полученная в работе «полезная модель» может иметь большое практическое значение, позволит получать смеси определенной пробы, концентрации или цены. Дальнейшее её развитие и целесообразность использования при проведении химических опытов, при составлении смесей разной природы с различным содержанием входящих компонентов и т. п. наглядно представит простоту, удобство и широту применения алгоритма Л. Ф. Магницкого [4] [5] [6].
Литература:
- Магницкий, Леонтий Филиппович Арифметика [Электронный ресурс] // Математическая библиотека. URL: http://math.ru/lib/176 (дата обращения 15.04.2022).
- Математические этюды [Электронный ресурс] // URL: http://www.etudes.ru/ (дата обращения 10.04.2022).
- Олесник, С. Н. Старинные занимательные задачи: / С. Н. Олесник, Ю. В. Нестеренко, М. К. Потапов. — М.: 1985. — 224 с, ил.
- Макарова, Н. В. Системно-информационная концепция курса школьной информатики / Н. В. Макарова // Информатика и образование. — 2002 — № 8 — с. 17–19.
- Сандалова, С. Я. Линейные, разветвляющиеся и циклические алгоритмы: / С. Я. Сандалова. — Хабаровск: ЛИТ, 2003. — 278 с.
- Газизова Н. Н., Зиннурова О. В., Фаттахов Д. А. Построение математической модели смешения веществ // Современные решения научных и производственных проблем в химии и нефтехимии. — 2021, — c.341–351.
Основные термины (генерируются автоматически): математическая модель, алгоритм, задача, проба, проба смеси, смесь, благородный металл, большая проба, вид схемы, старинный алгоритм.
Задачи на смешивание
(смеси, растворы, сплавы) очень часто встречаются на практике, и, как показывает
опыт, вызывают некоторые трудности при решении. Условно разделяют два вида
задач на смешивание:
– задачи на смешивание первого рода;
– задачи на смешивание второго рода.
К задачам первого
роду относятся задачи, в которых дано количество смешиваемых растворов (сплавов)
и их процентные концентрации (пробы), а необходимо найти процентную концентрацию
(пробу) полученной смеси (сплава).
Задачи на смешивание
первого роду ещё иначе называются
задачами на нахождение среднего арифметического, или задачами на среднее взвешенное.
Распространёнными задачами на смешивание первого рода это задачи на нахождение
средней цены, средней температуры, средней скорости, среднего часа и другие. В этих
задачах необходимо определить “цену” смеси по данным “ценам” и количеством отдельных
сортов (слово “цена” тут употребляется в широком смысле). Поэтому, речь идёт
про нахождение среднего арифметического некоторой суммы слагаемых, взятых группами
(говорят также “среднее взвешенное”). Искомым может быть не только среднее
арифметическое, а и цена одного из сортов. Известные задачи на нахождение среднего
арифметического нескольких чисел есть отдельные случаи названных выше задач.
В условиях задач на
растворы фигурирует термин концентрация. Необходимо пояснить значение этого
понятия.
Концентрацией раствора называется количество (масса или объём) растворённого
вещества, которое содержится в некотором количестве (массы или объёму) раствора.
Процентной концентрацией раствора называется выражение в процентном
отношении массы растворённого вещества n к массе
всего раствору m:

Концентрацию раствора
можно выразить не только в процентах, а и в частях. Говорят, например, что
концентрация соли в морской воде равна 1/20 (по массе).
Промилле – это одна тысячная часть числа, или десятая часть процента.
Обозначается так: ‰
‰ = 0,001;
‰ =
0,1%
Сплав можно рассматривать
как раствор, в котором один из компонентов (любой) будет растворителем, а второй
растворённым веществом. Среди задач на сплавы отдельное место занимают задачи
на “пробы”.
Проба – это количество граммов
чистого золота (серебра, латуни и т. д.) в одном килограмме сплава. Так,
золото 875 пробы – это сплав, 1000 г в котором содержится 875 г чистого
золота.
Следует обратить внимание на основную зависимость между количеством
веществ, взятых до смешивания и полученных после смешивания, которую часто применяют,
решая задачи на смешивание. Эту зависимость часто формулируют так:
Количество веществ, взятых до смешивания,
равно количеству этих веществ, полученных после смешивания.
ПРИМЕР:
Если к раствору, в котором находится
m граммов
соли, долить воды, то и в полученном растворе будет m граммов этой соли.
Если смешать два раствора,
в одном из которых будет m, а во втором n граммов соли, то в полученном растворе будет m + n граммов этой соли.
Общая масса смеси всегда
равна сумме масс их составных частей.
В задачах на смешивание (сплавы) обычно речь идёт про массы m1, m2,…, их процентную
концентрацию (пробу) p1, p2,…, а также про массу m и концентрацию (пробу) полученной смеси
(сплава) p. В этом случае всегда правильным считается соотношение:
m1p1 + m2p2
= (m1 + m2)p.
Если в задаче известны
значения m1, m2,
p1, p2 и необходимо определить p, то это задача на смешивание первого рода. Её
можно решить за формуле:

При решении задач
не обязательно пользоваться готовой формулой. Можно постепенно делать расчёты, связанные
с определением массы растворённого вещества,
пользуясь понятием концентрации. Решая задачи на концентрацию кислот и сплавов,
необходимо помнить, что крепость кислоты или спирта обычно выражается в сотых
долях, или процентах, которые в этом случае называются градусами.
Решение задач путём
последовательных вычислений.
ЗАДАЧА:
Сплавили 180
г золота
920-й пробы со 100
г 752-й пробы. Какой пробы получился сплав ?
РЕШЕНИЕ:
В первом слитке чистого золота было 0,92 от 180
г, т. е.
180 × 0,92 = 165,6 (г).
Во втором слитке чистого золота было 0,752 от 100
г, т. е.
100 × 0,752 = 75,2 (г).
Следовательно, в полученном сплаве чистого золота
содержится:
164,6 + 75,2 =
240,8 (г).
Общий вес сплава равен
180 + 100 = 280 (г).
Его проба равна

ОТВЕТ:
Получен сплав 860 пробы.
ЗАДАЧА:
К 2
кг воды прибавили 8
кг 70-процентного
раствора серной кислоты. Определить процентную концентрацию полученного
раствора.
РЕШЕНИЕ:
Сначала определим, сколько в растворе чистой (безводной) кислоты
8 кг × 0,7 = 5,6 кг.
Найдём вес раствора
2 кг + 8 кг = 10 кг.
Теперь найдём процентную концентрацию раствора
5,6 кг : 10 кг = 0,56 =
56%.
ОТВЕТ:
Концентрация получившегося раствора 56%.
Если количество
кислоты выражено не в килограммах, а в литрах, то подобные задачи можно решать
только с помощью таблиц удельных весов растворов серной кислоты.
ЗАДАЧА:
К 2
л воды прибавили 8
л 70-процентного
раствора серной кислоты. Определить процентную концентрацию полученного
раствора.
РЕШЕНИЕ:
В таблице находим удельный вес 70-процентного
раствора серной кислоты. Он равен 1,6.
Следовательно, 8 л этого раствора
весят
1,6 × 8 = 12,8 (кг).
Безводной кислоты в нм содержится
12,8 × 0,7 = 8,96 (кг).
Концентрация раствора равна
8,96 : 14,8 ≈ 0,6 = 60%.
ОТВЕТ: 60%
Задания к уроку 38
