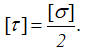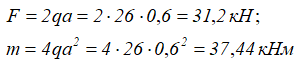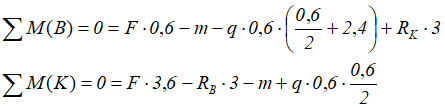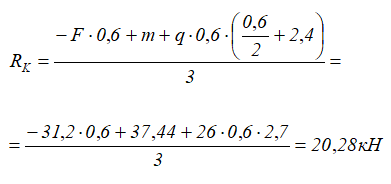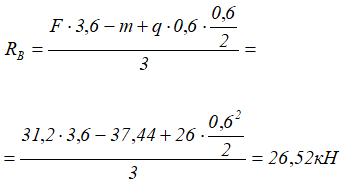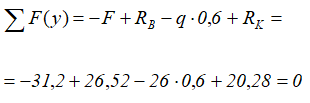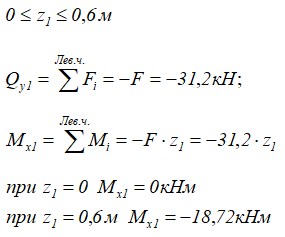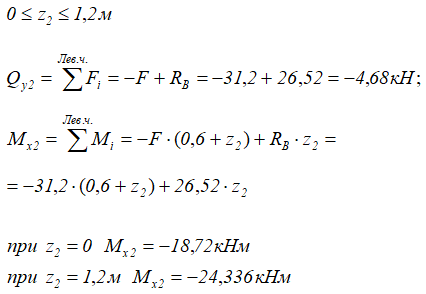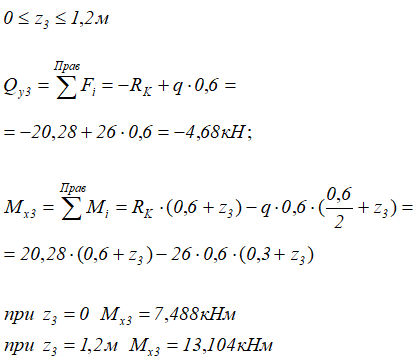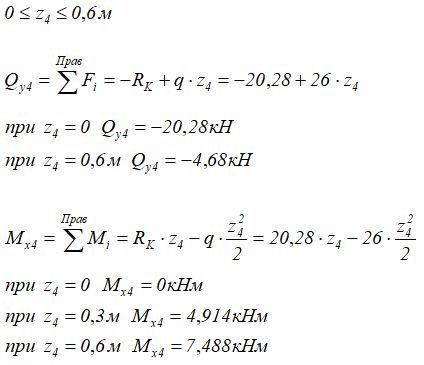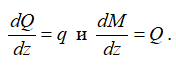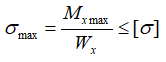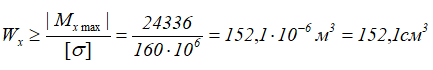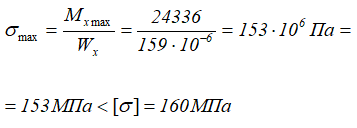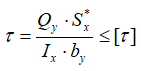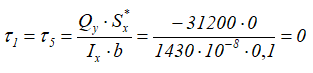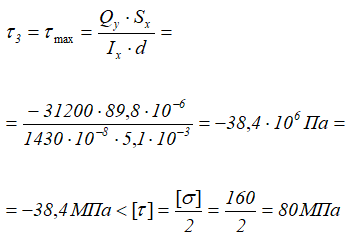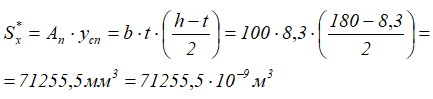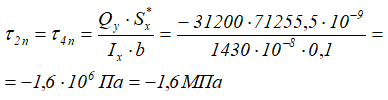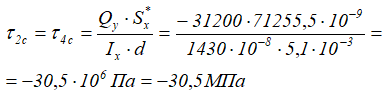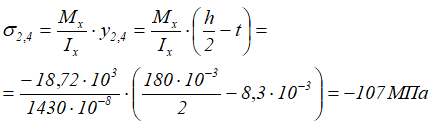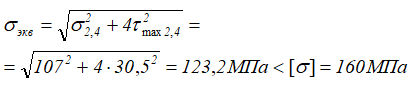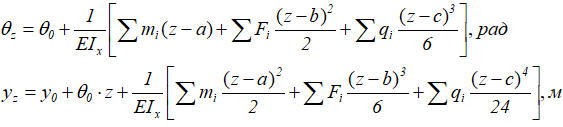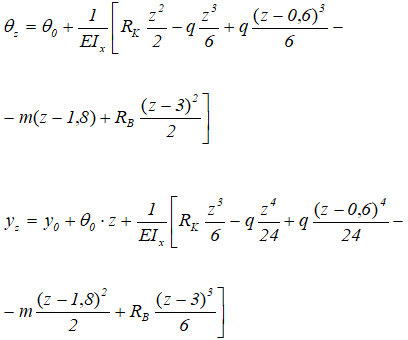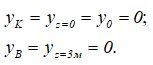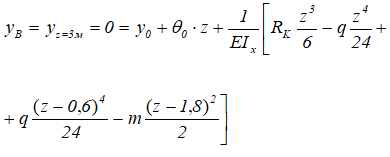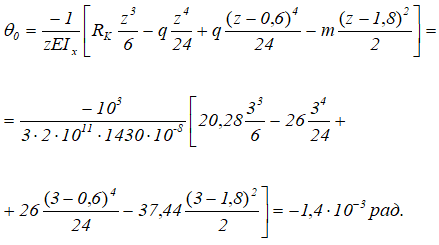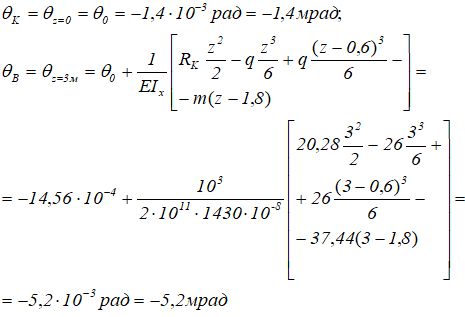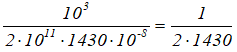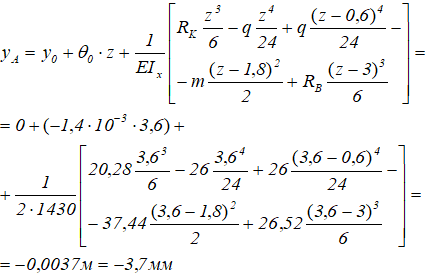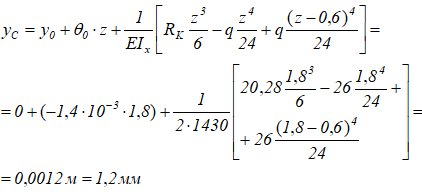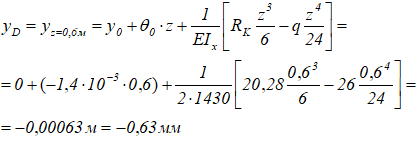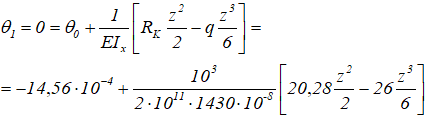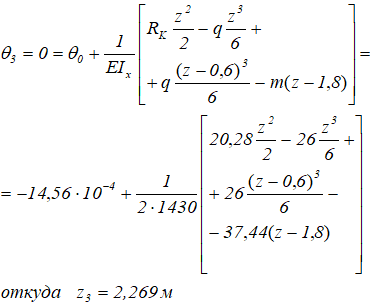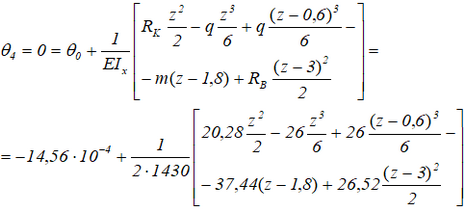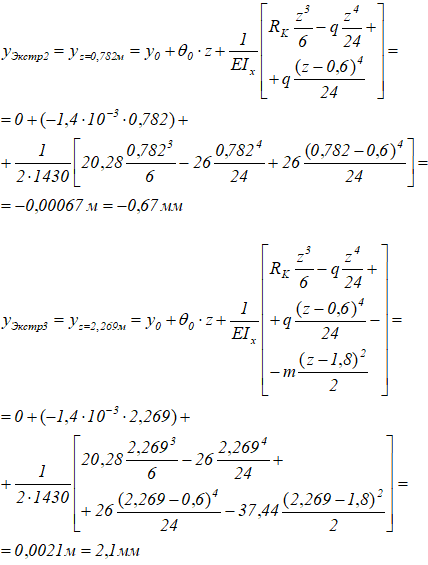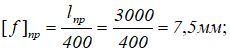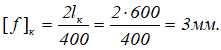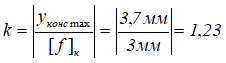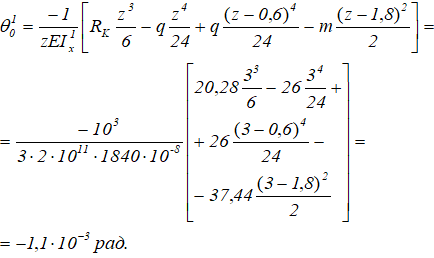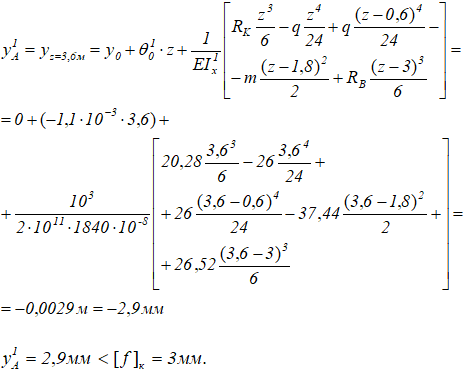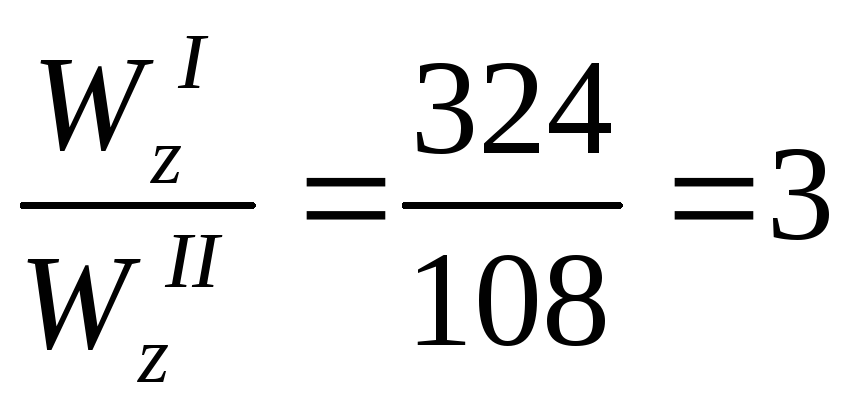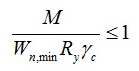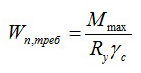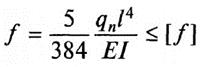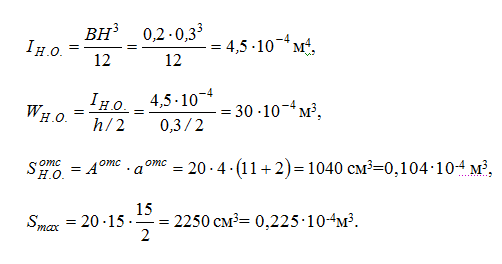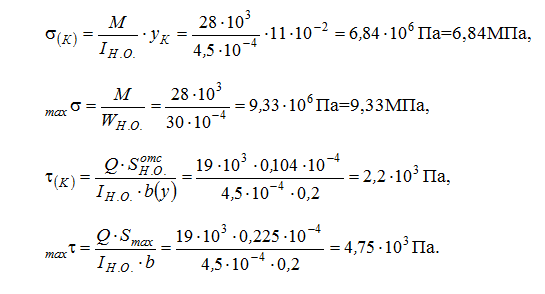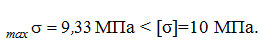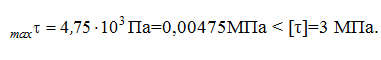Как найти прочность балки

Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки при заданной системе внешних изгибающих нагрузок.

Задача

Выполнить полный расчёт на прочность и проверить жёсткость стальной, двутавровой, статически определимой балки на двух опорах

при следующих данных:
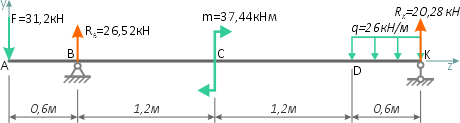
Интенсивность равномерно распределенной нагрузки q=26кН/м, продольный размер a=0,6м, сосредоточенная сила F=2qa, изгибающий момент m=4qa².
Допускаемые нормальные напряжения [σ]=160МПа,
Модуль упругости I рода Е=200ГПа.
Допустимый прогиб балки [f]=l/400.

Другие примеры решений >
Помощь с решением задач >

Последовательность решения задачи
Для расчета балки на прочность

1. Вычерчивается схема нагружения в масштабе, с указанием числовых значений приложенных нагрузок;
2. Строятся эпюры внутренних силовых факторов Q_y и M_x;
3. По условию прочности подбирается двутавровое сечение (№ двутавра) стальной балки:
4. Для балки двутаврового профиля выполняется полная проверка на прочность, приняв
   
5. Проверяется прочность по главным напряжениям в опасных точках сечения по III гипотезе прочности
   
6. По результатам расчетов дается заключение о прочности балки при выбранном сечении.
7. В случае невыполнения условия прочности по главным напряжениям, подбирается новый номер двутавра.

Для расчета балки на жесткость

1. С использованием универсальных уравнений метода начальных параметров (МНП) определяются углы поворота θ над опорами и прогибы в характерных сечениях (2-3 сечения), а также, максимальные прогибы балки в пролете и консольной части;
2. По этим данным, в соответствии с эпюрой M_x, строится линия изогнутой оси балки;
3. Проверяется выполнение условия жесткости балки.
4. Если условие жесткости не удовлетворяется, подбирается новое двутавровое сечение, обеспечивающее необходимую жесткость.

Решение

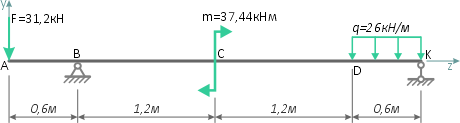
Рассчитаем численные значения силы F и момента m, которые были заданы в виде переменных.

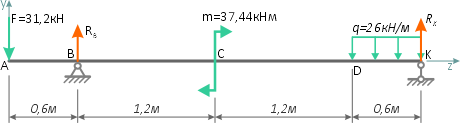
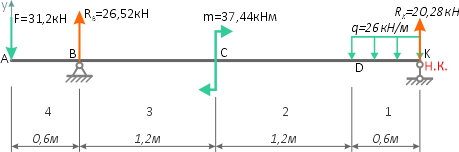
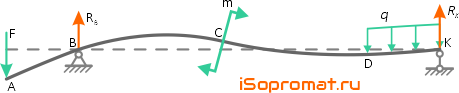
Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.

Показываем оси системы координат y-z и обозначаем характерные сечения балки.

Полный расчет стальной балки на прочность

Определение реакций в шарнирных опорах балки

Направим реакции опор вверх и запишем суммы моментов относительно точек на опорах, нагрузок приложенных к балке

Из составленных уравнений выражаем и находим реакции.
Из первого уравнения

из второго

Положительные значения указывают на то, что произвольно заданное направление реакций вверх оказалось верным.

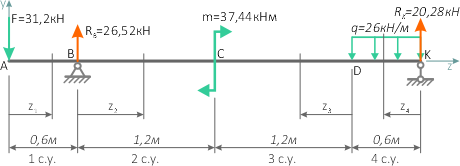
Выполним проверку найденных реакций опор спроецировав все силы на ось y

Равенство суммы проекций сил нулю говорит о том что реакции опор определены правильно.

Более подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

Другие видео

Построение эпюр внутренних силовых факторов

Рассчитаем значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.

Балка имеет 4 силовых участка.

1 участок (AB)

2 участок (BC)

3 участок (CD)

4 участок (DK)

Здесь, значения Q_y на границах участка имеют одинаковый знак, поэтому на этом участке, на эпюре M_x экстремума не будет.

Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки

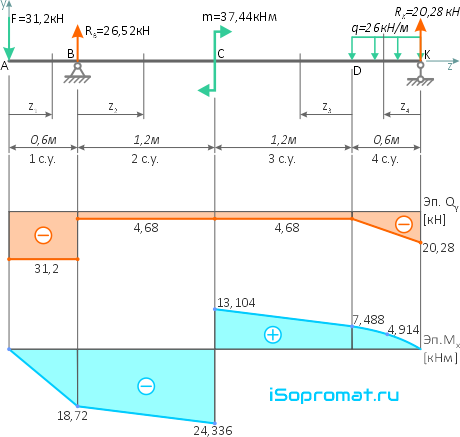
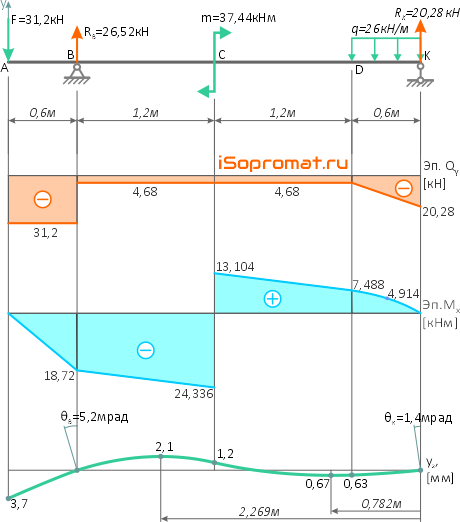
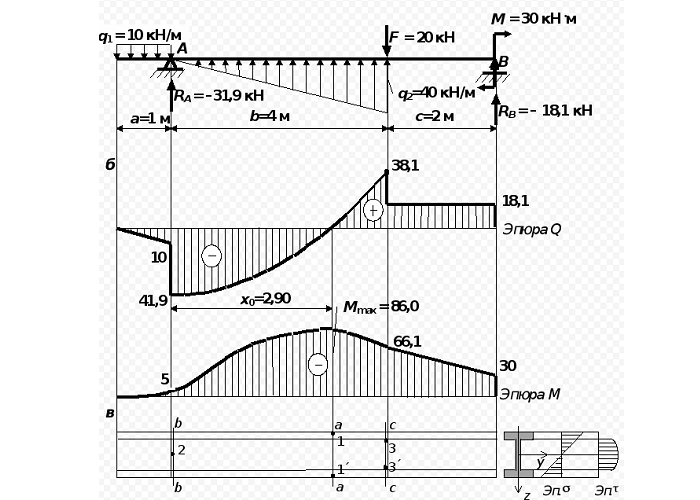
По полученным данным строим эпюры внутренних поперечных сил Q_y и изгибающих моментов M_x.

Проверка построенных эпюр:
— по дифференциальным зависимостям

— в сечениях балки, где приложены сосредоточенные силы, на эпюре Q_y имеются скачки значений на величину соответствующей силы;
— в сечениях балки, где приложены изгибающие моменты, на эпюре M_x скачки значений на величину соответствующего момента.
Все условия выполнены, следовательно, эпюры построены верно.

По эпюрам видно, что опасным является сечение балки в точке C, где:
M_x=M_{x max}=-24,336кНм
Q_y=-4,68кН

Подбор двутаврового сечения балки

Подберем двутаврового сечение балки по условию прочности по нормальным напряжениям

где
M_{x max} – максимальное значение внутреннего изгибающего момента в сечениях балки. Принимается с построенной эпюры M_x;
W_x – осевой момент сопротивления поперечного сечения балки относительно горизонтальной оси x;
[σ] – допустимые нормальные напряжения.

Подробнее о том, как подбирается сечение балки

Выразим и рассчитаем минимально необходимое значение осевого момента сопротивления поперечного сечения балки W_x обеспечивающего её прочность по нормальным напряжениям

По сортаменту прокатной стали выбираем номер двутавра имеющий осевой момент сопротивления близкий к расчетному W_x=152,1см³ в большую сторону.

Это двутавр №18а у которого W_x=159,0см³.

Максимальные нормальные напряжения в сечении

Этот двутавр будет работать при максимальных нормальных напряжениях в крайних слоях опасного сечения балки.

Максимальные нормальные напряжения выбранного номера двутавра не превышают допустимых значений, значит сечение подобрано верно.

Полная проверка на прочность двутаврового сечения

При изгибе тонкостенных прокатных профилей, таких как, например, двутавр или швеллер, в местах соединения стенки с полкой нормальные и касательные напряжения имеют не максимальные, но достаточно большие значения.

Их совместное действие, выраженное в виде главных (эквивалентных) напряжений, может превышать допустимые значения, что будет означать потерю прочности в этих точках поперечного сечения балки.

В отношении главных напряжений неблагоприятным является сечение балки B, в котором максимально значение поперечной силы при значительном изгибающем моменте:

Q_y=-31,2кН
M_x=-18,72кНм

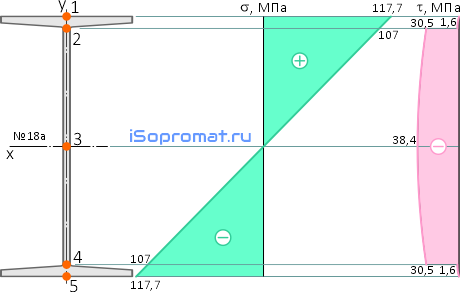
Для полной проверки на прочность построим эпюры нормальных и касательных напряжений в сечении B для выбранного номера двутавра.

Построение эпюр нормальных и касательных напряжений в сечении балки подробно рассмотрено здесь:

Построение эпюры нормальных напряжений

Построение эпюры касательных напряжений

Для выполнения расчетов, из сортамента выпишем необходимые геометрические характеристики выбранного номера двутавра:
Высота сечения
h=180мм;
Ширина сечения
b=100мм;
Толщина стенки
d=5,1мм;
Толщина полки
t=8,3мм;
Осевой момент инерции поперечного сечения
I_x=1430см⁴;
Статический момент сечения
S_x=89,8см³.

Двутавровое сечение по высоте имеет 5 характерных точек: верхнюю (1), нижнюю (5), среднюю (3) и две точки в местах перехода стенки в полку двутавра (2 и 4).

Для построения эпюр, определим значения напряжений в указанных точках сечения.

Нормальные напряжения в сечении балки распределяются по линейному закону, поэтому для построения эпюры достаточно найти максимальные значения

Касательные напряжения в характерных точках сечения рассчитываются по формуле Журавского

где
Q_y — поперечная сила в данном сечении. Принимается с эпюры с учетом знака;
I_x – осевой момент инерции поперечного сечения;
b_y – ширина сечения на уровне рассматриваемой точки;
S_x* — статический момент части сечения, расположенной между уровнем рассматриваемой точки и верхним (нижним) краем сечения.

Рассчитаем значения касательных напряжений

В точках 1 и 5

Так как выше точки 1 и ниже точки 5 площадь сечения равна нулю, то статический момент S_x* для этих точек тоже равен нулю, следовательно

В точке 3

В точке 3 будут максимальные касательные напряжения, т.к. для неё статический момент сечения S_x максимальный при минимальной ширине сечения d

Видно, что прочность сечения по касательным напряжениям обеспечена.

В точках 2 и 4

В точках, где стенка двутавра переходит в полку, будут скачки напряжений, так как на уровне этих точек резко меняется ширина сечения

Рассчитаем значения напряжений в этих точках для стенки (с) и полки (п)

Статический момент полки двутавра

Касательные напряжения в точках 2 и 4 полки

Касательные напряжения в точках 2 и 4 стенки

По этим данным строим эпюры нормальных и касательных напряжений для выбранного номера двутавра.

Рассчитаем величину главных напряжений в точках соединения полки со стенкой двутавра (т. 2 и 4)

Нормальные напряжения в рассматриваемых точках

Эквивалентные напряжения в опасных точках сечения

Как видно, величина эквивалентных напряжений не превышает допустимых значений, следовательно, выбранный номер двутавра удовлетворяет условию прочности и по главным напряжениям.

Полный расчет балки на жесткость

Для того чтобы балка удовлетворяла условию жесткости, линейные перемещения (прогибы) балки y_z не должны превышать заданных допустимых значений [f], т.е. должно выполняться условие жесткости

Расчет перемещений сечений балки

Расчет перемещений сечений балки выполним методом начальных параметров (МНП).

Шаблоны уравнений метода начальных параметров имеют вид:

Здесь:
θ_z — угловое перемещение (угол наклона) рассматриваемого сечения;
y_z — вертикальное линейное перемещение (прогиб) рассматриваемого сечения балки;
z – расстояние от выбранного начала координат балки до рассматриваемого сечения (координата);
θ₀, y₀ — соответственно угловое и линейное перемещения балки в выбранном начале координат (начальные параметры);
E – модуль упругости I рода для материала балки;
I_x – осевой момент инерции сечения балки;
m, F, q – соответственно моменты, сосредоточенные силы и распределенные нагрузки, приложенные к балке (включая опорные реакции и компенсирующую распределенную нагрузку);
a, b – расстояние от начала координат до соответствующих моментов m и сил F;
c – расстояние от начала координат до сечения балки, где начинается действие распределенной нагрузки q.

Подробный пример расчета перемещений сечений балки методом начальных параметров.

Составляем уравнения МНП для заданной балки

Начало координат принимаем в крайнем правом сечении балки, так как оно расположено на опоре.

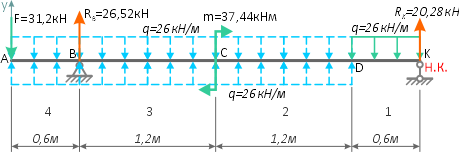
Распределенная нагрузка не доходит до конца балки, поэтому продляем её действие и на этой же длине добавляем компенсирующую нагрузку той же интенсивности но противоположного направления.

Запишем нагрузки в уравнения МНП последовательно по участкам с учетом знаков

Для определения начальных параметров θ₀ и y₀ запишем граничные условия.

На опорах прогибы балки равны нулю, т.е.

Из второго граничного условия, используя уравнение прогибов для точки B определим угол поворота сечения в начале координат θ₀

Откуда, при z=3м

Для построения линии изогнутой оси балки определим углы наклона сечений балки на опорах θ_B, θ_K и прогибы в характерных сечениях y_A, y_C, y_D.

Углы поворота сечений на опорах

Далее, для краткости, сократим дробь перед скобками

Линейные перемещения (прогибы) характерных сечений балки
Прогиб сечения A (y_z при z=3,6м)

Прогиб сечения C (y_z при z=1,8м)

Прогиб сечения D (y_z при z=0,6м)

Расчет максимальных прогибов балки

Экстремумы прогибов балки будут в точках, где угол наклона сечения балки равен нулю.

Для их определения, приравниваем к нулю уравнения углов наклона сечений по каждому участку балки, откуда определяем координаты z экстремумов прогибов на участке (если они есть).
1 участок (KD).

Уравнение решений не имеет (т.е. экстремумов на участке нет), это значит, что максимальный прогиб на этом участке будет на его левой границе (в сечении D), так как правая точка участка расположена на опоре.

2 участок (DC).

То есть, экстремум прогибов на втором участке будет на расстоянии z₂=0,782м от начала координат.

3 участок (CB).

Экстремум прогибов на третьем участке в сечении, на расстоянии z₃=2,269м от начала координат.

4 участок (BA).

Данное уравнение решений также не имеет, следовательно, максимальный прогиб на конце консоли, так как на правой границе участка – опора.

Значения максимальных прогибов балки на втором и третьем участках определяем из соответствующих уравнений прогибов для найденных значений z.

По полученным данным строим линию изогнутой оси балки в соответствии с эпюрой изгибающих моментов M_x и с указанием углов поворота сечений на опорах.

Проверка балки на жесткость

Проверяем балку на жесткость, сравнивая по модулю максимальные значения прогибов y_max в пролёте и на консольной части с допустимыми [f].

Балка считается жесткой, если прогибы её сечений не превышают допустимых значений, т.е.

Рассчитаем абсолютные значения допустимых прогибов заданной балки:
В пролете

На консольной части

Для проверки на жесткость сравниваем величину рассчитанных ранее максимальных прогибов сечений балки с соответствующими допустимыми значениями.

В пролете

На консоли

Как видно, максимальный прогиб на конце консольной части балки превышает соответствующее допустимое значение, следовательно, балка не удовлетворяет заданному условию жесткости.

Жесткость балки можно увеличить до требуемого значения путем увеличения момента инерции её сечения, т.е. подбором сечения большего размера.

Подберем двутавр другого номера, который будет обеспечивать необходимую жесткость балки.

Определяем, во сколько раз надо уменьшить величину максимального перемещения сечения.

Тогда, расчетный момент инерции нового сечения балки

По сортаменту выбираем двутавр №20 с осевым моментом инерции сечения I_x=1840см⁴.

Выполняем проверку:

Для начала требуется пересчитать угол наклона сечения балки в начале координат.

Рассчитываем прогиб сечения A с новым размером сечения

Условие жесткости выполняется.

Таким образом, двутавр №20 обеспечивает необходимую прочность и жёсткость заданной балки.
Полный расчет заданной балки на прочность и жёсткость выполнен.

Другие примеры решения задач >

Информация

Балка занимает роль основополагающего элемента в несущей конструкции. Её функция приравнивается к стержню всей конструкции, который прочно закрепили. При строительстве какого-либо сооружения очень важно осуществить грамотный расчет балки на прогиб и исключить допущение ошибки в расчетах. Прежде всего расчет требуется для определения того, на сколько балка деформируется в процессе эксплуатации сооружения. Если при расчете показатель деформации находится в пределах нормы, то можно определить нужные показатели будущей балки (сечение, материал, размер и так далее).

Делая расчет балки на прочность, необходимо четко знать виды материала, из которого изготавливаются балки (сталь, дерево, бетон, алюминий, стекло и медь). Далее нужно обратить внимание на то, что типы нагрузок, как и их схемы также различаются. Так, например, распределенная нагрузка означает, что давление оказывается не на одну точку, а распределено по всей площади балки. Сосредоточенный тип нагрузки характеризует направленность давления на один небольшой участок (точку) балки.

Вместе с типами, существуют четыре схемы нагрузок:

• Шарнир-Шарнир
• Заделка-Шарнир
• Заделка-Заделка»
• Свободный конец

Наш онлайн калькулятор позволяет сделать расчет, комбинируя все виды балок, типы и схемы нагрузок, при этом абсолютно исключив вероятность допущения ошибки в процессе расчета. Обычно рассчитывают деревянные балки, а также металлические. В процессе вычисления показателя определяется сумма сил, воздействующих на балку, которые направлены перпендикулярно конструкции. Расчет деревянной балки на прогиб осуществляется с учетом материала, т.е. учитывают вид древесины, её гибкость и многие другие параметры, также важно учесть форму сечения балки и нагрузка какого вида оказывается на балку. Сравнивая с расчетом балки из древесины, расчет металлической балки на прогиб существенно отличается, поскольку важное внимание уделяют виду соединения: электросварка, заклепки, болты и другие виды соединений.

Все перечисленные выше нюансы позволяют понять, что расчет балки на прогиб – крайне ответственный этап в процессе стройки какого-либо объекта. От него зависит надежность, долговечность и целостность всей конструкции. Наш калькулятор позволит Вам быстро и безошибочно провести предельно точный расчет.

Какие преимущества даёт наш калькулятор?

• экономия времени;
• исключение допущения ошибки;
• предельная точность в расчете;
• приятный и понятный интерфейс;
• дополнительный справочный материал.

Таким образом, созданный нами онлайн калькулятор является незаменимым инструментом в процессе работы специалиста, которому необходимо осуществить расчет балки или любого другого важного показателя.

Формула
(5.13) решает вопрос о величине и распределении
нормальных напряжений по сечению. Она
выведена в предположении наличия чистого
изгиба, когда сечения остаются плоскими.

Исследования
показали, что когда поперечная сила
не равна нулю, сечения не только
поворачиваются, но и несколько искривляются
под влиянием касательных напряжений.
Однако это искривление для двух смежных
сечений таково, что оно не меняет
установленного выше закона распределения
деформаций волокон, заключающихся между
этими сечениями. Поэтому формула (5.13)
может быть применена и в том случае,
когда поперечная силане равна нулю.

Для проверки
прочности балки по нормальным напряжениям
необходимо найти наиболее напряженные
растянутые или сжатые волокна сечения.
Для этого необходимо применить формулу
(5.13) к опасному сечению, т.е. подставить
в нее вместо изгибающего момента его
наибольшее значение
,
которое назовем расчетным изгибающим
моментом, а вместоподставить
расстояние от нейтральной линии сечения
до наиболее удаленных от нее точек.
Тогда для наибольшего нормального
напряжения получаем формулу:

.
(5.14)

Обычно эту формулу
преобразовывают, деля числитель и
знаменатель на
:

.

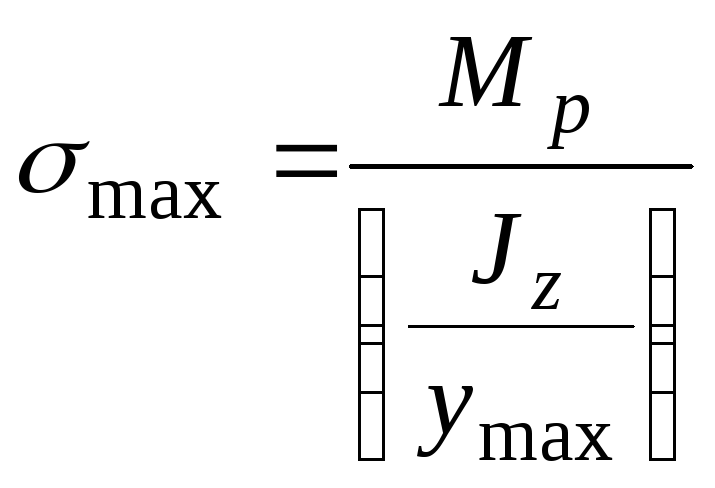
Величина
называется осевым моментом сопротивления
сечения и обозначается буквой.
Измеряется осевой момент сопротивления
единицами длины в третьей степени,
например (см³).
Физический смысл момента сопротивления
состоит в следующем: чем больше
,
тем больший изгибающий момент может
принять на себя балка, не подвергаясь
опасности разрушения. Таким образом,
величина момента сопротивления
характеризуетвлияние
формы и размеров поперечного сечения
балки на ее способность сопротивляться
внешним нагрузкам, не разрушаясь.

Максимальные
напряжения, действующие в балке, могут
быть найдены из выражения

.
(5.15)

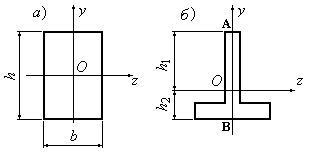
При симметричном
относительно нейтральной линии сечении,
например, прямоугольном, расстояния до
крайних растянутых и сжатых волокон
одинаковы и такое сечение имеет одно
вполне определенное значение момента
сопротивления относительно оси
.
Так, при высоте прямоугольника (Рис.5.7),
равной

и
.

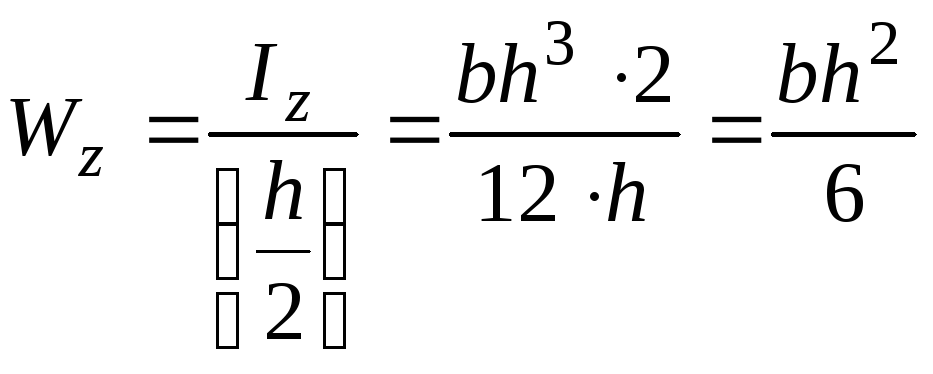
Рис.
5.7

Если сечение
несимметрично относительно нейтральной
линии – тавр, мы получим два момента
сопротивления: один для волокон А
(Рис.5.7,б):
и другой для волокон В:.
Теперь в формулу (5.15) следует вводить:
при вычислении напряжений в точке А и

при вычислении напряжений в точке В.

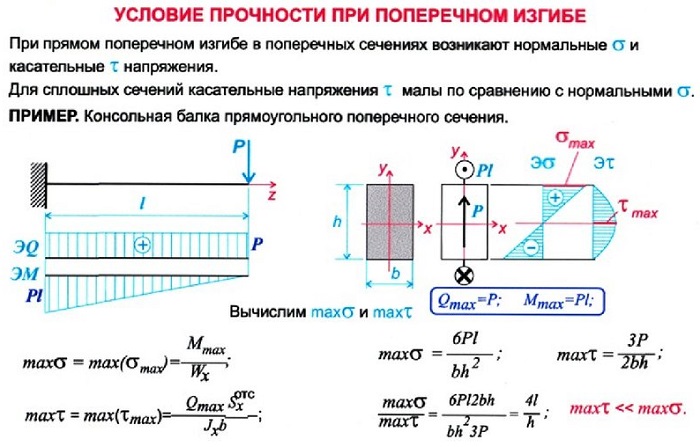
Запишем условие
прочности при изгибе. Это условие
выражает ту мысль, что наибольшее
действительное напряжение должно быть
не больше допускаемого:

(5.16)

Условие
прочности (5.16) решает три задачи:

1. Задача проверочного
расчета, заключающаяся в вычислении
максимальных действительных напряжений
в изгибаемой балке и сравнении этих
напряжений с допускаемым. Если
действительные напряжения не превышают
допускаемой величины, считается, что
прочность не нарушена и конструкцию
можно эксплуатировать дальше.

2.
Задача подбора величины допускаемой
нагрузки. В результате решения этой
задачи определяется допускаемое значение
для расчетного изгибающего момента, а
затем находятся допускаемые значения
самих внешних нагрузок, функцией которых
является расчетный изгибающий момент:

.
(5.17)

3.
Задача проектировочного расчета,
заключающаяся в определении размеров
поперечного сечения балки при известном
расчетном изгибающем моменте и известном
допускаемом напряжении:

.
(5.18)

Здесь:
требуемый момент сопротивления.

При
расчете балок на прочность следует
различать два случая. Первый случай,
наиболее часто встречающийся при изгибе,
когда материал одинаково сопротивляется
растяжению и сжатию; в этом случае
допускаемые напряжения для того и
другого вида деформации равны между
собой:

.

Тогда
при симметричном сечении безразлично,
проверять ли прочность растянутых или
сжатых волокон, ибо для тех и других
момент сопротивления
и наибольшие действительные напряжения
будут иметь одну и ту же величину. При
несимметричном сечении в формулу (5.16)
вместонадо подставить меньшее значение изи;
оно будет относиться к наиболее удаленному
волокну.

Второй
случай имеет место, когда материал балки
неодинаково сопротивляется растяжению
и сжатию; тогда вместо одного условия
прочности мы получаем два: одно -–для
растянутых, другое – для сжатых волокон:

;
.
(5.19)

В
зависимости от того, чему лучше
сопротивляется материал, что больше

⁺или,
приходится соответствующим образом
конструировать сечение, выбирая его
форму и размеры так, чтобыиудовлетворяли условию прочности.

Рассмотрим
несколько примеров определения моментов
сопротивления сечений и расчета балок
на прочность.

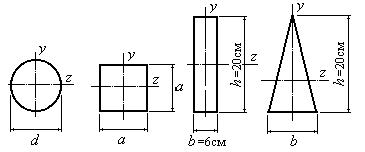
Пример 5.2.
У которой из фигур (Рис.5.8), имеющих
одинаковую площадь, момент сопротивления
относительно оси
,будет
наибольшим?
Определить
наибольший момент сопротивления.

Рис.5.8

Решение:

В
примере 4.8 были найдены моменты инерции
каждого из сечений относительно
центральной оси сечения
.

Найдем
моменты сопротивления:

для
сечения круглой формы:

см³;

для
сечения квадратной формы:

см³;

для
сечения прямоугольной формы:

см³;

для
сечения треугольной формы:

см³.

Таким
образом, наибольший момент сопротивления
оказался у сечения прямоугольной формы:
см³.

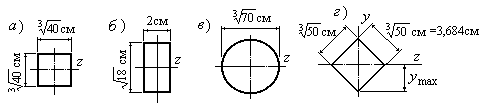
Пример
5.3.На рисунке изображены поперечные
сечения 4х балок
(Рис.5.9), изготовленных из одинакового
материала. Которая из балок является
наиболее прочной?

Рис.5.9

Решение:

Наиболее
прочной будет балка, у которой момент
сопротивления относительно оси
будет наибольший. Вычислим моменты
сопротивлениядля каждого из сечений.

Квадратное сечение.

см³.

Прямоугольное
сечение.

см³.

Круглое сечение.

см³;

Ромбовидное
сечение. Рассматриваемое сечение
получилось путем поворота горизонтальной
оси квадратного сечения на 45⁰. В
результате момент инерции сечения
относительно осине изменился и может быть вычислен как
для квадратного сечения:

см⁴.

Осевой
момент сопротивления найдем, разделив
момент инерции на
:

см³.

Таким
образом, наибольший момент сопротивления
оказался у круглого поперечного сечения:
см³.
Следовательно, балка с круглым поперечным
сечением обладает наибольшей прочностью.

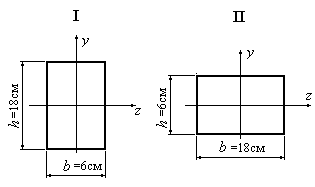
Пример
5.4.Как изменится прочность балки,
если поперечное сечение будет переведено
из положения “I” в положение “II”
(Рис.5.10)?

Рис.5.10

Решение:

1.
Вычислим осевой момент сопротивлениядля положения сеченияI :

см³.

2.
Вычислим осевой момент сопротивлениядля положения сеченияII:

см³.

3.
Найдем отношение осевых моментов инерции
для положения сеченияI

и
II:

Таким
образом, при переводе сечения из положения
I в положениеII
прочность балки уменьшается в 3
раза.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации. 

Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению. 

Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.

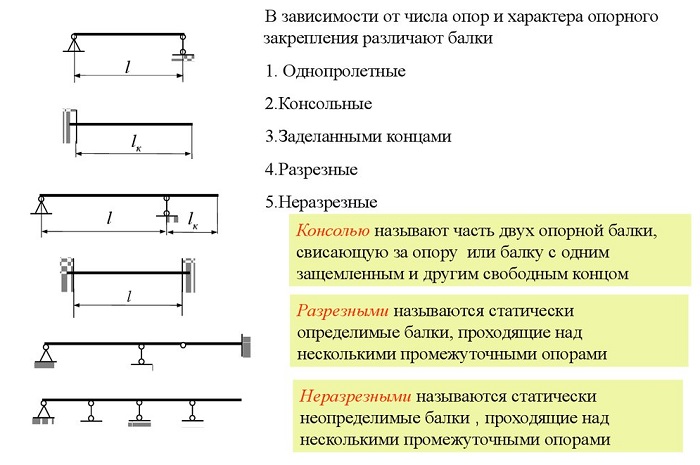
Виды балок

При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.

Виды балок:

1. Деревянные – их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.

2. Металлические – такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.

Прочность и жесткость балки

При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.

На эти параметры влияют следующие факторы:

• величина наружных нагрузок, их положение;

• параметры, характер, нахождение поперечного сечения;

• продольные величины;

• материал;

• число опор, метод их закрепления.

Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты. 

Построение эпюр балки

Эпюра распределения величины нагрузки на объект:

Расчет на жесткость

Алгоритм исчисления:

В формуле обозначены:

• M – max момент, возникающий в брусе;

• W_n,min – момент сопротивления сечения (табличный показатель);

• R_y – сопротивление на изгиб (расчётный показатель);

• γ_c – показатель условий труда (табличный показатель).

Такой расчет не трудоемок, но для более верного значения требуется следующее:

• рабочий план объекта;

• определение характеристик балки, характер сечения;

• определение max нагрузки, воздействующей на брус;

• оценка точки max прогиба;

• проверка прочности max изгибающего момента.

Расчет моментов инерции и сопротивления сечения

Алгоритм исчисления:

Где:

• J – момент инерции сечения;

• W – момент сопротивления.

Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.

Нахождение максимальной нагрузки и прогиба

Формула для вычисления:

Здесь обозначены:

• q – нагрузка равномерно-распределенная;

• E – гибкость (табличный показатель);

• l – длина;

• I – момент инерции сечения.

Нагрузки учитываются статические и периодические.

Расчет на прогиб и его особенности

Он необходим для всех перекрытий при высоких эксплуатационных нагрузках. 

При применении соответствующих коэффициентов, придерживаются следующего:

• балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;

• балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;

• нагрузка консольного типа;

• воздействие комплексной нагрузки.

Пример расчет балки на прогиб

Рассмотрим задачу из курса сопромата.

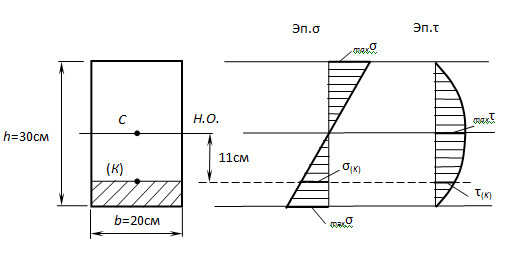
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм. 

Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.

Решение.

Чтобы узнать σ_(К), τ_(К), σ_max, τ_max
определяем значение осевого момента инерции общего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсеченного ряда и статического момента середины сечения S_max:

Из этого следует:

Определение прочности по нормальному напряжению:

Определение прочности по касательному напряжению:

Задача решена.

При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки. 

Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.