1.3.1. Расчет винтовых цилиндрических пружин
Основными
геометрическими параметрами винтовых
цилиндрических пружин являются:
d– диаметр проволоки;DН– наружный диаметр пружины;DС– средний диаметр пружины;– индекс пружины; α – угол подъема витков;L– длина развернутой
пружины;t– шаг пружины.
Рис. 1.2. Схема
нагружения пружины
При
известных размерах пружины ее проверяют
на прочность
|
|
(1.25) |
где τ – расчетное
максимальное напряжение в поперечных
сечениях витков пружины, МН/м2(МПа); [τ] – допускаемое
напряжение для проволок пружины, МН/м2(МПа); Р – максимальная сила, сжимающая
или растягивающая пружину, Н; к –
коэффициент, учитывающий влияние на
величину напряжений кривизны витков и
поперечной силы. Значение коэффициента
к в зависимости от индекса пружиныСпринимают из таблицы:
|
С |
4 |
5 |
6 |
8 |
10 |
12 |
|
к |
1,37 |
1,29 |
1,24 |
1,17 |
1,14 |
1,11 |
Зная
конструктивные размеры пружины,
определяют диаметр проволоки, мм:
|
|
(1.26) |
После
нахождения диаметра проволоки dустанавливают средний и наружный диаметр
пружины, мм:и
.
При
расчетах различают следующие силы,
действующие на пружину: Р1–
усилие, при котором происходит
предварительная деформация; Р2–
рабочая деформация (соответствует
наибольшему перемещению подвижного
звена в механизме); Р3– максимальная
деформация (допускаемая).
Обычно
пружина устанавливается с действующей
на нее начальной нагрузкой (Н): Р1= (0,1 – 0,5)Р2.
Максимальная
сила пружины (Н)
|
|
(1.27) |
При
изменении силы пружины от Р1до
Р2жесткость (Н/мм) определяют:
|
|
(1.28) |
где h– рабочий ход пружины, величина которого
назначается или вычисляется по условиям
работы механизма.
Жесткость
одного витка пружины:
,
Число
рабочих витков пружины:
,
Полное
число витков пружины:
,
где n2– число опорных витков,n2= 1,5 – 2,0
Деформация
пружины, мм:
|
|
(1.29) |
Подставив
в эту формулу вместо Р силы Р1,
Р2, Р3соответственно получим
деформацииF1–
предварительную,F2– рабочую иF3–
максимальную. Максимальная деформация
одного витка пружины, мм:
Шаг
пружины в ненагруженном состоянии (мм)
определяют:
для пружин сжатия
,
для пружин растяжения
.
Высота
пружины при максимальной ее деформации,
мм:
|
|
(1.30) |
где n3– число зашлифованных витков.
Высота
пружины в свободном состоянии, мм:
для
пружин сжатия
;
для
пружин растяжения
1.3.2. Привод валковой дробилки.
Привод
валков осуществляется ременной передачей
каждого валка (рис. 1.3) или одного валка,
а второго – зубчатой передачей от
первого. В дробилках во время работы
расстояние между валками постоянно
изменяется на величину деформации
пружины. Вследствие этого уменьшается
межосевое расстояние в ременной передаче
и увеличивается межцентровое в зубчатой
паре.
Рис. 1.3. Типы приводов
дробилки:
а – ременная
передача, б – индивидуальный привод.
Ременная
передача. В большинстве дробилок
применяется плоскоременная передача,
в паре подвижного валка – натяжной
ролик, который предохраняет ремень от
проскальзывания.
Площадь
сечения ремня определяется по формуле
|
|
(1.32) |
где Р – окружное
усилие, Н; F– площадь
ремня, м2; [k0]
– допускаемое полезное напряжение,
Н/см2, зависимое от
и от типа ремня;C-
коэффициент,C=C0·Cα·CV·CN;C0– коэффициент
учитывающий натяжение ремня,C0= 0,8 – 1,0;Cα– коэффициент, учитывающий влияние угла
обхвата,Cα= 0,91 – 0,94;CV– скоростной коэффициент,CV= 0,88 – 0,95;CN
– коэффициент динамичности режима
и нагрузки,CN= 0,6 – 0,7.
При
установке натяжного ролика диаметр его
,
где Dmin– минимальный диаметр шкива, м.
Расстояние
(м) между роликом и малым шкивом принимают:
.
Угол
обхвата ролика β > 600.
Зубчатые
передачи, как правило, устанавливают
открыто. Высота зуба удлинена на
деформации пружины. Зуб абразивно
изнашивается в двух направлениях – от
перемещения зуба в горизонтальной и
радиальной плоскостях и в зацеплении
зуба вследствие наличия неодинаковой
скорости скольжения.
Напряжения
в зубе определяются по формуле
|
|
(1.33) |
где N– передаваемая мощность, кВт;k– коэффициент нагрузки,k= 1,3 – 1,5;m– модуль, см;b– ширина зуба, см;z–
число зубьев колеса;n–
число оборотов в минуту;y– коэффициент формы зуба.
После
определения напряжений в основании
зуба проводят проверку напряжения для
удлиненного зуба (МПа) по формуле
Задаваясь
желаемым сроком службы Т зубчатого
колеса, определяем его модуль из условия
изнашивания, см:
|
|
(1.34) |
Здесь
μ – коэффициент трения для открытой
зубчатой передачи, μ = 0,1 – 0,2; ψ –
коэффициент ширины зуба, ψ =
;z– число зубьев шестерен;
Т – продолжительность изнашивания в
часах.
|
|
(1.35) |
где Киз–
коэффициент износостойкости материала,
мм3/Вт·ч (для сырых углеродистых
сталей Киз= 0,037; для стального
литья Киз= 0,008; для никелевых
улучшенных сталей Киз= 0,018);Uпр– предельный износ зубьев,Uпр= 0,2m; α – угол обхвата.
Соседние файлы в папке СДМ
- #
- #
- #
- #
- #
- #
- #
- #
Пружины сжатия навивают с просветом между витками. Для образования опорной поверхности, перпендикулярной к продольной оси пружины, крайние витки поджимают и сошлифовывают (см. рис. 18.1, а и рис. 18.2). Пружины растяжения обычно навивают без просвета между витками. Для соединения с другими деталями на концах пружины образуют зацепы в виде изогнутых витков (см. рис. 18.1, в).

Рис. 18.2. Пружина сжатия с поджатыми и сошлифованными крайними витками
Из рассмотрения равновесия отсеченной части пружины (см. рис. 18.2) можно установить, что в сечении витка действует крутящий момент 

Условие прочности для пружин из проволоки круглого сечения имеет вид:

где 




Зазор между витками во избежание соприкосновения их при сжатии пружины 
На рис. 18.2 показан шаг пружины Р.
Для пружин растяжения с зацепами в виде отогнутых витков значения 

При проектировочном расчете диаметр проволоки, из которой свита пружина, определяют по формуле

После определения диаметра по формуле окончательное значение 
Выбирая индекс пружины, следует придерживаться следующей рекомендации: при диаметрах 


Конические пружины сжатия из проволоки круглого сечения (см. рис. 18.1, г) рассчитывают на прочность по формуле (18.1) по витку с наибольшим диаметром.
Условие прочности для пружин с витками прямоугольного сечения:
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = – k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем – в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
Пружиной называют объект, способный с помощью деформации, вызванной внешними силами, накапливать и сохранять упругую потенциальную энергию, а после прекращения их воздействия восстанавливаться до прежнего состояния. Реально существующие пружины абсолютно точно восстановить свою прежнюю форму не в состоянии т.к. при внешнем воздействии в той или иной степени нарушается структура их материала, в результате чего возникают так называемые пластичные деформации. Чем они меньшее, тем более качественным считается изделие.

Какие бывают типы пружин
В первую очередь их принято делить на предназначенные для работы в режиме растягивания и предназначенные для работы в режиме сжатия.
Пружины растяжения при действии на них полезной нагрузки растягиваются. Они не нуждаются в жёстком захвате и, как правило, имеют нулевой шаг, т. е. витки у них прилегают вплотную друг к другу. В обычной жизни подобные изделия большинство людей может заметить, проходя через двери с механическим механизмом закрытия или при пользовании пружинными весами. В технике пружины растяжения используются для соединения элементов, положение которых меняется при их работе. В качестве примера можно привести завес рычагов.
Пружины сжатия под нагрузкой по длине уменьшаются. Для правильной работы их концы должны быть жёстко зафиксированы. Витки проволоки в свободном состоянии не касаются друг друга, т.к. им необходим некоторый промежуток, чтобы под внешней нагрузкой было куда перемещаться. В качестве примера использования таких изделий можно привести пружину в шариковой ручке или автомобильную подвеску.
В технике широкое применение находят и другие типы пружин: пружины кручения (в точных весах), плоские спиральные (как заводные в часах), плоские (в автомобильных рессорах), тарельчатые (в грузовых весах). В некотором роде пружинами можно назвать некоторые изделия из резины и из других полимерных эластичных материалов. Все они работают по одной и той же схеме – запасают кинетическую энергию в виде энергии упругости, а затем, когда нагрузка ослабнет или вовсе перестанет действовать, её возвращают.
Основные характеристики пружин
Зная материал и диаметр проволоки, форму её сечения, длину и диаметр пружины, как единого целого, можно с очень высокой достоверностью судить, насколько пружина может сопротивляться попыткам деформировать себя. Существуют также другие характеристики, от которых работоспособность пружины может зависеть очень серьёзно. К таковым относятся усталость материала проволоки, шаг витка, индекс пружины и т. д.
Материал и сила жесткости пружины
Зависимость между этими характеристиками пружин индивидуальная и вычисляется опытным путём. Чаще всего для изготовления металлических пружин используют высокоуглеродистые стали, легированные ванадием, кремнием и марганцем. Для изделий, предназначенных для длительной работы в агрессивных средах используют нержавеющую сталь, оловянносвинцовую, бериллиевую и кремнемарганцевую бронзу, различные чугуны, а также некоторые из титановых сплавов.
Небольшие пружины изготавливают из уже закалённой проволоки. Крупные изделия делают из отожжённой стали, а закалку проводят уже после формовки.
Как связана жесткость пружины с диаметром и формой сечения проволоки, из которой она сделана
Чем он меньше, тем пружина более эластична. Способность запасать энергию с уменьшением диаметра тоже становится меньше. Пружины сжатия, как правило, делают из более толстой проволоки.
Следует отметить, что не всегда сечение проволоки для пружин бывает круглым, в пружинах сжатия оно иногда бывает уплощённым. Это обеспечивает лучшую посадку одного витка на другой и делает конструкцию более устойчивой.
Длина и диаметр
Определение
Под длиной пружины понимают её длину в свободном, недеформированном состоянии.
Также следует различать длину собственно изделия и длину проволоки, из которой оно сделано. Это две совершенно разные величины. Не малое значение имеет число витков. В пружинах сжатия, чем их больше, тем выше вероятность соскальзывания изделия с опоры и, как следствие, выхода детали из строя.
О понятии жесткости. Жесткость пружины: формула
Определение
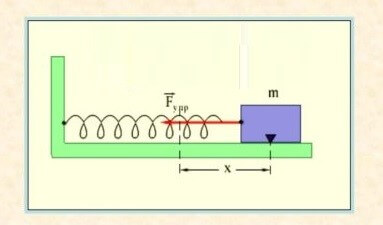
Жёсткостью пружины называют коэффициент, который связывает силу прилагаемую к ней с удлинением или сжатием.
Посмотрите на закон Гука.
Формула
Fупр = –kx
Зако́н Гу́ка — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе.
k – это и есть жёсткость пружины.
Fупр — сила жесткости или упругости пружины.
x — расстояние, на которое изменилась длина изделия после того как та была уравновешена.
Минус в формуле свидетельствует о том, что сила F имеет по сравнению с нагрузкой противоположное направление.
Закон Гука является одним из основных законов физики.
Как найти жесткость пружины? Формулу из выше приведённого уравнения понять достаточно легко:
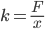
Коэффициент жесткости пружины можно вычислить и экспериментальным путём. Для этого нужно подвесить на вертикально закреплённую пружину груз с известной массой.
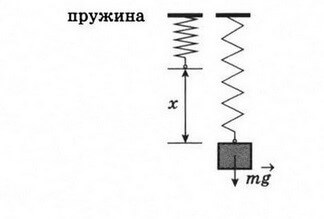
Имеем два уравнения:
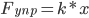
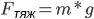
Т. к. Fупр =Fтяж, получаем
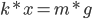
Отсюда разделив обе части уравнения на x, найдём, что жёсткость равна
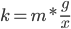
Массу самой пружины считаем равной нулю. Для исключения случайных ошибок проводим несколько измерений с грузами разной массы.
Нет времени решать самому?
Наши эксперты помогут!
Как рассчитать жесткость цилиндрической пружины
В плоской пружине в момент её изгиба расстояния между молекулами, находящимися в одном месте уменьшаются, а в другом увеличиваются. Сила электромагнитных межмолекулярных связей стремится вернуть изделие в прежнее положение.
С цилиндрической пружиной всё несколько иначе. В ней энергия запасается не из-за деформации изгиба, а благодаря скручиванию проволоки вдоль своей оси навивания.
Давайте мысленно увеличим выполненное перпендикулярно её оси плоскостью сечение проволоки. Это нам позволит не учитывать спиральную форму изделия. Разобьём весь объём проволоки на очень много касающихся друг друга своими торцами цилиндров. Их диаметр совпадает с диаметром проволоки, а высота бесконечно мала. Торцам не дают разъединится действующие между ними межмолекулярные силы. Именно они препятствуют деформации.
Когда пружина растягивается или сжимается, цилиндры вынуждены вращаться друг относительно друга в противоположных направлениях вокруг общей оси. В каждом из сечений запасается некоторая энергия. Отсюда легко сделать вывод, что чем проволока длиннее, тем больше энергии такая пружина способна запасти. Увеличение проволоки по диаметру тоже способствует возрастанию её энергоёмкости.
Окончательная формула для жёсткости цилиндрической пружины такова:
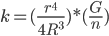
Буквой R у нас обозначен радиус цилиндра пружины, n – количество витков проволоки, r—её радиус, G – коэффициент, индивидуальный для материала проволоки.
Чтобы по данной формуле сделать расчёт жёсткости, достаточно просто подставить вместо букв, обозначающих величины, их числовые значения.
















