Свойство материалов и конструкций оказывать в определенных пределах сопротивление разрушению или заметному изменению формы.
По способу приложения нагрузки различают статическую и динамическую прочность.
Поскольку именно динамические нагрузки наиболее часто встречаются на практике, то говоря о прочности часто имеют в виду именно динамическую прочность – свойство оказывать сопротивление действию динамических нагрузок.
Динамическая прочность является характеристикой сопротивления материала деформированию или разрушению при динамической нагрузке.
Различают динамическую прочность при многократной циклической нагрузке и прочность при однократной нагрузке.
Динамическая прочность при циклических нагрузках
Характеристикой динамической прочности при повторно-переменных нагрузках является предел прочности (предел выносливости, усталости) материала, величина которого меньше величины статической прочности.
Максимальное по абсолютному значению напряжение цикла, при котором еще не происходит усталостное разрушение материала в течение заданного количества циклов нагрузки.
Величина предела прочности зависит от ряда факторов:
• вида, структуры и дефектов материала,
• технологии изготовления и обработки,
• среды и температуры испытаний,
• состояния поверхности,
• концентрации напряжений,
• размеров образца,
• режима нагрузки и т.д.
Предел прочности может изменяться в больших пределах – при самых неблагоприятных условиях может уменьшаться в 5-10 раз по сравнению с пределом прочности материала в обычных условиях. Эти изменения вызывают значительные сложности при проектировании машин и конструкций в связи с необходимостью исключения их усталостных разрушений.
Для каждого случая условий эксплуатации предел прочности определяется экспериментально в условиях действия переменных напряжений при определенном виде цикла изменения нагрузки.
Динамическая прочность при однократной нагрузке
Динамическое сопротивление материала деформированию в условиях однократной нагрузки при одноосном напряженном состоянии определяется диаграммой деформирования. В общем случае изменение сопротивления деформированию σ(t)σ (t) определяется изменением деформации ε(t)ε (t) в процессе испытания материала.
Диаграмма деформирования σ(ε)σ(ε) характеризует только тот закон нагрузки, который реализуется в процессе исследования.
Обобщение экспериментальных данных, полученных при испытаниях с различными законами нагрузки, обычно применяют в виде связи трех таких переменных: напряжение σσ, деформации εε и скорости деформирования ε(t)ε(t). То есть зависимостями вида (σ,ε,t)(σ, ε, t), которые в трехмерном пространстве изображаются соответствующими поверхностями нагрузок.
Аналогично кратковременной статической прочности динамическая прочность характеризуется динамичными пределом текучести, пределом прочности и тому подобное.
Для случая ударных нагрузок динамическая прочность характеризуется величиной максимального неразрушающего напряжения, возникающего в телах при ударном взаимодействии (может быть выше величины статической прочности), а также ударной вязкостью.
Прочность при кратковременной (длительностью порядка 10-3 с) динамической нагрузке ударного характера называют ударной прочностью.
Получение характеристик прочности
Характеристики прочности при увеличенных скоростях деформирования получают, используя пневмо-гидравлические устройства. Действие ударов и взрывов используют для деформирования с очень большими скоростями. Если скорость относительного деформирования меньше чем 104 с-1, кривую деформации определяют в квазистатических испытаниях, которые обеспечивают однородное напряженное состояние по всему объему рабочей части образца, при сохранении этой скорости. Влияние скорости деформирования незначительно для хрупких материалов высокой прочности и увеличивается с ростом их пластичности.
Наличие конструктивно-технологических концентраторов напряжений (отверстий, резких переходов форм, мест с неоднородной структурой материала) значительно снижает динамическую прочность элементов конструкции.
Тест по теме «Прочность»
Про́чность твёрдого те́ла, свойство сохранять на протяжении определённого времени сплошность, целостность, конфигурацию, размеры, способность к упругой деформации под действием внешних нагрузок различной природы (механических, термических, электрических, магнитных и др.). В узком смысле прочность – механическое свойство реальных твёрдых тел сопротивляться разрушению. Понятие прочности играет существенную роль в фундаментальных (физика твёрдого тела, механика сплошных сред и деформируемого твёрдого тела) и прикладных (сопротивление материалов, механика грунтов, материаловедение и др.) науках.
По характеру временно́го изменения, создаваемого внешними нагрузками, различают нагрузки: стационарные, квазистационарные, малоцикловые (действующие периодически с числом циклов <104), циклические (число циклов от 104 до 105), многоцикловые (число циклов >105), динамические и ударные. Соответствующие названия носят и различные типы прочности: статическая, динамическая, ударная (скорость деформации 10–4–10–7 с), мало- и многоцикловая усталость и т. п. В характеристику прочности добавляют также тип внешней нагрузки (например, термопрочность).
Физическая природа прочности
Прочность твёрдых тел обусловлена силами взаимодействия между атомами и ионами, составляющими тело. Эти силы зависят главным образом от взаимного расположения атомов. Например, сила взаимодействия двух соседних атомов (если пренебречь влиянием окружающих атомов) зависит лишь от расстояния между ними. При равновесном расстоянии (около 10 нм) эта сила равна нулю. При меньших расстояниях сила положительна и атомы отталкиваются, при бо́льших – притягиваются. На некотором критическом расстоянии rкрr_{кр}
сила притяжения по абсолютной величине максимальна и равна FтF_{т}. Например, если при растяжении цилиндрического стержня с поперечным сечением Stextit{S} действующая сила (нагрузка) Pboldsymbol{P}, направленная вдоль его оси, такова, что приходящаяся на данную пару атомов внешняя сила превосходит максимальную силу притяжения FтF_{т}, то атомы беспрепятственно удаляются друг от друга. Однако, для разрушения тела вдоль некоторой поверхности необходимо, чтобы все пáры атомов, расположенные по обе стороны от рассматриваемой поверхности, испытывали силу, превосходящую FтF_{т}. Напряжение, отвечающее силе FтF_{т}, называется теоретической прочностью на разрыв σт sigma_{т} (σт≈0,1E sigma_{т} ≈ 0,1text{E}, где Etext{E} – модуль Юнга). Однако на практике наблюдается разрушение при нагрузке P∗textit{P}^{∗}, которой соответствует напряжение σ=P∗/S sigma =textit{P}^{∗}/textit{S}, в 100 – 1000 раз меньшее σт sigma_{т}. Расхождение теоретической прочности с действительной объясняется неоднородностями структуры тела (границы зёрен в поликристаллическом материале, посторонние включения, дефекты структуры и др.), из-за которых нагрузка распределяется неравномерно по сечению тела.
Если на участке поверхности малых размеров (но значительно превышающем сечение одного атома) локальное напряжение окажется больше σт sigma_{т}, вдоль этой площадки произойдёт разрыв. Края разрыва разойдутся на расстояние, большее rкрr_{кр}, на котором межатомные силы уже малы, и образуется микротрещина. Зарождению микротрещин при напряжении ниже σт sigma_{т} способствуют термические флуктуации. Локальные напряжения особенно велики у края образовавшейся трещины, где происходит концентрация напряжений, причём они тем больше, чем больше её размер. Если этот размер больше некоторого критического, на атомы у края трещины действует напряжение, превосходящее σт sigma_{т}, и трещина растёт дальше по всему сечению тела, в результате чего наступает разрушение.
Теории прочности
В конструкциях при нагружении возникает, как правило, сложное напряжённое состояние, характеризующееся в каждой точке тремя главными напряжениями σ1 sigma_{1}, σ2 sigma_{2}, σ3 sigma_{3} (нумерация определяется условиями σ1⩾σ2⩾σ3 sigma_{1}⩾ sigma_{2}⩾ sigma_{3}). Для расчётов на прочность используют теории (критерии) прочности – формализованные соотношения, связывающие определённую комбинацию главных напряжений f(σ1,σ2,σ3)f (sigma_{1}, sigma_{2}, sigma_{3}) с опасным напряжением σоп sigma_{оп}, при котором начинается разрушение (пределом прочности), определённым из опытов на одноосное нагружение.
В первой теории прочности (теории максимальных нормальных напряжений) предполагается, что разрушение при сложном напряжённом состоянии наступает тогда, когда максимальное главное напряжение σ1 sigma_{1} равно опасному напряжению: σ1=σоп sigma_{1}= sigma_{оп}. Эта теория не учитывает влияние второго (а при трёхосном напряжённом состоянии и третьего) главного напряжения, однако она хорошо согласуется с экспериментальными данными для хрупких материалов, когда первое главное напряжение намного больше двух остальных.
В основе второй теории прочности (теории максимальных линейных деформаций) лежит предположение о том, что разрушение происходит при достижении максимальной линейной деформацией опасного значения: ε1=εоп varepsilon_{1}= varepsilon_{оп}. Деформацию εоп varepsilon_{оп} можно найти из закона Гука: εоп=σоп/E varepsilon_{оп}= sigma_{оп}/text{E}, где Etext{E} – модуль упругости (модуль Юнга). С учётом обобщённого закона Гука условие разрушения, соответствующее второй теории прочности, имеет вид: σ1−ν(σ2+σ3)=σоп sigma_{1}− nu ( sigma_{2}+ sigma_{3})= sigma_{оп}, где ν nu – коэффициент Пуассона. Данная теория хорошо подтверждается для хрупких материалов в опытах на трёхосное сжатие.
Третья теория прочности (теория максимальных касательных напряжений) основана на гипотезе, что причиной разрушения являются максимальные касательные напряжения τmax tau_{max}. Условие разрушения в этой теории прочности: σ1−σ3=σоп sigma_{1}− sigma_{3}= sigma_{оп}.
Согласно энергетической теории прочности, условие прочности имеет вид: (12)(σ1−σ2)2+(σ2−σ3)2+(σ3−σ1)2=σоп.( frac{1}{ sqrt{2}}) sqrt{( sigma_{1}− sigma_{2})^{2}+ ( sigma_{2}− sigma_{3})^{2}+( sigma_{3}− sigma_{1})^{2}}= sigma_{оп}.Третья теория и энергетическая теория прочности хорошо подтверждаются в опытах с пластичными материалами.
Для материалов, по разному сопротивляющихся растяжению и сжатию, часто используется теория прочности К. О. Мора, в которой условие прочности определяется равенством σ1−kσ3=σоп(ρ) sigma_{1}−textit{k}sigma_{3}= sigma_{оп}^{(rho)}, где k=σоп(ρ)/σоп(с)textit{k}=sigma_{оп}^{( rho)}/sigma_{оп}^{(с)}, σоп(ρ)sigma_{оп}^{(rho)} – опасное напряжение при растяжении, σоп(с)sigma_{оп}^{(с)} – при сжатии.
С развитием промышленного и транспортного машиностроения, строительством сложных инженерных сооружений возникла потребность в других критериях прочности. Были разработаны теории прочности, связывающие между собой напряжения, деформации, время и температуру. Это теория Губера – Генки – Мизеса, учитывающая энергию формоизменения нелинейно-упругих деформаций, обобщённая теория октаэдрических напряжений и др. В 1933 г. С. Н. Журков и А. П. Александров создали молекулярно-кинетическую теорию прочности, базирующуюся на термофлуктуационной физической природе элементарных актов межатомных и межмолекулярных перегруппировок и на активирующем влиянии механических напряжений. В 20 в. при строительстве летательных аппаратов, трубопроводов и пр. оказалась необходимой разработка критериев прочности, учитывающих процессы накопления повреждённостей. На основе решений задач о концентрации напряжений в теле с вырезами и разрезами в 1960-х гг. разработана теория трещин и введены параметры повреждённости различного масштаба, которые были использованы А. А. Ильюшиным при создании теоретических основ кинетической теории прочности и Ю. Н. Работновым в её практическом применении.
Современные проблемы
Решение актуальных задач прочности связано с развитием феноменологических глобальных критериев прочности при двух- и трёхосном напряжённо-деформированном состоянии в областях с разными знаками главных напряжений и деформаций, при наложении переменной нагрузки на статическую, особенно в зонах высокой концентрации напряжений. Рассматриваются: задачи расчёта прочности при нерегулярных и сложных режимах повторных нагружений, в т. ч. контактном переменном напряжённом состоянии; усталость при высоких и низких температурах, а также при импульсных нагрузках (импульсная обработка металлов); установление условий прочности при неоднородном распределении механических свойств конструктивных элементов из армированных волокнистых материалов, условий термопрочности тугоплавких материалов (вольфрама, молибдена, ниобия, тантала, различных сплавов на их основе). Разрабатываются теории и методы расчёта структурно-чувствительных свойств материалов (хрупкая прочность, накопление повреждений, связанных с расшатыванием, разрушением структуры, длительная прочность, усталость при средних и малых амплитудах колебаний). Решение задач прочности горных выработок, расчёт сейсмостойкости конструкций и сооружений связаны с развитием теории тектонических процессов и явлений с учётом реологических свойств и особенностей распространения возмущений в грунтах и реальных схем залегания пластов в земной коре.
Дата публикации: 21 февраля 2023 г. в 18:55 (GMT+3)
Про́чность
(в физике и материаловедении) — свойство
материала сопротивляться разрушению
под действием внутренних напряжений,
возникающих под воздействием внешних
сил.
Прочность
подразделяют на статическую, под
действием постоянных нагрузок,
динамическую и усталостную (выносливость),
имеющую место при действии циклических
переменных нагрузок.
Для
конструкций различают общую прочность
— способность всей конструкции
выдерживать нагрузки без разрушения,
и местную — та же способность отдельных
узлов, деталей, соединений.
Допускаемое
(допустимое) напряжение – это значение
напряжения, которое считается предельно
приемлемым при вычислении размеров
поперечного сечения элемента,
рассчитываемого на заданную нагрузку.
Можно говорить о допускаемых напряжениях
растяжения, сжатия и сдвига. Допускаемые
напряжения либо предписываются
компетентной инстанцией (скажем, отделом
мостов управления железной дороги),
либо выбираются конструктором, хорошо
знающим свойства материала и условия
его применения. Допускаемым
напряжением ограничивается максимальное
рабочее напряжение конструкции.
Запас
прочности.
Разность
напряжения, при котором материал теряет
прочность, и допускаемого напряжения
есть тот «запас прочности», который
необходимо предусматривать, учитывая
возможность случайной перегрузки,
неточностей расчета, связанных с
упрощающими предположениями и
неопределенными условиями, наличия не
обнаруженных (или не обнаружимых)
дефектов материала и последующего
снижения прочности из-за коррозии
металла, гниения дерева и пр
Коэффициент
запаса.
Коэффициент
запаса прочности какого-либо элемента
конструкции равен отношению предельной
нагрузки, вызывающей потерю прочности
элемента, к нагрузке, создающей допускаемое
напряжение. При этом под потерей прочности
понимается не только разрушение элемента,
но и появление в нем остаточных деформаций.
Поэтому для элемента конструкции,
выполненного из пластичного материала,
предельным напряжением является предел
текучести. В большинстве случаев рабочие
напряжения в элементах конструкции
пропорциональны нагрузкам, а поэтому
коэффициент запаса определяется как
отношение предела прочности к допускаемому
напряжению (коэффициент запаса по
пределу прочности). Так, если предел
прочности конструкционной стали равен
540 МПа, а допускаемое напряжение – 180
МПа, то коэффициент запаса равен 3.

![]()
Механическое
напряжение — это мера внутренних сил,
возникающих в деформируемом теле под
влиянием различных факторов. Механическое
напряжение в точке тела определяется
как отношение внутренней силы к единице
площади в данной точке рассматриваемого
сечения.
Напряжения
являются результатом взаимодействия
частиц тела при его нагружении. Внешние
силы стремятся изменить взаимное
расположение частиц, а возникающие при
этом напряжения препятствуют смещению
частиц, ограничивая его в большинстве
случаев некоторой малой величиной.
![]()
Q
— механическое напряжение.
F
— сила, возникшая в теле при деформации.
S
— площадь.
Различают
две составляющие вектора механического
напряжения:
Нормальное
механическое напряжение — приложено
на единичную площадку сечения, по нормали
к сечению (обозначается ).
Касательное
механическое напряжение — приложено
на единичную площадку сечения, в плоскости
сечения по касательной (обозначается
).
Совокупность
напряжений, действующих по различным
площадкам, проведенным через данную
точку, называется напряженным состоянием
в точке.
Более
строго механическое напряжение –
тензорная величина. Компоненты тензора
напряжений
![]()
равны отношению компоненты силы![]()
действующей на элементарную площадку![]()
к её площади:
![]()
Здесь
под![]()
понимаются компоненты вектора,
образованного из нормали к элементарной
площадке n
и её площади
![]()
:

Деформа́ция
(от лат. deformatio — «искажение») — изменение
взаимного положения частиц тела,
связанное с их перемещением относительно
друг друга. Деформация представляет
собой результат изменения межатомных
расстояний и перегруппировки блоков
атомов. Обычно деформация сопровождается
изменением величин межатомных сил,
мерой которого является упругое
механическое напряжение.
Деформации
разделяют на обратимые (упругие) и
необратимые (пластические, ползучести).
Упругие деформации исчезают после
окончания действия приложенных сил, а
необратимые — остаются. В основе упругих
деформаций лежат обратимые смещения
атомов металлов от положения
равновесия(другими словами, атомы не
выходят за пределы межатомных связей);
в основе необратимых — необратимые
перемещения атомов на значительные
расстояния от исходных положений
равновесия (то есть выход за рамки
межатомных связей, после снятия нагрузки
переориентация в новое равновесное
положение).
Пластические
деформации — это необратимые деформации,
вызванные изменением напряжений.
Деформации ползучести — это необратимые
деформации, происходящие с течением
времени. Способность веществ пластически
деформироваться называется пластичностью.
При пластической деформации металла
одновременно с изменением формы меняется
ряд свойств — в частности, при холодном
деформировании повышается прочность.
Простейшей
элементарной деформацией является
относительное удлинение некоторого
элемента:
![]()
где
— l1
длина элемента после деформации;
— l2
исходная
длина этого элемента.
Абсолютное
удлинение
Δl = l – l0, где l — длина деформированного
тела, l0 — длина тела в недеформированном
состоянии.
Деформация
растяжения (сжатия). Линейная деформация
возникает при приложении силы F
⃗ вдоль
оси стержня, закрепленного с одного
конца (рис. 3, а, б). При
линейных деформациях
слои
тела остаются параллельными друг другу,
но изменяются расстояния между ними.
Линейную
деформацию характеризуют абсолютным
и относительным удлинением.

На
практике чаще встречаются малые
деформации — такие, что e<<1
.
Соседние файлы в папке 6 вопрос
- #
- #
- #
- #
- #
- #
- #
твёрдых тел, в широком смысле — свойство тв. тел сопротивляться разрушению (разделению на части), а также необратимому изменению формы (пластич. деформации) под действием внеш. нагрузок. В узком смысле — сопротивление разрушению.
В зависимости от материала, вида напряжённого состояния (растяжение, сжатие, изгиб и др.) и условий эксплуатации (темп-ра, время действия нагрузки и др.) в технике приняты разл. меры П. (предел текучести, временное сопротивление, предел усталости и др.). Разрушение тв. тела — сложный процесс, зависящий от мн. факторов, поэтому величины, определяющие П., явл. условными.
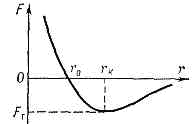
Рис. 1. Зависимость силы взаимодействия двух атомов от расстояния между ними.
Физическая природа прочности. П. тв. тел обусловлена в конечном счёте силами вз-ствия между атомами или ионами, составляющими тело. Напр., сила вз-ствия двух соседних атомов (если пренебречь влиянием окружающих атомов) зависит лишь от расстояния между ними (рис. 1). При равновесном расстоянии r0=0,1 нм (1 ?) эта сила равна нулю. При меньших расстояниях сила положительна и атомы отталкиваются, при больших — притягиваются. На критич. расстоянии rк сила притяжения по абс. величине максимальна и равна Fт. Напр., если при растяжении цилиндрич. стержня с поперечным сечением S0 действующая сила Р, направленная вдоль его оси, такова, что приходящаяся на данную пару атомов внеш. сила превосходит макс. силу притяжения Fт, то атомы беспрепятственно удаляются друг от друга. Однако, чтобы тело разрушилось вдоль нек-рой поверхности, необходимо, чтобы все пары атомов, расположенные по обе стороны от рассматриваемой поверхности, испытывали силу, превосходящую Fт. Напряжение, отвечающее силе Fт, наз. теор. прочностью на разрыв sт (sт»0,1 Е, где Е — модуль Юнга). Но на опыте наблюдается разрушение при нагрузке Р*, к-рой соответствует напряжение s=P*/S, в 100—1000 раз меньше sт. Расхождение теор. П. с действительной объясняется неоднородностями структуры тела (границы зёрен в поликрист. материале, посторонние включения и др.), из-за к-рых нагрузка Р распределяется неравномерно по сечению тела.
Механизм разрушения. Если на участке поверхности S малых размеров (но значительно превышающем сечение одного атома) локальное напряжение окажется больше sт, вдоль этой площадки произойдёт разрыв. Края разрыва разойдутся на расстояние, большее rк, на к-ром межатомные силы уже малы, и образуется трещина (рис. 2). Зарождению микротрещин при напряжении ниже sт способствуют термич. флуктуации. Локальные напряжения особенно велики у края образовавшейся трещины, где происходит концентрация напряжений, причём они тем больше, чем больше её размер. Если этот размер больше нек-рого критич. rс, на атомы у края трещины действует напряжение, превосходящее sт, и трещина растёт дальше по всему сечению тела с большой скоростью — наступает разрушение. rс определяется из условия, что освободившаяся при росте трещины упругая энергия материала покрывает затраты энергии на образование новой поверхности трещины: rс»Еg/s2 (где g — энергия единицы поверхности материала).
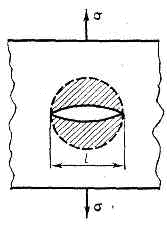
Рис. 2. Трещина Гриффита. Стрелки указывают направление растяжения, заштрихована область, в к-рой сняты напряжения.
Прежде чем возрастающее внеш. усилие достигнет необходимой для разрушения величины, отдельные группы атомов, особенно входящие в состав дефектов в кристаллах, обычно испытывают перестройки, при к-рых локальные напряжения уменьшаются («релаксируют»). В результате происходит необратимое изменение формы тела — пластич. деформация; ей также способствуют термич. флуктуации. Разрушению всегда предшествует большая или меньшая пластич. деформация. Поэтому при оценке rс в энергию g должна быть включена работа пластич. деформации gp, к-рая обычно на неск. порядков больше истинной поверхностной энергии g. Если пластич. деформация велика не только вблизи поверхности разрушения, но и в объёме тела, то разрушение в я з к о е. Разрушение без заметных следов пластич. деформации наз. х р у п к и м. Характер разрушения проявляется в структуре поверхности излома. В крист. телах хрупкому разрушению отвечает скол по кристаллографич. плоскостям спайности, вязкому — слияние микропустот и скольжение. При низкой темп-ре разрушение преим. хрупкое, при высокой — вязкое. Темп-ра перехода от вязкого к хрупкому разрушению наз. критич. темп-рой хладноломкости.
Поскольку разрушение есть процесс зарождения и роста трещин и пор, оно характеризуется скоростью или временем т от момента приложения нагрузки до момента разрыва, т. е. долговечностью материала. Исследования многих крист. и аморфных тел показали, что в широком интервале темп-р Т (по абс. шкале) и напряжений s, приложенных к образцу, долговечность при растяжении определяется соотношением:
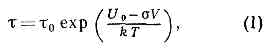
где t0— прибл. равно периоду тепловых колебаний атомов в тв. теле (10-12с), энергия U0 близка к энергии сублимации материала, активац. объём V составляет обычно неск. тысяч ат. объёмов и зависит от структуры материала, сформировавшейся в процессе предварительной термич. и механич. обработки и во время нагружения, k=l,38•10-16 эрг/град — постоянная Больцмана. При низких темп-рах долговечность очень резко падает с ростом напряжения, так что при любых важных для практики значениях т существует почти постоянное предельное значение напряжения s0, выше к-рого образец разрушается практически мгновенно, а ниже — живёт неограниченно долго. Это значение s0 можно считать п р е д е л о м п р о ч н о с т и (см. табл.).
НЕКОТОРЫЕ ЗНАЧЕНИЯ ПРОЧНОСТИ НА РАСТЯЖЕНИЕ, s0 в кгс/мм2 (1 кгс/мм2=10 МН/м2)
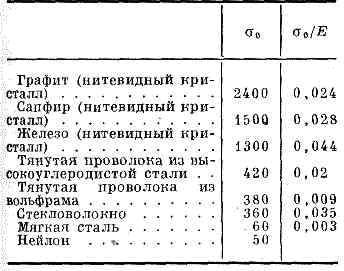
Время т затрачивается на ожидание термофлуктуац. зарождения микротрещин и на их рост до критич. размера rс. Когда к образцу прикладывают напряжение о, он деформируется сначала упруго, затем пластически, причём около структурных неоднородностей, имевшихся в исходном состоянии или возникших при пластич. деформации, возникают большие локальные напряжения (напр., в кристаллах — в результате скопления дислокаций). В этих местах зарождаются микротрещины. Их концентрация может быть очень большой (напр., в нек-рых ориентированных полимерах до 1015 трещин в 1 см3). Однако их размеры, определяемые масштабом структурных неоднородностей, значительно меньше rс. Под постоянным напряжением размеры и концентрация трещин растут медленно и тело не разрушается, пока случайно, напр. благодаря последовательному слиянию близко расположенных соседних трещин, одна из них не дорастёт до критич. размера. Поэтому при создании прочных материалов следует заботиться не столько о том, чтобы трещины не зарождались, сколько о том, чтобы они не росли. Случайное распределение структурных неоднородностей по объёму образца, по размерам и по степени прочности и случайный характер термич. флуктуации приводят к разбросу значений долговечности (а также предела П. s0) при испытаниях одинаковых образцов при заданных значениях а я Т. Вероятность встретить в образце «слабое» место тем больше, чем больше его объём. Поэтому П. (разрушающее напряжение) малых образцов (напр., тонких нитей) выше, чем больших из того же материала (т. н. масштабный эффект). Участки с повышенным напряжением, где легче зарождаются микротрещины, встречаются чаще у поверхности (выступы, царапины). Поэтому полировка поверхности и защитные покрытия повышают П. Напротив, в агрессивных средах П. понижена.
Физический энциклопедический словарь. — М.: Советская энциклопедия.
.
1983.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 марта 2021 года; проверки требуют 2 правки.
Преде́л про́чности — механическое напряжение 
Величины предела прочности[править | править код]
Статический предел прочности[править | править код]
Статический предел прочности, также часто называемый просто пределом прочности есть пороговая величина постоянного механического напряжения, превышая который постоянное механическое напряжение разрушит некое тело из конкретного материала. Согласно ГОСТ 1497-84 «Методы испытаний на растяжение», более корректным термином является временное сопротивление разрушению — напряжение, соответствующее наибольшему усилию, предшествующему разрыву образца при (статических) механических испытаниях. Термин происходит от представления, по которому материал может бесконечно долго выдержать любую статическую нагрузку, если она создаёт напряжения, меньшие статического предела прочности, то есть не превышающие временное сопротивление. При нагрузке, соответствующей временному сопротивлению (или даже превышающей её — в реальных и квазистатических испытаниях), материал разрушится (произойдет дробление испытываемого образца на несколько частей) спустя какой-то конечный промежуток времени (возможно, что и практически сразу, — то есть не дольше чем за 10 с).
Динамический предел прочности[править | править код]
Динамический предел прочности есть пороговая величина переменного механического напряжения (например при ударном воздействии), превышая которую переменное механическое напряжение разрушит тело из конкретного материала. В случае динамического воздействия на это тело время его нагружения часто не превышает нескольких секунд от начала нагружения до момента разрушения. В такой ситуации соответствующая характеристика называется также условно-мгновенным пределом прочности, или хрупко-кратковременным пределом прочности.
Предел прочности на сжатие[править | править код]
Предел прочности на сжатие есть пороговая величина постоянного (для статического предела прочности) или, соответственно, переменного (для динамического предела прочности) механического напряжения, превышая который механическое напряжение в результате (за конечный достаточно короткий промежуток времени) сожмет тело из конкретного материала — тело разрушится или неприемлемо деформируется.
Предел прочности на растяжение[править | править код]
Предел прочности на растяжение есть пороговая величина постоянного (для статического предела прочности) или, соответственно, переменного (для динамического предела прочности) механического напряжения, превышая который механическое напряжение в результате (за конечный достаточно короткий промежуток времени) разорвет тело из конкретного материала. (На практике, для детали какой либо конструкции достаточно и неприемлемого истончения детали.)
Другие прочностные параметры[править | править код]
Мерами прочности также могут быть предел текучести, предел пропорциональности, предел упругости, предел выносливости, предел прочности на сдвиг и др. так как для выхода конкретной детали из строя (приведения детали в негодное к использованию состояние) часто достаточно и чрезмерно большого изменения размеров детали. При этом деталь может и не разрушиться, а лишь только деформироваться. Эти показатели практически никогда не подразумеваются под термином «предел прочности».
Прочностные особенности некоторых материалов[править | править код]
Значения предельных напряжений (пределов прочности) на растяжение и на сжатие у многих материалов обычно различаются.
У композитов предел прочности на растяжение обычно больше предела прочности на сжатие. Для керамики (и других хрупких материалов) — наоборот, характерно многократное превышение пределом прочности на сжатие предела прочности на растяжение. Для металлов, металлических сплавов, многих пластиков, как правило, характерно равенство предела прочности на сжатие и предела прочности на растяжение. В большей степени это связано не с физикой материалов, а с особенностями нагружения, схемами напряженного состояния при испытаниях и с возможностью пластической деформации перед разрушением.
Прочность твёрдых тел обусловлена в конечном счёте силами взаимодействия между атомами, составляющими тело. При увеличении расстояния между атомами они начинают притягиваться, причем на критическом расстоянии сила притяжения по абсолютной величине максимальна. Напряжение, отвечающее этой силе, называется теоретической прочностью на растяжение и составляет σтеор ≈ 0,1E, где E — модуль Юнга . Однако на практике наблюдается разрушение материалов значительно раньше, это объясняется неоднородностями структуры тела, из-за которых нагрузка распределяется неравномерно.
Некоторые значения прочности на растяжение 
| Материалы |  , МПа , МПа
|

|
|---|---|---|
| Бор | 5700 | 0,083 |
| Графит (нитевидный кристалл) | 2401 | 0,024 |
| Сталь 60С2А рессорно-пружинная | 1570 (после термообработки) | 0,0074 |
| Сапфир (нитевидный кристалл) | 1500 | 0,028 |
| Железо (нитевидный кристалл) | 1300 | 0,044 |
| Тянутая проволока из высокоуглеродистой стали | 420 | 0,02 |
| Тянутая проволока из вольфрама | 380 | 0,009 |
| Стекловолокно | 360? | 0,035 |
| Сталь Ст0 обыкновенного качества | 300 | 0,0017 |
| Нейлон | 50 | 0,0025 |
См. также[править | править код]
- Теоретический предел прочности
Примечания[править | править код]
- ↑ Диапазон пределов прочности для стали составляет 500—3000 МПа (Б. Н. Арзамасов, В. А. Брострем, Н. А. Буше и др. Конструкционные материалы. Справочник. — М.: Машиностроение, 1990. — 688 с.).
