В школе часто рассказывают общие способы решения задачек. Они правильные, но не всегда самые простые и рациональные. Порой есть решения, которые позволяют решить задачку буквально в уме.
Взять к примеру задачки с процентами. В школе многим эта тема даётся сложно, нужно составлять пропорцию и решать. В уме мало кто справится.
Давайте рассмотрим пример. В магазине брюки стоят 3000 рублей, но сейчас на них скидка 40%. Как быстро узнать, сколько на самом деле стоят брюки и сколько удастся сэкономить?
I способ
Умножаем 3000 на 40 получаем 120 000. Отбрасываем два нуля и ответ готов. То есть скидка составляет 1200 рублей, а за пробки придётся заплатить 1800 рублей.
Наглядно показываю на этом видео.
II способ
Есть ещё один способ. Представьте, что вам нужно найти 18% от 50. Сложновато, не так ли? Можно воспользоваться первым способом, но 18 уменьшить на 50 в уме не так уж и просто для среднестатистического человека.
Но у процентов есть одно замечательное свойство: X% от Y это то же самое, что Y% от Х.
То есть 18% от 50 то же самое, что 50% от 18. Найти 50% от 18 легко, надо разделить 18 на 2, получается 9. Если посчитаться на калькуляторе 18% от 50, тоже получится 9. И это работает с любыми числами.
Вот ещё одно видео, где наглядно показывается этот способ.
Иногда удобнее использовать первый способ, а иногда второй, пользуйтесь на здоровье.
Основные определения
Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.
Чтобы узнать, как перевести проценты в десятичную дробь, нужно убрать знак % и разделить известное на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести натуральное число или десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%.
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а далее используем предыдущее правило и переведём десятичную дробь в проценты.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Проценты: правила
Рассмотрим четыре известных способа поиска процентов.
Нахождение одного процента от числа
Найти процент от числа можно несколькими способами.
Первый способ
-
Найдем, чему равен 1%.
-
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
-
48 : 100 = 0,48.
-
0,48 × 12 = 5,76.
Второй способ
-
Переведем проценты в десятичную дробь.
-
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
-
12 : 100 = 0,12.
-
48 × 0,12 = 5,76.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Как решаем:
- Переведем 15% в рубли:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит, 2,5 × 15 = 37,5 — это 15%.
- Вычислим цену со скидкой 15%: 250 − 37,5 = 212,5.
- 212,5 < 225.
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
- a, d — крайние члены
- b, c — средние члены
Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:
1390 руб. = 100%
x руб. = 14%
Перемножим крест-накрест и найдем x:
x = 1390 × 14 : 100
x = 194,6
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
- 100% – 25% = 75%,
значит, нужно заплатить 75% от первоначальной цены.
- Используем правило соотношения чисел:
75% — это 3/4 от числа, значит,
8500 : 4 × 3 = 6375 (рублей).
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Онлайн-калькулятор
Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:
- Для подсчета процента от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
- Чтобы вычесть проценты: введем известное, равное 100%, знак минус, размер процентной доли и знак %.
Содержание
- Проценты
- Что такое процент?
- Как найти процент?
- Второй способ нахождения процента
- Нахождения числа по его проценту
- Задачи на проценты: 3 способа решения с примерами
- Задачи на проценты: вся суть
- Решение задач на проценты с помощью формулы простого процента
- Задача 1
- Задача 2
- Задача 3
- Решение задач на проценты: метод пропорции
- Задача 4
- Задача 6
- Решение задач на проценты методом коэффициентов
- Задача 7
- Задача 8
- Задача 9
Проценты
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например, 
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, 
Проценты встречались настолько часто, что люди заменили дробь 
Эта запись читается как «один процент». Она заменяет собой дробь 

1% = 
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
Теперь полученный результат умножаем на 50
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти 
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись 

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
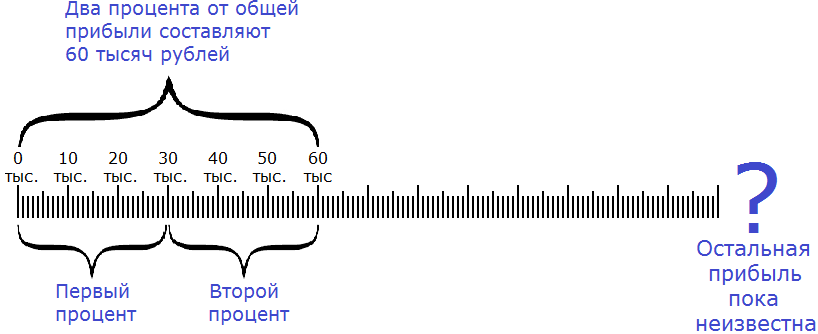
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. 
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это 
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Источник
Задачи на проценты: 3 способа решения с примерами
Как решать задачи на проценты? Есть 3 способа, выбирай тот, который для тебя проще и понятнее.
Умение быстро и правильно решать задачи на проценты важно, как для успешной сдачи ЕГЭ, так и для повседневной жизни. И если в ЕГЭ вы можете встретить такую задачу в задании 11, то в повседневной жизни такие задачи повсюду.
Зарплату повысили на 15%, а потом оштрафовали на 10%, после этого из зарплаты удержали налог 13% — сколько же мы получим в конце месяца? Коммунальные услуги повысили на 15%, сколько они теперь будут стоить? При возврате ж/д билета вернут только 20% стоимости, какую сумму мы получим? Все это задачи на проценты, которые нам приходится решать каждый день.
Поэтому умение быстро и правильно решать задачи на проценты – это полезно.
Задачи на проценты: вся суть
Задачи на проценты, как правило, описывают жизненную ситуацию. В ней присутствует какая-то величина, которая увеличивается или уменьшается на сколько-то процентов. Таким образом, в задаче на проценты упоминается такие данные, как первоначальная величина, конечная величина и процент, на который эта величина изменилась. Чаще всего в задаче требуется найти либо первоначальную величину, либо конечную величину, реже – процент, на который эта величина изменилась.
Решение задач на проценты с помощью формулы простого процента
Формула, которой мы пользуемся при решении задач на проценты, называется формула простого процента:
Хконечное – конечная величина
Хпервоначальное – первоначальная величина
k – процент, на который первоначальная величина изменилась
Из этой формулы всегда можно найти первоначальную величину или процент, на который происходит изменение.
Знак стоящий перед k зависит от того, увеличивается первоначальная величина или уменьшается. Так, если величина увеличивается на сколько-то процентов, то ставим знак плюс. Если уменьшается – минус.
Для наглядности приведем несколько простых примеров.
Задача 1
В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?
Решение: Очевидно, что в этой задаче нам известна первоначальная величина – 30 000 человек и процент, на который она увеличилась +6% Нужно найти конечную величину.
30 000 * ((100 + 6)/100) = х
х = 31 800 человек
Ответ: 31 800 человек
Задача 2
Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?
Решение: В этой задаче нам известна конечная величина – 5 килограмм и процент, на который происходит изменение -90%. Нужно найти первоначальную величину:
5 = х * ((100 – 90) / 100)
Задача 3
Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?
Решение: В данной задаче нам известна первоначальная (20 000 рублей) и конечная величина (22 000 рублей), а найти нужно процент, на который данная величина изменилась.
22 000 = 20 000 * ((100 + х) / 100)
22 000 / 20 000 = 1 + х/100
Решение задач на проценты: метод пропорции
Еще один способ решения задач на проценты – это метод пропорции. Это наиболее простой способ решения таких задач.
Напомним, что пропорция – это равенство двух отношений:
Для нас важно основное свойство пропорции, которое заключается в том, что произведение крайних членов пропорции равно произведению средних членов. Проще запомнить, что мы можем перемножить члены пропорции крест-накрест:
При решении задач на проценты с помощью метода пропорции необходимо руководствоваться следующим правилом:
Далее записываем пропорцию:
Давайте решим приведенные выше примеры задач на проценты с помощью метода пропорции.
Задача 4
В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?
Решение: Итак, в городе проживало 30 000 человек и это всё его население, т.е. 100%. Так и запишем:
Далее население выросло на 6%, т.е. всё его население стало составлять 100% + 6% = 106% и нам неизвестно, сколько это человек, т.е. Х человек. Запишем:
Таким образом, получаем:
Составим пропорцию: 

30 000 * 53 = 50х
Далее обе части полученного уравнения мы можем разделить на 50, получим:
Ответ: 31 800 человек
Задача 5
Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?
Решение: Нам неизвестно первоначальное количество всех яблок (всё количество), т.е. это Х, которое составляет 100%. Количество сушеных яблок (часть от первоначального количества яблок) составляет 5 кг. Причем известно, что количество сушеных яблок на 90% меньше от первоначального количества яблок (т.к. 90% — это вода, которая из них испарилась). Следовательно, количество сушеных яблок составит 100% — 90% = 10%. Запишем наши рассуждения:
Запишем наши рассуждения: 

Задача 6
Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?
Решение: Нам известно, что исходная цена – 20 000 рублей, следовательно, 20 000 рублей – это 100%. Тогда конечная цена 22 000 рублей – это неизвестное количество процентов, т.е. Х%. Так и запишем:
Теперь запишем пропорцию: 

В результате решения мы получили результат 110%, но он не является ответом! Ведь нам нужно найти, на сколько процентов изменилась стоимость холодильника. Чтобы это узнать, нужно из полученного числа процентов отнять 100%:
Решение задач на проценты методом коэффициентов
Можно назвать еще один метод решения задач на проценты, который является следствием из формулы простого процента. Так, формулу простого процента можно переписать следующим образом:
Таким образом, мы получили формулу для решения задач на проценты методом коэффициентов. Полученная формула удобна тем, что при достаточной практике простые задачи на проценты можно решать в уме, даже не задумываясь.
Например, яблоки стоили 150 рублей, затем они подорожали на 20%. Найдите новую стоимость яблок.
Применим полученную формулу и получим:
150 * 1,2 = 180 рублей
То есть мы интуитивно 20% превращаем в 0,2 прибавляем единицу, так как происходит увеличение на данное количество процентов, и умножаем на первоначальную стоимость.
Или другой пример. Зарплата работника составляла 25 000 рублей в месяц, в результате применения штрафа за опоздания зарплата сократилась на 10%. Найти сумму зарплаты, которую получит оштрафованный работник.
25 000 * 0,9 = 22 500 рублей
Опять же мы сразу понимаем, что 10% — это 0,1. Т.к. происходит уменьшение первоначальной величины на это количество процентов, то мы вычитаем из единицы этот процент и получаем 0,9. Затем умножаем полученное значение на первоначальную величину. Готово!
Давайте решим этим методом задачу про зарплату и налоги.
Задача 7
В России налог на доходы физических лиц составляет 13%. Зарплата Марии Ивановны после удержания налога на доходы составила 60 900 рублей. Найти сумму зарплаты Марии Ивановны до удержания налога.
Решение: Итак, 13% — это 0,13. Первоначальная зарплата уменьшилась на этот процент, значит, вычитаем из единицы и получаем 1 – 0,13 = 0,87. Подставляем в формулу:
Ответ: 70 000 рублей
Задача 8
В школе 1000 учеников, из них 20% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучают?
Решение: Для начала из общего количества учеников исключим тех, кто французский язык точно не изучает, т.е. учеников начальной школы. Ученики начальной школы – это 20%, т.е. 0,2, мы уменьшаем на этот процент, следовательно, вычитаем из единицы и получаем 1 – 0,2 = 0,8.
Из 800 полученных учеников французский язык изучают только 30%.
Обратите внимание, что здесь идет речь о проценте от числа. Т.е. мы не уменьшаем на 30% (в этом случае мы вычитаем значение процента в долях из единицы) и не увеличиваем на 30% (в этом случае мы прибавляем к значению процента в долях к единице), а берем 30% от заданного числа (в этом случае мы умножаем заданное число на значение процента в долях). Всегда внимательно читайте условия задачи!
В нашем случае нам нужно найти 30% от 800:
Это и есть ответ. 240 учеников изучают французский язык в школе.
Ответ: 240 учеников.
Задача 9
Разберем еще одну задачу на проценты, которая часто встречается на ЕГЭ и в которой легко можно допустить ошибку.
Задача: Зарплата рабочего составляла 30 000 рублей, затем зарплату повысили на 30%, а потом понизили на 30%. Какую зарплату стал получать рабочий?
Решение: быстро прочитав условие задачи, сходу хочется дать ответ – зарплата останется прежней, ее размер не изменился. Но это не так! Давайте разбираться.
Будем решать по формуле простого процента.
Первое событие – зарплату повысили на 30%. Следовательно, первоначальную сумму мы увеличиваем на 30%:

Данную задачу мы могли бы решить в одно действие, применяя формулу для вычисления сложного процента. Напомним ее:
S = P (1 + i) n , где
S – это конечная сумма;
P – это первоначальная сумма;
i – это процент/100;
n – количество периодов.
Т.к. 30% — это 0,3, то, применяя формулу для вычисления сложного процента к нашей задаче, мы получим:
30 000 * (1 + 0,3) 1 (1 – 0,3) 1 = 27 300 рублей
Результат получился тот же.
Ответ: 27 300 рублей
В этой статье были разобраны достаточно простые примеры задач на проценты, чтобы максимально доступно продемонстрировать методы решения задач на проценты. В профильном ЕГЭ с процентами вы можете столкнуться в задаче с экономическим содержанием по вкладам и кредитам. Такие задачи гораздо сложнее и подробное их решение вы можете посмотреть на нашем сайте.
Итак, надеюсь, что данная статья помогла вам понять, как решать задачи на проценты. Мы увидели, что задачи на проценты можно решать тремя способами – с помощью формулы простого процента, методом пропорции и методом коэффициентов. Выбирайте тот, который вам наиболее понятен, и которым вам решать такие задачи проще.
Источник
Простейшие формулы помогут узнать, выгодны ли скидки, и не нарушить пропорцию классного рецепта.
1. Как посчитать проценты, разделив число на 100
Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.
Пример 1
Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.
Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.
Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.
Умножьте 4,58 на 7, и вы получите 32,06 рубля.
Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.
Пример 2
Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.
Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.
Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.
100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.
2. Как посчитать проценты, разделив число на 10
Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.
Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.
Пример
Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.
В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.
Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.
Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.
В любом случае такими крупными числами оперировать довольно просто.
3. Как посчитать проценты, составив пропорцию
Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:
сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.
Или можно записать её так: a : b = c : d.
Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.
Пример 1
Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.
Сначала вычисляем процентную долю оставшегося шоколада.
90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.
Х = 70 × 100 / 90 = 77,7%.
Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:
200 г : 100% = Х : 77,7%, где Х — нужное количество масла.
Х = 77,7 × 200 / 100 = 155,4.
Следовательно, в тесто нужно положить примерно 155 г масла.
Пример 2
Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.
Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.
Составьте пропорцию: 1 499 : 100 = Х : 87.
Х = 87 × 1 499 / 100.
Заплатите 1 304,13 рубля и носите блузку с удовольствием.
4. Как посчитать проценты с помощью соотношений
В некоторых случаях можно воспользоваться простыми дробями. Например, 10% — это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.
- 20% — 1/5, то есть нужно делить число на 5;
- 25% — 1/4;
- 50% — 1/2;
- 12,5% — 1/8;
- 75% — это 3/4. Значит, придётся разделить число на 4 и умножить на 3.
Пример
Вы нашли брюки за 2 400 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:
100% — 25% = 75% — стоимость брюк в процентах от первоначальной цены после применения скидки.
2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.
5. Как посчитать проценты с помощью калькулятора
Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.
- Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
- Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
- Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.
6. Как посчитать проценты с помощью онлайн-сервисов
Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.
Planetcalc
На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.
Planetcalc→
Калькулятор — справочный портал
Ещё один сервис с калькуляторами на любой вкус.
Калькулятор — справочный портал→
Allcalc
Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.
Allcalc→
Читайте также 📑
- ТЕСТ: Умеете ли вы считать в уме?
- Математические игры — отличная разминка для мозга
- 11 книг, которые прокачают математическое мышление
- Как выучить таблицу умножения легко и быстро
В нашей повседневной жизни мы часто сталкиваемся с ситуациями, в которых необходимо что-то высчитать. Это может быть определение суммы выплат для погашения потребительского кредита, процентные скидки в магазинах или расчёт показателя инфляции. Давайте разберёмся, каким образом можно отыскать процент от какого-либо числа, а также приведём ряд соответствующих формул с подробными примерами.
- Особенности поиска процента от числа
- Формулы для определения необходимой доли от суммы
- Как найти процентное соотношение чисел
- Как найти базовую сумму исходя из ее процента
- Онлайн-сервисы для вычислений
- Заключение
Особенности поиска процента от числа
Как известно, само слово «процент» происходит от латинского «pro centum», что в переводе означает «со ста». Соответственно, под этим термином обычно понимается сотая часть от целого (или доля от целого). Процент обозначается всем нам известным знаком «%».
Нахождение процента требуется в трёх основных случаях:
- требуется найти долю от числа;
- определить соотношение чисел;
- найти базовое число исходя из его же процента.
Для нахождения этого параметра существуют различные варианты формул и способов решения. Давайте рассмотрим их пристальнее.
Это может быть интересно: Как выполнить орфографический разбор слова.
Формулы для определения необходимой доли от суммы
Есть несколько способов найти требуемый процент от любого числа.
Первый способ состоит в делении нужной суммы на 100, после чего полученный результат умножается на % который необходимо определить.
Формула расчёта в данном случае выглядит так:
A / 100 * B =
В данной формуле A – это базовое число, из которого нужно извлечь долю.
B – процент, который необходимо высчитать в числовом выражении.
Например, в каком-либо магазине вам отдают товар, цена которого 500 рублей, за 70% его стоимости. Используя приведённую выше формулу, высчитываем, сколько нам необходимо заплатить в конечном итоге (или сколько будет 70% от 500 рублей):
500 / 100 * 70 = 350 рублей
Таким образом, мы сможем приобрести нужный товар за 350 рублей.
Второй способ состоит в умножении базового числа A на коофициент 0,B
Где А – это базовое число, а B – количество процентов, которые необходимо определить.
Формула имеет следующую форму:
A * 0,B =
В случае упомянутого выше примера с 70% стоимости от 500 высчитываем стоимость товара:
500 * 0,70 = 350
Третий способ состоит в умножении базового числа на количество процентов, после чего полученный результат делим на 100.
Формула выглядит следующим образом:
A * B / 100 =
В нашем случае это:
500 * 70 / 100 = 350
На калькуляторе нужная доля от числа находится ещё проще:
- Набираете на калькуляторе базовое число (А).
- Жмёте на умножить, вводите искомое число процентов.
- После чего жмёте на кнопку %, а затем на кнопку =. Калькулятор тот час же отобразит требуемый результат.
500*70% = (результат)
Читайте также: Как проверить пунктуацию онлайн.
Как найти процентное соотношение чисел
Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.
Для определения такого результата существуют следующая формула:
B / A * 100 =
К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.
Используя приведённую формулу, выполняем несложные арифметические операции:
85 / 500 * 100 = 17%
Таким образом, число 85 составляет 17% от 500.
Проверяем полученное число по формуле первого способа:
500 / 100 * 17 = 85.
Всё сошлось.
Как найти базовую сумму исходя из ее процента
В некоторых случаях нам может быть известно какое-либо число и процент, которое оно составляет от базового числа. Нам необходимо определить значение. Например, нам может быть дана сумма 67, которое составляет 23% от базового числа. Каково же само базовое число?
Для решения этой задачи нам необходимо 67 разделить на 23 и умножить на 100. Формула вычисления процента выглядит следующим образом:
67 / B * 100 = A
Подставляем значения:
67 / 23 * 100 = 293, 31 (десятые после запятой можем округлить)
Проверяем полученный результат с помощью формулы из первого способа:
293, 31 / 100 * 23 = 67
Всё сошлось.
Онлайн-сервисы для вычислений
В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт fin-calc.org.ua имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.
Порядок действий:
- Перейдите на fin-calc.org.ua.
- Введите искомые показатели в соответствующие клетки.
- Нажмите на «Рассчитать». Вы сразу же получите искомый результат.
Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.
Заключение
В нашем материале мы разобрали, каким образом можно высчитать процент от любого числа, а также привели формулы с различными примерами. Наиболее просто высчитать долю с помощью калькулятора, который имеется в абсолютном большинстве современных гаджетов.