Онлайн калькулятор для вычисления процентного соотношения чисел.
Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.
Находится по формуле: R%= N1/N2×100%
Пример вычисления процентного соотношение между двумя числами:
Число 540 составляет 49.09% от числа 1100
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Частное двух чисел называют отношением этих чисел. Отношение можно записать как арифметическое действие «деление», а можно как обыкновенную дробь.
(a:b=frac{a}{b}) – так записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член.
Например: отношение 75 к 25 можно записать в виде: (75:25=frac{75}{25}=3).
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Процентное отношение
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например: вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: (52:400cdot100%=13 %).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Примеры.
Задача 1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий – это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 – 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 (Rightarrow 1100:1200cdot100%=91,7%).
2-й вариант
Решение:
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2 300 от 1 200 (Rightarrow 2300:1200cdot100%=191,7%).
2) На сколько процентов перевыполнен план?
(191,7%-100%=91,7%).
Ответ: на 91,7%.
Задача 2. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Решение:
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
(150:500cdot 100%=frac{150}{500}cdot 100% )(=frac3{10}cdot 100%=0,3cdot 100%=30%).
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Задача 3. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Решение:
Для ответа на вопрос задачи надо найти отношение (частное) числа 45 к 36 и выразить его в процентах: (45:36cdot 100%=1,25cdot 100%=125%).
Процент – это одна сотая доля числа, принимаемого за целое. Проценты используются для обозначения отношения части к целому, а также для сравнения величин.
1% = 1100 = 0,01
Онлайн калькулятор позволяет выполнить следующие операции:
Найти процент от числа
Чтобы найти процент p от числа, нужно умножить это число на дробь p100
Найдем 12% от числа 300:
300 · 12100 = 300 · 0,12 = 36
12% от числа 300 равняется 36.
Например, товар стоит 500 рублей и на него действует скидка 7%. Найдем абсолютное значение скидки:
500 · 7100 = 500 · 0,07 = 35
Таким образом, скидка равна 35 рублей.
Сколько процентов составляет одно число от другого числа
Чтобы вычислить процентное отношение чисел, нужно одно число разделить на другое и умножить на 100%.
Вычислим, сколько процентов составляет число 12 от числа 30:
1230 · 100 = 0,4 · 100 = 40%
Число 12 составляет 40% от числа 30.
Например, книга содержит 340 страниц. Вася прочитал 200 страниц. Вычислим, сколько процентов от всей книги прочитал Вася.
200340 · 100% = 0,59 · 100 = 59%
Таким образом, Вася прочитал 59% от всей книги.
Прибавить процент к числу
Чтобы прибавить к числу p процентов, нужно умножить это число на (1 + p100)
Прибавим 30% к числу 200:
200 · (1 + 30100) = 200 · 1,3 = 260
200 + 30% равняется 260.
Например, абонемент в бассейн стоит 1000 рублей. Со следующего месяца обещали поднять цену на 20%. Вычислим, сколько будет стоить абонемент.
1000 · (1 + 20100) = 1000 · 1,2 = 1200
Таким образом, абонемент будет стоить 1200 рублей.
Вычесть процент из числа
Чтобы отнять от числа p процентов, нужно умножить это число на (1 – p100)
Отнимем 30% от числа 200:
200 · (1 – 30100) = 200 · 0,7 = 140
200 – 30% равняется 140.
Например, велосипед стоит 30000 рублей. Магазин сделал на него скидку 5%. Вычислим, сколько будет стоить велосипед с учетом скидки.
30000 · (1 – 5100) = 30000 · 0,95 = 28500
Таким образом, велосипед будет стоить 28500 рублей.
На сколько процентов одно число больше другого
Чтобы вычислить, на сколько процентов одно число больше другого, нужно первое число разделить на второе, умножить результат на 100 и вычесть 100.
Вычислим, на сколько процентов число 20 больше числа 5:
205 · 100 – 100 = 4 · 100 – 100 = 400 – 100 = 300%
Число 20 больше числа 5 на 300%.
Например, зарплата начальника равна 50000 рублей, а сотрудника – 35000 рублей. Найдем, на сколько процентов зарплата начальника больше:
5000035000 · 100 – 100 = 1,43 * 100 – 100 = 143 – 100 = 43%
Таким образом, зарплата начальника на 43% выше зарплаты сотрудника.
На сколько процентов одно число меньше другого
Чтобы вычислить, на сколько процентов одно число меньше другого, нужно из 100 вычесть отношение первого числа ко второму, умноженное на 100.
Вычислим, на сколько процентов число 5 меньше числа 20:
100 – 520 · 100 = 100 – 0,25 · 100 = 100 – 25 = 75%
Число 5 меньше числа 20 на 75%.
Например, фрилансер Олег в январе выполнил заказы на 40000 рублей, а в феврале на 30000 рублей. Найдем, на сколько процентов Олег в феврале заработал меньше, чем в январе:
100 – 3000040000 · 100 = 100 – 0,75 * 100 = 100 – 75 = 25%
Таким образом, в феврале Олег заработал на 25% меньше, чем в январе.
Найти 100 процентов
Если число x это p процентов, то найти 100 процентов можно умножив число x на 100p
Найдем 100%, если 25% это 7:
7 · 10025 = 7 · 4 = 28
Если 25% равняется 7, то 100% равняется 28.
Например, Катя копирует фотографии с фотоаппарата на компьютер. За 5 минут скопировалось 20% фотографий. Найдем, сколько всего времени занимает процесс копирования:
5 · 10020 = 5 · 5 = 25
Получаем, что процесс копирования всех фотографий занимает 25 минут.
Процентное отношение двух чисел
Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.
Процентное отношение двух чисел можно записать следующей формулой: 
Пример процентного отношения
Например есть два числа: 750 и 1100.
Процентное отношение 750 к 1100 равно 
Число 750 составляет 68.18% от 1100.
Процентное отношение 1100 к 750 равно 
Число 1100 составляет 146.67% от 750.
Пример-задача 1
Норма завода по производству автомобилей составляет 250 машин в месяц. Завод собрал за месяц 315 машин. Вопрос: на сколько процентов завод перевыполнил план?
Процентное отношение 315 к 250 = 315:250*100 = 126%.
План выполнен на 126%. План перевыполнен на 126% — 100% = 26%.
Пример-задача 2
Прибыль компании за 2011 год составила 126 млн $, в 2012 году прибыль составила 89 млн $. Вопрос: на сколько процентов упала прибыль в 2012 году?
Процентное отношение 89 млн к 126 млн = 89:126*100 = 70.63%
Прибыль упала на 100% — 70.63% = 29.37%
9 оценок
Категории
НаукаМатематика
Читайте также
- ГНОМ ГНОМ СКАЛА
- ДОМ ВОДА ДАЧА
- Спряжение глагола “to relate” (Английский язык)
Комментарии
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 
и 
– члены отношения; число – предыдущий член отношения; – последующий член отношения.
Например:
14 : 7 – отношение числа 14 к числу 7;
6 : 25 – отношение числа 6 к числу 25;
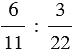– отношение числа 
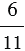к числу 
;
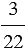1,15 : 0,36 – отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и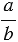 
.
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
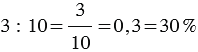
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел – это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
.
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
.
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб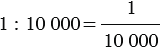 
, то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 
длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : = 1 : 10 000;
Решаем данное уравнение:
= 5
10 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 630,
Мерзляк, Полонский, Якир, Учебник
Номер 635,
Мерзляк, Полонский, Якир, Учебник
Номер 740,
Мерзляк, Полонский, Якир, Учебник
Номер 792,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Задание 778,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 825,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1311,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1495,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 149,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 846,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 303,
Мерзляк, Полонский, Якир, Учебник
