Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.
Задачи:
Образовательные
- повторить понятия проценты, отношения;
- закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
- показать практическую значимость математических знаний для решения задач на концентрацию.
Воспитательные
- показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
- воспитание у учащихся интереса к предмету.
Развивающие
- развивать наблюдательность, логическое мышление учащихся;
- развивать жизненную смекалку и интуицию.
Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.
План урока:
- Мотивационный момент (1 минута).
- Подготовка учащихся к сознательному усвоению нового материала (5 минут).
- Изучение нового материала (12 минут).
- Решение задач на отработку формул (3 мин).
- Физминутка (1 минута).
- Первичное закрепление нового материала (15минут).
- Рефлексия (1 минута).
- Подведение итогов. Домашнее задание (2 минуты).
Ход урока
I. Мотивационный момент.
Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.
II. Подготовка к сознательному усвоению нового материала.
(Слайд 2)
- Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
- Указать в виде процентов: 0,7; 0,04; 1,3.
- Найти 15% от числа 60.
- Найти число, 15% которого равны 30.
- Из 25 семян взошло 24 семени. Найдите процент всхожести.
- Итак, известные нам отношения: (Слайд 3)
Всхожесть = ![]() ;
; ![]() .
.
Значения данных отношений мы представляли в виде процентов.
III. Изучение нового материала.
Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?
В большом энциклопедическом словаре «концентрация (от новолат. concentratio) – сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].
Концентрация в химии – величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].
Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)
Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]
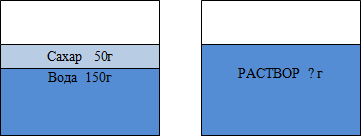
50+150=200 (г) – масса общая. (Слайд 5)
Раствор тщательно перемешиваем.
Найдите процентное содержание сахара в растворе.
50 : 200=1: 4 = 0,25;
0,25=25%
25% – процентное содержание сахара в данном растворе.
Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)
Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).
Концентрация = ![]() , т.е. К=
, т.е. К=![]() .
.
Как по этой формуле найти Мч.в? Мобщ?
Мч.в. = Мобщ · К
Мобщ = Мч.в: К
(Слайд 7)
IV. Решение задач на отработку формул:
(Слайд 8)
- В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
- 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
- Какова масса раствора, в котором 150 г сахара составляют 25%.
Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)
Рис.1.
Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».
Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.
V. Физминутка.
(Слайд 11)
Следите глазами за движениями черепашек.
VI. Первичное закрепление нового материала.
Решим несколько задач на «концентрацию».
(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.
Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)
Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.
Решение:
-
Какова масса раствора в первой банке?
480+120 = 600 (г) -
Какова концентрация сахара в растворе первой банки?
120:600 = 0,2; 0,2=20% -
Какова масса раствора во второй банке?
840+160 = 1000(г) -
Какова концентрация сахара в растворе второй банки?
160:1000 = 0,16; 0,16=16% -
В какой банке вода слаще?
20% > 16%
Ответ: в первой банке вода слаще.
Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)
Решение:
80% – это процентное содержание соли в 200г раствора (концентрация 0,8)
- Сколько г соли в этом растворе?
0,8 ·200=160(г)
20% – это содержание соли в 700 г раствора (концентрация соли 0,2)
- Сколько г соли во втором растворе?
0,2·700=140 (г) - Сколько г соли в полученном растворе?
160+140=300 (г)
Ответ: 300 г.
Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)
Решение:
50% – процентное содержание соли в 200 г растворе (концентрация 0,5).
-
Сколько г соли в этом растворе?
0,5·200=100 (г)
Что мы знаем про второй раствор? – Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25) -
Какова масса второго раствора?
150:0,25= 600 (г)
Чтобы найти концентрацию соли в новом растворе, что надо знать? – Массу соли и массу всего раствора. -
Какова масса соли в двух растворах?
100+150=250 (г) -
Какова масса нового раствора?
200+600 =800 (г) -
Какова концентрация соли в новом растворе?
250:800=0,3125; 0,3125 = 31,25%
Ответ: 31,25%.
Задача для самостоятельного решения (дома).
Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]
Решение:
-
Сколько кг соли в морской воде?
0,05·30=1,5 (кг)
Пресная вода содержит соль? – Нет. – Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015. -
Какова масса нового раствора (с добавлением пресной воды)?
1,5: 0,015= 100 (кг) -
Сколько пресной воды нужно добавить?
100 – 30 = 70 (кг)
Ответ: 70 кг.
VII. Этап рефлексии.
(Слайд 18)
Ответ на листочке:
- Сегодня я узнал….
- У меня получилось…
- Было трудно….
- Было интересно….
- Теперь я умею…
VIII. Итог урока. Домашнее задание.
(Слайд 19)
№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.
Используемая литература:
- Большой энциклопедический словарь. -2-е изд., перераб.и доп. – М.:Большая Российская энциклопедия, 1998. – 1456 с.: ил.
- slovari. yandex.ru
- urok.1sept.ru/articles/520040
- Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – 8-е изд.-М.: Просвещение, 2006. – 302 с. :ил.
- Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. – 7-е изд., перераб. и доп. – М.: Высш.шк., 1994. – 528 с.: ил.
Автор Русанова Людмила Васильевна
Название работы: «Решение задач на процентное содержание вещества»
Краткая аннотация работы: В современном мире обучение требует современных и новаторских подходов. Данный урок-исследование проведен в 6 классе, в соответствии с программой по математике 6 класса по теме «Нахождение части от целого». Ученик, получает знания не в готовом виде, а, добывает их сам, что способствует активному успешному формированию его общекультурных и деятельностных способностей, общеучебных умений. Предполагает снятие всех стрессообразующих факторов учебного процесса, создание в классе доброжелательной атмосферы, ориентированной на реализацию идей сотрудничества, развитие диалоговых форм общения. Разработка такого урока требует большой затраты сил, энергии и времени, но с лихвой окупается позитивной мотивацией и интересом учащихся к учебно- познавательной деятельности.
Тип урока: систематизация, обобщение и расширение знаний по теме «Нахождение части от целого».
Основная цель: получение учащимися субъективно нового научного знания «Процентное содержание вещества».
Цели:
- Организовать исследовательскую деятельность учащихся по решению задач на процентное содержание вещества;
- Формирование учебно- познавательной компетенции: самостоятельная познавательная деятельность, включающая элементы логической деятельности.
- Формирование информационной компетенции: поиск, анализ и отбор необходимой информации.
- Содействовать воспитанию активной личности, самостоятельно предлагать, реализовывать свои пути и пути решения.
Задачи урока:
- Повторить понятие процента;
- Вспомнить вид задачи «Нахождение части по его целому»;
- Научить решать задачи на растворы и сплавы.
Оборудование: компьютеры, весы,мензурка, вода, медный купорос, стеклянная палочка.
Ход урока
|
№ |
Этап урока |
Деятельность учителя |
Деятельность ученика |
|
1 |
Орг.момент |
Проверка готовности к уроку |
Организация рабочего места |
|
2 |
Мотивация |
Сегодня мы будем не просто математиками, а исследователями. Мы откроем новые знания. Внимание! Начинаем урок! |
|
|
3 |
Актуализация знаний |
5%=? Ответьте на данный вопрос. Задача 1. 60 г водного раствора содержит 5% медного купороса. |
Запись в тетради 5%= 0.05 Обратим в десятичную дробь |
|
4 |
Создание проблемной ситуации |
Задайте вопрос к данной ситуации. Вопрос: Как найти часть от его целого? |
Сколько медного купороса в растворе? Решение: Целое дробь часть 60 г 0.05 ? Чтобы найти часть от целого, надо целое умножить на дробь. 60 Ответ: 3 г медного купороса. 5% -это процентное содержание медного купороса |
|
5 |
Исследование |
Приготовим водный раствор, содержащий 5% медного купороса. |
Алгоритм: 1.Взвесим 3г медного купороса (на лабораторных весах); 2.Пересыпим в мензурку; 2.Нальем в мензурку воды до отметки 60 мл; 3.Размешаем стеклянной палочкой; 4. Получим данный раствор. |
|
6 |
Изучение нового материала |
Вы знаете формулу определения процентного содержания вещества? Формула
Процентного содержания некоторого вещества b в массе a (раствора, смеси, сплава). Чему равно b? Чему равно а? |
Нет
b=3г а=60г Вычислим процентное содержание:
|
|
7 |
Применение новых знаний в учебной деятельности |
Задача Итак, мы решали задачи на процентное содержание вещества. |
300×0,2=60 г- олова в первом куске 200×0,4=80 г – олова во втором куске 60+80=140 г – олова в полученном сплаве 300+200=500 г – масса полученного сплава
Ответ: 28%. |
|
8 |
Закрепление |
Класс делится на 4 группы: 1группа: Приготовить 10%солевой раствор; 2 группа:2% солевой раствор; 3 группа:3% солевой раствор; 4 группа: 15% солевой раствор |
Каждая группа отчитывается по выполнению работы. |
|
9 |
Рефлексия |
Кто осуществлял учебное исследование с удовольствием? Поднимите руку. Спасибо за совместное исследование. |
Все |
|
10 |
Домашнее задание |
Задачник Мордкович А.Г. №645 В 200 г раствора 8 г соли. Определите процентное содержание соли в растворе. №647 б Из 105 посеянных семян взошло 98. Определите процент всхожести семян. |
Результат по выполнению домашнего задания: все учащиеся справились. |
Задача на растворы
Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что называется концентрацией раствора.
Запомните! ![]()
Концентрация раствора — это часть, которую составляет масса растворённого вещества от массы всего раствора.
- 9% -я концентрация раствора соли — это 9 грамм соли в 100 граммах раствора.
Задача № 322 (2) из Петерсона 6 класс (2010 г.)
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
- 1 кг — масса растворённого вещества (соли)
- 9 кг — масса воды в растворе (не путать с общей массой раствора)
- 9 + 1 = 10 кг — общая масса раствора.
Ответ: 10% — концентрация раствора.
Задача № 353(2) из Петерсона 6 класс (2010 г.)
Теперь решим обратную задачу.
Сколько соли получится при выпаривании 375 граммов 12% -го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.

Ответ: 45 г соли.
Сложная задача на растворы
В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70 . Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за « x » первоначальную массу соли в растворе, а за « y » массу воды в растворе. Так как концентрация соли в исходном растворе 40% , то соответственно вода составляет
Изобразим графически условия задачи.

Составим пропорцию, связывающую эти величины до добавления соли.

Для решения задачи нам надо определить какая из неизвестных (« x » или « y ») остаётся неизменной после добавления соли.
Этой величиной является масса воды в растворе « y ».
Выразим её, учитывая изменения в растворе после добавления соли.
- (x + 120) г — масса соли в новом растворе
- (100% − 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.

Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.

Учитель математики . Здравствуйте, ребята. Сегодня на уроке математики мы познакомимся, и будем решать задачи, с которыми вы встретитесь и на уроках химии в старших классах. Помогать мне будет учитель химии нашей школы Абашеева Татьяна Васильевна.
Учитель химии . Ребята, в повседневной жизни мы встречаемся очень часто с растворами. Где? Кто может привести примеры растворов?
Дети перечисляют различные растворы.
Из чего состоят растворы?
Из растворителя и растворенного вещества.
На доске появляется запись: раствор = растворитель + растворенное вещество .
Роль растворителя могут выполнять разные жидкие вещества. Как вы думаете какие?
(Ученики называют бензин, керосин, спирт, воду).
В курсе химии вы встретитесь с различными растворами, в том числе и с «волшебными». Один такой волшебный раствор я хочу вам показать.
Демонстрационный опыт №1 .
В двух химических стаканах находится бесцветная жидкость (учитель в первый стакан налил раствор щелочи NaOH, а во второй фенолфталеин).
Учитель химии . Как вы думаете, каким будет цвет раствора, если мы смешаем эти две бесцветные жидкости?
Дети говорят, не задумываясь, что раствор останется бесцветным. И когда после смешивания он приобрел малиновую окраску, удивлению не было предела.
Учитель химии . Добавим в полученный раствор еще одну бесцветную жидкость (в стакане находится раствор серной кислоты). Какой станет окраска?
Теперь дети, учитывая предыдущий опыт, с ответом не торопятся. И предлагаются разные варианты ответов.
Раствор обесцветился. Этот демонстрационный опыт создал определенный эмоциональный настрой и активизировал мышление учащихся.
Учитель химии . Почему изменился цвет раствора, мы сможем сказать при изучении химии.
А сейчас давайте посмотрим на следующий опыт.
Демонстрационный опыт №2
Предлагаются к рассмотрению два химических стакана, в которых находится одинаковое количество жидкости. В первый стакан добавляем 5г вещества, а во второй 15г вещества. Получается разная окраска.
Учитель математики . Вы все видели, что в стаканах первоначально находилось одинаковое количество жидкости. В них добавили одно и тоже вещество . Почему же получилась разная окраска?
Учащиеся говорят, что добавили разное количество вещества, поэтому получилась разная окраска.
Учитель математики . Для того чтобы грамотно выразить различия этих и других растворов введем новое понятие «процентная концентрация».
Процентной концентрацией раствора называют процентное содержание растворенного вещества в единице массы раствора.
Масса раствора складывается из массы вещества и массы растворителя.
Давайте вернемся ко второму опыту. В первом стакане было 100 г жидкости, добавили 15г вещества. Какой стала масса раствора? 115г. А %-ная концентрация? ∙100%=13 %. А во втором стакане было 100 г жидкости, добавили 25г вещества. Какой стала масса раствора? 125г. А %-ная концентрация? ∙100%=20%
Ребята, зачем нам нужно понятие «%-ная концентрация»? Где мы с этим сталкиваемся
в повседневной жизни? Медицина, бытовая химия и т.д. Давайте устно решим с вами следующую задачу.
Для консервирования огурцов приготовили рассол: на 2л воды взяли 100г соли, а для консервирования томатов — рассол из 100г соли на 3л воды. Какой рассол получился более
В результате обсуждения ученики делают вывод, что чем больше растворителя при равном количестве растворенного вещества, тем меньше концентрация. Здесь проводим аналогию с правилом сравнения двух дробей с одинаковыми числителями.
Учитель обращает внимание на то, что только для воды 1л=1кг. Для других жидких веществ это равенство не выполняется. Необходимая запись делается на доске.
Учитель химии . Ребята, %-ную концентрацию Вы научились считать. Теперь я хочу усложнить вам задачу.
Демонстрационный опыт №3
Предлагаю к рассмотрению два химических стакана. В первом стакане 100г раствора и растворено 10 г вещества. Чему равна процентная концентрация этого раствора?
( Один ученик выполняет вычисления на доске. Получает ответ 10%.)
Во втором стакане 50г раствора и растворено 5 г вещества. Чему равна процентная концентрация этого раствора?
( Другой ученик выполняет вычисления на доске. Получает ответ 10%.)
Мы убедились, что процентная концентрация одинаковая. Давайте смешаем эти два раствора. Какая получилась концентрация получившегося раствора?
Учащиеся работают самостоятельно. Предлагаются разные варианты ответов. Идет обсуждение и записывается правильный ответ: %-ная концентрация= ∙100%=10%.
Учитель математики . Давайте подведем промежуточный итог. Ответьте мне на вопросы:
Из чего состоит раствор? ( Из растворителя и растворенного вещества).
Как найти массу раствора? ( Масса раствора складывается из массы вещества и массы растворителя) .
Как посчитать %-ную концентрацию раствора?
Хорошо. А теперь давайте рассмотрим еще несколько задач.
№1. На полке 280 книг. Из них 70% по математике. Сколько книг по математике на полке?
Дети решают самостоятельно в тетрадях, потом один ученик записывает решение на доске.
Сравни с предыдущей и реши такую задачу.
№2. Сколько граммов сахара содержится в 250 граммах 12%-ного раствора сахара?
Чем похожи эти задачи?
В результате обсуждения приходят к выводу, что обе задачи на нахождении части от целого.
№3. В шкафу 64 книги на английском языке, что составляет 40% от всех книг. Сколько всего книг в шкафу?
Дети решают самостоятельно в тетрадях.
Сравни с предыдущей и реши такую задачу.
№4. Найди массу 10%-ного раствора соли, если известно, что соли в растворе 0,2 кг.
Чем похожи эти задачи? Приходим к выводу, что эти две задачи на нахождение целого по его части.
Учитель химии . А я предлагаю вам такую задачу.
№5. В лаборатории имеется 2л 18%-ного раствора щелочи. В раствор добавили 2л воды. Каким стало процентное содержание щелочи в новом растворе?
Идет обсуждение решения.
Сколько щелочи было первоначально в растворе? 2∙0,18=0,36(л)
Какой стала масса раствора после добавления воды? 2+2=4(л)
Найдите %-ную концентрацию раствора. ∙100%=9%
Учитель химии . Сегодня на уроке у вас было первое знакомство с наукой химией. Мы начали урок с «волшебства», давайте и закончим его «волшебством».
Демонстрационный опыт №4
Предлагается опыт, напоминающий извержение вулкана.( В результате сжигания бихромата аммония выделяется азот, происходит изменение оранжевого цвета на серо-зеленый.)
Каталог статей
• 9%-я концентрация раствора соли — это 9 грамм соли в 100 граммах раствора.
Задача из Петерсона 6 класс (2010 г.) № 322 (2)
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
• 1 кг — масса растворённого вещества (соли)
• 9 кг — масса воды в растворе (не путать с общей массой раствора)
• 9 + 1 = 10 кг — общая масса раствора.
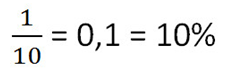
Ответ: 10% — концентрация раствора.
Задача из Петерсона 6 класс (2010 г.)
Теперь решим обратную задачу.№ 353(2)
Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.
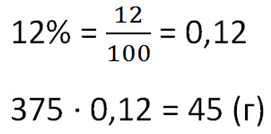
Ответ: 45 г соли.
Сложная задача на растворы
В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за x первоначальную массу соли в растворе, а за y массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
100% — 40%= 60%
Изобразим графически условия задачи. 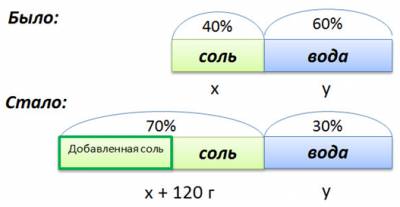
Составим пропорцию, связывающую эти величины до добавления соли.
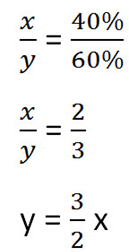
Для решения задачи нам надо определить какая из неизвестных (x или y) остаётся неизменной после добавления соли.
Этой величиной является масса воды в растворе (y).
Выразим её, учитывая изменения в растворе после добавления соли.
• (x + 120) г — масса соли в новом растворе
• 100% — 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.
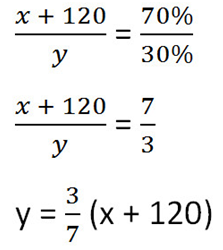
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.
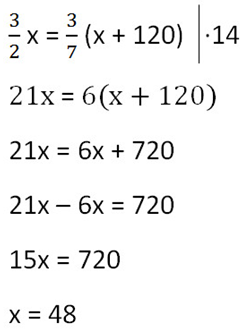
Ответ: 48 г — масса соли в первоначальном растворе.
Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что
называется концентрацией раствора.
Запомните!
![]()
Концентрация раствора — это часть, которую составляет масса растворённого вещества от
массы всего раствора.
- 9%-я концентрация раствора соли — это 9 грамм соли в
100 граммах раствора.
Разбор примера
Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора?
(Масса 1 л воды составляет 1 кг)
Используя определение концентрации данное выше, решим задачу следующим образом.
- 1 кг — масса растворённого вещества (соли)
- 9 кг — масса воды в растворе (не путать с общей массой раствора)
- 9 + 1 = 10 кг — общая масса раствора.
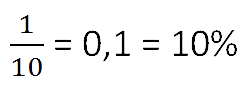
Ответ: 10% — концентрация раствора.
Разбор примера
Теперь решим обратную задачу.
Сколько соли получится при выпаривании 375 граммов 12%-го раствора?
Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации.
Не забудем предварительно перевести процент в десятичную дробь.
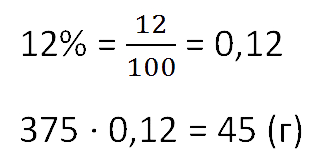
Ответ: 45 г соли.
Сложная задача на растворы
В растворе 40% соли. Если добавить 120 г соли,
то процентное содержание соли станет равным 70.
Сколько грамм соли было первоначально в растворе?
Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а
за «y» массу
воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
100% − 40%= 60%
Изобразим графически условия задачи.
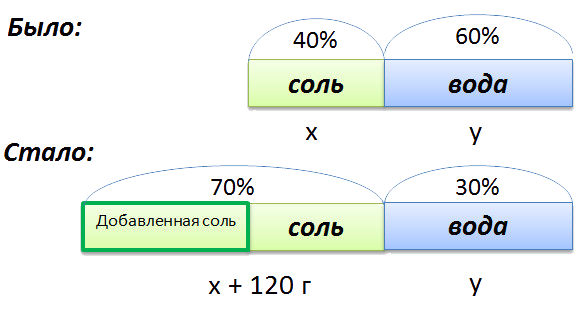
Составим пропорцию, связывающую эти величины до добавления соли.
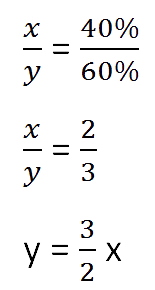
Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной
после добавления соли.
Этой величиной является масса воды в растворе «y».
Выразим её, учитывая изменения в растворе после добавления соли.
- (x + 120) г — масса соли в новом растворе
- (100% − 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших
после добавления соли.
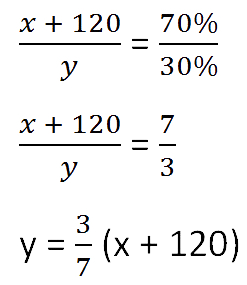
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и
после добавления соли и решим уравнение.
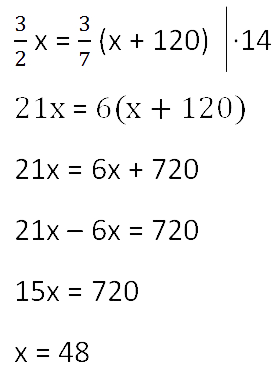
Ответ: 48 г — масса соли в первоначальном растворе.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
31 октября 2016 в 18:30
Роман Роршахов

Профиль
Благодарили: 0
Сообщений: 1

Роман Роршахов
Профиль
Благодарили: 0
Сообщений: 1
Сколько граммов 6%-ного раствора соли можно получить из 300 г жидкости содержащей 40% этой соли?
0
Спасибо
Ответить
5 ноября 2016 в 21:36
Ответ для Роман Роршахов
София Деревянко

Профиль
Благодарили: 0
Сообщений: 2

София Деревянко
Профиль
Благодарили: 0
Сообщений: 2
Если соли 40%, то воды — 60%. проценты характеризуют массовые доли, значит в растворе 120 г соли. Для нахождения массы раствора составляем пропорцию, которую можно прочитать так ЕСЛИ 120 Г СОЛИ СОСТАВЛЯЕТ 6 % ОТ ВСЕГО РАСТВОРА, ТО ВЕСЬ РАСТВОР (100%) БУДЕТ ВЕСИТЬ Х г, 120: 6=Х: 100, отсюда находим Х=120: 6 · 100, вес всего раствора 2 кг. проверяем, 2000 г · 0,06 получается 120г. Количество соли не изменилось))))
0
Спасибо
Ответить
6 сентября 2015 в 12:03
Дарья Сидорова

Профиль
Благодарили: 0
Сообщений: 1

Дарья Сидорова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
6 сентября 2015 в 13:43
Ответ для Дарья Сидорова
Настюша Кирпичева

Профиль
Благодарили: 0
Сообщений: 1

Настюша Кирпичева
Профиль
Благодарили: 0
Сообщений: 1
1 3-
0
Спасибо
Ответить
2 сентября 2016 в 15:56
Ответ для Дарья Сидорова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
= ? · = ? = ===8
0
Спасибо
Ответить
22 апреля 2015 в 16:36
Амина Загребельная

Профиль
Благодарили: 0
Сообщений: 1

Амина Загребельная
Профиль
Благодарили: 0
Сообщений: 1
в морской воде содержится 5% соли, какую часть морской воды состовляет соль?
0
Спасибо
Ответить
14 апреля 2016 в 13:37
Ответ для Амина Загребельная
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В статье подробно описано, как это делается: http://math-prosto.ru/index.php?page=pages/percent/percent1.php
А именно: «Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.»
5: 100=0,05=
0
Спасибо
Ответить
Правило 1. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.
Решение задач на понятия “процентное содержание”, “концентрация”, “%-й раствор”.
Процентное содержание. Процентный раствор.
Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Решение.10 . 0,15 = 1,5 (кг) соли.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение: Процентное содержание вещества в сплаве – это часть, которую составляет вес данного вещества от веса всего сплава.
1) 10 + 15 = 25 (кг) – сплав;
2) 10/25 . 100% = 40% – процентное содержание олова в сплаве;
3) 15/25 . 100% = 60% – процентное содержание цинка в сплаве;
Ответ: 40%, 60%.
Концентрация.
Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.
Решение. 300 . 0,87 = 261 (г).
В этом примере концентрация вещества выражена в процентах.
Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Сумма концентраций всех компонент, составляющих смесь, равна 1.
Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к – концентрация вещества; р – процентное содержание вещества (в процентах).
Пример. Имеется 2 сплава, в одном из которых, содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Решение: Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится 0,4 . 20 = 8 (кг) серебра, в х кг второго сплава содержится 0,2х кг серебра, а в (20+х) кг нового сплава содержится 0,32 . (20+х) кг серебра. Составим уравнение:
8 + 0,2х = 0,32 . (20 +х); х = 13 1/3.
Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
Пример. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение. Пусть добавили х л 5%-ного раствора соли. Тогда нового раствора стало (15 + х) л, в котором содержаться 0,8 . (15 + х) л соли. В 15 л 10%-ного раствора содержится 15 . 0,1 = 1,5 (л) соли, в х л 5%-ного раствора содержится 0,05х (л) соли.
Составим уравнение.
1,5 + 0,05х = 0,08 . (15 + х);
х = 10.
Ответ: добавили 10 л 5%-ного раствора






