Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
– масса раствора = масса воды + масса соли;
– масса сплава равна сумме масс металлов, входящих в этот сплав;
– масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
Концентрация соли или процентное содержание соли в растворе – это отношение массы соли к массе раствора, записанное в виде процентов:
K=(mc/M)*100%,
где mс – масса соли, M – масса всего раствора, К – концентрация (процентное содержание) соли.
Концентрация вещества или процентное содержание вещества в смеси – это отношение массы вещества к массе смеси, записанное в виде процентов: K=(mв/M)*100%, где mв – масса вещества, M – масса всей смеси, К – концентрация (процентное содержание) вещества
Концентрация вещества или процентное содержание вещества в сплаве – это отношение массы вещества к массе сплава, записанное в виде процентов : K=(mв/M)*100%, где mв – масса вещества, M – масса всего сплава, К – концентрация (процентное содержание) вещества.
Пример раствора. Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор, его масса равна 180 + 20 = 200 грамм. Определим концентрацию соли (процентное содержание соли) в растворе: К= (20/(180+20))*100%=10% . Тогда процентное содержание воды 90%. (100%-10%=90%). Процентное содержание воды можно определить и так: Кв=(180/(180+20))*100%=90%. Результаты запишем в виде таблицы.
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Пример смеси. Возьмем и перемешаем одно ведро цемента с тремя ведрами песка. Получим смесь цемента с песком, её масса равна 1 + 3 = 4 (единиц массы). Определим концентрацию (процентное содержание) цемента в смеси : К=(1/(1+3))*100%=25%.. Концентрация (процентное содержание) песка в смеси 100%-25%=75%.
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Км= (270/600)*100%= 45%.
Концентрация (процентное содержание) цинка в смеси:
100%-45%=55%. Или Кц=((600-270)/600))*100%= 55%.
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве.
Из формулы K=(m/M)*100%, где m масса вещества, М – масса всего раствора ( смеси, сплава), получим, что масса вещества в растворе находится по формуле: m=(M*K)/100%.
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
Решение: 1 способ. 100% – 64% = 36% цинка в смеси,
mц=(900*36%)/100%=324г.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Ответ: 324г.
.
Последнее изменение: Четверг, 24 июля 2014, 21:53
Решение задач на смеси, сплавы и растворы с помощью таблиц
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Ворончихина А.В. 1
1МБОУ “ООШ № 12” Асбестовского городского округа
Самофалова В.В. 1
1МБОУ “ООШ № 12” Асбестовского городского округа
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
В пятом классе на уроках математики мы впервые встретились с процентами и с задачами на смеси, сплавы, растворы при изучении тем «Нахождение процентов от числа» и «Нахождение числа по его процентам».
Пример задачи на нахождение процентов от числа:
Сплав содержит 8% меди. Сколько килограммов меди содержится в 360 кг сплава?
Решение: – масса меди в данном сплаве.
Ответ: 28,8 кг
Пример задачи на нахождение числа по его процентам:
Раствор содержит 14% соли. Сколько килограммов раствора нужно взять, чтобы получить 49 кг соли?
Решение: – раствора потребуется, чтобы получить требуемое количество соли.
Ответ: 350 кг
В шестом классе на уроках математики мы снова встретились с задачами на смеси, сплавы, растворы при изучении темы «Процентное отношение двух чисел» мы находили концентрацию вещества.
Пример задачи на нахождение концентрации вещества:
Найти процент содержания соли в растворе, если 400 г раствора содержит 34 г соли.
Решение: – концентрация соли в данном растворе.
Ответ: 8,5%
Меня заинтересовали задачи на смеси, сплавы, растворы, так как они имеют огромное практическое значение. Например, нужно знать, как правильно приготовить маринад для консервирования, как смешать клей для обоев, как приготовить раствор для заливки фундамента дома, как разбавить уксусную кислоту для употребления в пищу и так далее.
Кроме всего прочего, как оказалась, эти задачи есть на ОГЭ по математике в 9 классе (задание 22) и на профильном ЕГЭ по математике в 11 классе (задание 11), поэтому мне стало интересно, смогу ли я решить эти задачи уже сейчас?
Проанализировав информационные источники по данной теме, я обратила внимание на то, что существуют различные способы решения задач на смеси, сплавы, растворы: решение с помощью модели, решение с помощью таблицы, решение методом прямоугольников, правило квадрата, решение с помощью расчетной формулы, решение графическим способом. Благодаря информационным ресурсам я выяснила, чторешение этих задач вызывает у учащихся затруднения и самостоятельно справиться с ними могут немногие, так как данный тип задач ранее встречался только на вступительных экзаменах в ВУЗы и олимпиадах.
На уроках математики, начиная с начальной школы, и по сей день, решая текстовые задачи, мы часто оформляли условие задач в виде таблицы, которую продолжали заполнять в процессе решения задачи. С помощью таблицы ранее я успешно решала задачи на движение, задачи на работу, задачи о походе в магазин за покупками и другие, поэтому я захотела научиться решать задачи на смеси, сплавы, растворы именно с помощью таблицы.
Цель проекта: научиться решать задачи на смеси, сплавы, растворы с помощью таблицы.
Задачи:
Познакомиться с основными типами задач на смеси, сплавы, растворы.
Понять особенности решения задач на смеси, сплавы, растворы с помощью таблицы.
Разобрать решение основных типов задач на смеси, сплавы, растворы с помощью таблицы.
Отработать полученные знания при решении нетрудных задач.
Попробовать решить несколько сложных задач.
Гипотеза: опираясь на знания по математике, полученные в 5-6 классах, и познакомившись с особенностями решения задач на смеси, сплавы, растворы с помощью таблицы, можно решить любую задачу на смеси, сплавы, растворы из банка задач ОГЭ и ЕГЭ.
1. Теоретическая часть
1.1. Классификация и примеры задач на смеси, сплавы, растворы
Задачи на понижение или повышение концентрации:
Сироп содержит 18% сахара. Сколько кг воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?
В сосуд, содержащий 6 литров 20% водного раствора некоторого вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?
Задачи на «высушивание»:
Пчелы перерабатывают цветочный нектар в мед, освобождая его от воды. Нектар содержит 84% воды, а полученный мед – 20%. Сколько кг нектара нужно переработать пчелам для получения 1 кг меда?
Свежие фрукты содержат 72% воды, а сухие – 20% воды. Сколько сухих фруктов получится из 20 кг свежих?
Собрали 42 кг свежих грибов, содержащих по массе 95% воды. Когда их подсушили, они стали весить 3 кг. Каков процент содержания воды по массе в сухих грибах?
Задачи на смешивание растворов разных концентраций:
Один раствор содержит 20% соли, а второй 70 %. Сколько граммов первого и второго растворов нужно взять, чтобы получить 100 г 50% солевого раствора.
Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20% олова. Второй, массой 200 г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков.
Первый сплав содержит 5% меди, второй 14% меди. Масса второго сплава больше массы первого сплава на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найти массу третьего сплава.
1.2. Особенности решения задач на смеси, сплавы, растворы с помощью таблицы
Таблица для решения задач на понижение или повышение концентрации, а также задач на смешивание растворов разных концентраций имеет примерно такой вид:
|
1-ый |
2-ой |
Смешали |
|
|
общая масса |
|||
|
концентрация |
|||
|
масса чистого вещества |
В роли одного из растворов может быть вода или чистое вещество, например к сплаву меди добавляется медь; столбиков может быть больше, если смешивается более двух веществ; в сложных задачах, возможно, придется сделать не одну таблицу.
Таблица для решения задач на высушивание имеет вид:
|
«фрукт» |
«сухофрукт» |
|
|
общая масса |
||
|
концентрация |
||
|
масса чистого вещества |
(концентрация = 100% – процент воды)
Замечания по заполнению таблиц:
Сначала читаем условие задачи и вносим известные данные в таблицу (при необходимости можно что-то принять за ).
Затем заполняем таблицу преимущественно по столбикам.
Способ 1 (с помощью пропорции).
общая масса – 100%
масса чистого вещества – концентрация
можно выписать пропорцию:
далее можно действовать по правилам нахождения неизвестного члена пропорции:
Способ 2 (нахождение процента от числа, числа по его процентам, процентное отношение двух чисел).
Заполняя таблицу по строчкам, учитываем следующее:
при смешивании двух веществ
при переливании
по третьей строчке часто получается уравнение, поэтому в первую очередь стараемся заполнить столбики
Если в роли одного из растворов выступает вода, учитываем следующее:
Если в роли одного из сплавов выступает чистое вещество, учитываем следующее:
При решении задач на высушивание учитываем следующее:
2. Практическая часть
2.1. Решение задач на повышение или понижение концентрации
Задача №1 (способ 1)
Сироп содержит 18% сахара. Сколько кг воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?
Решение:
|
сироп |
вода |
смешали |
|
|
общая масса |
40 кг |
8 кг |
48 кг |
|
концентрация |
18% |
0% |
15% |
|
масса чистого вещества |
7,2 кг |
0 кг |
7,2 кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
40 кг – 100%
? кг – 18%
– масса чистого вещества в первоначальном сиропе;
– масса чистого вещества в разбавленном сиропе;
? кг – 100%
7,2 кг – 15%
– общая масса разбавленного раствора
– масса добавленной воды.
Ответ: 8 кг
Задача №1 (способ 2)
Сироп содержит 18% сахара. Сколько кг воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?
Решение:
|
сироп |
вода |
смешали |
|
|
общая масса |
40 кг |
8 кг |
48 кг |
|
концентрация |
18% |
0% |
15% |
|
масса чистого вещества |
7,2 кг |
0 кг |
7,2 кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
– масса чистого вещества в первоначальном растворе;
– масса чистого вещества в разбавленном сиропе;
– общая масса разбавленного раствора;
– масса добавленной воды.
Ответ: 8 кг.
Задача №1 (способ 3)
Сироп подержит 18% сахара. Сколько кг воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?
Решение:
|
сироп |
вода |
смешали |
|
|
общая масса |
40 кг |
х кг |
(40+х) кг |
|
концентрация |
18% |
0% |
15% |
|
масса чистого вещества |
(7,2)кг |
0 кг |
(0,15(40+х)) кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
пусть масса добавленной воды, тогда масса разбавленного сиропа
– масса чистого вещества в первоначальном сиропе;
– масса чистого вещества в разбавленном сиропе;
уравнение:
Ответ: 8 кг.
Задача №2
В сосуд, содержащий 6 литров 20% водного раствора некоторого вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение:
|
раствор |
вода |
смешали |
|
|
общая масса |
6 л |
6 л |
12 л |
|
концентрация |
20% |
0% |
10% |
|
масса чистого вещества |
1,2 л |
0 л |
1,2 л |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
– общая масса смеси;
– масса чистого вещества в первоначальном растворе;
-масса чистого вещества в смеси;
– концентрация получившейся смеси;
Ответ: 10%.
Задача №3
Сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?
Решение:
|
слав |
медь |
смешали |
|
|
общая масса |
36 кг |
х кг |
(х+36) кг |
|
концентрация |
45% |
100% |
60% |
|
масса чистого вещества |
16,2 кг |
х кг |
(0,6(х+36)) кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
пусть общая масса добавленной меди, тогда или общая масса получившейся смеси
– масса чистого вещества в первоначальном сплаве;
– масса чистого вещества в получившемся сплаве;
уравнение:
.
Ответ: 14,5 кг.
2.2. Решение задач на «высушивание»
Задача №4
Пчелы перерабатывают цветочный нектар в мед, освобождая его от воды. Нектар содержит 84% воды, а полученный мед – 20%. Сколько кг нектара нужно переработать пчелам для получения 1 кг меда?
Решение:
|
нектар |
мед |
|
|
общая масса |
5 кг |
1 кг |
|
концентрация |
16 % |
80% |
|
масса чистого вещества |
0,8 кг |
0,8 кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
– концентрация нектара;
– концентрация меда;
– масса чистого вещества в меде (и в нектаре);
– масса нектара, который потребуется.
Ответ: 5 кг.
Задача №5
Свежие фрукты содержат 72% воды, а сухие – 20% воды. Сколько сухих фруктов получится из 20 кг свежих?
Решение:
|
свежие фрукты |
сухие фрукты |
|
|
общая масса |
20 кг |
7 кг |
|
концентрация |
28% |
80% |
|
масса чистого вещества |
5,6 кг |
5,6 кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
– концентрация свежих фруктов;
– концентрация сухих фруктов;
– масса чистого вещества в свежих фруктах (и в сухих фруктах);
– масса сухих фруктов.
Ответ: 7 кг.
Задача №6
Собрали 42 кг свежих грибов, содержащих по массе 95% воды. Когда их подсушили, они стали весить 3 кг. Каков процент содержания воды по массе в сухих грибах?
Решение:
|
свежие грибы |
сухие грибы |
|
|
общая масса |
42 кг |
3 кг |
|
концентрация |
5 % |
70 % |
|
масса чистого вещества |
2,1 кг |
2,1 кг |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
– концентрация свежих грибов;
– масса чистого вещества в свежих грибах (и в сухих);
– концентрация сухих грибов.
Ответ: 70%.
2.3. Решение задач на смешивание растворов разных концентраций
Задача №7.
Один раствор содержит 20% соли, а второй 70 %. Сколько граммов первого и второго растворов нужно взять, чтобы получить 100 г 50% солевого раствора.
Решение:
|
1-ый |
2-ой |
смешали |
|
|
общая масса |
х г |
(100-х) г |
100 г |
|
концентрация |
20% |
70% |
50% |
|
масса чистого вещества |
(0,2х) г |
(0,7(100-х)) г |
50 г |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
пусть общая масса 1-го раствора, тогда общая масса 2-го раствора.
– масса чистого вещества в 1-м растворе;
– масса чистого вещества во 2-м растворе;
– масса чистого вещества в смеси;
уравнение:
Ответ: 40 г, 60 г.
Задача № 8
Даны два куска с различным содержанием олова. Первый, массой 300 г, содержит 20% олова. Второй, массой 200 г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков.
Решение:
|
1-ый |
2-ой |
смешали |
|
|
общая масса |
300 г |
200 г |
500 г |
|
концентрация |
20% |
40% |
28% |
|
масса чистого вещества |
60 г |
80 г |
500 г |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
– масса чистого вещества в 1-м сплаве;
– масса чистого вещества во 2-м сплаве;
– масса чистого вещества в получившемся сплаве;
– общая масса получившегося сплава;
– концентрация получившегося сплава.
Ответ: 28%
Задача №9
Первый сплав содержит 5% меди, второй 14% меди. Масса второго сплава больше массы первого сплава на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найти массу третьего сплава.
Решение:
|
1-ый |
2-ой |
смешали |
|
|
общая масса |
х г |
(х+10) г |
(2х+10) г |
|
концентрация |
5% |
14% |
11% |
|
масса чистого вещества |
(0,05х) г |
(0,14(х+10)) г |
(0,11(2х+10)) г |
Замечание: жирным шрифтом с подчеркиванием в таблицу внесены данные, которые находятся в процессе решения.
пусть общая масса 1-го раствора, тогда общая масса 2-го раствора и общая масса 3-го раствора.
– масса чистого вещества в 1-м растворе;
– масса чистого вещества во 2-м растворе;
– масса чистого вещества в 3-м растворе;
уравнение:
Ответ: 30 г
Заключение
Благодаря проделанной работе я убедилась в том, что решение задач на смеси, сплавы, растворы с помощью таблицы возможно, если знать особенности решения этих задач таким способом и опираться на знания по математике, полученные в 5-6 классах. Моя гипотеза была верной. Решение задач на смеси, сплавы, растворы с помощью таблицы часто можно осуществить даже без составления уравнения. В некоторых задач не обойтись без введения неизвестной, составления и решения уравнения.
Работая над проектом, я изучила типы задач на смеси, сплавы, растворы в банке задач ОГЭ и ЕГЭ по математике, и заметила, что большую часть задач могу решить уже сейчас (это шесть видов задач из восьми имеющихся). В банке задач я обратила внимание на две сложные задачи, при решении которых придется составить две таблицы, ввести две неизвестных, составить два уравнения (по одному из каждой таблицы). Я сделала вывод, что мне не достаточно имеющихся знаний, чтобы решить эти две задачи (при решении этих задач составляется система уравнений, а системы уравнений мы научимся решать на уроках алгебры в 7 классе).
Работая над проектом, я научилась решать основные типы задач на смеси, сплавы, растворы с помощью таблицы и поняла, что это очень удобный и понятный способ решения таких задач. Я уверенна, что полученные знания и умения пригодятся мне на ОГЭ и ЕГЭ по математике. Также я считаю, что эти знания и умения пригодятся мне на уроках химии и обязательно пригодятся в повседневной жизни. Я думаю, что без труда смогу научить своих одноклассников решать задачи такого типа с помощью таблиц. Материал моего проекта будет полезен учащихся выпускных классов как пособие для подготовки к ОГЭ и ЕГЭ.
Список использованной литературы
Задачи на смеси и сплавы. Журнал «Математика в школе». №17. №11 2004г.
Захарова А.Е. Учимся решать задачи на смеси и сплавы // Математика для школьников. 2006.
Образовательный портал для подготовки к экзаменам.- http://reshuege.ru
Интернет ресурс – [эл. ресурс] – режим доступа, http://ru.wikipedia.org
Прокопенко Н.И. Задачи на смеси и сплавы / Н.И. Прокопенко. – М.: Чистые пруды, 2010.
Цыганов Ш.И. Все задачи ЕГЭ по математике прошлых лет: Учебное пособие / Ш. И. Цыганов – 4-е изд., дополненное – Уфа: Центр педагогических измерений, 2008-324с.
Просмотров работы: 7889
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
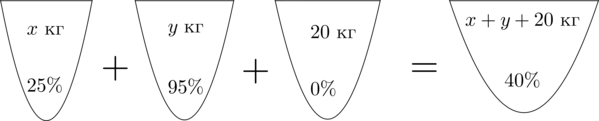
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
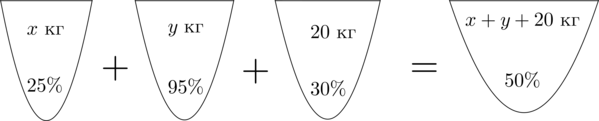
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

УСТАЛ? Просто отдохни
Здравствуйте, дорогие читатели, подписчики и гости канала. Продолжаем разбор текстовых задач из ОГЭ 2021 года, входящие в 21 задание. В этом выпуске рассмотрим решение задач на проценты.
Задача №1
Оформим задачи в виде таблицы.
Чтобы найти, сколько чистого вещества находится в растворе, нужно массу всего раствора умножить на его концентрацию. В четвертом столбце приведены расчеты, для вычисления чистого вещества (кислоты) в каждом растворе. Третий раствор получили смешиванием первого и второго раствора. В результате этого получили третий раствор массой 10 кг в котором содержится 6,2 кг кислоты.
Найдем концентрацию получившегося раствора:
Задача №2
Когда в задаче сказано, что массы сплавов или веществ одинаковы, то лучше всего брать их равными 1 кг.
Масса четвертого сплава равна сумме трех сплавов, взятых каждого по 1 кг, т.е. 3 кг. В четвертом столбце найдена масса никеля в каждом сплаве на 1 кг. Значит в четвертом сплаве на 1 кг сплава, содержится 0,75 кг никеля.
Найдем концентрацию никеля в четвертом сплаве и его процентное содержание:
Следующие две задачи будут немного сложней. Каждая задача будет состоять из двух частей.
Задача №3
Первая часть задачи, выделена зеленым цветом, первое предложение. Составим таблицу по первому предложению. За массу первого вещества возьмем Х, масса второго вещества – Y.
Вода добавляется в раствор, поэтому масса чистого вещества не изменится.
Составим уравнение:
Рассмотрим вторую часть задачи, в которой добавляется в раствор не вода, а водный раствор кислоты. Выделен красным цветом.
В данном случае в раствор добавляем 10 кг кислоты, чистое вещество увеличится на 5 кг.
Составим уравнение:
У нас получилось два уравнения. Составим систему уравнений, и найдем массу 30% – ного раствора кислоты, которую брали в начале задачи за Х.
Задача №4 Несколько раз встречалась на экзамене.
Первая часть задачи выделена синим цветом. В тексте написано “растворы различной концентрации”, значит на Х и Y возьмем концентрации раствором. Оформим все в таблицу:
Третий раствор, получаем сливанием вместе первого и второго вещества. В четвертом столбце найдем массу чистого вещества в первом и втором растворе. Составим уравнение по чистому веществу:
Составим таблицу по второй части задачи, которая выделена красным цветом. Во второй части сказано, что массы растворов взяты одинаковы. Возьмем массу первого и второго вещества равным 1 кг.
Второе уравнение составим также по чистому веществу:
У нас получилось два уравнения. Составим систему уравнений, и найдем массу кислоты во втором растворе.
Спасибо, что дочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.
Путеводитель по каналу здесь