Инфоурок
›
Математика
›Презентации›Презентация по теме “Процентное отношение двух чисел”, 6 класс
Скачать материал
без ожидания
Скачать материал
без ожидания
- Сейчас обучается 124 человека из 40 регионов
- Сейчас обучается 75 человек из 34 регионов
- Сейчас обучается 36 человек из 27 регионов
Описание презентации по отдельным слайдам:
-
1 слайд
16.12 Классная работа
Процентное отношение двух чисел. -
-
3 слайд
Такие задачи нам приходится решать в жизни каждый день. Учебный день в школе начинается с вопроса Сколько процентов учащихся отсутствуют в классе?
-
4 слайд
Всего: 30 ————100%
3 ———— х%Х = 3 30 *100% = 3 ∗100 30 = 300 30 = 10%
-
5 слайд
Вспомним сведения из 5 класса.
1.Что называется процентом?
Сотую часть рубля называют копейкой, сотую часть метра – сантиметром, сотую часть гектара – аром или соткой. -
6 слайд
Принято называть сотую часть величины или числа процентом. Значит одна копейка – один процент от одного рубля, а один сантиметр – один процент от одного метра, один ар – один процент гектара, две сотых – один процент от числа два.
-
7 слайд
ОДИН ПРОЦЕНТ – ЭТО ОДНА СОТАЯ ДОЛЯ ЧИСЛА.
-
8 слайд
Определение одного процента можно записать равенством:
1% = 0,01 ; а%=0,01*а.
Каждый быстро сообразит, что 5%=0,05, 23%=0,23, 130%=1,3 и т. д -
9 слайд
Как найти процент от числа?
Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов . -
10 слайд
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
-
11 слайд
В 6 классе учатся 12 девочек и 20 мальчиков. Найти процентное отношение количества девочек к количеству мальчиков.
Девочек – 12
Мальчиков – 20Процентное отношение количества девочек к количеству мальчиков равно:
12 20 *100 = 60%
-
12 слайд
А вот число
𝟐𝟎 𝟏𝟐 * 100= 166 𝟐 𝟑 %показывает, что количество мальчиков составляет 166 2 3 % от количества девочек.
𝟐𝟎 𝟑𝟐 * 100= 62,5%
показывает, какой процент составляет количество мальчиков от количества учащихся всего класса.
-
13 слайд
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100 и к результату дописать знак %.
Например: вычислить, сколько процентов составляет число 52 от числа 400.
52 от числа 400.
По правилу:
𝟓𝟐 𝟒𝟎𝟎 ×100%=13%. -
14 слайд
В парке растет 400 деревьев, из них 96 –ели. Сколько % -тов всех деревьев парка составляют ели?
-
15 слайд
Решение:
400деревьев ——100%
96 деревьев ——- х%Х = 96∗100 400 = 96∗1 4 = 24%
Ответ: 24%
-
16 слайд
Пример 2.
Стоимость товара возросла со 150 р. До 240 р. На сколько % – тов увеличилась стоимость товара -
17 слайд
Решение:
150р. ——-100%
240 р. ——- х %Х = 240∗100 150 = 240∗10 15 = 240∗2 3 = 80∗2 1 = 160%
160% – 100% = 60% – составляет увеличение товара.
Ответ: на 60% -
-
19 слайд
Устно:
стр. 125 №1,2 -
20 слайд
В классе:
№633, 634(1-3), 636(1-3), 638(1-3) стр125 -
21 слайд
Что вы узнали сегодня на уроке?
Чему вы научились сегодня?
Что вызывало у вас затруднения в начале урока и что стало понятно в течение урока?
2) Какие моменты урока особенно понравились? Когда вам было неуютно? Почему? -
22 слайд
Домашнее задание: п.21,выучить правила, № 635, 637.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 195 материалов в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Рейтинг:
5 из 5
- 21.01.2021
- 1315
- 121
- 20.01.2021
- 179
- 2
- 20.01.2021
- 360
- 24
- 20.01.2021
- 208
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Сороковикова Марина Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 3 года и 1 месяц
- Подписчики: 0
- Всего просмотров: 41664
-
Всего материалов:
68
Частное двух чисел называют отношением этих чисел. Отношение можно записать как арифметическое действие «деление», а можно как обыкновенную дробь.
(a:b=frac{a}{b}) – так записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член.
Например: отношение 75 к 25 можно записать в виде: (75:25=frac{75}{25}=3).
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Процентное отношение
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например: вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: (52:400cdot100%=13 %).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Примеры.
Задача 1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий – это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 – 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 (Rightarrow 1100:1200cdot100%=91,7%).
2-й вариант
Решение:
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2 300 от 1 200 (Rightarrow 2300:1200cdot100%=191,7%).
2) На сколько процентов перевыполнен план?
(191,7%-100%=91,7%).
Ответ: на 91,7%.
Задача 2. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Решение:
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
(150:500cdot 100%=frac{150}{500}cdot 100% )(=frac3{10}cdot 100%=0,3cdot 100%=30%).
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Задача 3. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Решение:
Для ответа на вопрос задачи надо найти отношение (частное) числа 45 к 36 и выразить его в процентах: (45:36cdot 100%=1,25cdot 100%=125%).
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 
и 
– члены отношения; число – предыдущий член отношения; – последующий член отношения.
Например:
14 : 7 – отношение числа 14 к числу 7;
6 : 25 – отношение числа 6 к числу 25;
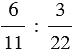– отношение числа 
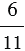к числу 
;
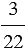1,15 : 0,36 – отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и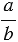 
.
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
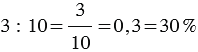
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел – это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
.
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
.
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб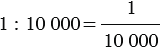 
, то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 
длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : = 1 : 10 000;
Решаем данное уравнение:
= 5
10 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 585,
Мерзляк, Полонский, Якир, Учебник
Номер 668,
Мерзляк, Полонский, Якир, Учебник
Номер 689,
Мерзляк, Полонский, Якир, Учебник
Номер 1070,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Задание 758,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 821,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 823,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 149,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 230,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 303,
Мерзляк, Полонский, Якир, Учебник
Отношение. Процентное отношение двух чисел
Частное двух чисел называют отношением этих чисел.
Так с помощью букв записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член. (Напоминание: дробная черта означает знак деления).
Процентное отношение.
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например, вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: 52 : 400 × 100 — 13 (%).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Решения задач на процентное отношение двух чисел редко предполагают только одно действие. Чаше решение таких задач состоит из 2-3 действий.
Примеры
Задача 1.
Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий — это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 — 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 => 1 100 : 1 200 × 100 = 91,7 (%).
2-й вариант
Решение:
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2 300 от 1 200 => 2 300 : 1 200 ×100 = 191,7 (%).
2) На сколько процентов перевыполнен план?
191,7 — 100 = 91,7 (%)
Ответ: на 91,7%.
Задача 2.
Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Решение
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
150/500 = 3/10 = 0,3 = 30 %
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Задача 3.
Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Решение
Для ответа на вопрос задачи надо найти отношение (частное) числа 45 к 36 и выразить его в процентах:
45 : 36 = 1,25 = 125 %.
Задача 4.
В семенах сои содержится 20 % масла. Сколько масла содержится в 700 кг сои?
Решение.
В задаче требуется найти указанную часть (20 %) от известной величины (700 кг). Такие задачи можно решать способом приведения к единице. Основное значение величины – 700 кг. Её мы можем принять за условную единицу. А условная единица и есть 100 %. Так как пропорциональная зависимость прямая Кратко условия задачи можно записать так:
Составим пропорцию и найдем неизвестный член пропорции:
Ответ: 140кг.
Нахождение числа по его процентам.
Задача 1.
Из хлопка-сырца получается 24 % волокна. Сколько надо взять хлопка-сырца, чтобы получить 480 кг волокна?
Решение
480 кг волокна составляют 24 % от некоторой массы хлопка-сырца, которую примем за Х кг. Будем считать, что Х кг составляют 100 %. Теперь кратко условие задачи можно записать так:
Ответ: 2000кг = 2т.
Эту задачу можно решить и иначе.
Если в условии этой задачи вместо 24 % написать равное ему число 0,24, то получим задачу на нахождение числа по известной его части (дроби). А такие задачи решают делением. Отсюда вытекает ещё один способ решения:
1) 24 % = 0,24; 2) 480 : 0,24 = 2000 (кг) = 2 (т).
Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби и решить задачу на нахождение числа по данной его дроби.
Вопросы к конспектам
В саду растет 5 кустов желтых роз. Это составляет 25% от всех роз в саду. Сколько кустов роз в саду?
Приведите отношение к отношению натуральных чисел:
В аэропорту ждут прибытия самолета 1200 пассажиров. 45% из них мужчины. 15% общего числа женщин и детей составляют дети. Найдите число мужчин и число детей?
В классе 25 учеников, 40% (сорок процентов) из них девочки. Сколько девочек в классе?
На стоянке стоит 40 машин, 8 из них фирмы Рено. Какой процент машин фирмы Рено от всех стоящих на стоянке?
Проволоку длиной 162 м разрезали на три части в пропорций 3:2:1. Найдите длину каждой части.
Разделить 70 на две части так, чтобы одна часть составляла 40% от другой
Разделить 85 на две части так, чтобы одна часть составляла 70% от другой
Сплав содержит 20 % железа и 40% меди, остальное – бронза. Определите массу бронзы, если масса сплава 5 кг.
Чтобы доехать до базы отдыха, турист проехал 80км, что составляет 40% всего пути. Какое расстояние осталось проехать, чтобы доехать до базы?
