Как найти процентное содержание для 6 классов

Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.

Задачи:

Образовательные

• повторить понятия проценты, отношения;
• закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
• показать практическую значимость математических знаний для решения задач на концентрацию.

Воспитательные

• показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
• воспитание у учащихся интереса к предмету.

Развивающие

• развивать наблюдательность, логическое мышление учащихся;
• развивать жизненную смекалку и интуицию.

Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.

План урока:

1. Мотивационный момент (1 минута).
2. Подготовка учащихся к сознательному усвоению нового материала (5 минут).
3. Изучение нового материала (12 минут).
4. Решение задач на отработку формул (3 мин).
5. Физминутка (1 минута).
6. Первичное закрепление нового материала (15минут).
7. Рефлексия (1 минута).
8. Подведение итогов. Домашнее задание (2 минуты).

Ход урока

I. Мотивационный момент.

Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.

II. Подготовка к сознательному усвоению нового материала.

(Слайд 2)

1. Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
2. Указать в виде процентов: 0,7; 0,04; 1,3.
3. Найти 15% от числа 60.
4. Найти число, 15% которого равны 30.
5. Из 25 семян взошло 24 семени. Найдите процент всхожести.
6. Итак, известные нам отношения: (Слайд 3)

Всхожесть = ; .

Значения данных отношений мы представляли в виде процентов.

III. Изучение нового материала.

Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?

В большом энциклопедическом словаре «концентрация (от новолат. concentratio) – сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].

Концентрация в химии – величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].

Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)

Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]

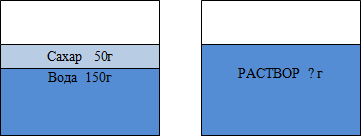
50+150=200 (г) – масса общая. (Слайд 5)

Раствор тщательно перемешиваем.

Найдите процентное содержание сахара в растворе.

50 : 200=1: 4 = 0,25;

0,25=25%

25% – процентное содержание сахара в данном растворе.

Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)

Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).

Концентрация = , т.е. К=.

Как по этой формуле найти М_ч.в? М_общ?

М_ч.в. = М_общ · К

М_общ = Мч.в: К

(Слайд 7)

IV. Решение задач на отработку формул:

(Слайд 8)

1. В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
2. 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
3. Какова масса раствора, в котором 150 г сахара составляют 25%.

Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)

Рис.1.

Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».

Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.

V. Физминутка.

(Слайд 11)

Следите глазами за движениями черепашек.

VI. Первичное закрепление нового материала.

Решим несколько задач на «концентрацию».

(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.

Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)

Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.

Решение:

1. Какова масса раствора в первой банке?
   480+120 = 600 (г)

2. Какова концентрация сахара в растворе первой банки?
   120:600 = 0,2; 0,2=20%

3. Какова масса раствора во второй банке?
   840+160 = 1000(г)

4. Какова концентрация сахара в растворе второй банки?
   160:1000 = 0,16; 0,16=16%

5. В какой банке вода слаще?
   20% > 16%

Ответ: в первой банке вода слаще.

Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)

Решение:

80% – это процентное содержание соли в 200г раствора (концентрация 0,8)

1. Сколько г соли в этом растворе?
   0,8 ·200=160(г)

20% – это содержание соли в 700 г раствора (концентрация соли 0,2)

1. Сколько г соли во втором растворе?
   0,2·700=140 (г)
2. Сколько г соли в полученном растворе?
   160+140=300 (г)

Ответ: 300 г.

Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)

Решение:

50% – процентное содержание соли в 200 г растворе (концентрация 0,5).

1. Сколько г соли в этом растворе?
   0,5·200=100 (г)
   Что мы знаем про второй раствор? – Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25)

2. Какова масса второго раствора?
   150:0,25= 600 (г)
   Чтобы найти концентрацию соли в новом растворе, что надо знать? – Массу соли и массу всего раствора.

3. Какова масса соли в двух растворах?
   100+150=250 (г)

4. Какова масса нового раствора?
   200+600 =800 (г)

5. Какова концентрация соли в новом растворе?
   250:800=0,3125; 0,3125 = 31,25%

Ответ: 31,25%.

Задача для самостоятельного решения (дома).

Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]

Решение:

1. Сколько кг соли в морской воде?
   0,05·30=1,5 (кг)
   Пресная вода содержит соль? – Нет. – Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015.

2. Какова масса нового раствора (с добавлением пресной воды)?
   1,5: 0,015= 100 (кг)

3. Сколько пресной воды нужно добавить?
   100 – 30 = 70 (кг)

Ответ: 70 кг.

VII. Этап рефлексии.

(Слайд 18)

Ответ на листочке:

• Сегодня я узнал….
• У меня получилось…
• Было трудно….
• Было интересно….
• Теперь я умею…

VIII. Итог урока. Домашнее задание.

(Слайд 19)

№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.

Используемая литература:

1. Большой энциклопедический словарь. -2-е изд., перераб.и доп. – М.:Большая Российская энциклопедия, 1998. – 1456 с.: ил.
2. slovari. yandex.ru
3. urok.1sept.ru/articles/520040
4. Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – 8-е изд.-М.: Просвещение, 2006. – 302 с. :ил.
5. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. – 7-е изд., перераб. и доп. – М.: Высш.шк., 1994. – 528 с.: ил.

Автор Русанова Людмила Васильевна

Название работы: «Решение задач на процентное содержание вещества»

Краткая аннотация работы: В современном мире обучение требует современных и новаторских подходов. Данный урок-исследование  проведен в 6 классе, в соответствии с программой  по математике 6 класса по теме «Нахождение части от целого». Ученик, получает знания не в готовом виде, а, добывает их сам, что способствует активному успешному формированию его общекультурных и деятельностных способностей, общеучебных умений. Предполагает снятие всех стрессообразующих факторов учебного процесса, создание в классе доброжелательной атмосферы, ориентированной на реализацию идей сотрудничества, развитие диалоговых форм общения. Разработка такого урока требует большой затраты сил, энергии и времени, но с лихвой окупается позитивной мотивацией и интересом учащихся к учебно- познавательной деятельности.

Тип урока: систематизация, обобщение и расширение знаний по теме «Нахождение части от целого».

Основная цель: получение учащимися субъективно нового научного знания «Процентное содержание вещества».

Цели:

• Организовать исследовательскую деятельность учащихся по решению задач на процентное содержание вещества;
• Формирование учебно- познавательной компетенции: самостоятельная познавательная деятельность, включающая элементы логической деятельности.
• Формирование информационной компетенции: поиск, анализ и отбор необходимой информации.
• Содействовать воспитанию активной личности, самостоятельно предлагать, реализовывать свои пути и пути решения.

Задачи урока:

• Повторить понятие процента;
• Вспомнить вид задачи «Нахождение части по его целому»;
• Научить решать задачи на растворы и сплавы.

Оборудование: компьютеры, весы,мензурка, вода, медный купорос, стеклянная палочка.

Ход урока

№	Этап урока	Деятельность учителя	Деятельность ученика
1	Орг.момент	Проверка готовности к уроку	Организация рабочего места
2	Мотивация	Сегодня мы будем не просто математиками, а исследователями. Мы откроем новые знания.  Внимание! Начинаем урок!
3	Актуализация знаний	5%=? Ответьте на данный вопрос. Задача 1. 60 г водного раствора содержит 5% медного купороса.	Запись в тетради 5%= 0.05 Обратим в десятичную дробь
4	Создание проблемной ситуации	Задайте вопрос к данной ситуации. Вопрос: Как найти часть от его целого?	Сколько медного купороса в растворе? Решение: Целое    дробь   часть         60 г          0.05         ? Чтобы найти часть от целого, надо целое умножить на дробь. 600,05=3 г- медного купороса Ответ: 3 г медного купороса. 5% -это процентное содержание медного купороса
5	Исследование	Приготовим водный раствор, содержащий 5% медного купороса.	Алгоритм: 1.Взвесим 3г медного купороса (на лабораторных  весах); 2.Пересыпим в мензурку; 2.Нальем в мензурку  воды до отметки 60 мл; 3.Размешаем стеклянной палочкой; 4. Получим данный раствор.
6	Изучение нового материала	Вы знаете  формулу определения процентного содержания вещества? Формула ×100% Процентного содержания некоторого вещества b в массе a  (раствора, смеси, сплава). Чему равно b? Чему равно а?	Нет ×100% b=3г а=60г Вычислим процентное содержание: ×100%=5%
7	Применение новых знаний в учебной деятельности	Задача Итак, мы решали задачи  на  процентное содержание вещества.	300×0,2=60 г- олова в первом куске 200×0,4=80 г – олова во втором куске 60+80=140 г – олова в полученном сплаве 300+200=500 г – масса полученного сплава ×100%=28% Ответ: 28%.
8	Закрепление	Класс делится на 4 группы: 1группа: Приготовить 10%солевой раствор; 2 группа:2% солевой раствор; 3 группа:3% солевой раствор; 4 группа: 15% солевой раствор	Каждая группа отчитывается по выполнению работы.
9	Рефлексия	Кто осуществлял учебное исследование с удовольствием? Поднимите руку. Спасибо за совместное исследование.	Все
10	Домашнее задание	Задачник  Мордкович А.Г. №645 В 200 г раствора 8 г соли. Определите процентное содержание соли в растворе. №647 б Из 105 посеянных семян взошло 98. Определите процент  всхожести семян.	Результат по выполнению домашнего задания: все учащиеся справились.

Предлагаю вашему вниманию легкий способ разобраться, как решать задачи на проценты в 6 классе.

При решении задачи на проценты первым делом нужно определить вид задачи. Задачи на проценты в 6 классе можно подразделить на  три вида:

1) Нахождение процентов от числа.

2) Нахождение числа по его процентам.

3) Нахождение процентного отношения двух чисел.

Определить вид задачи на проценты можно по записи ее условия. Если напротив 100% стоит число, то это — задача на нахождение процентов от числа. Если число напротив 100% неизвестно, то это — задача на нахождение числа по его процентам. Если же неизвестное значение стоит в колонке процентов, то это — задача на нахождение процентного отношения двух чисел.

Рассмотрим на примерах, как научиться определять вид задачи на проценты.

1. Из картофеля выходит 20% крахмала. Сколько крахмала выйдет из 45 т картофеля?

	тонны	%
Картофель	45т	100%
Крахмал	?	20%

Это задача на нахождение процентов от числа (так как напротив 100% стоит число).

2. Руда содержит 67% железа. Сколько нужно руды для получения 13,4 т железа?

	тонны	%
Руда	?	100%
Железо	13,4т	67%

Это задача на нахождение числа по его процентам (так как напротив 100% стоит ?)

3. Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.

	Зерна	%
Всего посеяли	400	100%
Взошло	360	?

Это задача на процентное отношение (так как в колонке процентов стоит ?). 

Как найти процент от числа 5 класс?

Рекомендуемый клип · 117 сек.

Математика 5 Проценты — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как найти процент от числа пример?

Чтобы найти, сколько процентов составляет первое число от второго, нужно разделить первое число на второе и результат умножить на 100%.

• Пример 1. Выразить проценты дробью или натуральным числом: 130%, 65%, 4%, 200%.
• Пример 2. Записать следующие числа в виде процентов: 1; 1,5; 0,4; 0,03.
• Пример 3.
• Пример 4.
• Пример 5.

Рекомендуемый клип · 118 сек.

Как найти процент от числа — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как найти процент от дроби?

Процент записывается с помощью знака «%».

1. Чтобы перевести проценты в дробь, нужно убрать знак «%» и разделить число на 100.
2. Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%».
3. Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.

Как определить процентное соотношение?

Правило. Чтобы найти процентное отношение двух чисел , нужно одно число разделить на другое, а результат умножить на 100. Например, вычислить, сколько процентов составляет число 52 от числа 400.

Как правильно решать задачи на проценты?

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

• Задача. В классе 30 учеников. 14 из них – девочки.
• Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%.

12 нояб. 2013 г.

Как правильно посчитать проценты на калькуляторе?

0:09

5:26

Рекомендуемый клип · 59 сек.

Как считать проценты на калькуляторе — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как правильно высчитать процент от суммы?

После этого есть два варианта:

1. Если нужно узнать, сколько процентов составляет другая сумма от первоначальной, нужно просто разделить ее на размер 1%, полученный ранее.
2. Если же нужен размер суммы, которая составляет, скажем, 27,5% от первоначальной, нужно размер 1% умножить на требуемое количество процентов.

Как высчитать процент от суммы?

набрать на калькуляторе сумму умножить на число (процент) и разделить на 100, или сумму умножить на процент и нажать значок процентов? например сумма 7000, надо взять 25%, тут надо 7000 поделить на 100% и умножить на 25%, получиться 1750,))) 1750-это 25 проценотов от суммы!

Как найти 1% от всего?

Чтобы найти проценты от числа, надо:

1) перевести % в десятичную дробь (для этого следует разделить количество процентов на 100); 2) умножить эту дробь на данное в задаче число.

Как рассчитать долю от суммы?

Если надо найти процент от числа (т. е. часть от целого) , надо число разделить на 100 и умножить на количество %. Если надо найти число (целое) по заданной его части (например знаем, что 24% это 78123), тогда мы число делим на процент и умножаем на 100.21 сент. 2012 г.

Как вычесть 13 процентов из суммы?

Существует еще один простой способ, как посчитать 13 от суммы. Для этого нужно общую сумму, от которой нужно выделить процент, разделить на 100, а результат умножить на 13. То есть если вы рассчитываете подоходный налог от заработной платы в 20 тыс. руб., получится 20000/100 х 13 = 2600 руб.4 мар. 2016 г.

Как проценты выразить в виде обыкновенной дроби?

Чтобы преобразовать проценты в обыкновенную дробь нужно выполнить следующие шаги:

• 1 Записать в виде дроби с знаменателем 100:
• 2 В случае если количество процентов было не целым нужно умножать числить и знаменатель на 10 за каждый знак после запятой.
• 3 Упростить(сократить) полученную дробь.

Как представить число в виде процентов?

Чтобы выразить число в процентах, нужно это число умножить на 100 и поставить знак %. Чтобы выразить проценты в виде десятичной дроби, нужно число процентов разделить на 100. 1)выразить проценты в виде дроби; 2)умножить эту дробь на данное число.

Как перевести десятичную дробь в обыкновенную дробь?

Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:

1. Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу.
2. Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая.

Ещё

1 янв. 2017 г.

Как посчитать процентное отношение двух чисел?

Рекомендуемый клип · 55 сек.

Процентное отношение двух чисел — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как рассчитать отношение одного числа к другому?

Отношение двух чисел показывает:

• во сколько раз одно число больше другого;
• какую часть одно число составляет от другого.

Как посчитать процент из двух чисел в Excel?

Как посчитать процент от числа в Excel

1. ввести сразу число со знаком «%» (ячейка автоматически установит нужный формат);
2. щелкнуть по ячейке правой кнопкой мыши, выбрать «Формат ячеек» — «Процентный»;
3. выделить ячейку и нажать комбинацию горячих клавиш CTRL+SHIFT+5.

Как правильно решать пропорции?

0:31

2:50

Рекомендуемый клип · 40 сек.

Как решать задачи на пропорции? — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа

Как правильно решать задачи по химии?

0:16

53:50

Рекомендуемый клип · 115 сек.

ТИПОВЫЕ ЗАДАЧИ ПО ХИМИИ. Часть 1. — YouTube

YouTube

Начало рекомендуемого клипа

Конец рекомендуемого клипа