Как найти процентную ставку за период

Подробнее про формулу

Банки в своей практике руководствуются несколькими формулами, позволяющими рассчитывать простые % и сложные. При их начислении применяется фиксированный и плавающий вид ставок. Фиксированную закрепляют договором при размещении вклада, она не меняется до конца периода его действия. Она может измениться в случае автоматических пролонгаций действия договора. Также она изменится в случае досрочного разрыва соглашения между клиентом и банком с выплатой % за фактический период размещения вложений, если вклад был размещен до востребования. Эти нюансы должны быть описаны в договорах.

В случае плавающих ставок, установленных изначально, их размер может изменяться на протяжении действия договоров.

При каких условиях и в каком порядке будет осуществляться этот процесс, нужно описывать в договорах. Изменение процентов привязано к изменениям:

• ключевой ставки;
• валютного курса;
• переводом депозита в иную категорию и др.

Для расчетов указываются все требуемые формой данные:

• сумма вклада;
• размер % ставки конкретного вклада;
• периодичность начислений % (поквартально, помесячно, ежедневно и др.);
• срок заключения договора;
• иногда нужно знать вид применяемой ставки – она может плавать или быть зафиксированной.

Общая формула расчета процентов по вкладу

Использование формулы простых процентов целесообразно в случае начисления процентов в конце срока размещения депозита или если они будут переводиться на отдельный счет – если капитализация договором не предусмотрена.

Выбирая вклад, клиент банка должен обратить внимание на порядок, который применяется при начислении процентов.

Формула расчета простых:

S = (P x I x t / K) / 100

Обозначения:

• S – прибыль со вклада (только проценты, без тела вклада);
• P – сумма, изначально внесенная на депозит;
• I – размер % ставки (за год);
• t – кол-во дней начисления %;
• K – кол-во дней за год по календарю.

A = P * (1 + r/n)^(n*t)

Здесь все более сложно, поскольку нужно высчитывать степень (^ – знак степени). Остальные обозначения:

• A – общая сумма денег (тело вклада + проценты), которую вы получите после того, как срок вклада закончится.
• P – стартовая сумма, которую вы кладете на счет вклада.
• r – процентная ставка по вкладу.
• n – количество расчетов прибыль в году, для ежедневной капитализации – 365 или 366, для ежемесячной – 12 и так далее.
• t – количество лет вклада. 6 месяцев – это 0.5 года.

Формула для вкладов с ежемесячной капитализацией

Чтобы рассчитать возможную прибыль в случае выбора вида депозита с капитализацией % с ежемесячным начислением % подойдет такая формула:

S = Р * (1 + (N/100)/12)^n, здесь используются следующие обозначения:

n – количество проведенных операций перевода процентов в тело вклада на протяжении полного срока действия договора (то есть месяцев вклада);

S – сумма вклада на дату окончания действия депозита, которую вкладчик получит на руки;

Р – изначально внесенная сумма на депозит с возможностью капитализации;

N – % ставка (годовая).

Формула для вкладов с ежедневной капитализацией

Если выбрана форма начисления % с ежедневной капитализацией, применяется следующая формула:

S = P * (1 + (N/100)/K)^T, где:

S – суммарный доход (тело вклада + проценты);

Р – внесенная при заключении договора сумма;

N – годовая % ставка;

К – 365 или 366 дней;

Т – кол-во дней, на которые открыт депозит.

Формула для вкладов с ежеквартальной капитализацией

В данном случае расчет процентов будет выглядеть следующим образом:

S=Р * (1+ (N/100)/4)^Т, где:

S – получаемый в конце срока доход (тело вклада + проценты);

Р – изначально размещенная сумма на депозите;

N – годовой %;

Т – количество кварталов, на протяжении которых открыт вклад.

Что такое эффективная ставка по депозиту?

Эффективная ставка = фактическая ставка + прибыль от капитализации. Если вклад – без капитализации, то эффективная ставка равна фактической ставке (указана в договоре); если вклад – с капитализацией, то эффективная ставка будет выше фактической, поскольку капитализация будет увеличивать тело вклада.

Как рассчитать через Excel?

Рассчитать в Excel доход от депозита можно на примере. Если необходимо положить на депозит 50 000 руб. с процентной ставкой 8% на три года с ежемесячной капитализацией и просчитать размер дохода через 24 месяца, нужно составить таблицу:

• A1-A24 – указываем месяцы, то есть 1,2,3…
• D1 – указываем сумму тела кредита.
• D2 – указываем ставку в процентах

Теперь нужно в ячейку B1 вставить специальную формулу для подсчета сложного процента: =БС($D$2/12;A1;;-$D$1). Первый аргумент ($D$2/12) – проценты, нужно делать на 12, поскольку считаем ежемесячное начисление. Второй аргумент (A1) – месяц, за который считаем. Третий аргумент оставляем пустым (комиссии/сборы). Четвертый (-$D$1) – тело вклада, ввиду некоторых особенностей работы функции БС его нужно указывать с минусом. Теперь выделяем ячейку B1, растягиваем ее содержимое на ячейки ниже, до B24. Получаем суммарное количество денег на счете в каждом месяце, через 24 месяца получим 58 644 рубля.

Как рассчитать онлайн?

Онлайн расчет процентов можно осуществлять на сайте банка, выбранного для размещения депозита. Для этого нужно найти на странице банка онлайн калькулятор вкладов, ввести в него требуемые данные и рассчитать:

• сумму;
• срок;
• дату начала размещения вклада;
• % ставку;
• период капитализации;
• пополнение (если возможно).

Пример расчета

Расчет при ежемесячной капитализации:

Исходные данные:

Сумма вклада – 50 000 руб.;

Годовая ставка – 8%;

Срок вклада – 12 мес.

50 000 х(1+0,08/12)^12= 54 150 руб.

Налоги на доход по вкладам

За 2021 и 2022 годы налог по вкладам не начисляли вовсе. На доход со вкладов, полученный с 1 января 2023 года, начисляется НДФЛ в размере 13%, но – только на доход, превышающий определенный порог. Порог рассчитывается так: берут максимальную ключевую ставку ЦБ РФ за год, после чего умножают ее на 1 000 000 рублей. Например, максимальная ключевая ставка составила 6% – значит, налогом не будет облагаться доход за год в 60 000 рублей. Если ваш доход за год превысил эту сумму – на сумму превышения начисляется 13%. Если вы получили за год 90 000 рублей дохода со вкладов – с 30 000 рублей нужно будет заплатить 13% НДФЛ, то есть 3 900 рублей. Налог рассчитывается автоматически, в 2024 году вам пришлют уведомление за 2023-й год. Это работает как для резидентов, так и для нерезидентов РФ.

На что вы обращаете внимание в первую очередь при выборе кредитной программы? Для большинства заемщиков решающее значение имеет величина процентной ставки. Принимать решение только на основе этого критерия не совсем верно. Стоит учитывать еще и то, по какой схеме банк начисляет проценты по кредиту. Это имеет значение, если вы планируете погашать заем досрочно.

В этой статье рассмотрим две схемы платежей — аннуитетную и дифференцированную, расскажем об отличиях между ними, а также приведем формулы расчетов с примерами. Зная это, вы сможете более обстоятельно подходить к выбору кредитной программы.

Из чего состоит платеж по кредиту

В структуре ежемесячного платежа принято выделять два элемента: основной долг (тело кредита) + проценты (плата банку за пользование заемными средствами). Их пропорция может меняться в зависимости от схемы платежей. В случае несвоевременного погашения к этим двум элементам добавляются штрафы и пени.

Платеж по кредиту включает процентную и долговую (основную) часть

Способы выплаты процентов по кредиту

Аннуитетная схема

Это наиболее распространенный вариант. На протяжении всего срока кредитования заемщик погашает кредит равными платежами. В графике платежей каждый месяц сумма одинаковая. Однако соотношение основного долга и начисленных процентов постоянно меняется: доля процентов (вознаграждение банку) снижается, а доля кредита (суммы займа) увеличивается. 

Если есть возможность возвращать такой кредит досрочно, то это имеет смысл в первую половину периода кредитования, когда вы гасите в основном проценты, а не сам долг. 

Дифференцированная схема

Если посмотреть на график ежемесячных взносов по займу, то в первый месяц заемщику приходится вносить самый крупный платеж, а в последний месяц — взнос наименьший. 

Принцип такой схемы следующий: в счет основного долга ежемесячно идет фиксированная сумма, а в счет погашения процентов сумма постоянно сокращается. Частичные досрочные погашения по такому кредиту выгодны в любой момент. Благодаря этому тело займа сокращается, а вместе с этим уменьшаются и начисляемые проценты. 

Подробнее об аннуитетной и дифференцированной схеме вы можете прочитать в этой статье.

Разница между дифференцированной и аннуитетной схемой

Что нужно для расчета суммы процентов по кредиту

Итак, кредит может предполагать аннуитетную или дифференцированную схему расчетов. А сколько именно идет в счет уплаты процентов каждый месяц? Чтобы рассчитать это, достаточно знать всего три параметра:

• размер займа,

• месячная процентная ставка (годовая ставка, поделенная на 12),

• период кредитования (в месяцах).

Как самостоятельно рассчитать проценты по кредиту

Принцип расчетов меняется в зависимости от схемы платежей. Посмотрим, как работают формулы в каждом из случаев.

Аннуитетная схема

Сначала посчитаем размер ежемесячного взноса (х):

Помните, что срок кредита в формуле всегда считается в месяцах!

Затем вычислим, какую долю (I) занимают проценты в ежемесячном платеже: 

Месячная процентная ставка — это годовая ставка, поделенная на 12

Давайте посмотрим, как это работает в конкретной ситуации. Предположим, вам одобрили ссуду на 400 тысяч рублей по ставке 12% годовых на 24 месяца.

Не упустите степень! 

Смотрите, как это будет отражаться графике платежей: 

Так выглядит график платежей по кредиту с аннуитетной схемой

Дифференцированная схема

При такой схеме, как мы уже выяснили ранее, в счет основного долга ежемесячно идет одинаковая сумма. Чтобы узнать эту часть ежемесячного платежа, достаточно сумму займа (тело кредита) поделить на количество месяцев кредитования. 

Используем эту формулу для расчета ежемесячного платежа по дифференцированной схеме

Остается только вычислить, какая сумма из ежемесячного взноса будет уходить в счет уплаты процентов (I). Делается это по уже знакомой нам формуле: 

Считаем процентную долю в ежемесячном платеже по кредиту

Теперь давайте посмотрим, как всё это выглядит в графике дифференцированных платежей. Обратите внимание, как размер ежемесячного платежа постоянно убывает за счет сокращения процентной доли.

Так выглядит график платежей по кредиту с дифференцированной схемой

Как рассчитать проценты по кредиту на калькуляторе

Если у вас нет времени или желания самостоятельно делать расчеты, эту задачу можно доверить кредитному калькулятору. Для того чтобы узнать размер ежемесячного платежа по займу, вам потребуются все те же данные: сумма + срок кредитования + процентная ставка.

Важно иметь в виду, что в базовом кредитном калькуляторе не учитываются персональные условия. Они могут меняться в зависимости от кредитной истории заемщика, финансового положения и прочих критериев, которые рассматриваются в индивидуальном порядке. 

Чтобы получить персональные условия кредитования, оставьте заявку на Кредит наличными от Почта банка. С услугой «Гарантированная ставка» ваша процентная ставка составит от 4,5%. При этом можно взять займ до 5 млн рублей на срок до семи лет. Далее на этой странице вы сможете рассчитать условия и заполнить онлайн-заявку.

Процентные ставки действительны на момент публикации статьи.

Почему важно считать кредит самому?

Кредитами сейчас сложно кого-то удивить. Каждый среднестатистический россиянин имеет или имел как минимум один-два кредита в своей жизни или собирается его взять. Если вы идете в банк для получения кредита и вам дают несколько предложений, то нужно выбрать самое дешевое и выгодное для вас. Для этого нужно рассчитать кредит самому, например в Excel. Нужно также знать размер ежемесячного платежа, чтоб понять нагрузку займа на ваш бюджет. Это тоже можно сделать самостоятельно.

Видео

Как рассчитать годовые проценты по кредиту?

Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:

10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.

При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.

То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.

При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.

Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.

Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.

Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.

Как самостоятельно рассчитать аннуитетный платеж

Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.

Стандартная формула расчета аннуитетного платежа выглядит так:

Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.

А вот как рассчитывается коэффициент аннуитета:

Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.

Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.

Количество платежей равно количеству месяцев — 18.

Подставляем данные в формулу и считаем коэффициент аннуитета:

0,0125 × (1 + 0,0125)¹⁸ / ((1 + 0,0125)¹⁸ − 1) = 0,062385

Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.

Какие данные нужны для расчета платежа по кредиту

Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.

Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:

• ставка,
• размер желаемого займа,
• срок, на который вы хотите занять деньги.

Воспользуемся банковскими калькуляторами

Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.

Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.

Виды ежемесячных выплат по кредитам

Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.

Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.

В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.

Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.

Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.

Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.

Самостоятельный подсчет при аннуитетных платежах

Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:

1. Процентная ставка — 18%.
2. Период кредитования — 24 месяца.
3. Сумма кредита — 500000 рублей.

Классическая формула для расчета аннуитетного платежа выглядит так:

Разовый аннуитетный платеж = Сумма кредита * Ка

где Ка — это коэффициент аннуитета.

Ка = ((ЕПС* (1 + ЕПС)ⁿ)/( (1 + ЕПС)ⁿ -1)

где ЕПС — ежемесячная процентная ставка.

Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.

Итоговый расчет примет вид:

500 000 * (0,015 * (1 + 0,015)²⁴)/((1 + 0,015)²⁴ -1) = 24 962,05 рублей в месяц.

Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.

Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:

24 962,05 * 24 = 599 089,24 рублей.

Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.

Из чего состоит ежемесячный платеж

Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.

Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.

Формула расчета процентов по кредиту

S = (s₃ x i x Kk / Kr) / 100

• S = вычисляемые проценты;
• S₃ = общая сумма кредита;
• i = процентная ставка по кредиту;
• Kk = кол-во дней по платежам;
• Kr = кол-во дней на календарный год.

Какие данные нужны для расчета

• Сумма, выданная в кредит;
• Процентная ставка за год;
• Кол-во календарных дней в текущем году.

Пример расчета процентов по кредиту

65000 рублей – сумма переплаты в год. Для того чтобы посчитать сумму переплаты в месяц нужно 65000 рублей разделить на 12.

Погашать долг можно по-разному

Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.

С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.

Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.

Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.

Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).

, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.

Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.

Как составить график платежей

Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.

Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.

Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.

При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р.

В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.

Сначала считаем проценты:

Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году

Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р.

Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р.

Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р.

На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).

Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.

График выплаты кредита с аннуитетными платежами

Номер платежа	Сумма платежа	Сумма в погашение тела кредита	Сумма платежа в погашение процентов	Остаток долга
1	18 715,44	15 016,81	3698,63	284 983,19
2	18 715,44	15 084,83	3630,61	269 898,37
3	18 715,44	15 387,92	3327,51	254 510,44
4	18 715,44	15 473,04	3242,39	239 037,40
5	18 715,44	15 670,17	3045,27	223 367,24
6	18 715,44	16 053,39	2662,05	207 313,85
7	18 715,44	16 074,31	2641,12	191 239,53
8	18 715,44	16 357,69	2357,75	174 881,84
9	18 715,44	16 487,49	2227,95	158 394,35
10	18 715,44	16 762,63	1952,81	141 631,73
11	18 715,44	16 911,09	1804,35	124 720,64
12	18 715,44	17 126,53	1588,91	107 594,11
13	18 715,44	17 388,93	1326,50	90 205,18
14	18 715,44	17 566,25	1149,19	72 638,93
15	18 715,44	17 819,89	895,55	54 819,04
16	18 715,44	18 017,06	698,38	36 801,98
17	18 715,44	18 246,59	468,85	18 555,40
18	18 768,91	18 555,39	213,51

Первый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 016,81

Сумма платежа в погашение процентов

3698,63

Остаток долга 284 983,19

Второй платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 084,83

Сумма платежа в погашение процентов

3630,61

Остаток долга 269 898,37

Третий платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 387,92

Сумма платежа в погашение процентов

3327,51

Остаток долга 254 510,44

Четвертый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 473,04

Сумма платежа в погашение процентов

3242,39

Остаток долга 239 037,40

Пятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 670,17

Сумма платежа в погашение процентов

3045,27

Остаток долга 223 367,24

Шестой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 053,39

Сумма платежа в погашение процентов

2662,05

Остаток долга 207 313,85

Седьмой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 074,31

Сумма платежа в погашение процентов

2641,12

Остаток долга 191 239,53

Восьмой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 357,69

Сумма платежа в погашение процентов

2357,75

Остаток долга 174 881,84

Девятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 487,49

Сумма платежа в погашение процентов

2227,95

Остаток долга 158 394,35

Десятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 762,63

Сумма платежа в погашение процентов

1952,81

Остаток долга 141 631,73

Одиннадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 911,09

Сумма платежа в погашение процентов

1804,35

Остаток долга 124 720,64

Двенадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 126,53

Сумма платежа в погашение процентов

1588,91

Остаток долга 107 594,11

Тринадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 388,93

Сумма платежа в погашение процентов

1326,50

Остаток долга 90 205,18

Четырнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 566,25

Сумма платежа в погашение процентов

1149,19

Остаток долга 72 638,93

Пятнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 819,89

Сумма платежа в погашение процентов

895,55

Остаток долга 54 819,04

Шестнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

18 017,06

Сумма платежа в погашение процентов

698,38

Остаток долга 36 801,98

Семнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

18 246,59

Сумма платежа в погашение процентов

468,85

Остаток долга 18 555,40

Восемнадцатый платеж Сумма платежа 18 768,91 Сумма в погашение тела кредита 18 555,39 Сумма платежа в погашение процентов 213,51 Остаток долга

При дифференцированном платеже проценты в первом месяце будут такими же — 3698,63 Р. Дальше же принцип расчета процентов аналогичен, а сумма основного долга будет каждый месяц уменьшаться равномерно — на 16 666,67 Р (300 000 / 18). Ежемесячный платеж будет складываться из этих двух сумм.

В результате в первые месяцы платеж будет больше, чем при аннуитетном способе, а итоговая переплата будет меньше.

График выплаты кредита с дифференцированными платежами

Номер платежа	Сумма платежа	Сумма в погашение тела кредита	Сумма платежа в погашение процентов	Остаток долга
1	20 365,30	16 666,67	3698,63	283 333,33
2	20 276,26	16 666,67	3609,59	266 666,67
3	19 954,34	16 666,67	3287,67	250 000,00
4	19 851,60	16 666,67	3184,93	233 333,33
5	19 639,27	16 666,67	2972,60	216 666,67
6	19 248,86	16 666,67	2582,19	200 000,00
7	19 214,61	16 666,67	2547,95	183 333,33
8	18 926,94	16 666,67	2260,27	166 666,67
9	18 789,95	16 666,67	2123,29	150 000,00
10	18 515,98	16 666,67	1849,32	133 333,33
11	18 365,30	16 666,67	1698,63	116 666,67
12	18 152,97	16 666,67	1486,30	100 000,00
13	17 899,54	16 666,67	1232,88	83 333,33
14	17 728,31	16 666,67	1061,64	66 666,67
15	17 488,58	16 666,67	821,92	50 000,00
16	17 303,65	16 666,67	636,99	33 333,33
17	17 091,32	16 666,67	424,66	16 666,67
18	16 858,45	16 666,67	191,78

Первый платеж

Сумма платежа

20 365,30

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3698,63

Остаток долга 283 333,33

Второй платеж

Сумма платежа

20 276,26

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3609,59

Остаток долга 266 666,67

Третий платеж

Сумма платежа

19 954,34

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3287,67

Остаток долга 250 000,00

Четвертый платеж

Сумма платежа

19 851,60

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3184,93

Остаток долга 233 333,33

Пятый платеж

Сумма платежа

19 639,27

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2972,60

Остаток долга 216 666,67

Шестой платеж

Сумма платежа

19 248,86

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2582,19

Остаток долга 200 000,00

Седьмой платеж

Сумма платежа

19 214,61

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2547,95

Остаток долга 183 333,33

Восьмой платеж

Сумма платежа

18 926,94

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2260,27

Остаток долга 166 666,67

Девятый платеж

Сумма платежа

18 789,95

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2123,29

Остаток долга 150 000,00

Десятый платеж

Сумма платежа

18 515,98

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1849,32

Остаток долга 133 333,33

Одиннадцатый платеж

Сумма платежа

18 365,30

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1698,63

Остаток долга 116 666,67

Двенадцатый платеж

Сумма платежа

18 152,97

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1486,30

Остаток долга 100 000,00

Тринадцатый платеж

Сумма платежа

17 899,54

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1232,88

Остаток долга 83 333,33

Четырнадцатый платеж

Сумма платежа

17 728,31

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1061,64

Остаток долга 66 666,67

Пятнадцатый платеж

Сумма платежа

17 488,58

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

821,92

Остаток долга 50 000,00

Шестнадцатый платеж

Сумма платежа

17 303,65

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

636,99

Остаток долга 33 333,33

Семнадцатый платеж

Сумма платежа

17 091,32

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

424,66

Остаток долга 16 666,67

Восемнадцатый платеж Сумма платежа 16 858,45 Сумма в погашение тела кредита 16 666,67 Сумма платежа в погашение процентов 191,78 Остаток долга

Теги

Это слайд-шоу требует JavaScript.

ФОРМУЛА ПРОСТЫХ ПРОЦЕНТОВ

Формула простых процентов для срока, который не кратен году, т.е. не составляет целое число лет, выглядит следующим образом:

S=P(1+t/K*i), где

S — сумма в конце срока

P — первоначальная сумма

i — годовая процентная ставка

t — число дней кредита

K — число дней в году, или временная база начисления процентов

При вычислении показателя по формуле простых процентов подразумевается, что процент, в отличие от расчетов по формуле сложных процентов, начисляется только на первоначальную сумму долга независимо от срока пользования заемными средствами. Например, если в кредит была получена сумма в размере 1 000 000 рублей на срок 5 лет под 20% годовых, то в первый год и последующие годы, ежегодные выплаты по кредиту составят 200 000 рублей.

Также следует учитывать, что данная формула верна, если в расчетах указана именно годовая процентная ставка.

ВЫЧИСЛЕНИЕ ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ

Формула для вычисления годовой процентной ставки по формуле простых процентов

i=(S/P-1)*K/t

Всего можно выделить четыре наиболее часто встречающихся варианта расчета простых процентов в зависимости точности срока кредита и количества дней в году.

1. Точное число в месяцах, точное число дней в году

Например, для периода с 01.01.2012 по 31.06.2012 включительно срок в виде дроби выглядит как 182/366. Всего 182 дня, так как январь (31) +февраль (29) + март (31)+апрель (30)+май (31)+июль (30)=182. В году 366 дней, так как год високосный.

2. Точное число дней в месяцах, число дней в году равно 360

Для  периода с 01.01.2012 по 31.06.2012, срок равен 182 дням и записывается дробью как 182/360.

3. 12 месяцев по 30 дней в каждом

Срок в виде дроби для периода с 01.01.2012 по 31.06.2012 будет выглядеть как 180/360, 6 месяцев*30 дней=180.

4. Точное число дней в месяцах, число дней в году принимается за 365

Срок в виде дроби для периода с 01.01.2012 по 31.06.2012 будет выглядеть как 182/365

Практикум

ПРИМЕР РАСЧЕТА ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ

Банк выдал клиенту кредит в размере 1 000 000 рублей на период  с 01.01.2012 г. по 30.06.2012 г. включительно. В качестве платы за пользование кредитом банк  ежемесячно начисляет  клиенту по 20 000 рублей. По условию кредита клиент обязался погасить всю сумму в конце срока. Требуется определить годовую процентную ставку по формуле простых процентов, применив четыре метода.

Расчет годовой процентной ставки по формуле простых процентов

Предварительно рассчитаем сумму к погашению, точное и приближенное число дней.

Точное число дней  182.

Приближенное число дней  180.

Сумма к погашению = 6 месяцев * 20 000 рублей + 1 000 000 рублей= 1 120 000 рублей

1. Точное число дней в месяцах, точное число дней в году

i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*366/182=0,2413 или 24,13%

2. Точное число дней в месяцах, число дней в году равно 360.

i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*360/182=0,23736 или 23,73%

3. 12 месяцев, по 30 дней в каждом

i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*360/180=0,24 или 24,00%

4. Точное число дней в месяцах, число дней в году принимается за 365

i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*365/182=0,24065 или 24,07%

Анализ динамики процентной ставки

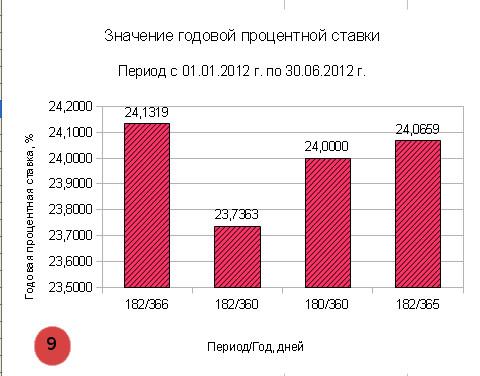
Проанализируем с помощью гистограммы значения годовой процентной ставки в зависимости от выбранного метода расчета.

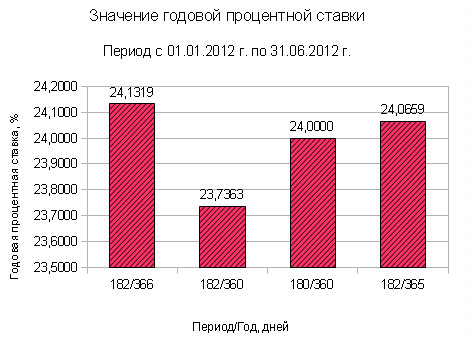
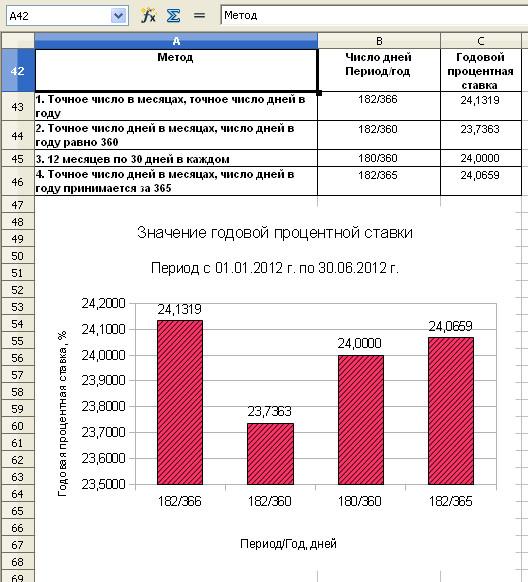
Годовая процентная ставка за кредит за период с 01.01.2012 г. по 30.06.2012 г.  по формуле простых процентов

Описание	Число дней Период/год	Годовой процент
1. Точное число дней в месяцах, точное число дней в году	182/366	0,2413 или 24,13%
2. Точное число дней в месяцах, число дней в году равно 360	182/360	0,23736 или 23,73%
3. 12 месяцев по 30 дней в каждом	180/360	0,24 или 24,00%
4. Точное число дней в месяцах, число дней в году принимается за 365	182/365	0,24065 или 24,07%

Openoffice Calc. Пример применения функции INTRATE для расчет годовой процентной ставки по формуле простых процентов

В OpenOffice Calc для расчета годовой процентной ставки по формуле простых процентов применяется функция INTRATE.

Синтаксис функции INTRATE

INTRATE(дата начала периода; дата окончания периода; первоначальная сумма; сумма в конце периода; Базис)

Базис – это метод вычисления года.
Базис	Метод	Вычисление
0 или отсутствует	1	Американский метод (NASD): 12 месяцев по 30 дней в каждом
1	2	Точное число дней в месяцах, точное число дней в году
2	3	Точное число дней в месяцах, число дней в году принимается за 360
3	4	Точное число дней в месяцах, число дней в году принимается за 365

1. Таблица с расчетами годовой процентной ставки по формуле простых процентов 4-мя методами

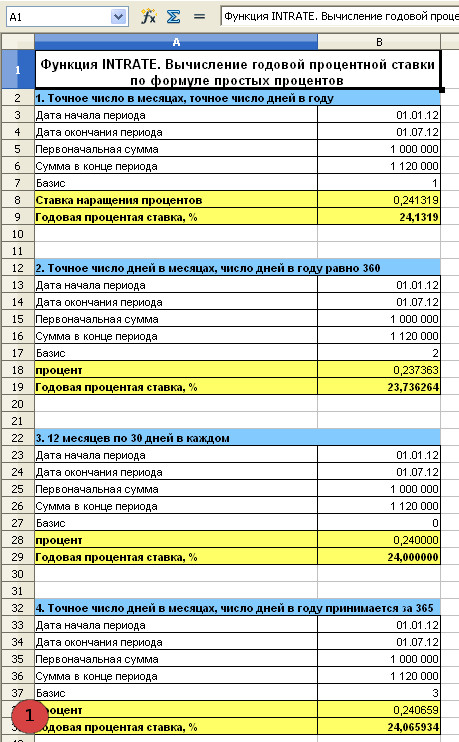
2. Вызов мастера функций

Вызовем Мастер функций, чтобы лучше понять, как применять функцию INTRATE. Для этого выделим ячейку с формулой (для первого примера это B8) и затем последовательно выберем Вставка/Функция…

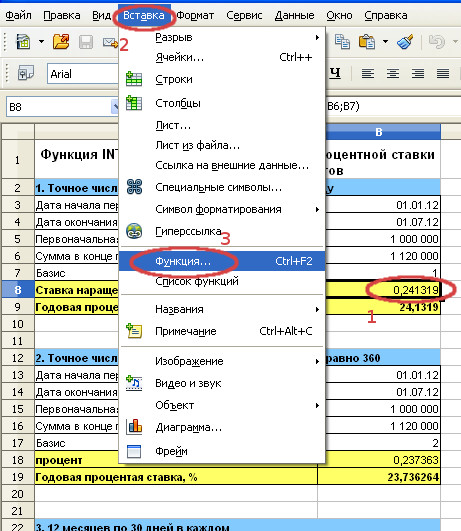
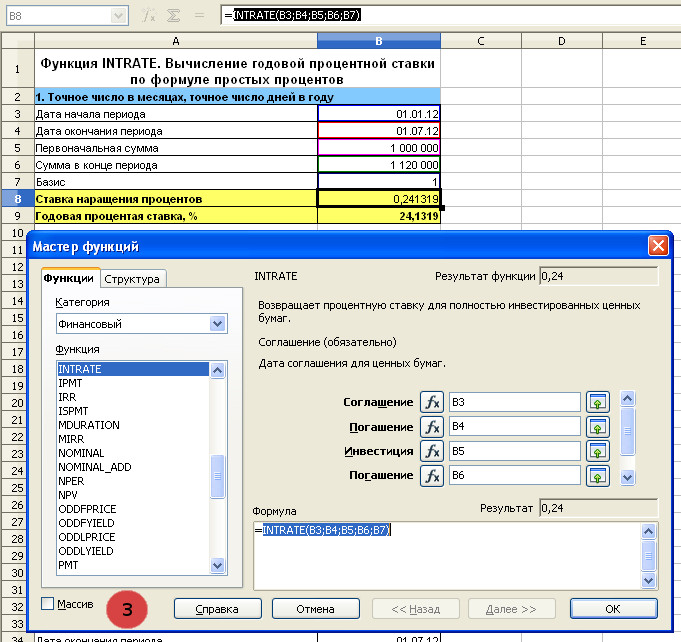
3. Базис 1.  Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов

Мастер функций с заполненными полями. Формула в ячейке B8. Необходимо нажать ОК, чтобы вернуться к исходной таблице.

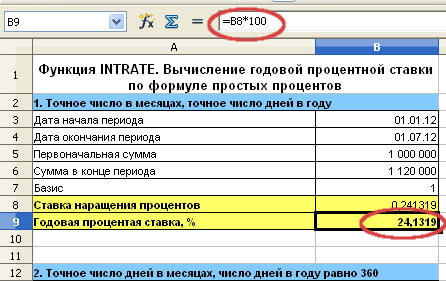
Переведём полученный результат в проценты умножив его на 100.

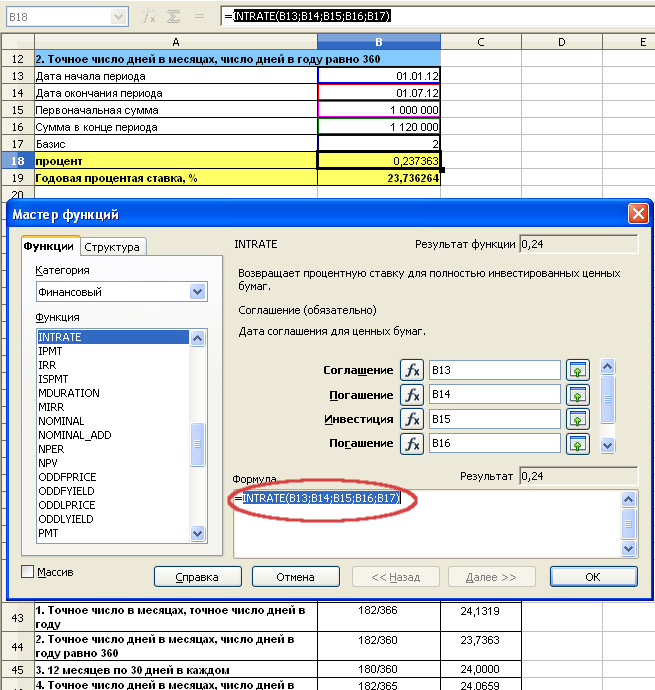
4. Базис 2.  Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов

Мастер функций с заполненными полями. Формула в ячейке B18. Необходимо нажать ОК, чтобы вернуться к исходной таблице.

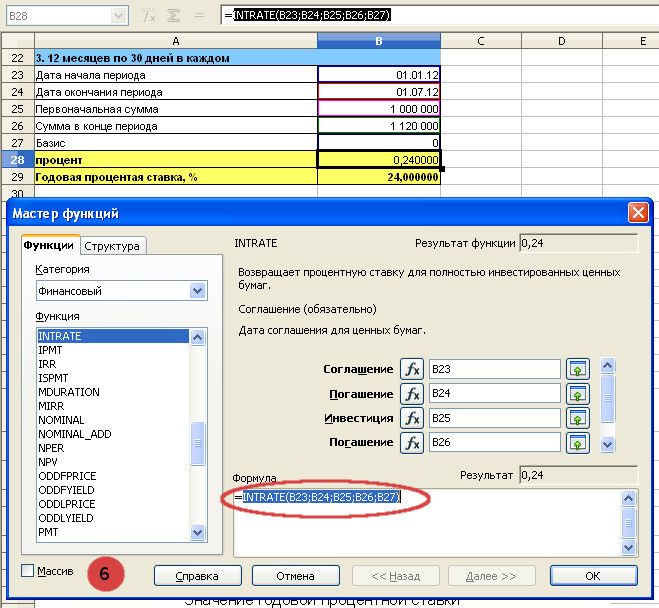
5. Базис 0.  Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов

Мастер функций с заполненными полями. Формула в ячейке B28. Необходимо нажать ОК, чтобы вернуться к исходной таблице.

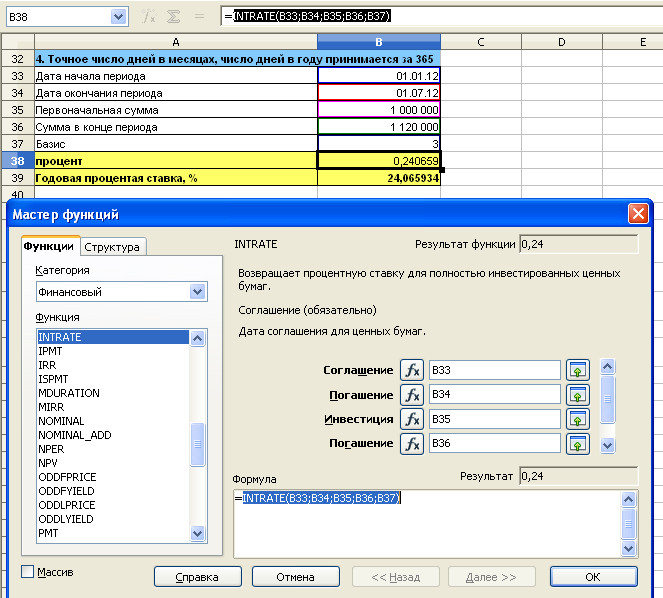
6. Базис 3.  Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов

Мастер функций с заполненными полями. Формула в ячейке B38. Необходимо нажать ОК, чтобы вернуться к исходной таблице.

7. Гистограмма значений годовых процентных ставок по формуле простого процента рассчитанных 4-мя методами