Как найти процентную точку

Приложение 2 Процентные точки распределения Фишера (при а = 0,05, f — т,/г = п — да—1)  [c.394]

Как обычно, если LM > Ха(1)> то гипотеза HQ отвергается при уровне значимости а, где Ха(1) -процентная точка распределения хи-квадрат с одной степенью свободы.  [c.378]

Таблица 2. Процентные точки распределения Стьюдента ta(n)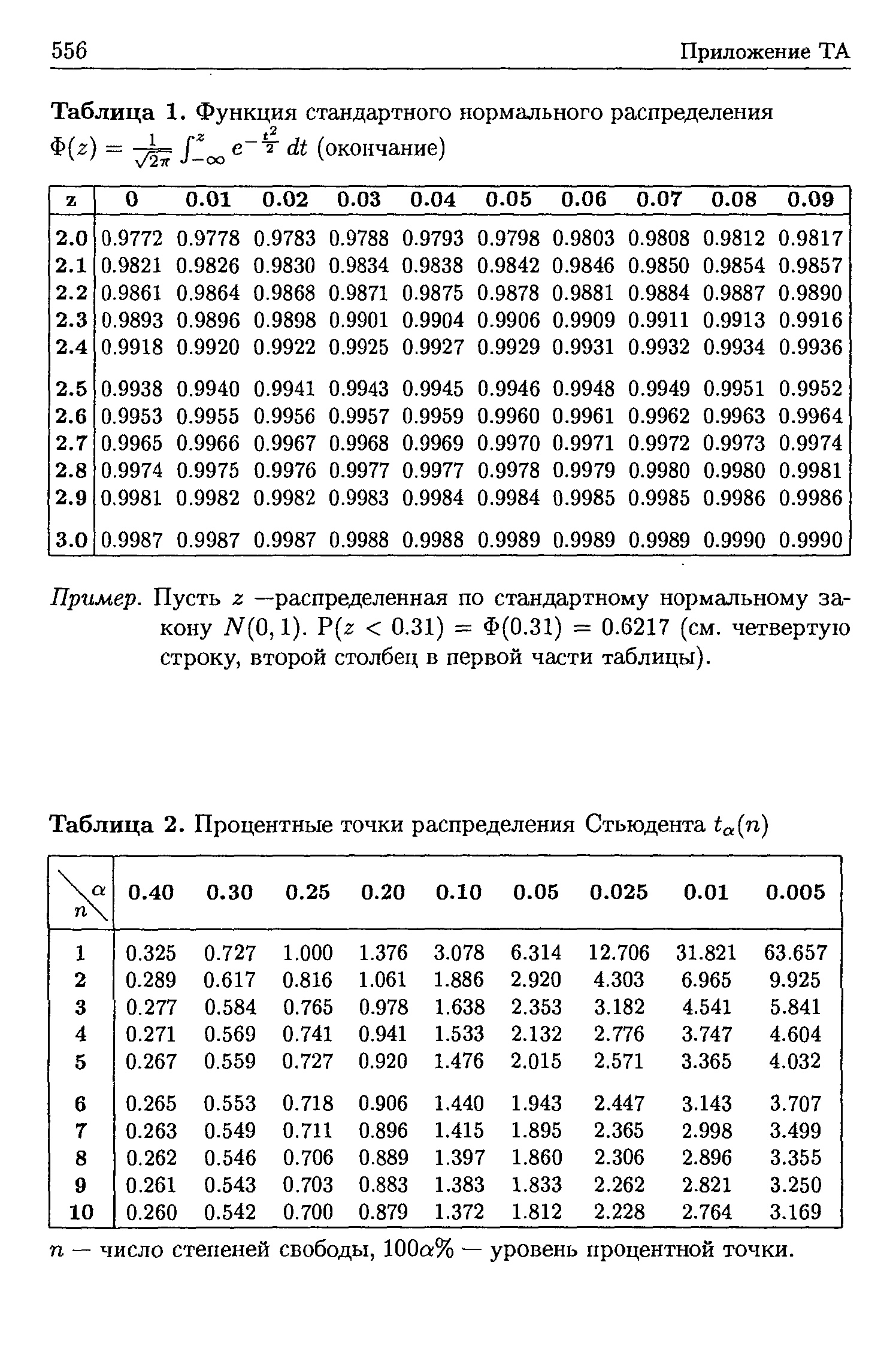

Но как же быть с теми случаями, когда статистика неопределенна Как быть с таким случаем на Рисунке 9.1, где средняя степень и продолжительность ставят текущую коррекцию на 40-процентный уровень распределения В таком случае шансы в пользу продолжения текущего нисходящего тренда — точнее, где-то 1,5 к 1. Это тот случай, когда основной акцент должен быть сделан на выборе сегмента рынка и конкретных акций, демонстрирующих силу (или слабость) относительно рынка в целом. Подробнее об этом поговорим в Главе 10.  [c.162]

Здесь, как и прежде, рч. и г — соответственно выборочные корреляционные отношения (г) по ) и коэффициент корреляции, вычисляемые по формулам (1.16) и (1.8 ). Логическая схема использования статистики (6.17) аналогична ранее изложенным критериям задаются достаточно малым (0,05 0,15) уровнем значимости а находят по табл. П.5 100 оь%-ную точку Va распределения F (k — 2, п — А) сравнивают величину и2, определенную с помощью (6.17), с процентной точкой и если оказывается, что v2 >> uj, то гипотезу о линейном виде регрессии считают статистически необоснованной.  [c.203]

Пусть теперь задано число 0 < а < 1. ЮОа- процентной точкой непрерывного распределения F(x) называется такое число гуа, что 1 — F(wa) — Р(Х > wa) — а. Для дискретной величины  [c.512]

Числитель данной формулы характеризует разницу средних. Кроме того, необходимо учесть различие формы двух кривых распределения. Это осуществляется в знаменателе формулы. Выборочное распределение теперь рассматривается как выборочное распределение разницы между средними (процентными мерами). Если нулевая гипотеза является справедливой, то распределение разницы является нормальной кривой со средней равной нулю и средней квадра-тической ошибкой равной 1.  [c.43]

Когда используется метод рентабельности продаж, процентная наценка включает только желаемую величину прибыли. Чтобы этот метод был эффективным, все затраты должны быть распределены по единицам продукции. Поскольку коммерческие, общие и административные расходы труднее отнести на конкретные виды продукции, чем переменные и постоянные производственные затраты, то для их распределения можно использовать произвольные методы. Однако, такое произвольное распределение коммерческих, общих и административных расходов может привести к ошибкам в определении цены изделия. Так как такие внешние факторы, как конкуренция и положение на рынке, должны быть учтены прежде установления окончательной цены, то метод ценообразования на основе рентабельности продаж может быть использован в качестве исходной цены в решении проблемы ценообразования. Для расчетов используются формулы  [c.258]

Как показывают данные табл. 3.10,распределению подлежало 227947 тыс. р. балансовой прибыли, в том числе 20192 тыс. р. сверхплановой. Структура платежей из прибыли в бюджет была близка к плановой и изменилась незначительно на 0,14 процентных пункта снизился удельный вес налога на недвижимость и на 0,42 процентных пункта возрос удельный вес налога на прибыль. В то же время при соблюдении плановых пропорций чистая прибыль предприятия могла бы составить 169251 тыс. р. (227947 0,7425). Фактически же чистая прибыль составила 168605 тыс. р., что на 646 тыс. р. меньше вследствие изменения структуры платежей из прибыли в бюджет. Чистая прибыль была распределена в следующих пропорциях резервный фонд – 4,96 %, фонд накопления -4,96, фонд потребления – 89,25, прочие цели – 0,84 %.  [c.170]

Второй аспект финансового риска — относительный разброс дохода держателей обыкновенных акций. Допустим, оценки ожидаемого дохода от основной деятельности на ближайшие 5 лет для фирм А и В есть субъективные случайные величины, ожидаемое значение распределения вероятностей будет 80 000 дол. для каждой, а стандартные отклонения равно 40 000 дол. Как и в предыдущем примере, предположим, что фирма А не имеет задолженности, а фирма В выпустила на 200 000 дол. 15-процентных облигаций. Если для простоты пренебречь федеральными налогами, то ожидаемый доход акционеров фирмы А составит 80 000 дол., а фирмы В — 50 000 дол. Поскольку величина стандартного отклонения одинакова для обеих фирм, относительная дисперсия ожидаемых доходов фирмы В больше, чем фирмы А. Коэффициент вариации для фирмы А есть стандартное отклонение, деленное на ожидаемую величину дохода  [c.450]

Право на получение дополнительных дивидендов позволяет привилегированным акционерам в установленном порядке принимать участие в распределении остаточной прибыли корпорации. Привилегированный акционер может иметь право участия на равных основаниях с обычными акционерами в любых дивидендах, превышающих определенную сумму. Предположим, что 6-процентные привилегированные акции (номиналом 100 дол.) дают право на получение дополнительных дивидендов, т. е. их владелец имеет право получить все дивиденды по обыкновенным акциям в объеме, превышающем 6 дол. на акцию. Если дивиденд по обыкновенным акциям составляет 7 дол. на акцию, привилегированный акционер получит 1 дол. дополнительных дивидендов на каждую имеющуюся у него акцию. Условия оговорки о праве на получение дополнительных дивидендов могут быть самыми различными. Существенным здесь является то, что привилегированные акционеры имеют преимущественное право на получение дополнительного дохода в том случае, когда дивиденды по обыкновенным акциям превосходят определенное установленное значение. К сожалению, для инвестора практически все привилегированные акции не дают права на получение дополнительных дивидендов, и максимальный доход по ним не превосходит заранее установленного уровня.  [c.624]

Если мы имеем дело с заказами и продуктами, то затраты на организацию групп I и II относятся на их себестоимость по процентной ставке от прямых производственных затрат (подробнее об этом см. в гл. В и Г, раздел 1). Таким образом, для системы контроллинга проблема учета затрат состоит в распределении расходов на организацию группы I. Необходимо так сгруппировать эти затраты, чтобы их можно было распределить по вызывающим их факторам, дабы на предприятии могли приниматься оптимальные управленческие решения.  [c.71]

Изучение рыночной системы при любом подходе приводит к мысли, что цены определяют распределение ресурсов в экономике. Процентная ставка — это цена кредита, которая определяет распределение кредита между домашними хозяйствами и фирмами. Фирмы конкурируют друг с другом за получение кредита, а процентная ставка распределяет кредит между разными фирмами и, следовательно, между инвестиционными проектами этих фирм. В условиях нерегулируемого (свободного) рынка ссудных капиталов поддержку получат такие инвестиционные (капитальные) проекты, прибыльность которых выше рыночной процентной ставки на кредитном рынке. Например, если ожидаемая норма прибыли от покупки нового завода равна 20%, а ссуду можно получить под 15%, то этот инвестиционный проект — покупка нового завода — будет осуществлен. Если, напротив, тот же проект сулит норму прибыли 9%, то он не получит поддержки. Ссудный капитал получают те, кто хочет и может обеспечить наиболее высокую норму прибыли. Практически ссудный капитал уходит к наиболее прибыльным фирмам. Таким образом, прибыльные фирмы получают возможность расширяться, а неприбыльные — вынуждены сворачивать деятельность или закрываться.  [c.146]

В модели структура—поведение—эффективность существует несколько прогнозов. Во-первых, с увеличением уровня концентрации на рынках банковских услуг прибыль банков должна расти. К тому же банки будут взимать более высокие процентные ставки по ссудам, выплачивая меньшие ставки по депозитам и выдавать меньшие объемы ссуд, чем если бы уровень концентрации на рынке был ниже. Следовательно, большинство исследователей модели структура—поведение—-эффективность особенно выделяли возможную зависимость между рыночной концентрацией и прибылью банков. Выводы этих исследователей различны. Многие из них пришли к выводу, что высокая степень концентрации приводит к росту банковской прибыли, как и предсказывает указанная модель. Другие же не поддерживают эту точку зрения. Таким образом, не существует единства мнений об адекватности модели структура— поведение—эффективность . Тем не менее большинство экономистов соглашаются, что результаты исследований в основном поддерживают точку зрения, что распределение банков по числу и размеру влияет на величину процентных станок, которые банки взимают по ссудам и выплачивают по депозитам.  [c.281]

Процент платы за основные производственные фонды выступает в виде налога, введенного в целях улучшения их использования, тогда как процент за кредит должен обеспечивать оптимальность использования заемных средств в строго установленные сроки. Если установить, например, процентную ставку и норму платы за фонды на уровне нормативного коэффициента экономической эффективности основных фондов и капитальных вложений, как это предлагает, например, Д. С. Львов [55], то, исходя из положений теории экономической эффективности, лучшим следует признать такое распределение капитальных вложений, при котором соблюдается равенство фактического и нормативного коэффициентов эффективности. Но в этом случае разработчикам нововведений невыгодно брать кредит на приобретение нового оборудования, совершенствование технологии и внедрение в производство новых изделий,  [c.182]

В ее основу может быть положена существующая на практике дифференциация ссудного процента при долгосрочном кредитовании капитальных вложений. В отличие от действовавшей шкалы опорных процентных ставок, установленных в зависимости от одного фактора — сроков проведения работ, разрабатываемая модель должна учитывать другие факторы. С целью сохранения преемственности разрабатываемой шкалы в число факторов необходимо включить срок кредитования работ. Дифференциация по сроку кредитования по своему содержанию близка к дифференциации в зависимости от экономической эффективности кредитуемого предприятия. В условиях конкурсного отбора мероприятий по созданию новой техники приоритет должен принадлежать работам с более коротким сроком окупаемости, а следовательно, и возврата ссуд. Скорость погашения кредитов в современных условиях зависит не от той ее доли, которая поступит в распоряжение предприятия в соответствии с нормативом распределения. Возвратность кредита будет тем скорее, чем больше доля прибыли. В нынешних условиях хозяйствования срок кредитования оказывается зависимым от финансовых  [c.184]

По горизонтали указаны процентные группы населения, а по вертикали — проценты дохода, получаемые этими группами. Если бы существовало абсолютное равенство, то 20% населения получали бы 20% всего дохода общества, 30% населения — 30% всего дохода, 40% населения — 40% дохода и т.д. Появилась бы линия ОА, которая означала бы абсолютное равенство в распределении доходов. В жизни распределение осуществляется иначе. Например, 10% населения получают 50% всех доходов, 50% населения — 20% и т.д. В этой ситуации на графике возникает кривая ОСА, которая называется кривой Лоренца. Чем дальше эта кривая от прямой ОА, тем больше различие в доходах членов общества. Степень дифференциации дохода определяется с помощью коэффициента Джини. Чем больше величина этого показателя, тем больше отклонение фактического распределения доходов от идеального равенства. Рассчитывается он путем деления площади ОСА на площадь треугольника ОАВ.  [c.188]

Изучая функции ценообразования, необходимо учитывать, что одни и те же экономические процессы можно выполнять с помощью различных элементов хозяйственного механизма. Разница состоит в том, что финансовый, кредитный, плановый аппараты воздействуют на производство и распределение, как правило, административными методами, цена же воздействует всегда на экономические интересы. Например, налоги, которые платят производители, потребители, они не в силах отменить, не в силах отменить процентную ставку за кредит, в то время как цены они могут снижать, повышать или покупать товары, сырье с разным уровнем цен. Даже в период диктатуры плана предприятия  [c.246]

За последние несколько десятилетий значительно повысилась скорость внедрения инноваций, которые облегчают управление риском. Причина тому — изменения, которые произошли, с одной стороны, в области спроса и, а с другой — в области предложения на рынках, связанных с распределением риска. Новые открытия в области телекоммуникаций, обработки информации и финансовой теории значительно снизили издержки достижения более масштабной диверсификации и специализации при принятии риска. В то же время возросшая изменчивость валютных курсов, процентных ставок и товарных цен повысили спрос на адекватные способы управления риском. Таким образом, стремительное и повсеместное развитие фьючерсов, опционов и свопов, которое началось в 70-80-е годы, в значительной степени можно объяснить реакцией рынка. Наряду с удешевлением затрат на использование инструментов по Управлению риском, произошло увеличением спроса на них.  [c.178]

Функциональная связь между одаренностью и квалификацией может быть выявлена и в иных группировках материала анкеты, помимо вышеприведенной. Так, если в основание группировки положить средний балл общей одаренности, выведенной по каждому бланку, то получим такое весьма характерное процентное распределение обследованных ученых (табл. 32).  [c.89]

Уравнения с (2. 10а) по (2. 10в) дают разные ответы в зависимости от того, какая была открыта позиция длинная или короткая. Например, если акция куплена за 80, а продана за 100, выигрыш составит 25%. Однако если акция продана по 100, а закрыта по 80, то выигрыш составит только 20%. В обоих случаях позицию открыли по 80 и закрыли по 100. Таким образом, последовательность — хронология трансакций — должна приниматься во внимание. Так как хронология трансакций затрагивает распределение процентных выигрышей и проигрышей, мы допускаем, что будущая хронология скорее всего будет подобна прошлой. Конечно, мы можем игнорировать хронологию сделок (используя 2.10в для длинных позиций и цену выхода в знаменателе 2.10в для коротких позиций), но это означало бы уменьшение информации в исторических данных. Более того, риск торговли является функцией хронологии торговли, и этот факт мы были бы вынуждены игнорировать.  [c.76]

Уравнение (5.11) не учитывает разницу между фондовыми опционами и товарными опционами. Согласно общепринятому подходу, в цену фондового опциона включается доход по простой бескупонной облигации, которая будет погашена в момент истечения срока опциона и номинал которой равен цене исполнения. Опционы на товарные фьючерсы, как считается, имеют процентную ставку 0. Мы же не учитываем это обстоятельство. Если ценная бумага и товар имеют абсолютно одинаковое распределение ожидаемых результатов, т.е. их арифметические математические ожидания равны, то разумный инвестор выберет более дешевый инструмент. Эту ситуацию хорошо иллюстрирует пример, когда вы рассматриваете покупку одного из двух одинаковых домов, и один из них оценен выше только потому, что продавец платил более высокую процентную ставку по ипотечному кредиту  [c.162]

Чтобы оценить динамику изменения кредитоспособности компании за ряд лет, можно использовать простой коэффициент — отношение суммы долга к чистой посленалоговой прибыли, то есть показатель того, сколько лет нужно компании, чтобы погасить долги. Поскольку при этом мы игнорируем расходы на выплату процентов (хотя они и вычитаются из чистой прибыли, пригодной для распределения среди акционеров), изменение процентных ставок оказывает незначительное влияние на величину этого показателя.  [c.477]

Если ожидаемая норма чистой прибыли дополнительного реального капитала, скажем, в отрасли промышленности, выпускающей компьютеры, равна 12%, а необходимые фонды могут быть обеспечены при ставке, равной 8%, то данная отрасль в состоянии с точки зрения прибыли прибегать к займу и расширять свой основной капитал. Если ожидаемая норма чистой прибыли дополнительного капитала, скажем, в сталелитейной промышленности составит только 6%, то для этой отрасли будет невыгодным накапливать больше средств производства при процентной ставке в размере 8%. Короче говоря, процентная ставка способствует распределению денег и в конечном счете реального капитала между теми отраслями, где они окажутся наиболее производительными и соответственно наиболее прибыльными. Такое распределение средств производства — явно в интересах общества в целом.  [c.643]

Неэффективность. Мы только что обсудили, каким образом равновесная процентная ставка выделяет деньги на те инвестиционные проекты, где ожидаемая ставка (эффективность) будет наибольшей. Распределение кредита в соответствии с законами о ростовщичестве, скорее всего, не обеспечит финансирование наиболее эффективных проектов. Рассмотрим пример. Предположим, у Холли есть настолько многообещающий проект, что она готова платить 8% за кредит на его финансирование. У Бена тоже есть проект, менее многообещающий, и он не захочет платить более 6% за его финансирование. Если бы фонды распределял рынок, то на высокопродуктивный проект Холли деньги бы нашлись, а на проект Бена – нет. Такое распределение фондов в интересах как Холли, так и всего общества. Но при установлении предела ставки в 6% существует 50%-ная вероятность, что деньги получит Бен, а не Холли. Законодательное установление максимальной процентной ставки приводит к выделению фондов и для менее эффективного использования.  [c.644]

Для купонных облигаций корпораций налогооблагаемым ежегодным доходом являются купонные выплаты. Более того, если при выпуске облигация была продана по номинальной цене, а затем приобретена инвестором на вторичном рынке со скидкой к номиналу (как отмечалось ранее, такие бумаги называются рыночными дисконтными облигациями), то инвестору обычно приходится платить подоходный налог как на купонные выплаты, так и на дисконт. Используя либо метод постоянного процента, либо метод равномерного распределения дисконта на период до погашения облигации, инвестор может определить часть дисконта как ежегодный процентный доход от обли-  [c.402]

Это уменьшение составило от 1 до 4 процентных пунктов. Во-вторых, значительно возросла доля пятой группы с 38,3 до 46,9%. Это означает, что в ней произошла существенная концентрация доходов. В-третьих, резко усилилась неравномерность распределения денежных доходов в нашей стране. Если у 40% населения с наименьшими доходами душевой доход здесь в 1995 г. был в 2,5 раза ниже среднего уровня (для всех групп), то у 20% населения из пятой группы душевой доход в 2,3 раза превысил средний уровень.  [c.458]

Важной социально-экономической проблемой является распределение дохода. Его рассматривают, прежде всего, с функциональной точки зрения, то есть распределения полученного совокупного дохода между факторами производства. Функциональное распределение дохода, как было ранее показано в главе 4, свидетельствует о том, какая доля национального дохода или богатства присваивается соответствующим фактором производства. Основная часть текущих доходов в рыночной макроэкономике приходится на заработную плату (с включением в нее всей суммы социальных налогов и выплат, а также доходов индивидуальных предпринимателей, не использующих наемных рабочих). Практика развитых стран показывает, что доля заработной платы в составе национального дохода при длительном, стабильном и прогрессирующем макроэкономическом развитии не должна опускаться ниже 80—85%. Заработная плата является основным фактором, побуждающим граждан к использованию всей совокупности рыночных ценностей как стимулов хозяйственного й социального прогресса. На прибыль предприятий негосударственного сектора в итоге конечного распределения национального дохода обычно приходится около 14%, включая как предпринимательскую прибыль в реальном секторе экономики, так и процентные доходы. Из этой величины основная сумма расходов приходится на реальные инвестиции (они образуются в результате трансформации сбережений в расходы на закупку оборудования, производственное строительство и т.п. расходы). Иначе говоря, в социально ориентированной экономике функциональное распределение национального дохода признается эффективным, если темп прироста желаемого в определенном структурном качестве реального национального дохода, взвешенный по показателю прироста инвестиционной емкости сбережений участников рынка и при требуемом объеме совокупной заработной платы является максимальным  [c.291]

Для статистической проверки этого факта можно воспользоваться сравнением подсчитанного значения статистики у с процентной точкой / “-распределения (см. табл. П.5). А при достаточно больших объемах п исходных выборок ВЛ можно непосредственно проверять факт F-распределенности случайных  [c.200]

В математической статистике широко используются квантили и процентные точки распределения случайной величины. Пусть случайная величина X имеет непрерывную функцию распределения F(x) и пусть задано число 0 < q < 1. Квантилъю уровня q (или q- квантилъю) распределения F(x) называется такое число uq, что F(uq) = Р(Х . uq) = q. Если величина X дискретна, то может случиться, что такого числа uq либо не существует, либо их бесконечно много. Но всегда можно найти два числа x q < xq такие, что F(x ) q, F(x ) > q. Тогда g-квантиль определяется как любое число, лежащее между x q и х .  [c.512]

Фуллер затабулировал процентные точки распределений оценки а и -статистики для проверки гипотезы а = 1 в такой ситуации.  [c.127]

США — не маленькая страна. Политика правительства США влияет на международные рынки капитала. Тем не менее важно помнить, что наша экономика не закрытая, и хотя громадный дефицит 1986 г. равен более четверти сбережений страны15, он представляет гораздо меньшую часть суммарных мировых сбережений. Дефицит может вылиться в до некоторой степени более высокие процентные ставки, он также вызывает увеличение притока капитала из-за границы (выше, чем он был бы в ином случае). Тот факт, что выросший в начале 1980-х гг. дефицит государственного бюджета хорошо соответствовал увеличившимся займам за границей, был на этом фоне не случайным16. Из этих дефицитов возникло бремя, ложащееся на будущие поколения. Желательно это или нет — вопрос распределения доходов во времени, будь то распределение дохода в пользу нынешнего поколения или нет.  [c.633]

Для определения вероятности того, что чистая текущая стоимость проекта будет меньше нуля, мы должны обратиться к таблице нормального распределения (см. приложение Б в конце данной главы). Видим, что с вероятностью 0,4013 результат наблюдения будет находиться менее чем на -0,25 стандартного отклонения от математического ожидания данного распределения с вероятностью 0,3821 — менее, чем на -0,30 стандартного отклонения от математического ожидания. Интерполируя, мы найдем, что существует приблизительно 40-процентная вероятность того, что чистая текущая стоимость будет меньше нуля. Отсюда с вероятностью 60% чистая текущая стоимость проекта будет больше нуля. При нормальном распределении 68% распределения попадают в область, ограниченную одним стандартным отклонением в ту и другую сторону от математического ожидания. То есть мы знаем, что с вероятностью 2/3 чистая текущая стоимость предложения будет находиться в пределах 116 дол. – 444 дол. = -328 дол. и 116 дол. + 444 дол. = 560 дол. Выражая отклонение от математического ожидания в стандартных отклонениях, мы можем определить вероятность того, что чистая текущая стоимость инвестиционного предложения будет больше или меньше определенной величины.  [c.397]

Причем, наличие некоторых экономических рычагов, тесно связанных со стимулированием, обусловлено принятой системой финансирования предпроизводственного этапа СОНТ. При использовании заемных средств таким рычагом является процентная ставка и принятый метод отнесения средств по уплате процентов на результаты хозяйственной деятельности предприятий и поощрительные фонды. Но, как уже отмечалось, эффективность воздействия процентной ставки на результаты проведения кредитуемых работ сегодня еще весьма незначительна. Основными причинами такого положения являются следующие неточность планирования расходов на уплату процентов банку, приводящая в результате к большим расхождениям между запланированными и фактическими суммами уплаты за кредит. Предприятия-разработчики новой техники предусматривают в своих финансовых планах часть прибыли на уплату процентов за плановые ссуды, причем эта прибыль позволяет часто покрывать перерасход средств по уплате при нарушении плановых сроков работ по СОНТ. Если устранение первой причины связано в основном с перестройкой банковской системы взаимоотношений с ссудополучателями и совершенствованием расчетных операций, то вторая причина вызывается механизмом распределения прибыли предприятиями при формировании фондов стимулирования. Не  [c.208]

Таким образом, в соответствии с моделью Блэка для фьючерсов справедливая стоимость колл-опциона с ценой исполнения 600, сроком исполнения 15 сентября 1991 года, при цене базового инструмента на 1 августа 1991 года 575, при вола-тильности 25%, с учетом 252-дневного года и R = 0 составляет 10,1202625. Интересно отметить связь между опционами и базовыми инструментами, используя вышеперечисленные модели ценообразования. Мы знаем, что 0 является наименьшей ценой опциона, но верхняя цена — это цена самого базового инструмента. Модели демонстрируют, что теоретическая справедливая цена опциона приближается к верхнему значению (стоимости базового инструмента U) при росте любой или всех трех переменных Т, R или V Это означает, что если мы, например, увеличим Т (время до срока истечения опциона) до бесконечно большого значения, тогда цена опциона будет равна цене базового инструмента. В этой связи мы можем сказать, что все базовые инструменты в действительности эквивалентны опционам с бесконечным Т. Таким образом, все сказанное верно не только для опционов, но и для базовых инструментов, как будто они являются опционами с бесконечным Т. Модель фондовых опционов Блэка-Шоулса и модель опционов на фьючерсы Блэка построены на определенных допущениях. Разработчики этих моделей исходили из трех утверждений. Несмотря на недостатки этих утверждений, предложенные модели все-таки довольно точны, и цены опционов будут стремиться к значениям, полученным из моделей. Первое из этих утверждений состоит в том, что опцион не может быть исполнен до истечения срока. Это приводит к недооценке опционов алгериканского типа, которые могут исполняться до истечения срока. Второе утверждение предполагает, что мы знаем будущую волатильность базового инструмента, и она будет оставаться постоянной в течение срока действия опциона. На самом деле это не так (т.е. волатильность изменится). Кроме того, распределение изменений волатильности логарифмически нормально, и эту проблему модели не учитывают1. Еще одно допущение модели состоит в том, что безрисковая процентная ставка остается постоянной в течение времени действия опциона. Это также не обязательно. Более того, краткосрочные ставки логарифмически нормально распределены. То обстоятельство, что, чем выше краткосрочные ставки, тем выше будут цены опционов, и утверждение относительно неизменности краткосрочных ставок может привести к еще большей недооценке опциона по отношению к ожидаемой цене (его правильному арифметическому математическому ожиданию). Еще одно утверждение (возможно наиболее важное), которое может привести к недооценке стоимости опциона, рассчитанной с помощью модели, по отношению к действительно ожидаемой стоимости, состоит в том, что логарифмы изменений цены распределяются нормально. Если бы опционы характеризовались не числом дней до даты истечения срока, а числом тиков вверх или вниз до истечения, а цена за один раз могла бы изменяться только на 1 тик и он был бы статистически независим от предыдущего тика, то мы могли бы допустить существование нормального распределения. В нашем случае логарифмы изменений цены не имеют таких характеристик. Тем не менее теоретические справедливые цены, полученные с помощью моделей, используются профессионалами на рынке. Даже если некоторые трейдеры применяют модели, которые отличаются от показанных здесь, большинство из них дадут похожие теоретические справедливые цены. Когда реальные цены расходятся с теоретическими до такой степени, что спекулянты могут получить прибыль, цены начинают снова сходиться к так называемой теоретической справедливой цене . Тот факт, что мы можем спрог-нозировать с  [c.160]

При ожидаемой инфляции распределение дохода между кредитором и дебитором также могло бы быть иным. Предположим, что кредитор (например, коммерческий банк или ссудо-сберегательная ассоциация) и заемщик (домохозяйство) договариваются о том, что 5% — это справедливая процентная ставка по займу сроком на 1 год в том случае, если уровень цен останется неизменным. Но допустим, что инфляция все-таки есть и на будущий год она ожидается на уровне 6%. Если банк дает заемщику ссуду в размере 100 дол. под 5% годовых, то в конце года он получит обратно 105 дол. Но если инфляция действительно достигнет 6% в течение этого года, то покупательная способность этих 105 дол. упадет примерно до 99 дол. Фактически кредитор платит заемщику 1 дол. за то, что последний в течение года пользовался его деньгами.  [c.175]

Но процентная ставка не полностью выполняет задачу распределения капитала в целях его наиболее эффективного производительного применения. Крупные заемщики — олигополисты находятся в лучшем положении, чем конкурирующие заемщики, поскольку у них есть возможность перекладывать затраты на погашение процентов на потребителей, контролировать предложение и манипулировать ценами. Большой размер и высокий престиж крупных промышленных концернов также позволяет им получать денежный капитал на более выгодных условиях, в то время как менее известным фирмам трудно выйти на рынок денежного капита-  [c.643]