|
Один из способов решения задач на проценты – это использование пропорций. Как правильно составлять и решать подобные пропорции? Существует много практических задач, использующих понятие процентов. Часто для их решения используется понятие пропорции. В простых случаях можно решать вот таким образом: все мы знаем, что 50% это половина от числа, 25% – это его четвёртая часть, 20% – это пятая часть, 10% -это 10 часть , 5 % – 20 часть, 1% – 100 часть. Итак, найти один процент от 2000 это 2000/100=20. Найти 50 % от 60 это 60/2=30. А можно использовать универсальный способ – понятие пропорции. Предположим надо найти 13% от 180. Тогда составим: 180 – 100% Х – 13 % Мы должны числа писать под числами, проценты под процентами. Далее раскрывает пропорцию крест накрест. То с чем икс не в паре перемножаем, а с чем в паре по диагонали – делим. У нас получаем 180*13/100=23,4 система выбрала этот ответ лучшим
Ксарфакс 4 года назад Пропорция с процентами составляется по следующему принципу:
Вот как выглядет такая пропорция: A / B = 100% / p% Например: 1000 / 50 = 50% / 5%. Или можно записать по-другому: 1000 – 100%. 50 – 5%. При решении задач на проценты с помощью пропорции неизвестный её член (а здесь может быть 3 варианта) обычно обозначается за x. Решить пропорцию (то есть найти неизвестный член) можно благодаря её основному свойству: произведение крайних членов пропорции равно произведению средних (другими словами, нужно перемножить члены пропорции крест-накрест).
Далее рассмотрим несколько простых примеров. Пример 1. Зарплата составляет 30000 рублей, а премия – 10% от зарплаты. Нужно определить размер премии. 30000 – 100%. x – 10%. Вспоминаем, что произведение крайних членов равно произведению средних: 30000 * 10 = 100 * x. x = (30000 * 10) / 100 = 3000. Значит, премия равна 3000 рублей. Пример 2. Сделано 20 выстрелов, 4 из них – мимо мишени. Нужно определить процент попадания. 20 – 100%. 4 – x%. Умножаем крест-накрест и приравниваем: 20 * x = 100* 4. x = (100 * 4) / 20 = 20. Здесь нужно учесть, что 20% – это процент выстрелов мимо мишени (так как рядом с неизвестным x были записаны именно промахи). Процент попадания в свою очередь равен 100% – 20% = 80%. Пример 3. За месяц было продано 30 ноутбуков, что составляет 20% от всего количества ноутбуков, имеющихся в продаже. Нужно найти, сколько всего ноутбуков было в магазине изначально. x – 100%. 30 – 20%. Умножаем крест-накрест: 20 * x = 100 * 30. x = (100 * 30) / 20 = 150. Таким образом, изначально в продаже было 150 ноутбуков.
Zummy out off 3 года назад Я как-то со школы запомнила принцип пропорции и способ ее решения называю «крест-накрест», не помню, кто это мне подсказал. Никогда не нахожу проценты по принципу умножения на сотую часть, мне не удобно, всегда использую свой «крест», единственное неудобство – нужно наглядно записывать это. Это не страшно – бумага всегда под рукой. Составляю пропорцию по условию, одно из значений неизвестное обозначаю Х. Затем решаю: перемножаю цифры, расположенные «на углах» слева и справа от Х, делю на число, расположенное на противоположном углу от Х. Пример: нужно найти 5% от числа 420. Пишу пропорцию. 420 – 100 % Х – 5 % Х = 5 • 420 : 100 = 21% Вот моя запись с крестом
Ещё пример: сколько процентов от 200 составляет число 20. Составляю пропорцию. 200 – 100 % 20 – Х % Решение: X = 20 • 100 : 200 = 10%
Алиса в Стране 3 года назад Странно, конечно, для таких простых задач составлять какие-то дополнительные пропорции, они решаются в уме и очень быстро, но способ такой есть, давайте его рассмотрим, возможно, кому-то он пригодится. Допустим, нам надо найти сколько процентов составляет число 18 от числа 90, в принципе, мы и так сразу видим что 18 это одна пятая, то есть 20 процентов от числа 90, но давайте составим пропорцию, приняв за х искомое количество процентов, пропорция у нас будет такая: 90 – 100 % 18 – х %, откуда х = 100 х 18 / 90 = 20 процентов. Еще один пример для закрепления материала, найдем, сколько процентов составляет 24 от 250, пропорция: 24 – х 250 – 100 х = 24 х 100 /250 = 9,6 %.
Go Green 3 года назад Для определения процентного соотношения от числа нужно иметь представление об основных простых процентных соотношениях и о принципе вычисления любых из них. Для простоты давайте приведем примеры с числом 100. 1 % от ста – это одна сотая часть или один процент. 2% от ста – две сотых части от ста. 7% от ста – семь сотых части от ста и так далее. То есть сначала нам нужно узнать, сколько составляет один процент любого числа, разделив его на сто, а затем узнавать заданное процентное соотношение. Например, нам нужно найти, сколько будет равно 7 процентам от 200. Делим 200 на 100. Получится 2. Умножим 2 на 7, получится 14. Итого: 7% от 200 будет равняться числу 14. СТА 1106 3 года назад Всегда любила задачки на пропорции. Главное- правильно ее составить, а потом все просто, крест на крест и решение готово. Простейший пример. Найти на сколько процентов цех выполнил план по сборке за смену, если общий план 250 механизмов( штук), а всего за смену было собрано 262 ? Итак решаем. 250 штук – 100 % 262 штуки – х % Решение: 262 × 100:250= 104,8 %. Пример 2. Выяснить, сколько столовой нужно картофеля на год, если 20 тонн закрывают потребность лишь на 82%. Решение. Опять пропорция, где известно доля от потребности и в тоннах и процентах. Общая потребность , разумеется берется за 100. 20 тонн – 82 % Х тонн – 100 %. 20 × 100:82= 24,4 тонны.
Бекки Шарп 3 года назад Допустим по условию задачи нам известно сколько всего было единиц (1000 кг яблок) и надо узнать сколько единиц (кг сухого вещества) составляют 18%. Составляем пропорцию, в которой 1000 – это 100%, а неизвестной х – 18 %. То есть в пропорции у нас есть единицы и проценты. Соотносим соответственно кг к кг и проценты к процентам. это обязательное условие пропорции. Пропорция будет выглядеть так:
Бархатные лапки 3 года назад Обычно в таких задачах задано общее число единиц, кг, км и нужно узнать сколько этих единиц составит определенное количество процентов. Или наоборот сколько процентов составляет количество единиц. То есть даны два известных, но мы помним что есть еще проценты, что общее количество чего-то это всегда 100%. Например нам нужно узнать сколько процентов составляет 38 рублей от 40 рублей. Составим пропорцию: 40/38=100/х, где 40 рублей это 100%, х – сколько рублей 38%. Из пропорции находим х = 95 %.
Точно в цель 3 года назад Посчитать пропорцию с процентами очень легко. В задачах на пропорции с процентами нам нужно посчитать проценты от числа. Для решения задачи нам нужно знать, что 50% – это половина от числа, 25% – одна четвертая от числа. То есть для того, чтобы найти пропорцию с процентами, нам нужно разделить число на 100 и умножить на процент. Например, мне нужно найти 20 процентов от числа 230. Сначала я 230 делю на 100, получается 2.3, а затем умножаю его на 20 – получаю 46. 50 процентов является половиной от числа, 25 является четвертой частью, 20 – пятой, 10 – 10, 5 является 20, а 1 процент – 100 часть. Один процент от 2000 найти не сложно. 2000 делим на 100 получим 20. Для того чтобы найти 50 процентов от 60 вам потребуется поделить на 2 = 30. Если нужно найти 13 процентов от 180 то 180 = 100 процентам , х = 14 получится 180 умножим на 13 делим на 100 и получаем 23,4. [пользователь заблокирован] 4 года назад Всё очень просто. Всегда нужно начинать с того, что процент – это одна сотая часть. Ну, а далее – пропорция составляется исходя из этой посылки. Знаете ответ? |
Задачи на проценты: считаем проценты с помощью пропорции
11 ноября 2013
В прошлом видеоуроке мы рассматривали решение задач на проценты с помощью пропорций. Тогда по условию задачи нам требовалось найти значение той или иной величины.
В этот раз исходное и конечное значения нам уже даны. Поэтому в задачах будет требоваться найти проценты. Точнее, на сколько процентов изменилась та или иная величина. Давайте попробуем.
Задача. Кроссовки стоили 3200 рублей. После повышения цены они стали стоить 4000 рублей. На сколько процентов была повышена цена на кроссовки?
Итак, решаем через пропорцию. Первый шаг — исходная цена была равна 3200 рублей. Следовательно, 3200 рублей — это 100%.
Кроме того, нам дана конечная цена — 4000 рублей. Это неизвестное количество процентов, поэтому обозначим его за x. Получим следующую конструкцию:
3200 — 100%
4000 — x%
Что ж, условие задачи записано. Составляем пропорцию:
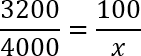
Дробь слева прекрасно сокращается на 100: 3200 : 100 = 32; 4000 : 100 = 40. Кроме того, можно сократить на 4: 32 : 4 = 8; 40 : 4 = 10. Получим следующую пропорцию:
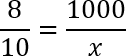
Воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получаем:
8 · x = 100 · 10;
8x = 1000.
Это обычное линейное уравнение. Отсюда находим x:
x = 1000 : 8 = 125
Итак, мы получили итоговый процент x = 125. Но является ли число 125 решением задачи? Нет, ни в коем случае! Потому что в задачи требуется узнать, на сколько процентов была повышена цена на кроссовки.
На сколько процентов — это значит, что нам нужно найти изменение:
∆ = 125 − 100 = 25
Получили 25% — именно настолько была повышена исходная цена. Это и является ответом: 25.
Задача B2 на проценты №2
Переходим ко второй задаче.
Задача. Рубашка стоила 1800 рублей. После снижения цены она стала стоить 1530 рублей. На сколько процентов была снижена цена на рубашку?
Переводим условие на математический язык. Исходная цена 1800 рублей — это 100%. А итоговая цена 1530 рублей — она нам известна, но неизвестно, сколько процентов она составляет от исходной величины. Поэтому обозначим ее за x. Получим следующую конструкцию:
1800 — 100%
1530 — x%
На основе полученной записи составляем пропорцию:
![]()
Давайте для упрощения дальнейших вычислений разделим обе части данного уравнения на 100. Другими словами, у числителя левой и правой дроби мы зачеркнем два нуля. Получим:
![]()
Теперь снова воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних.
18 · x = 1530 · 1;
18x = 1530.
Осталось найти x:
x = 1530 : 18 = (765 · 2) : (9 · 2) = 765 : 9 = (720 + 45) : 9 = 720 : 9 + 45 : 9 = 80 + 5 = 85
Как видите, мы не стали считать полученное частное уголком, а просто несколько раз сократили нашу дробь. При этом нам потребовалось разложить на множители числитель и
Мы получили, что x = 85. Но, как и в прошлой задаче, это число само по себе не является ответом. Давайте вернемся к нашему условию. Теперь мы знаем, что новая цена, полученная после снижения, составляет 85% от старой. И для того, чтобы найти изменения, нужно из старой цены, т.е. 100%, вычесть новую цену, т.е. 85%. Получим:
∆ = 100 − 85 = 15
Это число и будет ответом: Обратите внимание: именно 15, а ни в коем случае не 85. Вот и все! Задача решена.
Внимательные ученики наверняка спросят: почему в первой задаче мы при нахождении разности вычитали из конечного числа начальное, а во второй задаче поступили в точности до наоборот: из исходных 100% вычли конечные 85%?
Давайте проясним этот момент. Формально, в математике изменением величины всегда называется разность между конечным значением и начальным. Другими словами, во второй задаче у нас должно было получиться не 15, а −15.
Однако этот минус ни в коем случае не должен попасть в ответ, потому что он уже учтен в условии исходной задачи. Там прямо сказано о снижении цены. А снижение цены на 15% — это то же самое, что повышение цены на −15%. Именно поэтому в решении и ответе задачи достаточно написать просто 15 — без всяких минусов.
Все, надеюсь, с этим моментом мы разобрались. На этом наш сегодняшний урок закончен. До новых встреч!
Смотрите также:
- Задачи на проценты: стандартный расчет с помощью пропорций

- Процент: неизвестно начальное значение (метод пропорции)

- Тест к уроку «Что такое числовая дробь» (легкий)

- Сводный тест по задачам B15 (1 вариант)

- Деление многочленов уголком

- Задача B4: строительные бригады

Простейшие формулы помогут узнать, выгодны ли скидки, и не нарушить пропорцию классного рецепта.

1. Как посчитать проценты, разделив число на 100
Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.
Пример 1
Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.
Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.
Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.
Умножьте 4,58 на 7, и вы получите 32,06 рубля.
Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.
Пример 2
Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.
Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.
Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.
100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.
2. Как посчитать проценты, разделив число на 10
Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.
Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.
Пример
Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.
В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.
Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.
Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.
В любом случае такими крупными числами оперировать довольно просто.
3. Как посчитать проценты, составив пропорцию
Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:
сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.
Или можно записать её так: a : b = c : d.
Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.
Пример 1
Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.
Сначала вычисляем процентную долю оставшегося шоколада.
90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.
Х = 70 × 100 / 90 = 77,7%.
Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:
200 г : 100% = Х : 77,7%, где Х — нужное количество масла.
Х = 77,7 × 200 / 100 = 155,4.
Следовательно, в тесто нужно положить примерно 155 г масла.
Пример 2
Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.
Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.
Составьте пропорцию: 1 499 : 100 = Х : 87.
Х = 87 × 1 499 / 100.
Заплатите 1 304,13 рубля и носите блузку с удовольствием.
4. Как посчитать проценты с помощью соотношений
В некоторых случаях можно воспользоваться простыми дробями. Например, 10% — это 1/10 числа. И чтобы узнать, сколько это будет в цифрах, достаточно разделить целое на 10.
- 20% — 1/5, то есть нужно делить число на 5;
- 25% — 1/4;
- 50% — 1/2;
- 12,5% — 1/8;
- 75% — это 3/4. Значит, придётся разделить число на 4 и умножить на 3.
Пример
Вы нашли брюки за 2 400 рублей со скидкой 25%, но у вас в кошельке только 2 000 рублей. Чтобы узнать, хватит ли денег на обновку, проведите серию несложных вычислений:
100% — 25% = 75% — стоимость брюк в процентах от первоначальной цены после применения скидки.
2 400 / 4 × 3 = 1 800. Именно столько рублей стоят брюки.
5. Как посчитать проценты с помощью калькулятора
Если без калькулятора вам жизнь не мила, все вычисления можно делать с его помощью. А можно поступить ещё проще.
- Чтобы посчитать проценты от суммы, введите число, равное 100%, знак умножения, затем нужный процент и знак %. Для примера с кофе вычисления будут выглядеть так: 458 × 7%.
- Чтобы узнать сумму за вычетом процентов, введите число, равное 100%, минус, размер процентной доли и знак %: 458 – 7%.
- Аналогично можно складывать, как в примере с депозитом: 530 000 + 5%.
6. Как посчитать проценты с помощью онлайн-сервисов
Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.
Planetcalc
На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.
Planetcalc→
Калькулятор — справочный портал
Ещё один сервис с калькуляторами на любой вкус.
Калькулятор — справочный портал→
Allcalc
Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.
Allcalc→
Читайте также 📑
- ТЕСТ: Умеете ли вы считать в уме?
- Математические игры — отличная разминка для мозга
- 11 книг, которые прокачают математическое мышление
- Как выучить таблицу умножения легко и быстро
Метод решения задач с процентами
Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
все – 100%
часть – часть в %
которые можно записать в виде пропорции
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
Примеры решения задач на проценты
Пример 1.
Найти число B составляющее 15% от числа 30.
Решение:
30 соответствует 100%
x соответствует 15%
Запишим пропорцию
решим полученное уравнение
Ответ: 15% от 30 равно 4.5.
Пример 2.
Найти сколько процентов составляет число 35 от числа 20.
Решение:
20 соответствует 100%
35 соответствует x
Запишим пропорцию
решим полученное уравнение
Ответ: 35 составляет 175% от 20.
Пример 3.
Найти число, 5% которого равны 20.
Решение:
x соответствует 100%
20 соответствует 5%
Запишим пропорцию
решим полученное уравнение
Ответ: 400.
При изучении процентов вам также будут полезны:
Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.
Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.
Задачи про проценты вокруг нас
Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.
А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.
Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.
А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.
Что такое процент?
Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.
Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.
Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.
Типы задач на проценты
Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.
Тип 1: Находим процент (дробь) от числа.
- Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
- Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.
Тип 2: Находим число по его проценту (дроби).
- Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
- Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.
Тип 3: Находим процентное отношение двух чисел (часть от целого числа).
- Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
- Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.
Тип 4: Увеличиваем число на процент.
- Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
- Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.
Тип 5: Уменьшаем число на процент.
- Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
- Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.
Тип 6: Задачи на простые проценты.
- Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
- Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.
Тип 7: Задачи на сложные проценты.
- Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
- Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% – процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)3 = 38021,875 – искомая сумма.
Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще. Давайте решим задачу №3 про класс и процент девочек в нем, составив пропорцию.
- Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:
30 – 100%
14 – х%
Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.
Задачи на проценты с решением
Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.
Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?
Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.
Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х2 = 0,96 ↔ х2 = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.
Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.
Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.
Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.
Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67% – 6% = 27%.
Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?
Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.
Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.
Заключение
Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.
Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.
Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.


