Формулы расчета процентов
Онлайн калькулятор
- Процент
- это одна сотая доля, обозначается знаком %. Само слово процент происходит от латинского pro centum, что означает сотая доля. Используется для обозначения части чего-либо по отношению к целому, выражается в сотых долях. Например, 5 процентов это пять сотых долей.
Проценты незаменимы в страховании, финансовой сфере, в экономических расчетах. В процентах выражаются ставки налогов, доходность капиталовложений, плата за заемные денежные средства (например, кредиты банка), темпы роста экономики и многое другое.
Содержание
Формула расчета доли в процентном отношении
Формула расчета процента от числа
Формула увеличения числа на заданный процент. Сумма с НДС
Формула уменьшения числа на заданный процент
Формула расчета исходной суммы. Сумма без НДС
Формула расчета простых процентов. Расчет процентов на банковский вклад
Формула расчета сложных процентов
Формула сложных процентов если процентная ставка дана не в годовом исчислении
1. Формула расчета доли в процентном отношении
Пусть задано два числа: A1 и A2. Надо рассчитать, какую долю в процентном отношении составляет число A1 от A2.
P = A1 / A2 * 100
В финансовых расчетах часто пишут
P = A1 / A2 * 100%
Пример 1.1 Рассчитаем какую долю в процентном отношении составляет 10 от 200
P = 10 / 200 * 100 = 5 (%).
Онлайн калькулятор
Доля в процентах
P =
2. Формула расчета процента от числа
Пусть задано число A2. Надо вычислить число A1, составляющее заданный процент P от A2.
A1= A2 * P / 100
Пример 2.1 Банковский кредит 10 000 рублей под 5% за весь срок кредита. Сумма процентов составит:
A1 = 10000 * 5 / 100 = 500
Онлайн калькулятор
Процент от числа
A1 =
3. Формула увеличения числа на заданный процент. Сумма с НДС
Пусть задано число A1. Надо вычислить число A2, которое больше A1 на заданный процент P. Используя формулу расчета процента от числа, получаем:
A2= A1 + A1 * P / 100
или
A2= A1 * (1 + P / 100)
Пример 3.1 Банковский кредит 10 000 рублей под 5% за весь срок кредита. Общая сумма долга составит:
A2= 10000 * (1 + 5 / 100) = 10000 * 1.05 = 10500
Пример 3.2 Сумма без НДС равна 1000 рублей, НДС 18%.
Рассчитаем сумму с НДС:
A2= 1000 * (1 + 18 / 100) = 1000 * 1.18 = 1180
Онлайн калькулятор
Увеличение числа на заданный процент
Сумма с НДС
A2 =
4. Формула уменьшения числа на заданный процент
Пусть задано число A1. Надо вычислить число A2, которое меньше A1 на заданный процент P. Используя формулу расчета процента от числа, получаем:
A2= A1 – A1 * P / 100
или
A2= A1 * (1 – P / 100)
Пример 4.1 Оклад за минусом подоходного налога (13%).
Пусть оклад составляет 10 000 рублей. Тогда сумма к выдаче составляет:
A2= 10000 * (1 – 13 / 100) = 10000 * 0.87 = 8700
Онлайн калькулятор
Уменьшение числа на заданный процент
A2 =
5. Формула расчета исходной суммы. Сумма без НДС
Пусть задано число A1, равное некоторому исходному числу A2 с прибавленным процентом P. Надо вычислить A2. Например, знаем денежную сумму с НДС, надо рассчитать сумму без НДС.
Обозначим p = P / 100, тогда:
A1= A2 + p * A2
или
A1= A2 * (1 + p)
тогда
A2= A1 / (1 + p)
окончательная формула расчета:
A2= A1 / (1 + P/100)
Пример 5.1 Сумма с НДС равна 1180 рублей, НДС 18%.
Стоимость без НДС составляет:
A2= 1180 / (1 + 0.18) = 1000
Онлайн калькулятор
Вычисление исходной суммы
Сумма без НДС
A2 =
6. Формула расчета простых процентов. Расчет процентов на банковский вклад
Если проценты на депозит начисляются один раз в конце срока вклада, то расчет процентов выполняется по формуле простых процентов:
Sp = K * P/100 * d/D
Формула расчета вклада с процентами:
S = K + K * P/100 * d/D
Иногда удобнее использовать формулу расчета в таком виде:
S = K * (1 + P/100 * d/D)
Где:
S — сумма банковского вклада с процентами,
Sp — сумма процентов (доход),
K — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — количество дней начисления процентов по привлеченному вкладу,
D — количество дней в календарном году (365 или 366).
Пример 6.1 Банком принят вклад 100 тыс. рублей сроком на 1 год по ставке 20%.
S = 100000 + 100000 * 20/100 * 365/365 = 120000
Sp = 100000 * 20/100 * 365/365 = 20000
Пример 6.2 Банком принят вклад 100 тыс. рублей сроком на 30 дней по ставке 20% годовых.
S = 100000 + 100000 * 20/100 * 30/365 = 101643.84
Sp = 100000 * 20/100 * 30/365 = 1643.84
Онлайн калькулятор
Расчет вклада с процентами
S =
Расчет процентов
Sp =
7. Формула расчета сложных процентов. Расчет процентов на банковский вклад при начислении процента на процент
Если проценты на депозит начисляются несколько раз через равные промежутки времени и зачисляются во вклад, то расчет вклада с процентами выполняется по формуле сложных процентов.
S = K * ( 1 + P/100 * d/D )N
Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — годовая процентная ставка,
d — продолжительность периода в конце которого начисляются проценты,
N — количество периодов начисления процентов.
При расчете сложных процентов проще вычислить общую сумму с процентами, а потом вычислить сумму процентов (доход), вычтя сумму начального вклада (капитал).
Формула расчета процентов:
Sp = S – K
или
Sp = K * ( 1 + P/100 * d/D )N – K
Иногда удобнее использовать формулу расчета в таком виде:
Sp = K * (( 1 + P/100 * d/D )N – 1)
Пример 7.1 Принят вклад 100 тыс. рублей сроком на 90 дней по ставке 20% годовых с начислением процентов каждые 30 дней.
S = 100000 * (1 + 20/100 * 30/365)3 = 105 013.02
Sp = 100000 * ((1 + 20/100 * 30/365)3 – 1) = 5 013.02
Онлайн калькулятор
Расчет вклада с процентами
S =
Расчет процентов
Sp =
Пример 7.2 Проверим формулу расчета сложных процентов для случая из предыдущего примера.
Разобьем срок вклада на 3 периода и сделаем расчет процентов для каждого периода, использую формулу простых процентов.
S1 = 100000 + 100000*20/100 * 30/365 = 101643.84
Sp1 = 100000 * 20/100 * 30/365 = 1643.84
S2 = 101643.84 + 101643.84*20/100 * 30/365 = 103314.70
Sp2 = 101643.84 * 20/100 * 30/365 = 1670.86
S3 = 103314.70 + 103314.70*20/100 * 30/365 = 105013.02
Sp3 = 103314.70 * 20/100 * 30/365 = 1698.32
Общая сумма процентов с учетом начисления процентов на проценты (сложные проценты)
Sp = Sp1 + Sp2 + Sp3 = 5013.02
Таким образом, формула расчета сложных процентов верна.
8. Формула сложных процентов если процентная ставка дана не в годовом исчислении
Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула расчета сложных процентов выглядит так:
S = K * ( 1 + P/100 )N
Где:
S — сумма вклада с процентами,
К — первоначальный вклад (капитал),
P — процентная ставка,
N — количество периодов начисления процентов.
Формула расчета процентов на вклад:
Sp = S – K
или
Sp = K * ( 1 + P/100 )N – K
Иногда удобнее использовать формулу расчета в таком виде:
Sp = K * (( 1 + P/100 )N – 1)
Пример 8.1 Принят депозит 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5% в месяц.
S = 100000 * (1 + 1.5/100)3 = 104 567.84
Sp = 100000 * ((1 + 1.5/100)3 – 1) = 4 567.84
Онлайн калькулятор
Расчет вклада с процентами
S =
Расчет процентов
Sp =
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Математика, 6 класс по учебнику «Математика» Н Я Виленкина, В И Жохова, А С Чеснокова, С И Шварцбурда.
Тема: «Решение экономических задач на проценты».
Цели:
Предметные:
-
повторить виды задач на проценты;
-
способствовать формированию умений решать задачи с помощью «сложных процентов»;
-
тренировка в умении решать задачи на проценты с экономическим содержанием разными способами.
Личностные:
-
преодолеть в сознании учеников неизбежно возникающее представление о формальном характере предмета, оторванности от жизни и практики;
-
способствовать созданию отношений взаимной ответственности и зависимости в группах;
-
содействовать развитию исследовательских умений.
Метапредметные:
-
формировать умение сравнивать, создавать обобщение, устанавливать аналогию , моделировать выбор способов деятельности.
Тип урока: урок-исследование.
Оборудование урока:
Для учителя:
1Мультимедиа-проектор,
2.презентация к уроку.
Для учащихся:
1.Раздаточный материал: карточки задания для групповой работы; листы «новых знаний»; сигнальные карточки;
2.Плакат с заданием для проведения самостоятельной работы (на обороте правильные ответы для самопроверки).
3.Карточки: с индивидуальными заданиями; с планом исследования.
Ход урока.
-
Актуализация знаний.
Вступительное слово учителя:
«Мы сегодня находимся в бизнес классе. В этом классе решают экономические задачи. Как бы вы определиnt цель нашего урока?»
Вариант ответа: «Научиться решать экономические задачи».
Подтверждает цель. «Но добиться достижения этой цели можно при одном условии: вы должны владеть некоторыми знаниями и умениями. Как вы думаете : какие знания и умения необходимы для решения экономических задач на проценты?»
Возможные варианты ответов:
-знания по теме «Проценты»;
-знание правила нахождение дроби от числа;
-умение решать задачи на проценты;
-умение выполнять вычисления;
-умение находить дробь от числа.
И т. п.
Формируемые УУД: Проверяется умение оформлять свои мысли в устной форме (коммуникативные УУД).
2. Операционно-исполнительный этап.
Нам необходимо извлечь из тайников памяти кое-что ценное по теме «Проценты».
2.1 а)Создание проблемной ситуации.
Устно (Разминка).
Разминка.
1). Что называется процентом?
Правильные ответы:
Один процент – это одна сотая доля числа.
(Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
В школьном учебнике «Математика, 5»,авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Проценты не просто пустое слово, а это универсальная величина измерения, которая появилась из практической необходимости измерения различных величин и не только денежных.)
2)Представьте проценты десятичной дробью и прочитайте предложение: а). Каждый работающий платит государству 12% своей зарплаты в качестве подоходного налога . Правильный ответ
Каждый работающий платит государству 0,12 своей зарплаты в качестве подоходного налога.
б). Налог на продажу дома составляет 3% его стоимости.
Правильный ответ
Налог на продажу дома составляет 0,03 его стоимости
в)Как найти 1% от числа?
Правильный ответ
Определение одного процента можно записать равенством: 1 % = 0,01 * а
3)Найдите, сколько будет:
5% от 200 рублей;
120% от 10 литров;
4% отличников от 25 учащихся.
Ответы (выберете правильный ): 10, 2, 1, 28, 12.
4) Найти 42% от числа 180.
Решений будет 3.
1 решение. 1) 42%=42/100=0,42
2) 180х0,42=75,6
2 решение. 1) 180 : 100=1,8 – 1% от 180
2) 1,8х42=75,6
3 решение. Число 180 – это 100%, нужно найти 42% от этого числа. Обозначим эту величину за х, тогда 180 – 100%
Х – 42%
Х=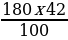
=
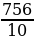=75,6.
Ответ : 75,6
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.
4)В задачах на проценты частенько встречаются обратная ситуация. Нам дают величины (какие угодно), а надо найти проценты.
Задача. Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?
Правильный ответ
Решение:
16 делим на общее количество арбузов и умножаем на 100 %.
Ответ: 8 % – составляют незрелые арбузы от всех арбузов.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
5) Задача.При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?
Решение: (66:60)х100=110(%)- такую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%
Ответ: 110%
Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.
6)найти число, 35% которого равно 280.
Решений будет 3
1 решение. 35%=0,35 ; 280:0,35=800.
2 решение. 280 – это 35%, значит на 1% приходится 280:35=8;
2) 8х100=800.
3 решение. Обозначим искомое число за х и составим пропорцию: х – 100%
280 – 35%
Х=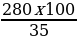
=800
Ответ:800.
Правило 4. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.
Формируемые УУД: Проверяется умение проговаривать последовательность действий (регулятивные УУД); оформлять свои мысли в устной форме (коммуникативные УУД); уметь ориентироваться в своей системе знаний(познавательные УУД).
« А теперь проверим, не забыли вы как решаются задачи на проценты. Сделаем это с помощью математического диктанта».
Перед диктантом вызывает двух учащихся решать у доски одну и ту же задачу разными способами.
Задача
Банк предлагает вклад «студенческий». По этому вкладу, сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик положил 1 января 1000 руб. и в течение 2 лет не производил со своим вкладом никаких операций. Какова сумма вклада на конец срока?
Задание записано на доске. Ребята решают и возвращаются на свои места.
1.Задача. Зарплату увеличили на 60%. Во сколько раз увеличилась зарплата?
Решение.
-
100+60=160(%)-увеличенная зарплата.
-
160:100=1,6 (раза0
Ответ: в 1, 6 раза.
2.Задача.
Что больше четверть или 30% площади?
Решение.
-
Четверть -25% от 100%
-
30%
25%.
25%.Ответ: 30% площади больше.
3.Задача.После понижения цены товара на 10% товар стал стоить 540 рублей. Какова первоначальная цена товара?
Решение.
-
100-10-90(%)- стал стоить товар в %
-
540:90х100=600(руб)- первоначальная цена товара.
Ответ: первоначальная цена товара 600 рублей.
4.Задача. Проезд на автобусе стоит 14 рублей. В дни школьных каникул для учащихся ввели скидку 25%. Сколько стоит проезд на автобусе в дни школьных каникул?
Решение.
-
14:100=0,14 – одна сотая часть или 1%.
-
25х0.14=3,5 (руб) – 25%.
-
14-3,5=10.5(руб)-новая цена.
. Ответ : 10.5 рубля новая цена билета.
Формируемые УУД: оформлять свои мысли в устной форме (коммуникативные УУД); уметь ориентироваться в своей системе знаний(познавательные УУД).
Письменное. Математический диктант с контролем.
Вопрос: кто получил верный ответ в первом задании?
Вопрос: кто получил верный ответ во втором задании?
Вопрос: кто справился со всей работой?
Организует взаимопомощь в парах, остальные сдают учащиеся работы.
Оценка: учитель просит оценить свою работу по повторению и устную, и письменную по пятибалльной системе.
Анализируют свое участие при повторении изученного материала и ставят отметку на лист с математическим диктантом.
Формируемые УУД: уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок (регулятивные УУД)
2.1 б) Постановка проблемы исследования.
Проверка задач решенных у доски.
Задача
Банк предлагает вклад «студенческий». По этому вкладу, сумма, имеющаяся на 1 января, ежегодно увеличивается на 10 процентов. Вкладчик положил 1 января 1000 руб. и в течение 2 лет не производил со своим вкладом никаких операций. Какова сумма вклада на конец срока?
Решение.
-
10%=0,1; 1000х0,1=100(рублей)-составят 10%
-
1000+100=1100(рублей)- в конце 1 года
-
1100х0,1=110(рублей)-составят 10% после второго года вложений
-
1100+110=1210(рублей)-в конце второго года вложений.
Ответ: 1210 рублей.
Вопрос: сколько способов решения этой задачи мы знаем?
Проблема: сколько будет действий в решении задачи, если надо узнать сумму вклада через 19 лет, через 15 лет?
Если надо узнать сумму вклада через 19 лет, то в решении задачи будет 20 действий, 15 лет – 16 действий.
Можно предположить, что есть рациональный способ решения.
Может с помощью какой-нибудь формулы?
Формируемые УУД: уметь оформлять свои мысли в устной форме (коммуникативные УУД); умение проговаривать последовательность действий (регулятивные УУД);
3 Формулировка цели исследования
Можно предположить, что есть рациональный способ решения.
2.4 Выдвижение гипотезы
Может с помощью какой-нибудь формулы?
Формируемые УУД: уметь ориентироваться в своей системе знаний :отличать новое от уже известного (познавательные УУД)
2.5 выбор метода решения проблемной ситуации
Листы новых знаний.
-
Давайте попытаемся решить задачу с помощью формулы. Используя формулу увеличения положительного число на p%, получим, что через год сумма вклада составит a*(1+0,01р), а через два года a*(1+0,01р)х(1+0,01р)= a*(1+0,01р)2 через t лет a*(1+0,01р)t– это так называемая формула сложных процентов. С условием, что никаких действий с вкладами не производятся, т е прийти в банк в конце срока хранения вклада. А если в конце каждого года хранения вклада снимать проценты по вкладу за tлет вы получите a*(1+0,01р)t- это так называемая формула простых процентов.
2.6 Составление плана исследования
Ребята работают с листами знаний, один ученик читает вслух текст.
Формируемые УУД: уметь выполнять работу по предложенному плану (регулятивные УУД)
2.7 «Открытие « нового знания.
Задача. Вкладчик положил 20 000 руб в банк, годовая процентная ставка которого 20%. Каким станет вклад через 3 года, если банк начисляет:
а ) простые проценты;
б) сложные проценты.
Решение.
а )по формуле простых процентов имеем:
p=20%=0,2
a=20 000 (рублей)
t=3 года
А=20.000 х (1+0,2х3)=32 000 (рублей)
б )Решение задачи по формуле.
p=20%=0,2
а=20 000 (рублей)
t=3(года)
A=(1+0,2)3*20000=34560(рублей)
Ответ : 34560 рублей.
Выбирают рациональный способ вложения денег в банк.
Зачем нужно научиться решать задачи с экономическим содержанием?
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Учитель :
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
Формируемые УУД: уметь добывать новые знания: находить ответы на вопросы, используя информацию, полученную на уроке (познавательные УУД); слушать и понимать речь другого (коммуникативные УУД).
3.Оценочно-рефлексивный этап
Работа в группах по 3-4 человека.
Каждая группа представляют какую-либо организацию, предприятие, отдел или просто семью. Получают задание. Руководитель группы организует работу по поиску решения задачи. Решение записывают в тетрадь, а руководитель на карточку. Обсуждают , делают вывод.
Учитель следит за работой в классе.
Формируемые УУД: уметь добывать новые знания: находить ответы на вопросы, используя информацию, полученную на уроке (познавательные УУД); слушать и понимать речь другого (коммуникативные УУД).
3.1Вывод по результатам исследовательской работе.
Отчет о проделанной работе.
–Сравните результаты с результатами на доске.
Если результат неверен, то учитель предлагает карточку с готовым решением.
Делает общий вывод.
Члены групп зачитывают ответ, делают вывод.
Проверяют результат по готовому решению.
Формируемые УУД: слушать и понимать речь другого (коммуникативные УУД); уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок (регулятивные УУД)
3.3 Применение новых знаний в учебной деятельности
Ребята (называет имена) вели наблюдение за ростом цен на товары в течении двух месяцев. И по результатам их наблюдений была
Составлена задача.
Задача. Вклад в Сбербанке «Сохраняй (пенсионный)» .
Первоначальный взнос: 100 000 руб.Процентная ствка 8%.Срок вклада: 2 год
Какова будет сумма вклада, если расчет идет по формуле сложных процентов.
Учащиеся читают условие задачи и решают ее самостоятельно. Один из учеников решает ее у доски (на оборотной стороне).
A= 100 000 x (1+0,08)2=116 4 00
Задача. Вклад в Сбербанке «Подари жизнь».Процентная ставка 8%, первоначальный взнос 100 000рублей. Какова будет сумма вклада через 2 года, если расчет идет по формуле простых процентов?
A= 100 000x(1+0,08х2)=116 000
Учитель Проводит контроль, используя запись решения, сделанную учеником на доске.
Проверяют решение по записи на доске. При необходимости исправляют ошибки.
Формируемые УУД: уметь выполнять работу по предложенному плану (регулятивные УУД);способность к самооценке на основе критерия успешности учебной деятельности (личностные УУД).
3.4 Итоги урока. Самооценка детьми собственной деятельности.
Учитель просит оценить степень сформированности умения решать задачи на проценты с экономическим содержанием.
На сигнальных карточках ставят один из символов: « ? », « ! », « . ».
. – умею решать предложенные задачи.
! – прекрасно справляюсь с решением.
? – затрудняюсь при решении.
Возможны варианты: «!?» и др
Формируемые УУД: уметь оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки (регулятивные УУД); способность к самооценке на основе критерия успешности учебной деятельности (личностные УУД).
4. Домашнее задание.
Кто справился с задачей? Для тех домашнее задание творческого характера: составить задачу на проценты, используя газетные статьи, специальную литературу, экономические знания родителей.
Кто допустил вычислительную лишь ошибку? Для тех задача дана на листе контроля и по желанию тоже можно придумать задачу.
Кто совсем не справился с работой? Для тех домашнее задание: стр.75, задача4(образец), №484, 491.
Привет всем читателям Блога Вебинвестора! Думаю, каждый из вас сталкивался с начислением процентов на денежную сумму — по депозиту, по кредиту, расчётом доходности инвестиций и так далее. Так вот, если повторить эту процедуру много раз, вложения начинают расти всё быстрее и быстрее благодаря эффекту сложного процента! Воистину, это один из главных секретов, как с помощью инвестирования увеличить количество нулей в сумме на вашем банковском счёте.
Эта статья входит в бесплатное обучение инвестициям с нуля на Блоге Вебинвестора. В комментариях к статье вы можете оставлять любые вопросы по теме и я постараюсь подробно на них ответить.
Приглашаю подписываться на мой Telegram-канал Блог Вебинвестора! Там вы найдёте еженедельные отчёты по инвестициям, аналитические материалы, комментарии по важным новостям и многое другое. Также прошу делиться ссылкой на блог в социальных сетях и мессенджерах:
Что такое простой и сложный процент
и чем они отличаются
Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.
Простой процент — прибыль в % начисляется только на первоначальную сумму вклада и сразу выводится.
Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:
Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Понятия «реинвестирование» и «капитализация» по сути означают использование сложного процента.
Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:
В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:
Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:
без капитализации депозит растёт линейно,
а с капитализацией — по экспоненте
Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 🙂 Конечно, 50 лет это много, но правило сложного процента неплохо работает и на более коротких промежутках времени — всё зависит от доходности вклада. Если хочется заработать больше, стоит использовать более прибыльные способы инвестирования: акции, драгоценные металлы, криптовалюты, валютный рынок и так далее.
Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.
⬆️ К СОДЕРЖАНИЮ ⬆️
Формулы простых и сложных процентов
Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:
- К0 — начальная сумма вклада;
- К — конечная сумма вклада;
- R — ставка доходности, переводится из процентов в число (10% = 0.1);
- N — количество периодов (лет).
Формула простого процента
По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:
Формула сложного процента
По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:
На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:
где D — сумма регулярных пополнений банковского депозита. Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N).
Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.
⬆️ К СОДЕРЖАНИЮ ⬆️
Примеры решения задач
по сложным процентам
В этом разделе мы пройдемся по некоторым типичным задачам на сложные проценты. Также вы найдете шаблоны расчётов в Excel, в которых можно поменять вводные данные и получить нужное вам решение.
Задача №1. Рассчитать прибыль по вкладу на 5 лет под 10% годовых, начальная сумма вложений 100000 рублей (с капитализацией).
Находим конечную сумму вклада по формуле сложных процентов:
Вычисляем прибыль:
Результат: инвестор через 5 лет получит 61051 рублей прибыли.
Задача №2. Рассчитать прибыль по вкладу на 10 лет под 10% годовых с капитализацией. Начальная сумма вложений 50000 рублей, дополнительно каждый год начиная с первого счёт пополняется на 10000 рублей.
Сначала находим конечную сумму по формуле сложного процента с регулярными пополнениями:
Учитывая, сколько инвестировано за 10 лет (50000 сразу и еще 9 раз по 10000), вычисляем прибыль:
Результат: инвестор через 10 лет получит 139061 рубль прибыли, инвестировав 140000 рублей.
Задача №3. Рассчитать, сколько времени понадобится инвестору, чтобы увеличить капитал с 500000 до 1000000 рублей. Средняя доходность портфеля — 12% годовых, прибыль реинвестируется.
У нас есть все необходимые данные, используем одну из производных формул сложных процентов:
Решение: инвестору понадобится чуть больше 6 лет.
Задача №4. Посчитать среднюю процентную ставку, которая позволит превратить 100000 рублей в 500000 рублей за 10 лет путём инвестирования. Прибыль реинвестируется.
Используем одну из производных формул сложных процентов:
Решение: инвестору нужно вложить деньги под 17.5% годовых (довольно сложно на практике, кстати).
Думаю, этого достаточно. Если ваша задача не похожа ни на одну из предыдущих, возможно вам поможет информация из следующего раздела статьи.
⬆️ К СОДЕРЖАНИЮ ⬆️
Калькулятор сложных процентов в Excel
Конечно же, задачи на сложные проценты целесообразнее решать в MS Excel по уже известным вам из предыдущих разделов формулам. По ходу статьи вы уже могли скачать некоторые примеры типичных задач, но если этого мало — предлагаю полную подборку калькуляторов по сложным процентам, реализованную в одном Excel-файле. Получить его можно бесплатно, просто заполните форму ниже:
Если письмо не пришло, проверяйте папку «Спам», иногда попадает туда. Если не видите форму подписки, оставьте комментарий к статье и я добавлю ваш электронный адрес вручную.
Вот какие задачи по простым и сложным процентам может решать «Коллекция калькуляторов для инвестора»:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт необходимой процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом регулярных пополнений и капитализацией;
- ожидаемый пассивный доход в каждом из случаев.
В будущем я планирую добавить много калькуляторов по самым разным темам, оставляйте свои пожелания в комментариях!
Пример одного из калькуляторов для расчёта сложных процентов в Excel:
Дополнительно к каждому калькулятору автоматически строится график доходности вклада с капитализацией и без:
А также уже знакомые вам таблицы:
Думаю, файл будет полезен и для практического использования, и в обучающих целях — в готовом виде есть все формулы, по которым можно считать сложные проценты в Excel.
⬆️ К СОДЕРЖАНИЮ ⬆️
Как использовать сложные проценты
в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Статья в тему: Как деньги делают еще больше денег или Что такое реинвестирование
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:
Источники: statbureau.org
Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:
Источник: ru.investing.com
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
- Акции, в особенности американские. Сейчас это один из немногих активов, которые растут большую часть времени. Кроме того, многие компании платят дивиденды, которые можно реинвестировать и еще сильнее разгонять сложный процент. Плюс, рост цен на сами акции способен перекрыть влияние инфляции, а комиссии зависят от объема торгов, а не от вашего вклада. Взгляните на самых богатых людей планеты — почти все сделали состояние, владея большим количеством акций в своих компаниях.
- Инвестиционные фонды (в т.ч. ETF). Чаще всего это тоже инвестиции в акции, но вам не нужно самостоятельно подбирать портфель — аналитики фонда все сделают за вас. Если в портфеле фонда есть дивидендные акции, вы опять же сможете реинвестировать выплаты. При комиссии за участие ниже 1% в год катастрофического влияния на доходность ваших инвестиций не будет.
- Облигации. Обычно они дают чуть большую доходность, чем банковский депозит и способны практически без рисков приносить небольшую прибыль с учётом инфляции. В любом случае в вашем инвестиционном портфеле должны быть надёжные долгосрочные вложения, и облигации для этих целей подходят неплохо. Расходы при вложении в облигации идут на услуги фондового брокера и не зависят от общей суммы инвестиций.
Оптимальный портфель инвестора предполагает использование всех этих инструментов, поскольку генерируемый ими денежный поток позволяет гибко управлять вложениями: делать ребалансировку, выводить прибыль или реинвестировать. Использовать правило сложных процентов можно в любых инвестициях, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
⬆️ К СОДЕРЖАНИЮ ⬆️
Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.
Удачных инвестиций и не болейте!
Простые и сложные проценты
С помощью калькулятора вычисляются параметры финансовых операций по простой и сложной банковской ставке (см. также вычисления при учетной ставке).
- Ввод данных
- Решение
Здесь будет показано решение
Существуют два способа начисления процентов: декурсивный и антисипативный. При декурсивном способе проценты начисляются в конце каждого интервала начисления. При антисипативном (предварительном) способе проценты начисляются в начале каждого интервала (процентная ставка называется учётной).
Простые проценты
На практике применяются три варианта расчета простых процентов:
- точные проценты с точным числом дней ссуды (английская практика). Обозначается как 365/365 или АТС/АТС.
- обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Обозначается как 365/360 или АТС/360.
- обыкновенные проценты с приближенным числом дней ссуды (германская практика). Обозначается как 360/360.
По схеме 360 количество дней к году принимается равным 360 (в каждом месяце по 30 дней).
Пример. Определить приближённое число дней между 12.02.2019 и 27.08.2020.
Если год рассматривается как промежуток, содержащий 12 месяцев продолжительностью 30 дней (дивизор равен 360 дней), то приближённое число дней рассчитывается следующим образом:
n = 360*(y2-y1)+30*(m2-m1)+(d2-d1)
где y – номер года, m – номер месяца в году, d – номер дня в месяце.
n = 360*(2020-2019)+30*(8-2)+(27-12) = 555 дней
Наращение основной суммы: S = P(1+i*n)
где P – исходная сумма, i – проценты, n – количество лет.
Когда срок финансовой сделки не равен целому числу лет:
S=P·(1+tT·i)
где t – срок в днях, T – временная база (365 или 360)
Примеры задач на простые проценты
Выберите необходимый вид задачи (кнопка Решить) и заполните требуемые поля.
- Ссуда в размере P = 1 млн.руб. выдана d1 = 20.01 до d2 = 05.10 включительно под i = 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить три метода расчёта срока ссуды.
Решить аналогичную
Начальная дата: 20.01, конечная дата: 05.10, количество дней между датами: 258
Январь, 11 дней: с 21.01 по 31.01
Февраль, 28 дней: с 01.02 по 28.02
Март, 31 день: с 01.03 по 31.03
Апрель, 30 дней: с 01.04 по 30.04
Май, 31 день: с 01.05 по 31.05
Июнь, 30 дней: с 01.06 по 30.06
Июль, 31 день: с 01.07 по 31.07
Август, 31 день: с 01.08 по 31.08
Сентябрь, 30 дней: с 01.09 по 30.09
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 11 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 5 = 258
S=P·(1+tT·i)
1) Точные проценты с точным числом дней ссуды (365/365)
S=1 000 000·(1+258365·0.18)=1 127 232.88 руб.
2) Обыкновенные проценты с точным числом дней (365/360)
S=1 000 000·(1+258360·0.18)=1 129 000 руб.
3) Обыкновенные проценты с приближённым числом дней (360/360)
Количество дней между датами: 255
Январь, 10 дней: с 21.01 по 30.01
Февраль, Март, Апрель, Май, Июнь, Июль, Август, Сентябрь по 30 дней
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 10 + 30*8 + 5 = 255
S=1 000 000·(1+255360·0.18)=1 127 500 руб. - Через d = 180 дней после подписания договора должник уплатит S = 310 тыс.руб. Кредит выдан под i = 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
Решить аналогичную
P=S(1+tT·i)
Находим современную стоимость P=310 000(1+180365·0.16) = 287 328.59 руб.
Сложные проценты
Выберите необходимый вид задачи (кнопка Решить) и заполните требуемые поля.
Сложная процентная ставка наращения – это ставка, при которой база начисления является переменной, то есть проценты начисляются на проценты. Формула наращения для сложных процентов имеет вид:
S=P·(1+i)n
Если в качестве периода наращения процентов используется не год, а, например, месяц (m=12), квартал (m=4) или другой период, то наращенная сумма определяется по формуле:
S=P·(1+im)m·n
Если срок ссуды измеряется дробным числом лет, то наращенную сумму можно найти смешанным методом:
S = P·(1+i)[n]·(1+{n}·i)
где [n] – целая часть числа; {n} – дробная часть числа n.
Современная стоимость Р величины S находится в случае сложной процентной ставки по формуле:
P=S(1+i)n
Примеры задач на сложные проценты
- Какой величины достигнет долг, равный P = 1 млн.руб., через n = 5 лет при росте по сложной ставке i = 15,5% годовых, если проценты начисляются раз в год, ежемесячно, поквартально и два раза в год?
Решить аналогичную
1) Сложные проценты начисляются раз в год:S = 1 000 000·(1+0.155)5 = 2 055 464,22 руб
2) Сложные проценты начисляются два раза в год:
S=1 000 000·(1+0,1552)2·5 = 2 109 467,26 руб.
3) Сложные проценты начисляются 4 раза в год (поквартально):
S=1 000 000·(1+0,1554)4·5 = 2 139 049,01 руб.
4) Сложные проценты начисляются ежемесячно (12 раз в год):
S=1 000 000·(1+0,15512)12·5 = 2 159 847,20 руб. - Через n = 5 лет предприятию будет выплачена сумма S = 1 млн.руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов i = 10% годовых.
Решить аналогичную
P=S(1+i)n
P=1 000 000(1+0,1)5 = 620 921,32 руб.
Если проценты начислялись ежеквартально.
P=S(1+im)m·n
P=1 000 000(1+0,14)4·5 = 610 270,94 руб. - Определить современную стоимость S = 20 тыс.руб., которые должны быть выплачены через четыре года (n = 4). В течение этого периода на первоначальную сумму начислялись сложные проценты по i = 8 %годовых: а)ежегодно; б)ежеквартально.
Решить аналогичную
P=S(1+i)n
P=20 000(1+0,08)4 = 14 568,92 руб.
Если проценты начислялись ежеквартально.
P=S(1+im)m·n
P=20 000(1+0,084)4·4 = 14 570 руб. - За взятые в долг деньги под сложную процентную ставку i=35% годовых должник обязан уплатить кредитору 30 тыс. руб. 1 июля 1997 г. Какую сумму необходимо уплатить должнику, если он вернет долг: а) 1 января 1997 г.; б) 1 января 1998 г.; в) 1 июля 1999 г.?
Количество дней в 1997 году: T=365.
а) 1 января 1997 г.;
Эта дата ранее 1 июля 1997 г., поэтому речь идет о поиске исходной суммы P (S=30000). Количество дней между 1 января 1997 г. и 1 июля 1997 г. составляет d=181 дн..
б) 1 января 1998 г.;
Эта дата позже 1 июля 1997 г., поэтому находим наращенную сумму S (P=30000). d1=01.07.1997 и d2=01.01.1998.
в) 1 июля 1999 г.
Количество лет между 1 июля 1997 г. и 1 июля 1999 г. составляет n=2 года.
S=P·(1+i)n=30000·(1+0.35)2 = 54 675 руб.
Список источников
- Финансовая математика (детерминированные модели): конспект лекций/Н.А.Шиловская.-Архангельск:Сев. (Аркт.) фед.ун-т, 2011. -104с.
- Ширшов Е.В. Финансовая математика: учебное пособие / Е.В. Ширшов, Н.И. Петрик, А.Г. Тутыгин, Т.В. Меньшикова. – 5-е перераб. и доп. – М.: КНОРУС, 2010. – 144 с.
Стоимость подключения зависит от срока использования:
- 1 месяц: 100 руб.
- 3 месяца: 200 руб.
- 6 месяцев: 300 руб.
- 1 год: 600 руб.
Возможности:
- Скачивать решение в формате Word (форматы rtf, docx, xlsx).
- Использовать калькуляторы без рекламы.
Оплата осуществляется в Личном кабинете в разделе Платные услуги
.
