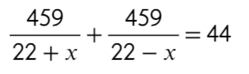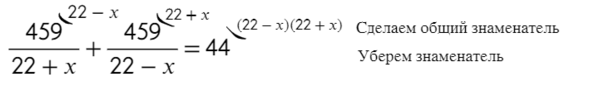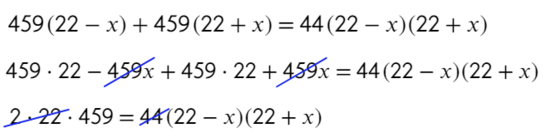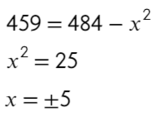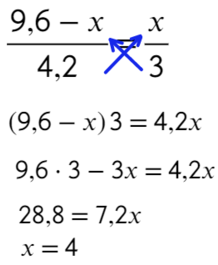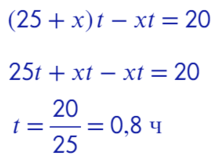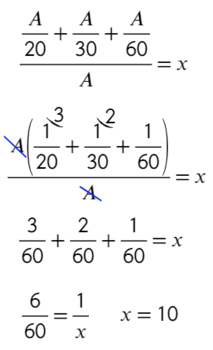Владимир Замятин
Оракул
(64975)
6 лет назад
[сек/метр] – это не скорость. Это время прохождения единицы расстояния (величина, обратная скорости).
А решение элементарное: 0,2/0,77 = 0,26 = 26%.
Самолёты игрушечные, что ли? Больно скорости маленькие.
АлександрГуру (2853)
6 лет назад
Действительно, путаница сплошная… и с цифрами, и с буквами… 🙂
XCMerГуру (2898)
6 лет назад
Знали бы вы какие я формулы настроил. ..спасибо. затупил так затупил
Андрюха Доропей
Гуру
(3831)
6 лет назад
((1/0.77)/(1/0.2))*100%
Владимир ЗамятинОракул (64975)
6 лет назад
Неверно.
Андрюха Доропей
Гуру
(3831)
а, не заметил размерность, это не скорость тогда, вообще говоря.
((1/0.77)/(1/0.2))*100%
White RabbitИскусственный Интеллект (313265)
6 лет назад
0,2/0,77 – у него НЕ скорость, обратная величина)))
Андрюха Доропей
Гуру
(3831)
да, понял уже)
Формулы. Вычисление по формулам. Решение текстовых задач (на движение, на проценты и т.д.)
В задачах на движение рассматриваются три взаимосвязанные величины:
S – расстояние (пройденный путь),
t – время движения и
V – скорость – расстояние, пройденное за единицу времени.
Расстояние – это произведение скорости на время движения; S = V t
Скорость – это расстояние, которое тело проходит за единицу времени;
Скорость – это частное от деления расстояния на время движения; V = S / t
Время – это частное от деления расстояния на скорость движения t = S / V
Какие могут быть ситуации?
Ситуация первая.
Два объекта движение начинают одновременно навстречу друг другу. Встречное движение.
Ситуация вторая.
Два объекта движение начинают одновременно в противоположных направлениях. Движение в противоположных направлениях из одного пункта
Ситуация третья.
Два объекта движение начинают одновременно в одном направлении.
При решении этих задач надо использовать понятия «скорость сближения» и « скорость удаления».
Задача №1.
В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого -68 км /ч., и они выезжают навстречу друг другу одновременно?
1-ый способ:
1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов.
2)140×2 = 280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.
3) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.
2 – й способ решения.
1)72 × 2 =144 (км) – такое расстояние проедет один таксист за 2 часа.
2) 68 × 2 = 136 (км) – такое расстояние проедет другой таксист за 2 часа.
3)144+ 136 =280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.
4) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.
Задача № 2
Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км /ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
Решение.
1)80×2=160(км) -прошёл скорый поезд за 2 часа.
2)720-160=560(км) -осталось пройти поездам.
3)80+60=140(км/ч) -скорость сближения 2 поездов.
4)560:140=4(ч) -был в пути пассажирский поезд.
Ответ:4часа.
Задача № 3.
Из двух пунктов навстречу друг другу одновременно выехали два автобуса. Скорость одного автобуса 45 км /ч, а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.
Найдите расстояние между пунктами.
Решение.
1-ый способ: .
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2)72×3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.
2 – й способ решения.
1)135 : 45 = 3 (часа) – ехали автобусы до встречи.
2)45 +72 = 117 (км/ ч.). – скорость сближения автобусов .
3)117 × 3 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.
Что такое скорость сближения?
Задача № 4.
Машина и автобус выехали из двух городов, находящихся на расстоянии 740 км навстречу друг другу со скоростями 70 км/ч и 50 км/ч. Какое расстояние будет между машинами через 5 часов?
Решение.
1 –й способ решения.
1)50 × 5 = 250 (км) – проедет машина до встречи.
2)70 × 5 = 350 (км) – проедет автобус до встречи.
3) 250 + 350 = 600 (км) – на такое расстояние они приблизятся друг к другу.
4) 740 -600 = 140 (км) – такое расстояние будет между ними через 5 часов.
Ответ: 140 км.
2 – й способ решения.
1)50 + 70 = 120 (км /ч.) – скорость сближения автобуса и машины.
2)120 × 5 = 600 (км) – на такое расстояние они приблизятся друг к другу.
3) 740 – 600 = 140 (км) – такое расстояние будет между ними через 5 часов.
Ответ: 140 км.
Задача №5.
Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч. Через какое время они встретятся?
Решение.
1)100+120=220(км/ч)- скорость сближения машин .
2)660:220=3(ч) -через такое время встретятся гоночные машины.
Ответ: через 3 часа.
Задача № 6.
Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч., а другого – 54 км ч. Какое расстояние будет между тиграми через 2 часа?
Решение.
1-ый способ:
1)48 × 2 = 96 (км) – пробежит один тигр за 2 часа.
2)54 × 2 = 108 (км) – пробежит другой тигр за 2 часа.
3)96 + 108 = 204 (км) – будет между тиграми через 2 часа.
Ответ: 204 км.
2 – й способ
1)48 + 54 =102 (км /ч.) – скорость удаления тигров.
2)102 × 2 =204 (км) – будет между тиграми через 2 часа.
Ответ: 204 км.
Задача № 7.
Максат и Нурдаулет вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут Рома догонит Максата и Нурдаулета?
Решение.
1) 80 – 50 = 30 (км /ч.) –скорость сближения мальчиков.
2)50 × 6 = 300 (км) – такое расстояние было между мальчиками перед выходом из школы Ромы.
3)300 : 30 = 10 (мин.) – через такое время Рома догонит друзей.
Ответ: через 10 мин.
ИТОГИ:
1) При решении задач на движении двух объектов применяются понятия «скорость сближения» и «скорость удаления».
2)При решении задач на встречное движение и движение в противоположных направлениях скорость сближения и скорость удаления находятся сложением скоростей движущихся объектов.
3)При решении задач на движение в одном направлении скорость сближения и скорость удаления находятся вычитанием скоростей движущихся объектов.
Решение задач на проценты
Найдем 20% от 300 :
1-ый способ: 20% от 300 =300:100×20 = 60 ;
2-ой способ: 20% от 300 = 0,20 ×300 = 60 .
Задача №1
В классе 25 учеников, 40% (сорок процентов) из них девочки. Сколько девочек в классе?
Решение:
25:100 × 40 = 10 девочек ; или 25 × 0,40 = 10 девочек ;
Ответ: в классе 10 девочек.
Задача №2
В саду растет 5 кустов желтых роз. Это составляет 25% от всех роз в саду.
Сколько кустов роз в саду?
Решение:
5:25 ×100 = 20 кустов роз; или 5 : 0,25 = 20 кустов роз;
Ответ : в саду растет 20 кустов роз.
Задача №3
На стоянке стоит 40 машин, 8 из них фирмы Рено. Какой процент машин фирмы Рено от всех стоящих на стоянке?
Решение:
8 :40 ×100 = 20 % .
Ответ: на стоянке 20% машин фирмы Рено.
Вопросы к конспектам
Лыжнику необходимо было пробежать расстояние в 50 км. Начав бег на 30 мин позже назначенного срока, лыжник бежал со скоростью, больше предполагавшейся на 5 км/ч и прибежал к месту назначения вовремя. Определите скорость, с которой бежал лыжник.
На сколько процентов изменится площадь прямоугольника, если его длину уменьшить на 15% а ширину увеличить на 20%
Рабочий день уменьшился с 8 до 7 часов. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках заработная плата возросла на 5%?
Турист прошел по проселочной дороге 6 км и по шоссе 3 км, затратив на весь путь 2ч. По шоссе он прошел со скоростью на 2 км/ч больше, чем по проселочной дороге. С какой скоростью шел турист по проселочной дороге?
Автомобиль за 4 часа проезжает путь в 240 км. Если скорость автомобиля увеличится на 20 км/ч, то за сколько часов он проедет тот же путь?
В аэропорту ждут прибытия самолета 1200 пассажиров. 45% из них мужчины. 15% общего числа женщин и детей составляют дети. Найдите число мужчин и число детей?
Пассажир в метро спускается вниз по движущемуся эскалатору за 24с. Если пассажир идет с той же скоростью по неподвижному эскалатору, то он спустится за 42с. За сколько секунд он спустится стоя на ступеньках движущегося эскалатора?
Сколько воды нужно добавить к 54 кг 5%-го раствора соли в воде, чтобы получить 3%-ый раствор?
Скорость моторной лодки по течению реки равна 10,2 км/ч, а против течения реки 7,8км/ч. Найдите скорость течения реки.
Скорость течения реки 2 км/ч, собственная скорость лодки в 2,5 раза больше. Найдите расстояние, которое проплыла лодка против течения за 3 часа
Сторону квадрата увеличили на 20%. На сколько процентов увеличится периметр квадрата?
Текстовые задачи на движение, работу, проценты
Пример решения задачи на движение по воде
Теплоход проходит по течению реки до пункта назначения 459 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 22 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 54 часа после отплытия из него. Ответ дайте в км/ч.
Разберем по пунктам:
- Задачу прочитали.
- Определяемся, про что задача: работа, движение, проценты? Движение.
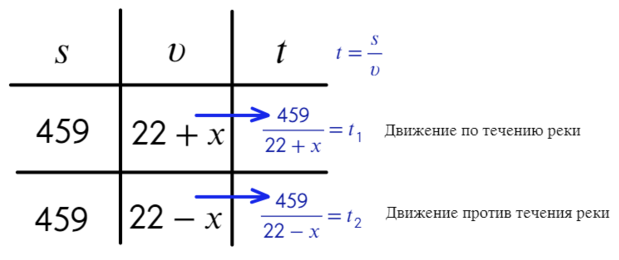
- Точные данные: расстояние между пунктами назначения 459 км = S.
- За X берем скорость течения. Теперь стоит вернуться к пункту 4 и пояснить, чему равна скорость лодки. Скорость лодки по течению равна 22 + Х (Представим, что мы отправились на плоту и не прилагаем никаких усилий, плывем по течению – двигаемся со скоростью течения реки. Теперь, если мы начнем грести по направлению течения, наша скорость будет равна скорости течения плюс скорость, которую мы получаем от наших усилий – то есть наши усилия с рекой суммируются). Скорость лодки против течения 22 – Х (теперь мы преодалеваем усилия реки и движемся наперекор ей, для этого нам нужно затратить столько же скорости, сколько и реке).
- Теперь выразим время (t) через скорость (v) и путь (s). Время = путь / скорость.
6 Дополнительное условие: теплохода не было в пункте, из которого он выплыл 54 часа, из них он был на стоянке 10 часов, то есть его время в пути 54 – 10 = 44 часа = t. Это сумма времени по течению (t₁) и против (t₂).
Решим это уравнение:
Так лихо убрать знаменатель можно в связи с тем, что скорость не может равняться 22, тогда скорость теплохода была бы равна скорости течения, и силушки у теплохода не хватило бы, чтобы идти против течения.
Ответ: 5.
Пример решения задачи на прямолинейное движение
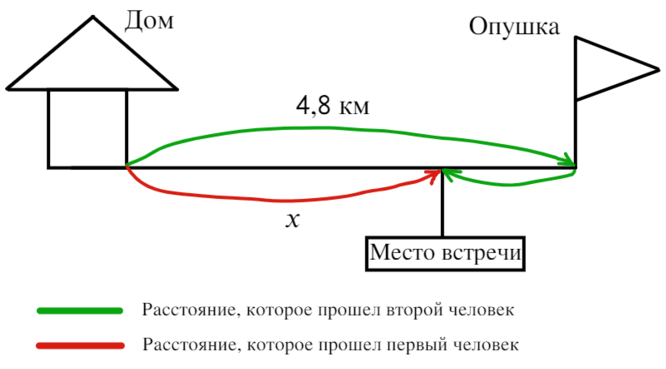
Два человека одновременно отправляются из одного дома до опушки леса, находящейся в 2,4 км. от дома. Один идёт со скоростью 3 км/ч, а другой — со скоростью 4,2 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? Ответ дайте в километрах.
- Задачу прочитали.
- Определяемся, про что задача: работа, движение, проценты? Движение.
- Точные данные: скорость первого 3 км/ч, второго – 4,2 км/ч.
- За Х берем расстояние от дома до места их встречи, то есть путь, который прошел первый человек. Второй двигается быстрее первого, то есть он первый дойдет до опушки леса и повернет обратно, пока первый человек будет двигаться к опушке.
5 Тогда путь, который прошел второй человек – это расстояние от дома до опушки (4,8 км) и путь от опушки до места встречи ((4,8 – Х) км) => Путь второго человека: 4,8 + 4,8 – Х = 9,6 – Х. Путь первого человека: Х.
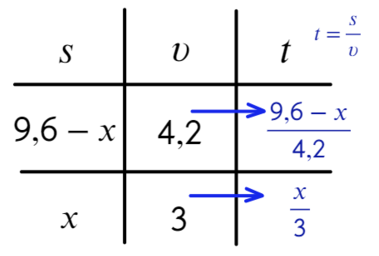
Теперь выразим время (t) через скорость (v) и путь (s). Время = путь / скорость.
6 Дополнительное условие: его тут нет. Все данные в задачке мы уже использовали. Тогда к чему же приравнять их время в движении? Ко времени друг друга. Вышли они одновременно, и все время, пока шел первый человек, шел и второй.
Ответ: 4.
Пример решения задачи на движение по окружности
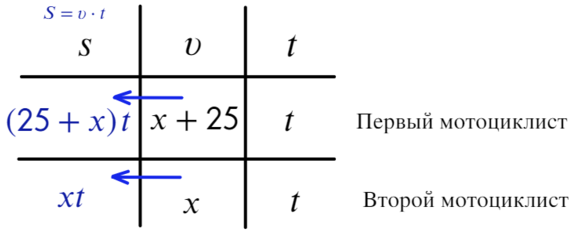
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 40 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?
- Условие прочитали.
- Определяемся, про что задача: работа, движение, проценты? Движение.
- Точные данные: скорость одного на 25 км/ч больше чем у другого. (важно – стартовали мотоциклисты из двух диаметрально противоположных точек трассы, изначальное расстояние между ними 20 км). Сложность в этой задачи в том, что длину трассы пока не нужно использовать.
- За t берем время, сколько им потребуется, чтобы встретиться. А за х скорость медленного мотоциклиста.
- Выражаем путь (S) через время и скорость.
- Еще никак не использовано расстояние между мотоциклистами – 20 км. Тогда путь, который проехал более быстрый до место их встречи минус путь, который проехал более медленный равно 20 км!
Ответ: 48.
Пример решения задачи на работу
Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
- Условие прочитали.
- Определяемся, про что задача: работа, движение, проценты? Работа.
- Точные данные: время первого 20 мин., второго 30 мин., третьего 60 мин. (важно – время каждого насоса выразить или в минутах, или в часах).
- За Х берем время, за которое все три насоса наполнят бассейн.
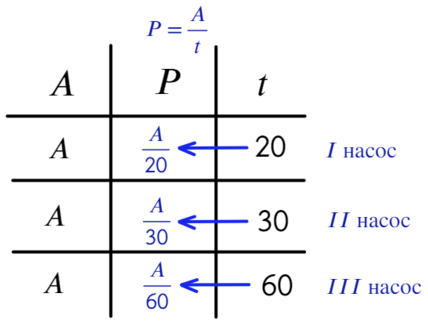
- Производительность P = A / t первого насоса – A/20, второго – A/30, третьего – A/60.
Теперь выразим производительность (Р) через работу (A) и время (t). P = A / t
6 Последнее действие: всю работу (А) разделим на сумму производительностей всех трех насосов и получим время, за которое все три насоса, работая вместе, наполняют бак.
Проверьте себя на глупость: 3 насоса должны наполнить бак быстрее, чем каждый по отдельности.
Ответ: 10.
Пример решения задачи на проценты
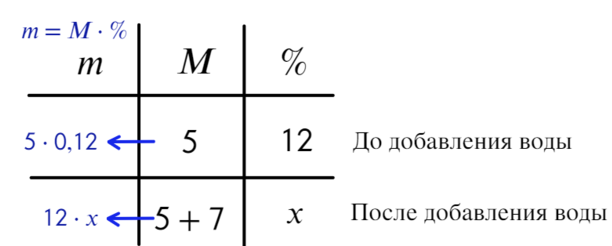
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
- Задачу прочитали.
- Определяемся, про что задача: работа, движение, проценты? Проценты.
- Точные данные: объем первого расствора до добавления воды – 5 литров, после – 5 + 7 = 12 литров (в формуле говорится о массе, но эта формула так же справедлива и для объемов, то есть весь объем жидкости умножить на процент равняется объему какого-то вещества), тогда раз у нас изменения происходят после добавления воды, возьмем первую строку – до добавления воды, вторую – после добавления воды.
- За Х берем процент после добавления воды.
- Объем активного вещества найдем как произведение всего объема жидкости на процент (Почему так? – В аптеке продается медицинский спирт, на котором написано содержание спирта 95% и воды 5%, допустим, объем его 1 литр, тогда объем чистого спирта составляет 1*95/100=0,95 литра или 950 миллилитров, а объем воды 1*5/100=0,05 литра или 50 миллилитров. То есть от всего объема 0, 95 составляет спирт. Чтобы найти процент содержания спирта, нужно объем спирта разделить на весь объема и умножить на 100 (для перевода в проценты). Тогда получим 0,95/1*100=95%).
6 5 * 12 / 100 – объем некоторого вещества. После добавления воды, объем нашего вещества не изменится. А вот объем всего водного раствора составит в итоге 12 литров.
Ответ: 5%.
Задачи с подсказками для закрепления.
Будь в курсе новых статеек, видео и легкого математического юмора.
На сколько процентов, с которой едут Ваня с дедушкой по тропинке, меньше их скорости по шоссе.
По тропинке 15км/ч
По шоссе 20км/ч
Остались вопросы?
Новые вопросы по предмету Математика
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Приветствую, сообщество Хакнем! До сих пор неизвестно будет ли проводиться ОГЭ в 2020 году. Пока решение не принято, девятиклассники готовятся к экзаменам. И я, как обещала, подготовила статью с решением задач про автомобильные шины. Задания взяты из сборника экзаменационных работ для подготовки к ОГЭ под ред. И.В. Ященко.
Прежде, чем решать задачи, давайте выпишем все величины и формулы, которые нам понадобятся, из условия задачи:
По условию шина с завода имеет маркировку 265/70 R17
В — ширина протектора, в мм, В = 265 мм
Н — высота боковины, при этом Н/В = 70% или Н = В×0,70
d — диаметр диска в дюймах, d = 17 дюймов, 1 дюйм = 25,4 мм
D — диаметр колеса, в мм, по рисунку 2 можно понять, что
D = 2H + d
Задание 1.
Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 20 дюймов?
Решение:
Работаем с таблицей из условия: смотрим на столбец с диаметром диска 20 дюймов, к нему разрешены размеры шин 275/55 и 285/50, т.е. с шириной шин В = 275 мм и В = 285 мм, а наименьшая из них равна 275 мм. Вот и всё решение.
Ответ: 275.
Задание 2
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение
Итак, требуется найти диаметр колеса D из условия: 265/70 R17
Напоминаю, что D = 2H + d
1) Переведём значение d из дюймов в мм:
d = 17× 25,4 = 431,8 мм;
2) Найдём Н:
Н = В×0,70 = 265×0,7 = 185,5 мм;
3) Найдём D = 2×185,5 + 431,8 = 802,8 мм.
Ответ: 802,8 мм.
Задание 3
На сколько миллиметров увеличится диаметр колеса, если заменить шины, установленные на заводе, на шины 275/70 R17?
Решение
Это задание практически повторяет задание 2, опять нужно найти диаметр колеса D, но для шины 275/70 R17, а затем найти разницу между ним и диаметром колеса с завода (265/70 R17), найденным в задании 2.
1) Из задания 2: D = 802,8мм (шина с завода);
2) Новая шина отличается только шириной шины В = 275 мм,
Тогда рассчитаем Н = В×0,70 = 275×0,7 = 192,5 мм и
D = 2H + d = 2×192,5 +431,8 = 816,8 мм;
3) Найдём на сколько увеличится диаметр колеса:
816,8 – 802,8 = 14 мм.
Ответ: 14.
Задание 4
На сколько метров увеличится путь, пройденный автомобилем, когда колесо сделает 1000 оборотов, если заменить шины, установленные на заводе, шинами с маркировкой 275/70 R17? Округлите результат до целых.
Решение
В этом задании нужно чётко понять, что 1 оборот колеса — это длина окружности (колеса). Из курса геометрии мы знаем, что длина окружности вычисляется по формуле: С = 2πr, где r в нашей задаче — радиус колеса, при этом, надеюсь все понимают, что диаметр колеса D = 2r.
Тогда формула перепишется в следующем виде: С = Dπ — это и есть путь 1 оборота колеса, а если колесо сделает 1000 оборотов, путь автомобиля будет равен 1000× Dπ.
Итак, наша задача заключается в том, чтобы найти путь автомобиля, равный 1000 оборотам колеса с завода (265/70 R17) и 1000 оборотам колеса с маркировкой 275/70 R17, и сравнить их.
1) Для колеса с маркировкой 265/70 R17:
1000 × Dπ = 1000 ×802,8π = 802 800π (D = 802,8 мм — из задания 2)
2) Для колеса с маркировкой 275/70 R17:
1000 × Dπ = 1000 ×816,8π = 816 800π (D = 816,8 мм — из задания 3)
Не спешите умножать на значение π = 3,14, ещё успеется…
3) Их разница: 816 800π – 802 800π = 14000π.
Умножим на π:
14000π = 14000 ×3,14 = 43 960 мм.
Переведём в м: 43960 мм = 43,96 м.
В задаче требуется округлить до целых, итого 44 м.
Ответ: 44.
Задание 5
Спидометр автомобиля, собранного на заводе, показывает скорость точно. На сколько процентов показания спидометра будут отличаться от реальной скорости, если заменить шины, установленные на заводе, шинами с маркировкой 275/70 R17? Округлите результат до десятых.
Решение
Решим эту задачу, как обычную задачу на проценты, будем снова использовать значения диаметров колёс, найденных в заданиях 2 и 3.
1) Пусть для автомобиля с колесом с завода (265/70 R17), D = 802,8 мм скорость составляет 100 %, а для автомобиля с колесом маркировки 275/70 R17 с D = 816,8 мм скорость x %.
802,8 — 100 %
816,8 — x %
Составим и решим уравнение:
802,8х = 816,8×100
х = 101,74 (приближенно до сотых)
2) Найдём изменение скорости 101,74 – 100 = 1,74 %, результат округлим до десятых, получим 1,7 %.
Ответ: 1,7.
Согласна с девятиклассниками — задача не из простых, очень объёмная, предполагает много вычислений. Но опять же нерешаемой её не назовёшь. Если нашли ошибку или опечатку пишите в комментариях, буду благодарна.
Сегодня (13 мая) уже после выхода статьи я получила информацию о том, что обязательные экзамены по русскому языку и математике для 9 классов отменены. Девятиклассникам повезло!
#хакнем_математика (👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳
Автор: #ирина_чудневцева координатор канала Хакнем Школа, 42 года, город Ярославль, мама 16-летнего подростка.