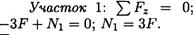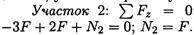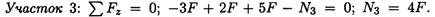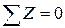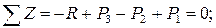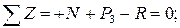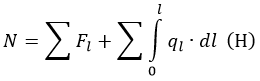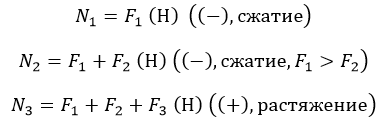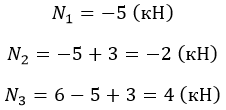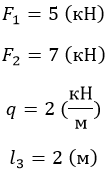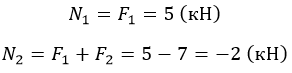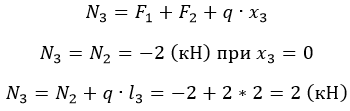Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
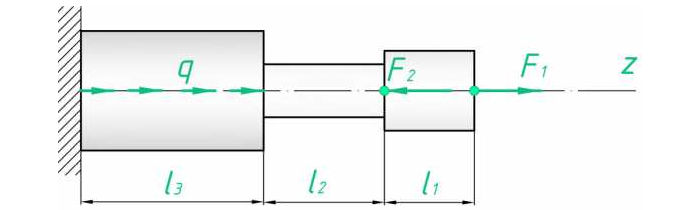
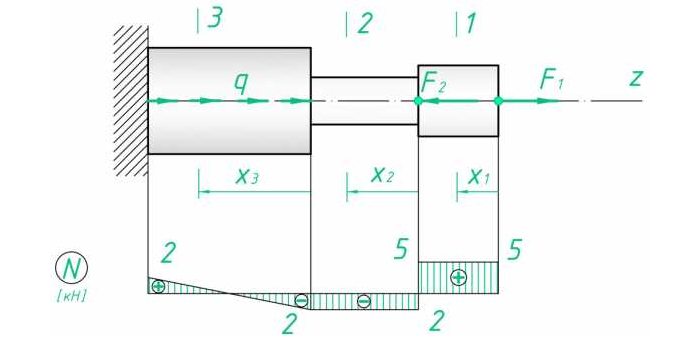
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

Внутренние силы при растяжении-сжатии
Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие (продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.
Из условий равновесия отсеченной части стержня $N = F$.
Продольная сила при растяжении считается положительной, при сжатии – отрицательной.
Пример определения внутренних сил.
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.
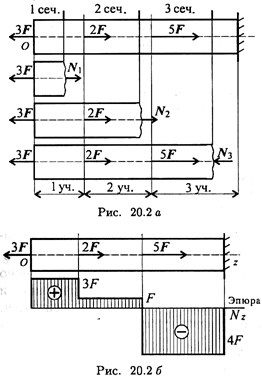
Участком нагружения считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Продольная сила положительна, участок 1 растянут.
Продольная сила положительна, участок 2 растянут.
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Напряжения. Действующие и допускаемые напряжения
Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.
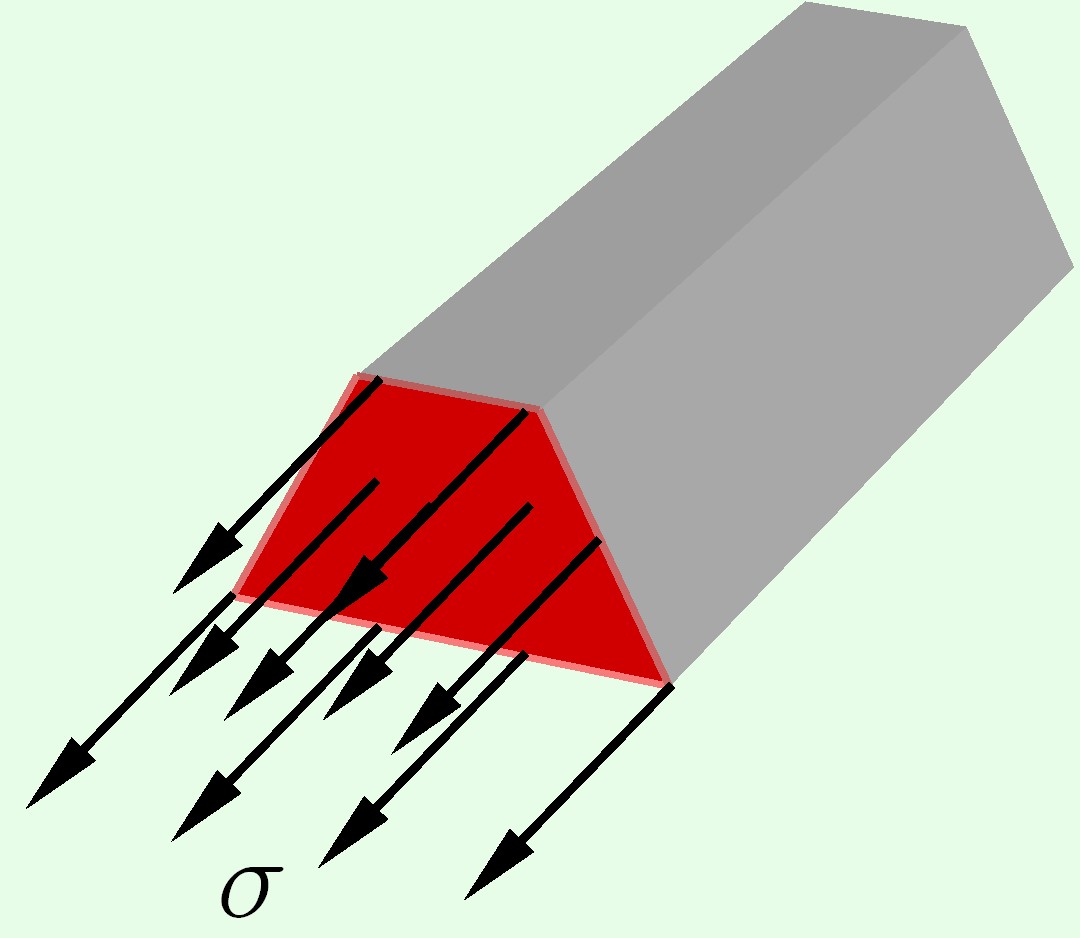
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными.
$sigma = frac{N}{A}$
Единицы измерения напряжений – Па, кПа, МПа.
Знаки напряжений принимают так, как и для продольной силы.
Действующие напряжения – напряжения, которые возникают в рассматриваемом сечении.
Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.
Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.
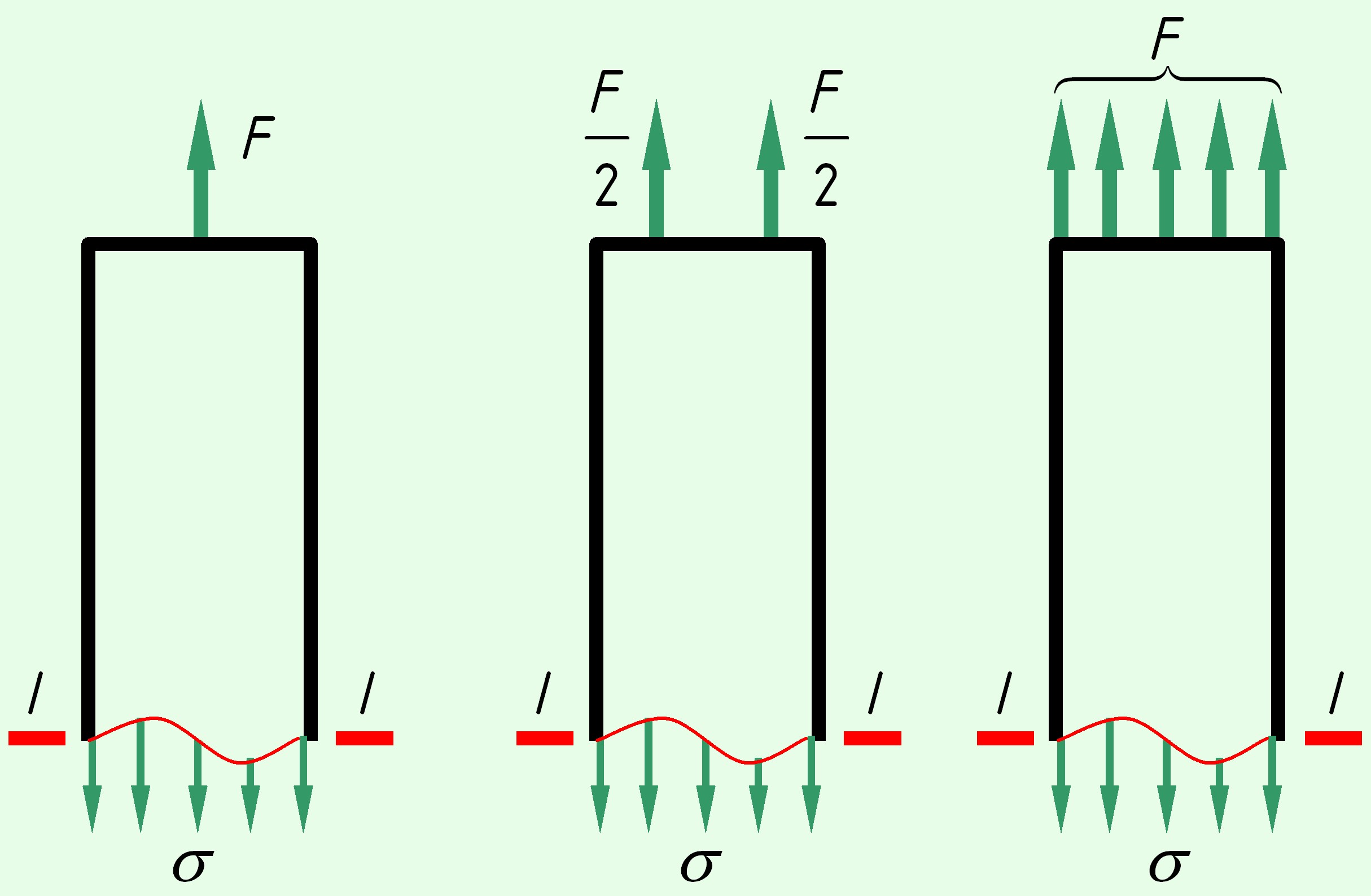
Принцип Сен-Венана: в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.
то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.
Рисунок – иллюстрация принципа Сен-Венана
Абсолютная и относительная деформация
При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией.
$Delta l = {l_1} – l$
Относительная деформация – отношение абсолютной деформации к первоначальной длине.
$varepsilon = frac{{Delta l}}{l}$
$sigma = E cdot varepsilon $
Таблица – физико-механические характеристики материалов
|
Материал |
Модуль упругости, х1010 Па |
Коэффициент Пуассона |
|
Сталь |
19 – 21 |
0,25 – 0,33 |
|
Чугун |
11,5 – 16 |
0,23 – 0,27 |
|
Медь, латунь, бронза |
10 |
0,31 – 0,42 |
|
Алюминий |
7 |
0,32 – 0,36 |
|
Кирпичная кладка |
0,3 |
0,2 |
|
Бетон |
1 – 3 |
0,1 – 0,17 |
|
Каучук |
0,0008 |
0,47 |
Эпюра продольных сил
Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение 
Как строить эпюру продольных сил?
Для построении эпюры N используется метод сечений. Продемонстрируем его применение на примере (рис. 2.1).
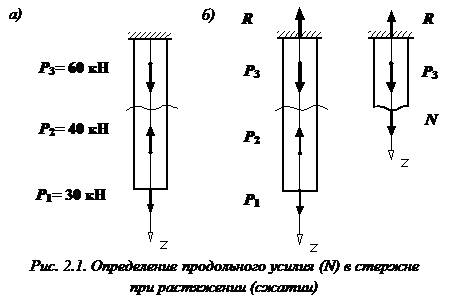
Разрежем стержень в этом месте и мысленно отбросим нижнюю его часть (рис. 2.1, а). Далее мы должны заменить действие отброшенной части на верхнюю часть стержня внутренней продольной силой N.
Для удобства вычисления ее значения закроем рассматриваемую нами верхнюю часть стержня листком бумаги. Напомним, что продольное усилие N, возникающее в поперечном сечении, можно определить как алгебраическую сумму всех продольных сил, действующих на отброшенную часть стержня, то есть на ту часть стержня, которую мы видим.
При этом применяем следующее правило знаков: силы, вызывающие растяжение оставленной части стержня (закрытой нами листком бумаги) входят в упомянутую алгебраическую сумму со знаком «плюс», а силы, вызывающие сжатие – со знаком «минус».
Итак, для определения продольной силы N в намеченном нами поперечном сечении необходимо просто сложить все внешние силы, которые мы видим. Так как сила 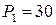
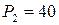
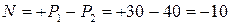
Знак «минус» означает, что в этом сечении стержень испытывает сжатие.
Можно найти опорную реакцию R (рис. 2.1, б) и составить уравнение равновесия для всего стержня, чтобы проверить результат:
или
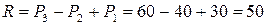
Теперь заменим действие отброшенной нижней части неизвестным внутренним усилием N, направив его, например, от сечения, что соответствует растяжению.
Уравновешиваем оставленную нами верхнюю часть стержня:
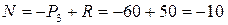
Знак «минус» сигнализирует, что мы не угадали направление продольного усилия N. Оно будет не растягивающим, как мы предполагали, а сжимающим.
Таким образом, мы получили тот же самый результат.
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.
Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
-
Fl – действующие на участке l силы (Н);
-
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
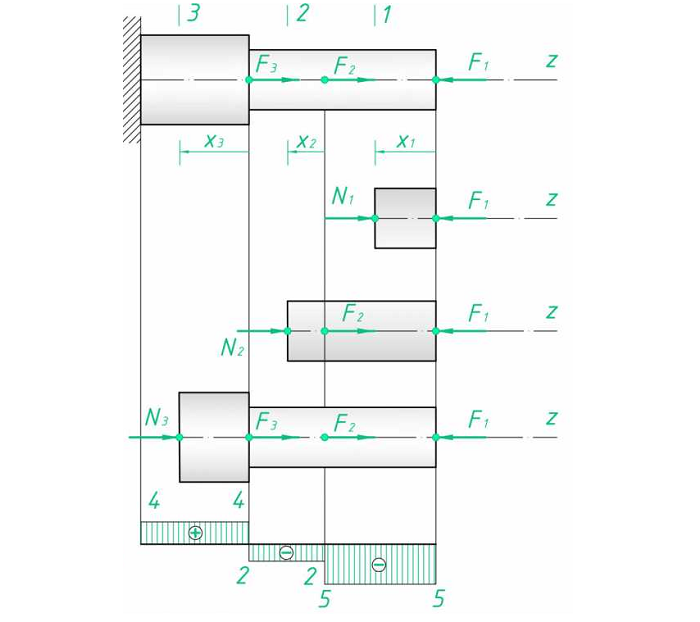
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
По полученным данным строим эпюру (рис. 3).
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Эпю́ра (фр. epure —
чертёж) — особый вид графика,
показывающий распределение величины
нагрузки на объект. Например, для стержня
продольнаяось
симметрииберётся заобласть
определения,и составляются эпюры
для сил, напряжений и разных деформаций
в зависимости отабсциссы.
Расчёт эпюр напряжения
является базовой задачей такой дисциплины,
как сопротивление
материалов.
В частности, только при помощи эпюры
возможно определить максимально
допустимую нагрузку на материал.
Построение
эпюр продольных сил Nz
Продольная
сила в сечении численно равна алгебраической
сумме проекций всех сил, приложенных
по одну сторону от рассматриваемого
сечения, на продольную ось стержня.
Правило знаков
для Nz: условимся считать продольную
силу в сечении положительной, если
внешняя нагрузка, приложенная к
рассматриваемой отсеченной части
стержня, вызывает растяжение и
отрицательной – в противном случае.
Построение
эпюр крутящих моментов Мкр.
Крутящий
момент в сечении численно равен
алгебраической сумме внешних моментов,
приложенных по одну сторону от
рассматриваемого сечения, относительно
продольной оси Z.
Правило знаков
для Мкр: условимся считать крутящий
момент в сечении положительным, если
при взгляде на сечение со стороны
рассматриваемой отсеченной части
внешний момент виден направленным
против движения часовой стрелки и
отрицательным – в противном случае.
Определение поперечных сил и изгибающих моментов – сечение 1
Отбросим
правую часть балки и заменим ее действие
на левую часть поперечной силой и
изгибающим моментом .
Для удобства вычисления закроем
отбрасываемую правую часть балки листком
бумаги, совмещая левый край листка с
рассматриваемым сечением 1.
Поперечная
сила в
сечении 1 балки равна алгебраической
сумме всех внешних сил, которые видим
после закрытия
Видим
только реакцию опоры, направленную
вниз. Таким образом, поперечная сила
равна:
кН.
Знак
«минус» нами взят потому, что сила вращает
видимую нами часть балки относительно
первого сечения против хода часовой
стрелки (или потому, что одинаково
направлена с направлением поперечной
силы по правилу
знаков)
Изгибающий
момент в
сечении 1 балки, равен алгебраической
сумме моментов всех усилий, которые мы
видим после закрытия отброшенной части
балки, относительно рассматриваемого
сечения 1.
Видим
два усилия: реакцию опоры и
момент M. Однако у силы плечо
практически равно нулю. Поэтому изгибающий
момент равен:
кН·м.
Здесь
знак «плюс» нами взят потому, что внешний
момент M изгибает видимую нами часть
балки выпуклостью вниз. (или потому, что
противоположно направлен направлению
изгибающего момента по правилу знаков)
Определение поперечных сил и изгибающих моментов – сечение 2
В
отличие от первого сечения, у силы
реакциипоявилось
плечо, равное а.
поперечная
сила:
кН;
изгибающий
момент:
кН·м.
Определение
поперечных сил и изгибающих моментов
– сечение 3
поперечная
сила:
кН;
изгибающий
момент:
кН
·м.
Определение
поперечных сил и изгибающих моментов
– сечение 4
Теперь
удобнее закрывать
листком левую часть балки.
поперечная
сила:
кН;
изгибающий
момент:
кН
·м.
Определение
поперечных сил и изгибающих моментов
– сечение 5
поперечная
сила:
кН;
изгибающий
момент:
кН
·м.
Определение
поперечных сил и изгибающих моментов
– сечение 1
поперечная
сила и изгибающий момент:
.
По
найденным значениям производим построение
эпюры поперечных сил (рис.
7.7, б) и изгибающих моментов (рис.
7.7, в).
КОНТРОЛЬ
ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР
Убедимся
в правильности построения эпюр по
внешним признакам, пользуясьправилами
построения эпюр.
Проверка
эпюры поперечных сил
Убеждаемся:
под незагруженными участками эпюра
поперечных сил идет
параллельно оси балки, а под распределенной
нагрузкой q – по наклоненной вниз прямой.
На эпюре продольной силы три
скачка: под реакцией –
вниз на 15 кН, под силой P – вниз на 20 кН
и под реакцией –
вверх на 75 кН.
Проверка
эпюры изгибающих моментов
На эпюре
изгибающих моментов видим
изломы под сосредоточенной силой P и
под опорными реакциями. Углы изломов
направлены навстречу этим силам. Под
распределенной нагрузкой q эпюра
изгибающих моментов изменяется по
квадратичной параболе, выпуклость
которой направлена навстречу нагрузке.
В сечении 6 на эпюре изгибающего момента –
экстремум, поскольку эпюра поперечной
силы в этом месте проходит через нулевое
значение.
4) Стержень, балка,
вал, брус, пластина, плита, оболочка
Основными
расчетными типовыми элементами на
которые делится целая конструкция,
являются стержень, брус, оболочка,
пластина, массивное тело, балка, ферма.
Стержень
– тело, длина которого существенно
превышает характерные размеры поперечного
сечения.
Брус
– это тот же стержень.
Балка
– стержень или брус, работающий на изгиб.
Пластина
– тело, у которого толщина существенно
меньше двух других размеров.
Оболочка
– тело, ограниченное криволинейными
поверхностями (искривленная пластина).
Массивное
тело – элемент конструкции с размерами
одного и того же порядка.
Ферма
– стержневая конструкция, работающая
только на растяжение или сжатие.
Остальное
см.конспект.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #