| Период | |
|---|---|
 |
|
| Размерность | T |
| Единицы измерения | |
| СИ | с |
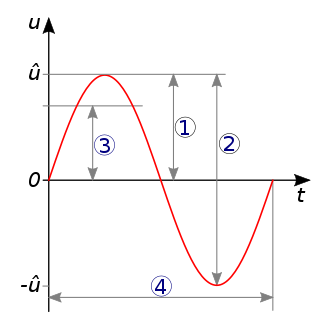
Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором она находилась в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: (хотя могут применяться и другие, наиболее часто это 
, иногда 
и т. д.).
Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.
Период колебаний связан соотношением взаимной обратности с частотой:
Для волновых процессов период связан кроме того очевидным образом с длиной волны 
где 
— скорость распространения волны (точнее[2] — фазовая скорость).
В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота[3] колебаний его волновой функции).
Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).
Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).
Периоды колебаний в природе[править | править код]
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот электромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
- от 5·10−5с до 0,2с
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне
- от 1,1·10−15с до 2,3·10−15с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц.
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.
Периоды колебаний простейших физических систем[править | править код]
Пружинный маятник[править | править код]
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
,
где 
— масса груза, 
— жёсткость пружины.
Математический маятник[править | править код]
Период малых колебаний математического маятника:
где 
— длина подвеса (к примеру, нити), 
— ускорение свободного падения. Отсюда видно, что период колебаний маятника зависит только от длины подвеса и ничего более.
Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью[5] равен 2 секундам.
Физический маятник[править | править код]
Период малых колебаний физического маятника:
где 
— момент инерции маятника относительно оси вращения, — масса маятника, — расстояние от оси вращения до центра масс.
Крутильный маятник[править | править код]
Период колебаний крутильного маятника:
где 
— момент инерции маятника относительно оси кручения, а 
— вращательный коэффициент жёсткости маятника.
Электрический колебательный (LC) контур[править | править код]
Период колебаний электрического колебательного контура (формула Томсона):
,
где 
— индуктивность катушки, 
— ёмкость конденсатора.
Эту формулу вывел в 1853 году английский физик Уильям Томсон.
Примечания[править | править код]
- ↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки[править | править код]
- [bse.sci-lib.com/article088257.html Период колебаний] — статья из Большой советской энциклопедии
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
Физика > Период и частота
Как найти период и частоту – определение и формула. Читайте, что такое угловая частота, цикл, частоты синусоидальных волн, единицы измерения, уравнения.
Период – продолжительность цикла повторяющегося события, а частота – количество циклов за временной промежуток.
Задача обучения
- Преобразование между частотой и периодом.
Основные пункты
- Регулярно повторяющееся движение – периодическое. Одно полное повторение – цикл.
- Продолжительность цикла – период.
- Частота отображает число циклов, осуществленное за определенный временной промежуток. Это обратная величина периода и определяется формулой f = 1/T.
- Некоторые перемещения лучше всего характеризовать угловой частотой (ω). Она относится к угловому смещению за временной промежуток. Вычисляется по формуле: ω = 2πf.
Термины
- Угловая частота – угловое смещение за временной промежуток.
- Период – длительность одного цикла в повторяющемся событии.
- Частота – соотношение количества раз (n) периодического явления за временную единицу (t): f = n/t.
Пример
Когда-то существовал викторианский трюк. Человеку нужно было вслушаться в звук мухи, воспроизвести музыкальную ноту на пианино и сказать, сколько раз летучая мышь ударила крыльями за секунду. Если это 200 раз в секунду, то частота движения – f = 200/1 с = 200 Гц. Период составляет 1/200-ю секунду: T = 1/f = (1/200) с = 0.005 с.
Период и частота
Эти термины используют для выражения повторного движения. Период – время, которое тратится на одно повторение. Один полноценный проход – цикл. Частота – количество циклов за конкретный временной промежуток (f).
Синусоидальные волны разных частот. Нижние обладают более высокими частотами, а горизонтальная ось отображает время.
Понятия выражаются в формуле: F = 1/T.
Допустим, частота сердца новорожденного составляет 120 раз в минуту, а период – половина секунды. Если вы отточите интуицию на ожидание сопряженности больших частот с короткими периодами (и наоборот), то избежите ошибок.
Единицы
Чаще всего частота рассчитывается в герцах (Гц). 1 Гц указывает на то, что событие происходит раз в секунду. Традиционная единица, применимая во вращающихся механических приборах, – обороты в минуту (об/мин). Единица периода – секунда.
Угловая частота
Частота периодического движения лучше всего передается через угловую частоту – ω. Она относится к угловому смещению на единицу времени или скорости перемены состояния синусоидальной формы волны. В виде формулы:
Колеса совершают вращение с частотой f циклов в секунду, что можно описать как ω радиан в секунду. Механическая связь позволяет линейным колебаниям поршней парового двигателя руководить колесами
у (t) = sin(θ(т)) = sin(ωt) = sin(2πft)
ω = 2πf
Угловая частота часто отображается в радианах на секунду.
Вычисляем период оборота оборотных активов (ОА): основные формулы
Период оборота оборотных активов — показатель, который отражает срок, в течение которого вложения фирмы в ОА вернутся к ней обратно. Данный показатель в общем случае вычисляется по формуле:
ПО = ПЕРИОД / (В / ОА),
где:
ПО — период оборота ОА;
ПЕРИОД — длительность анализируемого периода в днях;
В — выручка за анализируемый период;
ОА — средний остаток по ОА за анализируемый период.
В случае если анализируемый период — 1 год (ПЕРИОД составляет 365 дней), показатель В будет равен значению в строке 2110 годового отчета о прибылях и убытках фирмы. Показатель ОА составит среднюю величину между значениями в строке 1200 бухгалтерского баланса по состоянию на начало и конец года. Период оборота ОА показывает время, которое необходимо для замещения оборотных средств предприятия полученной выручкой.
Данный показатель прямо связан с коэффициентом оборачиваемости ОА, который определяется по формуле:
КО = В / ОА,
где:
КО — коэффициент оборачиваемости ОА;
В, ОА — те же показатели, что применяются в предыдущей формуле.
Рассматриваемый коэффициент показывает, сколько оборотов (возвратов каждого рубля, вложенного в оборот активов, относимых к оборотным) осуществляется в рамках производственного процесса в течение анализируемого периода. Фактически чем больше соответствующий коэффициент, тем меньше будет период оборота активов, и наоборот.
Если анализируемый период — 1 год, то источником данных для исчисления показателя КО, как и в случае с предыдущим показателем, может быть бухгалтерский баланс предприятия, а также отчет о финансовых результатах.
В КонсультантПлюс есть множество решений по анализу хозяйственной деятельности предприятия. Например, в этой статье вы узнаете, как рассчитать текущую (общую) ликвидность по балансу. Получите бесплатный демо-доступ к К+ и переходите в материал, чтобы узнать все подробности данной процедуры.
Рассмотрим теперь, какое значение может иметь период оборота ОА (и сопутствующий ему коэффициент) при оценке результатов хозяйственной деятельности предприятия.
Период оборачиваемости ОА: нормы по отраслям
В общем случае о высокой эффективности бизнес-модели предприятия свидетельствует низкий показатель по длительности оборота ОА и, соответственно, большой коэффициент оборачиваемости оборотных активов предприятия — относительно нормативных значений.
Данные нормативные значения могут определяться, прежде всего, исходя из отраслевой специфики бизнеса.
- Так, наибольшие значения период оборачиваемости ОА, как правило, принимает в отраслях с «длинными» инвестициями — в промышленности (особенно наукоемкой, поскольку в данном сегменте производство товаров может осуществляться в рамках очень длинных технологических цепочек при задействовании широкого спектра различных фондов), в сельском хозяйстве. В соответствующих отраслях период оборота ОА может составлять порядка 180–250 дней (в то время как коэффициент оборачиваемости будет равен примерно 1,5–2).
- В мелкосерийном производстве период оборота ОА может быть в 2–3 раза ниже (в свою очередь, в пропорционально большей величине будет представлен коэффициент оборачиваемости), в торговле — в 10–20 раз ниже (коэффициент, соответственно, выше).
ОБРАТИТЕ ВНИМАНИЕ! Такой показатель, как период оборота ОА, равно как и коэффициент оборачиваемости, может иметь весьма ограниченную информативность при оценке эффективности бизнес-модели отдельно взятого предприятия (вне зависимости от отрасли), но крайне информативным при сопоставлении показателей деятельности 2 фирм одной и той же отрасли при сопоставимых оборотах и условиях ведения бизнеса на рынке.
Так, если сравниваются 2 фирмы, имеющие доступ к рынкам с одинаковой емкостью, имеющие сопоставимый штат, доступ к кредитным ресурсам, сырью, транспортной инфраструктуре, и выяснится, что у первой — в разы выше период оборота ОА (и ниже, соответственно, коэффициент оборачиваемости), то у заинтересованных лиц — действующих инвесторов, акционеров, кредиторов — могут возникнуть вопросы к менеджерам второй фирмы. Потенциальные же акционеры, инвесторы и кредиторы, рассматривая возможности для вложений в бизнес или его кредитования, вероятнее всего, предпочтут работать с первой фирмой.
Период оборота ОА и сопутствующий данному показателю коэффициент также имеет смысл сравнивать в динамике — чтобы определить тренд, характеризующий повышение или снижение эффективности управления бизнесом.
Таким образом, наиболее информативными рассматриваемые показатели будут:
- при сопоставлении результатов хозяйственной деятельности 2 предприятий одного сегмента;
- при рассмотрении данных показателей в контексте отраслевых нормативов;
- при сопоставлении показателей в динамике.
Одна из распространенных интерпретаций изменений в динамике показателей оборачиваемости ОА — определение экономического эффекта от соответствующих изменений. Изучим его специфику подробнее.
Изменение оборачиваемости ОА: экономический эффект
Данный эффект может выражаться в высвобождении свободных денежных средств, вкладываемых в ОА, по причине повышения динамики оборота соответствующих ОА (или же, в свою очередь, в необходимости привлечения дополнительных средств по причине замедления оборота ОА).
С точки зрения бизнеса экономический эффект здесь может быть, таким образом, положительным или отрицательным. Вычисляться он будет с использованием формулы:
ЭИ = (СПО1 — СПО2) × СВ,
где:
ЭИ — эффект от использования ОА;
СПО1 — период оборота ОА за анализируемый период;
СПО2 — период оборота ОА за период, предшествующий анализируемому.
СВ — среднедневная выручка в анализируемом периоде.
Если СПО1 меньше СПО2, в то время как ЭИ будет меньше 0, то это будет означать, что фирма смогла высвободить денежные средства по причине повышения динамики хозяйственного применения ОА. Это свидетельствует о положительном развитии бизнеса.
Если СПО1 больше СПО2, в то время как ЭИ будет больше 0, то это будет показателем того, что фирме пришлось осуществлять в целях воспроизводства бизнес-модели дополнительные инвестиции в оборотные активы по причине снижения динамики их хозяйственного применения. Это свидетельствует о замедлении развития бизнеса.
В свою очередь, конкретное значение показателя ЭИ (оно будет зависеть от показателя СВ) в данном случае полезно наблюдать в динамике: при сохранении положительного экономического эффекта уменьшение его значения может свидетельствовать о снижении эффективности управления предприятием.
Как снизить период и повысить коэффициент оборачиваемости ОА
Существует большое количество факторов, влияющих на формирование показателя ОА (и сопутствующего ему коэффициента). Ключевыми можно назвать:
- темпы рыночного спроса на товар (продукцию);
- эффективность управления производственными процессами.
Увеличить темпы рыночного спроса на товар можно, прежде всего, используя маркетинговые инструменты (такие как изучение закономерностей спроса, реализация стратегий повышения лояльности покупателей, налаживание обратной связи с потребителем), задействуя методы эффективной рекламы, расширяя рынки сбыта.
Эффективность управления различными процессами на производстве зависит от квалификации отвечающих за соответствующее управление сотрудников, от качества инфраструктуры производства, проработанности механизмов контроля над этапами выпуска товаров, общей эффективности системы локальных норм, регламентирующих работу сотрудников предприятия.
Итоги
Период оборачиваемости оборотных активов на предприятии показывает количество времени, в течение которого 1 рубль вложений в оборотные средства возвращается организации в виде денежных потоков от выручки и иных доходов. Чем ниже соответствующий показатель относительно отраслевых нормативных значений и иных, что могут быть ориентиром (например, показателей другого предприятия, ведущего деятельности в аналогичных условиях), тем более эффективным оценивается управление бизнесом.
Узнать больше о применении различных показателей по оборотным активам в рамках анализа хозяйственной деятельности предприятия вы можете в статьях:
- «Оборотные активы предприятия и их показатели (анализ)»;
- «Собственные оборотные средства и их оборачиваемость».
1.Чтобы определить ЭРУ мы берём те даты, которые нам даны (например, от 350
до 285 млн лет назад) и вычитаем бОльшую из указанного возраста для Эры. Например:
(Эра) Палеозойская, 541.
541-350=191
(Эра) Мезозойская, 252.Она совсем дитё и сосчитать не получится :)Поэтому мы выбираем палеозойскую. И так в принципе всегда : мы выбираем ту эру, по расчетам с которой меньше всего отрыв.
2. Чтобы определить ПЕРИОД нужно взять начало Эры и из него начинать вычитать продолжительность периодов. Например :
(Периоды) Пермский, 47
Каменноугольный, 60
Девонский, 60
Силурийский, 25
Ордовикский, 41
Кембрийский, 56
Нашей эре 541 годик, а период нужно найти, чтобы колебался от 350 до 285.Начинаем “с низов”.То есть, с самых поздних Поеехали :
541-56=485
485-41=444
444-25=419
419-60=359
359-60=299-ТАДААМ! Период найден
НО! Обязательно внимательно читайте задание, ибо в некоторых простят указать периодЫ .Это значит, что Вы указываете не только тот, который у вас получился по расчетам, но и тот, что выше, который также подходит по ним самым.
Удачи и всего доброго 🙂
Период и частота колебаний, теория и онлайн калькуляторы
Период и частота колебаний
Период колебаний
Определение
Период – это отрезок времени, которое необходимо для совершения одного цикла периодического процесса.
Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.
За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:
[T=frac{2pi }{{omega }_0}left(1right).]
Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.
Гармонические колебания некоторого параметра $xi $ описываются уравнением:
[xi =A{cos ({omega }_0t+varphi ) } left(2right),]
где $A={xi }_{max}$ – амплитуда колебаний; ${omega }_0$ – циклическая (круговая) частота колебаний; $varphi $ – начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ –
фаза колебаний. Величина $xi $ лежит в пределах $-Ale sle $+A.
Формулы для вычисления периода простейших колебательных систем
Период колебаний пружинного маятника определим как:
[T=2pi sqrt{frac{m}{k}} left(3right),]
на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.
Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)
[T=2pi sqrt{frac{l}{g}}left(4right).]
Формула для вычисления периода колебаний физического маятника представляет собой выражение:
[T=2pi sqrt{frac{J}{mga}left(5right),}]
где $J$ – момент инерции маятника относительно оси вращения; $a$ – расстояние от центра масс тела до оси вращения.
Единицами измерения периода служат единицы времени, например секунды.
[left[Tright]=c.]
Частота колебаний
Определение
Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $).
Частота – это количество полных колебаний, которые колебательная система совершает за единицу времени.
[nu =frac{1}{T}left(6right).]
Частота колебаний связана с циклической частотой как:
[{omega }_0=2pi nu left(7right).]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
[left[nu right]=с^{-1}=Гц.]
Примеры задач с решением
Пример 1
Задание. Каковы период ($T$) и частота ($nu $) колебаний, которые происходят в соответствии с уравнением: $x=A{sin ({omega }_0(t+tau )) }$, где ${omega }_0=2,5 pi (frac{рад}{с})$; $tau =0,4 $с?
Решение. Из уравнения колебаний:
[x=A{sin left({omega }_0left(t+tau right)right)left(1.1right), }]
заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:
[T=frac{2pi }{{omega }_0}left(1.1right).]
Подставляя имеющиеся данные, вычислим период колебаний:
[T=frac{2pi }{2,5pi }=0,8 left(сright).]
Частоту колебаний найдем как величину, обратную периоду:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту:
[nu =frac{1}{0,8}=1,25 left(Гцright).]
Ответ. $T=0,8$ с; $nu =1,25 Гц$
Пример 2
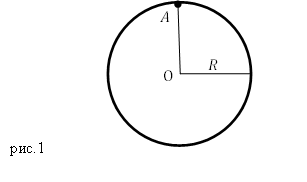
Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.
Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:
[T=2pi sqrt{frac{J}{mga}left(2.1right).}]
Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:
[a=R left(2.2right).]
Найдем момент инерции обруча относительно оси, перпендикулярной плоскости обруча, проходящей через точку $A$. Для этого воспользуемся теоремой Штейнера:
[J=J_0+mR^2 left(2.3right),]
где $J_0=mR^2$ – момент инерции обруча, относительно оси, проходящей через его центр (т.О), перпендикулярно плоскости обруча; расстояние между осями равно радиусу обруча. Получаем, момент инерции обруча относительно гвоздя равен:
[J=mR^2+mR^2=2mR^2left(2.4right).]
Используя формулы (2.1) (2.2) и (2.4), имеем:
[T=2pi sqrt{frac{2mR^2}{mgR}}=2pi sqrt{frac{2R}{g}}.]
Отталкиваясь от полученного результата, найдем частоту колебаний как:
[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{g}{2R}}.]
Ответ. $T=2pi sqrt{frac{2R}{g}},$ $nu =frac{1}{2pi }sqrt{frac{g}{2R}}$
Читать дальше: полная энергия колебаний.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
