Перпендикуляр и наклонная к прямой
Если через какую-нибудь точку, взятую вне прямой, провести прямую, перпендикулярную к ней, то отрезок от данной точки до прямой для краткости называют одним словом перпендикуляр.
Отрезок СО — перпендикуляр к прямой АВ. Точка О называется основанием перпендикуляра СО (рис).
Если прямая, проведённая через данную точку, пересекает другую прямую, но не перпендикулярна к ней, то отрезок её от данной точки до точки пересечения с другой прямой называют наклонной к этой прямой.
Отрезок ВС — наклонная к прямой АО. Точка С называется основанием наклонной (рис.).
Если из концов какого-нибудь отрезка опустим перпендикуляры на произвольную прямую, то отрезок прямой, заключённый между основаниями перпендикуляров, называется проекцией отрезка на эту прямую.
Отрезок А’В’ — проекция отрезка АВ на ЕС. Отрезок ОМ’ — также называется проекцией отрезка ОМ на ЕС.
Проекцией отрезка КР, перпендикулярного к ЕС, будет точка К’ (рис.).
2. Свойства перпендикуляра и наклонных.
Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой.
Отрезок АС (рис.) является перпендикуляром к прямой ОВ, а АМ — одна из наклонных, проведённых из точки А к прямой ОВ. Требуется доказать, что АМ > АС.
В ΔМАС отрезок АМ является гипотенузой, а гипотенуза больше каждого из катетов этого треугольника. Следовательно, АМ > АС. Так как наклонная АМ взята нами произвольно, то можно утверждать, что всякая наклонная к прямой больше перпендикуляра к этой прямой (а перпендикуляр короче всякой наклонной), если они проведены к ней из одной и той же точки.
Верно и обратное утверждение, а именно: если отрезок АС (рис.) меньше всякого другого отрезка, соединяющего точку АС любой точкой прямой ОВ, то он является перпендикуляром к ОВ. В самом деле, отрезок АС не может быть наклонной к ОВ, так как тогда он не был бы самым коротким из отрезков, соединяющих точку А с точками прямой ОВ. Значит, он может быть только перпендикуляром к ОВ.
Длина перпендикуляра, опущенного из данной точки на прямую, принимается за расстояние от данной точки до этой прямой.
Теорема 2. Если две наклонные, проведённые к прямой из одной и той же точки, равны, то равны и их проекции .
Пусть ВА и ВС — наклонные, проведённые из точки В к прямой АС (рис.), причём АВ = ВС. Нужно доказать, что равны и их проекции.
Для доказательства опустим из точки В перпендикуляр ВО на АС. Тогда АО и ОС будут проекции наклонных АВ и ВС на прямую АС. Треугольник АВС равнобедренный по условию теоремы. ВО — высота этого треугольника. Но высота в равнобедренном треугольнике, проведённая к основанию, является в то же время и медианой этого треугольника.
Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой.
Пусть АС и СВ — наклонные к прямой АВ (рис.). СО ⊥ АВ и АО = ОВ.
Требуется доказать, что АС = ВС.
В прямоугольных треугольниках АОС и ВОС катеты АО и ОВ равны. СО — общий катет этих треугольников. Следовательно, ΔAOС = ΔВОС. Из равенcтва треугольников вытекает, что АС = ВС.
Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.
Пусть АВ и ВС — наклонные к прямой АО; ВО ⊥ АО и АО>СО. Требуется доказать, что АВ > ВС.
1) Наклонные расположены по одну сторону перпендикуляра.
Угол АСЕ внешний по отношению к прямоугольному треугольнику СОВ (рис.), а поэтому ∠АСВ > ∠СОВ, т. е. он тупой. Отсюда следует, что АВ > СВ.
2) Наклонные расположены по обе стороны перпендикуляра. Для доказательства отложим на АО от точки О отрезок ОК = ОС и соединим точку К с точкой В (рис.). Тогда по теореме 3 имеем: ВК = ВС, но АВ > ВК, следовательно, АВ > ВС, т. е. теорема справедлива и в этом случае.
Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую.
Пусть КС и ВС — наклонные к прямой КВ (рис.), СО ⊥ КВ и КС > ВС. Требуется доказать, что КО > ОВ.
Между отрезками КО и ОВ может быть только одно из трёх соотношений:
КО не может быть меньше ОВ, так как тогда по теореме 4 наклонная КС была бы меньше наклонной ВС, а это противоречит условию теоремы.
Точно так же КО не может равняться ОВ, так как в этом случае по теореме 3 КС = ВС, что также противоречит условию теоремы.
Следовательно, остаётся верным только последнее соотношение, а именно, что КО > ОВ.
Как найти проекцию наклонной
Раздел ІІ. СТЕРЕОМЕТРИЯ
§8. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. ПРОЕКЦИЯ НАКЛОННОЙ НА ПЛОСКОСТЬ.
2. Свойства перпендикуляра и наклонной.
Рассмотрим свойства перпендикуляра и наклонной.
1) Перпендикуляр, опущенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к плоскости.
На рисунке 411: АН АК.
2) Если две наклонные, проведенные из данной точки к плоскости, равны, то равны их проекции.
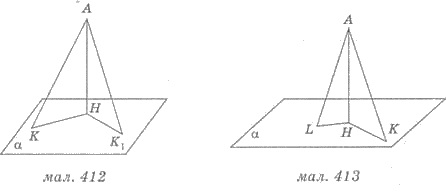
На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K 1 и перпендикуляр АН и АК = АК 1 . Тогда по свойству: НК = НК1.
3) Если две наклонные, проведенные из данной точки к данной плоскости, имеют равные проекции, то они равны между собой.
На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K 1 и перпендикуляр АН, причем КН = К 1 Н. Тогда по свойству: АК = АК 1 .
4) Если из данной точки проведены к плоскости две наклонные, то большая наклонная имеет большую проекцию.
На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, A К > AL . Тогда по свойству: H К > HL .
5) Если из данной точки проведены к плоскости две наклонные, то большей из них является та, которая имеет большую проекцию на данную плоскость.
На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, НК > Н L . Тогда по свойству: АК > А L .
Пример 1. Из точки к плоскости проведены две наклонные, длины которых 41 см и 50 см. Найти проекции наклонных, если они относятся, как 3 : 10, и расстояние от точки до плоскости.
Решения. 1) А L = 41 см; АК = 50 см (рис. 413). По свойством имеем Н L НК. Обозначим Н L = 3 х см, НК = 10 х см, АН = h см. АН — расстояние от точки А до плоскости α .
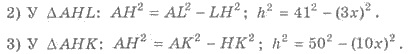
4) Приравнивая, получаем 41 2 — 9х 2 = 50 2 — 100 х 2 ; х 2 = 9; х = 3 (учитывая х > 0). Итак, Н L = 3 ∙ 3 = 9 (см), НК = 10 ∙ 3 = 30 (см).
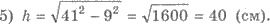
Пример 2. С данной точки к плоскости проведены две наклонные, каждая по см. Угол между наклонными равен 60°, а угол между их проекциями — прямой. Найти расстояние от точки до плоскости.
1) АС = ВС = см — наклонные, ВАС = 60°; ВНС = 90° (рис. 414). Необходимо найти АН.
2) В рівнобедреному треугольнике АВС: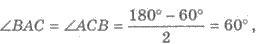 
поэтому ∆ АВС — равносторонний; ВС = см.
3) Так как АВ = АС, то НВ = НС ; обозначим НВ = НС = х см. Тогда в ∆ ВНС :
Как найти проекцию наклонной
Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
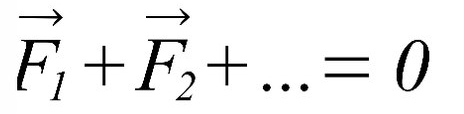
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
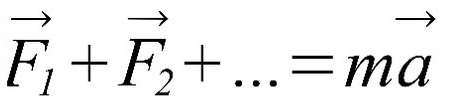
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
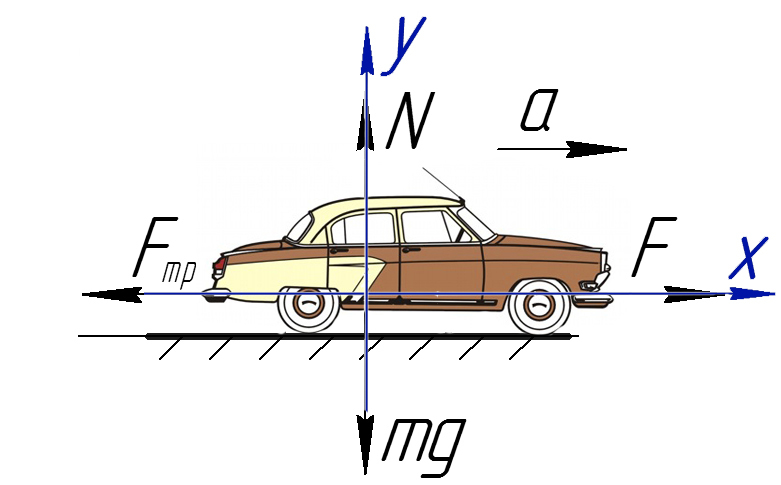
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
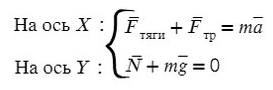
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
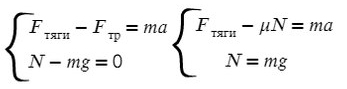
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
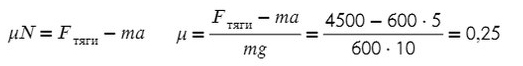
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
Сделаем рисунок, покажем силы, которые дествуют на груз
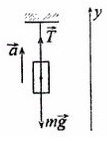
T — сила натяжения нити
На ось X: нет сил
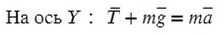
Разберемся с направлением сил на ось Y:
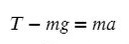
Выразим T (силу натяжения) и подставим числительные значения:
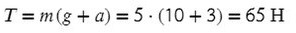
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
Простой пример: мальчик тянет санки
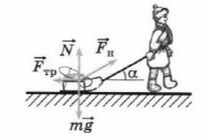
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
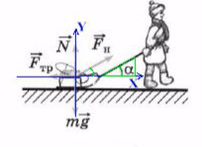Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.
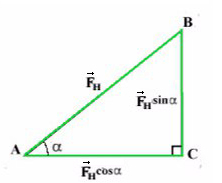
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
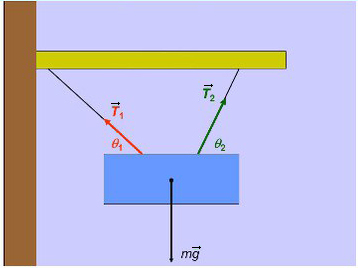
Введем оси и спроецируем силы:
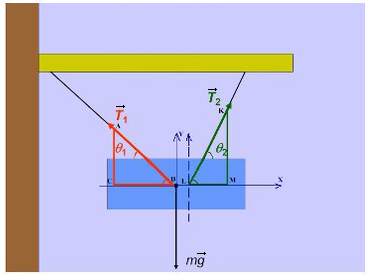
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
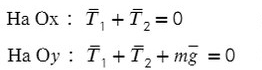
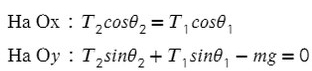
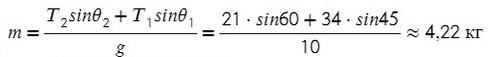
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
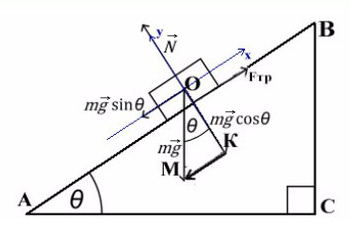
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
Рассмотрим поподробнее ΔKOM:
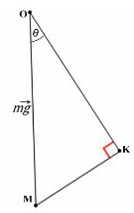
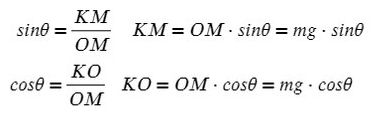Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).
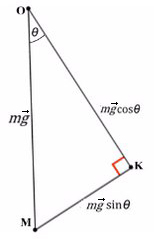
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
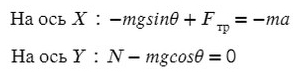
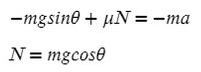
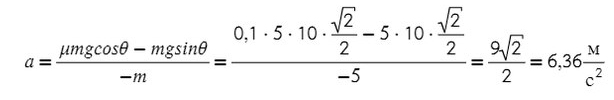
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
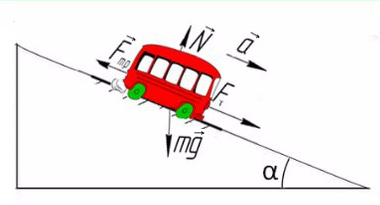
Введем оси X и Y. Спроецируем mg на оси:
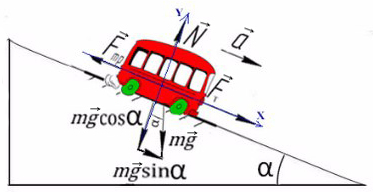
Запишем второй закон Ньютона на X и Y:
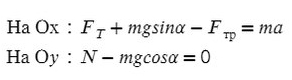
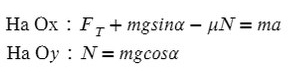
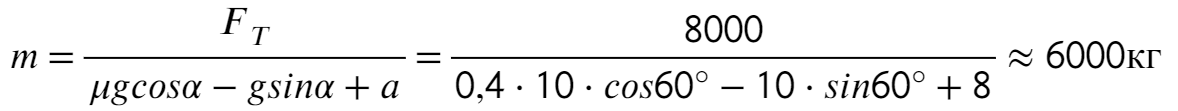
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.
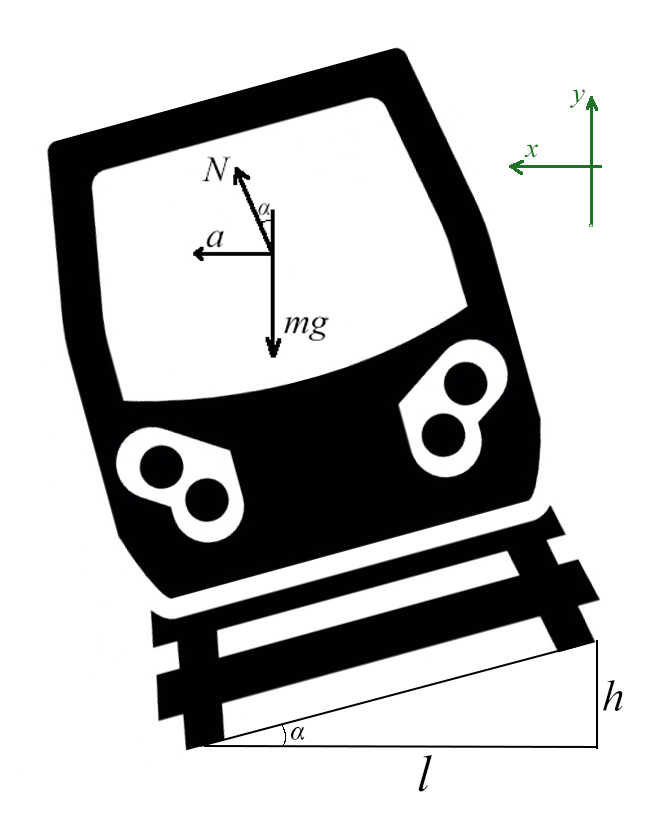
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
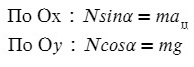
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
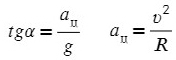
Тангенс — это отношение противолежащего катета к прилежащему:
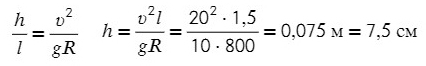
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
На чтение 8 мин Просмотров 3.7к. Опубликовано 04.07.2019
Содержание
- Теоретические материалы
- Предупреждение
- Проекция точки на плоскость − теория, примеры и решения
- Проекция прямой на плоскость
- Угол между прямой и плоскостью
- Теорема о трех перпендикулярах
Теоретические материалы
Глава 9. Прямые и плоскости в пространстве
9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.
Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).
Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.
Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.
Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.
Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).
Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.
Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.
Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
Для нахождения проекции точки M на плоскость α, необходимо:
- построить прямую L, проходящую через точку M и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
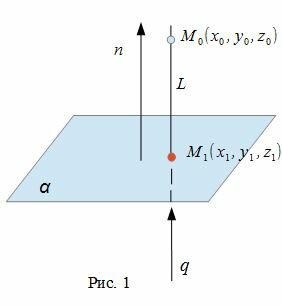
Общее уравнение плоскости имеет вид:
 |
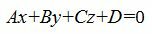(1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M(x, y, z) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
 |
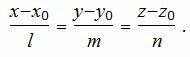(2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M(x, y, z) и ортогональной плоскости (1) имеет следующий вид:
 |
(3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
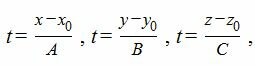
Выразим переменные x, y, z через рараметр t.
 |
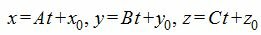(4) |
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
A(At+x)+B(Bt+y)+C(At+z)+D=0,
A 2 t+Ax+B 2 t+By+C 2 t+Cz+D=0,
 |
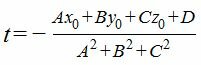(5) |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M на плоскость (1).
Пример 1. Найти проекцию M1 точки M(4, -3, 2) на плоскость
 |
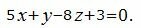(6) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M и нормального вектора плоскости в (5), получим:
 |
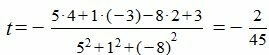(7) |
Из выражений (7) находим:
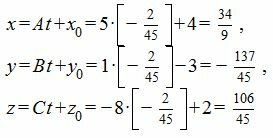
Проекцией точки M(4, -3, 2) на плоскость (6) является точка:
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
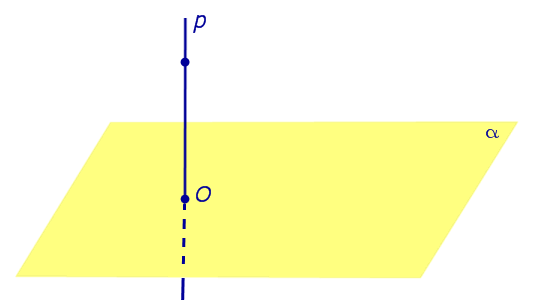
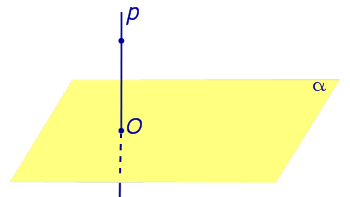
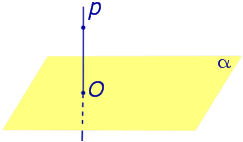
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
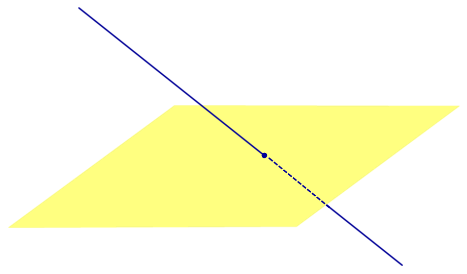
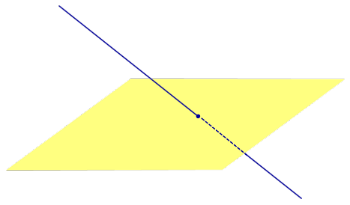
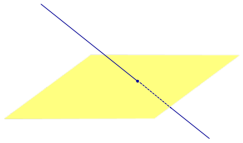
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
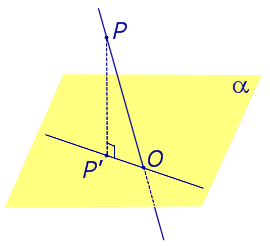
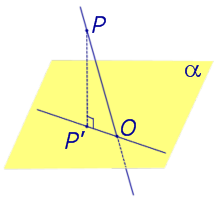
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
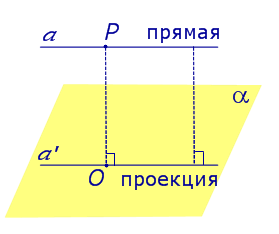
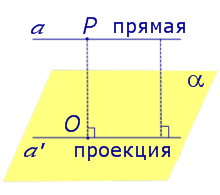
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
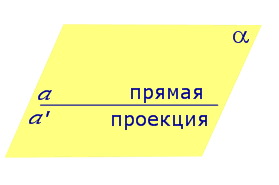
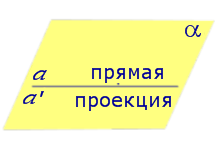
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
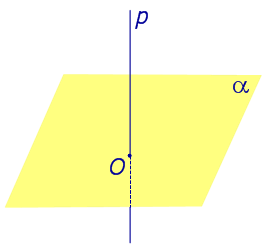
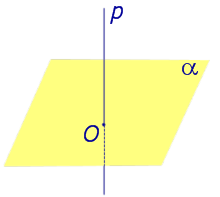
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.
| Фигура | Рисунок | Свойство проекции |
| Наклонная к плоскости α | |
|
| Прямая, параллельная плоскости | |
|
| Прямая, лежащая на плоскости | |
|
| Прямая, перпендикулярная к плоскости | |
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
радиан).
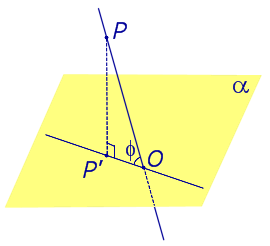
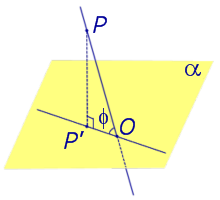
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )
На рисунке это угол φ
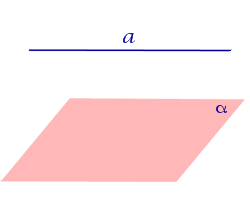
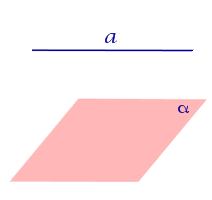
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
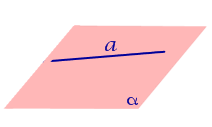
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
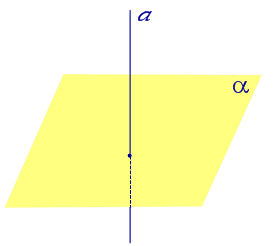
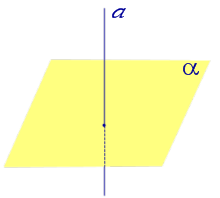
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).
Теорема о трех перпендикулярах
Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.
Доказательство. Рассмотрим следующий рисунок 3.
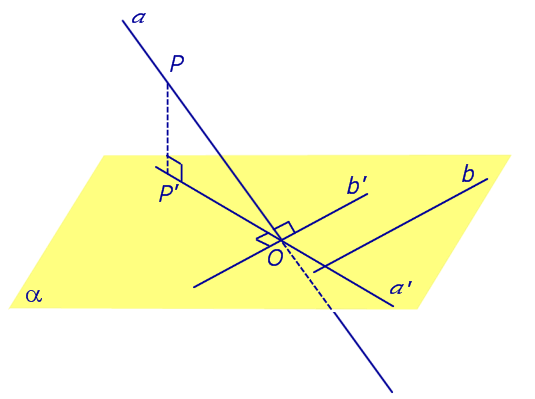
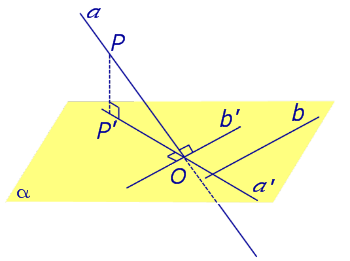
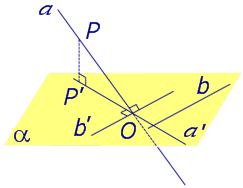
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.
Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.
Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.
Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.
Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.
| Фигура | Рисунок | Определение |
| Наклонная к плоскости α | |
|
| Прямая, параллельная плоскости | |
|
| Прямая, лежащая на плоскости | |
|
| Прямая, перпендикулярная к плоскости | |
Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Конец отрезка, лежащий в плоскости, называется основанием наклонной.
(AB) — наклонная;
(B) — основание наклонной.
Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
(AC) — перпендикуляр;
(C) — основание перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, проведённого из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.
(CB) — проекция наклонной (AB) на плоскость
α
.
Треугольник (ABC) прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
(CBA) — угол между наклонной (AB) и плоскостью
α
.
Если (AD > AB), то (DC > BC).
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
(DAB) — угол между наклонными;
∠
(DCB) — угол между проекциями.
Отрезок (DB) — расстояние между основаниями наклонных.
Источники:
Рис. 1-5. Наклонная, перпендикуляр к плоскости, © ЯКласс.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Наклонная к прямой
Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?
Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.
Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).
Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.
На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.
Точка B — основание перпендикуляра, точка C — основание наклонной AC.
Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.
Из точки к прямой можно провести бесконечно много наклонных.
Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.
На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.
На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.
BC — проекция наклонной AC на прямую a,
BD — проекция наклонной AD на прямую a.
CD — расстояние между основаниями наклонных
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
В следующий раз рассмотрим свойства наклонных.
2 Comments
Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме длин проекций этих наклонных.
Косые треугольники: характеристика, примеры, упражнения
Содержание:
В косые треугольники Это те, у которых нет прямого угла, поэтому ни один из их внутренних углов не равен 90º. Итак, косой треугольник может быть острый угол или тупой.
В первом случае внутренние углы треугольника острые или что то же самое: меньше 90º, а во втором всегда есть угол больше 90º, то есть угол тупой. Давайте посмотрим на пример каждого из них на следующем рисунке:
Чтобы найти длины сторон и меры внутренних углов этого класса треугольников, при отсутствии прямых углов невозможно применить теорему Пифагора.
Однако есть альтернативы решению треугольника: теоремы косинусов и синусов и тот факт, что сумма внутренних углов равна 180 °.
Примеры наклонных треугольников
Руководствуясь рисунком 1, мы легко можем распознать наклонные треугольники по двум критериям, которые мы приведем ниже.
Острый треугольник
Пусть треугольник сторон a, b и c будет углом перед стороной a.
Если квадрат стороны a, противоположной острому углу α, равен Меньше чем сумма квадратов остальных сторон, треугольник равен острый угол. Алгебраически:
к 2 2 + c 2 ; α 2 > б 2 + c 2 ; α > 90º
Например, треугольник с внутренними углами 105º, 60º и 15º является тупым наклонным треугольником. Обратите внимание, что 105º + 60º + 15º = 180º.
Теоремы о синусе и косинусе
Чтобы решить наклонные треугольники, то есть найти меры всех их сторон и всех углов, требуются теоремы о синусе и косинусе.
Пусть a, b и c – стороны треугольника, а α, β и γ – его внутренние углы. Так:
Теорема синуса
Теорема синусов утверждает следующее:
Где α – угол, противоположный стороне a, β – угол, противоположный стороне b, а γ – угол, обращенный к стороне c.
Мы решили применить теорему синуса, когда собираемся решить треугольник, для которого известно больше углов, чем сторон.
Теорема косинусов
Согласно теореме косинусов:
c 2 = а 2 + b 2 – 2⋅a⋅b⋅cos γ
Угол γ снова находится перед стороной c. Мы также можем написать эквивалентные выражения для сторон a и b следующим образом:
к 2 = b 2 + c 2 – 2⋅b⋅c⋅cos α
б 2 = а 2 + c 2 – 2⋅a⋅c⋅cos β
Теорема косинуса предпочтительно применяется, когда известны значения двух сторон и угол между ними. Точно так же, как только три стороны треугольника известны, теорема позволяет нам вычислить косинус угла между двумя из них.
Решенные упражнения
– Упражнение 1
Убедитесь, что треугольник, стороны которого составляют 20, 10 и 12 условных единиц, тупой.
Решение
Мы не знаем ни одного из внутренних углов, но, принимая во внимание критерий, используемый для распознавания тупых треугольников, мы можем сформулировать неравенства с квадратами сторон, чтобы проверить, истинно ли это.
Сначала находим квадраты с каждой стороны:
И мы видим, что в действительности это: 400> 100 + 144, поскольку 400> 244. Следовательно, треугольник содержит угол больше 90º, расположенный напротив стороны, которая измеряет 20. Следовательно, этот треугольник, помимо того, что он наклонен, это тоже тупо.
– Упражнение 2.
Учитывая наклонный треугольник, показанный на рисунке 2, размеры которого даны в произвольных единицах, определите:
а) Значение х. Треугольник острый или тупой?
б) Остальные внутренние углы треугольника
Решение для
Известны две смежные стороны треугольника, размеры которых равны 38,0 и 45,8, а угол между ними равен 30 °, поэтому теорема косинусов имеет непосредственное применение:
Икс 2 = 38.0 2 + 45.8 2 – 2 x 38,0 x 45,8 x cos 30º = 527,18
х = (527,18) 1/2 = 22.96
Рисунок предполагает, что α> 90º и треугольник тупой и наклонный. Чтобы это проверить, находим квадраты сторон, как это было сделано в предыдущем упражнении:
Угол α больше 90 °, если квадрат на противоположной стороне: 45,8 2 больше суммы квадратов других сторон, которая равна 22,96 2 + 38.0 2 .
Посмотрим, будет ли это так:
527.18 + 1444.00 = 1971.2
Следовательно, угол α больше 90º.
Решение б
Теперь мы можем применить теорему синусов, чтобы найти один из недостающих углов. Поднимем его на угол β:
грех 30º / 22,96 = грех β / 38
sin β = 38 x (sin 30º / 22,96) = 0,8275
β = арксен (0,8275) = 55,84º
Недостающий угол можно найти, зная, что сумма внутренних углов любого треугольника равна 180 °. Таким образом:
55.84º + 30º + α = 180º
Если хотите, вы также можете использовать теорему косинусов, чтобы найти косинус угла между любыми двумя соседними сторонами. После получения функция арккосинуса используется для определения угла.
Результаты могут немного отличаться до десятичных знаков, в зависимости от выполняемого округления.
Решение c
Периметр P – это контур фигуры, эквивалентный сумме измерений трех сторон:
P = 22,96 + 38,00 + 45,80 = 106,76 условных единиц.
Решение d
Формула для вычисления площади любого треугольника:
A = (1/2) x основание x высота
Нам нужно выбрать одну из сторон в качестве основы и определить высоту. Например, выбрав сторону размером 45,8, мы строим высоту час до вершины A, которая является красной линией на рисунке 2b.
Делая это, мы делим исходный треугольник на два прямоугольных треугольника, оба с час как общая нога. Любой из них работает, так как мы знаем сторону и острый угол.
Мы собираемся взять отрезок с гипотенузой, равной 38, отрезок, который измеряет час, что является искомой высотой и острым углом, равным 30º.
С помощью тригонометрических соотношений острого угла 30º определяем величину час:
sin 30º = катет напротив 30º / гипотенуза = h / 38
h = 38 x sin 30º = 19
A = (1/2) x 45,8 x 19 = 435,1 условных единиц площади.
В качестве основы мы могли бы выбрать другую из сторон, например сторону 38, в данном случае высоту час отличается, поскольку образуется еще один прямоугольный треугольник, но результат по площади такой же. Читателю остается проверить это в качестве упражнения.
– Упражнение 3.
Для треугольника ABC, такого что A = 45º, B = 60º и a = 12 см, вычислите другие данные треугольника.
Решение
Учитывая, что сумма внутренних углов треугольника равна 180º, мы имеем:
C = 180º-45º-60º = 75º.
Три угла уже известны. Затем по закону синусов вычисляются две недостающие стороны.
Возникают следующие уравнения: 12 / sin (45º) = b / sin (60º) = c / sin (75º).
Из первого равенства мы можем решить для «b» и получить, что:
b = 12 * sin (60º) / sin (45º) = 6√6 ≈ 14,696 см.
Вы также можете решить для «c» и получить:
c = 12 * sin (75º) / sin (45º) = 6 (1 + √3) ≈ 16,392 см.
– Упражнение 4.
Учитывая треугольник ABC, такой что A = 60º, C = 75º и b = 10 см, вычислите другие данные треугольника.
Решение
Как и в предыдущем упражнении, B = 180º-60º-75º = 45º. Кроме того, используя закон синусов, мы получаем, что a / sin (60º) = 10 / sin (45º) = c / sin (75º), из чего получается, что a = 10 * sin (60º) / sin (45º ) = 5√6 ≈ 12,247 см и c = 10 * sin (75º) / sin (45º) = 5 (1 + √3) ≈ 13,660 см.
– Упражнение 5.
Дан треугольник ABC такой, что a = 10 см, b = 15 см и C = 80º, вычислите другие данные треугольника.
Решение
В этом упражнении известен только один угол, поэтому его нельзя начинать, как в предыдущих двух упражнениях. Кроме того, нельзя применить закон синусов, потому что никакое уравнение не может быть решено.
Поэтому переходим к применению закона косинусов. Вот тогда:
c² = 10² + 15² – 2 (10) (15) cos (80º) = 325 – 300 * 0,173 ≈ 272,905 см,
Итак, c ≈ 16,51 см. Теперь, зная 3 стороны, используется закон синусов и получается, что:
10 / sin (A) = 15 / sin (B) = 16,51 см / sin (80º).
Следовательно, решение для B приводит к sin (B) = 15 * sin (80º) / 16,51 ≈ 0,894, что означает, что B ≈ 63,38º.
Теперь мы можем получить, что A = 180º – 80º – 63,38º ≈ 36,62º.
– Упражнение 6
Стороны наклонного треугольника равны a = 5 см, b = 3 см и c = 7 см. Найдите углы треугольника.
Решение
Опять же, закон синусов не может быть применен напрямую, поскольку никакое уравнение не может служить для получения значения углов.
Используя закон косинуса, мы имеем c² = a² + b² – 2ab cos (C), из которого при вычислении получаем cos (C) = (a² + b² – c²) / 2ab = (5² + 3²-7²) / 2 * 5 * 3 = -15/30 = -1/2 и, следовательно, C = 120º.
Теперь мы можем применить закон синусов и, таким образом, получить 5 / sin (A) = 3 / sin (B) = 7 / sin (120º), из которого мы можем решить относительно B и получить, что sin (B) = 3 * sin (120º) / 7 = 0,371, так что B = 21,79º.
Наконец, последний угол рассчитывается с использованием того, что A = 180º-120º-21,79º = 38,21º.
Ссылки
- Клеменс, С. Геометрия с приложениями. Эддисон Уэсли.
- Ибаньес, П. 2010. Математика III. Cengage Learning.
- Хименес, Р. Математика II: геометрия и тригонометрия. 2-й. Издание. Пирсон.
- Математика для вас. Тупой треугольник. Получено с: matematicasparaticharito.wordpress.com.
- Стюарт, Дж. 2007. Precalculus. 5-е. Издание. Cengage Learning.
Что такое слезы и слезы?
Что такое самоисполняющееся пророчество? (Психология)
[spoiler title=”источники:”]
http://ru1.warbletoncouncil.org/triangulos-oblicuangulos-ejercicios-resueltos-8172
[/spoiler]
Стереометрия
Глава 9. Прямые и плоскости в пространстве
9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью
Определение 1
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.
Определение 2
Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).
Определение 3
Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.
Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.
Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.
Следствие
Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).
Определение 4
Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.
Определение 5
Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.
Теорема 5
Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.
