Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
Задача
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.

Решение
- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L1 лежит на фронтальном следе плоскости γ.
- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.

Алгоритм построения
- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L”1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’1.
- Находим точку L”2 на пересечении фронтальных следов пл. α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L”2.
- Проводим прямые l’ и l” через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

Алгоритм построения
- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f0σ и 5”=A”С”∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f0σ на одной линии связи с N’.
-
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
- Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.
Определение видимости
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N”K” видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Дополнительные материалы:
- Способы задания плоскости на чертеже
- Точка пересечения прямой и плоскости
Л иния
иния
пересечения двух плоскостей – прямая
линия. Рассмотрим сначала частный случай
(рис. 3.9), когда одна из пересекающихся
плоскостей параллельна горизонтальной
плоскости проекций (α ׀׀
π1,
f0α
׀׀Х).
В этом случае линия пересечения а,
принадлежащая плоскости α,
будет также параллельна плоскости π1,
(рис. 3.9. а) т.
е. будет совпадать с горизонталью
пересекающихся плоскостей (а ≡ h).
Если одна из
плоскостей параллельна фронтальной
плоскости проекций (рис. 3.9. б), то линия
пересечения а, принадлежащая этой
плоскости, будет параллельна плоскости
π2
и будет совпадать с фронталью
пересекающихся
плоскостей (а ≡ f).

а)
б)
Рис. 3.9. Частный
случай пересечения плоскости общего
положения с плоскостями: а) горизонтального
уровня; б) фронтального уровня
Пример построения
точки пересечения (К) прямой а (АВ) с
плоскостью α (DEF)
показан на рис. 3.10. Для этого прямая а
заключена в произвольную плоскость β
и определена линия пересечения плоскостей
α и β.
В рассматриваемом
примере прямые АВ и MN
принадлежат одной плоскости β и
пересекаются в точке К, а т. к. прямая MN
принадлежит заданной плоскости α (DEF),
то точка К является и точкой пересечения
прямой а (АВ) с плоскостью α. (рис. 11).

Рис. 3.10. Построение
точки пересечения прямой с плоскостью
Для решения подобной
задачи на комплексном чертеже необходимо
уметь находить точку пересечения прямой
общего положения с плоскостью общего
положения.
Рассмотрим пример
нахождения точки пересечения прямой
АВ c
плоскостью треугольника DEF
представленный на рис. 3.11.
Для нахождения
точки пересечения через фронтальную
проекцию прямой А2В2
проведена фронтально-проецирующая
плоскость β которая пересекла треугольник
в точках M
и N.
На фронтальной плоскости проекций (π2)
эти точки представлены проекциями M2,
N2.
Из условия принадлежности прямой
плоскости на горизонтальной плоскости
проекций (π1)
находятся горизонтальные проекции
полученных точек M1
N1.
В пересечении горизонтальных проекций
прямых А1В1
и M1N1
образуется горизонтальная проекция
точки их пересечения (К1).
По линии связи и условиям принадлежности
на фронтальной плоскости проекций
находится фронтальная проекция точки
пересечения (К2).
В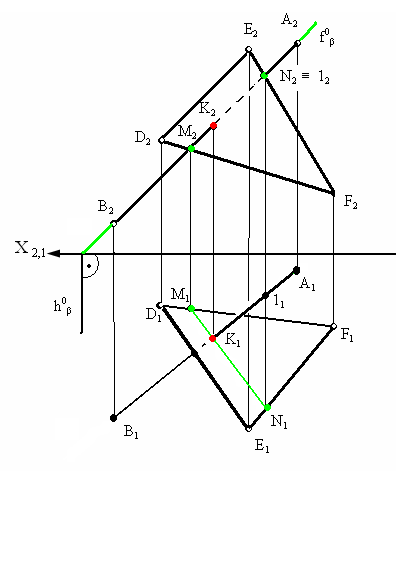 идимость
идимость
отрезка АВ относительно треугольника
DEF
определена методом конкурирующих
точек.
На плоскости π2
рассмо- трены две точки NEF
и
Рис. 3.11. Пример
определения точки
пересечения прямой
и плоскости
1АВ.
По горизонтальным проекциям этих
точек можно установить, что точка N
рас- положена ближе к наблюда-
телю (YN>Y1
), чем точка 1 (направление луча
зрения параллельно S).
Следовательно, прямая АВ, т. е. часть
прямой АВ (К1)
закрыта плоскостью DEF
на плоскости π2
(ее проекция К212
показана штриховой линией). Аналогично
установлена видимость на плоскости
π1.
Вопросы для
самоконтроля
-
В чем заключается
сущность метода конкурирующих точек
? -
Свойства прямой.
-
Каков алгоритм
определения точки пересечения прямой
и плоскости ? -
Каков алгоритм
определения линии пересечения плоскостей
? -
Какие задачи
называются позиционными ? -
Сформулируйте
условия принадлежности прямой плоскости.
Соседние файлы в папке Лекции нг
- #
- #
- #
- #
- #
- #
- #
- #
§11. Построение линии пересечения двух плоскостей. (Вторая позиционная задача).
Результатом пересечения двух плоскостей является прямая . Для построения этой прямой достаточно найти две точки, принадлежащие обеим плоскостям и провести через них прямую линию.
Если мы возьмем прямую, принадлежащую одной плоскости и найдем точку ее пересечения с другой плоскостью, то эта точка будет общей для обеих плоскостей. Таким образом, построение линии пересечения двух плоскостей сводится к решению первой позиционной задачи, повторенному дважды.
Задача 11.1. Построить линию пересечения плоскости α, заданной треугольником АВС, и плоскости β, заданной двумя пересекающимися прямыми МЕ и МК (рисунок 11.1). Определить видимость плоскостей.
Решение.
1. Возьмем прямую АВ, принадлежащую плоскости α, и найдем точку ее пересечения с плоскостью β. Для этого заключим ее в проецирующую плоскость и найдем точку пересечения, используя алгоритм для решения первой позиционной задачи (см. §7).
На рисунке 11.2 продемонстрирован этот этап решения – точка N является точкой пересечения прямой АВ и плоскости β(МК, МЕ). В данном случае мы заключили прямую в фронтально-проецирующую плоскость ФП, прямая 1-2 является результатом пересечения плоскости ФП и плоскостиβ.
Не нужно забывать о том, что все точки на чертеже отображены в проекциях. Так, например, на рисунке 11.2. точка N представлена проекциями N1 и N2.
2. Возьмем прямую МК, принадлежащую плоскости β, и найдем точку ее пересечения с плоскостью α. Заключив ее в горизонтально-проецирующую плоскость, и проведя аналогичные построения, найдем точку L (рисунок 11.3).
3. Проведем прямую NL, являющуюся линией пересечения плоскостей α и β (рисунок 11.4).
4. Определяем видимость плоскостей (рисунок 11.5).
Применяем метод конкурирующих точек – для определения видимости на фронтальной проекции берем конкурирующие точки, проекции которых совпадают с точкой 22, для определения видимости на горизонтальной проекции берем точки с проекцией в 41. Конкурирующие точки 22 принадлежат фронтальной проекции АВ и МК. Пройдя по стрелке взгляда вниз, видим, что точка, лежащая на прямой АВ находится ближе к наблюдателю, так как у нее координата у больше, поэтому в районе проекции прямая АВ видимая, а МК – невидимая. Следовательно, проекция М2К2 в точке 22 меняет свой вид с видимой на невидимую.
Точка 41 лежит на горизонтальной проекции ВС и МК. Видимой будет та прямая, которая по стрелке взгляда находится выше на фронтальной проекции, в данном случае это прямая ВС.
Нужно обратить внимание на то, что прямые АВ и ВС меняют видимость в точках пересечения с прямой NL. Линия пересечения плоскостей всегда видимая.
На рисунке 11.6 показано окончательное решение задачи, для наглядности плоскости затонированы.
Задача 11.2. Построить линию пересечения плоскостей α и β, заданных следами (рисунок 11.7). Определить видимость плоскостей.
Решение.
Поскольку следы плоскости – это прямые, принадлежащие этой плоскости, а точки пересечения 1 и 2 одноименных проекций следов являются общими для обеих плоскостей, то очевидно, что результат пересечения плоскостей – это прямая, проходящая через эти точки. На эпюре Монжа определяем фронтальные и горизонтальные проекции точек 1 и 2 (рисунок 11.8).
Как видно на рисунке 11.8, горизонтальная проекция точки 1, являющейся точкой пересечения фронтальных следов α и β, а также фронтальная проекция точки 2 – лежат она оси х, поскольку сами прямые принадлежат плоскостям проекций. Соединив одноименные проекции точек 1 и 2, получим линию пересечения плоскостей (рисунок 11.9).
Определив видимость плоскостей в проекциях, получим окончательное решение задачи (рисунок 11.10)
Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям. Так, прямая K1К2 (рис. 163), по которой пересекаются между собой плоскость, заданная треугольником АВС, и пл. β, заданная прямыми DE и DF, проходит через точки K1 и K2; но в этих точках прямые АВ и АС первой плоскости пересекают пл. β т. е. точки К1 и К2 принадлежат обеим плоскостям.
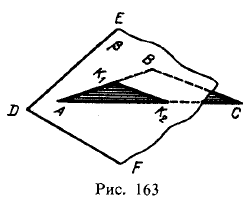
Следовательно, в общем случае для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям; эти точки определяют линию пересечения плоскостей.
Для нахождения каждой из таких двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна к плоскости проекций, то построение проекций линии пересечения упрощается. Начнем с такого случая.
На рис. 164 показано пересечение двух плоскостей, из которых одна (заданная треугольником DEF) расположена перпендикулярно к пл. π2. Так как треугольник DEF проецируется на пл.π2 в виде прямой линии (D”F”), то фронтальная проекция отрезка прямой, по которому пересекаются оба треугольника, представляет собой отрезок К”1К”2 на проекции D”F”. Дальнейшее построение ясно из чертежа.
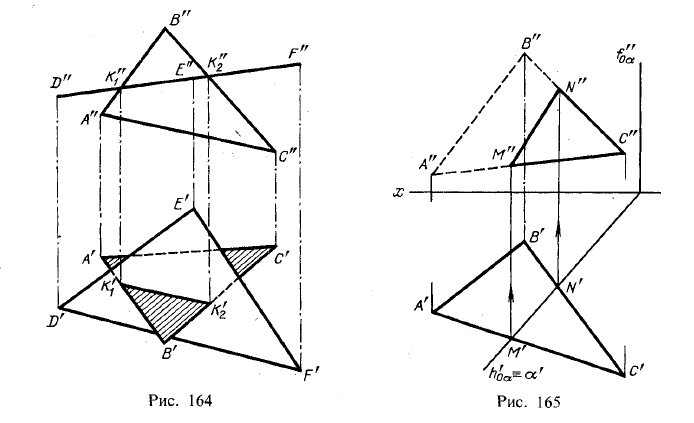
Другой пример дан на рис. 165. Горизонтально-проецирующая плоскость α пересекает плоскость треугольника АВС. Горизонтальная проекция линии пересечения этих плоскостей — отрезок M’N’ — определяется на следе α’.
Теперь рассмотрим общий случай построения линии пересечения двух плоскостей. Пусть одна из плоскостей, β, задана двумя пересекающимися прямыми, а другая, γ,— двумя параллельными прямыми. Построение показано на рис. 166. В результате взаимного пересечения плоскостей β и γ получена прямая K1K2. Выразим это записью: β × γ = К1K2.
Для определения положения точек K1 и К2 возьмем две вспомогательные фронтально-проецирующие плоскости (α1, и α2), пересекающие каждую из плоскостей β и γ. При пересечении плоскостей β и γ плоскостью α1. получаем прямые с проекциями 1″2″, 1’2′ и 3″4″, 3’4′. Эти прямые, расположенные в пл. α1, в своем пересечении определяют первую точку, К1, линии пересечения плоскостей β и γ.
Введя, далее, ил. α2, получаем в ее пересечении с β и γ прямые с проекциями 5″6″, 5’6′ и 7″8″, 7’8′. Эти прямые, расположенные в пл. α2, в своем пересечении определяют вторую точку, К2, общую для β и γ.
Получив проекции К’1 и К’2 находим на следах и α”1 и α”2 проекции К”1 и К”2. Этим определяются проекции К’1К’2 и К”1К”2 искомой прямой пересечения плоскостей β и γ(проекции проведены штрихпунктирной линией).
При построении можно иметь в виду следующее: так как вспомогательные секущие плоскости α1 и α2 взаимно параллельны, то, построив проекции 1’2′ и 3’4′ следует для проекций 5’6′ и 7’8′ взять по одной точке, хотя бы 5 и 8, так как 5’6’||1’2′ и 7’8’||3’4′.
В рассмотренном построении были взяты в качестве вспомогательных две фронгально- проецирующие плоскости. Конечно, можно было взять и иные плоскости, например две горизонтальные или одну горизонтальную, другую фронтальную и т. д. Сущность построений от этого не меняется. Однако может встретиться такой случай. Положим, что были взяты в качестве вспомогательных две горизонтальные плоскости и полученные при пересечении ими
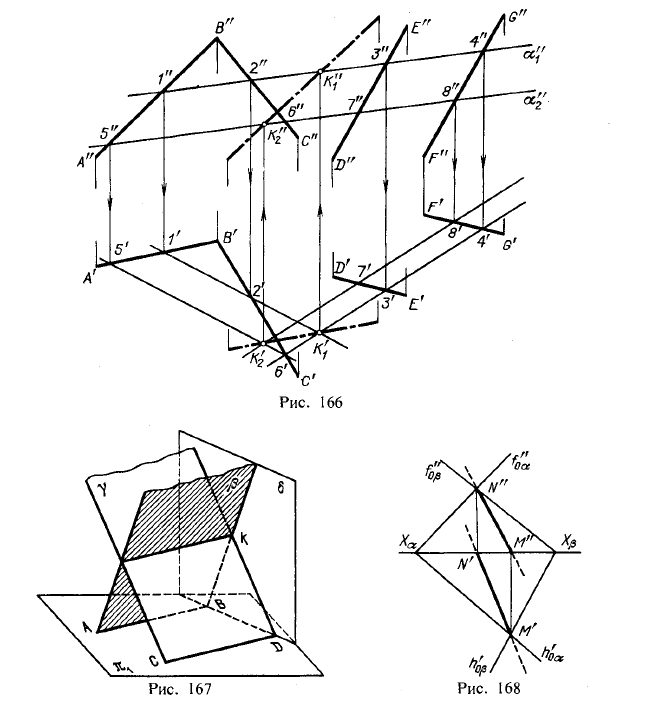
плоскостей β и γ горизонтали оказались взаимно параллельными. Но рис. 167 показывает, что β и γ пересекаются между собой, хотя их горизонтали параллельны. Следовательно, получив взаимно параллельные горизонтальные проекции горизонталей АВ и CD и зная, что плоскости при этом не обязательно параллельны, а могут пересекаться (по общей для них горизонтали), надо испытать плоскости β и γ при помощи хотя бы, горизонгально-проецирующей плоскости (см. рис. 167); если прямые, по которым эта вспомогательная плоскость σ, пересечет β и γ, также оказались бы параллельны одна другой, то плоскости β и γ не пересекаются, а параллельны одна другой. На рис. 167 эти прямые пересекаются в точке К, через которую и проходит линия пересечения плоскостей β и γ параллельно прямым ВА и CD.
Если плоскости заданы их следами на плоскостях проекций, то естественно искать точки, определяющие прямую пересечения плоскостей, в точках пересечения одноименных следов плоскостей (рис. 168): прямая, проходящая через эти точки, является общей для обеих плоскостей, т. е. их линией пересечения.
Схему построения линии пересечения двух плоскостей (см. рис. 166) можно, конечно, распространить и на случай задания плоскостей их следами. Здесь роль вспомогательных секущих плоскостей исполняют сами плоскости проекций:
α × π1=h’0α; β× π1=h’0β; h’0α × h’0β=M;
α × π2=f”0α; β× π2=f”0β; f”0α × f”0β=N.
Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей. Поэтому для построения проекций линии пересечения плоскостей α и β (рис. 168) надо: 1) найти точку М’ в пересечении следов h’0α и h’0β
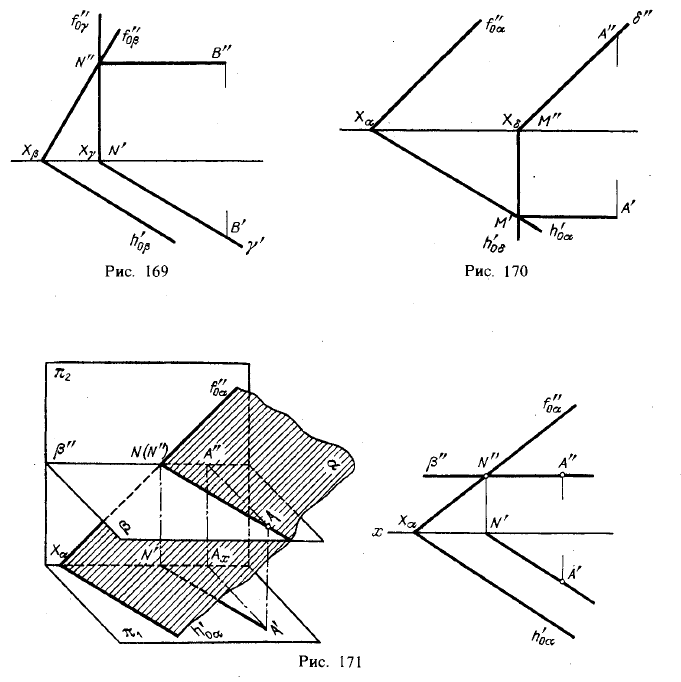
и точку N” в пересечении f”0α и f”0β, а по ним — проекции М” и N’; 2) провести прямые линии M”N” и M’N’,
На рис. 169—171 показаны случаи, когда известно направление линии пересечения. Поэтому достаточно иметь лйшь одну точку от пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов.
Вопросы к §§ 22-24
- Какое взаимное положение могут занимать две плоскости?
- Каков признак параллельности двух плоскостей?
- Как взаимно располагаются фронтальные следы двух параллельных между собой фронтально-проецирующих плоскостей?
- Как взаимно располагаются горизонтальные следы двух параллельных между собой горизонтально-проецирующих плоскостей?
- Как взаимно располагаются одноименные следы двух параллельных между собой плоскостей?
- Служит ли признаком взаимного пересечения двух плоскостей пересечение хотя бы одной пары их одноименных следов?
- Как установить взаимное положение прямой и Плоскости?
- Как строится точка пересечения прямой линии с плоскостью, перпендикулярной к одной или к двум плоскостям проекций?
- Какая точка из числа расположенных на общем перпендикуляре к а) пл. π1 б) пл. π2 считается видимой соответственно на π1, на π2?
- Как строится линия пересечения двух плоскостей, из которых хотя бы одна перпендикулярна к пл. π1 или к пл. π2?
- В чем заключается общий способ построения линии пересечения двух плоскостей?
Задание 2. Построение линии пересечения плоскостей
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
2.1. Условие задания
По заданным координатам точек А, В, С, D, E, F (Таблица 2) построить горизонтальную и фронтальную проекции треугольников ∆АBC и ∆DEF, найти линию их пересечения и определить видимость элементов треугольников.
2.2. Пример выполнения задания № 2
Второе задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам шести точек А, В, С, D, E, Fпостроить горизонтальную и фронтальную проекции 2-х плоскостей, заданных ∆АBC и ∆DEF;
2. Плоскости общего и частного положения, пересечение прямой и плоскости, пересечение плоскостей, конкурирующие точки: построить линию пересечения заданных плоскостей и определить видимость их элементов.
Построить горизонтальные и фронтальные проекции заданных плоскостей ∆АBC и ∆DEF (Рисунок 2.1).
Для построения искомой линии пересечения заданных плоскостей необходимо:
1. Выбрать одну из сторон треугольника и построить точку пересечения этой стороны с плоскостью другого треугольника: на Рисунке 2.1 построена точка М пересечения прямой EF c плоскостью ∆АBC; для этого прямую EF заключают во вспомогательную горизонтально-проецирующую плоскость δ;
2. Построить фронтальную проекцию 1222 линии пересечения плоскости δ с плоскостью ∆АBC;
3. Найти фронтальную проекцию М2 искомой точки М на пересечении фронтальную проекцию 1222 с фронтальной проекцией E2 F2прямой EF;
4. Найти горизонтальную проекцию М1 точки М с помощью линии проекционной связи;
5. Аналогично построить вторую точку N, принадлежащую искомой линии пересечения заданных плоскостей: заключить во фронтально-проецирующую плоскость β прямую ВС; найти линию пересечения 34 плоскости с плоскостью ∆DEF; на пересечении линии 34 и прямой ВС найти точку N;
6. Определить с помощью конкурирующих точек, для каждой плоскости отдельно, видимые участки треугольников.
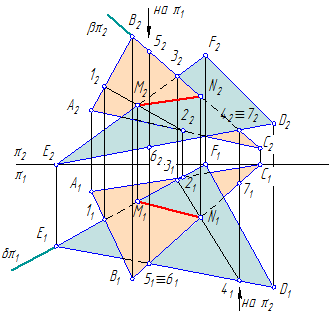
Рисунок 2.1 – Построение линии пересечения двух плоскостей, заданных треугольниками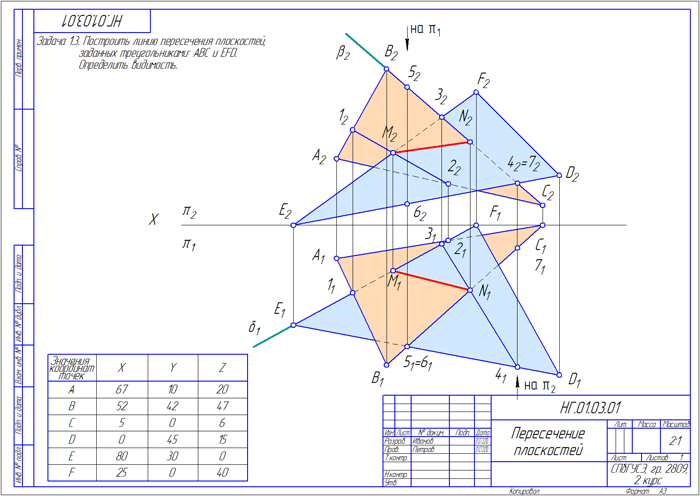
Рисунок 2.2 – Пример оформления задания 2
Видеопример выполнения задания №2
2.3. Варианты задания 2
Таблица 2– Значения координат точек
| Вариант | Координаты (x, y, z) вершин треугольников | |||||
|---|---|---|---|---|---|---|
| А | В | С | D | E | F | |
| 1 | 20; 65; 30 | 40; 15; 65 | 80; 30; 35 | 15; 35; 70 | 70; 75; 80 | 35; 0; 0 |
| 2 | 75; 75; 5 | 60; 20; 60 | 20; 10; 40 | 30; 55; 50 | 90; 50; 35 | 60; 5; 10 |
| 3 | 0; 30; 75 | 30; 65; 15 | 80; 25; 15 | 45; 65; 75 | 95; 40; 0 | 10; 0; 10 |
| 4 | 90; 5; 70 | 65; 60; 15 | 15; 15; 20 | 25; 45; 70 | 95; 60; 35 | 65; 10; 0 |
| 5 | 30; 0; 10 | 70; 15; 15 | 15; 55; 16 | 70; 55; 60 | 5; 30; 60 | 20; 0; 0 |
| 6 | 20; 25; 0 | 60; 5; 80 | 90; 75; 40 | 0; 60; 60 | 75; 80; 70 | 90; 10; 0 |
| 7 | 0; 60; 20 | 20; 10; 60 | 85; 10; 20 | 50; 70; 65 | 75; 35; 0 | 10; 0; 5 |
| 8 | 10; 20; 15 | 55; 70; 5 | 80; 20; 45 | 20; 60; 55 | 100; 35; 20 | 60; 10; 5 |
| 9 | 0; 50; 10 | 60; 70; 70 | 80; 10; 10 | 20; 10; 70 | 90; 50; 60 | 60; 85; 0 |
| 10 | 85; 70; 10 | 25; 20; 25 | 90; 10; 60 | 15; 70; 65 | 105; 10; 45 | 70; 0; 0 |
| 11 | 25; 5; 25 | 60; 60; 5 | 95; 20; 50 | 36; 45; 55 | 105; 45; 60 | 70; 0; 0 |
| 12 | 95; 30; 65 | 15; 15; 10 | 70; 80; 5 | 35; 70; 70 | 115; 80; 55 | 85; 20; 0 |
| 13 | 20; 5; 60 | 50; 60; 5 | 90; 15; 30 | 60; 60; 60 | 100; 5; 10 | 25; 10; 0 |
| 14 | 10; 5; 70 | 80; 20; 25 | 40; 65; 10 | 70; 70; 70 | 0; 35; 60 | 30; 5; 0 |
| 15 | 20; 45; 55 | 60; 70; 10 | 90; 10; 60 | 20; 0; 10 | 95; 20; 10 | 75; 60; 75 |
| 16 | 5; 10; 60 | 40; 65; 10 | 70; 5; 40 | 70; 50; 75 | 0; 70; 45 | 15; 0; 5 |
| 17 | 10; 45; 5 | 90; 5; 10 | 50; 70; 70 | 15; 5; 50 | 95; 15; 65 | 60; 70; 0 |
| 18 | 65; 20; 70 | 0; 20; 15 | 50; 70; 5 | 15; 60; 55 | 90; 60; 40 | 60; 5; 5 |
| 19 | 20; 20; 70 | 50; 50; 10 | 70; 10; 30 | 80; 60; 70 | 5; 40; 60 | 25; 0; 10 |
| 20 | 85; 10; 45 | 70; 50; 0 | 20; 20; 10 | 55; 60; 60 | 0; 0; 60 | 75; 0; 0 |
| 21 | 0; 70; 60 | 30; 10; 80 | 70; 15; 20 | 60; 50; 70 | 0; 0; 50 | 15; 70; 5 |
| 22 | 0; 70; 25 | 45; 10; 70 | 90; 30; 20 | 65; 60; 70 | 90; 10; 15 | 15; 0; 15 |
| 23 | 10; 20; 40 | 50; 60; 10 | 75; 10; 40 | 75; 60; 75 | 5; 70; 55 | 35; 0; 0 |
| 24 | 10; 10; 10 | 90; 80; 20 | 65;10;60 | 15; 70; 65 | 100; 70; 40 | 80; 10; 0 |
| 25 | 60; 65; 10 | 0; 10; 25 | 85; 5; 60 | 20; 65; 60 | 105; 35; 35 | 55; 0; 0 |
| 26 | 10; 70; 20 | 50; 10; 60 | 90; 25; 10 | 70; 65; 45 | 5; 35; 55 | 25; 0; 50 |
| 27 | 10; 5; 70 | 40; 70; 10 | 90; 5; 40 | 100; 55; 25 | 25; 65; 80 | 50; 0; 0 |
| 28 | 0; 50; 5 | 25; 0; 60 | 85; 10; 15 | 50; 50; 50 | 90; 0; 55 | 20; 0; 0 |
| 29 | 10; 70; 10 | 40; 10; 50 | 80; 20; 20 | 80; 55; 55 | 10; 50; 70 | 20; 0; 0 |
| 30 | 75; 70; 20 | 10; 35; 10 | 60; 20; 60 | 20; 70; 70 | 100; 60; 50 | 75; 5; 0 |
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
