Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.
Проекцией вектора на ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.
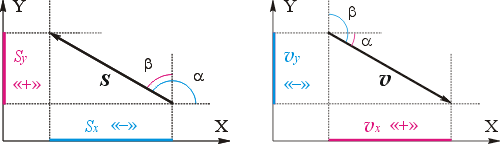
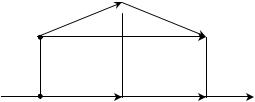
На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол 150° с направлением оси X. Пользуясь определением, найдём проекцию перемещения на ось X:
sx = s · cos(α) = 50 км · cos( 150°) = –43 км
Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:
sy = s · cos(β) = 50 км · cos( 60°) = +25 км
Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.
На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:
υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c
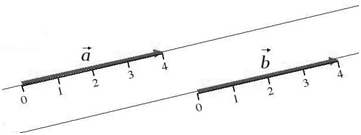
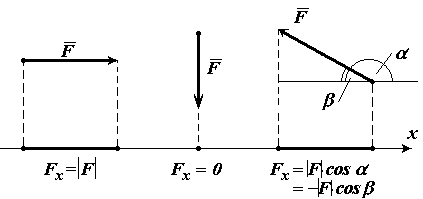
Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.
Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.
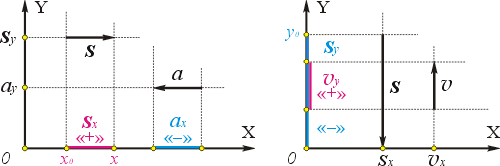
Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .
Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .
На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Для понятия проекции вектора на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
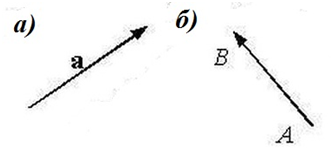
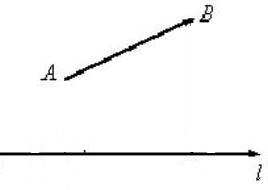
Обозначение: Двумя буквами: $overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
«Проекция вектора на ось. Как найти проекцию вектора» 👇
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A’$ – начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B’$ – конец искомого вектора. Вектор $overline{A’B’}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
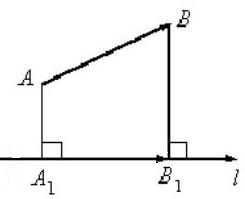
Постройте геометрическую проекцию $overline{AB}$ на ось $l$, изображенные на рисунке 6.
Решение.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A’$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B’$ (рис. 7).
Полученный на оси $l$ вектор $overline{A’B’}$ и будет искомой геометрической проекцией.
Замечание 1
Заметим, что если угол между вектором и осью острый, то проекция сонаправлена с осью, а если тупой, то проекция противоположно направлена с осью.
Числовая проекция
Как мы уже знаем, результатом алгебраической проекции будет неотрицательное действительное число.
Определение 9
Числовой (алгебраической) проекцией на ось будем называть неотрицательное число, равное длине вектора геометрической проекции.
Рассмотрим это понятие на примере задачи:
Пример 2
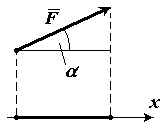
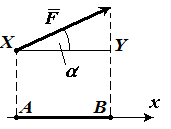
Найти числовую проекцию вектора $overline{F} на сонаправленную ему ось $x$, если угол между ними равняется $α$ (рис. 8). (рис. 8).
Решение.
Введем на рисунке следующие обозначения:
Видим, что длина вектора геометрической проекции, равняется длине $XY$. Из определения косинуса получим, что
$XY=|overline{F}|cosα$
где $|overline{F}|$ – длина вектора $overline{F}$. Это и будет искомая алгебраическая проекция на ось.
Другие случаи можете видеть на рисунке 9.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Преподаватель который помогает студентам и школьникам в учёбе.
Проекция вектора на ось в физике – формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка 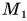
Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 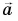 на ось Ох обозначена через
на ось Ох обозначена через 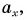 а проекция вектора
а проекция вектора 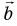 — через
— через 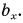
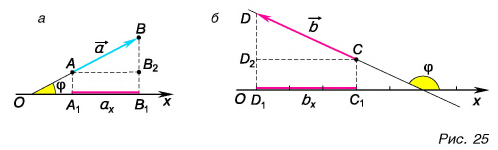
Проекция  — число положительное, т. к. угол
— число положительное, т. к. угол 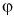 на рисунке 25, а — острый. Проекция
на рисунке 25, а — острый. Проекция 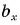 — число отрицательное
— число отрицательное 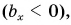 т. к. угол
т. к. угол 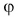 на рисунке 25, б — тупой.
на рисунке 25, б — тупой.
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
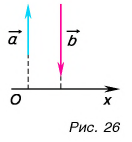
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник  на рисунке 25, а. Его гипотенуза
на рисунке 25, а. Его гипотенуза 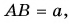 катет
катет 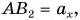 а угол между ними равен
а угол между ними равен 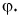 Следовательно,
Следовательно,

Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
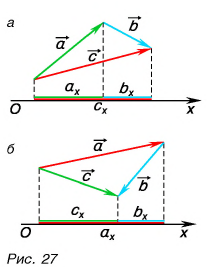
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 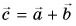 следует равенство для проекций:
следует равенство для проекций: 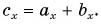 Не забывайте о знаках проекций.
Не забывайте о знаках проекций.
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
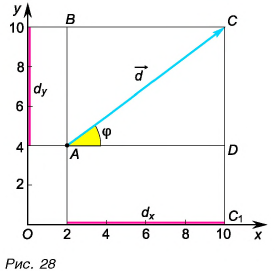
Рассмотрим вектор 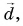 лежащий в плоскости
лежащий в плоскости 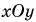 (рис. 28). Его проекции на оси
(рис. 28). Его проекции на оси 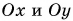 определим из рисунка:
определим из рисунка: 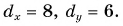
Модуль вектора 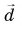 находим по теореме Пифагора из треугольника ACD:
находим по теореме Пифагора из треугольника ACD: 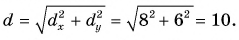 Разделив
Разделив  на
на 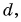 получим:
получим: 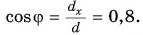 По значению косинуса находим угол
По значению косинуса находим угол 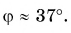
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
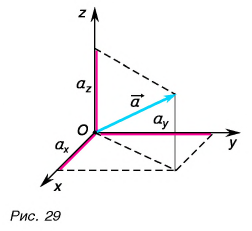
Вектор в пространстве определяется тремя проекциями: 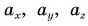 (рис. 29).
(рис. 29).
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
1. Определите сумму и разность взаимно перпендикулярных векторов  (рис. 30). Найдите модули векторов суммы
(рис. 30). Найдите модули векторов суммы  и разности
и разности 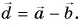
Решение
Сумму векторов 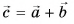 находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы
находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы  взаимно перпендикулярны, модуль вектора
взаимно перпендикулярны, модуль вектора 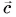 находим по теореме Пифагора:
находим по теореме Пифагора: 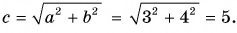 Разность векторов
Разность векторов 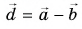 определим по правилам вычитания векторов (рис. 32, а, б).
определим по правилам вычитания векторов (рис. 32, а, б).

Модуль вектора 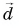 находим аналогично:
находим аналогично:
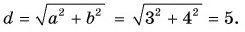
Ответ: 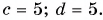
- Заказать решение задач по физике
Пример №2
Выразите вектор 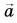 через векторы
через векторы 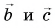 (рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?
(рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?
Решение
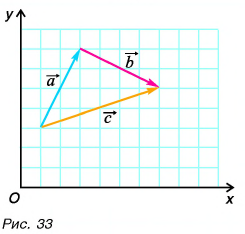
По правилу треугольника находим: 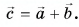 Отсюда
Отсюда 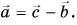 Определив координаты
Определив координаты  начальных и конечных точек векторов
начальных и конечных точек векторов 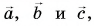 находим проекции этих векторов:
находим проекции этих векторов: 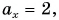

Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы: 
Ответ: 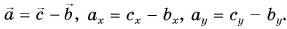
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними

|
x |
x1 x2 |
, |
y |
y1 y2 |
, |
z |
z1 z2 |
. |
(8. |
) |
||
|
2 |
2 |
2 |
||||||||||
|
3 |
Замечание. На плоскости (в двумерном пространстве) можно также задать прямоугольную систему координат Oxy. С помощью введенной системы координат любую точку или ее радиус-вектор можно представить парой чисел (x, y). Все соотношения, полученные нами ранее для координат векторов и точек трехмерного пространства, будут справедливы и на плоскости с той лишь разницей, что из них нужно всюду убрать третью координату z. Аналогичные рассуждения можно повторить и для произвольной прямой (одномерного пространства).
Определение 9.1. Осью называется прямая с лежащим на ней единичным вектором (ортом), задающим положительное направление на прямой.
На рисунке ось будем изображать в виде направленной прямой. Пусть в пространстве задана ось l и точка А, не принадлежащая оси.
Определение 9.2. Основание перпендикуляра, опущенного из точки А на пря-
мую l, точка A‘ называется проекцией (ортогональной проекцией) точки на ось.
В случае, если точка А принадлежит оси l, то проекция точки на ось совпадает с самой точкой А.
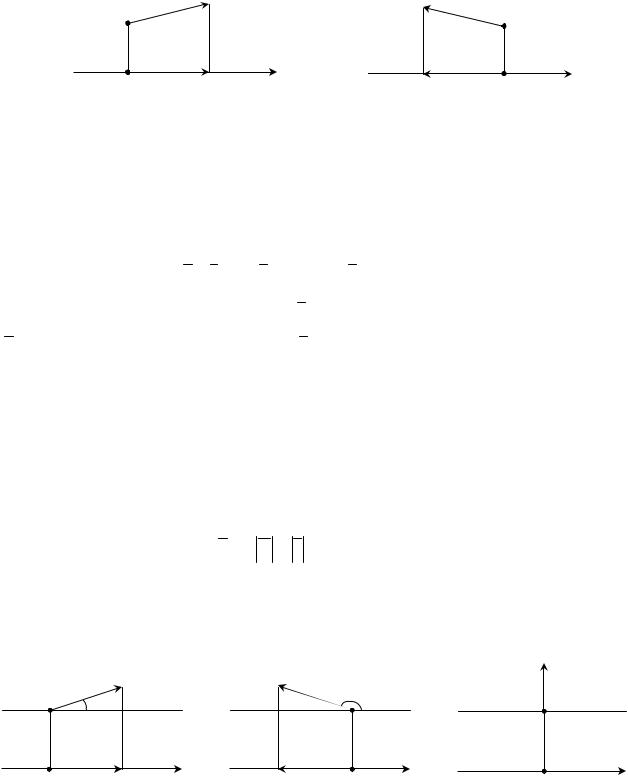
Пусть задан некоторый вектор a AB . Находя проекции начала и конца вектора a на ось l, получим вектор a‘ A‘ B‘ , где A‘, B‘ — соответственно проекции точек А, В на ось l.
Определение 9.3. Проекцией вектора a на ось l будем называть положительное число, равное a‘ , если вектор a‘ и ось l направлены одинаково (см. рис. 12) и отрица-
тельное число a‘ , если вектор a‘ и ось l направлены противоположно (см. рис. 13).
26
|
a |
В |
В |
|||||||||||||||||||||
|
a |
|||||||||||||||||||||||
|
А |
А |
||||||||||||||||||||||
|
a |
l |
a |
l |
||||||||||||||||||||
|
А’ |
В’ |
B’ |
A’ |
||||||||||||||||||||
|
Рис. 12 |
Рис. 13 |
||||||||||||||||||||||
|
Проекцию вектора |
на |
ось l |
будем обозначать прl |
. Таким образом, соглас- |
|||||||||||||||||||
|
a |
a |
||||||||||||||||||||||
|
но определению прl |
или прl |
||||||||||||||||||||||
|
a |
a |
a |
a |
. |
Замечание. Если a 0 или a l , то прl a 0 .
Теорема 9.1. Проекция вектора a на ось l равна произведению длины вектора a на косинус угла между вектором a и осью l, где под углом понимается наименьший из двух углов, образуемых вектором и осью.
Таким образом,
|
прl |
cos |
(0 ) . |
(9.1) |
||||
|
a |
a |
||||||
|
Доказательство. В зависимости от величины угла |
возможны следующие |
случаи (рис. 14):
1. Если 900 , то прl a a a cos .
|
2. Если |
900 1800 , то прl |
cos( ) |
cos . |
||||||||||||||||||||||||
|
a |
a |
a |
a |
||||||||||||||||||||||||
|
3. Если |
900 , то пр |
0 |
cos . ▲ |
||||||||||||||||||||||||
|
a |
a |
||||||||||||||||||||||||||
|
l |
|||||||||||||||||||||||||||
|
a |
a |
a |
|||||||||||||||||||||||||
|
a |
a |
||||||||||||||||||||||||||
|
l |
l |
l |
Рис. 14
27
Следствие 9.1. Проекция вектора на ось есть число положительное, если уголмежду вектором и осью острый, и отрицательное, если угол тупой. Если уголпрямой, то проекция вектора на ось равна нулю.
Следствие 9.2. Проекции равных векторов на одну и ту же ось равны между
собой.
Свойства проекций векторов на ось
|
1) прl |
прl |
прl ( |
). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
b |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) прl ( |
) прl |
, |
R. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Доказательство: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) обозначим c a b . Рассмотрим прl c |
a |
прl |
a прl b (рис.15); ▲ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
с |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
l |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
с |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рис. 15 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) в зависимости от знака возможны следующие случаи: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прl ( |
по теореме 9.1 |
cos прl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a) 0 : |
a |
) |
a |
cos |
a |
a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прl ( |
по теореме 9.1 |
( cos ) прl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b) 0 : |
a |
) |
a |
cos( ) |
a |
a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прl ( |
см. замечание копр.9.3 |
0 прl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c) 0 : |
a |
) прl (0) |
a |
. ▲ |
Таким образом, линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов.
Замечание. Все рассуждения, приведенные выше, будут также справедливы, если вместо оси l рассматривать произвольный ненулевой вектор. Проекцию (ортого-
28
нальную проекцию) вектора a на вектор b (на направление вектора b ) будем обо-
значать прb a .
Теорема 9.2. Декартовы прямоугольные координаты a1 , a2 , a3 вектора a рав-
ны соответственно проекциям этого вектора на оси Ox, Oy и Oz.
Можно дать еще одно определение координат вектора.
Определение 9.4. Координатами вектора a в прямоугольной декартовой системе координат Oxyz называются проекции этого вектора на соответствующие координатные оси.
Рассмотрим задачу о нахождении длины вектора по его координатам.
Задача. Пусть дан вектор a , который относительно прямоугольного декар-
тового базиса {i, j, k} имеет координаты: a {a1 , a2 , a3}. Найдем длину вектора a .
Решение. Найдем проекции вектора a OA на координатные оси и обозначим их OA1,OA2 иOA3 . Согласно теореме 9.2, OA1 a1 , OA2 a2 , OA3 a3 . Построим пря-
моугольный параллелепипед так, что его три измерения равны OA1,OA2 иOA3 . Вектор
a в построенном параллелепипеде совпадает с диагональю (см. рис. 9). Так как квадрат диагонали в прямоугольном параллелепипеде равен сумме квадратов его сторон, то
|
a2 |
a2 |
a2 . |
(9.2) |
||
|
a |
|||||
|
1 |
2 |
3 |
Таким образом, длина вектора равна корню квадратному из суммы квадратов координат этого вектора.
Замечание. Длина вектора AB , где A(x1 , y1 , z1 ) , B(x2 , y2 , z2 ) , согласно формулам (8.2), (9.2), находится по формуле
|
(x |
x )2 |
( y |
y )2 |
(z |
z )2 . |
(9.3) |
||||
|
AB |
2 |
2 |
2 |
|||||||
|
1 |
1 |
1 |
29
Соседние файлы в папке Вектора
- #
- #
- #
- #
- #
- #
В математике существуют два определения:
1) геометрическая проекция вектора — вектор;
2) проекция вектора на ось — число.
Геометрическая проекция вектора — это вектор, который можно получить, если провести перпендикуляры от концов вектора до выбранной оси. Проекция начала вектора соответствует началу геометрической проекции, а проекция конца вектора соответствует концу геометрической проекции.

Ваш браузер не поддерживает HTML5 видео
Для вектора
v→
геометрическая проекция на оси (t) — это вектор
vt→
.
Для вектора
n→
геометрическая проекция на оси (y) — это вектор
ny→
.
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.

ax=4bx=−3
Если длина вектора
a→
равна
a→
и
α
— это острый угол, созданный вектором и осью (x), то скалярная проекция вектора вычисляется по формуле:
ax=a→⋅cosα
.
Знак проекции вектора выбирается в зависимости от направления оси.

На рисунке видно, что эту формулу можно получить из соотношения в прямоугольном треугольнике:
.
Обрати внимание!
Если вектор и ось проекций параллельны, то скалярная проекция на этой оси — число, которое равно длине вектора, если направления вектора и оси совпадают, или число, противоположное длине вектора, если направления вектора и оси — противоположные.
Если вектор и ось проекций перпендикулярны, то проекция вектора на этой оси равна (0).

at=3bt=−5ct=0dt=0