Проекционное черчение – это учебная дисциплина, которая устанавливает правила выполнения и чтения чертежей.
Проекционное черчение является основным разделом курса черчения, в котором изучаются правила, условности и практические приемы построения изображений в ортогональных и аксонометрических проекциях, установленные стандартами (ЕСКД, ГОСТ). На данной странице собран курс лекций по всем темам проекционного черчения с примерами по предмету “Проекционное черчение“.
Для построения изображений (проекций) объектов или предметов на плоскости применяют метод проецирования. Чертежи которые сделаны таким методом, называются проекционными. При выполнении чертежей технических форм используются метод ортогонального проецирования.
Содержание:
Любое техническое изделие (прибор, машина, отдельная деталь и пр.) изготавливают на предприятии по чертежам. Чертеж должен содержать полную информацию, необходимую для изготовления изделия, и в первую очередь его изображение. Главным требованием, предъявляемым к изображениям, является то, что они должны точно воспроизводить форму внешних и внутренних поверхностей изделий. Для обеспечения этого требования необходимо, чтобы изображения на чертежах были построены определенным способом по определенным правилам, которые изложены в ГОСТ 2.305 -2008 [1].
Часть курса «Начертательная геометрия и инженерная графика», в которой изучают правила построения изображений, называют проекционным черчением.
В проекционном черчении в качестве объекта для построения изображений выступает предмет – обезличенная деталь, а сами изображения должны быть построены по методу ортогонального (прямоугольного) проецирования.
Чертежи должны быть оформлены по единым и обязательным для всех правилам, изложенным в стандартах ЕСКД.
Метод ортогонального проецирования
Проецирование – это процесс получения изображения предмета на плоскости, например бумаге, экране и т. д. (рис. 1). При этом:
- предмет располагается между наблюдателем и этой плоскостью (она называется плоскостью проекций);
- через опорные и другие точки предмета проводятся проецирующие лучи до пересечения их с плоскостью проекций;
- множество точек пересечения будет образовывать на плоскости проекций изображение предмета или, как его еще называют, проекцию предмета.
Таким образом, можно назвать проецированием фотографирование предмета или получение его тени в солнечный день на любом экране.
Ортогональное проецирование характеризуется тем, что проецирующие лучи параллельны между собой и перпендикулярны к плоскости проекций. Метод ортогональных проекций является основным при построении машиностроительных чертежей, так как позволяет точно передавать форму и размеры предметов на их проекциях.
Принципы построения изображений предметов на чертежах
По изображению предмета, полученному на одной плоскости проекций, даже если оно построено по методу ортогонального проецирования, нельзя полностью представить формы всех его поверхностей. Так, по фронтальной проекции предмета, показанного на рис. 1, можно судить только о двух его измерениях – высоте и длине. Остаются невыявленными ширина предмета, форма отверстия и паза. Очевидным является вывод: чтобы получить полную информацию о форме всех частей предмета, необходимо построить его изображения со всех сторон. Поэтому при составлении технических чертежей предмет проецируют не на одну, а на несколько взаимно перпендикулярных плоскостей проекций.
По ГОСТ 2.305 – 2008 [1] основные изображения предмета получают на гранях пустотелого куба, внутри которого помещен предмет (рис. 2). Грани выступают в качестве основных плоскостей проекций. Построение ортогональной проекции на каждой грани производится так, как показано на рис. 1, т. е. наблюдатель располагается таким образом, чтобы предмет находился между ним и соответствующей гранью куба. На рис. 3 указаны направления взгляда наблюдателя при таком проецировании. Проецирование в направление 2 на рис. 3 приведет к построению изображения па грани 2 и т. д. Разрезая куб по ребрам, развертывают все его грани до совмещения с фронтальной плоскостью проекций. Получают чертеж предмета, включающий шесть изображений (см. под разд. 3.1).
При ортогональном проецировании необходимо соблюдать следующие правила:
- предмет ориентируют внутри куба так, чтобы большинство его граней и ребер были расположены параллельно граням куба (в этом случае грани и ребра предмета проецируются без искажений их формы и размеров);
- изображение на фронтальной плоскости проекций (см. рис. 2, грань 1) принимают за главное. Предмет размещают так, чтобы изображение на этой плоскости давало наиболее полное представление о его форме. Длинные предметы принято располагать горизонтально.
Изображения в зависимости от содержания делят на виды, разрезы и сечения.
Виды
Вид – это изображение обращенной к наблюдателю видимой части поверхности предмета. Виды разделяют на основные, дополнительные и местные.
Основные виды
Проекции предмета, полученные на гранях куба (см. рис. 2), развернутых в одну плоскость, называются основными видами. На рис. 4 приведена схема расположения основных видов на чертеже и их наименование.
Наименование каждого вида определяется направлением взгляда наблюдателя при проецировании. За основу построения чертежа принимают вид спереди – главный вид предмета. Все шесть видов располагаются в проекционной связи относительно главного вида. Такое расположение видов утверждено ГОСТ 2.305 – 2008 [1] и является обязательным при выполнении чертежей. Нарушение проекционной связи в расположении видов допускается при действительной необходимости в этом. Видимые контуры предмета на чертеже принято изображать основной линией (сплошной толстой линией толщиной от 0,5 до 1,4 мм включительно), контуры невидимых поверхностей – штриховой линией. Оси симметрии изображений и центровые линии окружностей показывают штрихпунктирной линией. Штриховые и штрихпунктирные линии выполняют линией в 2 … 3 раза тоньше основной линии. Начертание линий дано в ГОСТ 2.303 – 68 [4].
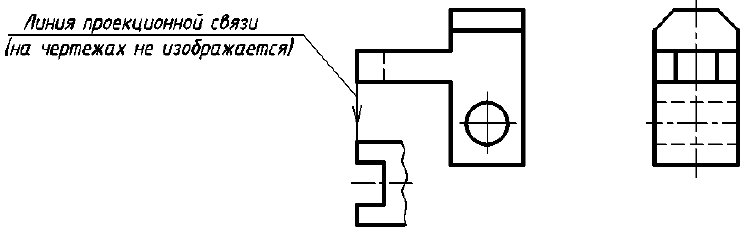
Контуры граней куба и линии проекционной связи на чертежах не изображают.
При выполнении чертежа любого технического изделия необходимо руководствоваться очень важным стандартным правилом: количество изображений па чертеже должно быть минимальным, но достаточным для полного представления о конструкции всех элементов предмета. Анализ основных видов на рис. 4 показывает, что вид справа несет такую же информацию о форме предмета, что и вид слева. То же можно сказать о видах снизу и сверху, сзади и спереди. Таким образом, для рассматриваемого предмета можно ограничиться тремя основными видами: спереди, сверху и слева (рис. 5).
Рис. 5. Оптимальное количество видов предмета, показанного на рис. 2
Рассмотрим обозначение основных видов. Если основные виды находятся в проекционной связи с главным видом (т. е. так, как показано на рис. 4 и рис. 5), то они не обозначаются.
На практике иногда приходится отдельные основные виды располагать на чертежах с нарушением их проекционной связи с главным видом. Как правило, это выполняют с целью уменьшения формата чертежа, что достигается рациональной компоновкой изображений. Рациональной считается такая компоновка, при которой изображения располагаются на поле чертежа равномерно, т. е. приблизительно с одинаковым расстоянием между ними и от изображений до внутренней рамки чертежа. Рассмотрим этот случай. Пусть предмет имеет форму, для пояснения которой на чертеже необходимо построить четыре основных вида. При стандартном расположении видов они заполнят поле чертежа нерационально (рис. 6). Если же вид справа разместить под видом слева, то изображения займут меньший формат и будут расположены на нем рационально (рис. 7).
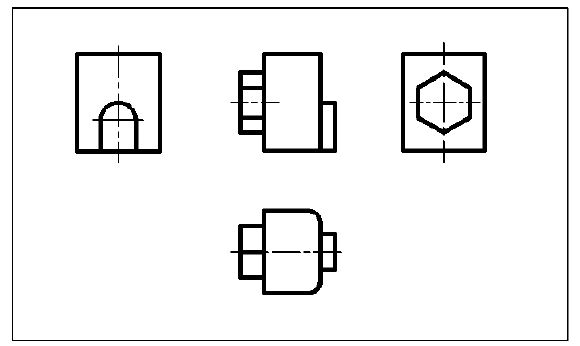
Рис. 7. Рациональная компоновка основных видов (вид справа находится не в проекционной связи с главным и должен быть обозначен)
Если какой-либо основной вид не находится в проекционной связи с главным, то он должен быть обозначен (см. вид справа на рис. 7):
- должно быть указано стрелкой около соответствующего вида (как правило главного) направление проецирования;
- над стрелкой и построенным по указанному стрелкой направлению видом должна быть нанесена одна и та же прописная буква русского алфавита.
Для обозначения основных, местных и дополнительных видов, а также разрезов и сечений, применяют прописные буквы русского алфавита, кроме букв Ё, 3, Й, О, Ч, X, Ь, Ы, Ъ, начиная с буквы А в порядке их расположения без пропусков и повторений.
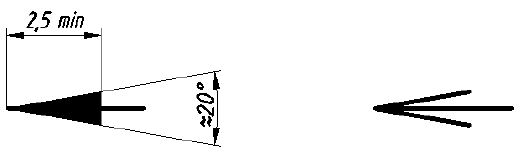
Стрелки, применяемые для указания направления взгляда, должны иметь форму и размеры, приведенные на рис. 8, а. На рис. 8, б, в даны другие варианты начертания стрелок.
Рис. 8. Размеры и допустимые варианты формы стрелок, указывающих направление взгляда
Местные виды
Если руководствоваться правилом о том, что на чертеже должно быть минимальное количество изображений (см. подразд. 3.1), то при анализе изображений, представленных на рис. 7, видно, что вид справа (вид Л) нужен исключительно для того, чтобы показать форму выступа, а остальная часть вида А -габаритный контур предмета – повторяет такой же контур на виде слева. Для того чтобы в подобных случаях исключить повторяющуюся информацию, применяют местные виды (рис. 9, а, б; вид Л).
Местным видом называется изображение отдельного ограниченного места поверхности предмета, параллельной плоскости проекций (грани куба). Местный вид может быть частью основного вида, а может быть видом на участок внутренней поверхности предмета.
Местный вид может быть ограничен линией обрыва (см. рис. 9, а), по возможности в наименьшем размере, или не ограничен (см. рис. 9, б). 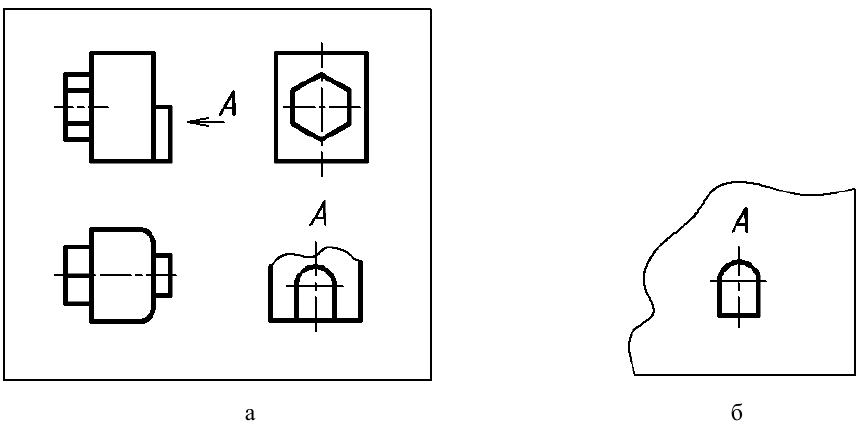
а – ограниченного линией обрыва; б – не ограниченного линией обрыва
Обозначение местных видов
Если местный вид не находится в проекционной связи с соответствующим изображением предмета, то он должен быть обозначен. Пример обозначения см. на рис. 9, а. Здесь местный вид А – это часть основного вида справа, который не находится в проекционной связи с главным.
Если местный вид находится в непосредственной проекционной связи с соответствующим изображением, то он не обозначается (рис. 10).
Дополнительные виды
В разд. 2 было указано, что при ортогональном проецировании предмет ориентируют внутри куба так, чтобы большинство его плоских поверхностей были параллельны граням куба. Только при таком расположении на гранях куба будут получены проекции, которые передадут действительную без искажений форму и размеры указанных плоских поверхностей предмета.
Если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, непараллельных основным плоскостям проекций (рис. 11).
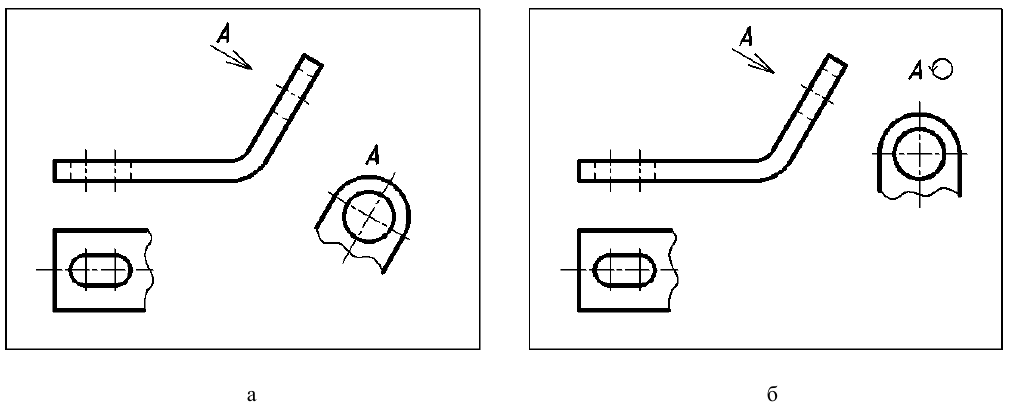
а – дополнительный вид не повернут; б – дополнительный вид повернут
Обозначение дополнительных видов
При обозначении всех видов, в том числе и дополнительных, действует одно правило: если вид не находится в проекционной связи с соответствующим изображением предмета, то он должен быть обозначен (см. рис. 11, а), если же вид находится в непосредственной проекционной связи с соответствующим изображением, то он не обозначается (рис. 12).
Дополнительный вид допускается поворачивать, но с сохранением, как правило, положения, принятого для данного предмета на главном изображении (см. рис. 11, б); при этом обозначение вида должно быть дополнено условным графическим обозначением 
Рис. 12. Пример дополнительного вида, который находится в проекционной связи с основным изображением и не обозначается
Разрезы
Основным назначением видов является определение формы внешних поверхностей предмета. Выявление на видах формы внутренних поверхностей при помощи штриховых линий не принято, так как это может привести к неправильному пониманию конструкции предмета. Поэтому для определения внутреннего строения применяют разрезы и сечения.
Разрез – это изображение предмета, мысленно рассеченного одной и более секущими плоскостями. Отсеченную часть предмета, расположенную между наблюдателем и секущей плоскостью, мысленно удаляют, в результате чего становятся видимыми контуры внутренних, ранее закрытых поверхностей. В разрезе показывают то, что лежит в секущей плоскости, и то, что расположено за ней. Невидимые контуры, которые в разрезе стали видимыми, изображают сплошной толстой линией, а фигуру, полученную в результате пересечения предмета плоскостью, заштриховывают. Штриховку выполняют по ГОСТ 2.306 – 68 [6]. Мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений. На чертеже может быть представлено несколько разрезов предмета.
Секущие плоскости должны проходить по плоскостям симметрии предмета, по осям отверстий и пересекать полости, как правило, по их центру.
Разрезы могут быть расположены:
- на месте основных видов;
- на свободном поле чертежа.
Построение разреза показано на рис. 13. Предмет рассечен секущей плоскостью, параллельной фронтальной плоскости проекций (см. рис. 13, б). На ортогональных проекциях (см. рис. 13, а) отсеченная часть предмета мысленно удалена, а оставшаяся часть изображена на месте вида спереди.
Допускается показывать невидимые поверхности на видах штриховыми линиями только тогда, когда контуры этих поверхностей являются простыми фигурами и не затемняют виды.
Допускается изображать нс все, что расположено за секущей плоскостью, если этого не требуется для понимания конструкции предмета.
Рис. 13. Образование фронтального разреза: а – ортогональные проекции; б – аксонометрическая проекция предмета
Простые разрезы
В зависимости от количества секущих плоскостей разрезы разделяются на простые и сложные. Простые разрезы получают при применении одной секущей плоскости, они легко читаются, поэтому им следует отдавать предпочтение.
В зависимости от положения секущей плоскости простой разрез может быть:
- горизонтальным – секущая плоскость параллельна горизонтальной плоскости проекций (см. рис. 14, разрез А-А).
- вертикальным – секущая плоскость перпендикулярна к горизонтальной плоскости проекций (например разрезы на рис. 13, 15);
- наклони ы м – секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого (рис. 16, разрез А-А)- Допускается наклонный разрез поворачивать до ближайшего горизонтального или вертикального положения (рис. 17).
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций (см. рис. 13), и профильным, если секущая плоскость параллельна профильной плоскости проекций (см. рис. 15).
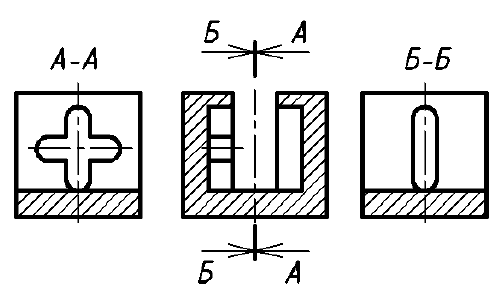
Если секущая плоскость направлена вдоль длины или высоты предмета, то разрез называется продольным (рис. 18, разрез А-А). Если секущая плоскость перпендикулярна длине или высоте предмета, то разрез называют поперечным (см. рис. 18, разрез Б-Б).
Разрезы, образованные одной секущей плоскостью, но со встречным направлением взгляда наблюдателя, выполняются так, как показано на рис. 19.
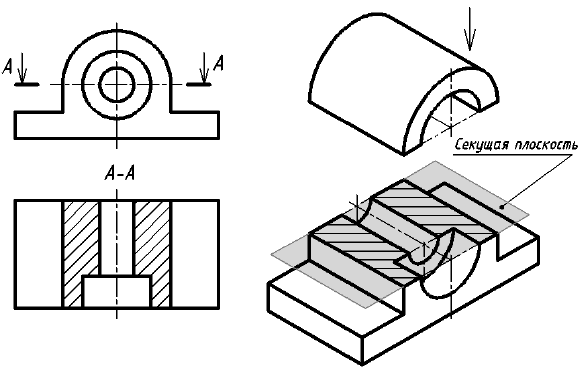
Рис. 15. Образование профильного разреза
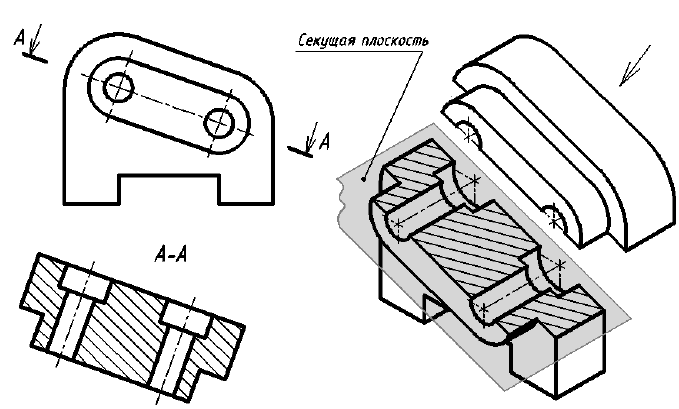
Рис. 17. Повернутый наклонный разрез 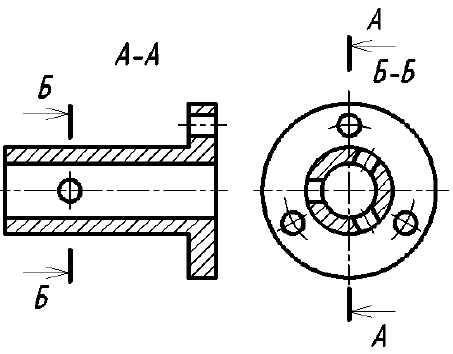
Местные разрезы
Местные разрезы представляет собой часть простого разреза (рис. 20), который располагается на виде и ограничивается сплошной волнистой линией. Местный разрез применяется для выявления внутренней формы предмета в отдельном ограниченном месте. С помощью местных разрезов показывают форму невидимых отверстий, пазов, канавок и других элементов в том случае, если они занимают по отношению к виду его малую часть и делать полный разрез нерационально. Волнистая линия, ограничивающая местный разрез, не должна совпадать с другими линиями изображения.
Обозначить разрез – это значит:
- показать положение секущей плоскости;
- сопроводить надписью сам разрез.
Положение секущей плоскости указывается на чертеже разомкнутой линией, причем начальный и конечный штрихи не должны пересекать контур соответствующего изображения. К начальному и конечному штрихам проводятся стрелки, указывающие направление взгляда наблюдателя. Стрелки должны располагаться на расстоянии 2 … 3 мм от наружных по отношению к «разрезаемому» изображению концов штрихов. Со стороны внешнего угла около стрелок ставится одна и та же прописная буква русского алфавита. Построенный при сечении указанной плоскостью предмета разрез должен быть отмечен надписью с применением той же буквы по типу А-А (всегда двумя буквами через тире). Пример обозначения разреза приведен на рис. 13.
Однако, как видно из рис. 13 … 20, одни разрезы на чертежах обозначены, другие не обозначены. Необходимо четко уяснить, когда разрезы обозначаются, а когда нет.
Простой разрез не обозначается, если секущая плоскость совпадает с плоскостью симметрии предмета в целом, а соответствующие изображения располагаются в непосредственной проекционной связи и не разделены какими-либо другими изображениями. Примеры таких разрезов приведены на рис. 13, 15.
Во всех остальных случаях простые горизонтальные, фронтальные и профильные разрезы должны быть обозначены.
Наклонные разрезы обозначаются всегда.
Местные разрезы не обозначаются.
Примечание. Не допускается при обозначении разреза применять ту же букву, которая была употреблена для обозначения других изображений на чертеже. По ГОСТ 2.305 — 2008 [1] для ограничения местных разрезов и в качестве линий обрыва изображений может применяться сплошная тонкая линия с изломами, начертание которой см. в ГОСТ 2.303 – 68 [4].
Структура обозначения положения секущей плоскости на чертеже показана на рис. 21. 
Стрелки, применяемые для указания направления взгляда, должны иметь такую же форму и размеры, как и стрелки для обозначения видов (см. рис. 8). Обратите внимание, что направление стрелок при обозначении положения секущей плоскости, должно соответствовать направлению взгляда при построении того вида, в границах которого полностью или частично будет располагаться разрез.
Совмещение разрезов с видами
Изображений на чертеже должно быть минимальное количество. Для уменьшения количества изображений применяется совмещение разрезов с видами. В большинстве случаев разрез совмещается с тем видом, который располагается по направлению взгляда наблюдателя на плоскости проекций, параллельно которой ориентирована секущая плоскость. Фронтальный разрез размещают на месте вида спереди или сзади (см. рис. 13), горизонтальный – на месте вида сверху или снизу (см. рис. 14), профильный – на месте вида слева или справа (см. рис. 15).
Возможны три варианта совмещения:
- в границах вида располагают полный разрез, т. е. выполняют полное совмещение разреза с соответствующим видом, как на рис. 13, 15, 18. Такое совмещение делают тогда, когда разрез представляет собой несимметричную фигуру, а на виде нет видимых контуров конструктивных элементов, форму которых нужно раскрыть;
- в границах вида располагают часть вида и часть соответствующего разреза, разделяя их сплошной волнистой линией (рис. 22). Такое совмещение выполняют тогда, когда разрез или вид представляют собой несимметричные фигуры и на виде имеются видимые контуры конструктивных элементов, форму которых нужно раскрыть (на рис. 22, для того, чтобы форма паза на передней стенке предмета была понятна, необходимо оставить видимой часть вида спереди с этим пазом). Как правило, при подобном совмещении простые разрезы не обозначают;
- в границах вида располагают половину вида и половину соответствующего разреза, разделяя их штрихпунктирной линией, являющейся осью симметрии вида и разреза (рис. 23). Таким образом, этот вариант совмещения можно применить, только если полный вид и полный разрез в отдельности представляют собой симметричные фигуры. Тогда по половине симметричного изображения легко понять полную форму. Вид принято располагать слева от оси симметрии, а разрез справа или вид располагать сверху, а разрез снизу. Обозначение разрезов в этом случае производится по правилу, изложенному в подразд. 4.3.
Примечания:
- Если совмещаются часть вида и часть соответствующего разреза или половина вида и половина разреза, то на части вида штриховые линии не проводят.
- Если при совмещении на одном изображении симметричных частей вида и разреза, какая-либо линия (например ребро) совпадает с осью симметрии, то эта линия (ребро) должна быть показана, и тогда вид от разреза отделяется сплошной волнистой линией, которая проводится левее (рис. 24, а) или правее (рис. 24, б) оси симметрии.
На рис. 13 … 16, 20 были приведены примеры с одним разрезом предметов. Для предметов сложной формы приходится выполнять несколько разрезов (рис. 18, 25 … 27), причем отдельные разрезы приходится иногда располагать вне видов на свободном поле чертежа.
Рис. 22. Совмещение несимметричных вида и разреза
Рис. 23. Совмещение симметричных вида и разреза (половины вида и половины разреза): а – разрез не обозначается; б – разрез обозначается
Рис. 24. Совмещение симметричных вида и разреза, когда ребро совпадает с осыо симметрии: а – ребро показано на разрезе; б – ребро показано на виде
Рис. 25. Выполнение разрезов на видах спереди, сверху и слева (совмещены половины видов и половины разрезов)
Рис. 26. Возможный вариант совмещения половины вида и половины разреза на изображении сверху на рис. 25
Сложные разрезы
Выявление формы внутренних полостей предметов, имеющих сложное внутреннее устройство, при помощи простых разрезов приводит к необходимости выполнять их большое количество, что затрудняет чтение чертежа. В таких случаях применяют сложные разрезы. Сложные разрезы всегда обозначают.
Сложным разрезом называют разрез, который получают при помощи двух и более секущих плоскостей. Сложные разрезы разделяются на ступенчатые и ломаные.
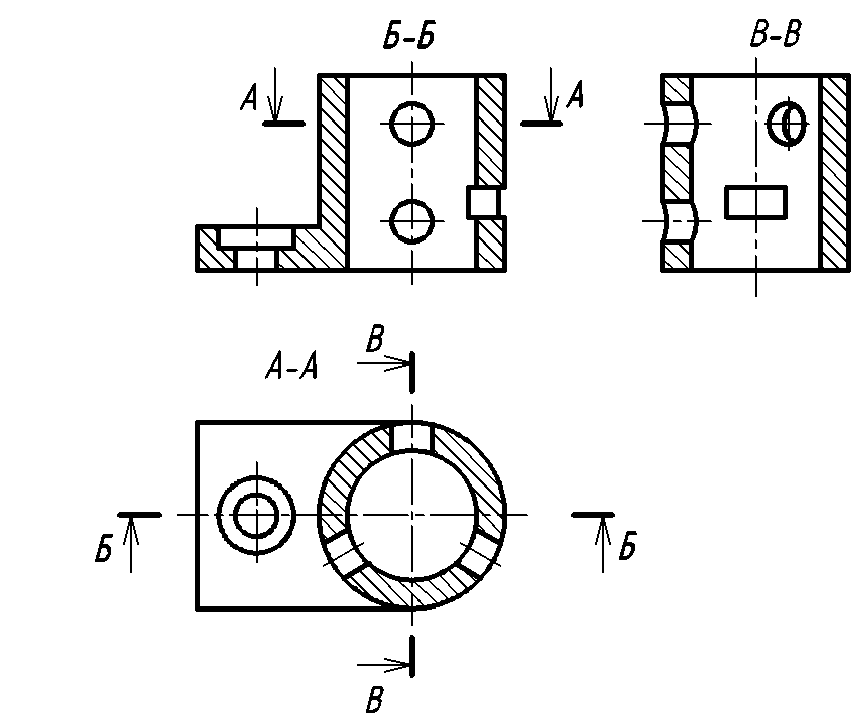
Ступенчатый разрез – это разрез, образованный несколькими параллельными секущими плоскостями (рис. 28).
При построении разреза секущие плоскости совмещают в одну, и ступенчатый разрез приобретает форму простого. Ступенчатые разрезы, так же как и простые, могут быть горизонтальными, фронтальными, профильными и наклонными (рис. 28 … 31).
Положение каждой секущей плоскости обозначают штрихами разомкнутой линии, места перехода от одной плоскости к другой (ступеньку) выполняют такими же штрихами. У начального и конечного штрихов указывают стрелкой направление взгляда наблюдателя и ставят одну и ту же букву. То есть, несмотря па то, что секущих плоскостей несколько, буквенные обозначения их одинаковы.
На ступенчатом разрезе линия перехода от одной плоскости к другой (ступенька) не изображается. На чертеже может быть несколько ступенчатых разрезов.
Примечание. Правая плоскость (см. рис. 28) может пересекать как нижнее, так и верхнее квадратное отверстие.
Рис. 28. Образование фронтального ступенчатого разреза.
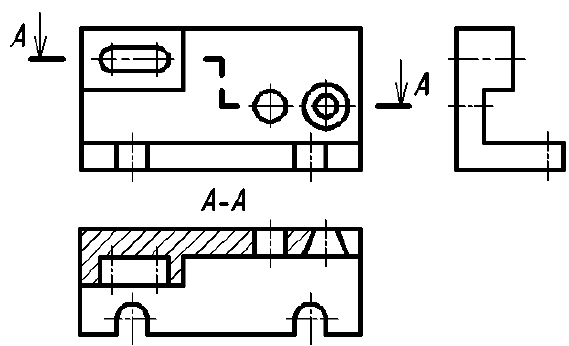
Рис. 30. Профильный ступенчатый разрез
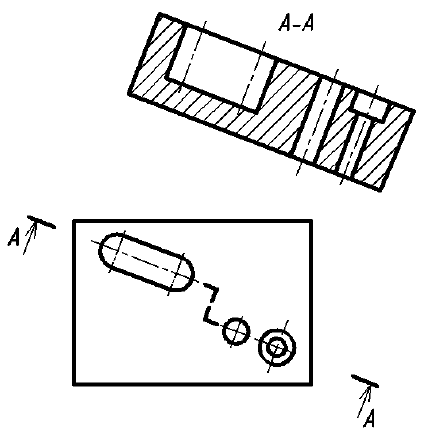
Для симметричных предметов рекомендуется рассекать их плоскостями так, чтобы полный ступенчатый разрез стал симметричной фигурой, что позволит соединить половину вида и половину разреза (рис. 32).
Не следует стремиться выявлять все внутреннее строение предмета одним сложным разрезом. Для образования ступенчатого разреза рекомендуется применять не более трех секущих плоскостей.
Рис. 32. Совмещение половины ступенчатого разреза с половиной вида спереди
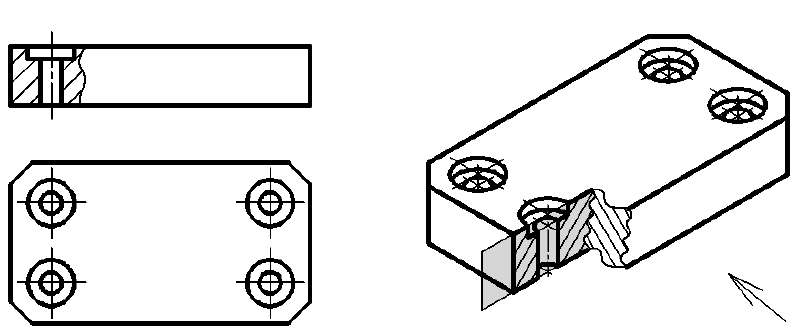
Ломаный разрез – это разрез, образованный двумя пересекающимися секущими плоскостями (рис. 33). Первая секущая плоскость выбирается параллельной, а вторая наклонной по отношению к основной плоскости проекций. При выполнении ломаного разреза наклонную секущую плоскость условно поворачивают до совмещения с первой секущей плоскостью, и из этого положения осуществляется проецирование получившейся фигуры сечения на параллельную ей плоскость проекций. При повороте наклонной секущей плоскости элементы предмета, видимые за ней, поворачивать не нужно, а следует строить их изображение в прямой проекционной связи с той плоскостью проекций, на которую производится проецирование. Подобным образом построен на верху цилиндрического выступа предмета (см. рис. 33) прямоугольный паз, который не связан с наклонной секущей плоскостью. Исключением из этого правила является вариант, когда видимые элементы конструктивно связаны с рассекаемым элементом. В подобном случае эти видимые за секущей плоскостью элементы поворачиваются вместе с рассекаемым элементом (рис. 34).
Ломаные разрезы в зависимости от того, на какой плоскости проекций (на каком виде) они будут располагаться, делятся на фронтальные, горизонтальные и профильные.
Положение каждой секущей плоскости обозначают штрихами разомкнутой линии. В месте пересечения секущих плоскостей также ставятся такие штрихи. У начального и конечного штрихов указывают стрелкой направление взгляда наблюдателя и ставят одну и ту же букву. Обратите внимание, что буква у наклонного штриха независимо от наклона плоскости изображается прямо.
Примечание. На рис. 33 наклонная секущая плоскость может пересекать как нижнее, так и верхнее отверстия. Построение ломаного разреза и в том, и в другом случае будет одинаковым.
Рис. 33. Образование фронтального ломаного разреза
Рис. 34. Проецирование элементов, конструктивно связанных с наклонной секущей плоскостью
Сечения
Сечением называется изображение, которое получается при мысленном рассечении предмета плоскостью. В отличие от разреза на сечении показывают только то, что расположено непосредственно в секущей плоскости. На рис. 35 показано отличие сечения от разреза.
Сечения применяются для выявления формы отдельных элементов предмета в тех случаях, когда на разрезе определяемые контуры нужного элемента затемняются изображениями других элементов второго плана. 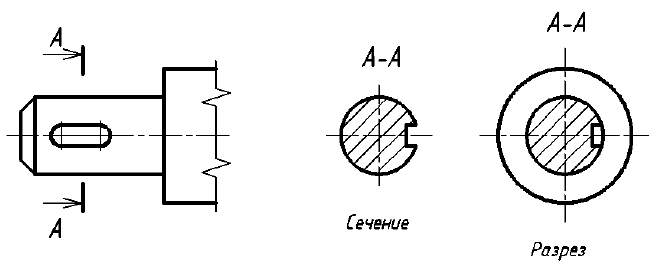
При выполнении сечений следует руководствоваться следующим правилом: фигура сечения должна представлять собой замкнутый контур. Не допускается сечение в виде разомкнутых частей. Так, если для пояснения формы паза на рис. 35 целесообразнее выполнить сечение, то для пояснения сквозного овального отверстия на рис. 36 следует выполнять разрез.
Рис. 36. Иллюстрация правильного и неправильного выявления формы отверстия на изображениях А-А
Однако существует исключение из приведенного выше правила: если секущая плоскость проходит по оси вращения круглого отверстия, то в сечении показывают полный контур этого отверстия, т. е. показывают и линии заднего плана, относящиеся к данному отверстию (рис. 37).
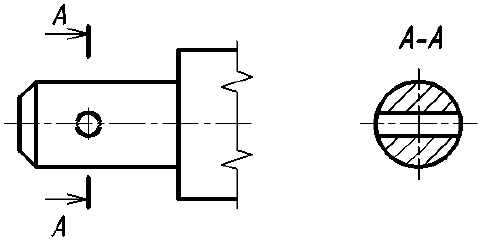
Сечения разделяют на входящие в состав разреза и не входящие в состав разреза (см. рис. 35, где видно, что сечение полностью входит в состав разреза).
Классификация сечений дана на рис. 38, 39. Сечения, не входящие в состав разреза, по месту своего расположения разделяются на вынесенные и наложенные. Контур вынесенного сечения обводится сплошной толстой линией, контур наложенного – сплошной тонкой. И вынесенные, и наложенные сечения могут быть симметричными и несимметричными.
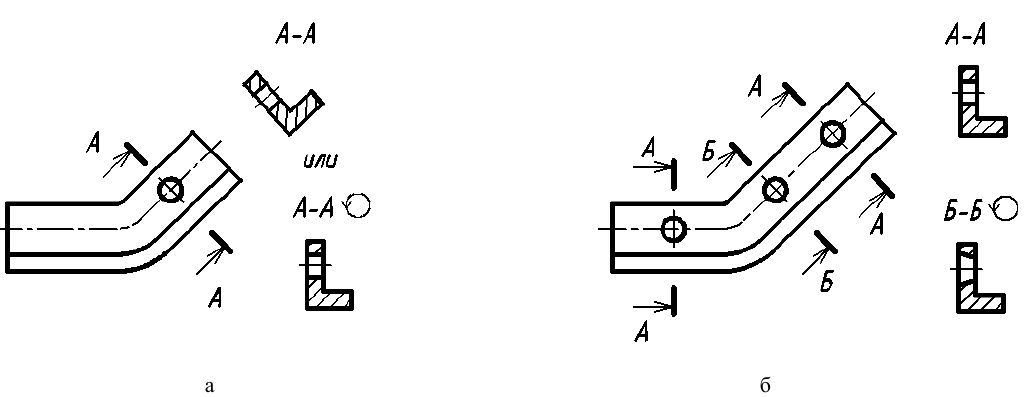
Вынесенным называется сечение, которое размещено вне основных изображений предмета. Вынесенное сечение может располагаться:
- на свободном поле чертежа в любом удобном месте. Такое сечение должно быть обозначено (см. рис. 38, а, б);
- в разрыве вида. При этом, если сечение симметрично, то оно не обозначается (см. рис. 38, в); если несимметрично, то оно должно быть обозначено указанием положения секущей плоскости и направления взгляда наблюдателя без буквенных обозначений (см. рис. 38, г);
- на продолжении следа секущей плоскости. Так могут быть выполнены только симметричные сечения, и они не обозначаются (см. рис. 38, д).
Наложенным называется сечение, которое располагается па виде предмета. Если наложенное сечение имеет симметричную форму, то в качестве линии секущей плоскости выступает ось симметрии сечения (см. рис. 39, а). Если наложенное сечение несимметрично, то оно должно быть обозначено указанием положения секущей плоскости и направления взгляда наблюдателя без буквенных обозначений (см. рис. 39, б).
Рис. 38. Вынесенные сечения

Сечение наклонного участка предмета по построению и расположению должно соответствовать направлению, указанному стрелками; допускается такое сечение поворачивать с добавлением условного графического обозначения 
Выносные элементы
Выносной элемент – это дополнительное отдельное изображение какой-либо части предмета (рис. 41), которое выполняется с целью уточнения ее формы и размеров. Как правило, выносной элемент вычерчивается в более крупном масштабе (см. рис. 41, а, б). Выносной элемент может отличаться от соответствующего исходного изображения и по содержанию, т. е. исходное изображение может быть видом, а выносной элемент разрезом (см. рис. 41, б). Рекомендуется выносной элемент вычерчивать на свободном поле чертежа как можно ближе к исходному изображению.
При выполнении выносного элемента необходимо тонкой сплошной линией обвести на исходном изображении геометрической фигурой (чаще окружностью или овалом) часть предмета, требующую пояснений. От этой фигуры проводят линию-выноску, на полке которой указывают буквенное обозначение выносного элемента. Эту же букву с указанием в скобках масштаба увеличения наносят над выносным элементом.
Рис. 41. Выносные элементы
Условности и упрощения на чертежах
Для уменьшения трудоемкости выполнения чертежей ГОСТ 2.305 – 2008 [1] предусматривает следующие условности и упрощения, которые могут быть применены при выполнении заданий проекционного черчения:
1. Если вид, разрез или сечение представляет симметричную фигуру, то допускается вычерчивать половину симметричного изображения (рис. 42, вид слева) или немного более половины с проведением в последнем случае линии обрыва (рис. 42, вид сверху).
Рис. 42. Выполнение части симметричного изображения
2. Допускается упрощенно изображать линии пересечения поверхностей вращения, если не требуется их точного построения. Например, вместо геометрически точно построенных кривых можно проводить дуги окружностей или прямые (рис. 43, а, б). Однако если пересекаются поверхности вращения, описанные около условной сферы, линиями пересечения которых являются прямые, то эти прямые необходимо показывать (рис. 44).
Рис. 43. Упрощенное изображение линий пересечения поверхностей вращения
Рис. 44. Изображение линий пересечения поверхностей вращения с одинаковым диаметром
3. Плавный переход одной поверхности в другую показывают условно тонкой линией (рис. 45, а) или вообще не показывают (рис. 45, б).

4. Плоские участки поверхности допускается выделять диагоналями, проводимыми тонкими линиями (рис. 46). Как правило, такое выделение выполняют, если плоские поверхности находятся на цилиндрических поверхностях или соседствуют с ними.
Рис. 46. Пример выделения плоских участков поверхностей диагональными линиями
5. Если секущая плоскость рассекает тонкую стенку параллельно большей грани, то ее условно показывают нерассеченной, отделяя от остальной части предмета основной линией (рис. 47, фронтальный разрез), и не штрихуют. В поперечных разрезах тонкие стенки изображают рассеченными и заштриховывают по общим правилам (рис. 47, разрез А-А). Если в тонкой стенке имеются отверстия, то их следует показывать местными разрезами (см. рис. 47, местный разрез на левом ребре жесткости).
Примечание. Тонкими стенками в техническом черчении называют конструктивные элементы (как правило ребра жесткости), у которых одна грань явно больше других.
Рис. 47. Изображение тонких стенок на разрезах
6. Если предмет имеет несколько одинаковых равномерно расположенных элементов, то на изображении этого предмета полностью показывают один такой элемент, а положение остальных задают условно, например центровыми линиями. На рис. 48 продублирован вид сверху предмета, изображенного на рис. 47, но уже с условным обозначением отверстий.
Рис. 48. Условное изображение одинаковых отверстий
7. Допускается на разрезах не показывать элементы, видимые за секущей плоскостью, если форма этих элементов уже выявлена. Особенно это касается элементов, которые видны на заднем плане под углом и проецируются с искажением формы. Так, на рис. 49 три одинаковых ребра жесткости. Однозначно определена форма правого ребра, поэтому в левой части разреза ребро на заднем плане не показано.
Рис. 49. Пример разреза, на котором левое ребро не изображается
Нанесение размеров
Предметы обладают формой и величиной. Форму предмета на чертеже передают изображения. Величину предмета определяют размеры. ГОСТ 2.307 – 68 [8] устанавливает правила нанесения размеров. Ниже приведены правила, знание которых необходимо при выполнении заданий проекционного черчения.
Размеры на чертеже наносятся один раз без повторения.
Различают размеры линейные (рис. 50, а) и угловые (рис. 50, б). Линейные размеры указывают в миллиметрах, а угловые – в градусах.
Размеры наносят при помощи размерных чисел, размерных и выносных линий (см. рис. 50, а). Размерные числа должны отражать действительные размеры изображаемого предмета независимо от того, в каком масштабе выполнены изображения.
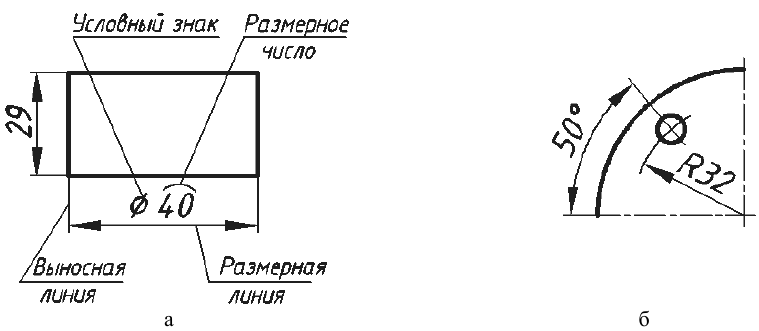
Рекомендуемое начертание размеров на чертежах показано на рис. 51.
Размерная линия – это линия, которая с двух сторон ограничена размерными стрелками. Опа в два – три раза тоньше основной линии на чертеже. Первая размерная линия должна отстоять от линии видимого контура изображения минимум па 10 мм, расстояние между параллельными размерными линиями минимум 7 мм. Не допускается использовать в качестве размерных линий линии контура, выносные, осевые и центровые. Необходимо избегать пересечения размерных линий между собой и с другими линиями чертежа.
Размерное число (рекомендуемый размер шрифта 5 мм) проставляют над размерной линией с зазором 1 … 1,5 мм. Размерное число наносят приблизительно на середине размерной линии. На параллельных размерных линиях размерные числа проставляют в шахматном порядке со сдвигом на 1 … 3 цифры относительно друг друга. Размерные числа не допускается пересекать или разделять любыми линиями чертежа.
Выносные линии (они выполняются в два – три раза тоньше основной линии), начинаются в опорных точках изображений и должны выходить за концы стрелок размерных линий на 1 … 5 мм.
Размерные стрелки должны иметь форму и размеры, показанные на рис. 52. Рекомендуемая длина стрелок – 5 или 7 мм. При компьютерном исполнении чертежа допускается в стрелках применять угол 30°.
Рис. 51. Начертание размеров
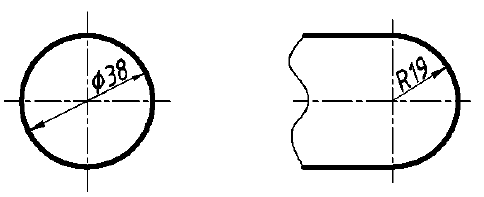
При нанесении размера окружности перед размерным числом размещают знак диаметра, перед размером дуги – знак радиуса (рис. 53).
При нехватке места размерные стрелки и размерные числа наносят на продолжении размерных линий (рис. 54).
Рис. 54. Варианты нанесения размерных чисел и стрелок размерных линий Размеры узких последовательно расположенных участков наносят так, как показано на рис. 55.
Рис. 55. Варианты нанесения размеров в узких местах
При выполнении чертежа всегда приходится задаваться вопросом, на каком изображении предпочтительнее нанести тот или иной размер. ГОСТ 2.307 – 68 [8] дает следующие рекомендации:
1. Размеры, определяющие форму элемента предмета, наносят на том изображении, на котором эта форма видна и понятна (рис. 56, а). В данном случае только на виде сверху видно, что отверстие имеет прямоугольную форму и именно здесь, а не на разрезе необходимо нанести размеры формы отверстия (размеры 15 и 9). Исключением из общего правила являются круглые отверстия, размеры диаметров которых наносят предпочтительно на их разрезах и сечениях (рис. 56, б; размер 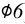
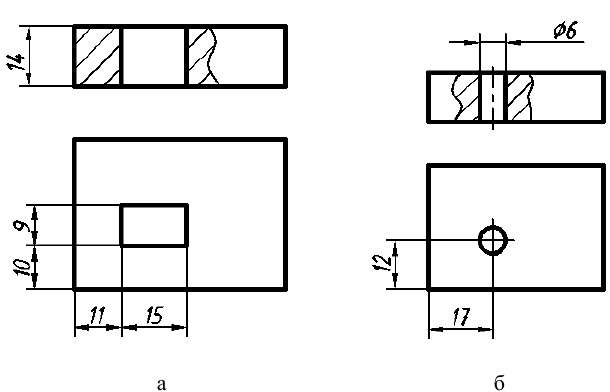
2. Размеры положения элемента относительно других поверхностей предмета наносят на виде, т. е. на том изображении, где можно произвести два измерения (см. рис. 56, а; размеры 10 и 11 и рис. 56, б; размеры 12, 17). Помните, что положение круглого отверстия или выступа задаются координатами только его центра.
3. Размеры наружных и внутренних элементов по возможности следует располагать по разные стороны изображения (рис. 57). Не следует наносить размер расстояния между наружной и внутренней поверхностями (см., например, зачеркнутый размер 7 на рис. 57).
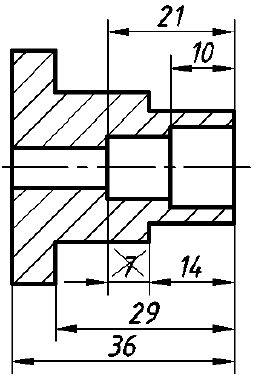
4. Размеры одинаковых круглых отверстий как простой, так и сложной формы наносят один раз с указанием их количества (рис. 58, а). Для отверстий допускается только следующая структура записи: 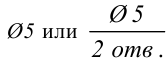
Рис. 58. Пример нанесения размеров одинаковых круглых отверстий: а – простой формы; б – сложной формы
5. Размеры симметрично расположенных элементов наносят так, как нанесен размер 24 на рис. 59, а. Если же имеется только половина симметричного изображения, то все равно должен быть указан его полный размер. В этом случае размерную линию проводят с обрывом, и обрыв размерной линии делают несколько дальше оси симметрии (см. рис. 59, б; размеры 24 и 34).
Рис. 59. Пример нанесения размеров симметрично расположенных элементов
Аксонометрические проекции предметов
На технических чертежах изделие изображается в виде ортогональных проекций (видов, разрезов, сечений). Недостатком ортогональных проекций является то, что они не дают непосредственного представления о форме изображенного предмета. Так, каждый основной вид представляет собой точное отображение только одной грани. Чтобы представить по этим видам полную форму предмета, необходимо иметь соответствующие навыки.
Для наглядного объемного представления о предмете применяют аксонометрические проекции по ГОСТ 2.317 – 69 [9], которые позволяют одним изображением передать общую форму предмета.
Аксонометрическая проекция – это проекция предмета на одну плоскость, относительно которой ни одна грань предмета в форме параллелепипеда не расположена параллельно или перпендикулярно. При таком проецировании видны три грани предмета (искаженные), и изображение получается наглядным. В общем случае для предметов любой формы, в том числе и круглых, для построения аксонометрического изображения предмет проецируют на некоторую плоскость вместе с осями прямоугольных координат X, Y и Z, к которым предмет отнесен в пространстве. Направление взгляда при этом не должно совпадать с направлениями координатных осей.
Аксонометрическое изображение дает общее наглядное представление о форме предмета, но не передает точно действительную форму и размеры поверхностей.
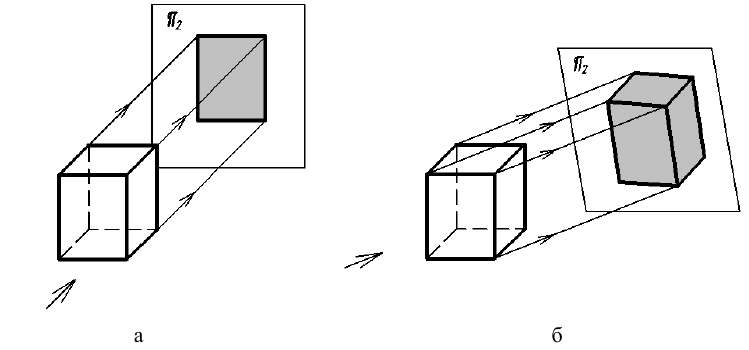
Если направление проецирования перпендикулярно к плоскости проекций, то на этой плоскости получают прямоугольную аксонометрическую проекцию (рис. 60, а), если не перпендикулярно -то косоугольную (рис. 60, б).
Для использования в учебной практике рекомендуются два вида аксонометрических проекций – прямоугольная изометрическая и косоугольная фронтальная диметрическая.
Прямоугольная изометрическая проекция
Прямоугольной изометрической проекцией (прямоугольной изометрией) называется аксонометрическая проекция, у которой углы между аксонометрическими осями равны 120°, а коэффициенты искажения по всем трем осям равны единице (рис. 61).
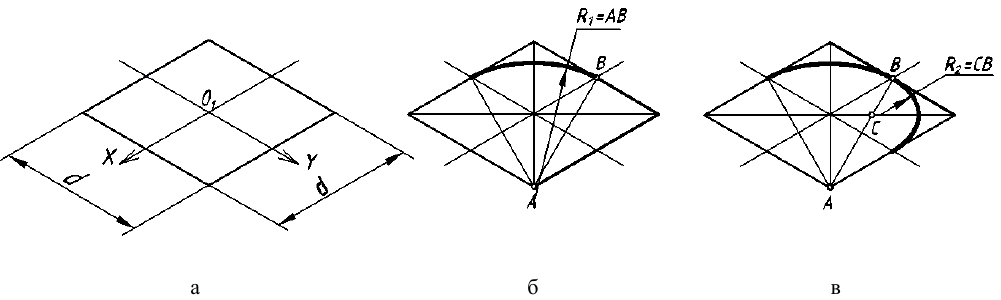
Прямоугольные грани, проецируются в виде параллелограммов, а окружности, лежащие на этих гранях проецируются в виде эллипсов. На рис. 62 показано изображение куба и окружностей на его гранях в прямоугольной изометрии. Построение эллипсов заменяется в учебном курсе более простым построением овалов, которое приведено на рис. 63. Эллипсы в каждой грани строятся одинаково.
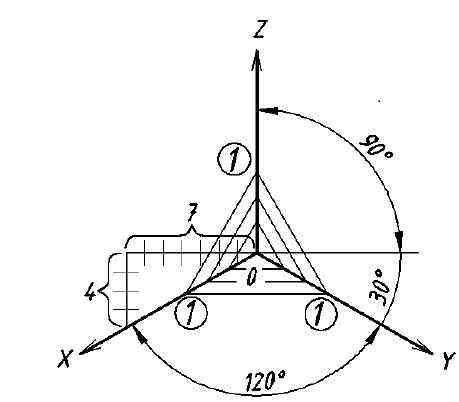
Рис. 62. Изображение куба и окружностей на его гранях в прямоугольной изометрии
Построение эллипсов. Построим эллипс на верхней грани куба.
- Этап 1 (рис. 63, а). Наметим на грани центр эллипса – точку
Проведем через нее изометрические оси X и Y (они параллельны сторонам верхней грани). Отложим в обе стороны от точки
на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.
- Этап 2 (рис. 63, б). Из вершины ромба в точке А проведем отрезок АВ и, взяв его в качестве радиуса Rt, построим верхнюю дугу. Аналогично построим нижнюю дугу (на рисунке она не показана).
- Этап 3 (рис. 63, в). На пересечении отрезка АВ с горизонтальной осью ромба определим точку С, из которой проведем правую дугу радиусом R2, равным отрезку СВ. Так же построим левую дугу, которая на рисунке не показана.
Косоугольная фронтальная диметрическая проекция
Косоугольной фронтальной диметрической проекцией (фронтальной диметрией) называется аксонометрическая проекция, у которой углы между аксонометрическими осями располагаются так, как показано па рис. 64. Коэффициенты искажения по осям Хи Z равны единице, а по оси Y- 0,5.
Особенностью этого вида аксонометрии является то, что грань, параллельная координатной плоскости X0Z, и находящаяся на ней окружность проецируются без искажений (рис. 65). Две другие видимые грани и окружности на них проецируются с искажениями: грани в виде равновеликих параллелограммов, а окружности в виде равновеликих эллипсов, причем большие оси этих эллипсов равны l,06d, а малые – 0,35d (d – диаметр исходной окружности). Построение упрощенных эллипсов как овалов показано на рис. 66.
Рис. 64. Расположение аксонометрических осей в косоугольной фронтальной диметрии
Рис. 65. Изображение куба и окружностей на его гранях Построение эллипсов. Построим эллипс, например, на верхней грани куба в плоскости X0Y (см. рис. 66).
Подобным образом на грани Z0Y построим эллипс с центром в точке 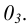
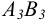
В плоскости X0Z построим окружность без искажения ее формы и размера с центром в точке
Рис. 66. Построение эллипсов во фронтальной диметрии
Разрезы в аксонометрических проекциях
В аксонометрических проекциях предметов для показа внутренней конфигурации, как правило, выполняют разрезы двумя и более взаимно перпендикулярными секущими плоскостями, параллельными координатным плоскостям X0Z, Y0Z или X0Y. Эти разрезы образуют вырез, на котором видно внутреннее строение предмета. Если предмет имеет две плоскости симметрии (вид сверху симметричен относительно двух осей), то обычно выполняют так называемый «четвертной вырез», при котором секущие плоскости совпадают с плоскостями симметрии (рис. 67). В предметах с одной плоскостью симметрии или несимметричных секущие плоскости должны проходить по осям отверстий и центрам полостей любой формы (рис. 68). Разрезы на ортогональных изображениях чертежа могут не совпадать с разрезами в аксонометрических проекциях. Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, построенных в соответствующих координатных плоскостях (см. рис. 61, 64). Штриховка пересекающихся сечений должна быть встречной. Ниже приведены примеры аксонометрических изображений предметов с «вырезами» (рис. 67, 68).
Рис. 67. Прямоугольная изометрическая проекция с «четвертным вырезом» 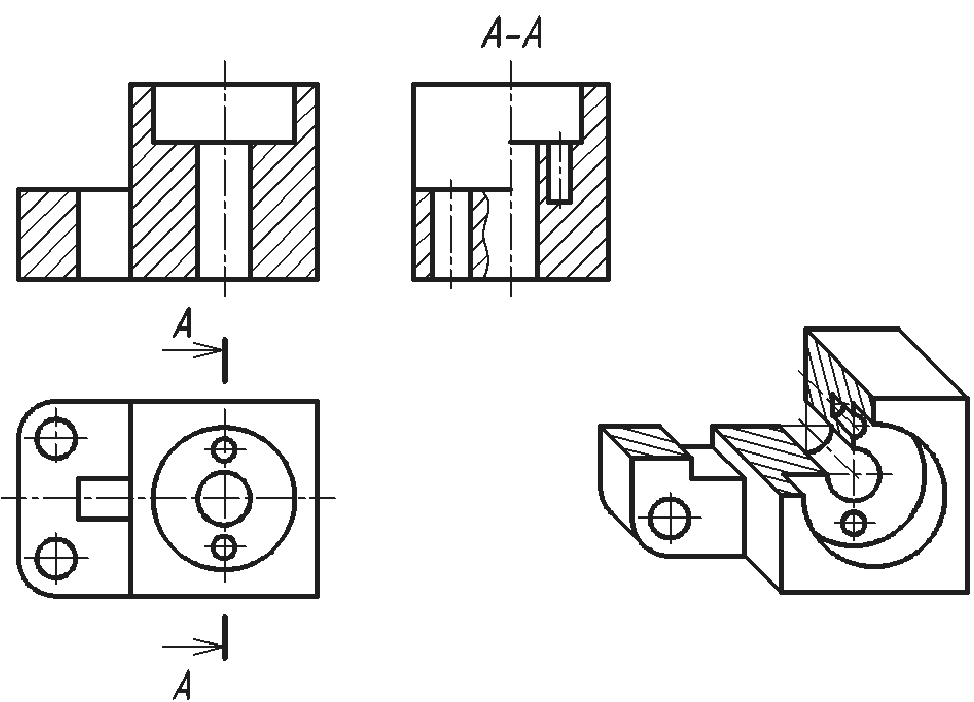
Выбор вида аксонометрии
Для изображения одного и того же предмета могут быть выбраны различные виды аксонометрии из разрешенных к применению ГОСТ 2.317 – 69 [9].
Как показала учебная практика, наиболее наглядной и понятной для студентов является прямоугольная изометрическая проекция, в которой предмет изображается в таком же положении, в каком он расположен на чертеже на виде спереди (см. рис. 67).
С точки зрения уменьшения трудоемкости чертежа рекомендуется:
- прямоугольную изометрию применять тогда, когда круглые отверстия и выступы располагаются на соседних гранях предмета, как на рис. 67;
- фронтальную диметрию применять тогда, когда подобные элементы находятся только на одной или на двух противоположных параллельных гранях предмета, как на рис. 68. Предмет в аксонометрии располагать так, чтобы грань с наибольшим количеством окружностей и дуг была параллельна плоскости проекций X0Z, при этом окружности и кривые изображаются без искажений.
Построение действительной формы сечения
В учебной практике широко распространены задачи на построение действительной величины сечения, образованного наклонной секущей плоскостью. Такие задачи хорошо развивают пространственное воображение.
Как правило, заданная секущая плоскость является проецирующей. Наиболее удобным способом построения действительной формы сечения является способ замены плоскостей проекций, который подробно изучается в курсе начертательной геометрии.
На рис. 69 показано построение действительной формы сечения предмета наклонной плоскостью А-А.
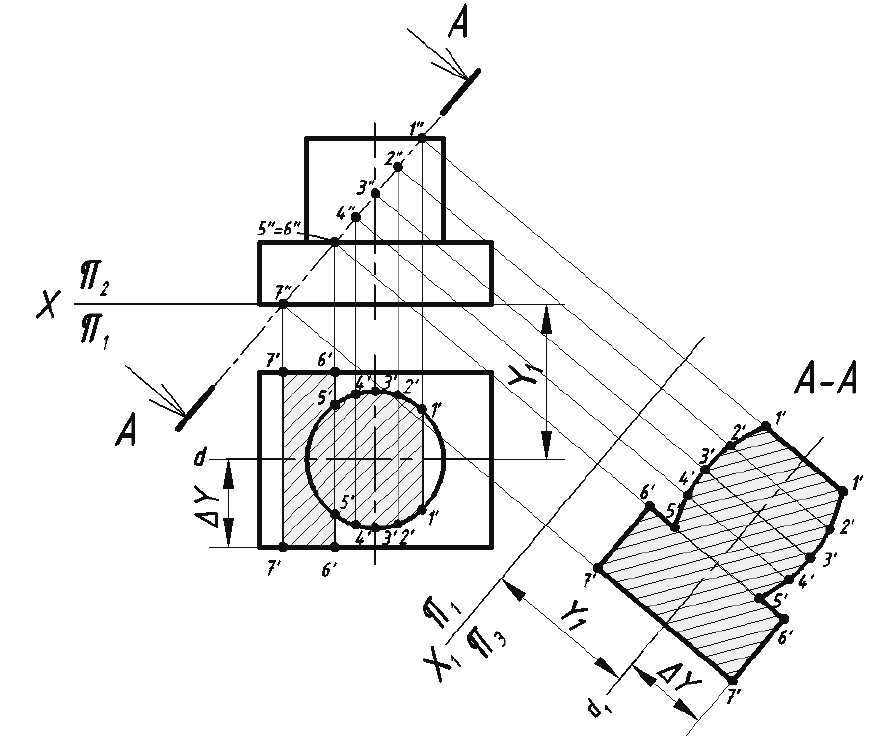
Показанный на рис. 69 предмет состоит из двух простых тел: параллелепипеда в основании и расположенного на нем цилиндра. Секущая плоскость А-А расположена под углом к оси вращения цилиндра и пересекает его боковую поверхность по эллипсу, а верхнее и нижнее основание – по прямым. Призматическое основание данная секущая плоскость пересекает по прямоугольнику. Горизонтальная проекция фигуры сечения, расположенная на виде сверху, представляет собой совмещение части эллипса с прямоугольником. Это искаженная проекция, так как при взгляде сверху фигура сечения видна под углом. Для построения действительной формы сечения по направлению взгляда, указанному стрелками секущей плоскости А-А, рекомендуется:
Примечание. Построенное таким образом сечение можно при необходимости переместить в другое место и даже повернуть. Пример повернутого сечения см. на рис. 38, а, б.
Задачи проекционного черчения с решением
Задача 1.
По заданным двум основным видам (рис. П.1.1) построить третий вид предмета, выполнить необходимые разрезы и построить аксонометрическую проекцию (на формате АЗ).
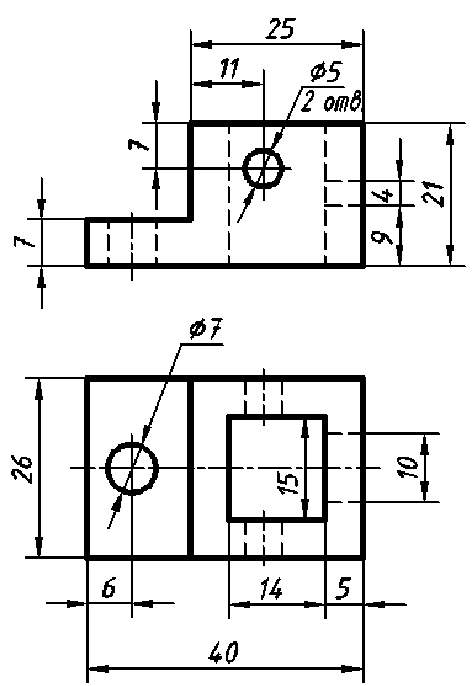
Рекомендуемая последовательность решения:
- Подготовить формат АЗ с упрощенной основной надписью.
- Перечертить заданные изображения предмета.
- Построить третье изображение – вид слева (рис. П.1.2). Для чего можно применить вспомогательную ось р или дуги окружностей с центром в точке 0.
- Построить необходимые разрезы. Для того чтобы невидимые поверхности, показанные штриховыми линиями, стали видимыми, применим три разреза (см. разд. 4):
- простой фронтальный разрез по плоскости симметрии предмета, который полностью совместим с видом спереди, так как и вид, и разрез представляют собой несимметричные фигуры. Этот разрез не обозначается (см. подразд. 4.3);
- сложный ступенчатый горизонтальный разрез А-А, который расположим на месте вида сверху, причем в силу их симметрии совместим половину вида с половиной разреза;
- простой профильный разрез Б-Б. Его расположим на месте вида слева и опять же в силу симметричности вида и разреза совместим их половины.
Построенные разрезы (рис. П.1.3) полностью выявят и сделают понятным внутреннее строение данного предмета.
Рис. П.1.2. Пример построения вида слева
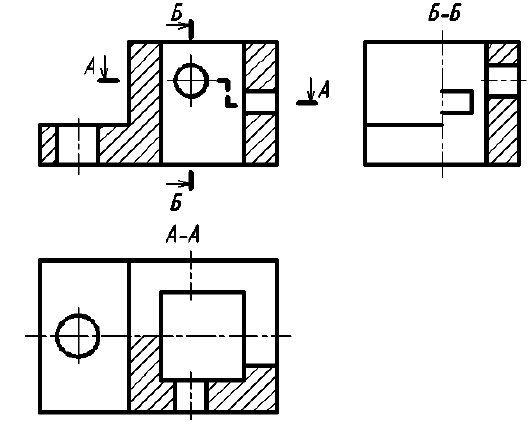
5. Построить аксонометрическую проекцию. Согласно рекомендациям по выбору вида аксонометрической проекции (см. подразд. 10.4) для данного предмета, у которого отверстия располагаются на всех гранях, целесообразнее построить прямоугольную изометрическую проекцию.
Этапы выполнения отражены на рис. П.1.4:
- построить аксонометрические оси X, У, Z. Воспользовавшись размерами, приведенными в задании (см. рис. П.1.1), выполнить изображение пластины, лежащей в основании предмета (рис. П. 1.4, а);
- построить изометрическую проекцию параллелепипеда, который расположен на пластине, и прямоугольное отверстие в нем (рис. П.1.4, б);
- по заданным размерам наметить центры круглых отверстий и выполнить их изометрические изображения – эллипсы (рис. П.1.4, в);
- определить секущие плоскости, которые позволят показать на аксонометрическом изображении внутреннюю структуру предмета. Плоскости, образующие «вырез», изображены на рис. П. 1.4, г толстой линией;
- построить «вырез» в предмете указанными секущими плоскостями (рис. П.1.4, д). Достроить отверстия, которые частично станут видны в «вырезе»;
- произвести обводку нужных линий, выполнить штриховку и удалить лишние линии. Построенная изометрическая проекция предмета показана на рис. П.1.4, е.
Рис. П.1.4. Этапы построения изометрической проекции
6. Нанести размеры, заполнить основную надпись. Полностью оформленный чертеж предмета представлен на рис. П.1.5. В обозначении чертежа ГУИР. 111814.009 первая цифра 1 обозначает номер темы, вторая цифра 1 – номер факультета, число 18 – номер кафедры, число 14 – номер рабочего места студента и число 009 – номер задания.
Рис. П.1.5. Пример выполнения проекционной задачи 1
Задача 2.
По заданным двум основным видам построить третий вид предмета, выполнить необходимые разрезы и построить действительную форму вынесенного сечения (рис. П.1.6).
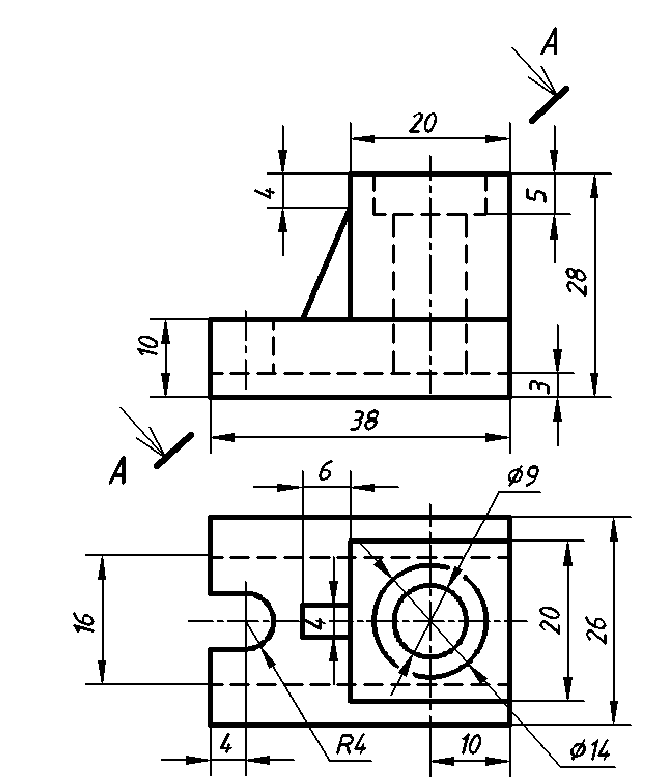
Рекомендуемая последовательность решения:
- Подготовить формат АЗ с упрощенной основной надписью.
- Перечертить заданные изображения предмета.
- Построить третье изображение – вид слева (рис. П. 1.7).
- Построить необходимые разрезы. Анализ конструкции предмета показывает, что для определения формы внутренних отверстий и паза достаточно выполнить простой фронтальный разрез по плоскости симметрии предмета. Разрез полностью совместим с видом спереди. Обратите внимание на то, как изображается в продольном разрезе ребро жесткости (см. разд. 8 рис. 46).
- Построить действительную форму сечения предмета плоскостью А-А. Методика построения рассмотрена в подразд. 10.5.
- Если это необходимо, то произвести корректировку компоновки изображений. При нехватке места следует иметь в виду, что допускается поворачивать сечение А-А до вертикального или горизонтального положения, а также выполнять половину любого, кроме главного, симметричного изображения (см. разд. 8, рис. 41).
- Произвести обводку нужных линий и удалить лишние.
- Выполнить штриховку сечения.
- Нанести размеры, заполнить основную надпись.
Полностью оформленный чертеж предмета представлен на рис. П.1.7. Обозначение чертежа производится по той же схеме, что и в задаче 1.
Рис. П.1.7. Пример выполнения проекционной задачи 2
Выдержки из стандартов по оформлению чертежей
ГОСТ 2.301 – 68. Форматы
Чертежи выполняют на листах бумаги определенного размера (формата).
Подготовленный для работы формат листа имеет вид, показанный на рис. П.2.1, и включает:
- внешнюю рамку, выполненную сплошной тонкой линией;
- внутреннюю рамку, которая проводится сплошной толстой линией на расстоянии 5 мм от правой, нижней и верхней стороны внешней рамки и на расстоянии 20 мм слева (это поле для подшивки чертежа);
- основную надпись (угловой штамп).
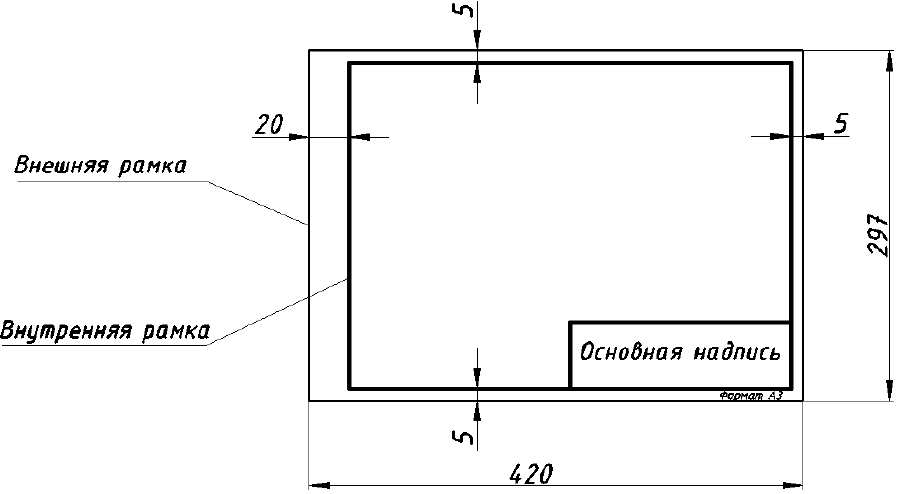
Формат листа определяется размерами сторон внешней рамки (см. на рис. П.2.1 размеры 420 и 297).
Форматы подразделяются на основные и дополнительные. Размеры и обозначения основных форматов приведены в табл. П.2.1.
Таблица П.2.1
Размеры основных форматов
Основную надпись чертежа выполняют по ГОСТ 2.104 – 2006 [7] и помещают в правом нижнем углу формата. На формате А4 ее располагают только вдоль короткой стороны листа, а на других форматах основная надпись может располагаться как вдоль короткой, так и вдоль длинной стороны листа.
ГОСТ 2.302 – 68. Масштабы
Масштабом называется отношение линейных размеров изображения предмета на чертеже к его действительным размерам.
Предметы следует изображать на чертеже предпочтительно в натуральную величину, так как такое изображение дает представление о действительных размерах и соотношениях сторон. Однако это не всегда возможно, и большие предметы изображают уменьшенными, а маленькие – увеличенными, что позволяет выполнять на стандартных форматах чертежи предметов практически любой величины.
Масштабы изображений на чертежах должны выбираться из следующих рядов: натуральная величина -1:1;
- масштабы уменьшения -1:2 1:2,5 1:4 1:5 1:10 1:15 и др;
- масштабы увеличения -2:1 2,5:1 4:1 5:1 10:1 20:1 и др.
Масштаб чертежа указывается в основной надписи в специально предназначенной для этого графе по типу 1:1 (рис. П.2.2). Если отдельное изображение на чертеже выполнено в масштабе, отличающемся от указанного в основной надписи, то этот масштаб записывают в скобках вслед за буквенным обозначением данного изображения. Подобным образом обозначен масштаб выносного элемента А на рис. П.2.2 (см. обозначение А(4:1)).
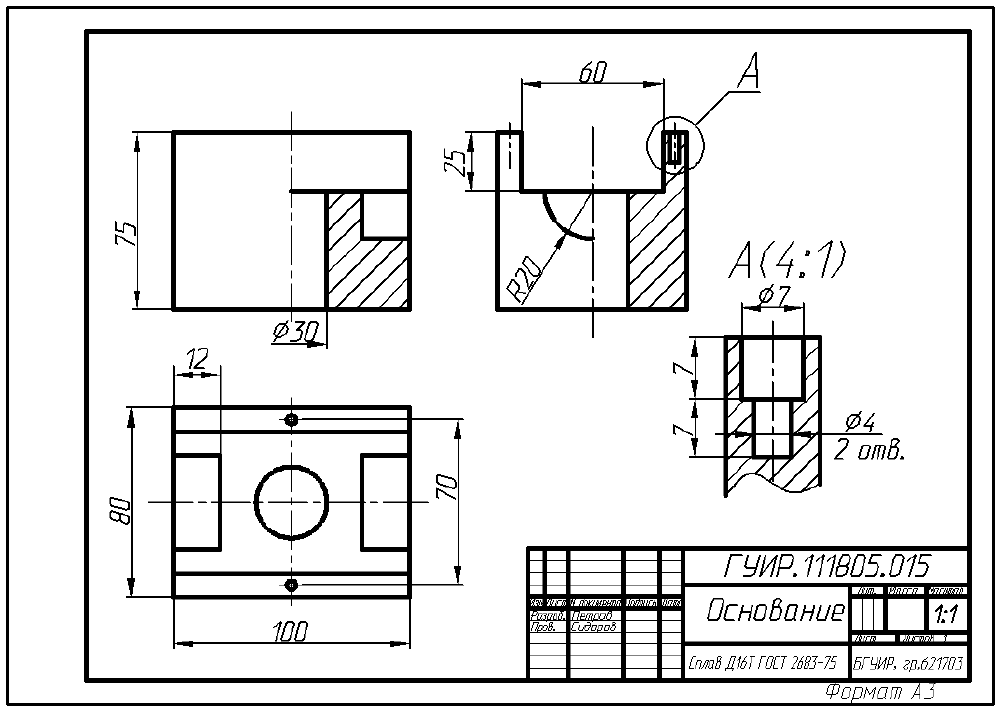
ГОСТ 2.303 – 68. Линии
Изображения на чертежах для большей их выразительности и наглядности выполняются линиями разного начертания и толщины. Установлены девять типов линий, которые представлены в табл. П.2.2. За исходную принята сплошная толстая основная линия. Ее толщина s должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения. Толщины остальных линий указываются отношением их к толщине основной.
Таблица П.2.2
Типы линий
При выполнении изображений на чертеже указанными линиями необходимо выполнять следующие требования:
- толщина линий каждого типа должна быть одинаковой для всех изображений на данном чертеже;
- штриховые и штрихпунктирные линии должны начинаться и заканчиваться штрихами;
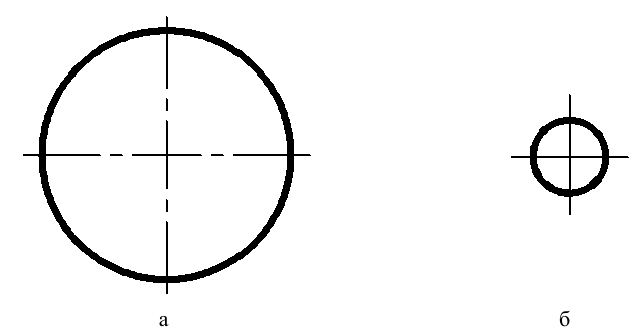
- в центре окружностей должны пересекаться штрихи центровых штрихпунктирных линий (рис. П.2.3, а);
- если диаметр окружности в изображении (т. е. при вычерчивании ее на чертеже независимо от действительного размера) получился меньше 12 мм, то центровые штрихпунктирные линии следует заменять сплошными тонкими (рис. П.2.3, б).
ГОСТ 2.304 – 81. Шрифты чертежные
Текстовую часть чертежей составляют надписи, числа и специальные знаки. Надписи должны быть выполнены стандартными чертежными шрифтами русского, латинского греческого алфавитов, а числа – арабскими и римскими цифрами. Шрифт каждого алфавита включает прописные (заглавные) и строчные (последующие) буквы.
Размер шрифта определяется высотой (h) прописных букв в миллиметрах. Установлены следующие его размеры: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.
В зависимости от толщины линий обводки букв (d) различают два типа шрифта:
- тип А с толщиной линии d = l/14h;
- тип Б с толщиной линий d = l/10h.
Оба типа шрифта выполняют с наклоном 75° или без наклона (прямой шрифт).
Для построения букв, цифр и знаков применяется вспомогательная сетка, шаг линий которой равен толщине линий шрифта (d). На рис. П.2.4 показано вписывание в такую сетку букв шрифта типа А с наклоном. Следует иметь в виду, что надписи на чертежах необходимо выполнять с применением первой прописной буквы и последующих строчных, т. е. так, как написано слово «Корпус» на рис. П.2.4. Высота строчных букв (с) берется на размер меньше, чем прописных, например, если в слове прописная буква выполняется высотой 7 мм, то строчные буквы должны быть высотой 5 мм. На чертежах, выполняемых карандашом, размер шрифта должен быть не менее 3,5 мм.
Кроме указанных выше параметров h, с, d, шрифты характеризуются еще шириной букв (g) и расстоянием между буквами (а).
В заданиях по курсу «Начертательная геометрия и инженерная графика» рекомендуется применять шрифт типа А с наклоном, который представлен на рис. П.2.5.
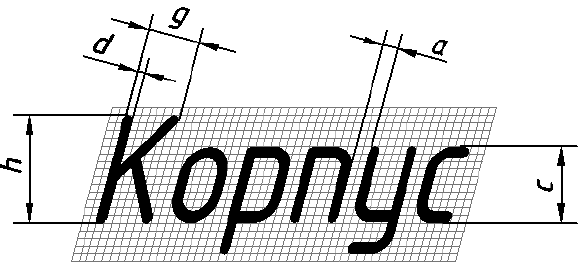
Рис. П.2.5. Начертание букв и цифр русского алфавита шрифта типа А с наклоном
ГОСТ 2.104 – 2006. Основные надписи
ГОСТ 2.104 – 2006 устанавливает формы, размеры и порядок заполнения основных надписей, установленных для применения в технических чертежах.
Для учебных чертежей, выполняемых по проекционному черчению, можно использовать два вида основных надписей:
- стандартную по указанному выше ГОСТу (рис. П.2.6). Ее применение предпочтительно;
- упрощенную учебную (рис. П.2.7). Ее рекомендуется применять по разрешению преподавателя на насыщенном изображениями чертеже по теме «Проекционное» черчение», когда стандартная основная надпись не помещается, (см. рис. П.1.5 и рис. П.1.7).

Рис. П.2.7. Форма и размеры упрощенной основной надписи
ГОСТ 2.306 – 68. Обозначения графические материалов и правила их нанесения на чертежах
Стандарт устанавливает правила штриховки материалов в сечениях. В курсе проекционного черчения, как правило, рассматриваются предметы (детали), которые сделаны из металлов и пластмасс.
Металлы заштриховываются параллельными прямыми тонкими сплошными линиями, проводимыми под углом 45° к горизонту (рис. П.2.8, а). Шаг штриховки (расстояние между линиями штриховки) принимается в пределах от I до 10 мм. В учебных чертежах рекомендуется шаг штриховки 2 … 5 мм в зависимости от площади штриховки. Наклон штриховки может быть влево или вправо.
Пластмассы штрихуются «в клеточку», т. е. перекрестными параллельными прямыми линиями с наклоном 45° (рис. П.2.8, б).
При выполнении любого чертежа необходимо придерживаться следующего правила: на всех изображениях чертежа, выполненных в одном масштабе, один и тот же предмет в сечениях должен быть заштрихован одинаково, т. е. с одинаковым шагом и одним наклоном линий штриховки. Имеются в виду все сечения, как входящие в состав разрезов, так и сечения выносные и наложенные.
Если линии штриховки совпадают по направлению с линиями контура или осевыми линиями, то вместо угла 45° следует брать угол 30° или 60° (см. рис. П.2.8, в). 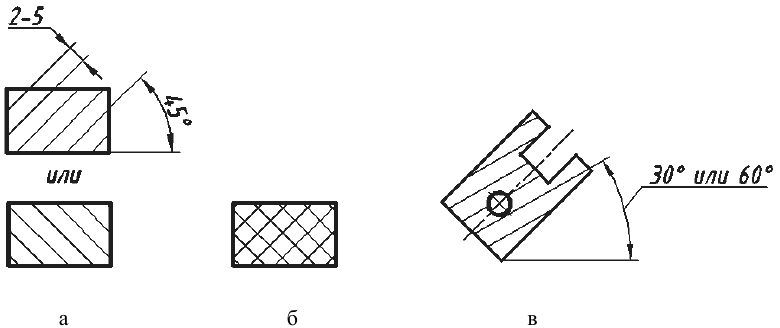
Изображения на технических чертежах
В основе правил построения изображений лежит метод проецирования, подробно рассмотренный в курсе начертательной геометрии. В машиностроении, как правило, применяются параллельные проекции, которые
можно разделить на прямоугольные (ортогональные) и аксонометрические.
Прямоугольные проекции наиболее распространены в машиностроении. В прямоугольных проекциях выполняются все производственные чертежи. Такие чертежи достаточно просты в исполнении, и по ним можно представить себе форму предмета и найти размеры всех его элементов. Однако прямоугольные проекции имеют существенный недостаток – отсутствие наглядности. Для того чтобы по этим проекциям представить истинную форму предмета, необходимо обладать достаточно развитым пространственным мышлением. Этот недостаток ортогональных проекций восполняют аксонометрические проекции, которые более сложны в исполнении, однако обладают наглядностью и выразительностью. Поэтому такие проекции широко применяются для наглядного изображения деталей, узлов, агрегатов машин и конструкций приборов на чертеже, особенно на начальных этапах конструирования. Аксонометрические проекции применяются как самостоятельно, так и в комплексе с ортогональными проекциями.
При выполнении проекционных чертежей полезно помнить, что какую бы сложную форму ни имели реальные изделия (рис. 1), их всегда можно представить как совокупность плоскостей и поверхностей вращения (цилиндрической, конической, сферической, торовой и винтовой). Таким образом, мысленно разбивая деталь на простейшие геометрические объекты и выполняя их проекционные изображения, можно получить прямоугольную или аксонометрическую проекцию изделия целиком.
Прямоугольное проецирование на несколько плоскостей проекций
В общем случае чертеж любого предмета должен содержать графические изображения видимых и невидимых его поверхностей. Согласно ГОСТ 2.305 – 68 ** изображения предметов необходимо выполнять по методу прямоугольного проецирования. При этом предмет предполагается расположенным между наблюдателем и соответствующей плоскостью проекций. Такой метод прямоугольного проецирования называется методом первого угла (или методом Е). За основные плоскости проекций принимают шесть граней куба (рис. 2, а), которые совмещают с плоскостью чертежа, как показано на рис. 2, б.
Изображение на фронтальной плоскости проекций принимают на чертеже в качестве главного. Предмет относительно фронтальной плоскости проекций следует располагать так, чтобы изображение на ней (главное изображение) давало наиболее полное представление о форме и размерах предмета. Изображения на чертеже в зависимости от их содержания согласно стандарту разделяются на виды, разрезы, сечения и выносные элементы.
Виды
Видом называется изображение обращенной к наблюдателю видимой части поверхности предмета. Все видимые элементы предмета выполняются сплошными толстыми (основными) линиями. Допускается на видах показывать невидимые части поверхности предмета штриховыми линиями для уменьшения количества изображений в тех случаях, когда невидимые очертания предмета являются несложными. Различают основные, дополнительные и местные виды.
Основными называются виды, получаемые проецированием на основные плоскости проекций. К основным видам (рис. 2, б) относятся:
1 – вид спереди (или главный вид); 2 – вид сверху; 3 – вид слева; 4 – вид справа; 5 – вид снизу; 6 – вид сзади.
Показанное на рис. 2, б расположение видов называется расположением в проекционной связи. Если какой-либо вид расположен с нарушением проекционной связи (смещен относительно главного изображения; отделен от главного изображения другими изображениями; вид расположен не на одном листе с главным изображением), то для него указывают стрелкой направление проецирования, обозначаемое прописной буквой кириллицы, той же буквой обозначают построенный вид (рис. 3).
Дополнительными называют виды, получаемые на плоскостях, не параллельных основным плоскостям проекции. Дополнительные виды применяются в тех случаях, когда какая-либо часть предмета не может быть показана ни на одном из основных видов без искажения формы и размеров и также отмечают стрелкой и надписью (вид А на рис. 4). Допускается поворачивать дополнительный вид, при этом к надписи добавляют знак «повернуто» (вид Б на рис. 4). При необходимости указывают угол поворота после знака «повернуто». Если дополнительный вид расположен в непосредственной проекционной связи с изображением, стрелку и надпись над видом не наносят (рис. 5, 6).
Местным видом называется изображение ограниченной части поверхности предмета. Если местный вид вычерчивают вместе с частью поверхности предмета, на которой находится изображаемый участок, то он ограничивается сплошной волнистой линией (рис. 7).
Если изображаемый элемент вычерчивают только по его контуру, без дополнительного указания части поверхности предмета, лежащей за этим контуром, то волнистую линию не проводят (вид Б на рис. 7).
Местный вид указывают на чертеже так же, как и дополнительный вид. В случаях, когда местные виды располагаются в непосредственной проекционной связи с изображением, допускается их не обозначать. Для удобства чтения чертежа рекомендуется располагать местные виды вблизи исходного изображения.
Кроме рассмотренных выше видов, для изображения искривленных (рис. 8, а) или гнутых предметов (рис. 8, б), которые можно развернуть в одну плоскость без искажения, применяют развертки (или, как их еще называют, развернутые виды). При таком изображении гнутых предметов контуры выполняют сплошной линией, а места изгиба обозначают тонкой штрихпунктирной линией с двумя точками (рис. 8, б). Над изображением развертки помещают знак «развернуто».
На рис. 9 приведены размеры стрелок, указывающих направление взгляда и знаков «повернуто» и «развернуто».
Разрезы
Разрезом называется изображение, полученное мысленным рассечением предмета одной или несколькими плоскостями. На разрезе показывают то, что расположено непосредственно в секущей плоскости и за ней (рис. 10). Допускается изображать не все, что расположено за секущей плоскостью, если этого не требуется для понимания конструкции предмета (рис. 11). Разрез может быть расположен на месте одного из основных видов или на свободном поле чертежа.
При выполнении разреза в определенном месте предмета мысленно проводят секущую плоскость, отбрасывают часть предмета, расположенную между наблюдателем и секущей плоскостью, а затем оставшуюся часть проецируют на соответствующую плоскость проекций. После чего наносятся необходимые обозначения.
Разрез является условным изображением, поскольку проведение секущей плоскости и удаление части предмета, лежащей между наблюдателем и секущей плоскостью, производится мысленно.
Выполняя разрезы, следует помнить, что разрез – это искусственный прием, при котором мысленное рассечение предмета относится только к данному разрезу и не изменяет другие изображения того же предмета. Каждому разрезу соответствует своя собственная секущая плоскость (или плоскости), причем эти плоскости между собой не связаны и один разрез от другого не зависит.
В зависимости от расположения секущих плоскостей относительно плоскостей проекций различают горизонтальные, вертикальные и наклонные разрезы. Горизонтальный разрез (рис. 12) получается при рассечении предмета горизонтальной плоскостью, вертикальный – при рассечении плоскостью,
перпендикулярной горизонтальной плоскости проекций. При этом вертикальный разрез называют фронтальным (рис. 13), если секущая плоскость параллельна фронтальной плоскости проекции, и профильным (рис. 14), если
секущая плоскость параллельна профильной плоскости проекций.
На практике встречаются случаи, когда вертикальный разрез выполняется секущей плоскостью, непараллельной ни фронтальной, ни профильной плоскостям проекций (рис. 15).
Такой разрез строится и располагается в соответствии с направлением взгляда, указанным стрелками на линии, обозначающей след секущей плоскости. Допускается изображать такой вертикальный разрез с поворотом. В этом случае к его обозначению добавляют знак «повернуто». Наклонный разрез (рис. 16) получается при рассечении предмета плоскостью, наклоненной к горизонтальной плоскости проекций. Наклонный разрез допускается изображать с поворотом. В этом случае к его обозначению добавляют знак «повернуто».
В зависимости от направления секущих плоскостей разрезы разделяют на продольные и поперечные. Разрез называется продольным (рис. 17), если секущая плоскость направлена вдоль длины или высоты предмета. Разрез называется поперечным (рис. 18), если секущая плоскость направлена перпендикулярно длине или высоте предмета.
В зависимости от числа секущих плоскостей различают простые и сложные разрезы. Простыми называются разрезы, полученные при мысленном рассечении предмета одной плоскостью. Сложными называются разрезы, полученные при мысленном рассечении предмета двумя или несколькими плоскостями.
Сложный разрез называют ступенчатым, если секущие плоскости параллельны между собой (рис. 19, 20), и ломаным, если секущие плоскости пересекаются под углом, большим 90° (рис. 21, 22).
При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, до которой производится совмещение (рис. 23).
Допускается применение сложных комбинированных разрезов, представляющих собой сочетание ступенчатого и ломаного (рис. 24). При необходимости допускается применять развернутые разрезы (рис. 25). В этом случае в качестве секущей применяют цилиндрическую поверхность, развертываемую затем в плоскость. При выполнении такого разреза над изображениями помещают знак «развернуто».
В зависимости от полноты произведенного разреза они подразделяются на полные и местные. Местные разрезы применяют для выяснения устройства детали лишь в отдельном ограниченном месте (рис. 26). Его ограничивают на виде или волнистой линией (рис. 26, а, б), или линией с изломами (рис. 26, б), и эти линии не должны совпадать с какими-либо другими линиями изображения. Концы ломаной линии должны выступать за контур изображения на 2…4 мм.
Допускается соединять часть вида и часть соответствующего разреза, разделяя их линией с изломами (рис. 27) или волнистой линией (рис. 29). При этом, как правило, разрезы располагают справа от вертикальной или внизу от горизонтальной оси симметрии. На изображениях симметричных изделий (рис. 28) границей вида и разреза служит ось симметрии (штрихпунктирная линия). В случае если на оси симметрии имеется линия видимого или невидимого контура, то ее видимость нужно сохранить, перенеся линию обрыва левее или правее оси симметрии (рис. 29).
Отметим, что если разрез выполнен на месте главного вида, то его называют главным изображением, а не главным видом.
Обозначение разреза (рис. 30) содержит указание положения секущей плоскости линией сечения (штрихами разомкнутой линии), указание направления проецирования (стрелками на начальном и конечном штрихах) и обозначение секущей плоскости и разреза одной и той же прописной буквой кириллицы, начиная с А, без пропусков и повторений. При сложном разрезе штрихи разомкнутой линии, обозначающие положение секущих плоскостей, проводят также у мест пересечения секущих плоскостей между собой. Начальный и конечный штрихи разомкнутой линии не должны пересекать контур изображения. Буквы наносят около стрелок (при необходимости и в местах перегиба) с внешней стороны угла. Высота буквенных обозначений должна быть на один-два размера шрифта больше размерных чисел чертежа.
Расстояние между изображением детали и штрихом принимается по обстановке, желательно не менее 3 мм. При необходимости начальный и конечный штрихи могут быть расположены внутри контура.
В случаях, подобных показанному на рис. 31, стрелки, указывающие направление взгляда, наносят на одной линии. Не указывают положение секущей плоскости, направление проецирования и не наносят буквенные обозначения, если секущая плоскость совпадает с плоскостью симметрии предмета и параллельна одной из основных плоскостей проекций, а соответствующие изображения расположены на одном и том же листе в непосредственной проекционной связи и не разделены какими-либо другими изображениями (см. рис. 13, 14).
Допускается указывать положение секущей плоскости и направление проецирования без буквенных обозначений для разреза, находящегося в
непосредственной проекционной связи, обеспечивающей однозначное понимание чертежа, как показано на рис. 32. Правила штриховки разрезов рассмотрены в п. 1.6.
Сечения
Сечением называется изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. При необходимости можно применять в качестве секущей цилиндрическую поверхность, развертываемую затем в плоскость. В отличие от разреза, в сечении показывают только то, что получается непосредственно в секущей плоскости. На рис. 33 для сравнения показаны разрез А – А и сечение Б – Б.
Сечения, не входящие в состав разреза, по месту своего расположения разделяют на вынесенные и наложенные. Вынесенным называется сечение, расположенное вне контура основного изображения (рис. 34, а). Наложенным называется сечение, расположенное на проекции предмета (рис. 34, б). Применение вынесенных сечений предпочтительно.
Наложенные сечения вычерчивают сплошными тонкими линиями непосредственно на самом виде, причем контур изображения в месте расположения наложенного сечения не прерывают (рис. 35). Вынесенные сечения располагают на свободном поле чертежа и ограничивают сплошными основными линиями (рис. 36). Допускается изображать вынесенное сечение в разрыве изображения (рис. 37).
В зависимости от расположения секущей плоскости относительно оси детали сечения подразделяются на нормальные и наклонные. Нормальным называется сечение в том случае, если секущая плоскость перпендикулярна оси предмета (рис. 38), наклонным – если секущая плоскость наклонена к оси предмета (рис. 39).
В зависимости от количества секущих плоскостей различают простые и сложные сечения. Простые сечения получаются при рассечении предмета одной секущей плоскостью, сложные – при рассечении предмета двумя или несколькими плоскостями. Наиболее часто применяют простые сечения. Сложные сечения допускается применять тогда, когда рассекаемые элементы предмета не параллельны друг другу. В общем случае положение секущей плоскости и надпись над сечением на чертежах указывают так же, как и для разрезов (рис. 38, 39).
Если вынесенное сечение имеет симметричную форму и расположено вблизи изображения на продолжении следа секущей плоскости, то след секущей плоскости обозначается тонкой штрихпунктирной линией, буквами не обозначается, направление взгляда не указывается и сечение не подписывается. Для симметричных наложенных сечений и сечений, расположенных в разрыве изображения, след секущей плоскости не указывается и сечение не подписывается (рис. 40).
При этом секущую плоскость следует располагать таким образом, чтобы на изображении получалось нормальное поперечное сечение.
Для несимметричных сечений, расположенных в разрыве или наложенных, линию сечения проводят со стрелками, но буквами не обозначают (рис. 41).
Сечения по построению и расположению должны соответствовать направлению, указанному стрелками. Допускается располагать сечение повернутым. В этом случае его изображение сопровождают знаком «повернуто» (рис. 42, а). Знак «повернуто» не ставят, если секущие плоскости расположены под разными углами (рис. 42, б).
Если на чертеже имеется несколько одинаковых сечений, относящихся к одному и тому же изделию, то линию сечения обозначают одной буквой и вычерчивают одно сечение (рис. 43). Если расположение одинаковых сечений точно определено размерами или изображением, то допускается наносить одну линию сечения и вычерчивать одно сечение (рис. 44). Допускается указывать количество сечений в надписи сечения (рис. 45).
Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, то контур отверстия или углубления в сечении показывают полностью (рис. 46).
Если сечение получается состоящим из отдельных частей, то необходимо применить разрез (рис. 47). Правила штриховки сечений рассмотрены в п. 1.6.
Выносные элементы
При изображении детали на чертеже в мелком масштабе конструкция отдельных ее частей может быть неясна. Поэтому возникает необходимость в применении выносных элементов, которые позволяют исключить необходимость увеличения масштаба всего изображения для конкретизации отдельных конструктивных особенностей изделия.
Выносным элементом называется дополнительное отдельное изображение (обычно увеличенное) какой-либо части предмета, требующей графического или иного пояснения в отношении формы, размеров и других данных ввиду мелкого ее изображения.
Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и может отличаться от него по содержанию (например, изображение может быть видом, а выносной элемент – разрезом).
При применении выносного элемента соответствующее место отмечают на виде, разрезе или сечении замкнутой сплошной тонкой линией (окружностью или овалом) с обозначением прописной буквой кириллицы на полке линии-выноски. Над выносным элементом указывается та же буква и масштаб, в котором выполнен выносной элемент (рис. 48).
Выносной элемент следует располагать как можно ближе к соответствующему месту на изображении предмета.
Графическое обозначение материалов в разрезах и сечениях
Для изготовления изделий в технике применяется большое число различных материалов. Материал, из которого должно быть изготовлено изделие, указывают соответствующим обозначением в основной надписи чертежа. Однако для удобства пользования чертежом в сечениях (в том числе и входящих в состав разрезов) наносят установленные ГОСТ 2.306 – 68* графические обозначения материалов, которые характеризуют их лишь в общих чертах. Некоторые из этих обозначений приведены в таблице, на с. 31.
Штриховка выполняется тонкими сплошными линиями. Параллельные линии штриховок проводят под углом 45° к линии рамки чертежа (рис. 49, а) или к оси вынесенного или наложенного сечения (рис. 49, б).
Расстояние между линиями выбирается в зависимости от площади сечения (чем больше площадь сечения, тем относительно реже штриховка) и необходимости разнообразить штриховку смежных сечений. Для учебных чертежей рекомендуется принимать расстояние между линиями штриховки, равным 2…3 мм. Расстояние между параллельными линиями штриховки должно быть одинаковым для всех выполненных в одном масштабе изображений данной детали на чертеже. Линии штриховки могут наноситься с наклоном влево или вправо, но в одну и ту же сторону на всех сечениях, относящихся к одной и той же детали, независимо от количества листов, на которых расположены чертежи этих сечений. При совпадении направления линий штриховки с контурными или осевыми линиями вместо угла наклона 45° применяют угол 30 или 60° (рис. 50).
Штриховку смежных сечений наносят для одного сечения вправо, для другого – влево или изменяют расстояние между линиями (рис. 51, а), кроме того, применяют сдвиги линий штриховки (рис. 51, б). При штриховке «в клетку» расстояние между линиями штриховки в каждом сечении должно быть разным (рис. 52).
Большие площади, а также при указании профиля грунта рекомендуется штриховать только у контурных линий узкой полоской равномерной толщины (рис. 53).
Узкие площади сечений, шириной на чертеже менее 2 мм, допускается зачернять (рис. 54), оставляя просвет между смежными сечениями 0,8…1,0 мм. Узкие и длинные площади сечений рекомендуется штриховать участками (рис. 55).
Таблица
Графические обозначения материалов:
Примечания:
- Композиционные материалы, содержащие металлы и неметаллические материалы, обозначают как металлы.
- Графическое обозначение древесины применяется в тех случаях, когда нет
- необходимости указывать направление волокон.
- Графическое обозначение керамики и силикатных материалов следует применять для обозначения кирпичных изделий (обожженных и необожженных), огнеупоров, строительной керамики, электротехнического фарфора, шлакобетонных блоков и т.п.
- Допускается применять дополнительные обозначения материалов, не предусмотренных в стандарте, поясняя их на чертеже.
Соприкасающиеся сечения одной и той же детали штрихуют в одну сторону без изменения шага штриховки (рис. 56). Графические обозначения, отличные от прямых линий штриховки, выполняют от руки.
Условности и упрощения, применяемые при выполнении изображений
В целях уменьшения трудоемкости и ускорения процесса разработки чертежей, уменьшения расхода бумаги на их оформление, повышения выразительности чертежей ГОСТ 2.305 – 68 ** устанавливает следующие условности и упрощения.
Если вид, разрез или сечение представляют собой симметричную фигуру, допускается вычерчивать половину изображения или немного более половины изображения с проведением в последнем случае волнистой линии (рис. 57).
Если предмет имеет несколько одинаковых, равномерно расположенных элементов (отверстий, зубьев, пазов, спиц и т. д.), то на его изображении полностью показывают один – два таких элемента, а остальные упрощенно или условно (рис. 58, а и рис. 59), с указанием их количества. Допускается также изображать лишь часть такого предмета (рис. 58, б) с надлежащими указаниями о количестве элементов, их расположении и т.д.
Плавный переход одной поверхности в другую показывают условно тонкой линией или совсем не показывают (рис. 60). Допускается упрощенно изображать линии пересечения поверхностей, если по условиям производства не требуется их точного построения. Например, вместо лекальных кривых можно проводить дуги окружности и прямые (рис. 61).
Такие элементы деталей, как спицы маховиков, шкивов, зубчатых колес, тонкие стенки типа ребер жесткости и т. п., показывают рассеченными, но для большей наглядности не заштрихованными, если секущая плоскость направлена вдоль их оси или длинной стороны элемента (рис. 58, 63). Если в подобных элементах детали имеется отверстие или углубление, то применяют местный разрез (рис. 24, 64).
При изображении деталей, имеющих постоянные или закономерно изменяющиеся поперечные сечения (стержни, валы, трубопроводы, цепи, фасонный прокат, шатуны, опоры и т.п.), для экономии места допускается
изображать их с разрывами (рис. 65). Место обрыва ограничивается сплошной волнистой линией, которая проводится от руки, или, для участков большой протяженности, сплошной линией с изломами. Плоские участки поверхности детали рекомендуется выделять диагоналями, проводимыми сплошными тонкими линиями (рис. 66).
На чертежах изделий с накаткой, сплошной сеткой, орнаментом, рифлением и т.д. эти элементы допускается изображать частично с возможным упрощением (рис. 67).
Для показа конструкции отверстий в ступицах шкивов, зубчатых и червячных колес и т.п. деталей, а также шпоночных пазов на валах допускается вместо второго изображения детали давать лишь контур отверстия (рис. 68, а) или паза (рис. 68, б).
Пластины, а также элементы деталей (отверстия, фаски, пазы, углубления и т.п.) размером на чертеже 2 мм и менее рекомендуется изображать с отступлением от масштаба, принятого для всего изображения, в сторону увеличения. Незначительный уклон допускается показывать с увеличением.
Незначительную конусность также допускается изображать с увеличением или проводить только одну линию, соответствующую меньшему диаметру конуса (рис. 69). При выполнении разрезов допускается показывать элементы детали,
расположенные перед секущей плоскостью (рис. 70). Такое изображение называется наложенной проекцией. Наложенная проекция выполняется
штрихпунктирной утолщенной линией.
Допускается изображать в разрезе отверстия, расположенные на круглом фланце, не попадающие в секущую плоскость (рис. 71).
Применение условностей и упрощений при построении изображений сокращает время, затрачиваемое на разработку графической документации, и ведет к сокращению сроков проектирования, повышению его качества. Однако следует иметь ввиду, что применение упрощений не должно приводить к снижению ясности чертежа.
Наглядные аксонометрические изображения
Сущность метода параллельного аксонометрического проецирования состоит в том, что предмет относят к некоторой прямоугольной системе координат и затем проецируют его параллельными лучами на произвольно выбранную плоскость аксонометрических проекций вместе с этой системой.
Сущность метода аксонометрического проецирования
Плоскость аксонометрических проекций называют также картинной плоскостью. На рис. 72 показана точка А, отнесенная к системе прямоугольных координат Oxyz. Проведем через нее проецирующий луч, параллельный вектору 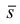
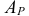
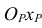
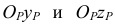
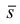
Аксонометрические проекции различаются по углу φ, который составляет вектор направления проецирования 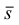
Известно, что положение любой точки в пространстве определяют три ее координаты – x, y и z. На рис. 73 показано построение аксонометрической проекции точки А, положение которой определяют координаты 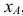
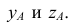
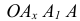
Коэффициентом (или показателем) искажения называется отношение длины проекции отрезка оси на картинной плоскости к его истинной длине.
Коэффициенты искажения по направлениям каждой из координатных осей или по направлениям, им параллельным, определяются по формулам:
Можно показать, что между коэффициентами искажения и углом φ существует следующая зависимость:
Для прямоугольной аксонометрии, когда φ = 90º, это соотношение принимает вид
В зависимости от соотношения коэффициентов искажения, различают изометрические, диметрические и триметрические аксонометрические проекции. Изометрической проекцией (или изометрией) называется такая
аксонометрическая проекция, у которой все коэффициенты искажения равны между собой (k = m = n). Если равны между собой лишь два коэффициента искажения (k = m ≠ n), то аксонометрическая проекция называется диметрической (или диметрией). Если же все три коэффициента искажения не равны между собой (k ≠ m ≠ n ≠ k), то аксонометрия называется триметрической (или триметрией). Понятно, что изометрические, диметрические и триметрические проекции могут быть как прямоугольными, так и косоугольными.
Обратимость аксонометрической проекции, т.е. возможность определения натуральных размеров изображенного объекта, обеспечивается путем указания на нем показателей искажения (или наличием условий для их определения) и возможности построения аксонометрической координатной ломаной любой точки поверхности, принадлежащей изображенному объекту. Построение аксонометрии при помощи координатных ломаных производят достаточно редко. Ими пользуются в тех случаях, когда нельзя применить какой-либо частный прием, например, для построения линий перехода и других кривых линий.
На практике аксонометрическую проекцию предмета строят, проводя отрезки
прямых соответствующей длинны (с учетом показателей искажения) параллельно аксонометрическим осям. На аксонометрической проекции могут быть нанесены размеры, обеспечивающие его обратимость. В этом случае нет необходимости в указании показателей искажения по осям.
Разрезы на аксонометрических проекциях выполняют, как правило, путем сечения объекта плоскостями, параллельными координатным. При этом линия, ограничивающая разрез, вычерчивается как линия видимого контура. Применяемые в отечественной конструкторской документации аксонометрические проекции стандартизованы по ГОСТ 2.317 – 69. К стандартным аксонометрическим проекциям относятся: прямоугольная изометрия, прямоугольная диметрия, косоугольные фронтальная и горизонтальная изометрии и косоугольная фронтальная диметрия.
Прямоугольная изометрия
В прямоугольной изометрии аксонометрические оси расположены под углами 120º друг к другу. При этом ось Оz располагают вертикально, а оси Оx и Оy под углами 30º к горизонтальному направлению (рис. 74, а).
Рассмотрим различные способы построения изометрических осей. Выполняя построение осей первым способом (рис. 74, б), на горизонтальной прямой, проходящей через центр аксонометрической системы координат, откладываем в обе стороны от точки О семь равных отрезков произвольной длины. Из крайних точек этих отрезков вниз по вертикали откладываем слева и справа по четыре таких же отрезка. Построенные точки соединяем с точкой О и получаем направления аксонометрических осей Ох и Оу.
Построение осей вторым способом (рис. 74, в) выполняется в следующей последовательности. Строим окружность произвольного радиуса R с центром в точке О. Затем из точки пересечения полученной окружности с вертикальной осью, проходящей через точку О, как из центра, проводим дуги окружностей такого же радиуса до пересечения с исходной окружностью. Построенные точки соединяем с точкой О и получаем направления аксонометрических осей Ох и Оу.
Третий способ (рис. 74, г) предполагает использование угольника с углами 30º, 60º и 90º. Порядок построения понятен из рисунка. Для построения изображения предмета в изометрии необходимо все его линейные размеры, параллельные осям, умножить на коэффициент искажения 0,82, а затем уже откладывать их на аксонометрическом чертеже. Полученное изображение называют нормальным или точным (рис. 75, а). Стандарт предусматривает построение и упрощенной изометрической проекции без сокращения размеров по осям координат. При этом получается увеличенное в 1,22 раза по отношению к оригиналу изображение
предмета без нарушения пропорций между отдельными элементами. Такое
изометрическое изображение называется увеличенным (рис. 75, б), а коэффициенты искажения становятся приведенными. На практике, как правило, применяется изометрическая проекция, дающая увеличенное изображение.
Изометрическими проекциями окружностей, расположенных в плоскостях проекций или плоскостях, параллельных им, являются эллипсы (рис. 76). Соотношения больших и малых осей эллипсов во всех плоскостях проекций одинаковы и равны: большие оси – 1,22d, малые – 0,71d, где d – диаметр изображаемой окружности.
Расположение осей эллипсов зависит от положения проецируемой окружности. В общем случае для всех видов прямоугольных аксонометрических проекций справедливо правило: большая ось эллипса всегда перпендикулярна к отсутствующей в плоскости данной окружности оси, а малая ось эллипса – направлена вдоль этой оси. Например, большая ось эллипса, в который проецируется окружность, лежащая во фронтальной плоскости проекций, расположена перпендикулярно оси Оy, а малая – направлена по этой оси, поскольку именно ось Оy отсутствует во фронтальной плоскости проекций (рис. 76).
Величина осей эллипса может быть вычислена по указанным соотношениям или определена графически. Графическое определение величин большой и малой осей эллипса в изометрии, в зависимости от диаметра d проецируемой окружности, показано на рис. 77. Как правило, на практике для упрощения построений эллипсы в изометрии заменяют четырехцентровыми овалами. Рассмотрим два способа построения таких овалов.
Для построения овала первым способом (рис. 78) проводим изометрические оси Ох и Оу и откладываем на них в обе стороны от точки О отрезки, равные радиусу заданной окружности (рис. 78, б). Через полученные точки 1, 2, 3, 4 проводим прямые, параллельные аксонометрическим осям, и получаем ромб ABCD, который представляет собой изометрию квадрата, описанного вокруг окружности (рис. 78, а). Вершины А и С полученного ромба, лежащие на короткой диагонали, являются центрами больших дуг овала.
Соединяем лучами точку А с точками 2 и 3 и на пересечении этих лучей с большой диагональю BD ромба получаем центры малых дуг овала – 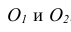
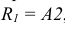
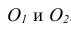
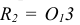
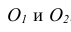
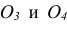
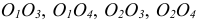
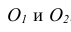
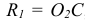
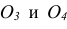
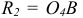
На рис. 80 показан пример построения наглядного изображения детали в прямоугольной изометрической проекции.
Прямоугольная диметрия
Стандарт регламентирует применение прямоугольной диметрической проекции, у которой ось Оz расположена вертикально, ось Ох наклонена под углом 7°10′, а ось Оу – под углом 41°25′ к линии горизонта (рис. 81). При построении прямоугольной диметрии сокращение длин по оси Оу принимают вдвое больше, чем по двум другим, т.е. полагают, что 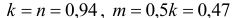
Построение аксонометрических осей диметрии можно проводить двумя способами (рис. 82). Выполняя построение осей первым способом (рис. 82, а), на горизонтальной прямой, проходящей через точку О, откладываем в обе стороны от точки О восемь равных отрезков произвольной длины. Из крайних точек этих отрезков вниз по вертикали откладываем слева один такой же отрезок, а справа – семь. Построенные точки соединяем с точкой О и получаем направления аксонометрических осей Ох и Оу. Построение осей вторым способом (рис. 82, б) выполняется в следующей последовательности. На вертикальной прямой вниз от точки О откладываем отрезок OD произвольной длины, а вверх – отрезок OA = 2ОD.
Затем из точки О, как из центра, проводим дугу окружности радиусом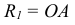
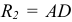
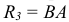
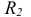
Диметрическими проекциями окружностей, расположенных в плоскостях проекций или плоскостях, параллельных им, так же как и в изометрии являются эллипсы, большие и малые оси которых расположены согласно правилу, сформулированному в п. 2.2 (рис. 83, а). Длина большой оси для всех эллипсов одинакова и равна 1,06d (где d – диаметр изображаемой окружности), длина малой оси различна: для фронтальной плоскости проекций и плоскостей, параллельных ей, она составляет 0,95d, для горизонтальной и профильной плоскостей проекций и плоскостей, параллельных им, – 0,35d.
При построении прямоугольной диметрической проекции эллипсы заменяют четырехцентровыми овалами. Построение четырехцентровых овалов для горизонтальной и профильной плоскостей проекций и плоскостей, параллельных им, производится в следующей последовательности (рис. 83, б). Через центр системы координат О проводят две взаимно перпендикулярные прямые и откладывают на горизонтальной оси от точки О влево и вправо половину большой оси эллипса (АО = ОВ =1,06d/2), а на вертикальной оси – вверх и вниз половину малой оси (СО = ОD =0,35d/2). Затем на вертикальной прямой от
точки О вверх и вниз откладывают отрезки 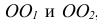
большой оси эллипса (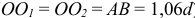
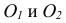
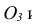
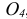
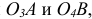
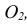
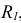
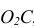
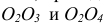
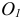
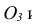
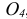
Построение овала, заменяющего эллипс во фронтальной плоскости проекций, показано на рис. 83, в. Проводят оси диметрии Ox, Оy, Оz и из точки О восставляют перпендикуляр к оси Оу (малая ось эллипса совпадает с направлением оси Оу, а большая – перпендикулярна к ней). На осях Ох и Оz откладывают величину радиуса заданной окружности, т. е. OМ = ON= OК = OL= d/2, и получают точки М, N, K, L, которые являются точками сопряжения дуг овала. Из точек М и N проводят горизонтальные прямые, которые в пересечении с осью Оу и перпендикуляром к ней дают точки 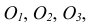
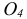
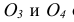
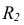
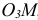
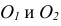
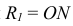
На рис. 84 показан пример построения наглядного изображения детали в прямоугольной диметрической проекции.
Косоугольные изометрии
Стандарт предусматривает применение двух видов косоугольной изометрической проекции: фронтальной и горизонтальной. Направление аксонометрических осей фронтальной косоугольной изометрической проекции показано на рис. 85, а. Угол наклона оси Оy к горизонтальной линии должен составлять 45º. Допускается применять фронтальную изометрию с углами наклона оси Оy в 30º или 60º. Все три показателя искажения по осям Оx, Оy и Оz равны единице.
Окружности, находящиеся в плоскостях, параллельных фронтальной плоскости проекций, изображаются в косоугольной фронтальной изометрии в натуральную величину, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям, проецируются в эллипсы (рис. 85, б). Большая ось эллипса в горизонтальной плоскости составляет угол 22º30′ с осью Ox, а в профильной плоскости – такой же угол с осью Oz. Большие оси этих эллипсов равны 1,3d, а малые – 0,54d, где d – диаметр изображаемой окружности. Эллипсы заменяются овалами, которые вычерчиваются по двум известным осям следующим образом (рис. 86). На прямой, соединяющей точки А и С,откладывают от точки С отрезок СМ, равный разности полуосей овала, т. е. СМ = ОK – ОС. Из середины отрезка AM восставляют перпендикуляр и продолжают его до пересечения с осями овала в точках 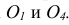
Затем определяют симметричные им точки 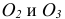
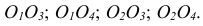
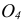
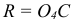
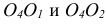
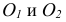
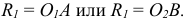
Направление аксонометрических осей горизонтальной косоугольной изометрической проекции показано на рис. 88, а. Угол наклона оси Оy к горизонтальной линии должен составлять 30º.Допускается применять горизонтальную аксонометрию с углами наклона оси Оy к горизонтальному
направлению в 45º и 60º, сохраняя угол 90º между осями Оx и Оy. Коэффициенты искажения по всем трем осям одинаковы и равны единице.
Окружности, находящиеся в плоскостях, параллельных горизонтальной плоскости проекций, изображаются в аксонометрии без искажения, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскости, проецируются эллипсами (рис. 88, б). Большая ось эллипса, который является проекцией окружности, расположенной во фронтальной плоскости, наклонена к оси Oz под углом 15º, величина большой оси этого эллипса равна 1,37d, а малой – 0,37d. Эллипс строится как овал по двум заданным осям (см. рис. 86). Большая ось эллипса, который является проекцией окружности, расположенной в профильной плоскости, наклонена к оси Oz под углом 30º, величина большой оси равна 1,22d, а малой – 0,71d. Сопряженные диаметры эллипсов, то есть диаметры, параллельные аксонометрическим осям, во всех случаях равны d. Построение эллипса выполняют по правилам построения проекций окружностей в прямоугольной изометрии.
На рис. 89 показан пример построения наглядного изображения детали в горизонтальной косоугольной изометрической проекции.
Косоугольная фронтальная диметрия
В косоугольной фронтальной диметрии ось Oz расположена вертикально, ось Ox – горизонтально, а ось Oy наклонена к горизонтальной оси под углом 45° (рис. 90, а). Допускается применение косоугольной фронтальной диметрии с углами наклона оси Oy, равными 30° или 60°. Коэффициенты искажения по осям Ox и Oz равны k = n = 1, а по оси Oy коэффициент m = 0,5. Следовательно, все плоские фигуры, размещенные параллельно фронтальной плоскости проекций, изображаются во фронтальной диметрии без искажения размеров и углов.
В косоугольной диметрии окружность, лежащая во фронтальной плоскости, изображается без искажения (рис. 90, б). Это обстоятельство представляет существенное преимущество при вычерчивании фронтальной диметрии деталей цилиндрической формы или с большим числом цилиндрических отверстий. Окружности, принадлежащие горизонтальной и профильной плоскостям, изображаются в виде эллипсов такой же формы и размеров, как и в
прямоугольной диметрии, то есть большая ось этих эллипсов равна 1,06d, а малая – 0,35d. В отличие от прямоугольной диметрии, большая ось эллипса в горизонтальной плоскости наклонена к оси Ox под углом 7º14′, а в профильной плоскости – под тем же углом к оси Oz (рис. 90, б). Упрощенное построение эллипсов в виде овалов выполняют по тем же правилам, что и в прямоугольной диметрии.
На рис. 91 показан пример построения наглядного изображения детали во фронтальной косоугольной диметрической проекции.
Условности и нанесение размеров в аксонометрии
При нанесении размеров на чертежах, выполненных в аксонометрических проекциях, выносные линии проводятся параллельно аксонометрическим осям, а размерные линии – параллельно измеряемому отрезку (рис. 92). В отличие от проекционных чертежей, в аксонометрии при рассечении поверхности предмета заштриховывают ребра жесткости, спицы маховиков, колес и другие подобные элементы (рис. 93), попавшие в секущую плоскость. Места плавных переходов изображают тонкими линиями.
Линии штриховки рассеченных поверхностей в аксонометрических проекциях выполняют параллельно одной из диагоналей квадратов, стороны которых расположены в соответствующих координатных плоскостях параллельно аксонометрическим осям. Направление штриховки рекомендуется выбирать в соответствии со схемами, показанными на рис. 94. Резьбу в аксонометрических проекциях изображают условно по ГОСТ 2.311 – 68. В случае необходимости, допускается частично изображать профиль резьбы (рис. 93).
Проекционное черчение
Проекционное черчение рассматривает построение изображений пространственных предметов на плоскости и имеет важное значение при изучении курса инженерной графики.
Изображение предметов на чертеже
На чертежах изображения предметов выполняются по способу прямоугольного проецирования, изложенном в курсе начертательной геометрии, с применением условностей, установленных правилами ГОСТ 2.305-2008 и других Государственных стандартов ЕСКД.
Прямоугольные проекции, построенные с применением указанных условностей, в ГОСТе называют изображениями. Для аксонометрических проекций, помимо прямоугольного, может применяться косоугольное проецирование.
В отличие от начертательной геометрии, где изображаются оси проекций, при выполнении чертежей применяется безосная система (без указания осей проекций и линий проекционной связи).
На чертежах в качестве баз для построения и определения формы и размеров изображения используются контуры, оси и центры симметрии проецируемого предмета. Вычерчивание изображения следует начать с проведения осей, нахождения центров симметрии и проведения линий видимого контура, от которых откладывают размеры и ведут построения.
При разработке технических чертежей деталей машин и других геометрических объектов (рис. 3,1) изображения должны выполняться по методу прямоугольного проецирования. При этом предполагается, что предмет расположен между наблюдателем и соответствующей плоскостью (рис. 3.2).
За основные плоскости проекций принимают шесть граней куба, которые разворачивают и совмещают с плоскостью так, как показано на рис. 3.2, причем грань 6 допускается размещать рядом с гранью 4. Изображения на фронтальной плоскости проекций называется главным. Относительно этой плоскости проекций предмет следует располагать так, чтобы изображение на ней давало наиболее полное представление о форме и размерах предмета.
Вес изображения на чертеже в зависимости от их содержания разделяются на виды, разрезы и сечения.
Видом называется изображение обращенной к наблюдателю видимой части поверхности предмета. Расположение видов на чертеже показано на рис. 3.3.
Разрезом называется изображение предмета, мысленно рассеченного одной или несколькими плоскостями, при этом мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений того же предмета. Па разрез показывается то, что получается на секущей плоскости и что расположено за ней. Допускается изображать не все, что расположено за секущей плоскостью, если этого нс требуется для понимания конструкции предмета. На чертеже предмет в разрезе заштриховывают.
Сечением называется изображение, получающееся при мысленном рассечении предмета одной или несколькими плоскостями. Па сечении показывается только то, что находится непосредственно в секущей плоскости.
Разрезы и сечения выявляют внутренние очертания изображаемого предмета.
Количество изображений (видов, разрезов, сечений) на чертеже должно быть наименьшим, но достаточным для полного понимания формы и размеров предмета. Это значит, что в каждом отдельном случае от исполнителя чертежа требуется, грамотно используя условные обозначения, знаки и надписи, согласно требованиям государственных стандартов, выбирать и располагать виды, разрезы и сечения так, чтобы свести к минимуму графические построения.
Виды
Виды, получаемые при проецировании предмета на шесть основных плоскостей проекций (граней куба), называются основными видами.
Наименование основных видов следующее:
- 1 – вид спереди (главный вид);
- 2 – вид сверху;
- 3 – вид слева;
- 4 – вид справа;
- 5 – вид снизу;
- 6 – вид сзади.
Основные виды располагаются в определенном порядке, как показано на рис. 3.3.
На чертеже виды располагают по отношению к главному виду (рис. 3.3) в такой последовательности: вид сверху – под главным видом, вид слева – справа от главного вида, вид снизу – над главным видом, а вид справа – слева от главного вида. Вид сзади разрешается помещать справа от вида слева или с левой стороны от вида справа.
Названия видов на чертежах не надписывают, за исключением случая, когда виды сверху, справа, слева, снизу, сзади не находятся в непосредственной проекционной связи с главным изображением (видом или разрезом, изображенным на фронтальной плоскости проекций). Тогда направление проектирования должно быть указано стрелкой около соответствующего изображения. Над стрелкой и над полученным изображением (видом) следует нанести одну и ту же прописную букву русского алфавита (рис. 3.4). Буквенные обозначения присваиваются в алфавитном порядке без повторений и без пропусков. Буквы И, О, X, Ъ,
Ы, Ь ,Ё, 3, Ч, согласно ГОСТу 2.316-2008, при выполнении чертежей не наносят.
Когда какая-либо часть предмета не может быть показана на одном из основных видов без искажения ее формы и размеров или можно ограничиться не целым видом, а изображением узко ограниченного места на поверхности предмета, применяют дополнительные и местные виды.
Дополнительными называются виды, получаемые на плоскостях, не параллельных ни одной из основных плоскостей проекций (рис. 3.5). Дополнительный вид на чертеже должен быть отмечен прописной буквой (рис. 3.5, о, б, г), а у изображения предмета, связанного с дополни-тельным видом должна быть поставлена стрелка, указывающая направление взгляда, где дополнительный вид обозначают той же буквой.
Когда дополнительный вид расположен в непосредственной связи с соответствующим изображением, стрелку и обозначение вида не наносят (рис. 3.5, а).
Дополнительный вид допускается повертывать (рис. 3.5, в, г), при этом буквенное обозначение вида должно быть дополнено знаком 
Местным видом называется изображение отдельного узко ограниченного места поверхности предмета.
Местный вид обозначается на чертеже подобно дополнительному виду и применяется в тех случаях, когда из всего вида только часть его необходима для уточнения формы предмета, остальная же часть вида не дает дополнительных сведений о предмете (рис. 3.6):
- – если изображение имеет ось симметрии, то допускается показывать его половину (рис. 3.6 – вид «А»);
- – если местный вид выполняется в проекционной связи по направлению взгляда, то стрелку и надпись над местным видом не наносят;
- – местный вид может быть ограничен линией обрыва;
- – местный вид может и не быть ограничен линией обрыва -вид «Б».
Разрезы
В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций разрезы бывают:
горизонтальные – секущая плоскость параллельна горизонтальной плоскости проекций (рис. 3.11, разрез А-А);
вертикальные — секущая плоскость перпендикулярна горизонтальной плоскости проекций (например, рис. 3.8, разрезы А-А, Б-Б);
наклонные — секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого.
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций (рис. 3.8, разрез А-А) и профильным, если секущая плоскость параллельна профильной плоскости проекции (рис. 3.8, разрез Б-Б).
В зависимости от числа секущих плоскостей разрезы бывают: простыми – при одной секущей плоскости (рис. 3.8, 3.9, 3.11); сложными – при двух и более секущих плоскостях.
Сложные разрезы в свою очередь подразделяют на ступенчатые, если секущие плоскости параллельны (рис. 3.12), и ломаные, если секущие плоскости пересекаются (рис. 3.13).
Форму предмета в отдельном узко ограниченном его месте определяет местный разрез (рис. 3.14, 3.15).
Положение (след) секущей плоскости показывают на чертеже разомкнутой линией (рис. 3.7, а), называемой линией сечения. При простом разрезе показывают только начальный и конечный штрихи линий сечения (рис. 3.8), а при сложном показывают се штрихи и в местах перегибов (рис. 3.12, 3.13). На начальном и конечном штрихах линии сечения ставят стрелки (рис. 3.7, а), указывающие направление взгляда (проецирования). Начальный и конечный штрихи этой линии не должны пересекать контур изображения.
У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита (рис. 3.7, б), разрез отмечается надписью по типу «А-А» (всегда только двумя буквами через тире).
В том случае, когда секущая плоскость совпадает с плоскостью симметрии детали и разрез расположен на одном листе в проекционной связи с другими изображениями детали, не обозначается положение секущей плоскости и разрез надписью не сопровождается.
На разрезе невидимые линии внутреннего контура становятся видимыми и изображаются сплошными основными линиями.
Мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений того же предмета.
Штриховка на всех изображениях детали выполняется в одном направлении, с правым или левым наклоном, под углом 45° к горизонтальной линии чертежа тонкими линиями, условно приняв, что все детали, приведенные в примерах, металлические. Расстояние между штриховыми линиями должно быть одинаковым.
Простые разрезы
Простым разрезом называется разрез, получаемый при рассечении детали одной секущей плоскостью. Чаще всего применяются вертикальные и горизонтальные разрезы.
Вертикальными называются разрезы, образованные секущими плоскостями, параллельными фронтальной или профильной плоскостям проекций.
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций, и профильным, если секущая плоскость параллельна профильной плоскости проекций.
Горизонтальными разрезами называются разрезы, образованные секущими плоскостями, параллельными горизонтальной плоскости проекций.
Горизонтальные, фронтальные и профильные разрезы могут размещаться на месте соответствующих основных видов.
На рис. 3.7 выполнены два вертикальных разреза: фронтальный (А-А) и профильный (Б-Б), где деталь не имеет осей симметрии, поэтому на чертеже указано положение секущих плоскостей и соответствующие им разрезы сопровождаются надписями.
Для упрощения построения чертежа на одном изображении допускается соединять часть вида и часть разреза.
При соединении симметричных частей вида и разреза, если с осью симметрии совпадает проекция какой-либо линии, например ребра (рис. 3.9), то вид от разреза отделяется тонкой сплошной волнистой линией, проводимой правее (рис. 3.9, а) или левее (рис. 3.9, 6) оси симметрии.
Если деталь симметрична (рис. 3.10), то можно соединить половину вида и половину разреза (рис. 3.11), разделяя их штрихпунктирной тонкой линией, являющейся осью симметрии. Часть разреза может располагаться правее (рис. 3.12, а, разрез А-А,) или ниже (рис. 3.12, б, разрез А-А) оси симметрии, разделяющей часть вида с частью разреза, причем разрез А-А на рис, 3.12, а предпочтительнее.
Сложные разрезы
Сложными называются разрезы, получаемые с помощью двух и более секущих плоскостей. Они применяются в случаях, когда количество элементов деталей, их форма и расположение не могут быть изображены на простом разрезе одной секущей плоскостью и это вызывает необходимость применения нескольких секущих плоскостей.
Сложные разрезы разделяются на ступенчатые и ломаные. Они могут быть так же, как и простые разрезы, горизонтальными, фронтальными и профильными. Сложные разрезы бывают и комбинированными, т. е. состоящими из ступенчатых и ломаных разрезов.
Ступенчатыми разрезами называются разрезы, выполненные нескольким и параллельным и секущими плоскостями.
Разрез на рис. 3.12 осуществлен тремя секущими фронтальными плоскостями. Положение секущих плоскостей указывается штрихами линии сечения со стрелками, отмеченными одной и той же буквой. Эти штрихи принимаются за начальный и конечный штрихи линии сечения. Линия сечения имеет также перегибы, показывающие места перехода от одной секущей плоскости к другой. Перегибы линии сечения еще выполняются штрихами разомкнутой линии. Наличие перегибов в линии сечения не отражается на графическом оформлении ступенчатого разреза, линии перехода между секущими плоскостями не показывают.
Ломаными называются разрезы, полученные от рассечения предмета пересекающимися плоскостями. Секущие плоскости условно повертывают около линии взаимного пересечения до совмещения с плоскостью (рис. 3.13), параллельной какой-либо из основных плоскостей проекций, при этом линия поворота может не совпадать с направлением взгляда.
Если совмещенные плоскости окажутся параллельными одной из основных плоскостей проекций, то ломаный разрез допускается помещать на месте соответствующего вида (рис. 3,13).
Вместе с секущей плоскостью поворачивается расположенная в ней фигура сечения детали. На рис. 3.13 для наглядности нанесены линии связи, эти построения на чертеже не должны быть показаны.
При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, с которой производится совмещение.
Разрез, служащий для выявления формы предмета лишь в отдельном ограниченном месте, называется местным и отделяется от вида сплошной волнистой тонкой линией (рис. 3.14) или сплошной тонкой линией с изломом. Эти линии не должны совпадать с какими-либо линиями изображения.
Если местный разрез выполняется на части изображаемого предмета, представляющей собой симметричную фигуру (рис. 3.15), где разделяющей линией служит ось симметрии, то местный разрез с видом может разделяться этой осевой линией или линией обрыва.
Сечения
Сечением называется изображение фигуры, получающееся при мысленном рассечении предмета одной или несколькими плоскостями. Секущие плоскости нужно выбирать так, чтобы получились нормальные поперечные сечения. В отличие от разреза на сечении показывается только то, что расположено непосредственно в секущей плоскости, а все, что расположено за ней, не изображается (рис. 3,16).
Сечения, не входящие в состав разреза, разделяют на вынесенные и наложенные.
Вынесенные сечения располагаются на свободном поле чертежа и более предпочтительны для однозначного чтения чертежа. Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями (рис. 3.16). Не обозначают вынесенные сечения, когда их располагают на линии сечения, если они имеют ось симметрии. При этом положение секущей плоскости показывают штрихпунктирной линией. В случае расположения сечения на свободном месте их обозначают аналогично разрезам (рис. 3.16, сечение А-А). Сечения необходимо обозначать, даже если они находятся в проекционной связи (рис. 3.16, сечение Б-Б).
Наложенные сечения располагаются непосредственно на изображении предмета (рис. 3.17, б, 3.18, б). Вынесенные сечения могут располагаться не только на свободном поле чертежа (рис. 3.16), но и в разрыве изображения предмета (рис. 3.17, а, 3.18, а). Вынесенное симметричное сечение может располагаться в непосредственной близости от изображения, причем его ось симметрии должна совпадать с положением секущей плоскости и пересекать контур изображения предмета.
На чертежах для несимметричных сечений, расположенных в разрыве (рис. 3.18, а) или наложенных сечениях (рис. 3.18, б), линии сечения обозначают разомкнутой линией со стрелкой, но нс буквами.
Несимметричное сечение по построению и расположению должно соответствовать направлению, указанному стрелками (рис. 3.18).
Контур выносного сечения, а также сечения, входящего в состав разреза, выполняется сплошной основной линией (толщиной 5), контур наложенного сечения выполняется сплошной тонкой линией (от S/2 до S/3), как показано на рис. 3.17, б и 3.18, б.
Выносные элементы
Дополнительное отдельное изображение какой-либо части фигуры, обычно увеличенное, требующее графического или других пояснений в отношении формы, размеров и иных данных, называется выносным элементом (рис. 3.19, 3.20).
Рис. 3.19. Выносной элемент
При применении выносного элемента соответствующее место изображения отмечают замкнутой сплошной тонкой линией (окружностью или овалом) с обозначением выносного элемента прописной буквой русского алфавита или сочетанием прописной буквы с арабской цифрой на полке линии-выноски (рис. 3.19, а и 3.20, а).
Над выносным элементом (рис. 3.19, б и 3.20, б) указывается та же цифра и масштаб, в котором выполнен выносной элемент (масштабы могут быть различные).
Выносной элемент следует располагать как можно ближе к соответствующему месту на изображении предмета. Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и отличаться от него по содержанию. Например, изображение может быть видом, а выносной элемент – разрезом.
Кстати вы всегда можете заказать чертежи.
Лекции по предметам:
- Инженерная графика
- Начертательная геометрия
- Компас
- Автокад
- Черчение
- Аксонометрическое черчение
- Строительное черчение
- Техническое черчение
- Геометрическое черчение
Проекционная связь
Cтраница 1
Проекционная связь на комплексном чертеже отражается линиями связи, соединяющими соответствующие проекции точки.
[1]
Проекционная связь частичного вида с основным изображением осуществляется с помощью оси. СТ СЭВ 363 – 76 рекомендует вычерчивать половину ( рис. V.19 a) или четверть ( рис. V.19, б) изображения, если оно представляет собой симметричную фигуру. При таком изображении контуры выполняют сплошной линией, а места изгибов обозначают тонкой штрих-пунктирной линией с двумя точками.
[2]
Проекционную связь между точками At и Аъ удобно осуществить с помощью вспомогательной прямой ОК, проведенной через О под углом 45 к прямым У.
[3]
Положения проекционных связей соответствуют направлениям проецирования на плоскости П ] и П4, отмеченным стрелками.
[5]
Проведя линии проекционной связи через точки А, B i, A и B i до пересечения с фронтальными проекциями траекторий соответственно точек А и В, получим их новые фронтальные проекции.
[6]
Проведя линии проекционной связи, перпендикулярно оси 0 х, а затем оси Ох, определим положение горизонтальных и фронтальных проекций – точек Е и К.
[7]
В этом случае проекционная связь частичного вида с основным изображением осуществляется с помощью оси.
[8]
Виды размещают в проекционной связи, как полагается по ГОСТ 2.305 – 68, при другом расположении видов металлоконструкций их отмечают по типу дополнительных видов. Размеры на чертежах металлоконструкций указывают без предельных отклонений, последние приводят в технических требованиях.
[9]
С помэщью линии проекционной связи определена искомая горизонтальная проекция а точки А. Заметим, что точка Е является низшей точкой кривой.
[10]
С помощью линии проекционной связи определена искомая горизонтальная проекция а точки А. Заметим, что точка Е является наинизшей точкой кривой. Ее горизонтальная проекция была получена с помощью горизонтали EN3, которая является касательной к заданной кривой.
[11]
На чертеже строго выдержана проекционная связь между изображениями, продумана компоновка, что значительно облегчает его чтение. Сплошные детали показывают неразрезанными.
[12]
Если виды расположены в проекционной связи, то их названия на чертежах не надписывают. Если виды смещены один относительно другого ( расположены на разных листах), то они должны быть обозначены прописной буквой русского алфавита, а направление взгляда должно быть указано стрелкой и также обозначено прописной буквой русского алфавита. При отсутствии изображения, на котором можно показать направление взгляда, название вида надписывают.
[14]
Страницы:
1
2
3
4
1.1. Центральное проецирование
Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.
Известны два метода проецирования: центральное и параллельное.
Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).
Рисунок 1.1 – Центральное проецирование
Введём следующие обозначения (Рисунок 1.1):
S – центр проецирования (глаз наблюдателя);
π1 – плоскость проекций;
A, B, C – объекты проецирования – точки;
SA, SB – проецирующие прямые (проецирующие лучи).
Примечание: левой клавишей мыши можно переместить КРАСНУЮ точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и её можно будет переместить по вертикали.
Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.
Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.
Докажем это утверждение.
На рисунке 1.1: точка А1 – центральная проекция точки А на плоскости проекций π1. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С1) на плоскости проекций π1 совпадает с проекцией точки А (А1):
- С ∈ SA;
- SC ∩ π1=C1 → C1 ≡ A1.
Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.
Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π2) и ещё один центр проецирования (S2) (Рисунок 1.2).
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств
Построим проекции точки А на плоскости проекций π2. Из всех точек пространства только точка А имеет своими проекциями А1 на плоскость π1 и А2 на π2 одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).
Свойство 2. Проекция прямой есть прямая.
Докажем данное свойство.
Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π1=А1В1, где А1В1 – центральная проекция прямой, заданной отрезком АВ.
Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.
1.2. Параллельное проецирование
Рассмотрим метод параллельного проецирования. Наложим три ограничения, которые позволят нам, пусть и в ущерб наглядности изображения, получить чертёж более удобным для использования его на практике:
- Удалим оба центра проекции в бесконечность. Таким образом, добьемся того, что проецирующие лучи из каждого центра станут параллельными, а, следовательно, соотношение истинной длины любого отрезка прямой и длины его проекции будут зависеть только от угла наклона этого отрезка к плоскостям проекций и не зависят от положения центра проекций;
- Зафиксируем направление проецирования относительно плоскостей проекций;
- Расположим плоскости проекций перпендикулярно друг другу, что позволит легко переходить от изображения на плоскостях проекций к реальному объекту в пространстве.
Таким образом, наложив эти ограничения на метод центрального проецирования, мы пришли к его частному случаю – методу параллельного проецирования (Рисунок 1.3).Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования P, называется параллельным.
Рисунок 1.3 – Метод параллельного проецирования
Введём обозначения:
Введём обозначения:
Р – направление проецирования;
π1 – горизонтальная плоскость проекций;
A, B – объекты проецирования – точки;
А1 и В1 – проекции точек А и В на плоскость проекций π1.
Параллельной проекцией точки называется точка пересечения проецирующей прямой, параллельной заданному направлению проецирования Р, с плоскостью проекций π1.
Проведём через точки А и В проецирующие лучи, параллельные заданному направлению проецирования Р. Проецирующий луч проведённый через точку А пересечёт плоскость проекций π1 в точке А1. Аналогично проецирующий луч, проведённый через точку В пересечет плоскость проекций в точке В1. Соединив точки А1 и В1, получим отрезок А1 В1– проекция отрезка АВ на плоскость π1.
1.3. Ортогональное проецирование. Метод Монжа
Если направление проецирования Р перпендикулярно плоскости проекций p1, то проецирование называется прямоугольным (Рисунок 1.4), или ортогональным (греч. ortos – прямой, gonia – угол), если Р не перпендикулярно π1, то проецирование называется косоугольным.
Четырехугольник АА1В1В задаёт плоскость γ, которая называется проецирующей, поскольку она перпендикулярна к плоскости π1 (γ⊥π1). В дальнейшем будем использовать только прямоугольное проецирование.
Рисунок 1.4 – Ортогональное проецирование
Рисунок 1.5- Монж, Гаспар (1746-1818)
Основоположником ортогонального проецирования считается французский учёный Гаспар Монж (Рисунок 1.5).
До Монжа строители, художники и учёные обладали довольно значительными сведениями о проекционных способах, и, всё же, только Гаспар Монж является творцом начертательной геометрии как науки.
Гаспар Монж родился 9 мая 1746 года в небольшом городке Боне (Бургундия) на востоке Франции в семье местного торговца. Он был старшим из пяти детей, которым отец, несмотря на низкое происхождение и относительную бедность семьи, постарался обеспечить самое лучшее образование из доступного в то время для выходцев из незнатного сословия. Его второй сын, Луи, стал профессором математики и астрономии, младший — Жан также профессором математики, гидрографии и навигации. Гаспар Монж получил первоначальное образование в городской школе ордена ораторианцев. Окончив её в 1762 году лучшим учеником, он поступил в колледж г. Лиона, также принадлежавший ораторианцам. Вскоре Гаспару доверяют там преподавание физики. Летом 1764 года Монж составил замечательный по точности план родного города Бона. Необходимые при этом способы и приборы для измерения углов и вычерчивания линий были изобретены самим составителем.
Во время обучения в Лионе получил предложение вступить в орден и остаться преподавателем колледжа, однако, вместо этого, проявив большие способности к математике, черчению и рисованию, сумел поступить в Мезьерскую школу военных инженеров, но (из-за происхождения) только на вспомогательное унтер-офицерское отделение и без денежного содержания. Тем не менее, успехи в точных науках и оригинальное решение одной из важных задач фортификации (о размещении укреплений в зависимости от расположения артиллерии противника) позволили ему в 1769 году стать ассистентом (помощником преподавателя) математики, а затем и физики, причём уже с приличным жалованием в 1800 ливров в год.
В 1770 году в возрасте 24-х лет Монж занимает должность профессора одновременно по двум кафедрам — математики и физики, и, кроме того, ведёт занятия по резанию камней. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке – начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года, книга вышла под названием Начертательная геометрия (Géométrie descriptive) (стенографическая запись этих лекций была сделана в 1795 году). Изложенный в ней подход к чтению лекций по этой науке и выполнению упражнений сохранился до наших дней. Еще один значительный труд Монжа – Приложение анализа к геометрии (L’application de l’analyse à la géometrie, 1795) – представляет собой учебник аналитической геометрии, в котором особый акцент делается на дифференциальных соотношениях.
В 1780 был избран членом Парижской академии наук, в 1794 стал директором Политехнической школы. В течение восьми месяцев занимал пост морского министра в правительстве Наполеона, заведовал пороховыми и пушечными заводами республики, сопровождал Наполеона в его экспедиции в Египет (1798–1801). Наполеон пожаловал ему титул графа, удостоил многих других отличий.
Метод изображения объектов по Монжу заключается в двух основных моментах:
1. Положение геометрического объекта в пространстве, в данном примере точки А, рассматривается относительно двух взаимно перпендикулярных плоскостей π1 и π2 (Рисунок 1.6).
Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте. Декартова система координат послужила основой для проекций Монжа. Монж заменил понятие координатных осей проекций на линию пересечения плоскостей проекций (ось проекций) и предложил совместить координатные плоскости в одну путем поворота их вокруг координатных осей.
Рисунок 1.6 – Модель построения проекций точки
π1 – горизонтальная (первая) плоскость проекций
π2 – фронтальная (вторая) плоскость проекций
π1∩π2 — ось проекций (обозначим π2/π1)
Рассмотрим пример проецирования точки А на две взаимно перпендикулярные плоскости проекций π1 и π2.
Опустим из точки А перпендикуляры (проецирующие лучи) на плоскости π1 и π2 и отметим их основания, то есть точки пересечения этих перпендикуляров (проецирующих лучей) с плоскостями проекций. А1 – горизонтальная (первая) проекция точки А;А2 – фронтальная (вторая) проекция точки А; АА1 и АА2 – проецирующие прямые. Стрелки показывают направление проецирования на плоскости проекций π1 и π2. Такая система позволяет однозначно определить положение точки относительно плоскостей проекций π1 и π2:
АА1⊥π1
А2А0⊥π2/π1 АА1 = А2А0 — расстояние от точки А до плоскости π1
АА2⊥π2
А1А0⊥π2/π1 АА2 = А1А0 — расстояние от точки А до плоскости π2
2. Совместим поворотом вокруг оси проекций π2/π1 плоскости проекций в одну плоскость (π1 с π2), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным (ортогональным) чертежом (Рисунок 1.7):
Рисунок 1.7 – Ортогональный чертеж
Прямоугольный или ортогональный носит название эпюр Монжа.
Прямая А2А1 называется линией проекционной связи, которая соединяет разноимённые проекции точки (А2 — фронтальную и А1 — горизонтальную) всегда перпендикулярна оси проекций (оси координат) А2А1⊥π2/π1. На эпюре отрезки, обозначенные фигурными скобками, представляют собой:
- А0 А1 – расстояние от точки А до плоскости π2, соответствующее координате yА;
- А0 А2 – расстояние от точки А до плоскости π1, соответствующее координате zА.
1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа
1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.
2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.
Убедимся в справедливости последнего утверждения, для чего повернём плоскость π1 в исходное положение (когда π1⊥π2). Для того, чтобы построить точку А необходимо из точек А1 и А2 восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π1и π2, соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А. Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).
Рисунок 1.8 – Построение эпюра точки
Введём третью (профильную) плоскость проекций π3 перпендикулярную π1 и π2 (задана осью проекций π2/π3).
Расстояние от профильной проекции точки до вертикальной оси проекций А‘0A3 позволяет определить расстояние от точки А до фронтальной плоскости проекций π2. Известно, что положение точки в пространстве можно зафиксировать относительно декартовой системы координат с помощью трёх чисел (координат) A(XA; YA; ZA) или относительно плоскостей проекций с помощью её двух ортогональных проекций (A1=(XA; YA); A2=(XA; ZA)). На ортогональном чертеже по двум проекциям точки можно определить три её координаты и, наоборот, по трём координатам точки, построить её проекции (Рисунок 1.9, а и б).
а б
Рисунок 1.9 – Построение эпюра точки по её координатам
По расположению на эпюре проекций точки можно судить о её расположении в пространстве:
- если на эпюре горизонтальная проекция точки А — А1 лежит под осью координат X , а фронтальная — А2 – над осью X, то можно говорить, что точка А принадлежит 1-му квадранту;
- если на эпюре горизонтальная проекция точки А — А1 лежит над осью координат X, а фронтальная — А2 – под осью X, то точка А принадлежит 3-му квадранту;
- если на эпюре горизонтальная и фронтальная проекции точки А — А1 и А2 лежат над осью X, то точка А принадлежит 2-му квадранту;
- если на эпюре горизонтальная и фронтальная проекции точки А — А1 и А2 лежат под осью X, то точка А принадлежит 4-му квадранту;
- если на эпюре проекция точки совпадает с самой точкой, то значит – точка принадлежит плоскости проекций;
- точка, принадлежащая плоскости проекций или оси проекций (оси координат), называется точкой частного положения.
Для определения в каком квадранте пространства расположена точка, достаточно определить знак координат точки.
| X | Y | Z | |
|---|---|---|---|
| I | + | + | + |
| II | + | — | + |
| III | + | — | — |
| IV | + | + | — |
Упражнение
Построить ортогональные проекции точки с координатами А (60, 20, 40) и определить в каком квадранте расположена точка .
Решение задачи: по оси OX отложить значение координаты XA=60, затем через эту точку на оси OX восстановить линию проекционной связи, перпендикулярную к OX, по которой вверх отложить значение координаты ZA=40, а вниз – значение координаты YA=20 (Рисунок 1.10). Все координаты положительные, значит точка расположена в I квадранте.
Рисунок 1.10 – Решение задачи
1.5. Задачи для самостоятельного решения
1. По эпюру определите положение точки относительно плоскостей проекций (Рисунок 1.11).
Рисунок 1.11
2. Достройте недостающие ортогональные проекции точек А, В, С на плоскости проекций π1, π2, π3 (Рисунок 1.12).
Рисунок 1.12
3. Постройте проекции точки:
- Е, симметричной точке А относительно плоскости проекций π1;
- F, симметричной точке В относительно плоскости проекций π2;
- G, симметричной точке С относительно оси проекций π2/π1;
- H, симметричной точке D относительно биссекторной плоскости второго и четвертого квадрантов.
4. Постройте ортогональные проекции точки К, расположенной во втором квадранте и удаленной от плоскостей проекций π1 на 40 мм, от π2 — на 15 мм.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Практическая работа № 3, «Обеспечение
проекционных связей в САПР Компас 3D v16»
Цель
работы: ознакомиться с основными приёмами выполнения линий чертежа в
Компас-график.
Задачи: Научиться
выполнять фигуры с использованием вспомогательных построений и привязок с
соблюдением проекционных связей.
1. Теоретическая часть.
Для
обеспечения проекционных связей в САПР Компас 3D предусмотрены такие
инструменты, как вспомогательные линии и привязки.
Рассмотрим
обеспечение проекционных связей на примере построения чертежа параллелепипеда с
выступом, рис. 1.1, для которого необходимо построить три проекции.
Рис. 1.1. Параллелепипед с
выступом.
Начнем
вычерчивание трех проекций заданного графического объекта с построения
взаимно-перпендикулярных вспомогательных линий, которые будут играть роль осей.
Для построения фронтального вида проводим горизонтальную линию параллельно
осевой на расстоянии 10 мм. Потом вертикальную линию на расстоянии 26 мм от
вертикальной оси, эта линия будет осью симметрии фронтального вида, рис. 1.2.
Рис. 1.2. Вспомогательные
линии для построения
фронтального вида.
Затем
размечаем вспомогательными линиями контур фронтальной проекции и обводим
основными линиями с помощью инструмента «Непрерывный ввод объектов» , а потом вычерчиваем осевую
линию, рис. 1.3.
Рис. 1.3. Контур фронтальной
проекции.
Для
обеспечения проекционных связей между фронтальной проекцией и видом сверху,
построение вида сверху следует делать на тех же вспомогательных линиях, что и
фронтальную проекцию.
Для
построения вида сверху необходимо провести горизонтальную ось симметрии на
расстоянии 23 мм от оси разделяющей фронтальную и горизонтальную плоскости.
Затем построить две горизонтальные вспомогательные линии на расстоянии 13 мм.
от оси горизонтальной проекции, рис. 1.4.
Рис. 1.4. Разметка вида
сверху.
После
этого следует обвести контур вида сверху основными линиями и построить оси,
рис. 1.5.
Рис. 1.5. Горизонтальная
проекция (вид сверху).
Для
обеспечения проекционных связей между фронтальной, горизонтальной и профильной
проекциями необходимо перенести вспомогательные линии с горизонтальной проекции
в профильную плоскость повернув их на 900. Для этого можно
воспользоваться инструментом «Дуга окружности», рис. 1.6.
Рис. 1.6. Кнопка «Дуга
окружности».
Выбрать
инструмент «Дуга окружности», назначить тип линии «Тонкая», установить курсор
мыши на пересечение осей разделяющих фронтальную, горизонтальную и профильную
плоскости, рис. 1.7.
Рис. 1.7. Пересечение осей
разделяющих плоскости.
Затем нажать леву клавишу
мыши, перенести курсор вниз до пересечения с горизонтальной вспомогательной
прямой проходящей через верхнюю границу горизонтальной проекции и нажать левую
клавишу, рис. 1.8.
Рис. 1.8. Начало построения
дуги связывающей горизонтальную и профильную
проекции.
Затем перевести курсор мыши до
пересечения с горизонтальной осью разделяющей фронтальную и горизонтальную
проекции, рис. 1.9.
Рисунок 1.9. Завершение построения дуги связывающей горизонтальную и профильную
проекции.
В результате получится дуга
связывающая горизонтальную и профильную проекции, аналогично построить дуги
связывающие горизонтальные вспомогательные прямые горизонтальной плоскости с
вертикальными прямыми профильной плоскости, рис. 1.10.
Рис. 1.10. Дуги связывающие
горизонтальные вспомогательные прямые горизонтальной плоскости с вертикальными
прямыми профильной плоскости.
Через пересечения дуг с осью
разделяющей фронтальную и горизонтальную плоскости построить вспомогательные
прямые линии, в результате в профильной проекции получится разметка профильной
проекции (вида слева), рис. 1.11.
Рис. 1.11. Разметка профильной
проекции.
Обвести основными линиями
разметку профильной плоскости, построить вертикальную ось и удалить
вспомогательные прямые и дуги, в результате получится чертеж трех проекций
заданного графического объекта, рис. 1.12.
Рис. 1.13. Три проекции
заданного графического объекта.
2. Практическая часть.
Самостоятельно
выполнить чертежи:
5.1 Основные понятия
и определения
Поверхность
– это множество l1,
l2
… li
последовательных положений линии l,
движение и форма которой подчинены
определенному закону. Под законом
следует понимать характер, порядок,
правила, траекторию перемещения линии
l
в пространстве таким образом, чтобы в
каждом новом положении члены множества
l1,
l2
… li
касались
друг друга, образуя оболочку поверхности.
В
формировании поверхности принимают
участие подвижные и неподвижные линии.
Подвижная линия, участвующая в формировании
поверхности, называется образующей;
неподвижная линия (или плоскость),
относительно которой перемещается
образующая (в большинстве случаев
пересекая ее), называется направляющей.
На рис. 48 представлен порядок формирования
цилиндрической (рис. 48а) и конической
(рис. 48б) поверхностей. В первом случае
образующая перемещается параллельно
самой себе, оставаясь в любом положении
перпендикулярной горизонтальной
плоскости проекций и пересекая
расположенную в ней горизонтальную
окружность. Во втором случае изменился
закон перемещения образующей: в
Рис.
48а
Рис.
48б
любом
положении она проходит через одну и ту
же точку S,
пересекая направляющую окружность.
Нетрудно догадаться, что если бы
направляющей была не окружность, а
многоугольник, то сохраняя вид перемещения
образующей, мы бы получили для первого
случая призматическую, а для второго –
пирамидальную поверхности. И это, опять
таки, за счет изменения закона перемещения
образующей (не по окружности, а по
многоугольнику).
Д
искретный
каркас поверхности – это конечное
множество образующих и направляющих
(или точек), задающих поверхность в
пространстве и на чертеже. Термин следует
понимать буквально, как сетку опорных
линий поверхности. На рис. 49 представлены
дискретные каркасы сферической
поверхности (рис. 49а) и конической
поверхности общего вида (рис. 49б).
Построение чертежа относительно сложной
поверхности сводится к построению
проекции ее дискретного каркаса. На
рис. 50а представлен чертеж конической
поверхности общего вида, дискретный
каркас которой показан на рис. 49б. Для
простейших поверхностей (сферы, кругового
конуса, кругового цилиндра и др.) с явно
выраженным законом их образования в
построении дискретного каркаса
необходимости нет, поскольку каждая из
них
Рис.
49а
Рис.
49б
исчерпывающе
полно может быть задана проекциями их
наружного контура (очерками, рис. 50б).
Рис.
50а
Рис.
50б
С
ледует
различать термины «очерк» поверхности
и «проекция» поверхности. Применительно
к термину «очерк» речь идет о проекциях
только наружного контура, ограничивающего
внешние линии проекции. Для сравнения
на рис. 51а дана чертеж пирамиды, а на
рис. 51б очерки этой же поверхности.
Отметим, что для упомянутых кругового
конуса, кругового цилиндра и сферы, не
имеющих вырезов, пересечений и т.д.,
очерки и проекции совпадают (рис. 50б).
Рис.
51а
Рис.
51б
Непрерывный
каркас поверхности – это множество l1,
l2
… li
последовательных
положении линии l,
заполняющих поверхность таким образом,
что через каждую точку поверхности
может быть проведена единственная линия
этого множества. В рамках нашего курса
термин носит больше теоретический
характер, но предоставляет наиважнейший
практический тезис: ЧЕРЕЗ ЛЮБУЮ ТОЧКУ
ПОВЕРХНОСТИ МОЖЕТ БЫТЬ ПРОВЕДЕНА
ЕДИНСТВЕННАЯ ОБРАЗУЮЩАЯ. Именно этот
тезис лежит в основе построения
недостающих проекций точек на поверхности,
предопределяя их единственное положение
на каждой из них.
П
Рис.
52а
Рис.
52б
орядок поверхности – это косвенная
характеристика ее сложности, численно
равная наибольшему количеству точек
пересечения прямой с поверхностью. Если
принять к сведению, что касание прямой
с поверхностью есть частный случай
пересечения, то при определении порядка
поверхности подобные случаи следует
исключать. В этой ситуации становиться
очевидным, что, например, сфера, конус,
цилиндр являются поверхностями второго
порядка (рис. 52а), а, например, тор –
поверхностью четвертого порядка (рис.
52б).
Критерием полноты
задания поверхности на чертеже является
возможность построения недостающих
проекций точки на поверхности по одной
заданной проекции этой точки. Для
построения недостающей проекции точки
на поверхности в общем случае необходимо:
-
через
заданную проекцию точки (1”, рис. 53а)
провести проекцию образующей (l”,
рис. 53б); -
по
закону формирования поверхности
простроить недостающую проекцию этой
образующей (l’,
рис. 53в); -
по
линии проекционной связи найти на ней
недостающую искомую проекцию этой
точки (1’, рис. 53г).
П
оскольку
на основании формулировки непрерывного
каркаса поверхности через любую точку
поверхности может быть проведена
единственная образующая, полученное
решение (положение точки 1’) тоже будет
единственным.
Рис.
53а
Рис.
53б
5.2 Классификация
поверхностей.
Предварительно
заметим, что предлагаемая здесь
классификация поверхностей является
наипростейшей, занимающей в рамках всех
возможных классификационных признаков
минимальную часть. Следует также принять
к сведению, что в нашем цикле начертательной
геометрии раздел «Поверхности»
рассматривается не более чем с точки
зрения формирования конфигурации
Рис.
53в
Рис.
53г
деталей,
имеющих переходы без учета взаимодействия
поверхности с окружающей средой.
Рассмотрим
классификацию поверхностей по двум
классификационным признакам.
В
Рис.
54
зависимости от формы образующей
поверхности подразделяются на линейчатые,
у которых образующая есть прямая линия
(цилиндр, конус, пирамида, призма и др.,
рис. 48,50) и нелинейчатые, у которых
образующая не является прямой (сфера,
тор, рис. 52). Линейчатые поверхности, в
свою очередь, подразделяются на
развертываемые и неразвертываемые.
Развертываемые поверхности, будучи
разрезанными по одной из образующих
могут быть развернуты в плоскость, т.е.
совмещены с плоскостью всеми своими
точками без складок, разрывов и выпучивания
поверхности или ее частей (цилиндр,
конус, призма и др.). Неразвертываемые
поверхности при этих же условиях не
могут быть совмещены с плоскостью
(гиперболический параболоид,
геликоид,
цилиндроид), хоть и являются линейчатыми
(рис. 54). Нелинейчатые поверхности (сфера,
тор и др.) являются неразвертываемыми.
В зависимости от
закона формирования (характера перемещения
образующей) поверхности подразделяются
на:
-
винтовые
(резьбы, шнеки, червяки, сверла и т.д. –
формируются вращательно-поступательным
перемещением образующей вокруг и вдоль
оси (рис. 55);
-
вращения,
– формируются вращением прямолинейной
или криволинейной образующей (дуги,
окружности, кривой общего вида) вокруг
оси. Так образуются цилиндрические,
конические, сферические, торовые и т.д.
поверхности (рис. 48, 49, 52); -
п
Рис.
55оверхности с плоскостью параллелизма
(Каталана), – формируются перемещением
прямолинейной образующей l
по двум прямолинейным или криволинейным
направляющим m
и
n
(рис. 56) таким образом, что в каждом
положении l1,
l2
… li
образующая остается параллельной
наперед заданной плоскости
(параллелизма).
Для отраслей
промышленности, имеющих дело с высокими
и сверхвысокими скоростями, при которых
среда (газовая, жидкостная и др.)
рассматривается как твердое тело
(турбиностроение, авиация, космонавтика,
военные отрасли) раздел «Поверхности»
инженерной графики является
основополагающим, поскольку через
геометрию поверхностей определяются
эксплуатационные, экономические и иные
(более высокого порядка) свойства
изделий. Естественно, что при таком
подходе к тематике требуется совершенно
иное количественное и качественное ее
рассмотрение.
Рис.
56
5.3 Точка на
поверхности
Раздел «Точка на
поверхности» в рассматриваемой тематике
является весьма ответственным, поскольку
его усвоение открывает путь к построению
проекций линий на поверхности (как
совокупности точек), к определению фигур
сечения поверхностей плоскостями общего
и частного положения, к построению
вырезов на поверхностях и телах (как
совокупности линий), к построению линий
пересечения поверхностей между собой.
Даже простое перечисление круга решаемых
задач наталкивает на весьма очевидный
вывод: не усвоив этого раздела, дальше
в начертательной геометрии делать
нечего. До тех пор, пока вы лично не
убедитесь в этом, (а это случится
непременно) советуем этот довод принять
на веру и отнестись к нижеизложенным
материалам с повышенным вниманием и
ответственностью.
5.3.1 Гранные
поверхности
На рис. 57 представлен
трехпроекционный чертеж трехгранной
пирамиды. Отметим несколько характерных
моментов.
Рис.
57
Во-первых,
студент должен понять, что на фронтальной
проекции все ребра AS,
BS,
CS
– видимые, но грань ASC
невидимая, причем ребра AS
и CS
являются
границами видимости для фронтальной
проекции. Для профильной проекции ребра
AS
и BS
являются границами видимости, ребро SC
– невидимое. Невидимые грани ASC
и BSC
закрыты гранью ASB.
Эти положения
определяют видимость точек, расположенных
на любой грани поверхности.
Во-вторых,
если проекция точки задана на любом
каком-либо ребре, ее недостающие проекции
следует искать только на соответствующих
проекциях этого ребра (вспомните свойство
параллельного проецирования: если точка
принадлежит прямой, проекции точки
принадлежат соответствующим проекциям
этой прямой). Заданная на фронтальной
проекции точка 1 (проекция 1’’) принадлежит
ребру AS
(проекция A’’S’’),
что однозначно определяет положение
ее горизонтальной и профильной проекций
1’ и 1’’’ на проекциях A’S’
и A’’’S’’’
этого ребра.
В-третьих, любая
грань пирамиды представляет собой
плоскость. Тогда задача на принадлежность
точки к пирамидальной поверхности
сводится к известному условию
принадлежности точки к плоскости: точка
принадлежит плоскости, если находится
на какой-либо прямой этой плоскости.
Применительно к поверхности пирамиды
в качестве такой «какой-либо» прямой
целесообразно принимать образующую, и
решение задачи в этом случае сводится
к общему алгоритму, показанному на рис.
53.
В-четвертых,
каждой видимой точке на фронтальной и
профильной проекциях пирамиды
соответствует парная невидимая точка,
находящаяся в створе видимой (на одной
линии визирования). Так, видимая на
фронтальной проекции точка 2 (проекция
2’’) и невидимая точка 3 (проекция 3’’
в скобках) находятся на одной линии
визирования 2-3 (горизонтальная проекция
2’ – 3’), но каждая из них лежит на своей
образующей l2
и l3,
на фронтальной проекции так же находящихся
в створе друг друга: образующая l2
видимой грани BSC
закрывает образующую l3
невидимой грани ASC
(l2’’
= (l3’’)).
Исходя из этих
характерных моментов аналогичным
образом (см. рис. 53) могут быть построены
недостающие проекции, например, точки
4, (рис. 57) заданной на горизонтальной
проекции или любой другой точки, заданной
на любой проекции пирамиды.
На рис. 58 показана
трехгранная призма. Здесь тоже следует
отметить узловые моменты. Во-первых,
каждая грань призмы представляет собой
горизонтально-проецирующую
плоскость, а их горизонтальные проекции,
– следы-проекции этих плоскостей.
Следовательно, горизонтальная проекция
любой точки, где бы она ни находилась,
может быть расположена только на
горизонтальном очерке этой призмы
(вспомните: любая точка, линия или плоская
фигура, расположенная в проецирующей
плоскости, отображается на ее
следе-проекции).
Рис.
58
Во-вторых, все
точки, расположенные на ее верхнем
срезе, на горизонтальной проекции будут
видимыми, на любом другом месте каждой
грани призмы, – невидимыми.
В-третьих,
вопросы видимости граней и точек на
них: грани ab
и bc
на фронтальной проекции – видимые,
грань ac
– невидимая; грань ab
на профильной проекции – видимая, грани
ac
и cb
– невидимые.
С
учетом этого точка 1, заданная на верхнем
конце фронтальной проекции ребра b
(1’’ расположена на b’’),
на других проекциях призмы будет видимой
(1’, 1’’’) и, естественно, принадлежать
соответствующим проекциям b’,
b’’’
ребра b.
Точка 2, заданная в средней части
фронтальной проекции ребра c
(см. 2’’), на остальных проекциях (2’,
2’’’) будет невидимой. Точки 3 и 4,
заданные на верхних срезах граней bc
и ac
(см. 3’’ и 4’’), на горизонтальной
проекции будут видимыми (см. 3’ и 4’), а
на профильной – невидимыми (см. (3’’’)
и (4’’’)), т.к. лежат на невидимых гранях.
Аналогично горизонтальные проекции
точек 7 и 8 будут невидимыми, как и
профильная проекция точки 8, находящаяся
на невидимой на W
грани ac.
Если точка 9 на горизонтальной проекции
задана как видимая, то ее фронтальная
и профильная проекции будут однозначно
видимыми. Если горизонтальная проекция
точки задана как невидимая (см. 10’), то
без дополнительной информации (например,
z
= 52) ее вертикальные проекции однозначно
построить невозможно, что отнюдь не
означает неполное задание поверхности.
В
заключение отметим еще одну деталь. У
студентов традиционно вызывает некоторые
осложнения построение профильной
проекции поверхности, особенно
несимметричной. Это свидетельствует о
неважном усвоении темы «проецирование
точки», необходимости повторить этот
материал и строить каждую проекцию
опорных линий поверхности и точек на
ней по координатам XYZ
(рис. 57). В инженерной практике, как
правило, поступают проще: оси y
и z
не указывают, а значения Y
точек откладывают от произвольной
точки, принятой по условиям компоновки
чертежа за начало координат (рис. 58,
фигурная скобка). Кстати, рассмотренные
выше соображения по определению
недостающих проекций точек на поверхности
пирамиды и призмы абсолютно приемлемы
для конических и цилиндрических
поверхностей соответственно.
5.3.2 Поверхность
вращения общего вида
Д
облегчения понимания последующего
материала предварительно рассмотрим
вращение точки А вокруг
горизонтально-проецирующей оси i
(рис. 59). Здесь важно отметить, что
точка А, последовательно перемещаясь
из крайнего левого положения А1
в крайне правое Аi,
находится на одном и том же расстоянии
от оси i,
равном радиусу вращения R.
Другими словами, траектория перемещения
точки в пространстве есть окружность
m
радиуса R.
П
Рис.
59
оскольку она находится в горизонтальной
плоскости ,
то на горизонтальную плоскость проекций
Н отобразится окружностью m’
действительной величины, а на фронтальную,
– в виде отрезка m’’=A1’’An’’
прямой, равного по длине диаметру
окружности и параллельного оси х. Это
утверждение справедливо для совокупности
любым образом расположенных точек
(окружности m1,
m2
… miбудут
параллельны друг другу и имеют обобщенное
название «параллели»).
А
теперь представим, что геометрическим
местом точек, вращающихся вокруг оси
i,
является произвольная плоская кривая
образующая l,
в начальном положении параллельная
фронтальной плоскости проекций V
(рис. 60). Ее горизонтальная проекция l’
есть прямая, параллельная оси х. При
Рис.
60
вращении
образующей l
вокруг оси ее точки 1…7 перемещаются по
параллелям m1
… m7,
представляющим собой совокупность
однотипных линий дискретного каркаса
поверхности. Вторую совокупность линий
дискретного каркаса составляют образующие
l1
… lI,
проекции которых необходимо построить.
Горизонтальные проекции образующей l
в любом положении останутся радиальными
прямыми, т.е. прямыми, продолжение которых
проходит через проекцию i’
оси вращения i.
Фронтальная
проекция образующей в крайнем правом
положении ln’’
будет зеркальным отображением крайней
левой образующей (l’’).
Любое промежуточное положение l1
… ln-1
образующей l
строится через горизонтальную проекцию
l1’
… ln-1’
по принадлежности каждой из точек 1…7
своей траектории (своей параллели) m1…m7
(на фронтальной проекции m1’’…m7’’).
Другими словами, для построения проекций
любого промежуточного положения l1
образующей l
необходимо:
-
провести
горизонтальную проекцию l1’
образующей l
(это будет радиальная прямая); -
найти
точки 11’…71’
ее пересечения с горизонтальными
проекциями параллелей m1’
…m7’; -
по
линиям проекционной связи снести
проекции точек 11’…71’
на соответствующие фронтальные проекции
m1’’
… m7’’параллелей
m1…m7
(точку 1’ сносим на m1’’
– получаем точку 11’’
и т.д. по всем точкам).
Проводим
через полученные точки 1’’…7’’
фронтальную проекцию l1’’
образующей l1.
Чтобы не затемнять чертеж на нем показано
только одно промежуточное положение
образующей l,
хоть аналогичным путем их можно было
провести сколько угодно. Таким образом,
дискретный каркас поверхности вращения
общего вида можно считать построенным.
Рассмотрим
характерные опорные линии дискретного
каркаса этой поверхности (рис. 60).
Параллель наименьшего диаметра называется
«горло» или «горловина» (m2).
Параллель наибольшего диаметра называется
экватором (m6).
Экватор является границей зоны видимости
для горизонтальной проекции поверхности:
все, что расположено выше экватора (и
не закрыто верхним «отворотом»
поверхности) на горизонтальной проекции
является видимым; точки и линии,
расположенные под экватором, на
горизонтальной проекции невидимые.
Л
инии
пересечения поверхности вращения
плоскостью, проходящей через ось вращения
i,
называется меридианом. Поверхность
вращения имеет множество меридианов.
Меридиан, параллельный фронтальной
плоскости проекций, называется главным
фронтальным меридианом. Его фронтальная
проекция – есть ничто иное как фронтальный
очерк поверхности. Главный фронтальный
меридиан является границей зоны видимости
для фронтальной проекции: все, расположенное
на поверхности проекции до главного
фронтального меридиана, на фронтальной
проекции является видимым (см. точку А,
рис. 60, 61), расположенное за ним, – невидимым
(точка В, рис. 61). Ну и, наконец, главный
профильный меридиан является границей
зоны видимости
Рис.
61
для
профильной плоскости проекций (рис.
60). Его фронтальная и горизонтальная
проекции есть вертикальные прямые,
проходящие через вертикальные оси
проекций поверхности, а профильная
проекция совпадает с профильным очерком
поверхности.
5.3.3 Поверхности
вращения второго порядка
Поверхности
вращения второго порядка можно
рассматривать как частные случаи
поверхности вращения общего вида со
всеми присущими им положениями и
свойствами.
5.3.3.1 Сферическая
поверхность
Образуется
вращениями окружности или ее части
относительно оси, проходящей через
центр окружности (дуги). Рассмотрим
опорные линии дискретного каркаса этой
поверхности. На рис. 62а показаны экватор
сферы и его проекции. Горизонтальная
проекция экватора совпадают с
горизонтальным очерком поверхности
(Экв’=Ф’). Фронтальная и профильная
проекции экватора представляют собой
прямые, параллельные осям x
и y
соответственно. Верхняя полусфера (со
всеми расположенными на ней точками)
на горизонтальной проекции, – видимая,
нижняя, – невидимая.
На
рис. 62б дополнительно к экватору показан
главный фронтальный меридиан ФМ и его
проекции. Внимательно изучите его
расположение на проекциях, сравните с
проекциями экватора. Отметьте для себя,
что фронтальная проекция ФМ’’
фронтального меридиана ФМ совпадает с
фронтальным очерком сферы (ФМ’’ = Ф’’),
а горизонтальная и профильная его
проекции есть прямые, параллельные осям
x
и z
соответственно. Ближняя полусфера на
фронтальной проекции – видимая, дальняя
– невидимая.
На рис. 62в показан
главный профильный меридиан ПМ и его
проекции (для упрощения восприятия
экватор и главный профильный
Рис.
62а
Рис.
62б
Рис.
62в
Рис.
62г
меридиан
не показаны). Профильная проекция ПМ’’’
профильного меридиана ПМ совпадает с
профильным очерком Ф’’’ поверхности,
а его горизонтальная и фронтальная
проекции и есть прямые, параллельные
осям y
и z
соответственно. Левая полусфера сферы
профильной проекции – видимая, правая
– невидимая.
А теперь мысленно
скомпонуйте рис. 62а, 62б, 62в в одно
изображение, представленное на рис.
62г. недостающие проекции точек, заданных
на каждой из опорных линий каркаса
сферической поверхности, следует
отыскивать на соответствующих проекциях
именно этих опорных линий с учетом их
видимости. Рассмотрите проекции точек
1 и 2 экватора на рис. 62а и 62г, убедитесь
в их адекватности. Разберитесь с точками
3, 4 заданными на горизонтальной проекции
главного фронтального меридиана (рис.
62г), и с точками 5, 6, заданными на профильной
проекции главного профильного меридиана.
На своем экземпляре методического
пособия можете нанести (карандашом)
точки 3, 4, 5, 6 и их проекции на рис. 62б, в.
Проекции точек сферы, не принадлежащих
опорным линиям ее каркаса, определяются
аналогично поверхности вращения общего
вида через проекции параллелей (рис.
60, 61 и текст к ним).
5.3.3.2 Коническая
поверхность
Как
отмечалось выше, в общем случае коническая
поверхность формируется перемещением
образующей по криволинейной направляющей
таким образом, что в каждом положении
образующая проходит через общую точку
S
и пересекает направляющую в какой-то
точке (рис. 49б, 50). Если направляющей
является окружность, а точка S
расположена на перпендикуляре к ее
центру, то полученная поверхность носит
название «прямой круговой конус» или
просто «конус» в общепринятом понимании
(рис. 48б).
Как и для любой
поверхности вращения, опорными линиями
каркаса прямого кругового конуса
являются главный фронтальный меридиан
(см. ФМ’, ФМ’’ рис. 63а) и главный профильный
меридиан (ПМ’, ПМ’’). Условным экватором
конуса является его основание. Это
означает, что горизонтальные проекции
любых точек на поверхности вертикального
конуса являются видимыми. Недостающие
проекции точек 1…5, заданных фронтальными
проекциями, определяются аналогично
сфере по принадлежности каждой из них
своей опорной линии. Недостающие проекции
точек, не принадлежащих опорным линия,
могут быть определены как через проекции
образующих (см. точки 1, 2 рис. 63б), так и
через проекции параллелей (точка 3).
Студентам
рекомендуется
определить горизонтальные проекции
точек 1, 2 через проекции параллелей, а
фронтальную проекцию точки 3 через
проекцию образующей и убедиться, что
результаты будут совпадать абсолютно.
Рис.
63а
Рис.
63б
3.3.3 Цилиндрическая
поверхность
Вопрос формирования
поверхности прямого кругового цилиндра
рассмотрен ранее. Опорные линии каркаса
поверхности представлены на рис. 64
(см. ФМ’, ФМ’’, ПМ’, ПМ’’). Отметим, что
экватора эта поверхность не имеет.
Некоторые характерные моменты, связанные
с этой поверхностью, сводятся к следующим.
В
на горизонтальной проекции все точки,
кроме расположенных на верхнем срезе
(4, 5, 8) будут невидимыми.
Во-вторых, поскольку
любая образующая такого цилиндра
является горизонтально-проецирующей
линией (как, кстати, и у прямой призмы)
горизонтальные проекции любых точек
поверхности будут отображаться только
на ее горизонтальный очерк Ф’) и сойти
с него не могут.
В-третьих,
горизонтальная проекция точки 8 (видимая),
однозначно говорит о том, что точка
расположена на верхнем срезе поверхности.
В
Рис.
64
-четвертых, горизонтальная
проекция точки 9 (невидимая) говорит о
том, что точка 9 находится где-то
ниже верхнего среза поверхности, и для
построения ее фронтальной проекции
дополнительно необходимо задать
аппликату точки (например, 9z=10).
В порядке самоконтроля студентам
рекомендуется самостоятельно построить
профильные проекции поверхностей и
точек, представленных на рис. 63 и 64.
5.4 Сечение поверхности
плоскостью частного положения
5.4.1 Общие замечания
Предлагаемая тема
является элементом теоретической
подготовки студентов к выполнению
графического модуля «Проекционное
черчение» учебного курса. Рассмотрим
ее на примерах решения нескольких
однотипных задач применительно к
различным поверхностям. Обобщенная
формулировка задачи выглядит следующим
образом: «построить проекции и
действительную величину фигуры сечения
поверхности плоскостью частного
положения». Обобщающая формализованная
запись условия задачи выглядит так:
Предварительно
заметим, что линия l
пересечения поверхности плоскостью
строится по отдельным точкам, общим для
плоскости и поверхности. Построение
следует начинать с так называемых
характерных точек: верхней, нижней,
ближней, дальней, левой, правой, границ
зон видимости. Если характерных точек
окажется недостаточно для выявления
формы искомой кривой, находят несколько
пар обыкновенных (рядовых) точек. Решают
вопрос о видимости точек и последовательности
их соединения. Следует отметить, что не
в любой задаче каждую из характерных
точек можно определить прямым построением.
В этом случае в предполагаемой области
характерной точки можно задать несколько
посредников и через них уточнить ее
положение.
5.4.2 Сечение сферы
плоскостью частного положения
Для
облегчения понимания материала процесс
построения линии l
разбит на несколько графических
фрагментов (рис. 65а-г). В порядке «входа
в тему» попытаемся ответить на вопрос
о форме искомой линии l
в пространстве
Рис.
65а
Рис.
65б
Рис.
65в
Рис.
65г
и
на проекциях. При этом полезно вспомнить,
что в сечении сферы любой некасательной
плоскостью всегда будет окружность. В
нашей задаче (рис. 65а) плоскость
перпендикулярна фронтальной плоскости.
Отсюда следует, что фронтальной проекцией
l’’
окружности
l
будет прямая внутри очерка сферы,
совпадающая со следом – проекцией
плоскости
(вспомните: «любая точка, линия или
плоская фигура, расположенная в
проецирующей плоскости, отображается
на ее след-проекцию», а линия l
принадлежит как поверхности, так и
плоскости ).
Горизонтальная проекция линии l
представляет собой эллипс, поскольку
плоскость
не параллельная горизонтальной плоскости
проекции. Таким образом, задача сводится
к, построению на горизонтальной плоскости
H
проекции эллипса l,
по однозначно определянной фронтальной
проекции l’’
= V
=
’’
окружности l.
Из
рис. 65б видно, что точка 1 является верхней
правой точкой линии l,
точка 1*
– нижней левой. Поскольку их проекции
1’’ и 1*’’
лежат на фронтальной проекции главного
фронтального меридиана Ф’’ (см. рис.
62б, г), горизонтальные проекции 1’ и 1*’
точек должны располагаться на
горизонтальной проекции фронтального
меридиана (рис. 65б). Так как точка 1*
расположена под экватором, на горизонтальной
проекции она будет невидимой (1*’).
Отрезок 1’-(1*’)
есть малая ось искомого эллипса. Поскольку
эллипс является фигурой симметричной,
его оси взаимноперпендикулярны и делят
друг друга пополам. Отсюда, разделив
отрезки 1′-(1*‘)
и 1’’-(1*‘’)
пополам (рис. 65б), получаем проекции
k’
и k’’
точки k
пересечения осей и заодно – направление
большей оси на горизонтальной
(перпендикулярно 1’-(1*‘))
и фронтальной (2’’ = (k’’)
= (2*’’))
проекциях. Концы 2 и 2*
большей оси эллипса на горизонтальной
проекции определяем с помощью параллели
m,
фронтальную проекцию m’’
которой предварительно проводим через
точку 2’’ = (k’’)
= (2*’’).
Отметим при этом, что точка 2 является
самой ближней, точка 2*
– самой дальней.
Если
точка 1 (рис. 65б) видимая, а точка 1*
– невидимая на горизонтальной проекции,
то, естественно, на кривой l
необходимо определить точку, в которой
видимость меняется на обратную. Такой
границей для сферы является ее экватор
и принадлежащие ему точки 4, 4*
(проекции 4’’ (4*’’))
кривой l
(рис. 65в), горизонтальные проекции которых
лежат на горизонтальном очерке сферы.
Для двухплоскостного чертежа характерные
точки определены, и остается определить
несколько пар обычных точек. Их положение
на горизонтальной проекции определяется
через параллели a,
n,
b,
предварительно произвольно заданные
на фронтальной проекции. А теперь
отдельные фрагменты (рис. 65а-в) объединим
на одном изображении, добавив сюда
обыкновенные точки 3, 3*
(рис. 65в), 5, 5*
и 6, 6*
(рис. 65г). Это и есть результат решения
поставленной задачи.
Действительная
величина |l|
фигуры сечения сферы плоскостью
в общем случае определяется известными
способами преобразования комплексного
чертежа, например, способом замены
плоскостей проекций. Применительно к
рассматриваемой задаче, когда форма
кривой наипростейшая и симметричная,
действительная величина фигуры сечения
может быть определена простой логикой:
если смотреть на сечение в направлении,
перпендикулярном плоскости
(стрелка А, рис. 65г), увидим фигуру сечения
в действительную величину в виде
окружности диаметром, равным отрезку
1’’-2’’. Проводим ее по линиям связи,
перпендикулярным .
5.4.3 Коники
Поверхность
прямого кругового конуса занимает
особое положение среди других
поверхностей. Она уникальна тем, что
является носителем совокупности кривых
второго порядка: окружности 2 (рис. 66а),
эллипса 3 (рис. 66а), параболы 5 (рис. 66б)
и гиперболы 6 (рис. 66в), которые получаются
при сечении конуса различно расположенными
плоскостями. Окружность получается
когда секущая плоскость 2
перпендикулярна оси конуса; эллипс –
когда плоскость 3
не перпендикулярна оси и пересекает
обе очерковые образующие конуса; парабола
– когда плоскость 5
параллельна очерковой
Рис.
66а
Рис.
66б
Рис.
66в
образующей,
а гипербола – когда плоскость 6
занимает положение между плоскостью
5
и параллельной оси конуса. Помимо этого,
сечение конуса плоскостью, проходящей
только через вершину S,
дает точку 1 (рис. 66а),
плоскостью
4,
касательной к конусу, – прямую (рис. 66б),
а плоскостью 7,
проходящей через вершину S
и основание конуса, – две прямые (рис.
66в).
Для самопроверки
студентам рекомендуется построить
горизонтальные и фронтальные проекции
линий 2 – 7, руководствуясь положениями
п. 5.3.3.2 и рис. 63.
5.4.4 Сечение конуса
плоскостью частного положения
У
задачи, его формализованная запись и
ход рассуждений при ее решении аналогичны
вышеописанным. Сразу определимся, что
за линии будут в сечении и на проекциях.
По расположению секущей плоскости
(рис. 67а) однозначно отвечаем: в
пространстве и на горизонтальной
проекции, – парабола, на фронтальной
проекции – прямая, совпадающая со следом
проекцией V
= ’’
секущей плоскости ;
то есть задача сводится к построению
горизонтальной проекции l’параболы
l
и ее действительной величины |l|.
О
Рис.
67а
пределяем характерные точки. Точка
1 – верхняя, правая; точки 2 и 2*
– нижняя ближняя и нижняя дальняя
соответственно.
Точка 1 находится на главном фронтальном
меридиане, точки 2, 2*
– на условном экваторе (на основании)
конуса, что и определяет их горизонтальные
проекции по принадлежности. Других
характерных точек нет. Остается взять
несколько пар обычных точек под номерами
3, 4, 5 (рис. 67б). Их положение на фронтальной
проекции задается совершенно произвольно
(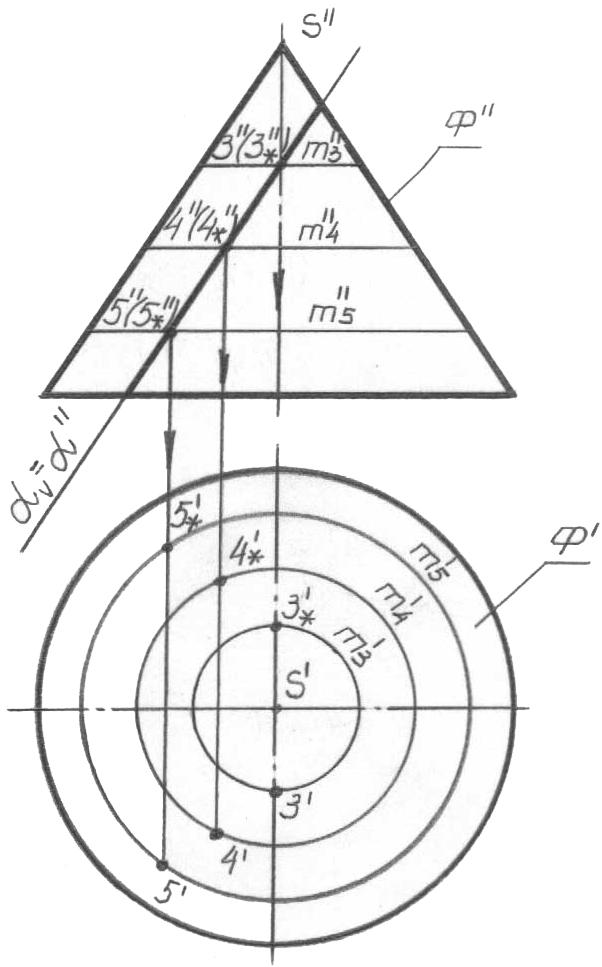
более-менее равномерно), а горизонтальные
проекции определяются через соответствующие
параллели m3,
m4,
m5
(см.
также раздел 5.3.3.2 и рис. 63). Сведите
изображения (рис. 67а, б) в обобщающее
изображение (рис. 67в), являющееся
результатом решения задачи.
В
Рис.
67б
основу построения действительной
величины фигуры сечения l
положен метод замены плоскостей проекций.
При этом рассуждаем следующим образом.
Поскольку на горизонтальной проекции
линия l
спроецировалась
с
искажением, логично эту
традиционно
горизонтальную плоскость проекций
заменить на другую тоже горизонтальную,
но не параллельную H,
а параллельную
плоскость. Тогда ось x1,1
новой системы плоскостей (см. раздел 4
«Способ замены плоскостей проекций»)
V/H1,
будет параллельна V’’.
Положение этой оси x1,1
можно задать на любом свободном поле
чертежа. Поскольку парабола является
симметричной кривой для удобства
построений начальную системы осей xyz
задаем через центр S’.
Тогда построение точек действительной
величины линии l
сведется к откладыванию отрезков равных
величин (см. размеры в фигурных скобках),
взятых с прежней горизонтальной проекции,
на соответствующую линии проекционной
связи новой системы x1,1
V/H1.
Эти отрезки есть ничто, иное как значения
Y
каждой точки, в старой системе плоскостей
проекций.
Рис.
67в
Например,
отрезок S’3*’
следует отложить в новую систему с осью
x1,1
вправо и влево от оси x1,1,
отрезок 4*’x
– по своей линии связи и т.д. до последней
пары точек под номером 2.
Действительную
величину фигуры сечения в общем случае
можно строить в проекционной связи, как
только что описано, со смещением (см.
изображением с осью x1,2)
и со смещением и поворотом (см. изображение
с осью x1,3).
В последних двух случаях из-за нарушения
проекционных связей следует обеспечить
вдоль осей x1,2
и
x1,3
равенство
расстояний между линиями связи отрезкам
1’’-3’’(3’’) – 4’’(4*’’)
и т.д. до точек 2’’(2*’’).
При этом за начало построений может
быть принята любая точка 10,
расположенная где угодно на новой оси.
Принятый Вами из трех вариантов построения
действительной величины фигуры сечения
определяется условиями компоновки
изображений на чертеже в каждом конкретном
случае. В заключение отметим, что
традиционное (кстати, более привычное
для студентов) расположение координатных
осей между горизонтальной и фронтальной
проекциями конуса привело бы к смещению
вправо изображения искомой линии |l|
относительно осей x1,1,
x1,2,
x1,3
без
нарушения ее формы и сделало бы менее
удобным само построение линии |l|.
5.4.5 Сечение пирамиды
плоскостью частного положения
П
Рис.
68
оскольку пирамида (рис. 68) представляет
собой гранную поверхность, искомая
линия l
в пространстве и на горизонтальной
проекции будет многоугольником (в нашем
случае – треугольником). Как и в предыдущих
случаях (см. рис. 65, 68), фронтальная
проекция l’’
линии l
совпадает со следом-проекцией секущей
плоскости .
Задача сводится к определению точек 1,
2, 3 (рис. 68) пересечения каждого из ребер
пирамиды с плоскостью .
Так как плоскость
перпендикулярна фронтальной плоскости
проекций искомые точки
1,
2, 3 являющиеся общими и для
ребер
и для плоскости ,
будут представлять собой точки 1’’,
2’’, 3’’ пересечения
проекции каждого ребра со следом
проекцией V
= ’’
плоскости .
Горизонтальные проекции 1’, 2’, 3’ точек
определяются по их принадлежности
каждому ребру. Так как плоскость
не параллельна основанию АВС пирамиды,
ни одна из сторон треугольника 1’2’3’
не должна быть параллельна соответствующим
сторонам основания A’B’C’.
Поскольку
форма сечения несимметричная, для
построения действительной величины
фигуры сечения расположение оси x
в начальной системе V/H
задаем традиционным, т.е. совпадающим
с основанием пирамиды. Проводим ось х1
параллельно плоскости
и линии проекционной связи (перпендикулярные
V
= ’’
из точек 1’’, 2’’, 3’’) для определения
местоположения на них точек 10,
20,
30.
По линии связи точки 3 откладываем на
сечении расстояние Y3,
взятое
от оси x
до горизонтальной проекции 3’ точки 3.
аналогично поступаем с точками 2 и 1,
получая в итоге точки 30,
20,
10,
определяющие истинную форму искомого
треугольника.
5.4.6 Сечение призмы
плоскостью частного положения
А
рассмотренным на рис. 65, 67, 68 примерам,
фронтальная проекция фигуры сечения
призмы плоскостью
(рис. 69) совпадает со следом-проекцией
плоскости .
В пространстве и на горизонтальной
проекции линия l
будет четырехугольником (по числу граней
призмы). Так как каждая грань рассматриваемой
призмы представляет собой
горизонтально-проецирующую плоскость,
а ребра a,
b,
c,
d
–
Рис.
69
горизонтально-проецирующие
прямые,
горизонтальные проекции 1’, 2’, 3’, 4’
точек пересечения ребер призмы с
плоскостью
совпадают с горизонтальными проекциями
a’,
b’,
c’,
d’
соответствующих ребер. Другими словами,
горизонтальная проекция фигуры сечения
совпадает с горизонтальным очерком
поверхности. Действительная величина
|l|
фигуры сечения l
построена в проекционной связи аналогично
рис. 68.
5.4.7 Сечение цилиндра
плоскостью частного положения
Н
Рис.
70
а рис. 70 показаны проекции и
действительная величина фигуры сечения
прямого кругового цилиндра
фронтально-проецирующей плоскостью .
Поскольку цилиндр занимает
горизонтально-проецирующее положение,
горизонтальные проекции всех точек
линии l,
располагаются на горизонтальном очерке
поверхности,
т.е. горизонтальная
проекция
линии l
представляет собой окружность.
Действительная
величина фигуры сечения представляет
собой эллипс, построенный со смещением
и поворотом. Порядок построения, его
аналогичен рис. 67. Текущие значения
координаты Y
точек 20,
30
и
др. показаны фигурными скобками.
Рассмотренная
тематика позволяет осуществить построение
проекций и действительной величины
фигуры сечения предметов практически
любой конфигурации, представляющей
собой совокупность нескольких элементарных
геометрических форм.
5.5 Пересечение
поверхностей
5.5.1 Общий алгоритм
построения линии пересечения поверхностей
Для построения
линии пересечения поверхностей Ф1
и Ф2 (рис. 71) необходимо.
-
П
ересечь
заданные поверхности вспомогательным
геометрическим элементом – посредником
(α1). -
Построить линии (m1 и
n1) пересечения
посредника (α1) с каждой поверхностью
в отдельности. -
Н
Рис.
71айти точки (1 и 1*) пересечения
полученных
линий
(m1 и n1).
-
Повторить этот алгоритм
необходимое количество раз (на рис. 71
это не показано). -
Соединить между собой
полученные точки (1, 1*, 2, 2* и
т.д.) в надлежащей последовательности.
Символическая запись порядка построения
выглядит следующим образом.
-
α1 ∩ Ф1 = m1;
α1 ∩ Ф2 = n1;
m1 ∩ n1 = 1, 1* – первый
шаг. -
α2 ∩ Ф1 = m2;
α2 ∩ Ф2 = n2;
m2 ∩ n2 = 2, 2* – второй
шаг.
и т.д.
i) αk∩
Ф1 = mk;
αk ∩ Ф2 = nk;
mk ∩ nk = k, k*
– последний шаг.
l = {1, 1*,
2, 2*, … k, k*}.
Для значительного
облегчения и обеспечения четкости
решения любой задачи на пересечение
поверхностей рекомендуется внутри
каждого шага алгоритма присваивать
один и тот же индекс всем элементам
построения, т.е. посредник, например с
индексом 5 дает линии m5
и n5, пересечение которых дает
точки под номером 5 со своими отличительными
признаками (5*, 50, 5., 5∆
и т.д.).
5.5.2 Общие
замечания
-
В общем случае в качестве
посредников могут приниматься плоскости
общего положения, плоскости частного
положения, концентрические или
эксцентрические сферы, цилиндры и т.д.
в зависимости от конкретной графической
задачи. -
Посредник должен выбираться
таким (по виду) и так (по расположению),
чтобы линии m и n
были наипростейшими (окружности, прямые,
совокупности прямых). -
Точки 1, 2 и т.д. искомой линии
l должны располагаться
в пределах площади взаимного наложения
проекций пересекающихся поверхностей
(затемненная зона рис. 71). -
Построение следует начинать
с так называемых “характерных”
точек: верхней, нижней, левой, правой,
ближней, дальней, границ зон видимости
и т.д. Если характерных точек окажется
недостаточно для однозначного определения
характера искомой линии, необходимо
найти несколько так называемых
“обыкновенных” точек. -
Если пересекающиеся
поверхности имеют общую плоскость
симметрии, параллельную какой-либо
плоскости проекций, то пересечение их
очерков дает пару характерных точек,
а остальные точки (в том числе и
характерные) находятся в створе друг
друга. -
Порядок линии пересечения
численно равен произведению порядков
пересекающихся поверхностей. -
Вопросы видимости –
невидимости точек и последовательности
их соединения решаются для каждой
задачи в отдельности.
5.5.3 Метод плоских
посредников
От наглядного
представления сути алгоритма, показанного
на рис. 71, перейдем непосредственно к
построению линии пересечения этих
поверхностей на двухплоскостном чертеже
(рис. 72). Формализованная запись условия
задачи выглядит следующим образом:
Ф
1,
Ф2; Ф1 ∩ Ф2 = l?
Рис.
72а
Анализ и решение
задачи.
-
Пересекаются две поверхности
вращения второго порядка, следовательно,
искомая линия l будет
четвертого порядка. -
Так как вид пересечения –
“врезка” (несквозное пересечение),
то линия l будет одна. -
Поверхности имеют общую
плоскость симметрии α1, параллельную
фронтальной плоскости проекций (рис.
72а), значит пересечение их фронтальных
очерков Ф1” и Ф2” дает пару
характерных точек: 1” – верхнюю и 1*”
– нижнюю. Кстати, заметим, что использование
плоскости α1 в
качестве первого посредника дает тот
же результат, поскольку линии m1”
и n1” есть ничто
иное, как фронтальные очерки поверхностей. -
В качестве посредников для
последующих построений в этой задаче
целесообразно принимать горизонтальные
плоскости α2, α3
и т.д., поскольку линии пересечения
ими каждой из поверхностей (см. рис. 72
а,б) являются наипростейшими (окружностями). -
Границей зоны видимости
искомой кривой l для
горизонтальной плоскости проекций
является экватор сферы, поэтому
плоскость – посредник α2,
проведенная через экватор сферы Ф2,
дает на втором шаге алгоритма принадлежащие
экватору точки 2 и 2*, являющиеся
границами зоны видимости для горизонтальной
плоскости проекций. Эти же точки являются
самыми левыми. -
Границами видимости для
фронтальной плоскости проекций являются
главные фронтальные меридианы
пересекающихся поверхностей и
принадлежащие им точки 1 и 1*. За
счет наличия общей плоскости симметрии
α1, параллельной
фронтальной плоскости проекций,
невидимая часть искомой линии l
на плоскости V полностью закроется ее
видимой частью кривой (о чем свидетельствует
двойное обозначение точек 2(2*)) и
т.д. Других характерных точек в
рассматриваемой задаче нет.
Рис.
72б
Таким образом,
построение линии пересечения поверхностей
сводится к следующему.
Во-первых, (рис.
72а) проводим плоскость α1,
параллельную фронтальной плоскости
проекций через оси i и j
поверхностей. На горизонтальной плоскости
проекций – это след-проекция α1Н
= α1‘, параллельная
оси х. На фронтальной проекции находим
точки 1” и 1*” пересечения очерков
Ф1” и Ф2”. Сносим полученные
точки на горизонтальный след-проекцию
α1Н = α1‘
плоскости α1 с учетом
их видимости (точка 1′ – видимая, точка
1*‘ – невидимая). Записываем
первый шаг алгоритма в виде:
1) α1
|| V; α1
i, j; α1
∩ Ф1 = m1; α1
∩ Ф2 = n1; m1
∩ n1 = 1, 1*.
Точка 1 – верхняя,
точка 1* – нижняя.
Отметим, что
алгоритм записывается для пространства,
а построение проекций точек и линии l
производится для каждой плоскости
проекций с обязательным обозначением
каждого элемента построения.
Во-вторых, через
экватор сферы Ф2 проводим
плоскость-посредник α2,
параллельную горизонтальной плоскости
проекций (см. α2V
= α2”). Параллели
m2 и n2
фронтальной проекции неразличимы,
так как их проекции m2”
и n2” частично
накладываются друг на друга. Поэтому
находим их горизонтальные проекции m2‘
и n2‘, как окружности
соответствующих радиусов и точки 2’ и
2*‘ их пересечения. Фронтальные
проекции 2” и 2*” этих точек находим
на следе-проекции α2V
= α2” плоскости
α2 по линиям
проекционной связи. Записываем второй
шаг алгоритма.
2) α2
|| Н; α2 ∩ Ф1 =
m2; α2
∩ Ф2 = n2; m2
∩ n2 = 2, 2*.
Обе точки –
границы видимости для плоскости Н.
В-третьих,
произвольно проводим плоскость α3,
параллельную плоскости Н. Аналогично
второму шагу, находим горизонтальные
проекции m3‘ и n3‘
линий пересечения этой плоскости с
каждой поверхностью и горизонтальные
проекции 3’ и 3*‘ точек 3 и 3*,
а затем на следе-проекции α3V
= α3” – фронтальные
проекции 3” и 3*” этих точек.
Записываем третий шаг алгоритма.
3) α3
|| Н; α3 ∩ Ф1 =
m3; α3
∩ Ф2 = n3; m3
∩ n3 = 3, 3* –
обычные точки.
Аналогично
можно было получить точки под номером
4:
4) α4
|| Н; α4 ∩ Ф1 =
m4; α4
∩ Ф2 = n4; m4
∩ n4 = 4, 4* –
обычные точки.
и этого для
рассматриваемой задачи достаточно.
Определяем
порядок соединения точек между собой,
предварительно объединив рис. 72а и рис.
72б в одно изображение (рис. 72в). Поскольку
искомая кривая l является
замкнутой, ее построение можно начинать
с любой точки и в любом направлении,
например 1, 2, 3, 4, 1*, 4*, 3*,
2*, 1. Заключительная фраза алгоритма
может быть записана в виде:
l = {1, 2,
3, 4, 1*, 4*, 3*, 2*, 1}
Пример оформления
задачи представлен на рис. 72в.
Рис.
72в
5.5.4 Метод
концентрических сфер
Применение
этого метода основано на теореме о
пересечении соосных поверхностей.
Соосными называются поверхности, имеющие
общую ось вращения. Сущность теоремы
сводится к следующему: линией l
пересечения двух соосных поверхностей
вращения является окружность (параллель),
проекция которой l’’ на
плоскость, параллельную общей оси
вращения есть прямая линия, а на плоскость,
перпендикулярную общей оси вращения,
– есть окружность l’
действительной величины (рис. 73а). Это
принципиальное положение справедливо
для любого пространственного положения
(сравните рис. 73а и рис. 73б) любых соосных
пересекающихся поверхностей. В заключение
отметим, что две пересекающиеся любым
образом сферы всегда соосны, поскольку
проходящая через их центры прямая всегда
является их общей осью вращения.
Рис.
73а
Рис.
73б
Рассмотрим
задачу построения линии пересечения
поверхностей с использованием метода
концентрических сфер на примере прямого
кругового конуса и кругового цилиндра.
Для упрощения понимания на рис. 74 дано
поэтапное решение задачи. Предварительно
сформулируем условия применения этого
метода. Их три. Во-первых, пересекающиеся
поверхности должны быть поверхностями
вращения. Во-вторых, оси поверхностей
должны пересекаться. В-третьих, поверхности
должны иметь общую плоскость симметрии,
параллельную одной из плоскостей
проекций. Эти условия должны выполняться
одновременно. Отметим, что применение
метода концентрических сфер не исключает
использования любых других посредников,
дающих нужный результат наипростейшим
путем.
Некоторые
преимущества метода концентрических
сфер заключаются в том, что он позволяет
получить искомую линию пересечения
поверхностей на единой проекции (без
привлечения построений на других
плоскостях проекций). Однако, и в учебном
процессе, и в инженерной практике это
преимущество не стоит преувеличивать.
Рис. 74а
Рис. 74б
Рис. 74в
Сферические
посредники должны проводиться из точки
пересечения осей поверхностей, поскольку
только в этом случае они (посредники)
окажутся соосными с каждой из пересекающейся
поверхностей. В качестве минимального
посредника должна приниматься большая
из сфер (Р2, рис. 74а), вписанных из
точки пересечения осей (i
и j) в каждую поверхность
в отдельности. Это связано с тем, что
меньшая из вписанных сфер (Р0) не
дает линии пересечения (или касания) с
другой поверхностью (Ф1) и,
следовательно, не дает точки, общей для
пересекающихся поверхностей. В качестве
максимального посредника принимается
сфера (Р1, рис. 74б), радиус которой
равен расстоянию от точки пересечения
осей i и j
до наиболее удаленной точки (1*,
рис. 74а) пересечения очерков поверхностей
Ф1 и Ф2. Остальные сферические
посредники должны быть больше минимального
и меньше максимального.
Анализ и решение
задачи.
-
Пункты 1-3 из предыдущей
задачи (рис. 72) один к одному справедливы
для рассматриваемого примера. -
Для определения минимального
посредника Р на фронтальной плоскости
проекций (рис. 74а) проводим сферы Р0
и Р2 (проекции Р0” и Р2”),
вписанные соответственно в поверхности
Ф2 и Ф1 (проекции Ф2”
и Ф1”). В качестве минимального
посредника принимаем сферу Р2
(проекция Р2”), отвергая Р0
(проекция Р0”), как не дающую
линию m0 пересечения
с поверхностью конуса Ф1 (проекция
Ф1”). Через точки касания сферы
Р2 (проекция Р2”) с конусом
Ф1 (проекция Ф1”) проводим
линию m2 (проекция
m2”) касания (напомним,
что касание – есть частный случай
пересечения) ее с конусом Ф1
(проекция Ф1”), а через точки
пересечения Р2 (проекция Р2”)
с цилиндром Ф2 (проекция Ф2”)
– линию n2 (проекция
n2”) пересечение
посредника Р2 с цилиндром Ф2.
Находим точки 2”, 2*” пересечения
линий (в пространстве – окружностей)
m2” и n2”.
Находим горизонтальную проекцию m2‘
параллели m2 и по
линии связи сносим на нее точки 2′, 2*‘.
Записываем второй шаг алгоритма.
2. Р2 > P0
– минимальная сфера. Р2 ∩ Ф1
= m2; Р2 ∩ Ф2
= n2; m2
∩ n2 = 2, 2* –
левые точки. В качестве максимального
посредника принимаем сферу Р1
(рис.74б), проходящую через ранее полученную
точку 1* (проекция 1*”).
Остальные сферические посредники должны
быть радиусом больше Р2 и меньше
Р1.
-
Для определения границы
зоны видимости горизонтальной проекции
искомой линии l через
условный экватор цилиндра Ф2
(через ось j) проводим
горизонтальную плоскость уровня α3
(след проекция α3V
= α3”). Эта плоскость α3
пересекает конус Ф1 по окружности
m3 (проекция m3”),
а цилиндр Ф2 по прямоугольнику,
фронтальная проекция которого есть
прямая n3”, а
горизонтальная проекция n3‘
совпадает с горизонтальным очерком
Ф2‘ цилиндра Ф2. Горизонтальные
проекции m3‘ и n3‘
линий m3 и n3,
пересекаясь, дают точки 3 и 3* (проекции
3′ и 3*‘). Фронтальные проекции 3”
и 3*” этих точек находятся на
следе-проекции α3V
= α3” плоскости α3 по
линиям проекционной связи. Записываем
третий шаг алгоритма.
3. α3
|| Н; α3 j;
α3 ∩ Ф1 = m3;
α3 ∩ Ф2 = n3;
m3 ∩ n3
= 3, 3*. – границы видимости для
горизонтальной плоскости проекций,
одновременно являющиеся ближней и
дальней точками.
На этом характерные
точки заканчиваются, и следует перейти
к построению обыкновенных точек.
-
Проводим сферический
посредник Р4, больший Р2 и
меньший Р1 (проекция Р4”).
Находим фронтальные проекции m4”
и n4” линий m4
и n4 пересечения
посредника Р4 с поверхностями
конуса и цилиндра и точки m4”
и n4”, пересечения
этих линий. Строим горизонтальную
проекцию m4‘ параллели
m4 и на ней по линии
связи – горизонтальные проекции 4′, 4*‘
искомых точек. Записываем четвертый
шаг алгоритма.
4. Р1 > P4
> P2; Р4 ∩ Ф1
= m4; Р4 ∩ Ф2
= n4; m4
∩ n4 = 4, 4*.
-
Аналогично решается и
записывается последний пятый шаг
алгоритма.
5. Р1 > P5
> P2; Р5 ∩ Ф1
= m5; Р5 ∩ Ф2
= n5; m5
∩ n5 = 5, 5*.
и заключительная
фраза алгоритма
l
{1,2,3,4,5,1*,5*,4*,3*,2*,1}
Объединив рис. 74а
и рис. 74б на одном изображении, получите
окончательное решение задачи в виде
рис. 74в, на котором дан пример оформления
этого задания.
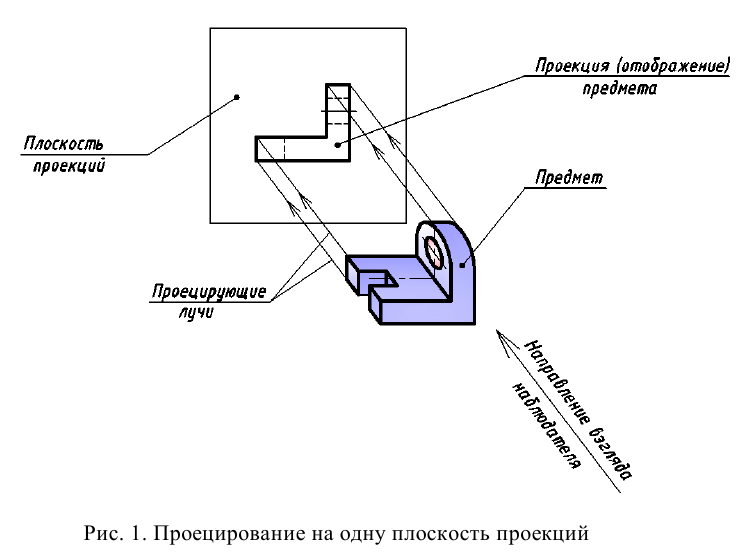
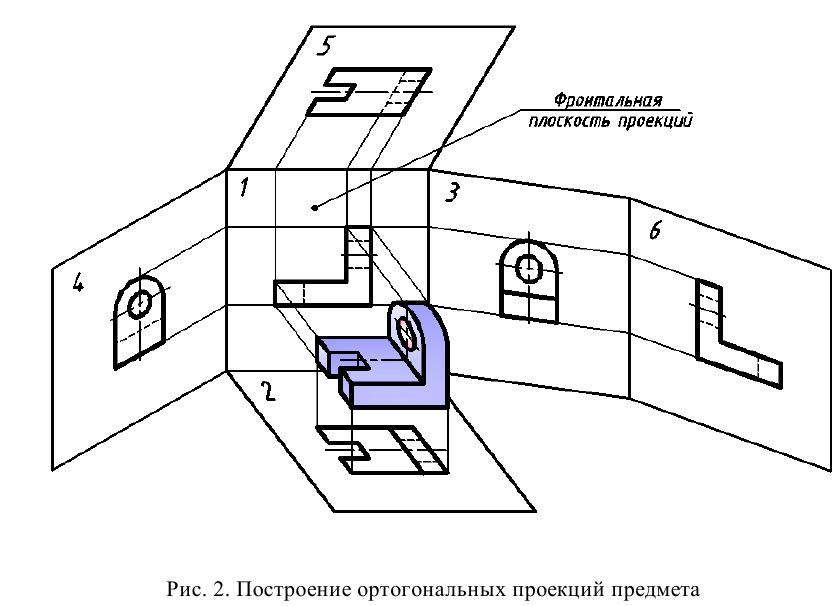
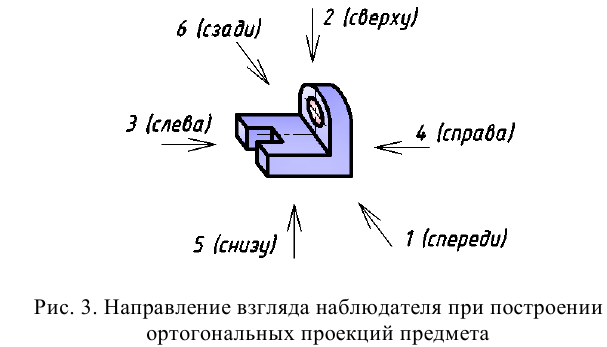
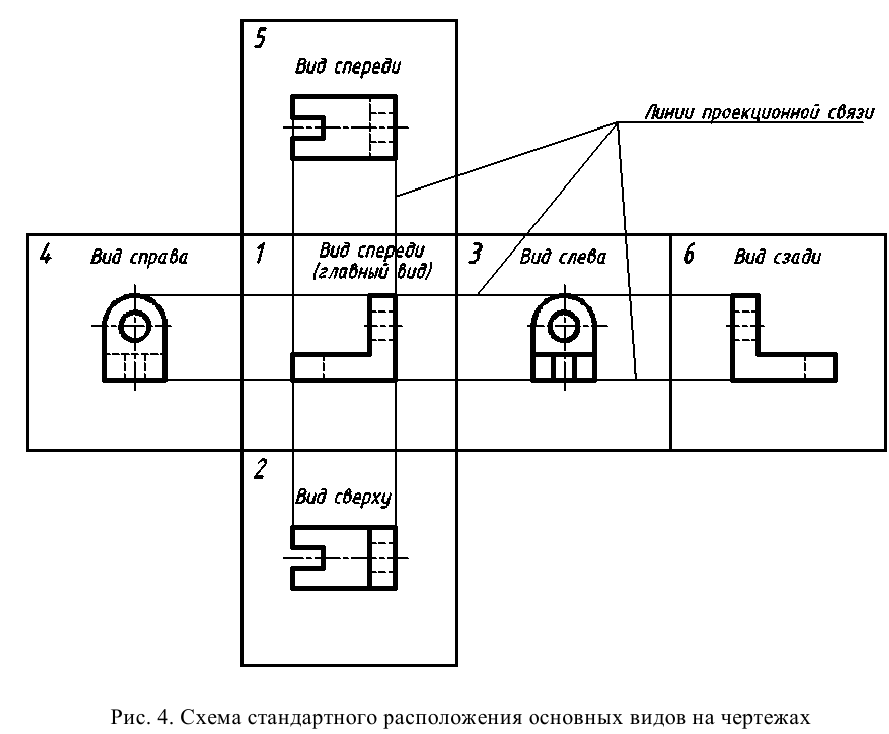
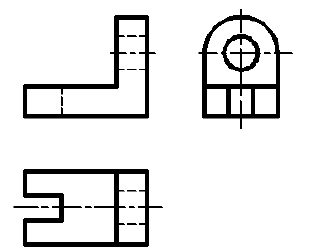
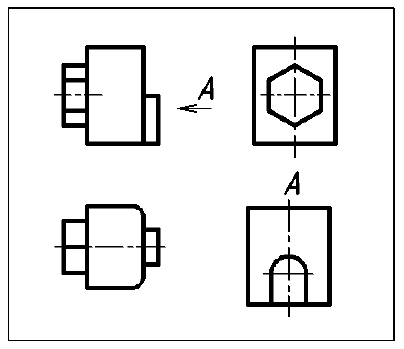
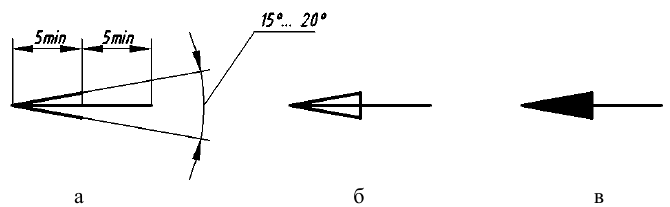
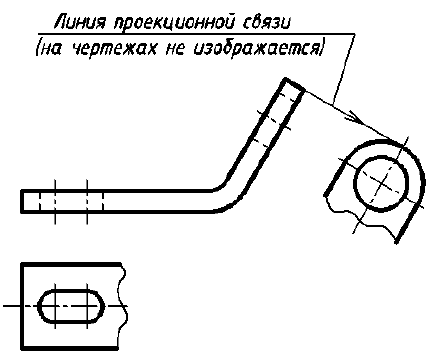
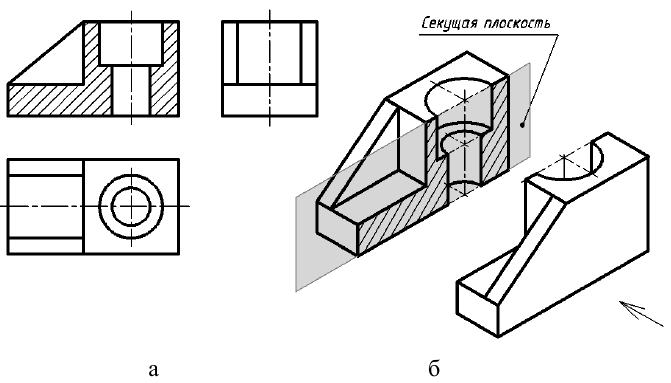
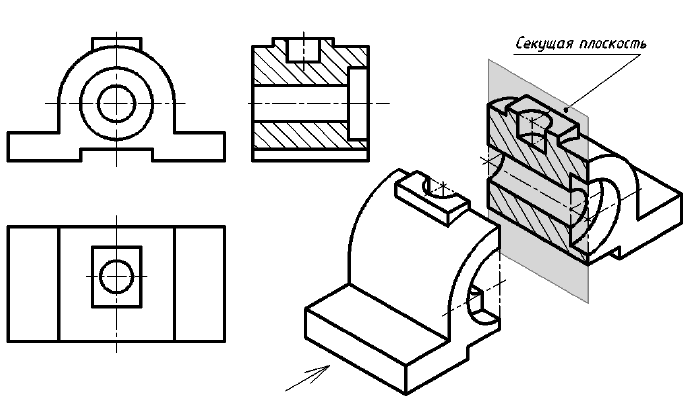
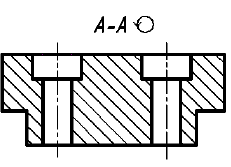
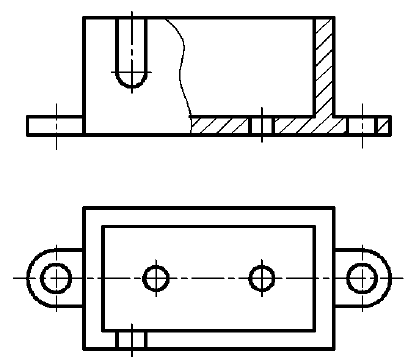
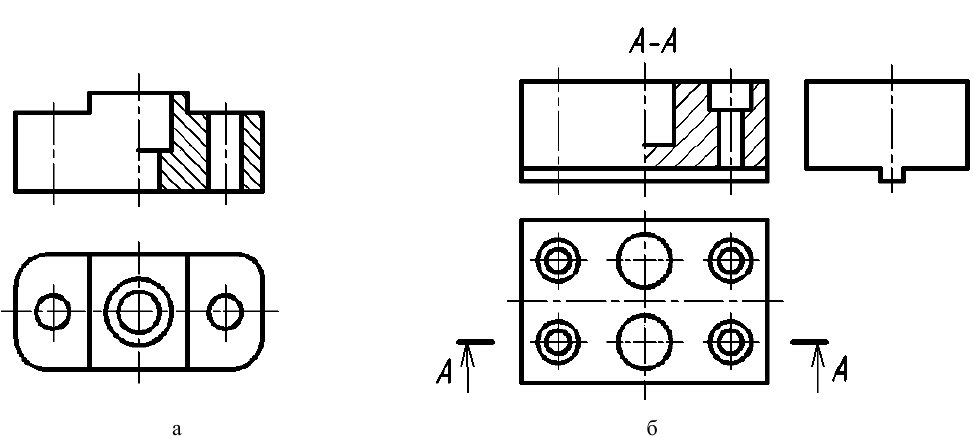
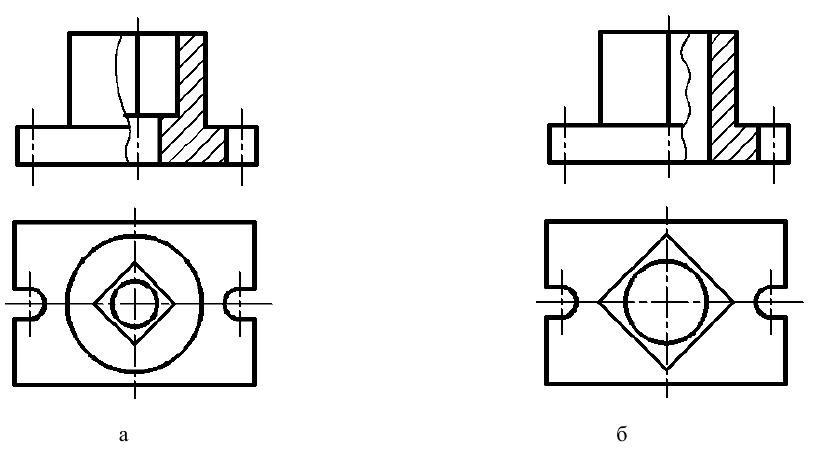
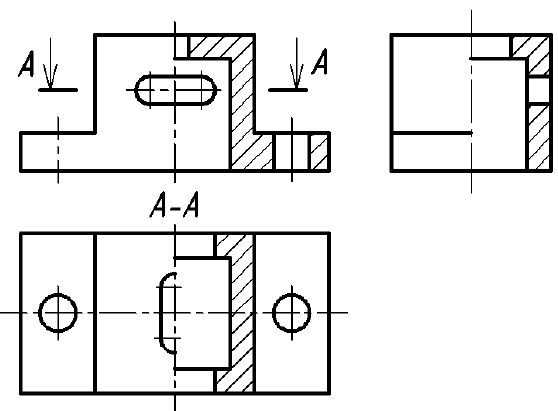
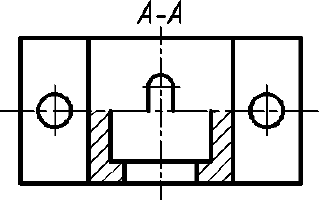
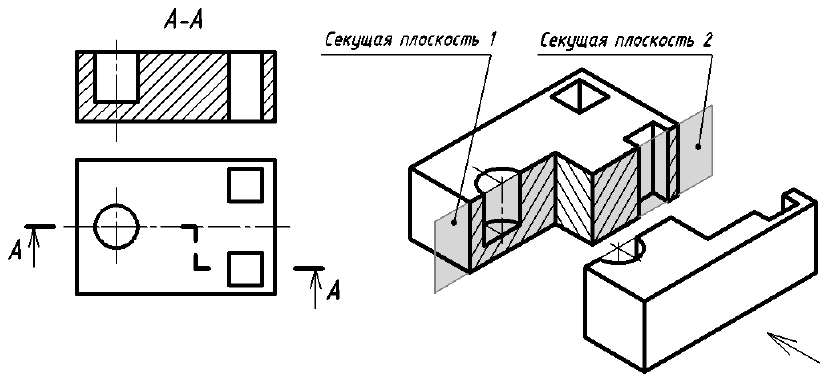
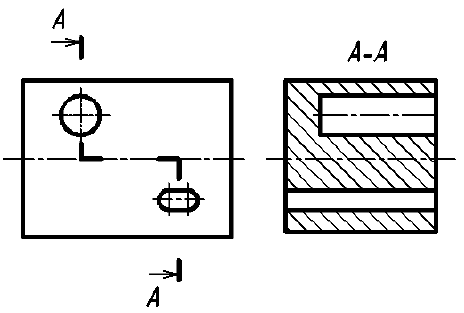
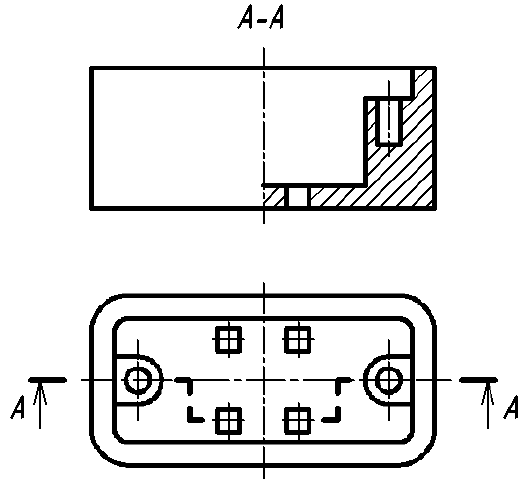
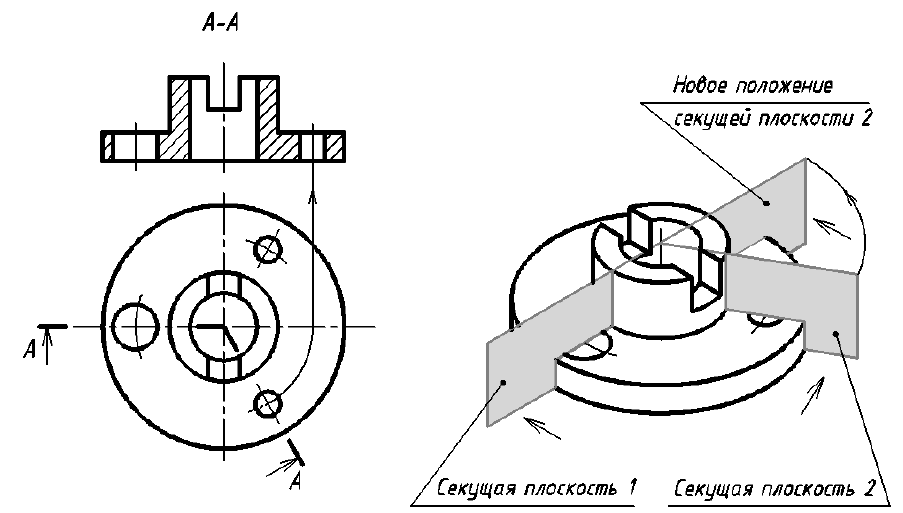
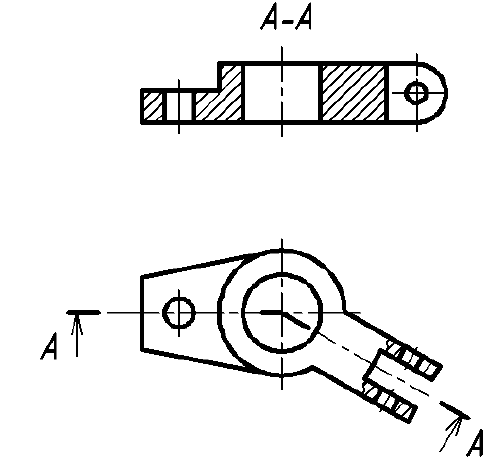
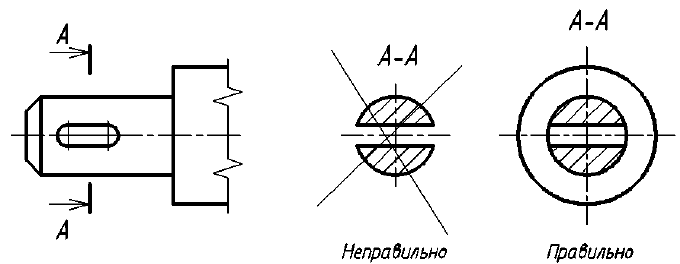
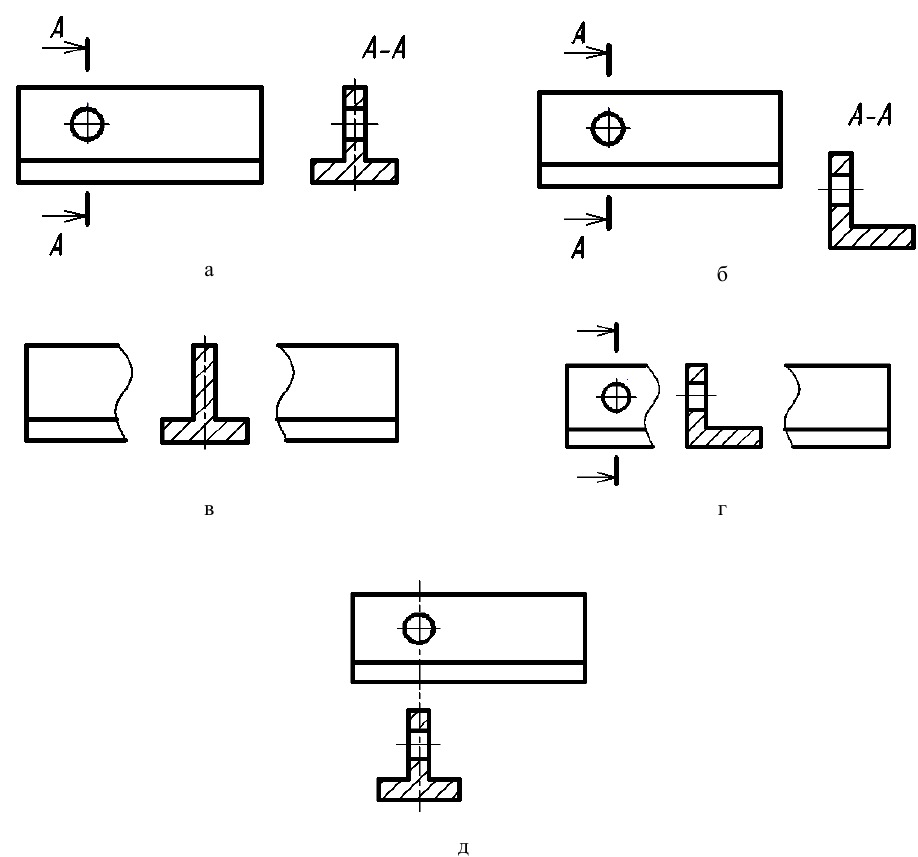
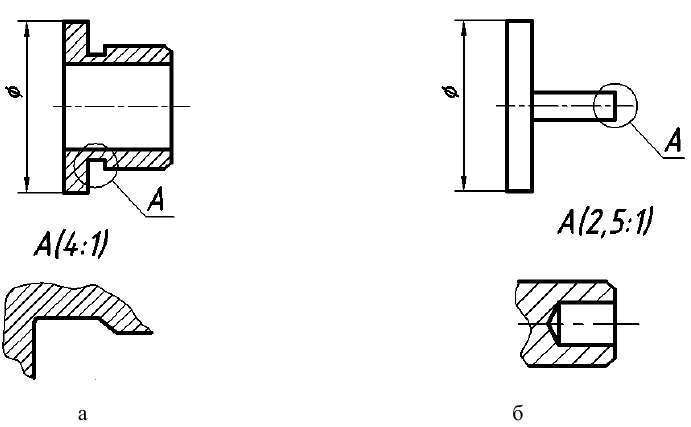
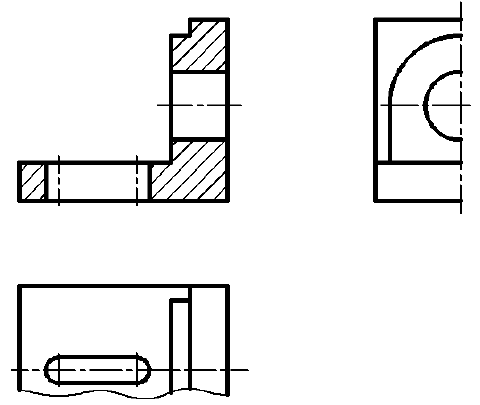
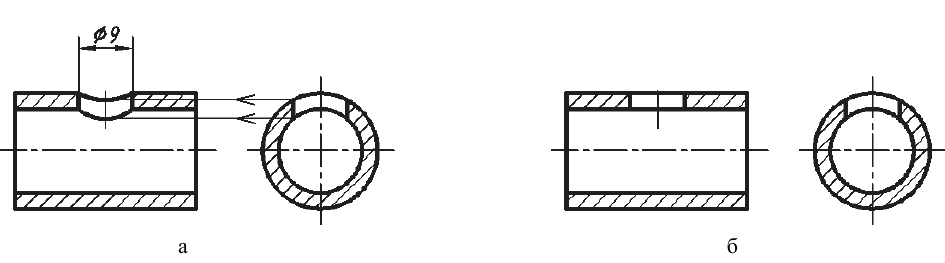
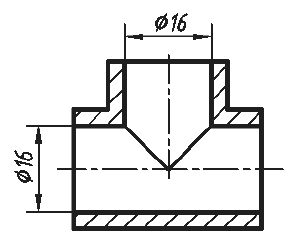
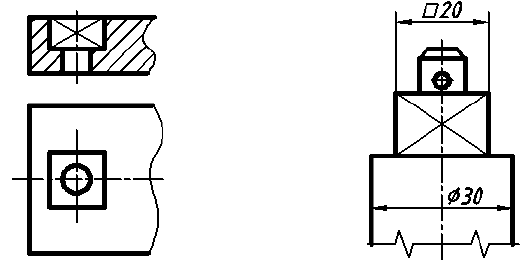
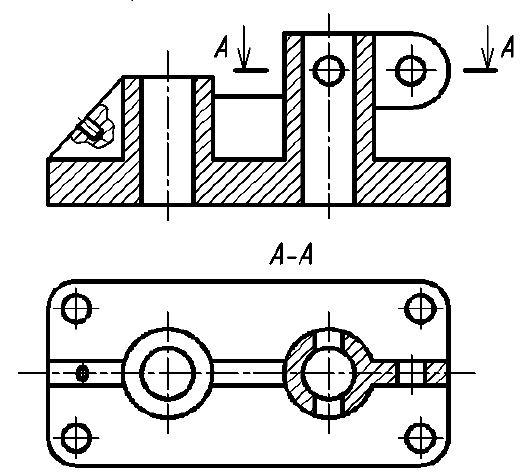
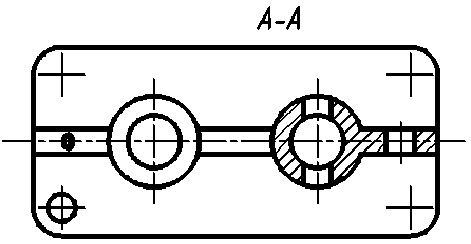
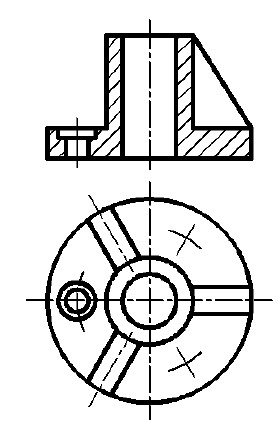
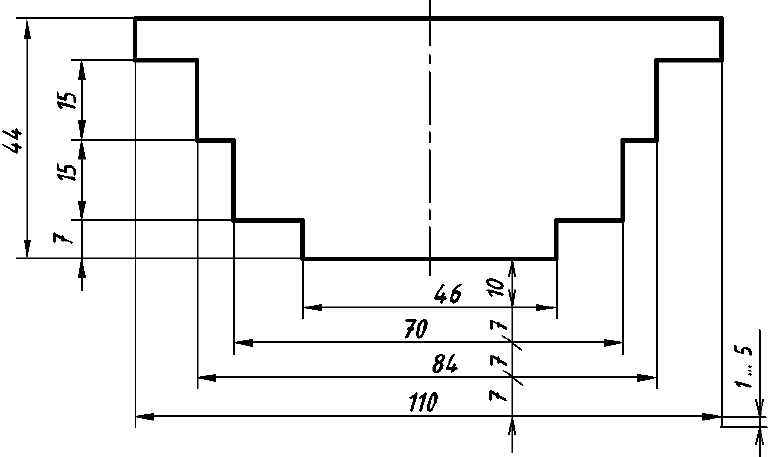
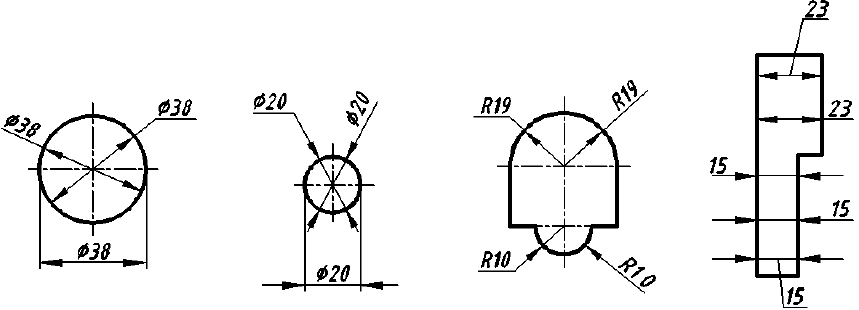
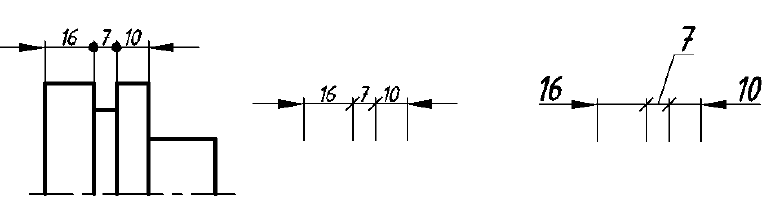
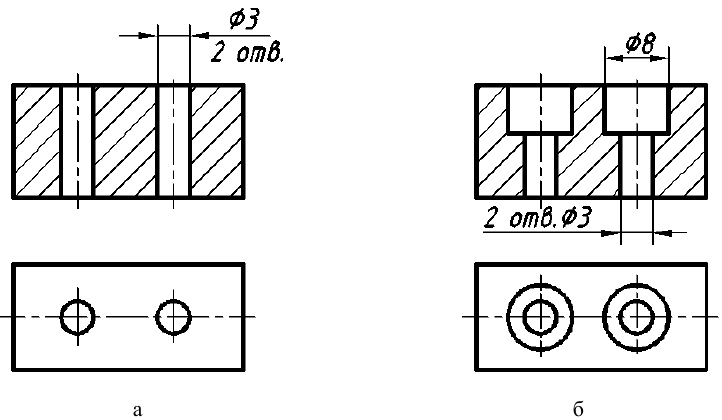
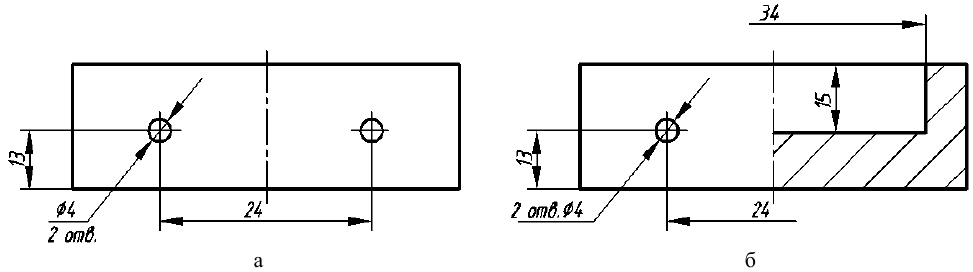
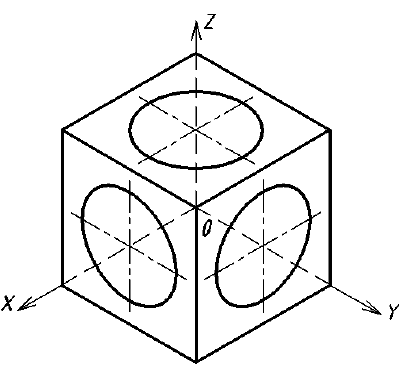
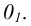 Проведем через нее изометрические оси X и Y (они параллельны сторонам верхней грани). Отложим в обе стороны от точки
Проведем через нее изометрические оси X и Y (они параллельны сторонам верхней грани). Отложим в обе стороны от точки 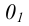 на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.
на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.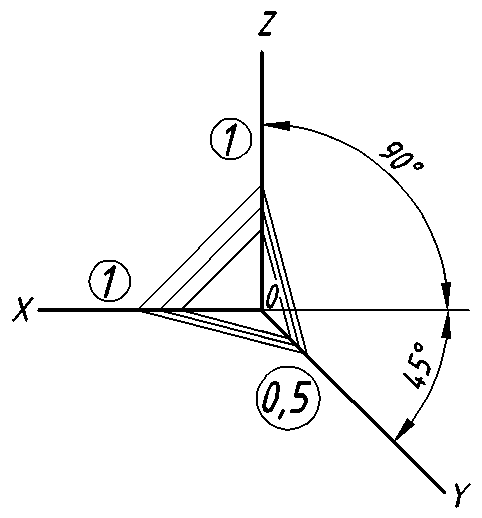
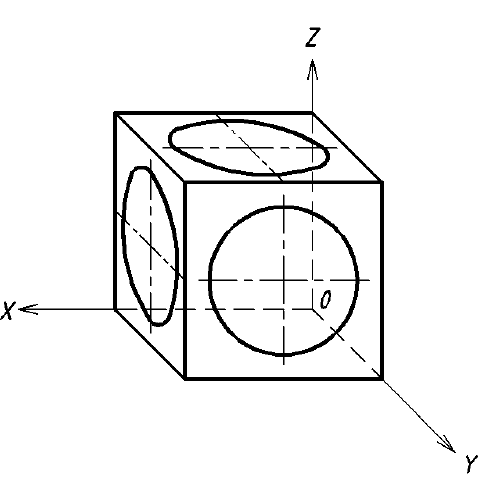
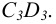
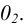
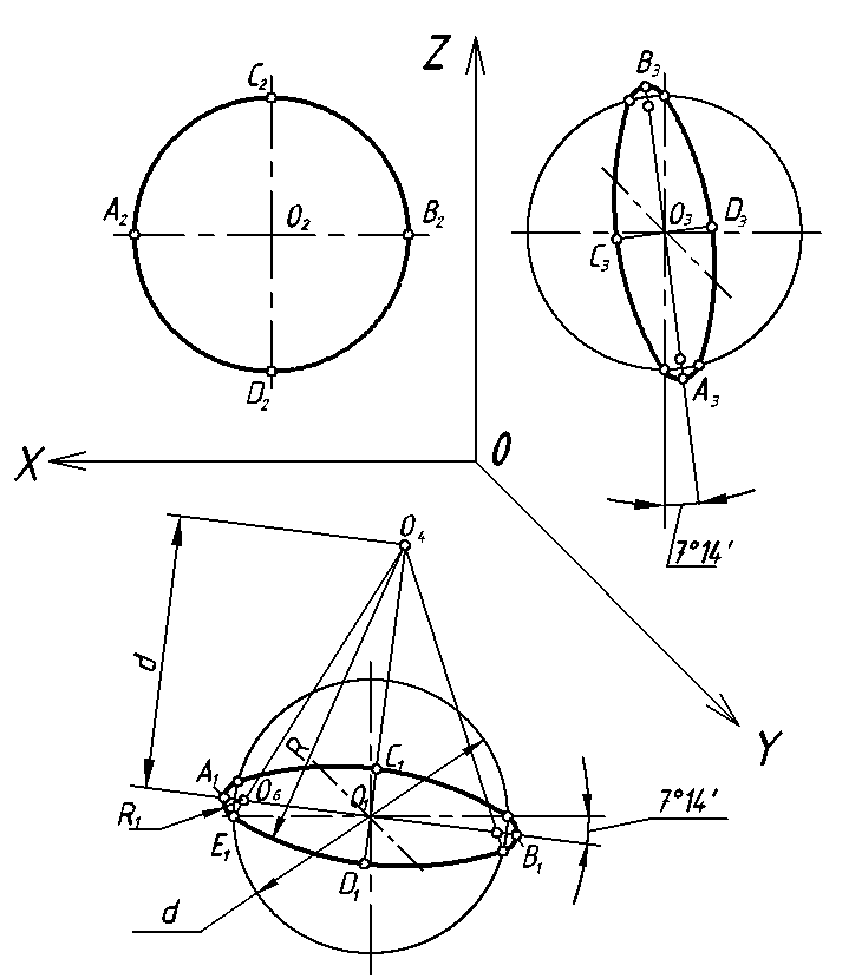
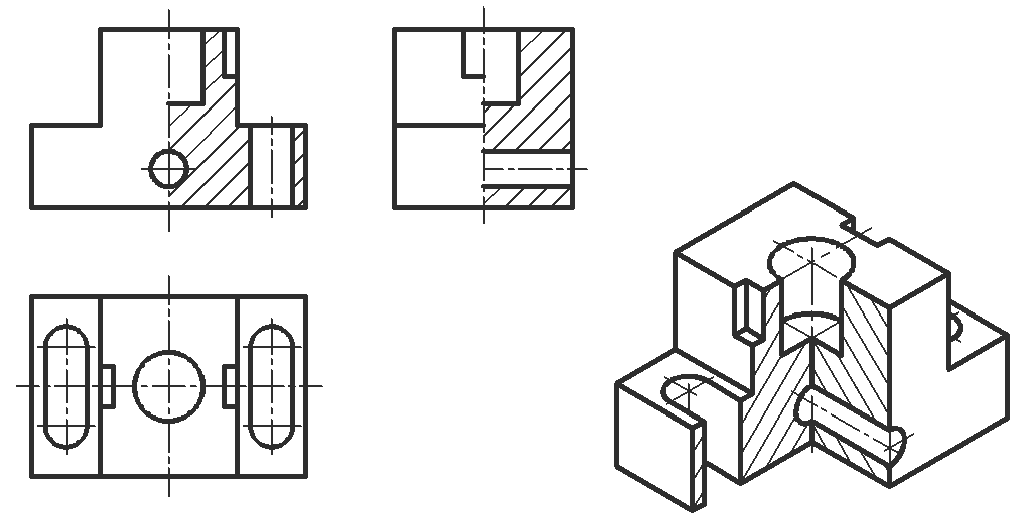
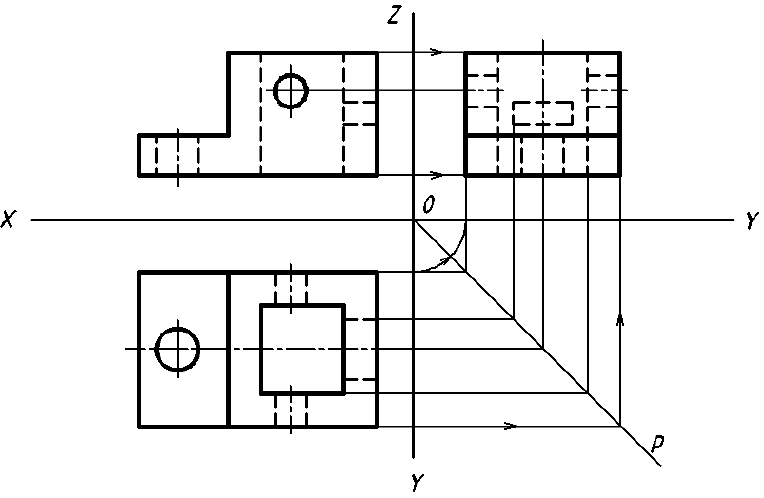
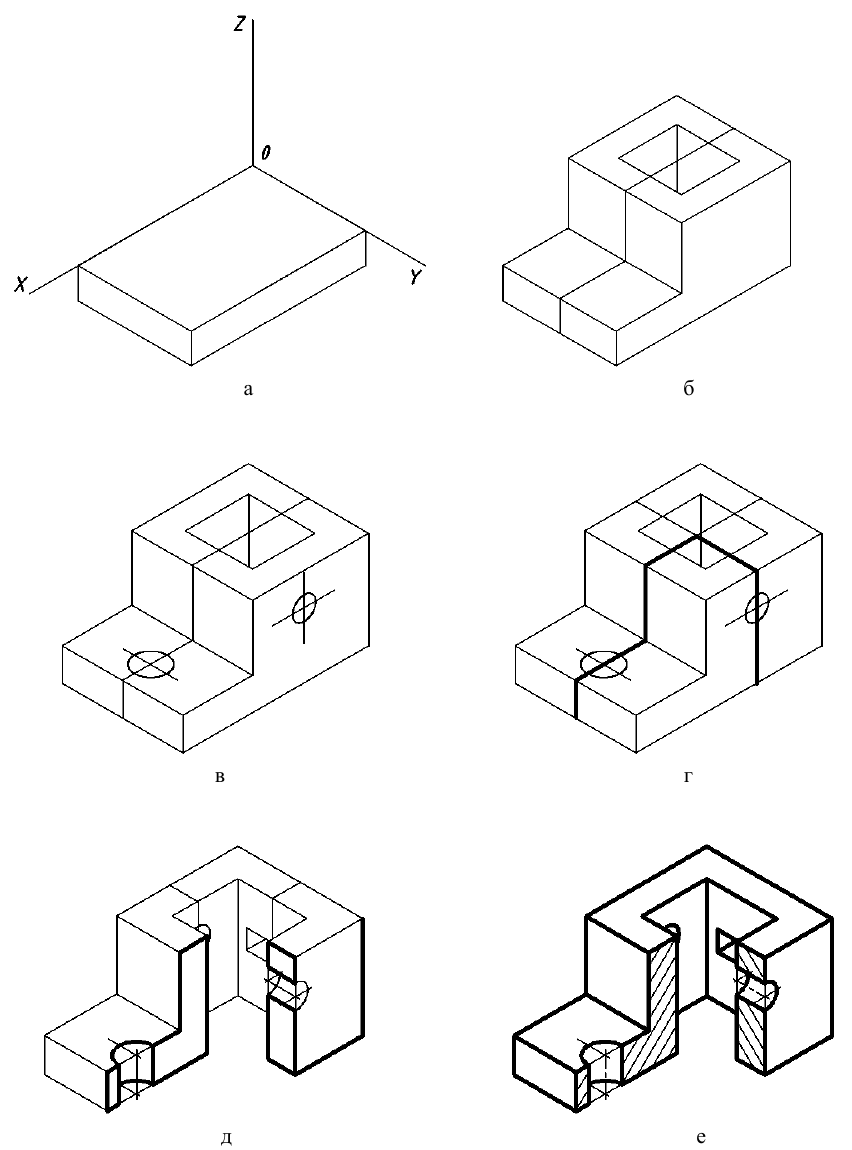
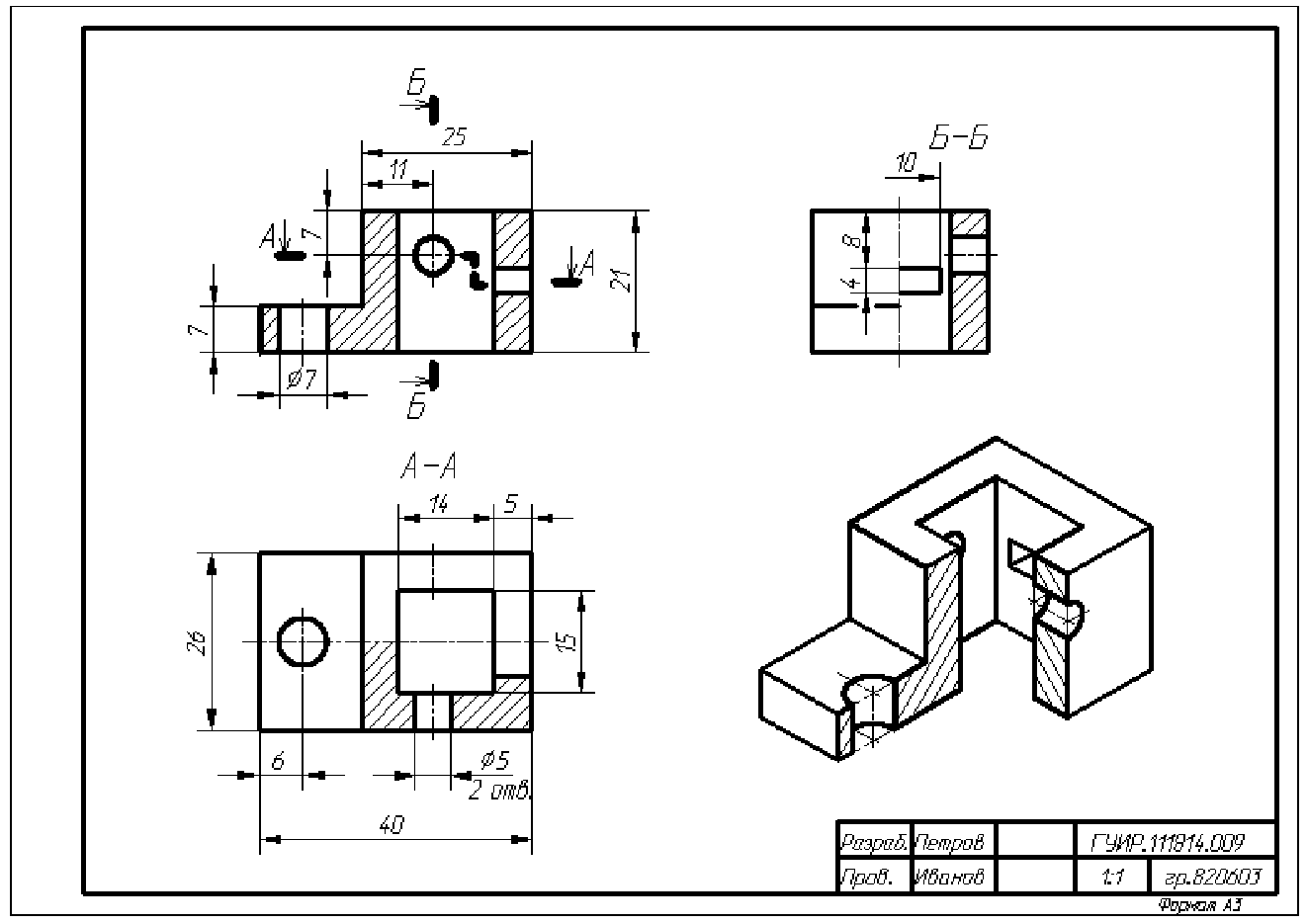
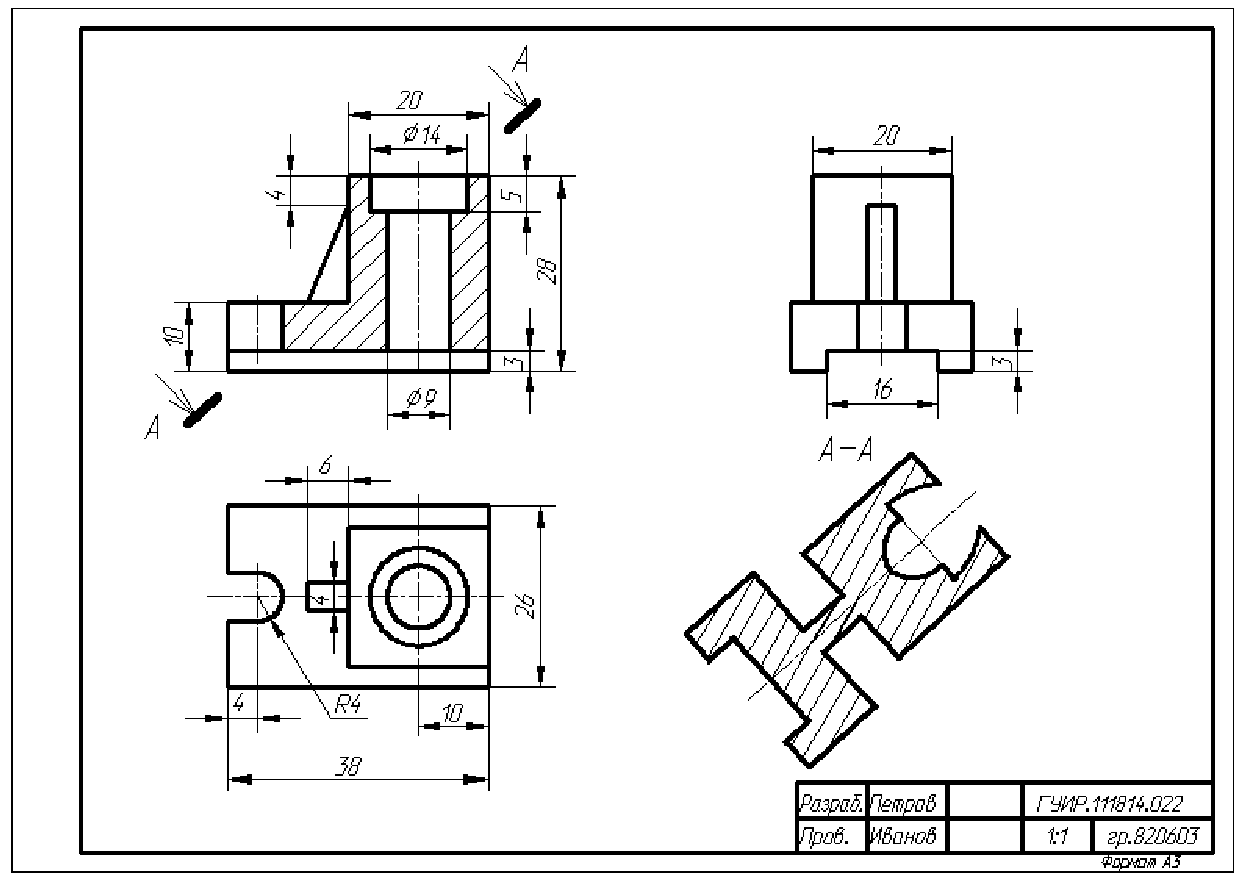

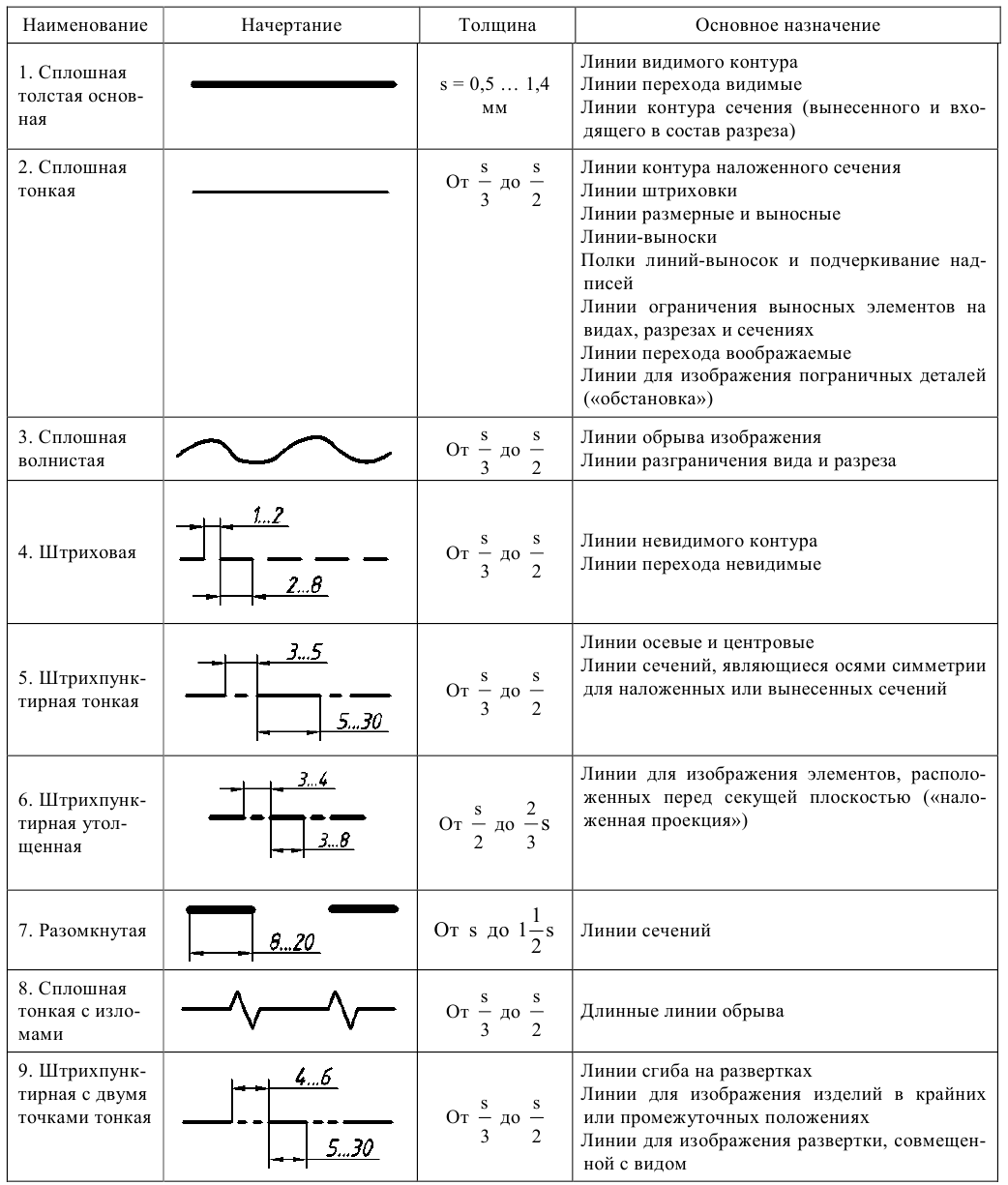

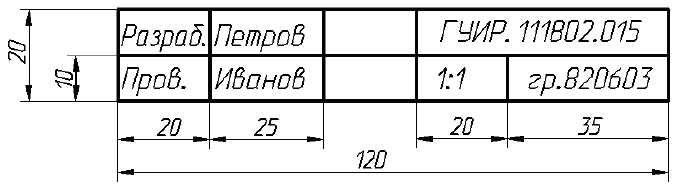
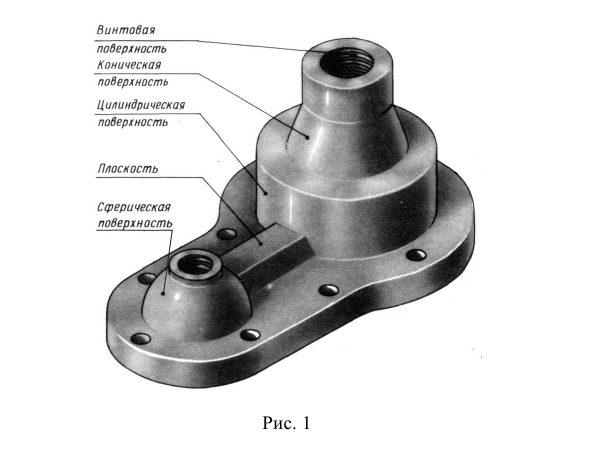
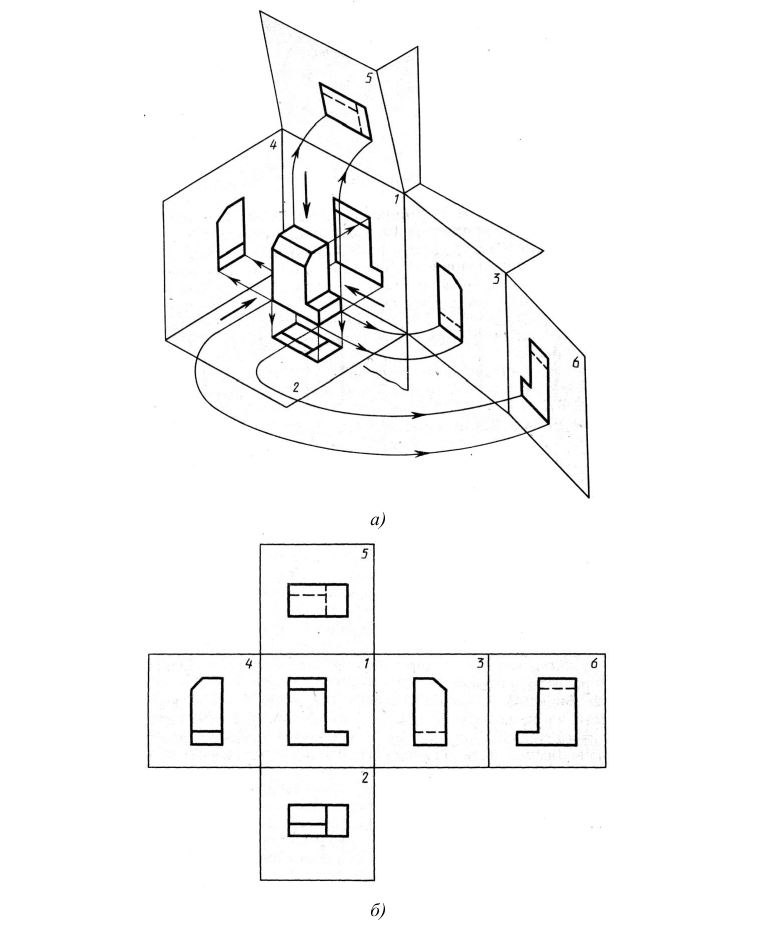

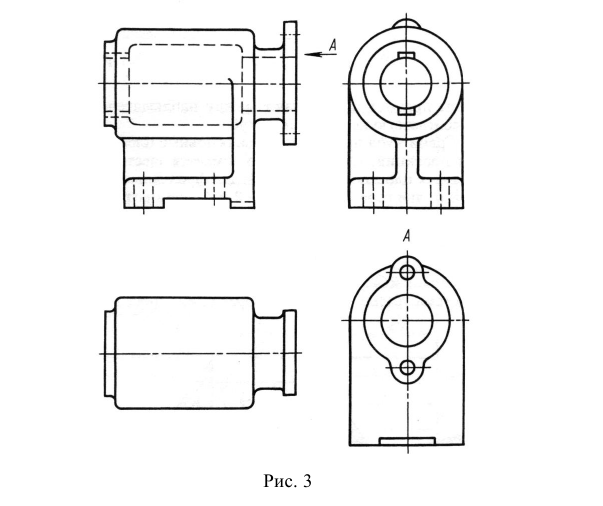

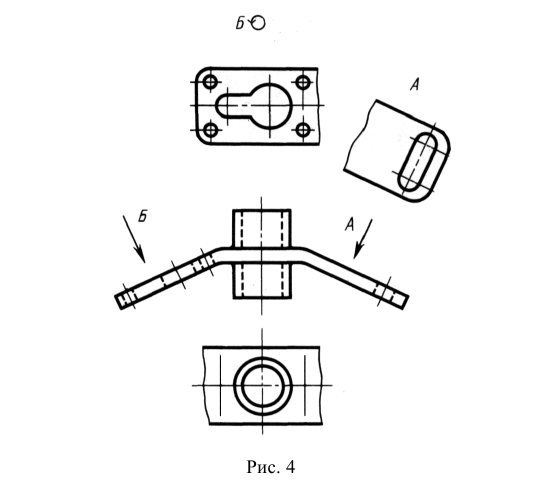
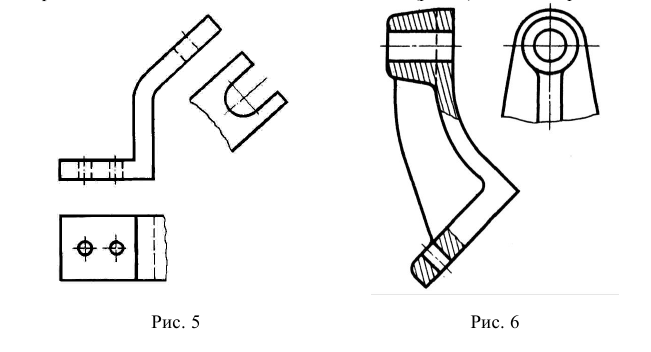
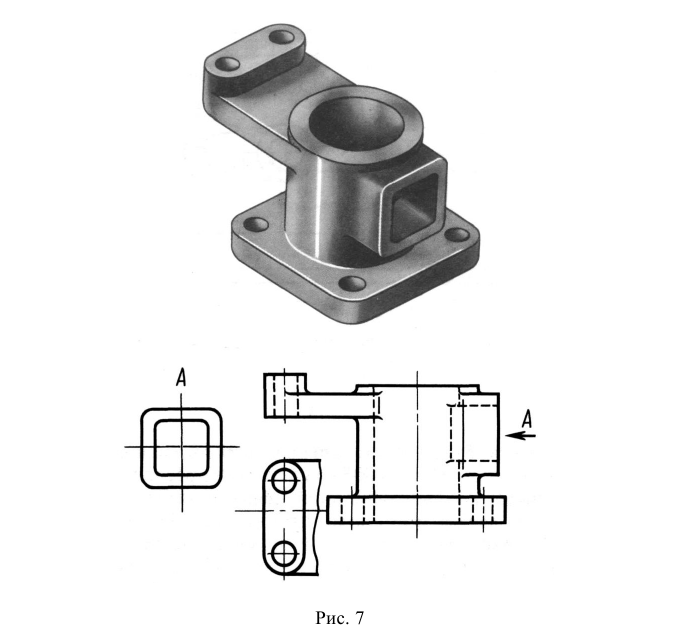
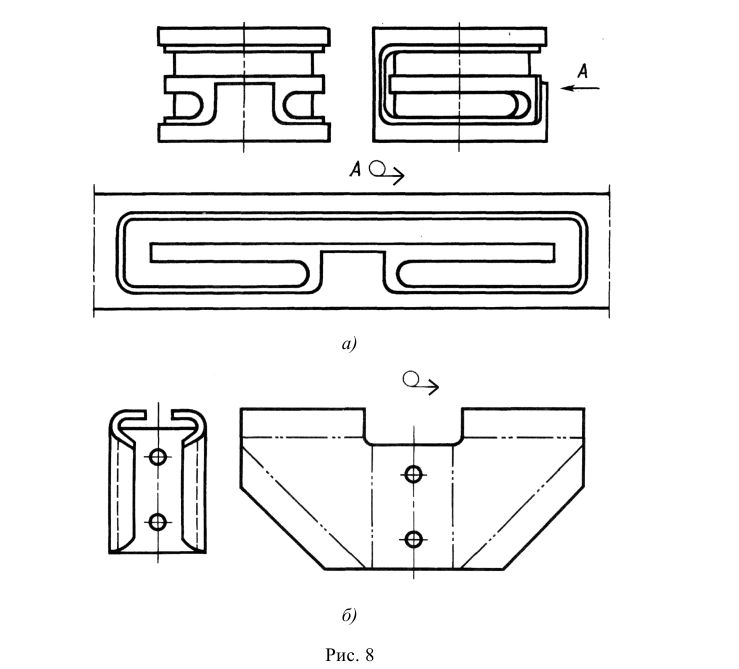
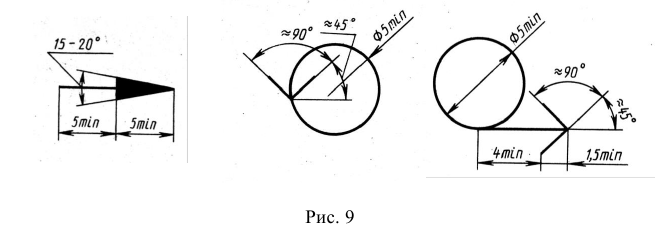
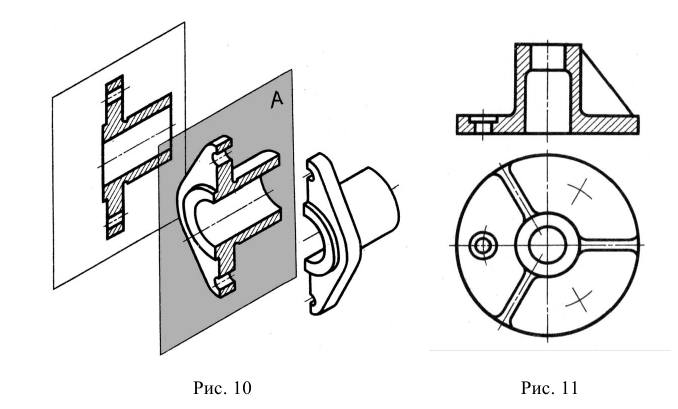
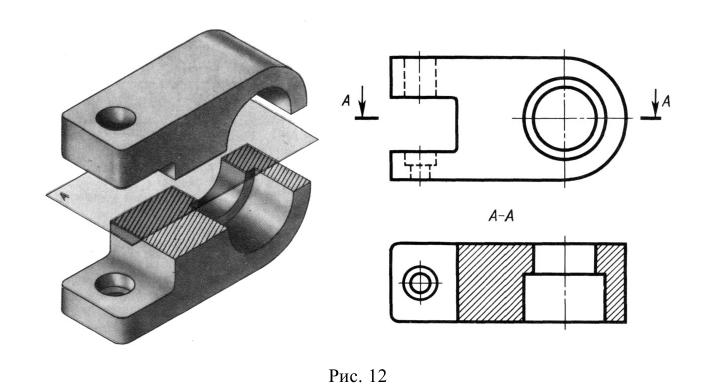
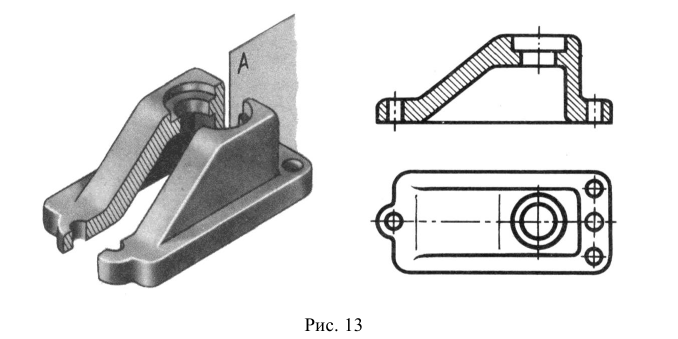
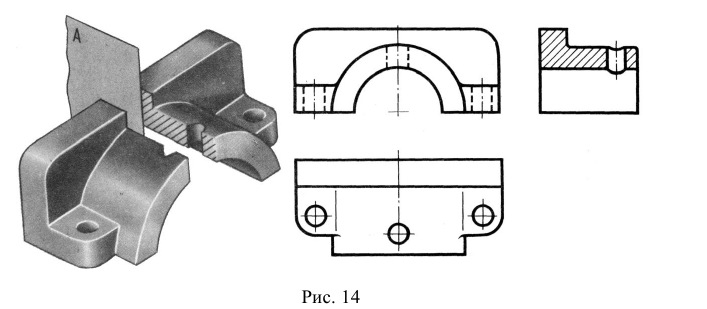
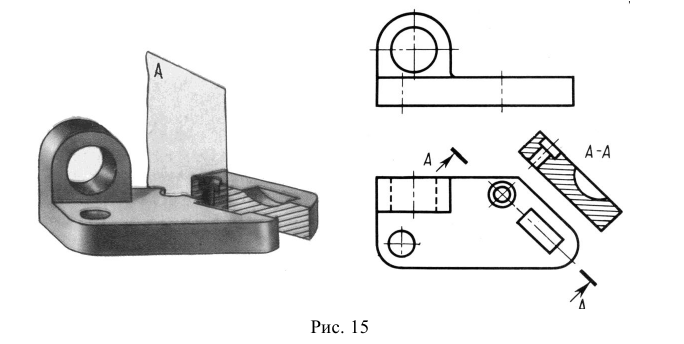
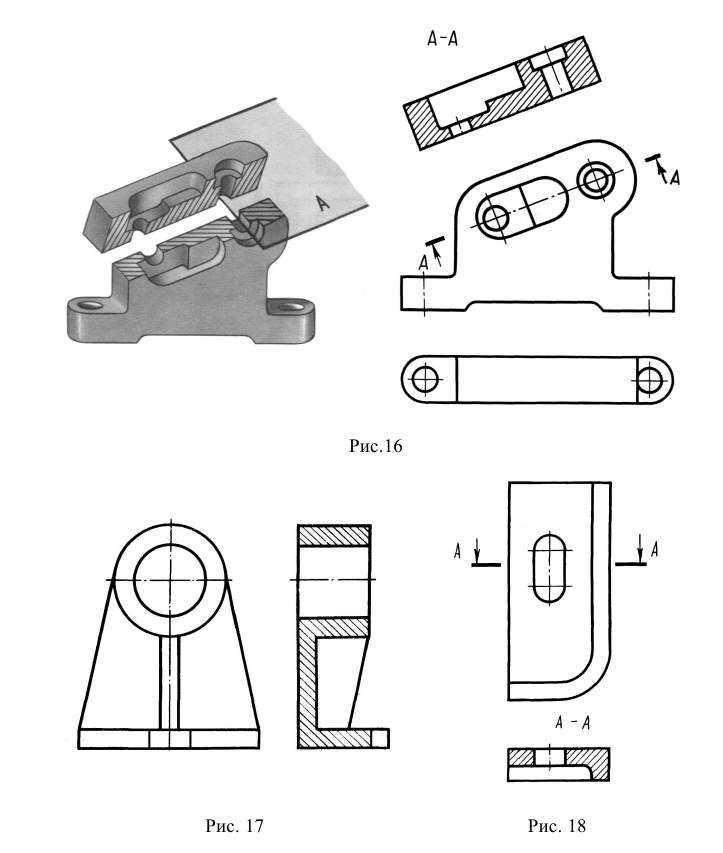
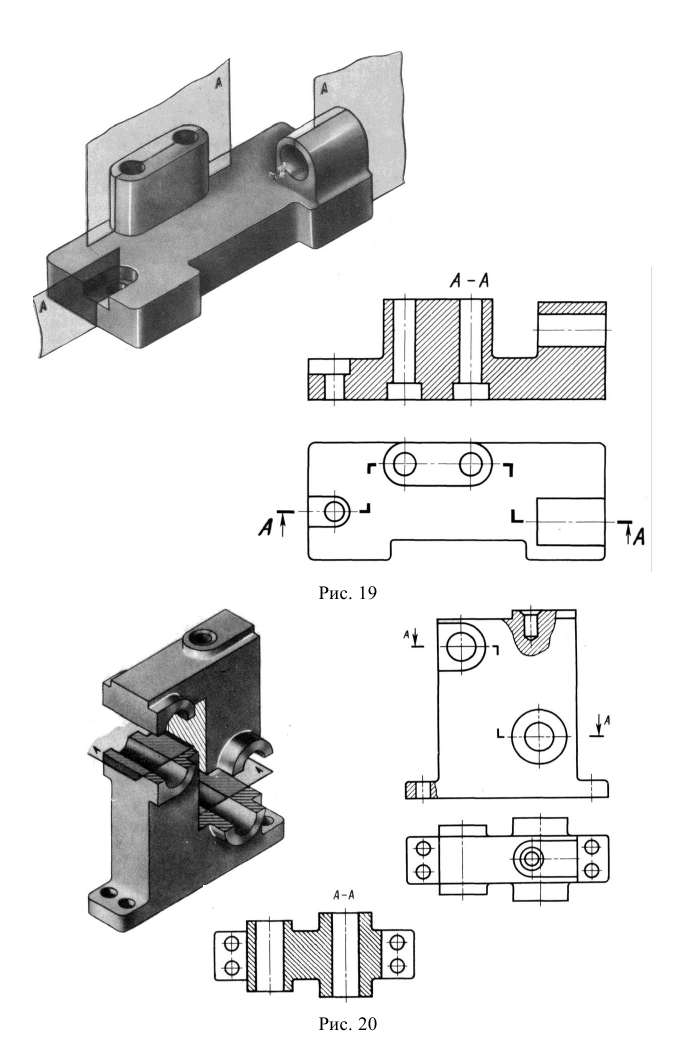
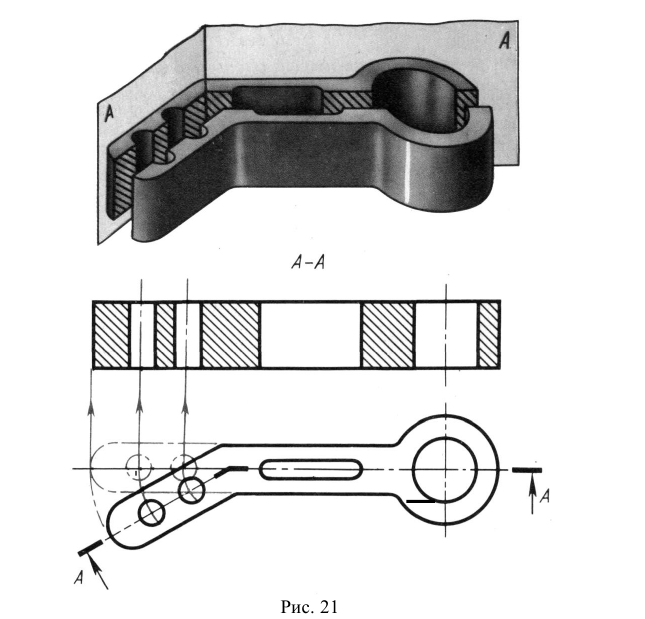
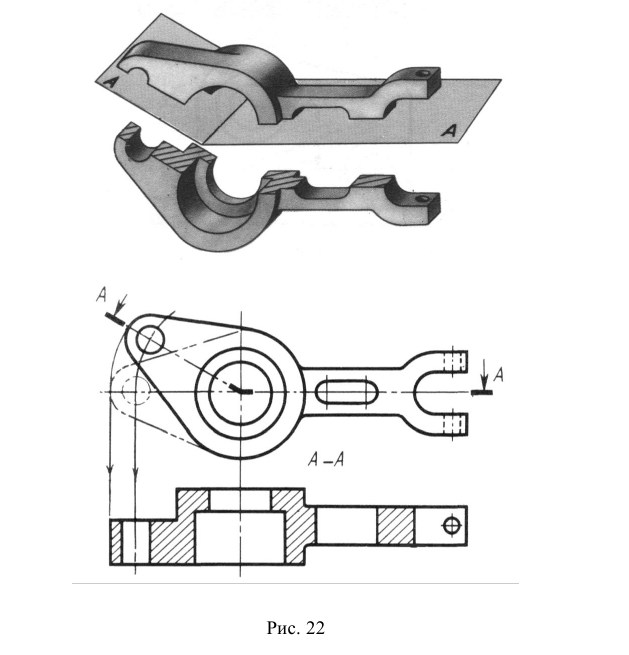
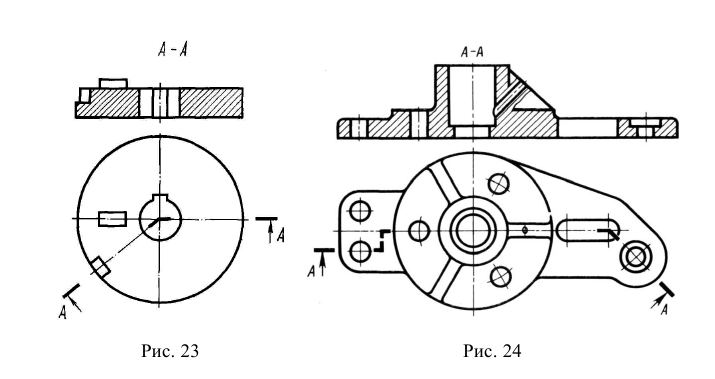
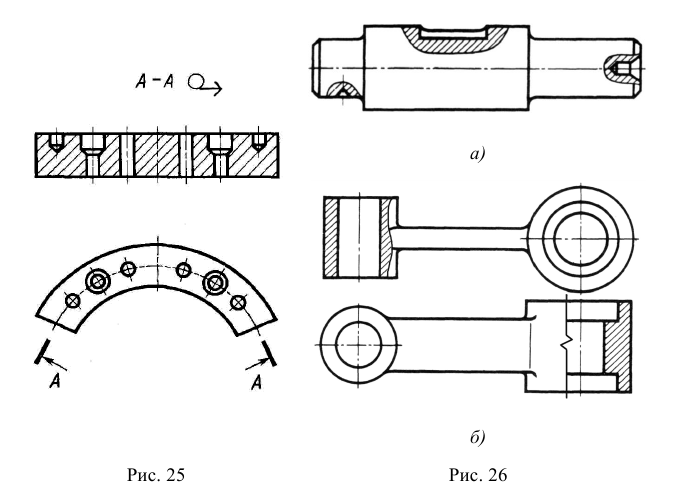
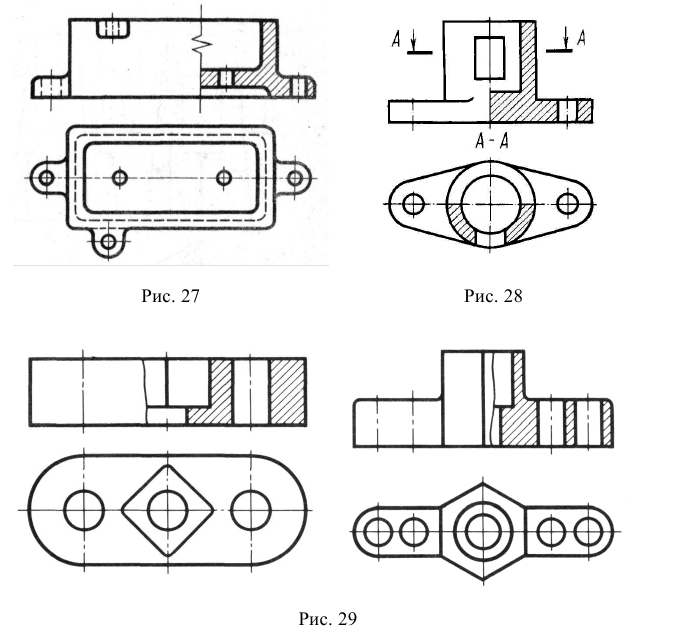
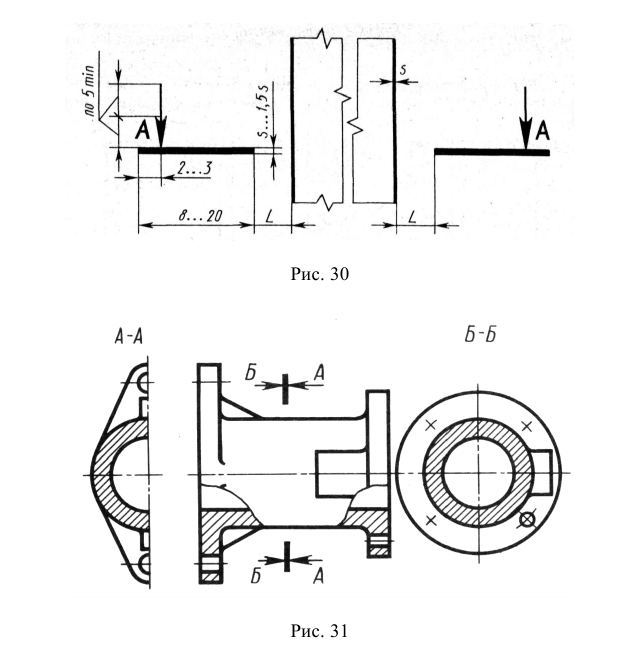
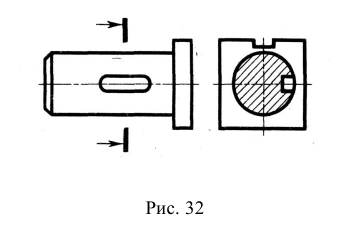
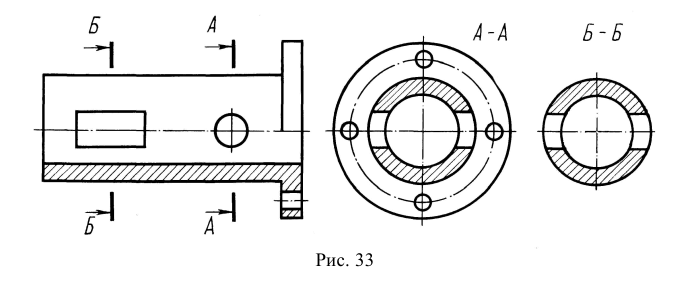
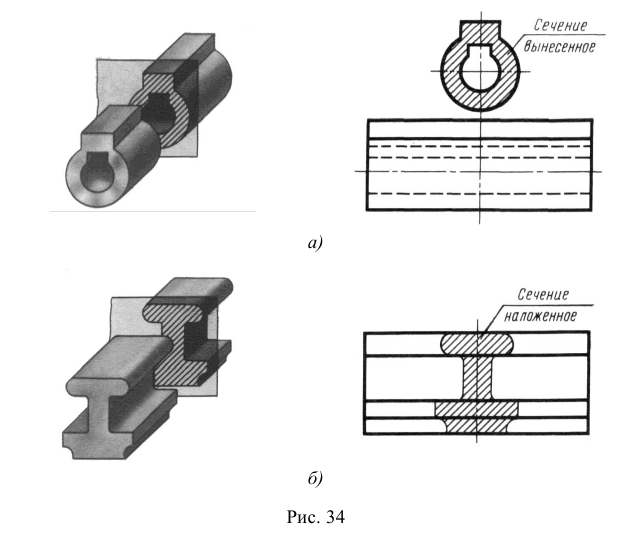
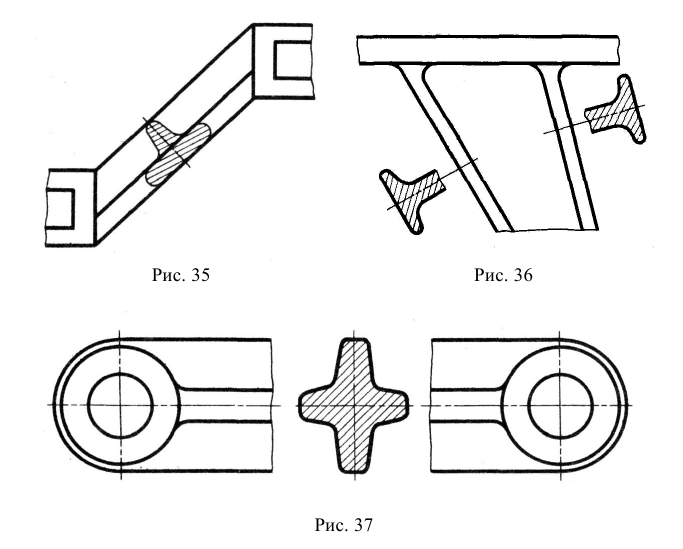
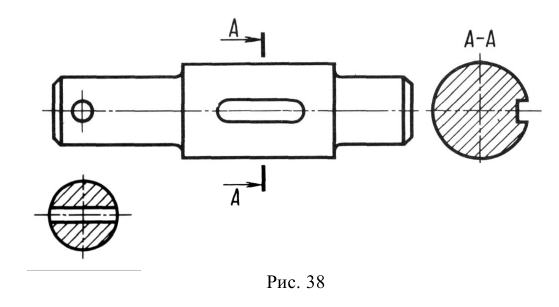
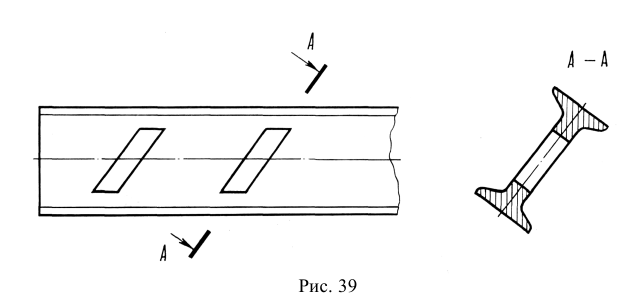
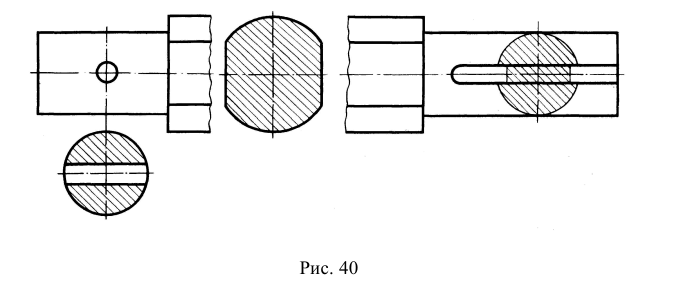
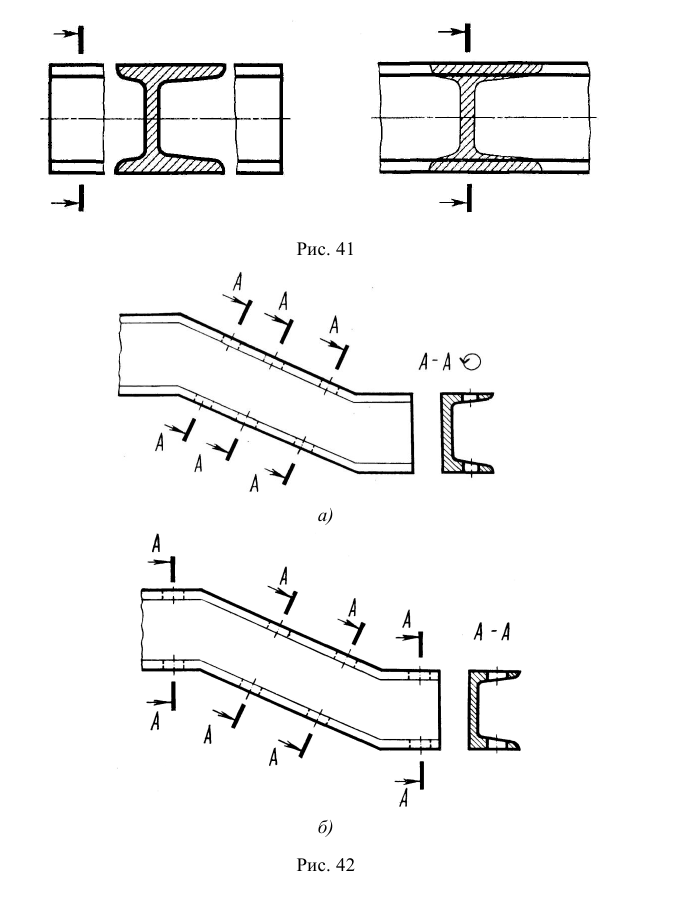
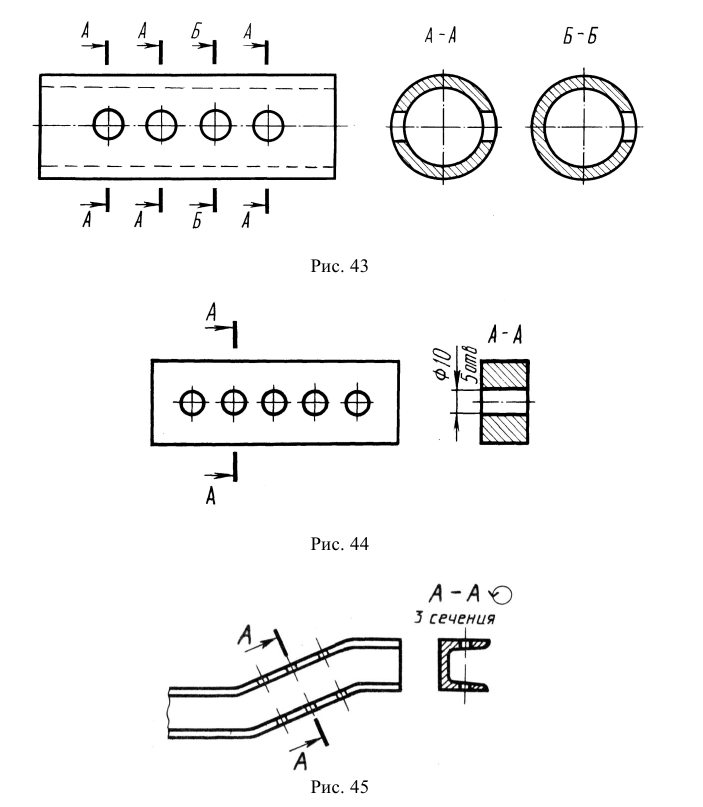
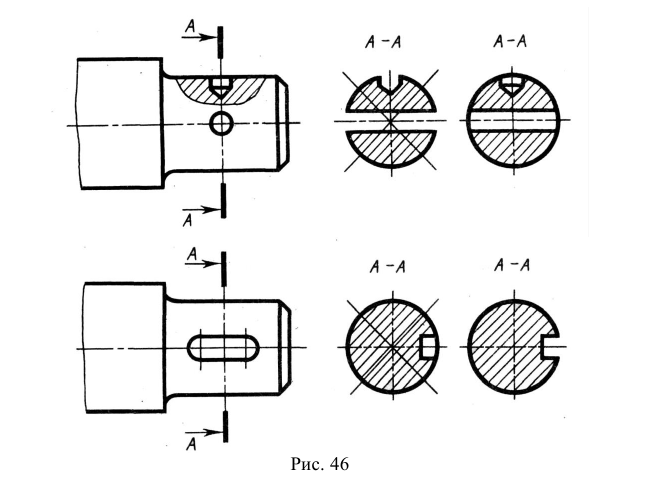
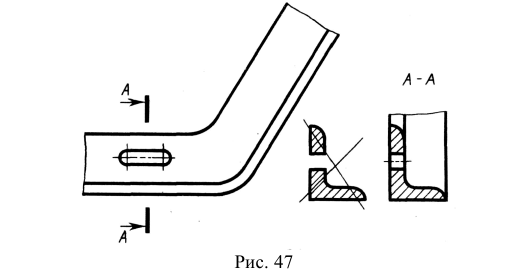
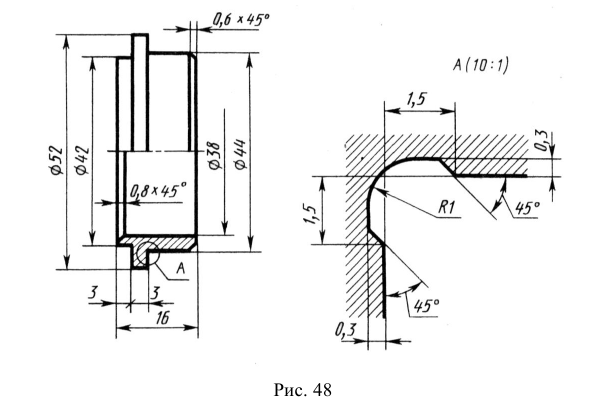

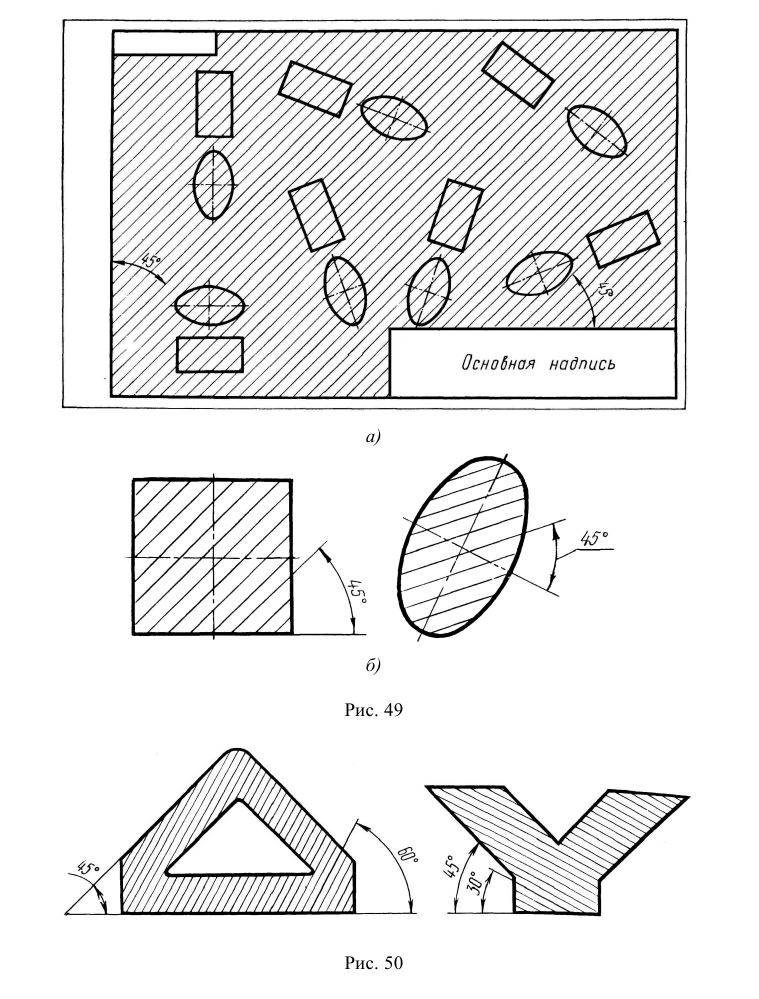
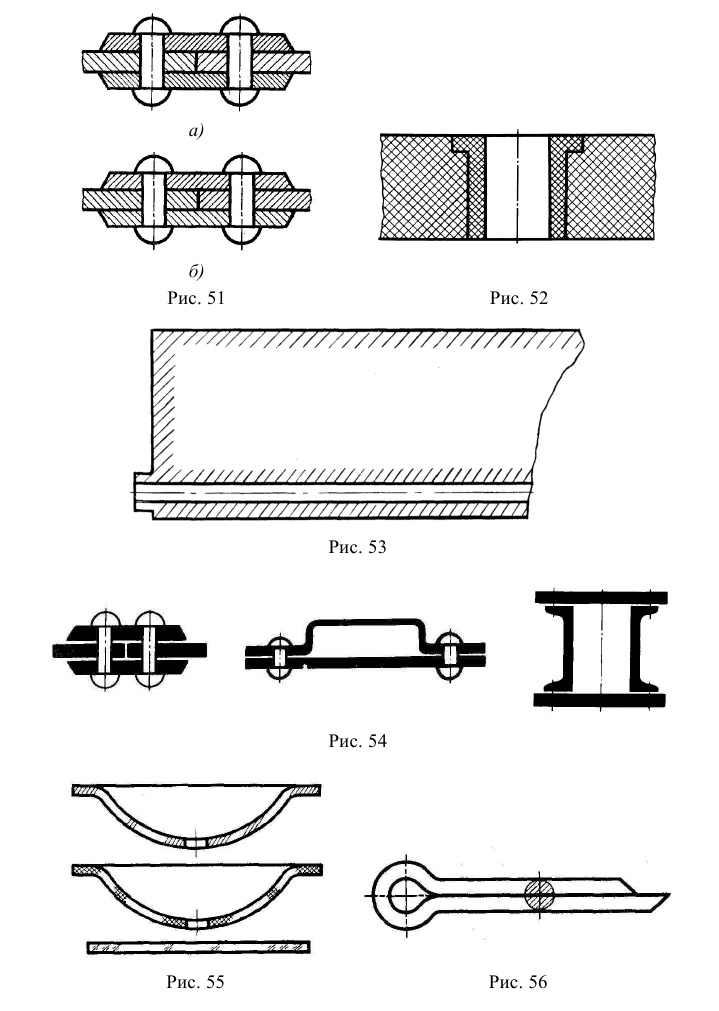
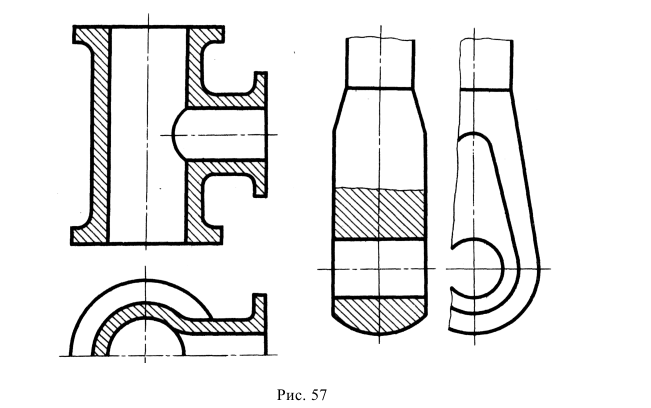
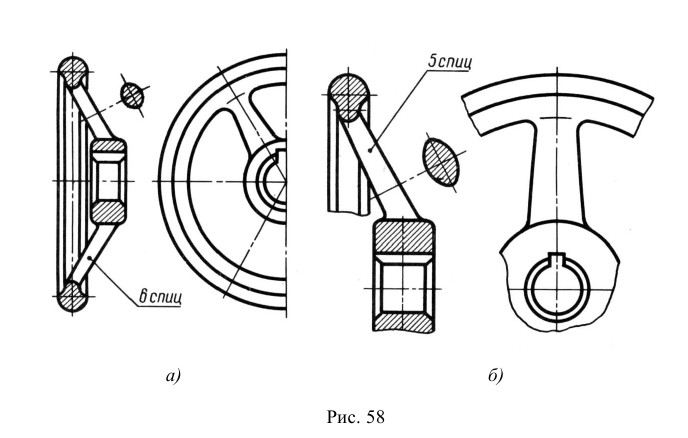
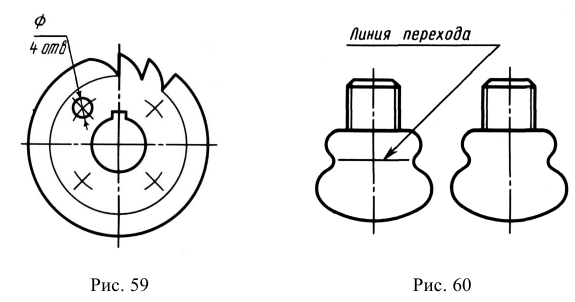
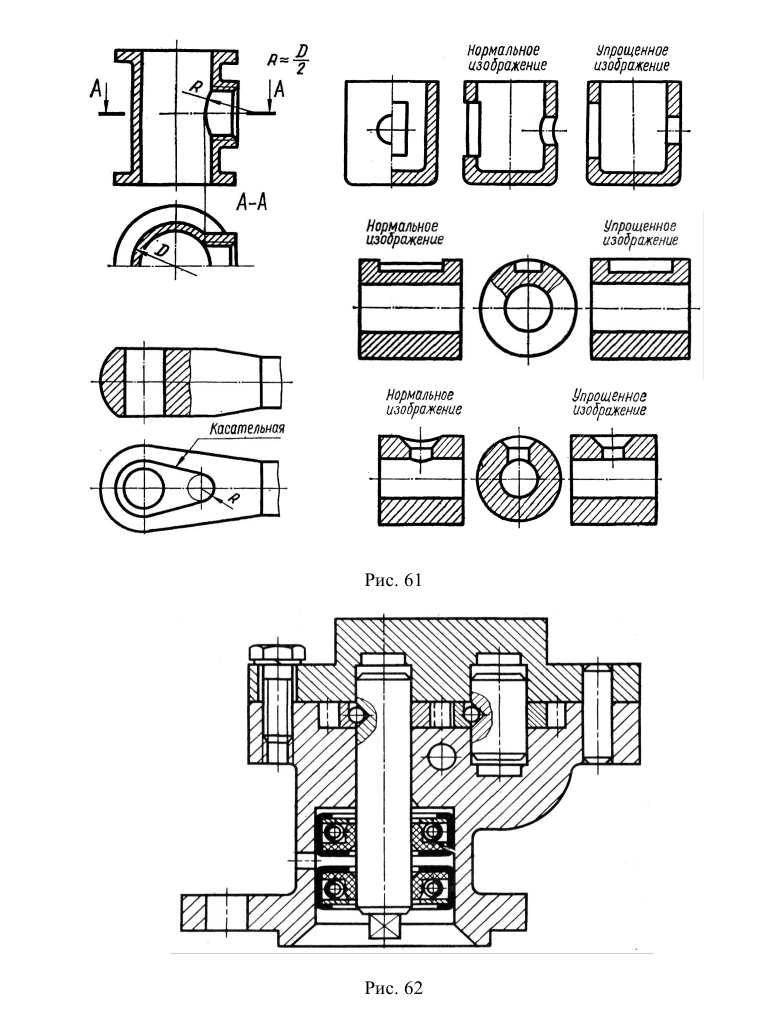
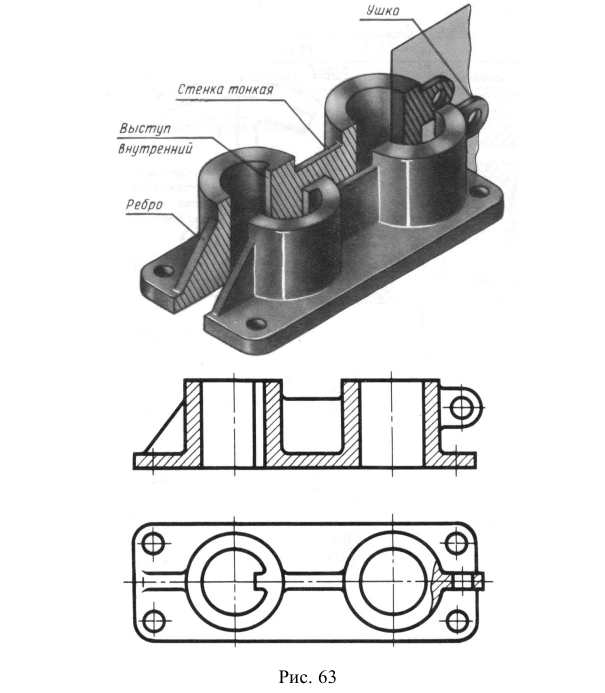
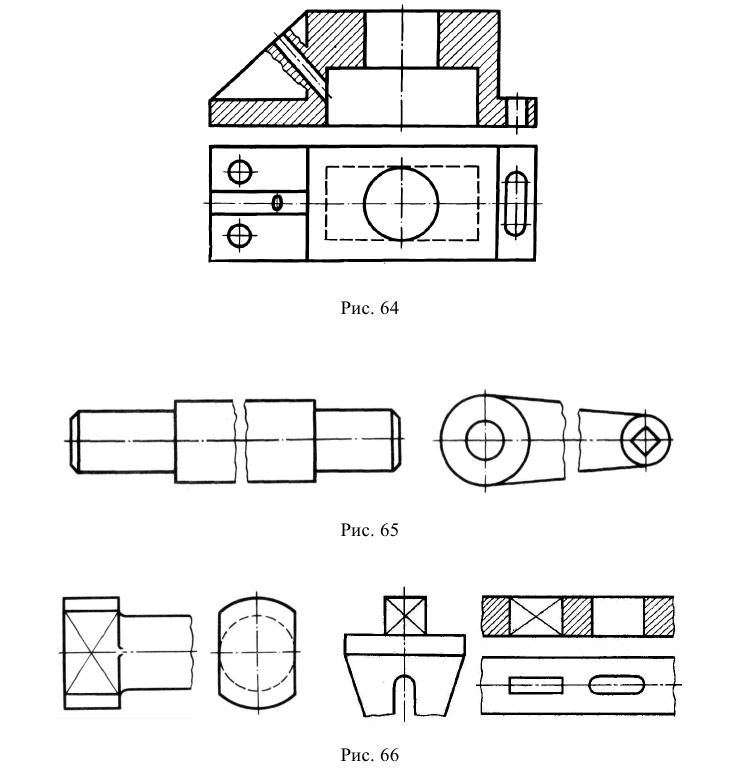
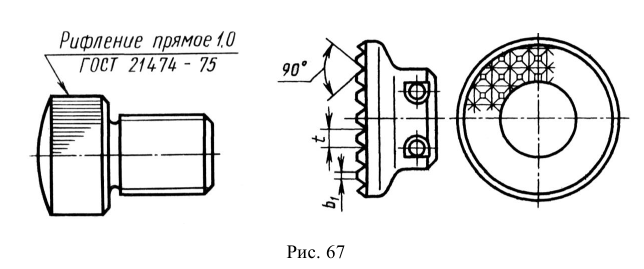
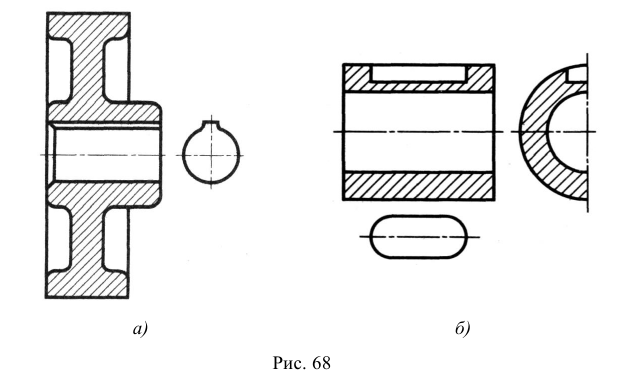
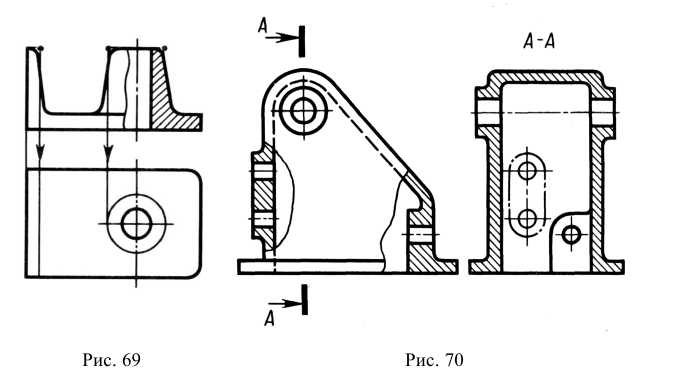
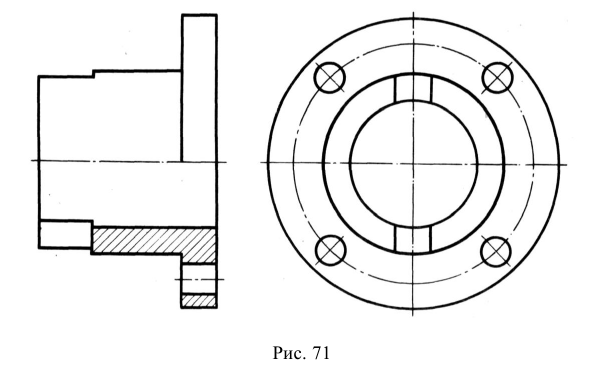
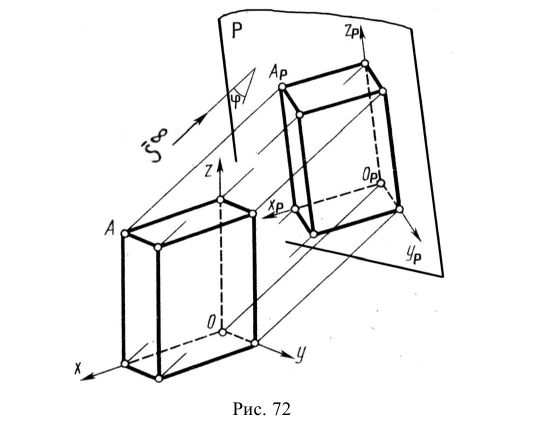
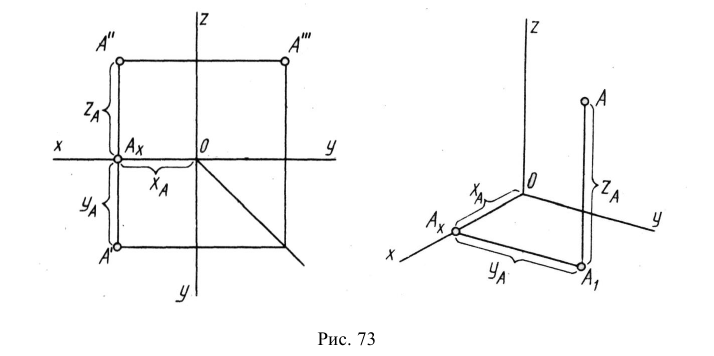
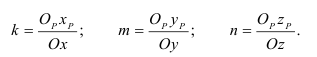
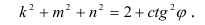
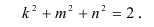
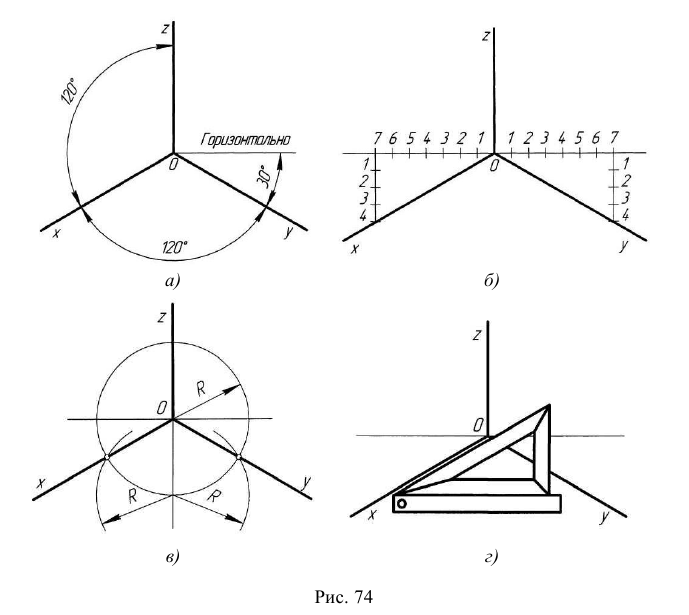
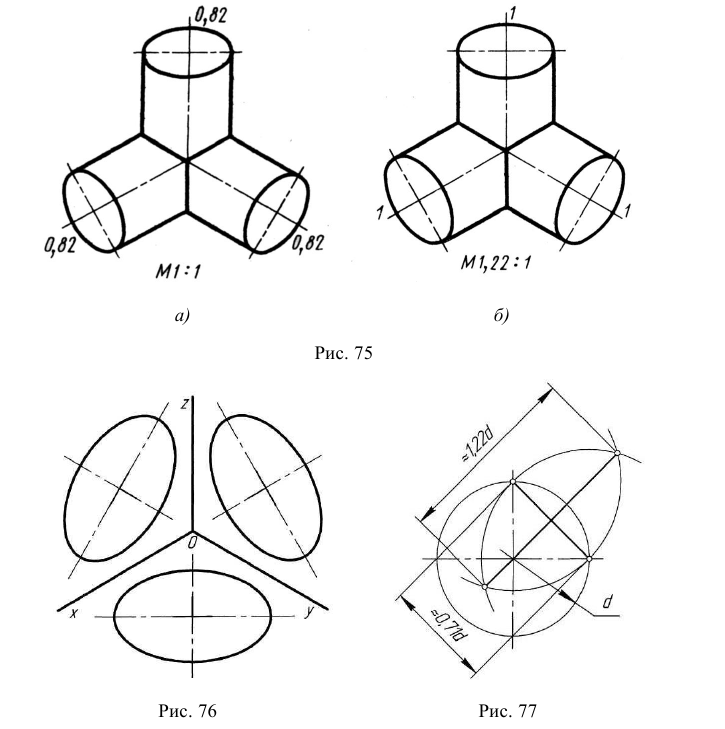
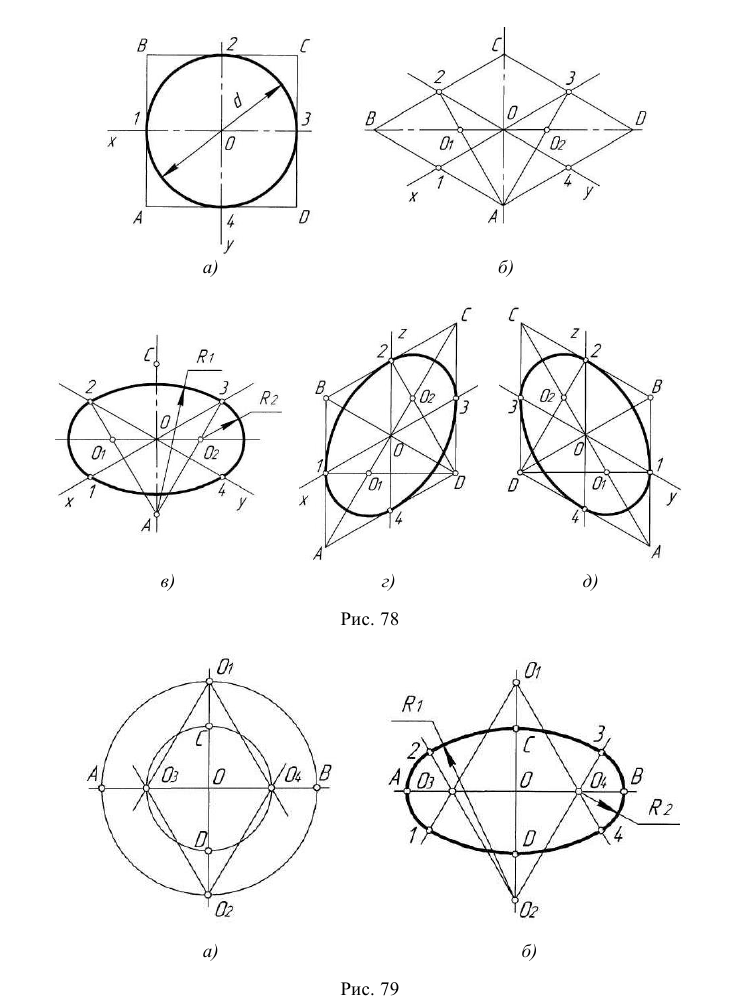
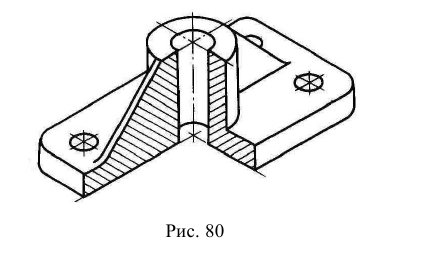
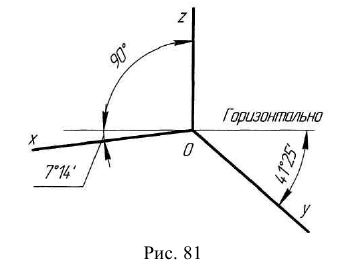
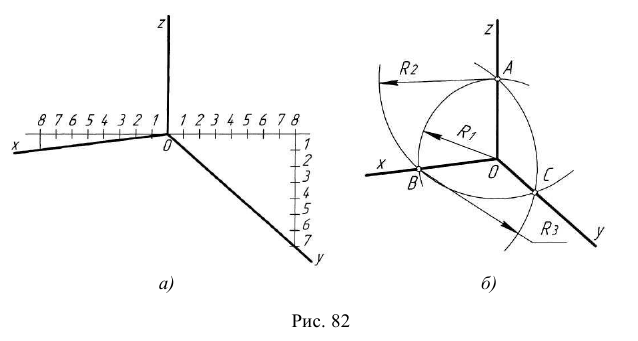
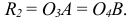
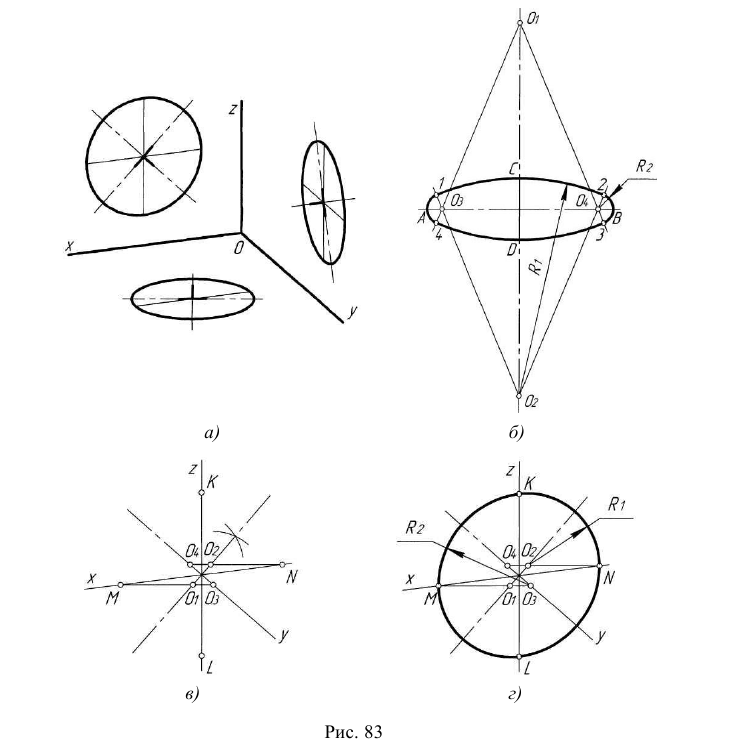
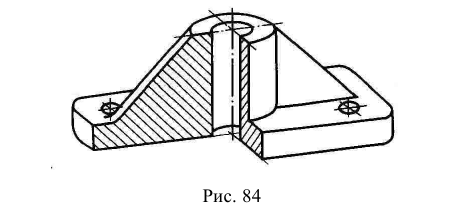
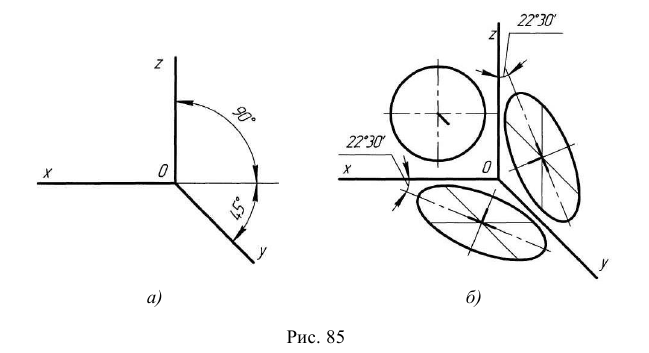
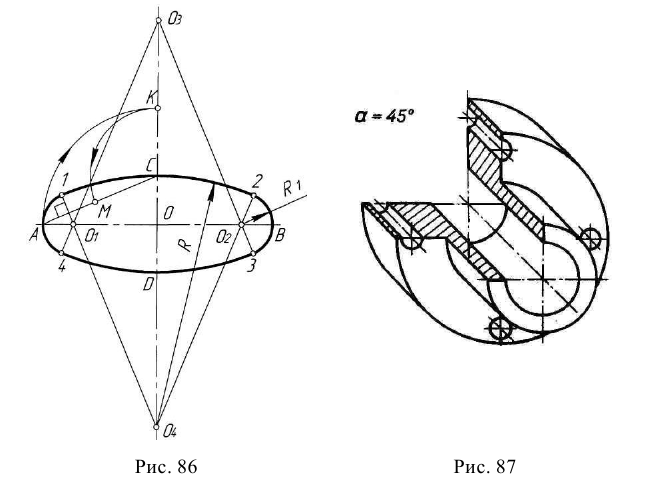
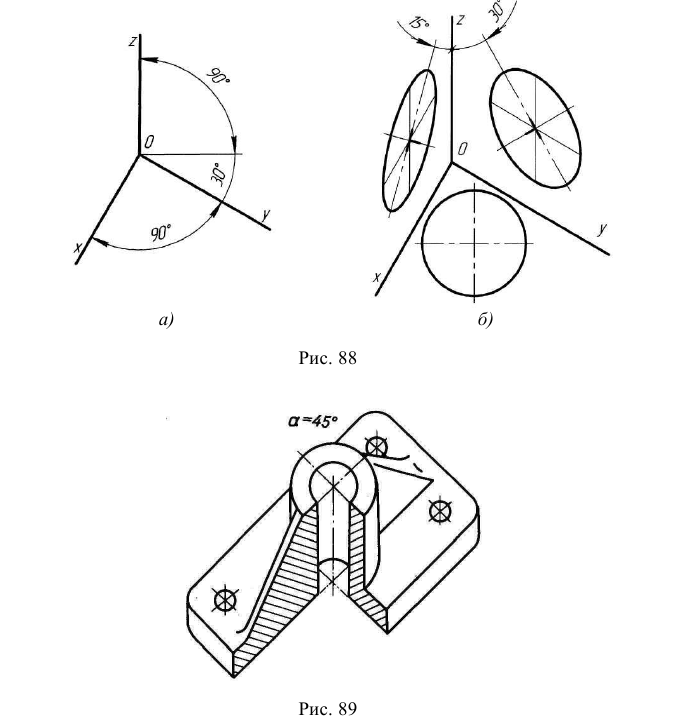
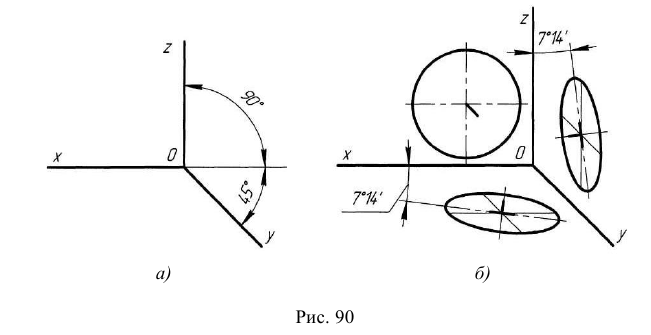
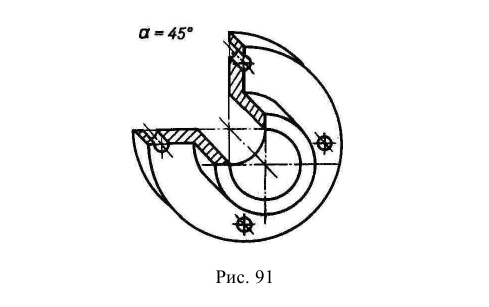
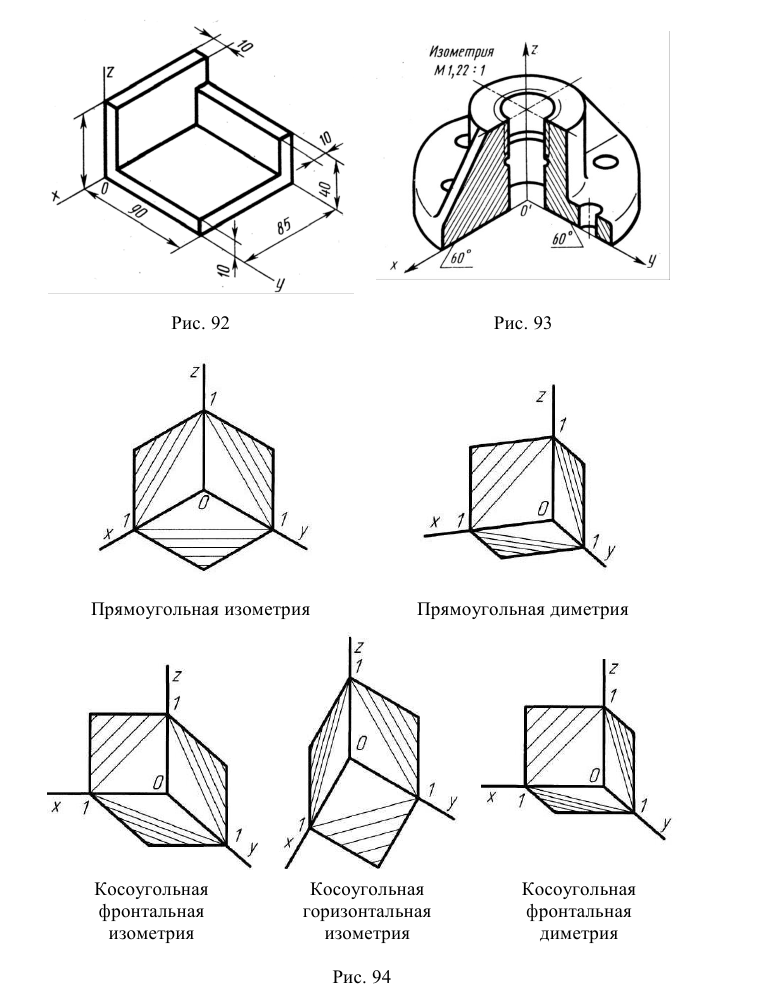
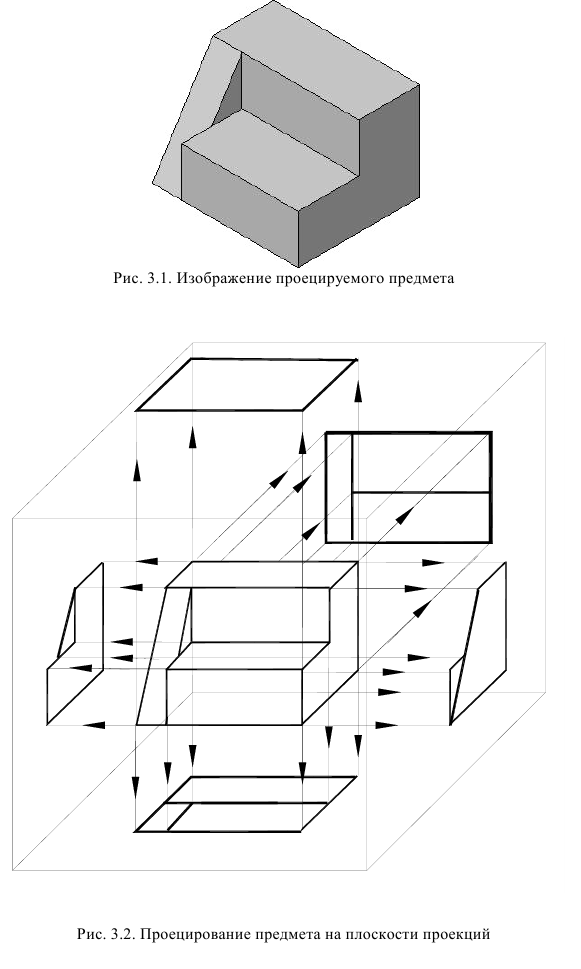
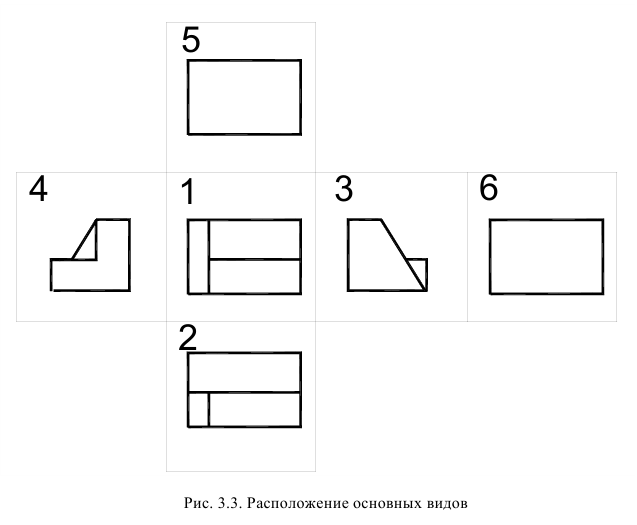
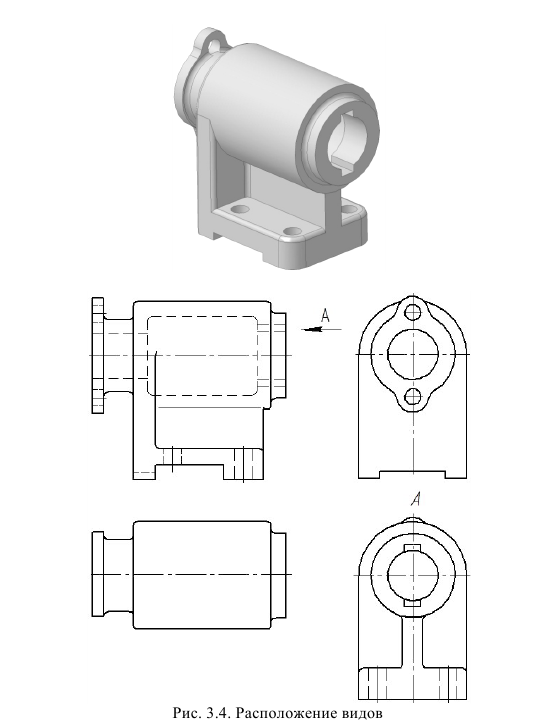
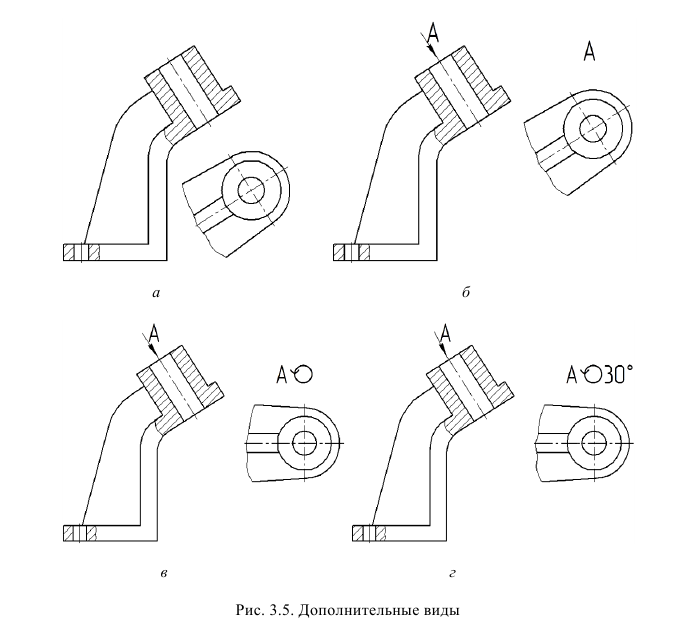
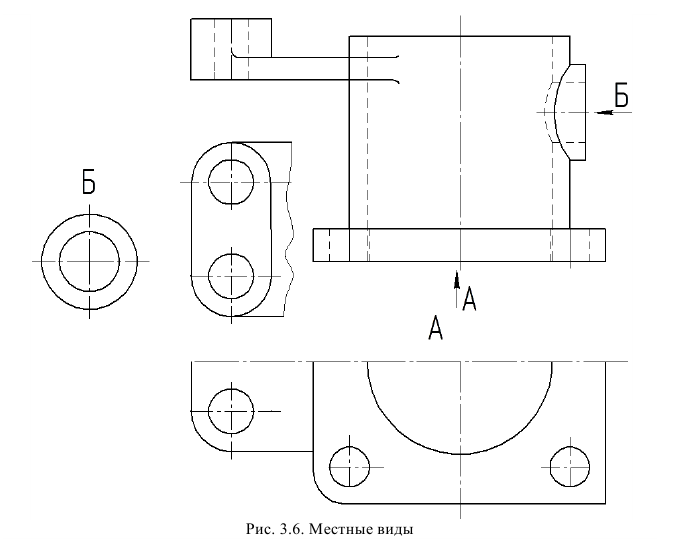
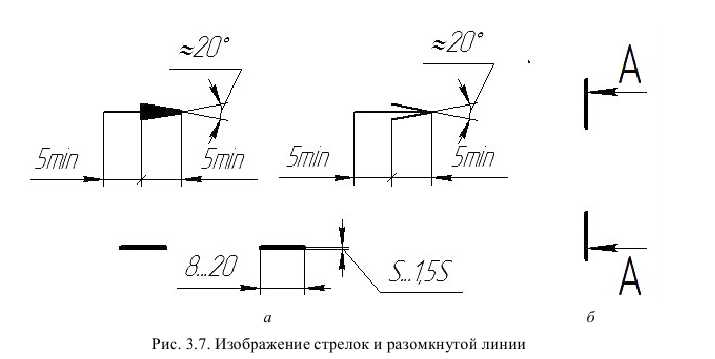

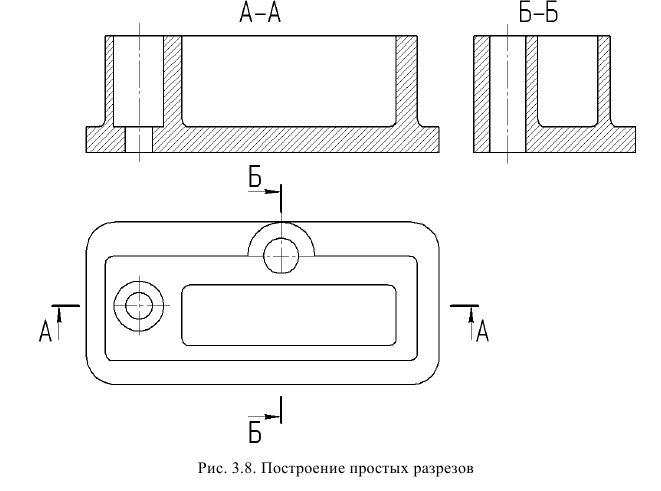
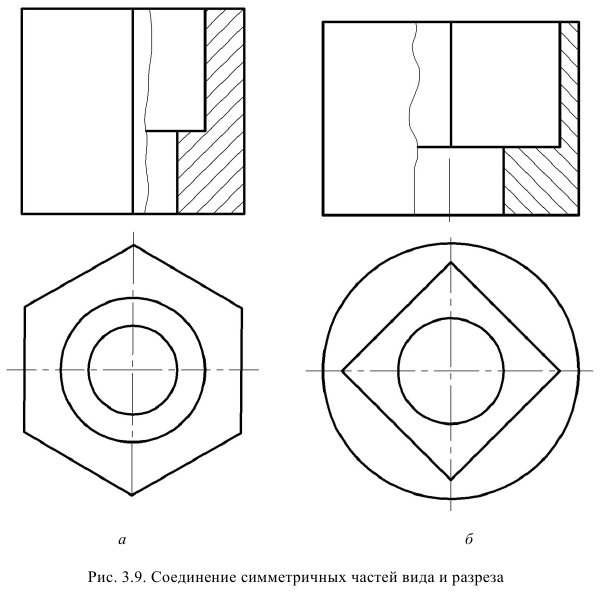

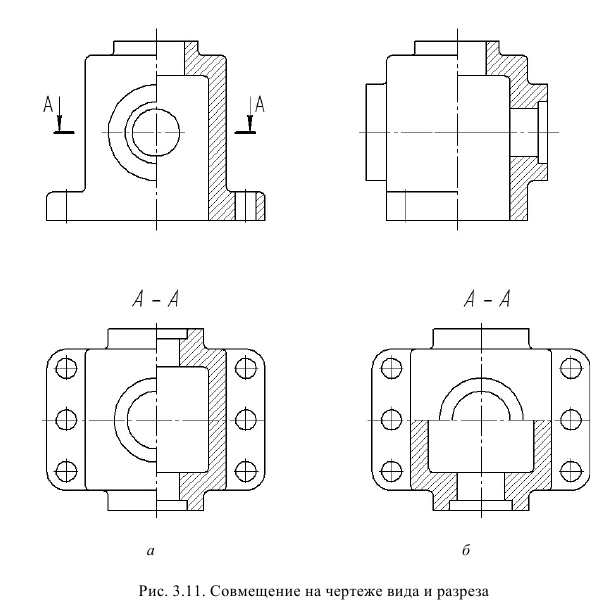
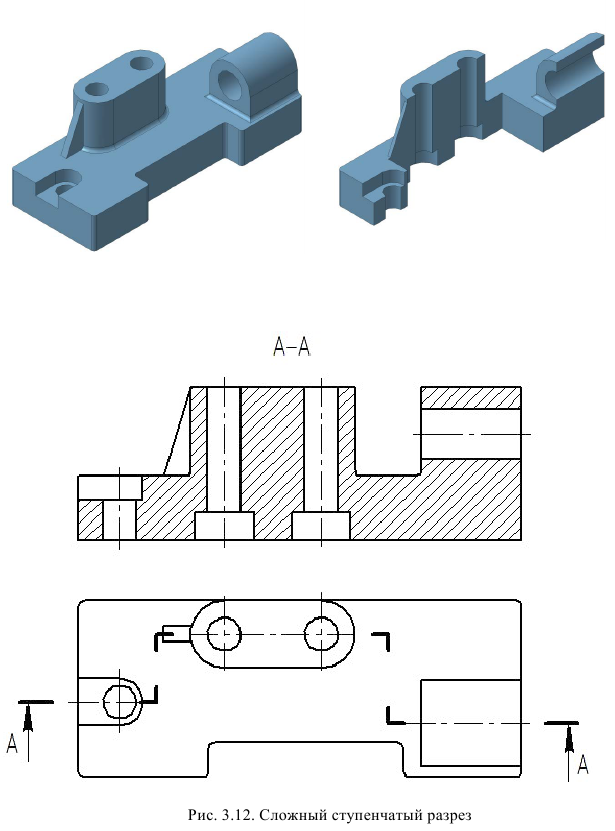
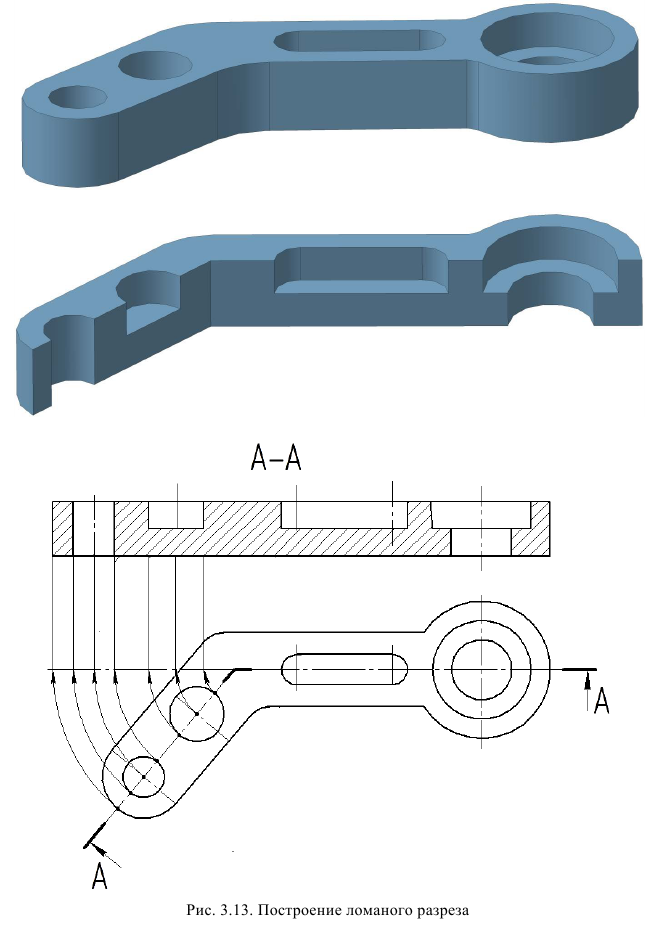
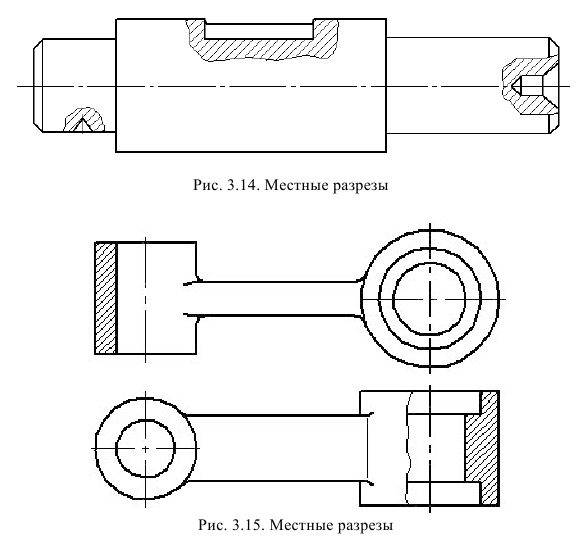
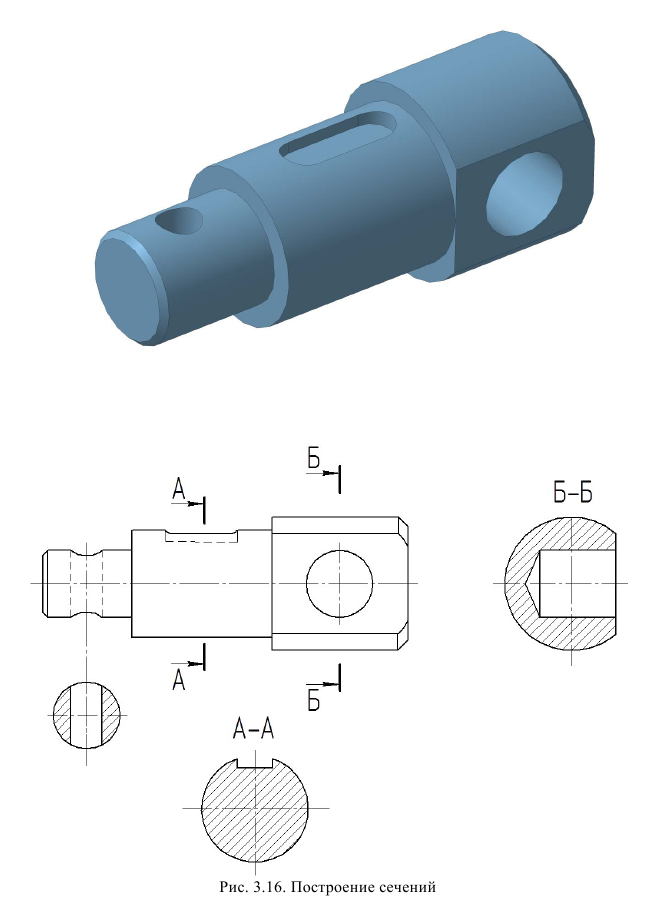
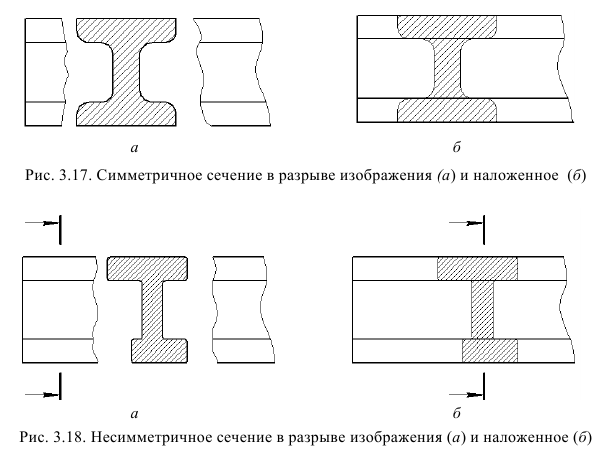
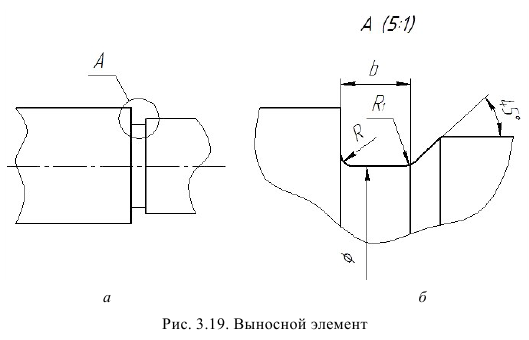
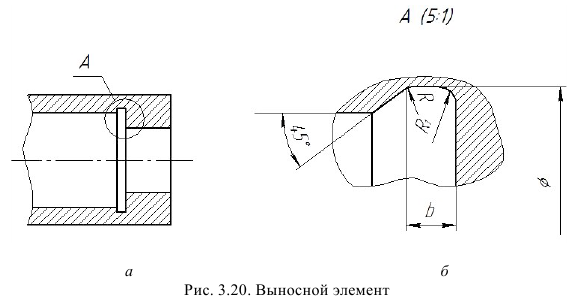
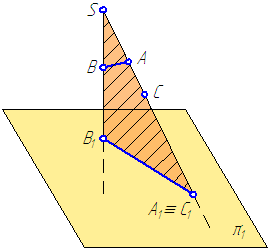
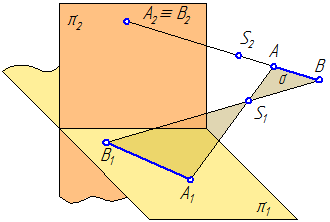
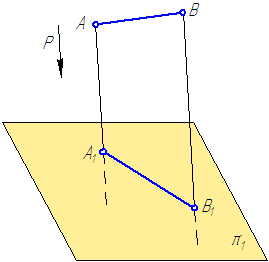
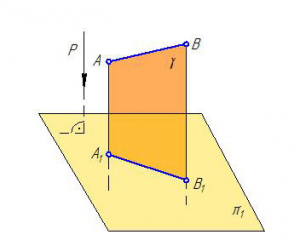

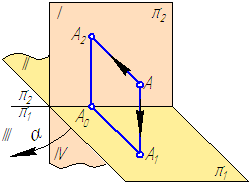
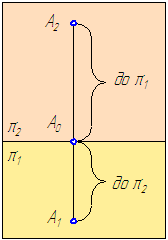
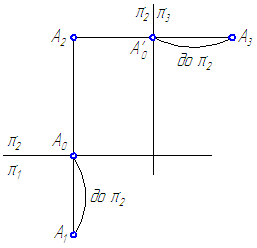
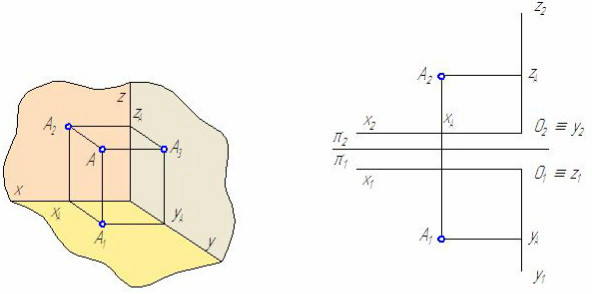
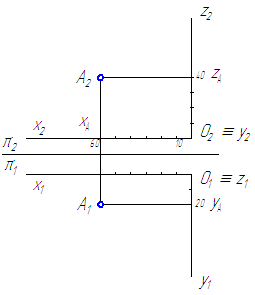
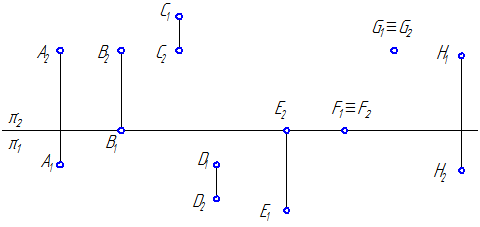
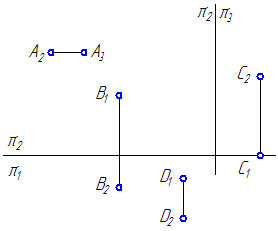



























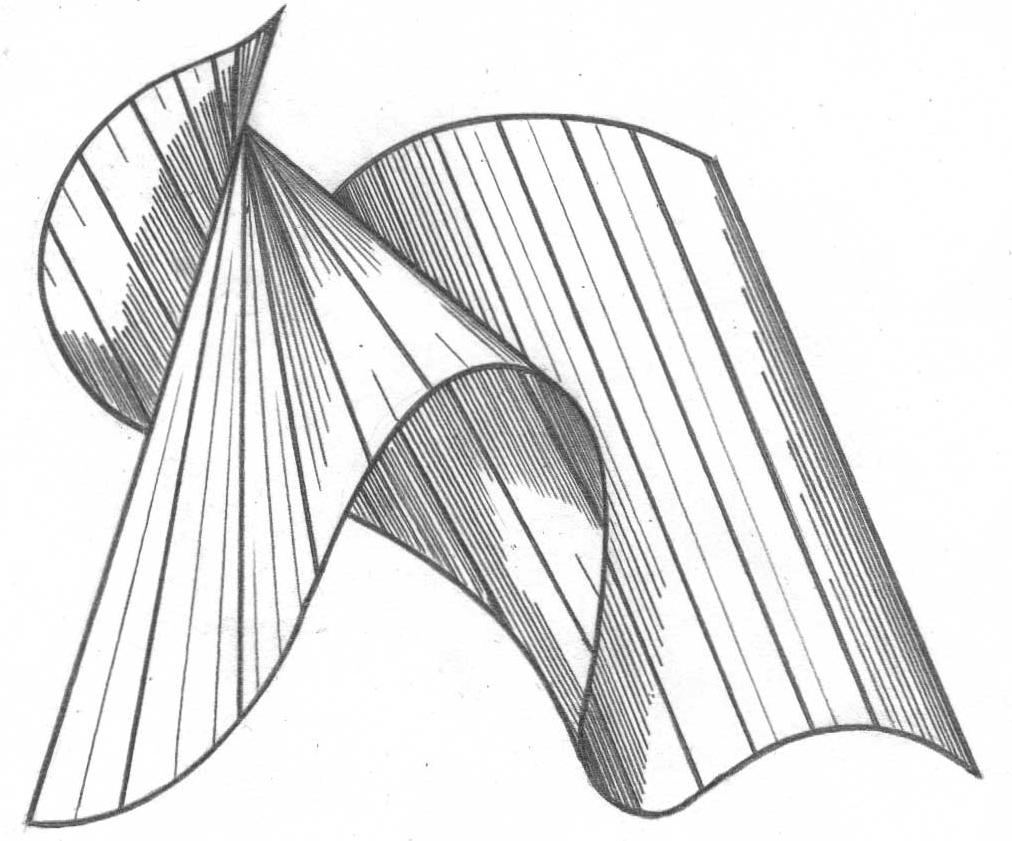
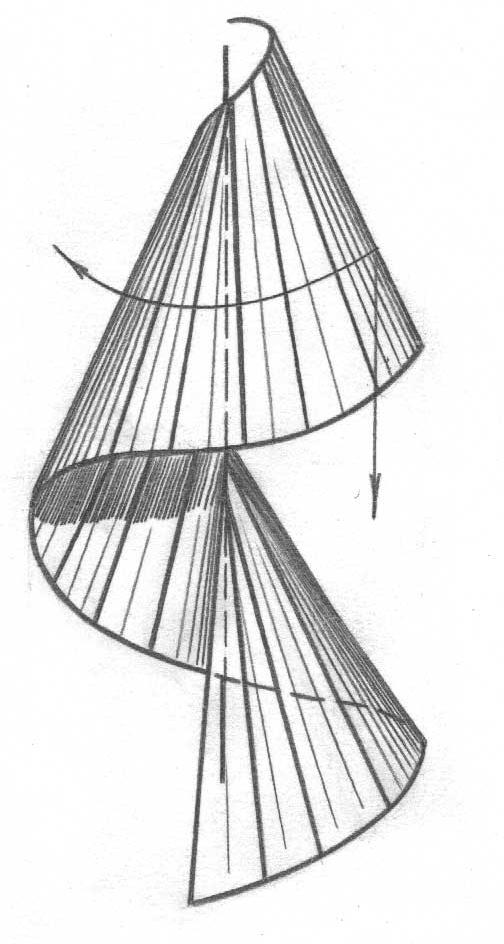

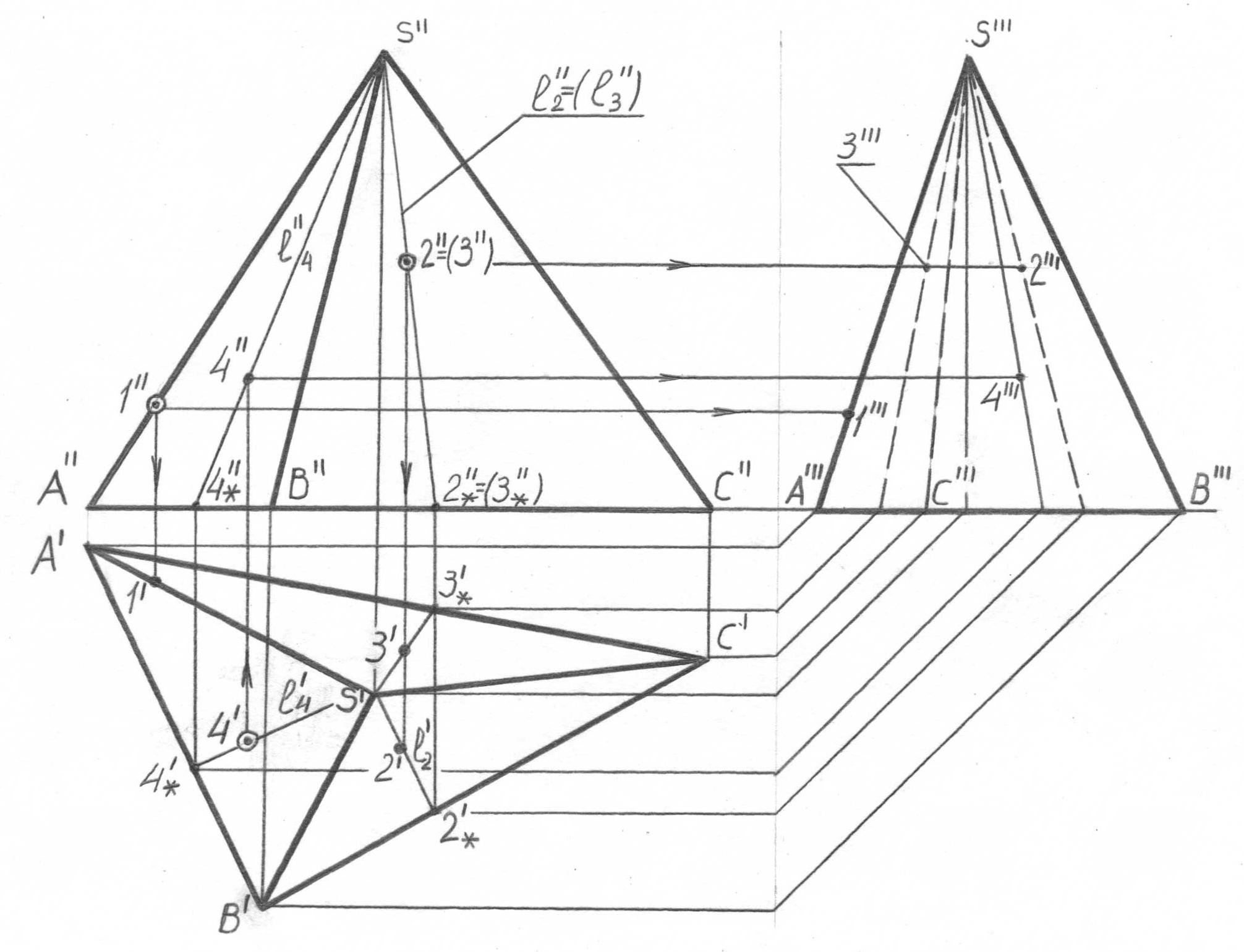












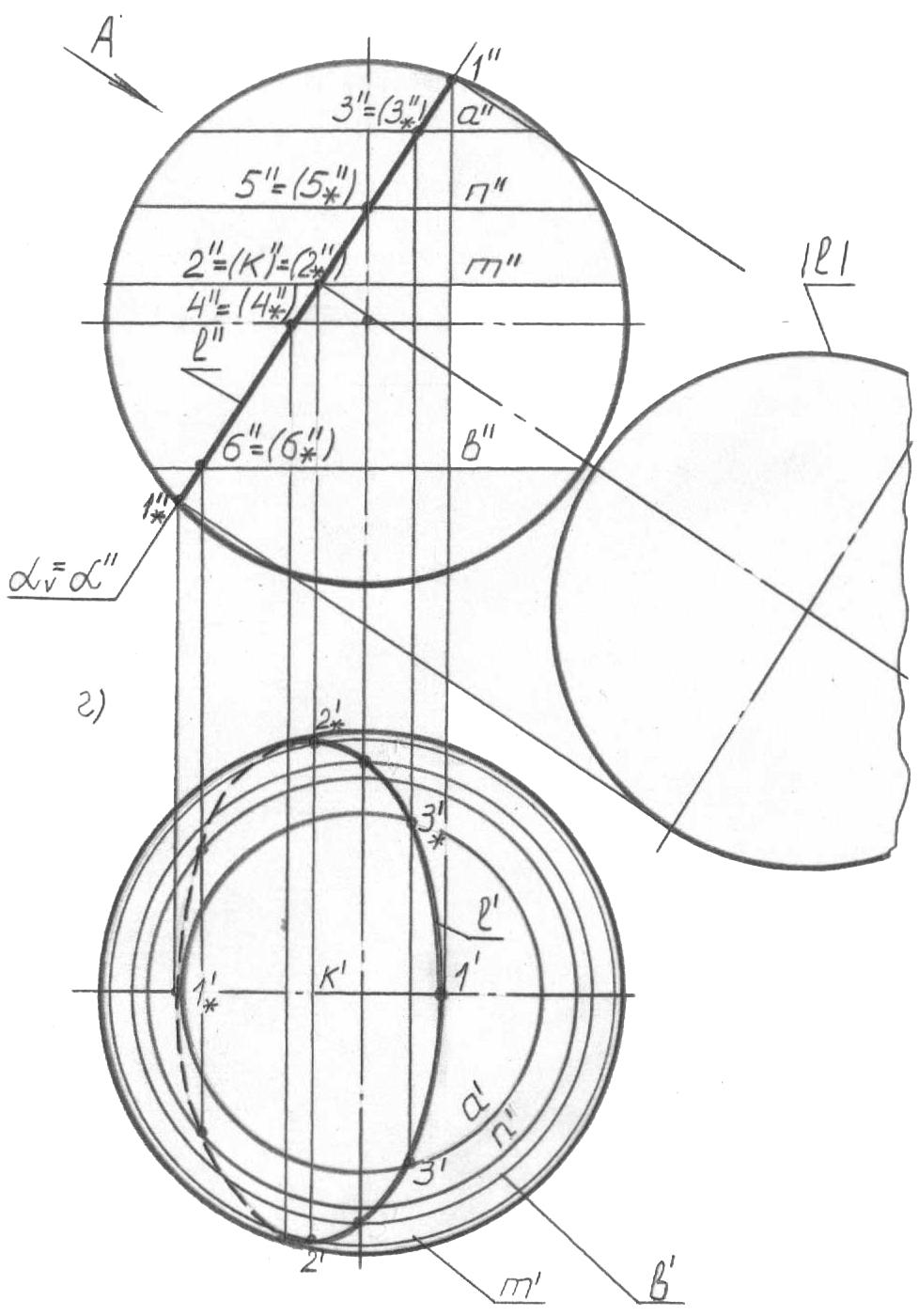


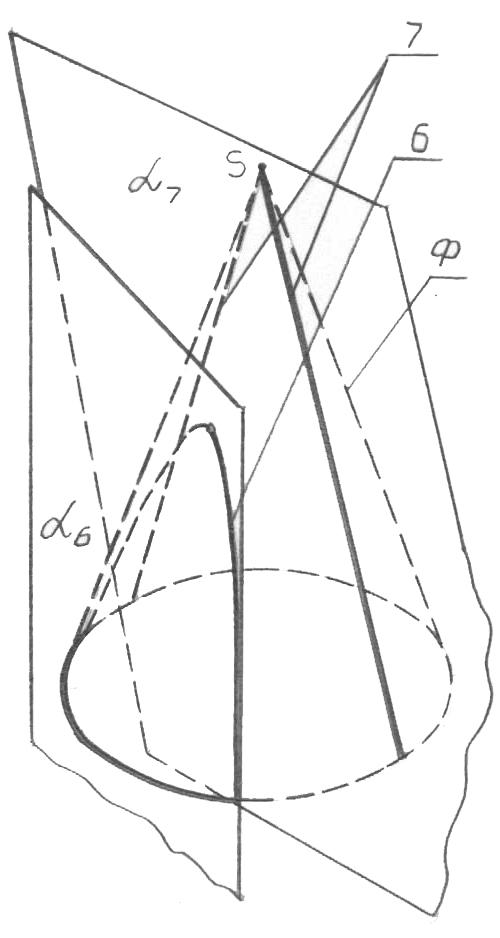



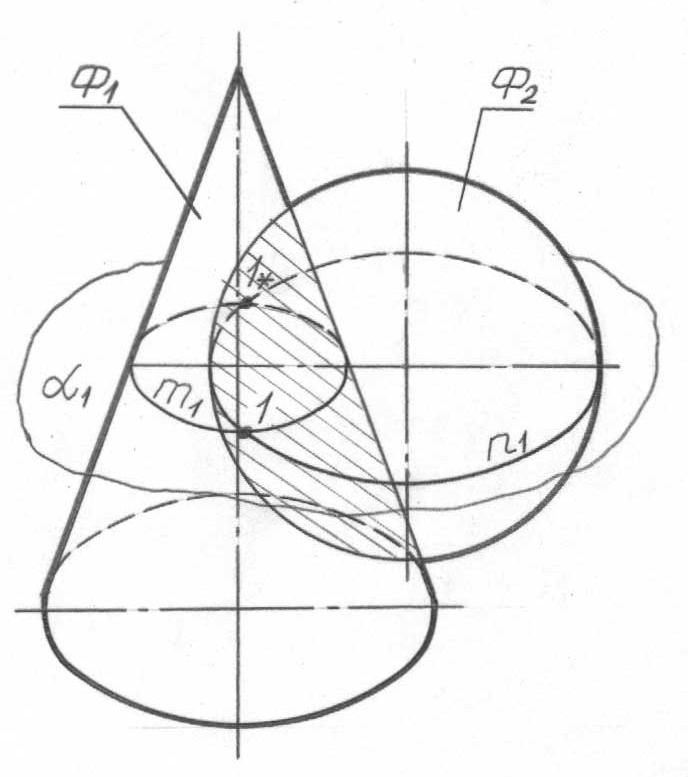 ересечь
ересечь






