Пример решения задачи по определению в заданный момент времени при сложном движении, абсолютной скорости и абсолютного ускорения точки, которая движется по ободу диска вращающегося вокруг оси.
Задача
Диск радиуса R=0,5 м вращается вокруг оси, лежащей в его плоскости и касающейся диска, с угловой скоростью ω=πt2 c-1 (рисунок 3.5). По ободу диска движется точка M по закону: ∪OM=πRt2/6 м.
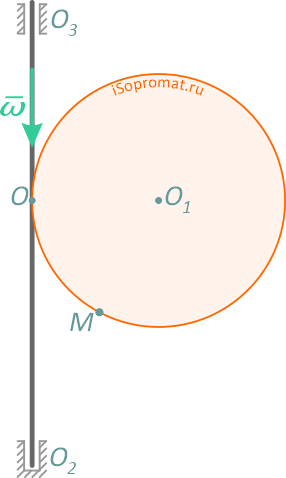
Рисунок 3.5
Требуется, в момент времени t=2c определить абсолютные скорость и ускорение точки M.
Другие примеры решений >
Помощь с решением задач >
Решение
Точка M в данном примере совершает сложное движение, которое может быть разложено на два движения: относительное движение — движение точки M по движущемуся диску (именно с ним может быть скреплена подвижная система отсчета) и переносное движение — вращение диска вместе с находящейся на нем точкой.
Поскольку переносное движение по определению это движение той точки диска, в которой находится в данный момент точка M, то сначала необходимо определить положение точки M на диске в момент времени t=2 c:
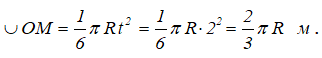
Центральный угол составит
![]()
Расчет скорости
В относительном движении закон движения задан естественным способом, поэтому скорость определяется как производная его дуговой координаты и направлена по касательной к траектории относительного движения в плоскости диска:
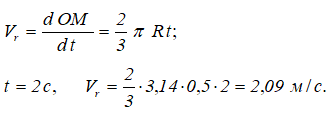
Переносное движение в данном случае — вращение вокруг неподвижной оси O2O3, расстояние до которой от точки M равно KM.
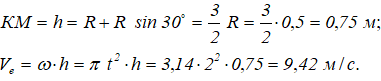
По направлению вектора угловой скорости ω определяем, что при вращении вокруг оси O2O3 точка M движется к нам, то есть вектор Ve перпендикулярен плоскости диска и для выбранной системы отсчета Mxyz, скрепленной с диском, направлен по оси Mx.
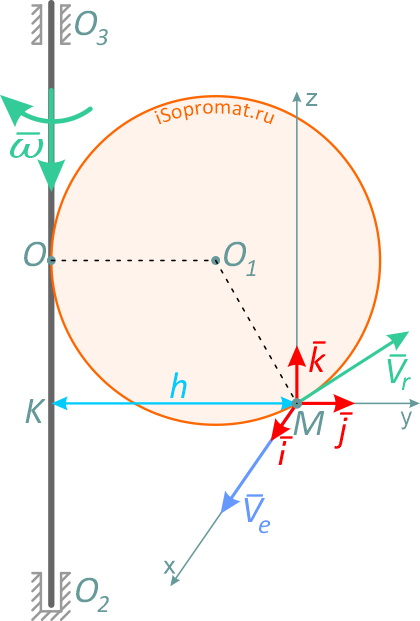
Рисунок 3.6
Абсолютная скорость точки в нашем примере определяется как геометрическая сумма векторов:
![]()
численная величина:
![]()
Спроецировав векторную сумму на выбранные оси координат, получим проекции абсолютной скорости на эти оси:
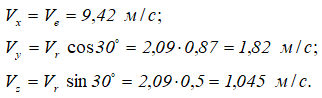
Направление вектора скорости определяют направляющие косинусы, то есть углы, которые вектор скорости составляет с выбранными осями:
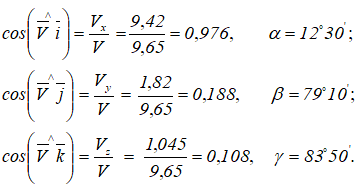
Расчет ускорения
В данном примере и переносные и относительные движения точки M — криволинейные, поэтому абсолютное ускорение определяется по формуле:
![]()
Составляющие ускорения определяются независимо друг от друга. В переносном движении точка M вращается вокруг оси O2O3 и движется по окружности радиуса h (рисунок 3.7).
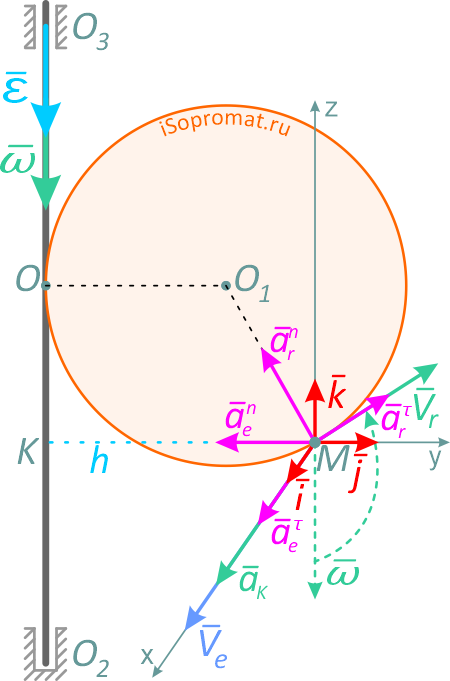
Рисунок 3.7
Нормальное ускорение в этом движении:
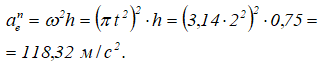
Этот вектор направлен от точки M к точке K (к оси вращения).
Касательное ускорение в переносном движении определится по формуле
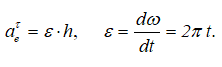
Знак производной положителен, то есть вращение ускоренное и направления векторов Ve и aeτ совпадают:
![]()
В относительном движении точка M движется по окружности радиуса R. Нормальное ускорение:
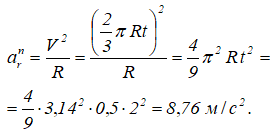
Этот вектор направлен от точки M к центру окружности — точке O1.
Касательное ускорение в относительном движении:
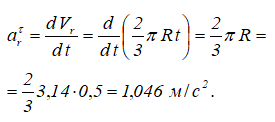
Производная от относительной скорости получена со знаком плюс, поэтому aeτ совпадает по направлению с Vr.
Кориолисово ускорение определяется по формуле
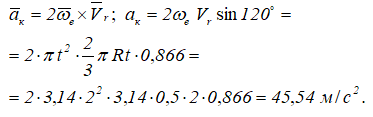
Вектор кориолисова ускорения должен быть перпендикулярен векторам ωe и Vr (в нашем случае перпендикулярен плоскости чертежа). Если смотреть навстречу вектору ak, то мы должны видеть поворот вектора ωe (мысленно перенесенного в точку) на кратчайший угол до совмещения с вектором Vr, происходящий против хода часовой стрелки. То есть в этом примере вектор ak направлен по оси Mx к нам.
Направление кориолисова ускорения может быть определено и по правилу Жуковского. Проецируем вектор V на плоскость, перпендикулярную вектору ωe (на плоскость Mxy; в данном примере эта проекция совпадает с осью My), и поворачиваем проекцию Vr на 90o в сторону вращения, то есть вектор ak направлен к нам по оси Mx.
Для определения абсолютного ускорения проецируем векторное равенство (3.6) на оси координат:
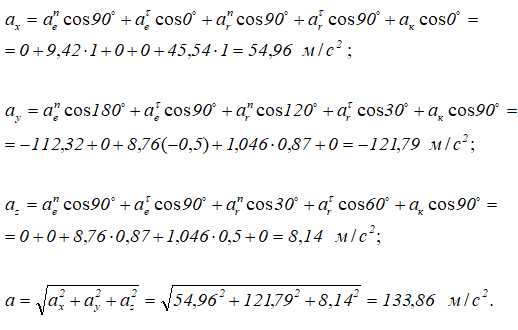
Направление вектора ускорения определяется с помощью направляющих косинусов (см. формулы (3.7)):
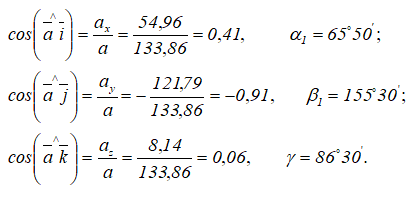
Другие примеры решения задач >
Напомним теорему сложения скоростей
при сложном движении точки:
абсолютная скорость точки равна
геометрической сумме относительной и
переносной скоростей:
![]()
Теорема сложения ускорений при сложном
движении точки имеет вид:
![]() ,
,
где вектор
![]()
называется ускорением Кориолиса.
Таким образом,
абсолютное ускорение точки равно
геометрической сумме относительного,
переносного и кориолисова ускорений.
Пример 3.3
Круглая трубка радиуса
![]() вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси![]() по часовой стрелке с постоянной угловой
по часовой стрелке с постоянной угловой
скоростью![]() .
.
Внутри трубки около ее точки![]() колеблется шарик
колеблется шарик![]() ,
,
причем так, что![]() (Рис. 3.5). Определить скорость, касательное
(Рис. 3.5). Определить скорость, касательное
и нормальное ускорения в абсолютном
движении шарика в любой момент времени.
|
|
|
Рис.3.5 |
Относительное движение шарика
представляет собой движение по окружности
радиуса![]() с центром в точке
с центром в точке![]() по закону
по закону![]() .
.
Определим закон изменения дуговой
координаты шарика в относительном
движении:
![]()
Вычислим относительную скорость и
относительное ускорение шарика:
![]()
![]()
![]()
Трубка сообщает шарику переносную
скорость
![]()
и переносное ускорение
![]()
Угол между осью вращения трубки,
вдоль которой направлен вектор ее
угловой скорости, и вектором относительной
скорости шарика равен
![]() ,
,
так что
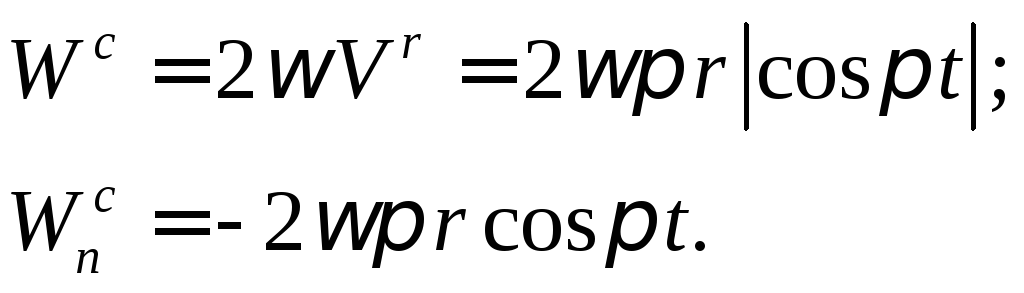
Для определения направления ускорения
Кориолиса удобнее всего воспользоваться
правилом Жуковского.
Абсолютная траектория шарика в
данном случае очевидна – это все та же
окружность с центром
![]() радиуса
радиуса![]() .
.
Используя теорему сложения скоростей,
получаем:
![]()
Используя теорему Кориолиса (3.12),
получаем:
![]()
![]()
Направления векторов указаны на Рис.
3.5. Ускорение Кориолиса и относительная
скорость представлены на рисунке для
случая
![]()
Пример 3.4
Лопатка
![]() рабочего колеса турбины, вращающегося
рабочего колеса турбины, вращающегося
против хода часовой стрелки замедленно
с угловым ускорением![]() ,
,
имеет радиус кривизны 0.2 м и центр
кривизны в точке![]() ,
,
причем![]() м. Частица воды
м. Частица воды![]() ,
,
отстоящая от оси![]() турбины на расстоянии 0.2 м, движется по
турбины на расстоянии 0.2 м, движется по
лопатке наружу и имеет скорость 0.25 м/с
и касательное ускорение 0.5 м![]() по отношению к лопатке. Определить
по отношению к лопатке. Определить
абсолютное ускорение частицы![]() в тот момент времени, когда угловая
в тот момент времени, когда угловая
скорость турбины равна 2 рад/с.
Подвижную систему координат свяжем
с рабочим колесом турбины (Рис. 3.6).
Относительной траекторией частицы воды
является кривая
![]() – лопатка турбины. Определим нормальное
– лопатка турбины. Определим нормальное
ускорение точки![]() в относительном движении
в относительном движении
![]()
Точка
![]() турбины описывает окружность с центром
турбины описывает окружность с центром![]() радиуса
радиуса![]() .
.
Определим переносное ускорение точки:
![]()
Направление ускорения Кориолиса
определяем по правилу Жуковского. Модуль
ускорения Кориолиса равен
![]()
Используя теорему Кориолиса, найдем
проекции абсолютного ускорения частицы
![]() на оси подвижной системы координат
на оси подвижной системы координат
(Рис. 3.6):
![]()
![]()
|
|
|
|
|
Рис. 3.6 |
Рис. 3.7 |
Остается определить
![]() и
и![]() .
.
Для этого используем теорему косинусов
(Рис. 3.7):
![]()
Отсюда
![]()
Таким образом,
![]()
Окончательно получаем:
![]()
Пример 3.5
Диск радиуса
![]() вращается вокруг неподвижной оси
вращается вокруг неподвижной оси![]() с постоянной угловой скоростью
с постоянной угловой скоростью![]() .
.
По ободу диска движется точка![]() ,
,
имея относительно диска постоянную по
модулю скорость![]() .
.
Определить абсолютную скорость и
абсолютное ускорение точки![]() .
.
Подвижную систему отсчета связываем
с диском (Рис. 3.8). По отношению к диску,
т.е. в относительном движении, точка
![]() движется равномерно со скоростью
движется равномерно со скоростью![]() ,
,
описывая окружность радиуса![]() с центром в точке
с центром в точке![]() .
.
Определяем относительное ускорение
точки:
![]()
Рассмотрим переносное движение –
его совершает диск. Точка
![]() диска описывает окружность с центром
диска описывает окружность с центром![]() ,
,
плоскость которой параллельна координатной
плоскости![]() .
.
Переносная скорость
![]()
направлена по касательной к этой
окружности в сторону вращения диска,
т.е. перпендикулярно плоскости диска в
отрицательном направлении координатной
оси
![]() .
.
Поскольку вращение диска по условию
равномерное, отличным от нуля оказывается
только осестремительное ускорение:
![]()
Вектор ускорения Кориолиса точки
![]() направлен перпендикулярно плоскости
направлен перпендикулярно плоскости
чертежа, в которой расположены векторы![]() и
и![]() ,
,
причем, в ту сторону, откуда кратчайшее
совмещение направления вектора![]() с направлением вектора
с направлением вектора![]() видно против хода часовой стрелки. В
видно против хода часовой стрелки. В
указанном на Рис. 3.9 положении точки![]() вектор ускорения Кориолиса направлен
вектор ускорения Кориолиса направлен
на нас, т.е. параллелен координатной
оси![]() в положительную сторону этой оси. На
в положительную сторону этой оси. На
Рис. 3.9 это направление условно обозначено
острием стрелки, заключенным в кружок.
Модуль ускорения Кориолиса вычисляется
по формуле:
![]() .
.
|
|
|
|
|
Рис.3.8 |
Рис.3.9 |
При перемещении точки
![]() по диску направление ускорения Кориолиса
по диску направление ускорения Кориолиса
не будет изменяться до тех пор, пока![]() ,
,
т.е. пока![]() (точка
(точка![]() ).
).
При пересечении точкой![]() координатной оси
координатной оси![]() ускорение Кориолиса обращается в нуль.
ускорение Кориолиса обращается в нуль.
При движении точки в нижней части диска,
т.е. при![]() ,
,
проекция ускорения Кориолиса на
направление оси![]() становится отрицательной и вектор
становится отрицательной и вектор![]() направлен от нас (точки
направлен от нас (точки![]() и
и![]() ).
).
Таким образом,
![]()
Используя теорему сложения скоростей
![]()
находим проекции вектора абсолютной
скорости на оси подвижной системы
координат:
![]()
![]()
![]()
Используя теорему Кориолиса
![]()
находим проекции абсолютного ускорения
точки на оси подвижной системы координат:
![]()
![]()
![]()
![]()
Примечание.
Последняя задача позволяет
проиллюстрировать некоторые явления,
связанные с вращением Земли, в частности,
размыв берегов рек. Как видно, вращение
Земли приводит к возникновению у частиц
воды кориолисова ускорения, направленного
перпендикулярно линии берегов. Наличие
такого ускорения приводит к тому, что
в северном полушарии дополнительно
подмывается правый берег, который на
прямолинейных участках рек заметно
выше левого берега. В южном полушарии
более высокий левый берег. Это явление
в географии отражено в законе Бэра.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 22.10;
22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19;
23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-23;
СР-24; СР-25.
КОНТРОЛЬНЫЕ
МЕРОПРИЯТИЯ:
-
После
практического занятия №7(15) проводится
тест «МОДУЛЬ КБ».
ЛИТЕРАТУРА:
-
Антонов В.И., Белов В.А., Егорычев О.О.,
Степанов Р.Н.//Курс теоретической
механики (теория и практика) – М.:
Архитектура – С, 2011 г. -
Мещерский И.В.//Сборник задач по
теоретической механике. – Спб.: Лань,
2010 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
Содержание:
- Сложное движение точки
- Абсолютный, относительный и переносной движения точки
- Теорема о сложении скоростей в сложном движении точки
- Теорема о сложении ускоренного в сложном движении точки (Теорема Кориолиса *)
- Кориолисово ускорения
- Правило Жуковского
- Примеры решения задач на сложное движение точки
- Сложное движение точки и решение задач
- Порядок решения задач на сложное движение точки
- Примеры решения задач
- Задание темы К4 (сложное движение точки)
- Пример решения задания темы К4
- Сложное движение точки образцы и примеры
- Относительное, переносное и абсолютное движение точки
- Относительные, переносные и абсолютные скорости и ускорение
- Сложение скоростей и ускорений при сложном движении точки
- Примеры решения задач
- Абсолютное, относительное и переносное движение точки
- Центральная операция кинематики и динамики. Абсолютная и относительная производные по времени от вектора функции
- Теорема о сложении скоростей
- Теорема о сложении ускорений
- Вращательное и осевое ускорение в случае вращения тела вокруг неподвижной оси
- Ускорение Кориолиса
- Случаи превращения в ноль ускорения Кориолиса
- Физические причины возникновения ускорения Кориолиса
- Сложное движение материальной точки. Относительное, переносное и абсолютное движение материальной точки
- Теорема о сложении скоростей в сложном движении материальной точки
- Теорема Кориолиса
- Модуль, направление и физические причины возникновения ускорения Кориолиса
- Методика решения задач на сложное движение материальной точки
Сложное движение точки – это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движениях. Примером сложного движения могут служить: движение пассажира. перемещающегося в вагоне движущегося поезда; движение человека, перемещающегося по лестнице движущегося эскалатора.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сложное движение точки
Сложное движение точки – это такое движение, при котором точка участвует одновременно в двух или нескольких движениях. Примеры сложного движения точки (тела): лодка, переплывающая реку; человек, идущий по движущемуся эскалатору; камень подвижной кулисы, поршень качающегося цилиндра; шары центробежного регулятора Уатта. Для описания сложного движения точки или для представления движения в виде сложного используются неподвижная система отсчета, связанная с каким-либо условно неподвижным телом, например, с Землей, и подвижная система отсчета, связанная с каким-либо движущимся телом.
Абсолютный, относительный и переносной движения точки
В разделе 2 изучалось движение точки по отношению к системе координат (системы отсчета), которую считали условно неподвижной. В то же время, рассматривая многие задачи механики, целесообразнее, а в некоторых случаях просто необходимо, проводить исследования движения точки одновременно по отношению в двух (или более) систем отсчета, из которых одна считается неподвижной, а другая (другие) движется определенным образом по отношению к ней.
Движение точки по отношению к нескольким системам отсчета называется сложным.
Например, в сложном движении находятся поршень двигателя движущегося автомобиля; груз, который поднимается краном, одновременно перемещается вдоль направляющих и поворачивается вокруг своей вертикальной оси; движение человека по вагону подвижного состава.
В этом разделе будем рассматривать движение точки относительно двух систем отсчета.
Рассмотрим движущееся тело А, которое в отдельных случаях будем называть переносной средой, в отношении которого движется точка М, которая не принадлежит телу (рис. 7.1). С телом А неизменно свяжем систему координат  которая движется относительно другой системы
которая движется относительно другой системы  которую условно считаем неподвижной.
которую условно считаем неподвижной.

Система координат  называется подвижной системой отсчета, а система
называется подвижной системой отсчета, а система  – неподвижной системе отсчета. Заметим, что неподвижную систему отсчета очень часто связывают с поверхностью Земли или неподвижными объектами на ней.
– неподвижной системе отсчета. Заметим, что неподвижную систему отсчета очень часто связывают с поверхностью Земли или неподвижными объектами на ней.
Поскольку точка М движется относительно двух систем отсчета, то ее движение, по определению, будет сложным. Введем основные понятия и обозначения в случае сложного движения точки.
Движение точки М по отношению к неподвижной системе отсчета называется абсолютным движением. Уравнения абсолютного движения точки можно записать в виде:

Траектория, скорость и ускорение точки в абсолютном движении называются абсолютной траекторией, скоростью и ускорением точки. Абсолютные скорость и ускорение будем обозначать  и
и
Движение точки М относительно подвижной системы отсчета  называется
называется
относительным движением точки, а траектория, скорость и ускорение – относительной траекторией, скоростью и ускорением. Относительные скорость и ускорение обозначают  и
и  (от латинского relativus – относительный). Уравнения относительного движения точки имеют вид:
(от латинского relativus – относительный). Уравнения относительного движения точки имеют вид:

Движение подвижной системы отсчета (а значит и тела А) относительно неподвижной
является для точки М переносным движением. Скорость и ускорение той точки тела А, с которой в данный момент времени совпадает движущаяся точка М, называется соответственно переносной скоростью и переносным ускорением точки в этот момент. Переносная скорость и ускорение обозначаются  и
и  (от латинского emporter – переносить).
(от латинского emporter – переносить).
В приведенном выше примере о человеке, что перемещается в вагоне подвижного состава, с вагоном можно связать подвижную систему координат, а с поверхностью Земли – неподвижную. Тогда движение вагона будет переносным, движение человека относительно вагона – относительным, а движение человека относительно поверхности
Земли – абсолютным. Переносной скоростью и переносным ускорением человека будет скорость и ускорение той точки вагона, в которой в заданный момент находится человек.
Основная задача кинематики сложного движения точки заключается в том, чтобы, зная кинематические характеристики относительного и переносного движений, найти соответствующие им характеристики абсолютного движения.
Теорема о сложении скоростей в сложном движении точки
Теорема. В сложном движении точки ее абсолютная скорость равна векторной сумме относительной и переносной скоростей.
Доказательство. Для доказательства рассмотрим движение точки М (рис. 7.1) относительно подвижной системы отсчета  связанной с телом А. Для общего случая, движение тела А рассмотрим как движение свободного твердого тела. Следовательно, точка М находится одновременно в двух движениях: относительном – относительно тела А и переносном – вместе с телом. Абсолютным движением точки М будет ее движение относительно неподвижной системы отсчета
связанной с телом А. Для общего случая, движение тела А рассмотрим как движение свободного твердого тела. Следовательно, точка М находится одновременно в двух движениях: относительном – относительно тела А и переносном – вместе с телом. Абсолютным движением точки М будет ее движение относительно неподвижной системы отсчета  Напомним, что поскольку переносным движением является свободное движение твердого тела, то его можно рассматривать, согласно § 6.1 раздела 6, как совокупность поступательного движения вместе с полюсом (Точка
Напомним, что поскольку переносным движением является свободное движение твердого тела, то его можно рассматривать, согласно § 6.1 раздела 6, как совокупность поступательного движения вместе с полюсом (Точка  ) и сферического вокруг полюса. Сферическую составляющую в каждый момент времени можно заменить (§ 5.1) вращением тела, а значит и подвижной системы координат
) и сферического вокруг полюса. Сферическую составляющую в каждый момент времени можно заменить (§ 5.1) вращением тела, а значит и подвижной системы координат  вокруг мгновенной оси
вокруг мгновенной оси  проходящей через
проходящей через
точку  с угловой скоростью переносного движения
с угловой скоростью переносного движения 
Положение точки М в подвижной системе координат  определяется радиусом-вектором
определяется радиусом-вектором  в неподвижной – радиусом-вектором
в неподвижной – радиусом-вектором  а положение начала подвижной системы координат (точка
а положение начала подвижной системы координат (точка  ) относительно начала О неподвижной – радиусом-вектором
) относительно начала О неподвижной – радиусом-вектором  Во время движения точки М между радиусами-векторами
Во время движения точки М между радиусами-векторами  и
и  согласно рис. 7.1 справедлива зависимость
согласно рис. 7.1 справедлива зависимость

Если координаты точки М в подвижной системе отсчета обозначить через  а орты осей этой системы –
а орты осей этой системы –  то
то

и тогда

Абсолютная скорость точки М равна производной по времени от радиусавектора что определяет ее положение в абсолютном движении. дифференцируя зависимость (7.5) и учитывая, что орты
что определяет ее положение в абсолютном движении. дифференцируя зависимость (7.5) и учитывая, что орты меняют свое направление в пространстве, получим
меняют свое направление в пространстве, получим

Изменение направлений ортов  происходит от вращения осей подвижной системы отсчета вокруг мгновенной оси
происходит от вращения осей подвижной системы отсчета вокруг мгновенной оси  с угловой скоростью
с угловой скоростью  Поэтому производные по времени от единичных ортов можно рассматривать как скорости концов этих ортов от этого вращения. Согласно формуле (3.17) раздела 3 запишем
Поэтому производные по времени от единичных ортов можно рассматривать как скорости концов этих ортов от этого вращения. Согласно формуле (3.17) раздела 3 запишем

После подстановки (7,7) в (7.6) и преобразований с учетом зависимости (7.7), получим
где скорость точки
скорость точки  начала подвижной системы координат.
начала подвижной системы координат.
Зависимость (7.8) определяет вектор абсолютной скорости точки М. Проведем ее анализ.
Поскольку в последних трех слагаемых зависимости (7.8) являются производные по времени от соответствующих уравнений относительного движения точки М (7.2), то согласно с (2.18) они являются проекциями вектора относительной скорости точки на оси
подвижной системы координат
 а сумма трех слагаемых выражает вектор относительной скорости точки М
а сумма трех слагаемых выражает вектор относительной скорости точки М

Покажем, что первые две слагаемых зависимости (7.8) определяют вектор переносной скорости точки М. Действительно, переносная скорость точки, по определению, это скорость точки, неизменно связанной с подвижной системой отсчета, с которой в данный момент времени совпадает движущаяся точка М. Такой точкой в нашем случае является точка М тела А, находящегося в свободном движении. А по формуле (6.3) скорость этой точки равна сумме скорости полюса  и вращательной скорости вокруг мгновенной
и вращательной скорости вокруг мгновенной
оси  то есть
то есть

Учитывая (7.9) и (7.10), зависимость (7.8) перепишем в виде

то есть абсолютная скорость точки равна векторной сумме переносной и относительной скоростей. Теорема доказана.
Следует заметить, что в случае, когда переносным движением является движение свободного твердого тела, то переносная скорость сама определяется диагональю
параллелограмма, построенного на векторах скорости полюса и скорости точки от вращения вокруг него
и скорости точки от вращения вокруг него  Если же переносное движение поступательное, то зависимость (7.10) принимает вид
Если же переносное движение поступательное, то зависимость (7.10) принимает вид

В случае вращательного переносного движения  где
где  – вектор, проведенный из любой точки на оси вращения к точке М.
– вектор, проведенный из любой точки на оси вращения к точке М.
Исходя из того, что в общем случае абсолютная скорость точки М определяется диагональю параллелограмма, построенного на векторах  и
и  модуль абсолютной скорости точки можно получить по формуле
модуль абсолютной скорости точки можно получить по формуле

Замечания. Если точка М находится в n движениях, то абсолютная скорость точки М равна векторной сумме векторов скоростей составляющих движений
Теорема о сложении ускоренного в сложном движении точки (Теорема Кориолиса *)
Теорема. В сложном движении точки ее абсолютное ускорение равно векторной сумме переносного, относительного и кориолисового ускоренний.
Доказательство. Вектор абсолютного ускорения точки М равна

и для его определения продифференцируем зависимость (7.6) по времени.
После возведения соответствующих членов, получим
Учитывая формулы (7.7),
Превратим зависимость (7.14), используя зависимости (7.5), (7.7), (7.9) и (7.15). Получим формулу, выражающую вектор абсолютного ускорения точки М
где  ускорения начала подвижной системы координат.
ускорения начала подвижной системы координат.
Проведем анализ зависимости (7.16).
Учитывая, что переносным движением в нашем случае является движение свободного твердого тела, то соответственно формуле (6.10) первые три слагаемых формулы (7.16) является вектором переносного ускорения точки

Поскольку в выражении есть вторые производные по времени от соответствующих уравнений относительного движения (7.2), то согласно (2.34) это выражение является вектором относительного ускорения точки
есть вторые производные по времени от соответствующих уравнений относительного движения (7.2), то согласно (2.34) это выражение является вектором относительного ускорения точки
Итак, мы установили механический смысл первых шести слагаемых зависимостях (7.16). Но, как видим, в формулу для вектора абсолютного ускорения точки М входит еще одно слагаемое.
Выражение 
называется вектором кориолисового или поворотного ускорения точки М.
Подставляя формулы (7.17), (7.18) и (7.19) в (7.16), получим

Теорема доказана.
В случае поступательного переносного движения а потому переносное ускорение точки М равна ускорению начала подвижной системы отсчета, то есть
а потому переносное ускорение точки М равна ускорению начала подвижной системы отсчета, то есть 
И одинаковое для всех точек переносного среды. Кроме этого, кориолисово ускорения в этом
случае также равна нулю и зависимость (7.20) принимает вид
и зависимость (7.20) принимает вид

Замечания. Относительные скорость и ускорение определяются в относительной системе отсчета по правилам кинематики точки: по координатного способа – через проекции на оси декартовой системы координат, как вторые производные от уравнений относительного движения точки (7.2) при натуральном способа – через проекции на оси натурального трехгранника относительной траектории.
Переносная скорость и ускорение определяются методами кинематики твердого тела. Если система  движется поступательно или вращается вокруг неподвижной оси, то используются методы раздела 3. В случае плоского движения переносного среды следует применить правила раздела 4, а для более сложных движений (сферический движение, движение свободного твердого тела) необходимо использовать методы, изложенные в
движется поступательно или вращается вокруг неподвижной оси, то используются методы раздела 3. В случае плоского движения переносного среды следует применить правила раздела 4, а для более сложных движений (сферический движение, движение свободного твердого тела) необходимо использовать методы, изложенные в
разделах 5 и 6. Методы определения кориолисового ускорения рассмотрены ниже.
Кориолисово ускорения
Кориолисовым ускорением называется составляющая абсолютного ускорения точки в ее сложном движении, равна удвоенному векторном произведения вектора переносной угловой скорости на вектор относительной скорости этой точки.
В начале выясним физические причины появления кориолисового ускорения. Как известно, вектор ускорения характеризует изменение вектора скорости как по величине, так и по направлению. Так, переносное ускорение характеризует изменение переносной скорости, а относительное -относительной скорости в соответствующих движениях точки М. Какие же изменения и которых кинематических характеристик движения точки, при ее сложном движении, характеризует кориолисово ускорения? Для ответа на этот вопрос рассмотрим движение точки М, равномерно перемещается вдоль радиуса платформы, которая равномерно вращается вокруг оси, перпендикулярной к плоскости платформы (рис. 7.2).
В этом случае переносным движением будет вращения платформы с 

относительным движением – прямолинейное движение точки вдоль радиуса
с 

Пусть в момент времени  точка занимала положение М, для которого векторы
точка занимала положение М, для которого векторы
переносной и относительной скоростей  и
и  За промежуток времени
За промежуток времени  платформа вернулась на некоторый угол
платформа вернулась на некоторый угол а точка переместилась из положения
а точка переместилась из положения и в
и в
момент времени векторы переносной и относительной скоростей будут соответственно
векторы переносной и относительной скоростей будут соответственно 
Поскольку относительное движение равномерное прямолинейный, то относительное ускорение  то есть за промежуток времени
то есть за промежуток времени  вектор
вектор  должен не измениться, а быть постоянным. Однако, как видно из рисунка, за время
должен не измениться, а быть постоянным. Однако, как видно из рисунка, за время  вектор относительной
вектор относительной
скорости  изменил свое направление от
изменил свое направление от  Это изменение вектора относительной
Это изменение вектора относительной
скорости состоялась за счет переносного движения.
Учитывая, что переносное движение – равномерное вращение и
и  то за промежуток времени
то за промежуток времени  не должна состояться изменение величины переносной скорости (это изменение характеризует вращательное ускорение, которое в нашем случае равна нулю 0).
не должна состояться изменение величины переносной скорости (это изменение характеризует вращательное ускорение, которое в нашем случае равна нулю 0).  Но, как видно из рис. 7.2, величина переносной скорости меняется от
Но, как видно из рис. 7.2, величина переносной скорости меняется от 
 Очевидно, что изменение вызвано перемещением точки с положения
Очевидно, что изменение вызвано перемещением точки с положения  которое произошло за счет относительного движения точки.
которое произошло за счет относительного движения точки.
Итак, появление кориолисового ускорения обусловлена взаимным влиянием переносного и относительных движений.
Ускорение Кориолиса характеризует изменение направления относительной скорости, обусловленной переносным движением, и величины переносной скорости за счет относительного движения.
Модуль кориолисового ускорения, исходя из (7.19), равна

Рассмотрим случаи отсутствия кориолисового ускорения точки.
Из формулы (7.22) следует, что  если:
если:
1)  то есть, когда переносное движение поступательное или угловая скорость переносного вращения равна нулю (в моменты, когда направление вращательного движения меняется на противоположный)
то есть, когда переносное движение поступательное или угловая скорость переносного вращения равна нулю (в моменты, когда направление вращательного движения меняется на противоположный)
2)  то есть в те моменты времени, когда относительная скорость равна нулю (например, в моменты времени, когда вектор
то есть в те моменты времени, когда относительная скорость равна нулю (например, в моменты времени, когда вектор  меняет свое направление на противоположный).
меняет свое направление на противоположный).
3) есть, когда векторы
есть, когда векторы  и
и  коллинеарны (параллельные).
коллинеарны (параллельные).
Направление вектора кориолисового ускорения определяется согласно правилу векторного произведения двух векторов  Во время практического решения задач целесообразно применять правило Жуковского.
Во время практического решения задач целесообразно применять правило Жуковского.
Правило Жуковского
Чтобы найти направление кориолисового ускорения, необходимо спроектировать вектор относительной скорости  на плоскость П, перпендикулярную оси переносного вращения, и вернуть эту проекцию
на плоскость П, перпендикулярную оси переносного вращения, и вернуть эту проекцию  на угол
на угол  в сторону переносного вращения (рис. 7.3).
в сторону переносного вращения (рис. 7.3).
Наличием кориолисового ускорения объясняются различные явления, которые происходят на поверхности Земли вследствие ее вращения. так замечено, что для рек, текущих в
северном полушарии, даже на прямолинейных участках, подмываются больше правы, чем левые берега; при аналогичных условиях на железнодорожных дорогах происходит интенсивнее износ правых рельсов колеи по сравнению с левыми. Все эти явления объясняются появлением кориолисова силы инерции, направленной в сторону, противоположную кориолисового ускорению, о чем пойдет речь в части «Динамика».

Примеры решения задач на сложное движение точки
Задача 1. Тележка А мостового крана, перемещает груз С в горизонтальной плоскости, движется по закону  в метрах,
в метрах,  -в секундах). Груз С при этом колеблется на подвесе
-в секундах). Груз С при этом колеблется на подвесе  длиной
длиной  по закону
по закону 
 – в радианах,
– в радианах,  – в секундах). Найти абсолютные скорость и ускорение груза С в момент времени
– в секундах). Найти абсолютные скорость и ускорение груза С в момент времени


Решение. Рассмотрим движение груза С, как материальной точки, находится в сложном движении. выберем неподвижную  и подвижную
и подвижную  системы координат, причем последнюю свяжем с подвижным тележкой (рис. 7.5). Тогда абсолютным движением груза С будет его движение относительно системы
системы координат, причем последнюю свяжем с подвижным тележкой (рис. 7.5). Тогда абсолютным движением груза С будет его движение относительно системы  переносным – движение подвижной системы
переносным – движение подвижной системы  относительно неподвижной
относительно неподвижной  или, что одно и тоже, поступательное движение тележки, а относительным движением – колебания груза на подвесе (криволинейное движение
или, что одно и тоже, поступательное движение тележки, а относительным движением – колебания груза на подвесе (криволинейное движение
точки С по кругу).

Для определения абсолютной скорости груза используем зависимость (7.11)

Чтобы определить переносную скорость, условно остановим относительное движение груза.
Тогда движение системы тележка-груз на подвесе рассматриваем как поступательное движение одного тела, происходит по закону 
Переносная скорость определится

Если  Вектор
Вектор направленный параллельно оси
направленный параллельно оси 
Чтобы найти относительную скорость груза, условно остановим переносное движение и тогда относительную скорость подсчитаем как скорость точки С при вращении вокруг точки  (криволинейное движение точки по окружности).
(криволинейное движение точки по окружности).

где  – относительная угловая скорость, в нашем случае
– относительная угловая скорость, в нашем случае

При 
Знак минус показывает, что вращение в данный момент времени происходит против положительного направления отсчета угла φ, то есть по часовой стрелки.
Итак,
Вектор  напрямлений перпендикулярно до
напрямлений перпендикулярно до  в сторону напрямку кутової швидкості.
в сторону напрямку кутової швидкості.
Модуль абсолютной скорости груза С определим по зависимости (7.12)
где α – угол между векторами и
и 
При 

Тогда 
Для определения абсолютного ускорения груза С используем зависимость (7.20)

Определим составляющие абсолютного ускорения груза. Методика определение переносного и относительного ускоренного аналогична определения переносной и относительной скоростей. переносное ускорение

Знаки  и
и  одинаковые, поэтому вектор
одинаковые, поэтому вектор  совпадает по направлению с
совпадает по направлению с 
Относительное ускорение точки, при ее движении по кругу, равна

Касательное ускорение

где  относительное угловое ускорение.
относительное угловое ускорение.
При 
Поскольку знаки  и
и одинаковые, то вращение ускоренное, и
одинаковые, то вращение ускоренное, и
совпадает по направлению с 
Тогда

Вектор  совпадает по направлению с вектором
совпадает по направлению с вектором 
Нормальное ускорение точки в относительном движении определится зависимостью

и при 
Вектор  направленный по
направленный по  от точки С до точки
от точки С до точки 
В этой задаче переносное движение является поступательным, так кориолисово ускорения равна нулю  Величину абсолютного ускорения груза найдем по его проекциями на оси неподвижной системы координат, учитывая, что при
Величину абсолютного ускорения груза найдем по его проекциями на оси неподвижной системы координат, учитывая, что при

Проекции абсолютного ускорения груза будут такими

Тогда модуль абсолютного ускорения груза С будет равняться

Задача 2. Прямоугольный треугольник АВС вращается вокруг своего катета АС ривносповильнено с угловым ускорением  при начальной угловой скорости
при начальной угловой скорости  По гипотенузе АВ движется точка М по закону
По гипотенузе АВ движется точка М по закону  в сантиметрах, t – в секундах). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени
в сантиметрах, t – в секундах). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени  (рис. 7.6).
(рис. 7.6).


Решение. Поскольку точка М одновременно находится в двух движениях, то
ее движение рассматриваем как сложный.
Выберем неподвижную  и подвижную
и подвижную системы координат (рис. 7.7).
системы координат (рис. 7.7).
Подвижная система связана с треугольником, вращающийся (на рис. 7.7 показана только ось  тогда переносним рухом буде обертання трикутника навколо катета АС, відносним — прямолінійний рух точки вздовж катета АВ за законом
тогда переносним рухом буде обертання трикутника навколо катета АС, відносним — прямолінійний рух точки вздовж катета АВ за законом

Абсолютная скорость точки М определится согласно (7.11)

Переносную скорость точки М определим как скорость той точки гипотенузы АВ треугольника, вращающийся с которой в данный момент времени совпадает подвижная точка М. Определим положение точки М на гипотенузе АВ при 

Переносная скорость равна

где DM – короткая расстояние от точки М до оси вращения АС;  угловая скорость вращения треугольника АВС.
угловая скорость вращения треугольника АВС.

Тогда 
Поскольку траектории переносного движения точки М в данный момент времени
является окружность радиуса DM, то вектор  будет направлен по касательной к
будет направлен по касательной к
круга в сторону вращения. Если плоскость треугольника АВС при совместить с плоскостью
совместить с плоскостью то вектор
то вектор  Относительная скорость точки М определится методами кинематики точки и будет равняться
Относительная скорость точки М определится методами кинематики точки и будет равняться

и при 
Вектор направлен по гипотенузе АВ в сторону увеличения S.
направлен по гипотенузе АВ в сторону увеличения S.
Поскольку угол между векторами  и
и  равна
равна  То модуль абсолютной
То модуль абсолютной
скорости будет равняться

В случае непоступального переносного движения абсолютное ускорение точки М в сложном движении по формуле (7.20) будет равняться

Переносное движение является вращательным, так переносное ускорение точки М в соответствии с (3.15) определится по формуле
Вектор  направлен к оси вращения треугольника вдоль радиуса MD, а вектор
направлен к оси вращения треугольника вдоль радиуса MD, а вектор  – перпендикулярно к
– перпендикулярно к  в сторону дуговой стрелки углового ускорения
в сторону дуговой стрелки углового ускорения  которое противоположное
которое противоположное  поскольку вращение замедлено.
поскольку вращение замедлено.
При прямолинейном относительном движении относительно ускорения точки М имеет только касательную составляющую, равную


векторы и
и  при
при совпадают по направлению.
совпадают по направлению.
Модуль кориолисового ускорения определится по зависимости (7.23)

Согласно принятому направлением вращения вектор  будет направлен по оси вращения в сторону положительного направления оси
будет направлен по оси вращения в сторону положительного направления оси  Поэтому угол между
Поэтому угол между  и
и  равна
равна и при
и при  кориолисово ускорения будет равняться
кориолисово ускорения будет равняться

Вектор  согласно правилу Жуковского, совпадает по направлению с вектором
согласно правилу Жуковского, совпадает по направлению с вектором 
Для нахождения модуля абсолютного ускорения точки М воспользуемся методом проекций. Для этого введем вспомогательную систему координат  оси которой направлены соответственно по касательной к переносной траектории, по радиусу MD и параллельно оси вращения (Рис. 7.7).
оси которой направлены соответственно по касательной к переносной траектории, по радиусу MD и параллельно оси вращения (Рис. 7.7).
тогда:

Модуль абсолютного ускорения точки М

Сложное движение точки и решение задач
Краткие сведения по теории:
Характер движения существенно зависит от того, в какой системе отсчета (подвижной или неподвижной) рассматривается это движение.
Движение точки относительно неподвижной системы отсчета называется абсолютным.
Движение точки по отношению к подвижной системе отсчета называется относительным.
Движение, которое имеет подвижная система отсчета со всеми неизменно связанными с ней точками пространства по отношению к условно неподвижной системы отсчета,
называется переносным.
Каждое из этих движений характеризуется своими скоростями и ускорениями.
В соответствии с законами сложения скоростей:

и ускорений:

где  абсолютные скорость и ускорение подвижной точки;
абсолютные скорость и ускорение подвижной точки;
 переносные скорость и ускорение подвижной точки;
переносные скорость и ускорение подвижной точки;
 относительные скорость и ускорение подвижной точки;
относительные скорость и ускорение подвижной точки;
 Кориолисовое ускорение.
Кориолисовое ускорение.
Величина Корриолисового ускорения определяется по формуле:

где  угловая скорость переносного движения;
угловая скорость переносного движения;
 угол между векторами
угол между векторами  и
и 
Вектор Корриолисового ускорения  направлен перпендикулярно к плоскости, в которой лежат векторы угловой скорости
направлен перпендикулярно к плоскости, в которой лежат векторы угловой скорости  и относительной скорости
и относительной скорости  в ту сторону, откуда наблюдатель видит наименьший поворот вектора
в ту сторону, откуда наблюдатель видит наименьший поворот вектора  к вектору
к вектору  против движения часовой стрелки.
против движения часовой стрелки.
Поскольку в случае плоского движения тела угол между векторами  и
и  равняется
равняется  то:
то:

При плоском движении направление  можно определить по правилу Жуковского Н.Е.: на направление Кориолисового ускорения укажет вектор относительной скорости
можно определить по правилу Жуковского Н.Е.: на направление Кориолисового ускорения укажет вектор относительной скорости  если его повернуть в плоскости расположения на
если его повернуть в плоскости расположения на  в сторону переносной угловой скорости
в сторону переносной угловой скорости 
В случае, если переносное движение является поступательным 
Если переносные и относительные движения являются криволинейными, переносными и относительными ускорениями можно изобразить в виде геометрических сумм соответствующих нормальных и касательных ускорений:

Порядок решения задач на сложное движение точки
При решении задач на сложное движение точки рекомендуется придерживаться такой последовательности:
1. Разложить движение точки на составляющие, определить абсолютное, относительное и переносное движения.
2. Выбрать две системы координат: абсолютную (неподвижную) и относительную (подвижную).
3. Мысленно остановить переносное движение, определить скорость и ускорение точки в относительном движении.
4. Мысленно остановить относительное движение, определить угловую скорость переносного движения, скорость и ускорение точки в переносном движении.
5. По известным угловым скоростям переносного движения и скоростью точки в относительном движении найти величину и направление кориолисового ускорения точки.
6. Используя метод проекций, определить проекции абсолютного ускорения и абсолютной скорости на оси неподвижной системы координат.
7. По определенным проекциям, найти модули и направления абсолютной скорости и абсолютного ускорения.
Примеры решения задач
Задача 1
Диск вращается вокруг оси, перпендикулярной к его плоскости, против хода часовой стрелки с угловой скоростью  в/c. По хорде диска от точки K к L движется точка M.
в/c. По хорде диска от точки K к L движется точка M.
Определить модуль и направление корриолисового ускорения точки M в изображенном на рис. 1 положении, если относительная скорость 

Решение. Точка M движется в плоскости диска которая перпендикулярна к оси вращения, то есть угол между векторами  и
и  составляет
составляет 
Учитывая  модуль ускорения Кориолиса равняется:
модуль ускорения Кориолиса равняется:

Поскольку вектор относительной скорости находится в плоскости перпендикулярной к оси вращения, то для определения направления ускорения Кориолиса согласно правилу
Жуковского надо повернуть вектор  по направлению угловой скорости
по направлению угловой скорости  переносного движения на угол
переносного движения на угол  (Рисс.1).
(Рисс.1).
Задача 2
Определить модуль и направление корриолисового ускорения точки M, которая движется по производной ВN кругового конуса от вершины В к точке N. Конус вращается вокруг своей оси с угловой скоростью  в/с. в направлении. показанном на рисунке, угол наклона производной к оси конуса
в/с. в направлении. показанном на рисунке, угол наклона производной к оси конуса  относительная скорость точки
относительная скорость точки 

Решение. Отложим вектор угловой скорости  переносного вращательного движения по оси вращения в сторону, с которой вращение видно против хода часовой стрелки. Относительную скорость
переносного вращательного движения по оси вращения в сторону, с которой вращение видно против хода часовой стрелки. Относительную скорость  направим от точки M до точки N. Тогда угол между
направим от точки M до точки N. Тогда угол между
векторами  и
и  (Рис.1) составит:
(Рис.1) составит:

Модуль ускорения Кориолиса точки M равен:


Чтобы найти направление ускорения Кориолиса (рис.1), спроектируем вектор относительной скорости  на плоскость S, перпендикулярную оси вращения конуса.
на плоскость S, перпендикулярную оси вращения конуса.
Проекция относительной скорости  направленная по прямой МК, которая является продолжением радиуса СМ.
направленная по прямой МК, которая является продолжением радиуса СМ.
Повернув проекцию  в направлении вращения конуса на угол
в направлении вращения конуса на угол  устанавливаем, что вектор
устанавливаем, что вектор  кориолисового ускорения направлен по касательной к кругу радиусом СМ в сторону вращения конуса.
кориолисового ускорения направлен по касательной к кругу радиусом СМ в сторону вращения конуса.
Задача 3
По хорде АВ диска, что вращается от точки А до точки В (рис.1) движется точка М, согласно уравнению  угол поворота диска изменяется по закону
угол поворота диска изменяется по закону 
Определить абсолютные скорости и ускорение точки М в момент времени, когда она находится на расстоянии  от оси вращения диска (рис.1).
от оси вращения диска (рис.1).

Решение. В данной задачи переносным движением будет вращение диска по закону
 и относительным – движение точки по хорде АВ по закону
и относительным – движение точки по хорде АВ по закону 
Запишем уравнение для определения абсолютной скорости точки М:

Для определения относительной скорости остановим переносное вращение диска и будем рассматривать движение точки по отношению к неподвижному диску.
Поскольку закон относительного движения  величина относительной скорости определяется как первая производная от пути по времени:
величина относительной скорости определяется как первая производная от пути по времени:

Вектор  относительной скорости направлен по хорде АВ (рис. 1) от точки А до точки В.
относительной скорости направлен по хорде АВ (рис. 1) от точки А до точки В.
Переносной скоростью  точки М будет скорость той точки диска, с которой в данный момент совпадает точка М.
точки М будет скорость той точки диска, с которой в данный момент совпадает точка М.
Из условия задачи следует, что точка М в данный момент времени находится посередине хорды АВ на расстоянии  от оси вращения диска.
от оси вращения диска.
Переносная скорость вращающегося движения определяется по формуле:

где  – угловая скорость переносного вращательного движения.
– угловая скорость переносного вращательного движения.
Угловую скорость переносного вращательного движения найдем как первую производную от угла поворота  по времени:
по времени:
 в/с.
в/с.
Таким образом, переносная скорость вращательного движения равна:

Вектор переносной скорости направлен перпендикулярно радиусу OM в сторону вращения диска.
Поскольку векторы  и
и  направленны вдоль одной прямой в разные стороны (рис. 1), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
направленны вдоль одной прямой в разные стороны (рис. 1), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
Тогда:

В зависимости от абсолютных значений скоростей  и
и  вектор
вектор  будет направлен или в сторону
будет направлен или в сторону  или в сторона
или в сторона 
Определить абсолютное ускорение точки M. Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:

Модуль относительного ускорения определим как производную от относительной скорости по времени:

Направленный вектор  вдоль хорды AB от точки A до точки B (рис.2).
вдоль хорды AB от точки A до точки B (рис.2).
Переносное ускорение  точки диска, которая совпадает с точкой M, учитывая, что она движется по кругу радиусом h, состоит из переносного тангенциального (касательного) ускорения
точки диска, которая совпадает с точкой M, учитывая, что она движется по кругу радиусом h, состоит из переносного тангенциального (касательного) ускорения  и переносного нормального ускорения
и переносного нормального ускорения 

Вычислим модули нормального  и тангенциального
и тангенциального  ускорений:
ускорений:

где  угловое ускорение переносного вращательного движения.
угловое ускорение переносного вращательного движения.
Переносное нормальное ускорение направлено вдоль радиуса к центру вращения O (рис.2).

Поскольку движение точки M происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:

Для определения направления ускорения Кориолиса (рис.2) необходимо вектор относительной скорости  повернуть на
повернуть на  в сторону угловой скорости
в сторону угловой скорости 
переносного вращательного движения, то есть против хода часовой стрелки.
Для определения величины и направления абсолютного ускорения  сначала добавим векторы
сначала добавим векторы  и
и  которые направлены вдоль одной прямой в противоположные стороны.
которые направлены вдоль одной прямой в противоположные стороны.
Найдена векторная сумма  направлена перпендикулярно к вектору
направлена перпендикулярно к вектору  и по модулю равняется
и по модулю равняется

Таким образом, абсолютное ускорение точки M равняется сумме векторов:

Поскольку вектор  перпендикулярный к вектору
перпендикулярный к вектору  вектор
вектор  будет изображаться диагональю прямоугольника со сторонами
будет изображаться диагональю прямоугольника со сторонами  и
и  (рис.2).
(рис.2).
Модуль абсолютного ускорения равняется:

Ответ: 
Задание темы К4 (сложное движение точки)
Вдоль стороны AB (см. задачу К3 и рис. К4.1) движется ползун 2, шарнирно
соединённый со стержнем EK, который движется в неподвижных направляющих параллельно оси  Точка E разделяет сторону AB в пропорции, которую указано в таблице К5 коэффициентом пропорциональности
Точка E разделяет сторону AB в пропорции, которую указано в таблице К5 коэффициентом пропорциональности 
Определить путем построения планов скоростей и ускорений по известным из задачи К3 кинематическим характеристикам движения фигуры АВС абсолютные скорости и
ускорение точек Е и К.


Пример решения задания темы К4
Изобразим на стороне AB тела 1 (рис.К4.2, а) ползун 2, который соединен шарниром Е со стержнем 3. Ползун 2 может двигаться поступательно по стороне AB, а стержень
3 – поступательно в вертикальных направляющих. Положение шарнира Е на стороне AB определяем по заданному коэффициенту пропорциональности 

1. Анализ движения стержня ЕК
Рассмотрим точку  принадлежащую одновременно ползуну 2 и стержню 3. Эта точка осуществляет сложное движение, двигаясь как по направляющей AB, так и вместе с фигурой ABC .
принадлежащую одновременно ползуну 2 и стержню 3. Эта точка осуществляет сложное движение, двигаясь как по направляющей AB, так и вместе с фигурой ABC .
Очевидно, скорость и ускорение точки  в ее поступательном движении вместе со стержнем ЕК относительно неподвижной опоры (которое видит неподвижный наблюдатель) следует считать абсолютным. Обозначим их соответственно
в ее поступательном движении вместе со стержнем ЕК относительно неподвижной опоры (которое видит неподвижный наблюдатель) следует считать абсолютным. Обозначим их соответственно  и
и 
Тогда движение точки  ползуна 2 вдоль направляющей AB будет относительным. Скорость
ползуна 2 вдоль направляющей AB будет относительным. Скорость  и ускорение
и ускорение  точки
точки  в относительном движении направлены вдоль стороны AB, поскольку ползун движется относительно стержня поступательно.
в относительном движении направлены вдоль стороны AB, поскольку ползун движется относительно стержня поступательно.
Одновременно ползун 2 движется вместе с фигурой ABC . Это движение для точки 
является переносным. Переносные скорость и ускорение  следует определить как скорость и ускорение той точки
следует определить как скорость и ускорение той точки  фигуры ABC, с которой в данный момент времени совпадает точка
фигуры ABC, с которой в данный момент времени совпадает точка  ползуна 2.
ползуна 2.
2. Определение переносной, абсолютной и относительной скорости точки Е2
Приняв точку A тела 1, осуществляющую плоское движение, за полюс (рис. К4.2, б), определим скорость точки  стороны AB используя свойство сходства фигур
стороны AB используя свойство сходства фигур
ABС тела 1 и abc плана скоростей, в соответствии с какой:

Из этой пропорции определим отрезок 

Отрезок откладываем на стороне ab фигуры abc плана скоростей (рис.К4.2, б) в направлении от точки “a” до точки “b”. Величине переносной скорости ползуна 2 на
плане будет соответствовать отрезок 

Запишем уравнение для абсолютной скорости точки  ползуна 2:
ползуна 2:

В этом уравнении нам известны:
- величина и направление переносной скорости
 (из плана скоростей);
(из плана скоростей); - направление относительной скорости
 (вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно; - направление абсолютной скорости
 (вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
Для решения уравнения (2) воспользуемся планом скоростей (рис.К4.2, б). Поскольку согласно уравнению до вектора  необходимо добавить вектор
необходимо добавить вектор  то с точки
то с точки 
проведем прямую  параллельную к AB, а с полюса
параллельную к AB, а с полюса  проведем направление абсолютной скорости
проведем направление абсолютной скорости  вертикальную прямую. Точка пересечения этих прямых “к” и будет решением уравнения (2), а отрезок
вертикальную прямую. Точка пересечения этих прямых “к” и будет решением уравнения (2), а отрезок  будет изображать
будет изображать
в масштабе  абсолютную скорость точек
абсолютную скорость точек  и К:
и К:

3. Определение переносного и абсолютного ускорения точки Е2
Определить переносное ускорение точки  ползуна 2.
ползуна 2.
Из условия сходства фигур ABС тела 1 и abc плана ускорений (рис.К4.2,в) следует, что точка  (конец вектора ускорения
(конец вектора ускорения  ) на плане ускорений будет лежать на отрезке ab. При этом расстояние
) на плане ускорений будет лежать на отрезке ab. При этом расстояние  может быть найдено из пропорции (1). Поскольку на плане
может быть найдено из пропорции (1). Поскольку на плане
ускорений  то:
то:


Тогда отрезок  будет изображать переносное ускорение точки
будет изображать переносное ускорение точки 
в масштабе плана ускорений 

Запишем векторное уравнение для абсолютного ускорения для точки  ползуна 2:
ползуна 2:

Определим сначала величину и направление Кориолисового ускорения.
Поскольку движение происходит в плоскости  то есть угол между векторами относительной скорости
то есть угол между векторами относительной скорости  и угол переносной скорости
и угол переносной скорости  равняется
равняется  то для определения величины
то для определения величины  воспользуемся формулой (4.4):
воспользуемся формулой (4.4):

Угловая переносная скорость  равняется угловой скорости тела 1, то есть
равняется угловой скорости тела 1, то есть 
Величину относительной скорости  определим из плана скоростей. (рис. К4.2, б). Измерение отрезка
определим из плана скоростей. (рис. К4.2, б). Измерение отрезка  который на плане скоростей в масштабе
который на плане скоростей в масштабе 
изображает  находим:
находим:

Тогда:

Направление Кориолисового ускорения определим по правилу Жуковского Н.Е., для этого вектор относительной скорости  что на плане скоростей (рис. К4.2, б) изображается вектором
что на плане скоростей (рис. К4.2, б) изображается вектором  повернем в сторону угловой переносной скорости
повернем в сторону угловой переносной скорости  направление которой показано на рис. К4.2,а, на
направление которой показано на рис. К4.2,а, на  (рис. К4.2, г).
(рис. К4.2, г).
Таким образом, в уравнении (3) нам известны:
- величина и направление переносного ускорения

- величина и направление Корриолисового ускорения

- направление относительного ускорения
 (вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно; - направление абсолютного ускорения
 (вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
Все это позволяет нам построить многоугольник ускорений в соответствии с уравнением (3) на плане ускорений, или отдельным чертежом. Учитывая, что величины отрезков, которые будут изображать некоторые ускорения, слишком большие и выходят за пределы чертежа, для нахождения абсолютного ускорения точки  построим отдельный план ускорений с масштабным коэффициентом:
построим отдельный план ускорений с масштабным коэффициентом:

Сначала из произвольной точки  (рис. К4.2, д) за направлением
(рис. К4.2, д) за направлением  (рис. К4.2, в) отложим вектор
(рис. К4.2, в) отложим вектор  который в масштабе
который в масштабе  будет изображать
будет изображать 

До этого вектора в направлении Кориолисового ускорения (рис. К4.2, г) добавим вектор  который в масштабе
который в масштабе  будет изображать
будет изображать 

Через конец вектора  параллельно AB проведем направление относительного ускорения
параллельно AB проведем направление относительного ускорения  (перпендикулярно
(перпендикулярно  или параллельно AB), а через полюс
или параллельно AB), а через полюс  направление абсолютного ускорения
направление абсолютного ускорения  (параллельно ЕК). Точка пересечения “к” этих двух направлений и будет решением уравнения (3), а вектор
(параллельно ЕК). Точка пересечения “к” этих двух направлений и будет решением уравнения (3), а вектор  в масштабе
в масштабе 
будет изображать абсолютное ускорение точек К и 
Замерив отрезок  получим:
получим:

Примечание. Поскольку все построения расчетные графических работ по кинематике К1, К3 и К4 рекомендуется выполнять на бумаге форматом А3, то после выполнения данной курсовой работы ее графическая часть будет иметь вид подобный изображенному на с. 188.

Сложное движение точки образцы и примеры
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Относительное, переносное и абсолютное движение точки
При исследовании движения точки выбирают некоторую систему отсчета (темы 1 и 2), относительно которой рассматривают движение точки.
В некоторых случаях приходится рассматривать движение точки относительно двух различных систем отсчета. Например, движение пассажира в поезде можно рассматривать как по отношению к поезду, так и по отношению к Земле.
При этом движение одной и той же точки относительно двух различных систем отсчета будет разным. Например, точка обода колеса движущегося железнодорожного вагона относительно Земли пишет циклоиду, а относительно вагона – окружение.
При рассмотрении движения точки по отношению к двум системам отсчета и система, которая в данной задаче условно принята за неподвижную, называется основной системой отсчета (неподвижной), а система, которая движется относительно основной, называется подвижной системой отсчета.
Движение точки относительно основной системы отсчета называется абсолютным движением, а ее движение относительно подвижной системы отсчета – относительным движением.
Пусть есть две системы координат  и
и  и некоторая подвижная точка
и некоторая подвижная точка  (рис.3.1).
(рис.3.1).

Выберем систему координат  за основную. Тогда движение системы
за основную. Тогда движение системы  относительно системы
относительно системы  будет переносным. Движение точки
будет переносным. Движение точки  относительно системы
относительно системы  будет относительным, а движение точки
будет относительным, а движение точки  относительно системы
относительно системы  будет абсолютным.
будет абсолютным.
Надо заметить, что переносным движением является движение не самой точки  , а того тела, с которым связана подвижная система координат
, а того тела, с которым связана подвижная система координат  , тогда как относительное и абсолютное движение является движением самой точки
, тогда как относительное и абсолютное движение является движением самой точки  , которое рассматривается соответственно относительно подвижной и основной систем отсчета. В переносном движении подвижная система координат может иметь любой вид движения.
, которое рассматривается соответственно относительно подвижной и основной систем отсчета. В переносном движении подвижная система координат может иметь любой вид движения.
Основная задача этого раздела состоит в том, чтобы по известным относительным и переносным движениям определить абсолютное движение точки (движение точки  относительно системы отсчета
относительно системы отсчета  ).
).
Выбор основной и подвижной систем отсчета, а соответственно, и разделение движения точки на абсолютное и относительное зависит от постановки конкретной задачи. В большинстве случаев за основную систему отсчета принимают систему, которую связано с Землей.
Относительные, переносные и абсолютные скорости и ускорение
Относительной скоростью  точки называется ее скорость в относительном движении, то есть по отношению к подвижной системе отсчета.
точки называется ее скорость в относительном движении, то есть по отношению к подвижной системе отсчета.
Абсолютной скоростью  точки называется ее скорость в абсолютном движении, то есть по отношению к основной системе отсчета.
точки называется ее скорость в абсолютном движении, то есть по отношению к основной системе отсчета.
Переносной скоростью  называется скорость относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
называется скорость относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Аналогично введем понятие относительного, абсолютного и переносного ускорения точки.
Относительным ускорением  точки называется ее ускорение в относительном движении, то есть по отношению к подвижной системе отсчета.
точки называется ее ускорение в относительном движении, то есть по отношению к подвижной системе отсчета.
Абсолютным ускорением  точки называется ее ускорение в абсолютном движении, то есть по отношению к основной системе отсчета.
точки называется ее ускорение в абсолютном движении, то есть по отношению к основной системе отсчета.
Переносным ускорением  называется ускорение относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
называется ускорение относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Обратим внимание на то, что переносное движение – это движение всей подвижной системы отсчета, то есть некоторого тела, с которым связана подвижная система координат, а переносная скорость и переносное ускорение – это скорость и ускорение конкретной точки этого тела.
Сложение скоростей и ускорений при сложном движении точки
Зависимость между абсолютной, переносной и относительной скоростями точки определяется теоремой сложения скоростей, согласно которой абсолютная скорость точки равна векторной сумме переносной и относительной скоростей:
 (3.1)
(3.1)
где  – абсолютная скорость точки;
– абсолютная скорость точки;
 – относительная скорость точки;
– относительная скорость точки;
 – переносная скорость.
– переносная скорость.
Для определения относительной скорости точки достаточно мысленно остановить переносное движение и найти по правилам кинематики скорость точки относительно системы отсчета, которая была подвижной.
Для определения переносной скорости – достаточно мысленно остановить относительное движение и найти переносную скорость как скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Зависимость между абсолютным, относительным и переносным ускорением точки при поступательном движении подвижной системы отсчета выражается векторным уравнением:
 (3.2)
(3.2)
где  – абсолютное ускорение точки;
– абсолютное ускорение точки;
 – относительное ускорение точки;
– относительное ускорение точки;
 – переносное ускорение точки.
– переносное ускорение точки.
Если переносным движением является вращательный, или сложный, то теорема о сложении ускорений приобретает вид:
 , (3.3)
, (3.3)
где  – ускорение Кориолиса (поворотное ускорение точки).
– ускорение Кориолиса (поворотное ускорение точки).
3.4. Ускорение Кориолиса
 .
.
Модуль ускорения Кориолиса равен:

где  – угол между векторами
– угол между векторами  и
и  .
.
Ускорение Кориолиса характеризует:
- изменение модуля и направления переносной скорости точки вследствие ее относительного движения;
- изменение направления относительной скорости точки вследствие вращательного переносного движения.
Ускорение Кориолиса равно нулю в трех случаях:
Направление ускорения Кориолиса определяется как направление вектора векторного произведения 

 .
.
Пусть точка  (рис.3.2) движется со скоростью
(рис.3.2) движется со скоростью  относительно тела, которое вращается вокруг оси
относительно тела, которое вращается вокруг оси  с угловой скоростью
с угловой скоростью  . Если построить в точке
. Если построить в точке  кроме
кроме  вектор
вектор  , то вектор векторного произведения
, то вектор векторного произведения 

 , то есть вектор ускорения Кориолиса
, то есть вектор ускорения Кориолиса  , будет направлен перпендикулярно плоскости, в которой лежат векторы
, будет направлен перпендикулярно плоскости, в которой лежат векторы  и
и  в ту сторону, откуда поворот вектора
в ту сторону, откуда поворот вектора  к вектору относительной скорости
к вектору относительной скорости  на наименьший угол виден против хода часовой стрелки.
на наименьший угол виден против хода часовой стрелки.

Для определения направления ускорения Кориолиса удобно пользоваться правилом Жуковского: чтобы найти направление ускорения Кориолиса надо спроектировать относительную скорость точки  на плоскость, перпендикулярную оси переносного вращения, и вернуть в этой плоскости полученную проекцию на
на плоскость, перпендикулярную оси переносного вращения, и вернуть в этой плоскости полученную проекцию на  в сторону переносного вращения (рис.3.3).
в сторону переносного вращения (рис.3.3).

Действительно, полученное направление  (рис.3.3) перпендикулярное плоскости треугольника, который образован относительной скоростью
(рис.3.3) перпендикулярное плоскости треугольника, который образован относительной скоростью  и ее проекцией
и ее проекцией  ‘отн, а эта плоскость совпадает с плоскостью векторов
‘отн, а эта плоскость совпадает с плоскостью векторов  и
и  , которой должен быть перпендикулярным вектор ускорения Кориолиса.
, которой должен быть перпендикулярным вектор ускорения Кориолиса.
Если вектор  перпендикулярен
перпендикулярен  , то есть
, то есть 

 и соответственно
и соответственно



 , то величина ускорения Кориолиса будет равна:
, то величина ускорения Кориолиса будет равна:

 . (3.5)
. (3.5)
Такой случай возможен, если относительное движение точки происходит в плоскости перпендикулярной оси переносного вращения. В этом случае векторы  ,
,  и
и  взаимно перпендикулярны (рис. 3.4).
взаимно перпендикулярны (рис. 3.4).

Рассмотрим два примера определения модуля и направления ускорения Кориолиса .
Пример 1. Диск вращается вокруг оси, которая перпендикулярна его плоскости, против хода часовой стрелки с угловой скоростью  . По хорде диска от точки
. По хорде диска от точки  к
к  движется точка
движется точка  .
.
Определить модуль и направление ускорения Кориолиса точки  в изображенном на рис. 3.5 положении, если относительная скорость
в изображенном на рис. 3.5 положении, если относительная скорость 
 .
.
Точка  движется в плоскости диска которая перпендикулярна оси вращения, то есть угол между векторами
движется в плоскости диска которая перпендикулярна оси вращения, то есть угол между векторами  и
и  составляет
составляет  . Учитывая, что
. Учитывая, что 


 , модуль ускорения Кориолиса равен:
, модуль ускорения Кориолиса равен:



Поскольку вектор относительной скорости лежит в плоскости перпендикулярной оси вращения, то для определения направления ускорение Кориолиса согласно правилу Жуковского надо повернуть вектор  по направлению угловой скорости
по направлению угловой скорости  переносного движения на угол
переносного движения на угол  (рис.3.5).
(рис.3.5).

Пример 2. Определить модуль и направление ускорение Кориолиса точки  , которая движется по образующей
, которая движется по образующей  кругового конуса от вершины
кругового конуса от вершины  к точке
к точке  . Конус вращается вокруг своей оси с угловой скоростью
. Конус вращается вокруг своей оси с угловой скоростью  в направлении, показанном на рис.3.6, угол наклона образующей к оси конуса
в направлении, показанном на рис.3.6, угол наклона образующей к оси конуса  , относительная скорость точки
, относительная скорость точки 
 .
.
Отложим вектор угловой скорости  переносного вращательного движения по оси вращения в сторону, из которой вращения видно против хода часовой стрелки. Относительную скорость
переносного вращательного движения по оси вращения в сторону, из которой вращения видно против хода часовой стрелки. Относительную скорость  направим от точки
направим от точки  к точке
к точке  . Тогда угол между векторами
. Тогда угол между векторами  и
и  (рис 3.6) составит:
(рис 3.6) составит:





Модуль ускорения Кориолиса точки  равен:
равен:














Чтобы найти направление ускорения Кориолиса (рис.3.6), спроектируем вектор относительной скорости  на плоскость
на плоскость  , которая перпендикулярна оси вращения конуса.
, которая перпендикулярна оси вращения конуса.

Проекция относительной скорости 

 направлена по прямой
направлена по прямой  , которая является продолжением радиуса
, которая является продолжением радиуса  .
.
Если повернуть проекцию 

 в направлении вращения конуса на угол
в направлении вращения конуса на угол  , устанавливаем, что вектор
, устанавливаем, что вектор  ускорения Кориолиса направлен по касательной к окружности радиусом
ускорения Кориолиса направлен по касательной к окружности радиусом  в сторону вращения конуса.
в сторону вращения конуса.
Примеры решения задач
Задача №1
Клин  (рис.3.7) с углом наклона рабочей поверхности
(рис.3.7) с углом наклона рабочей поверхности  , который движется поступательно по горизонтальной поверхности со скоростью
, который движется поступательно по горизонтальной поверхности со скоростью  , поднимает стержень
, поднимает стержень  , который движется в вертикальном направлении.
, который движется в вертикальном направлении.

Найти абсолютную скорость стержня  .
.
Решение. Учитывая, что стержень  в вертикальном направлении будет двигаться прямолинейно поступательно, то достаточно определить скорость любой его точки.
в вертикальном направлении будет двигаться прямолинейно поступательно, то достаточно определить скорость любой его точки.
Рассмотрим движение точки  стержня.
стержня.
Поскольку точка  стержня должна все время касаться клина
стержня должна все время касаться клина  , то рассмотрим ее движение как сложное – относительным будет движение точки
, то рассмотрим ее движение как сложное – относительным будет движение точки  по отношению к клину, а переносным – движение точки
по отношению к клину, а переносным – движение точки  вместе с клином.
вместе с клином.
По отношению к клину точка  стержня может двигаться только вдоль рабочей поверхности
стержня может двигаться только вдоль рабочей поверхности  . Таким образом, относительная скорость
. Таким образом, относительная скорость  будет направлена вдоль
будет направлена вдоль  .
.
Клин  движется поступательно горизонтальной поверхностью, то есть скорости всех его точек одинаковы. Таким образом, переносная скорость
движется поступательно горизонтальной поверхностью, то есть скорости всех его точек одинаковы. Таким образом, переносная скорость  точки
точки  стержня, которая совпадает с точкой
стержня, которая совпадает с точкой  клина будет равна
клина будет равна  .
.
Абсолютную скорость точки  стержня определим из векторного уравнения:
стержня определим из векторного уравнения:


 (1)
(1)
Для решения векторного уравнения (1) построим параллелограмм на векторах  и
и  (рис.3.7). При построении надо учесть, что
(рис.3.7). При построении надо учесть, что  , как диагональ параллелограмма, должна быть направлена вертикально.
, как диагональ параллелограмма, должна быть направлена вертикально.
Поскольку угол между векторами  и
и  прямой, то получим:
прямой, то получим:

Ответ: 
Задача № 2
Круг радиусом  (рис.3.8) равномерно вращается в своей плоскости вокруг центра
(рис.3.8) равномерно вращается в своей плоскости вокруг центра  по ходу часовой стрелки и делает
по ходу часовой стрелки и делает  оборотов в минуту. По кругу равномерно в противоположном направлении движется точка
оборотов в минуту. По кругу равномерно в противоположном направлении движется точка  и делает
и делает  оборотов в минуту.
оборотов в минуту.

Найти абсолютное ускорение точки  .
.
Решение. Движение точки  рассмотрим как сложное. Переносным движением будет вращение круга вместе с точкой
рассмотрим как сложное. Переносным движением будет вращение круга вместе с точкой  вокруг центра
вокруг центра  , а относительным – движение точки
, а относительным – движение точки  по кругу.
по кругу.
Абсолютное ускорение точки  , учитывая, что переносным будет вращательное движение, равно:
, учитывая, что переносным будет вращательное движение, равно:



Поскольку переносное движение вращательное, то переносное ускорение точки круга с которой совпадает точка  , будет иметь нормальную
, будет иметь нормальную  и тангенциальную
и тангенциальную  составляющую.
составляющую.
Учитывая, что при равномерном вращении угловое ускорение  , тангенциальная составляющая переносного ускорения
, тангенциальная составляющая переносного ускорения

Величина переносного нормального ускорения  определим из формулы:
определим из формулы:

где  – угловая скорость круга.
– угловая скорость круга.
Направлено это ускорение вдоль радиуса от точки  к точке
к точке  (рис.3.8).
(рис.3.8).
Учитывая то, что точка  по кругу радиуса
по кругу радиуса  движется равномерно, модуль относительного ускорения будет иметь тоже только одну нормальную составляющую
движется равномерно, модуль относительного ускорения будет иметь тоже только одну нормальную составляющую 

 :
:




где  – угловая скорость вращения точки
– угловая скорость вращения точки  по кругу.
по кругу.
Направлено это ускорение от точки  к точке
к точке  (рис.3.8).
(рис.3.8).
Поскольку точка  движется в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется по формуле:
движется в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется по формуле:

 .
.
Учитывая, что 
 , достанем:
, достанем:

Для определения направления ускорения Кориолиса повернем вектор относительной скорости  , который направлен по касательной к кругу, в направлении переносной угловой
, который направлен по касательной к кругу, в направлении переносной угловой  на
на  (рис.3.8). Таким образом, это ускорение направлено вдоль радиуса от центра вращения
(рис.3.8). Таким образом, это ускорение направлено вдоль радиуса от центра вращения  .
.
Поскольку все ускорения направлены вдоль одной прямой, то их можно сложить алгебраически:




 ,
,
или с учетом выражений для  ,
, 

 и
и  :
:

Подставив зависимости для угловых скоростей  и
и  , получим:
, получим:

Ответ: 
Задача №3
По хорде  вращающегося диска от точки
вращающегося диска от точки  к точке
к точке  движется точка
движется точка  согласно уравнению
согласно уравнению  , угол поворота диска изменяется по закону
, угол поворота диска изменяется по закону  .
.
Определить абсолютные скорости и ускорения точки  в момент времени, когда она находится на расстоянии
в момент времени, когда она находится на расстоянии  от оси вращения диска (рис.3.9).
от оси вращения диска (рис.3.9).
Решение. В данной задаче переносным движением будет вращение диска по закону  , а относительным – движение точки по хорде
, а относительным – движение точки по хорде  по закону
по закону  .
.
Запишем уравнение для определения абсолютной скорости точки  :
:



Для определения относительной скорости остановим переносное вращение диска и будем рассматривать движение точки по отношению к неподвижному диску. Поскольку закон относительного движения  , то величина относительной скорости определяется как первая производная от пути по времени:
, то величина относительной скорости определяется как первая производная от пути по времени:


Вектор относительной скорости направлен по хорде  (рис. 3.9) от точки
(рис. 3.9) от точки  к точке
к точке  .
.

Переносной скоростью  точки
точки  будет скорость той точки диска, с которой в данный момент совпадает точка
будет скорость той точки диска, с которой в данный момент совпадает точка  .
.
Из условия задачи вытекает, что точка  в данный момент времени находится посередине хорды
в данный момент времени находится посередине хорды  на расстоянии
на расстоянии  от оси вращения диска.
от оси вращения диска.
Переносная скорость вращательного движения определяется по формулой:

где  – угловая скорость переносного вращательного движения.
– угловая скорость переносного вращательного движения.
Угловую скорость переносного вращательного движения найдем как первую производную от угла поворота  по времени:
по времени:

Таким образом, переносная скорость вращательного движения равна:

Вектор переносной скорости направлен перпендикулярно радиусу  в сторону вращения диска.
в сторону вращения диска.
Поскольку векторы  и
и  направлены вдоль одной прямой в разные стороны (рис. 3.9), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
направлены вдоль одной прямой в разные стороны (рис. 3.9), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
Тогда:



В зависимости от абсолютных значений скоростей  и
и  , вектор
, вектор  будет направлен либо в сторону
будет направлен либо в сторону  , либо в сторону
, либо в сторону  .
.
Определим абсолютное ускорение точки  . Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:
. Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:



Модуль относительного ускорения определим как производную от относительной скорости по времени:


Направлен вектор  вдоль хорды
вдоль хорды  от точки
от точки  к точке
к точке  (рис.3.10).
(рис.3.10).

Переносное ускорение  точки диска, которая совпадает с точкой
точки диска, которая совпадает с точкой  , учитывая, что она движется по окружности радиусом
, учитывая, что она движется по окружности радиусом  , состоит из переносного тангенциального (касательного) ускорения
, состоит из переносного тангенциального (касательного) ускорения  и переносного нормального ускорения
и переносного нормального ускорения  :
:

Вычислим модули нормального  и тангенциального
и тангенциального  ускорений:
ускорений:

где  – угловое ускорение переносного вращательного движения.
– угловое ускорение переносного вращательного движения.
Переносное нормальное ускорение направлено вдоль радиуса к центру вращения  (рис.3.10).
(рис.3.10).
Поскольку движение точки  происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:
происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:



Для определения направления ускорения Кориолиса (рис.3.10) необходимо вектор относительной скорости  повернуть на
повернуть на  в бок угловой скорости
в бок угловой скорости  переносного вращательного движения, то есть против хода часовой стрелки.
переносного вращательного движения, то есть против хода часовой стрелки.
Для определения величины и направления абсолютного ускорения  сначала сложим векторы
сначала сложим векторы  и
и  , которые направлены вдоль одной прямой в противоположные стороны. Найденная векторная сумма
, которые направлены вдоль одной прямой в противоположные стороны. Найденная векторная сумма  направлена перпендикулярно вектору
направлена перпендикулярно вектору  и по модулю равнa
и по модулю равнa 
Таким образом, абсолютное ускорение точки  равно сумме векторов:
равно сумме векторов:

 .
.
Поскольку вектор от  перпендикулярен вектору
перпендикулярен вектору  , то вектор
, то вектор  будет изображаться диагональю прямоугольника со сторонами
будет изображаться диагональю прямоугольника со сторонами  и
и  (рис.3.10).
(рис.3.10).
Модуль абсолютного ускорения будет равен:

Ответ: 
Задача №4
В состав механизма Витворта (рис.3.11) входит: кривошип 1, ползун 2 и кулиса 3. Кривошип  механизма вращается с постоянной угловой скоростью
механизма вращается с постоянной угловой скоростью 

Определить скорость и ускорение точки  и угловую скорость и угловое ускорение кулисы 3 механизма в положении,
и угловую скорость и угловое ускорение кулисы 3 механизма в положении,
когда: 
Решение. Особенность этого механизма заключается в том, что в точке  между собой соединяются кривошип 1, ползун 2 и кулиса 3 (рис.3.12).
между собой соединяются кривошип 1, ползун 2 и кулиса 3 (рис.3.12).
Пересечение 

Кривошип 1 и ползун 2 между собой соединены цилиндрическим шарниром, что позволяет ползуну относительно кривошипа возвращаться, а на кулисе 3 параллельно ее оси сделаны направляющие, по которым ползун 2 может двигаться поступательно.
При повороте кривошипа 1 ползун 2 скользит по кулисе 3 и заставляет ее поворачиваться вокруг точки  . Расстояние от точки
. Расстояние от точки  к точке
к точке  на кулисе 3 с поворотом кривошипа 1 меняется.
на кулисе 3 с поворотом кривошипа 1 меняется.
Такой механизм позволяет преобразовать вращательное движение кривошипа в колебательное движение кулисы, если  , или в вращательное, с другим законом изменения угловой скорости чем у кривошипа, движение кулисы, если
, или в вращательное, с другим законом изменения угловой скорости чем у кривошипа, движение кулисы, если  .
.
Таким образом, в точке  механизма (рис.3.12) будем рассматривать три разные точки:
механизма (рис.3.12) будем рассматривать три разные точки:  , принадлежащая кривошипу 1;
, принадлежащая кривошипу 1;  – ползуну 2 и
– ползуну 2 и  – кулисе 3. Все эти точки лежат одна под второй на рис.3.11.
– кулисе 3. Все эти точки лежат одна под второй на рис.3.11.
Перед решением задачи в произвольном масштабе построим схему механизма (рис.3.13,а) для заданного положения кривошипа.
Первой определим скорость точки  , принадлежащей кривошипу 1, который вращается вокруг точки
, принадлежащей кривошипу 1, который вращается вокруг точки  с угловой скоростью
с угловой скоростью  :
:

Направлена скорость  перпендикулярно
перпендикулярно  в сторону вращения кривошипа 1 (рис.3.13, а).
в сторону вращения кривошипа 1 (рис.3.13, а).
Скорость точки  , принадлежащей ползуну 2, который соединен с кривошипом 1 шарниром, равна скорости точки
, принадлежащей ползуну 2, который соединен с кривошипом 1 шарниром, равна скорости точки  :
:

Для определения скорости точки  кулисы 3, примем движение ползуна 2 за переносное. Тогда кулиса 3 относительно ползуна 2 может двигаться поступательно и скорость точки
кулисы 3, примем движение ползуна 2 за переносное. Тогда кулиса 3 относительно ползуна 2 может двигаться поступательно и скорость точки  кулисы 3 относительно точки
кулисы 3 относительно точки  ползуна 2 будет направлена вдоль направляющих, то есть вдоль
ползуна 2 будет направлена вдоль направляющих, то есть вдоль  .
.

Запишем уравнение для скоростей при сложном движении точки  относительно
относительно  :
:

где  – переносная скорость точки
– переносная скорость точки  ползуна, которая в настоящий момент времени совпадает с точкой
ползуна, которая в настоящий момент времени совпадает с точкой  кулисы. Эта скорость уже определена;
кулисы. Эта скорость уже определена;
 – относительная скорость точки
– относительная скорость точки  относительно
относительно  . Направлена эта скорость вдоль
. Направлена эта скорость вдоль  ;
;
 – абсолютная скорость точки
– абсолютная скорость точки  кулисы 3. Учитывая, что кулиса 3 вращается вокруг неподвижной точки
кулисы 3. Учитывая, что кулиса 3 вращается вокруг неподвижной точки  , то эта скорость будет направлена перпендикулярно
, то эта скорость будет направлена перпендикулярно  .
.
Векторное уравнение (1) решим путем построения плана скоростей.
Поскольку направления скорости в правой и в левой части уравнения (1) известны, то из полюса плана скоростей сначала построим правую часть уравнения, а затем левую.
Согласно правой части уравнения (1) с полюса  (рис.3.13,б) откладываем вектор
(рис.3.13,б) откладываем вектор  по направлению
по направлению  (рис.3.13, а), который в масштабе будет изображать эту скорость. (Поскольку
(рис.3.13, а), который в масштабе будет изображать эту скорость. (Поскольку  , то скорости этих точек на плане будут изображаться одним вектором, то есть на плане скоростей точки
, то скорости этих точек на плане будут изображаться одним вектором, то есть на плане скоростей точки  и
и  совпадают). Через точку
совпадают). Через точку  проведем линию
проведем линию  параллельно
параллельно  , вдоль которой от точки
, вдоль которой от точки  будет направлен вектор, что будет изображать относительную скорость
будет направлен вектор, что будет изображать относительную скорость  (величина и направление этой скорости неизвестны).
(величина и направление этой скорости неизвестны).
Теперь построим левую часть уравнения (1). Поскольку абсолютная скорость  направлена перпендикулярно
направлена перпендикулярно  , то с полюса
, то с полюса  по этому направлению проводим линию к пересечению в точке
по этому направлению проводим линию к пересечению в точке  с линией
с линией  . Точка пересечения
. Точка пересечения  будет решением векторного уравнения (1).
будет решением векторного уравнения (1).
Вектор  на плане скоростей в масштабе изображает абсолютную скорость
на плане скоростей в масштабе изображает абсолютную скорость  , а вектор
, а вектор  – относительную скорость
– относительную скорость  .
.
Поскольку на плане скоростей вектор  перпендикулярен
перпендикулярен  , а
, а  перпендикулярен
перпендикулярен  , то угол между этими векторами равен углу между
, то угол между этими векторами равен углу между  и
и  на схеме механизма, то есть
на схеме механизма, то есть  .
.
Угол при вершине  плана скоростей будет прямым, поскольку линия
плана скоростей будет прямым, поскольку линия  перпендикулярна
перпендикулярна  , а линия
, а линия  параллельна
параллельна  .
.
Таким образом треугольник  на плане скоростей прямоугольный, с углами при вершинах:
на плане скоростей прямоугольный, с углами при вершинах:  и
и  .
.
Из плана скоростей определяем:
 или
или 
 или
или 
Учитывая, что кулиса 3 вращается вокруг точки  , то для угловой скорости кулисы
, то для угловой скорости кулисы  получим:
получим:

где  – длина кулисы для этого положения механизма. С
– длина кулисы для этого положения механизма. С  (рис.13.3,а):
(рис.13.3,а): 
Поскольку ползун 2 относительно кулисы 3 движется поступательно, то  .
.
Для определения направления угловой скорости  предварительно перенесем вектор
предварительно перенесем вектор  в точку
в точку  механизма (рис.3.13, а). Угловая скорость
механизма (рис.3.13, а). Угловая скорость  направлена против хода часовой стрелки.
направлена против хода часовой стрелки.
Определим ускорение точек механизма.
Поскольку кривошип 1 вращается вокруг центра  с постоянной угловой скоростью
с постоянной угловой скоростью  , то ускорение точки
, то ускорение точки  имеет только нормальную составляющую:
имеет только нормальную составляющую:

Направлено ускорение точки  вдоль кривошипа к центру вращения
вдоль кривошипа к центру вращения  (рис.3.14, а).
(рис.3.14, а).
Ускорение точки  ползуна 2, учитывая, что кривошип и ползун соединены шарниром, равно ускорению точки
ползуна 2, учитывая, что кривошип и ползун соединены шарниром, равно ускорению точки  :
:


Для ускорения точки  кулисы 3 запишем векторное уравнение для сложного движения точки, учтя при этом, что движение ползуна 2 принято за переносное
кулисы 3 запишем векторное уравнение для сложного движения точки, учтя при этом, что движение ползуна 2 принято за переносное

где  – абсолютное ускорение точки
– абсолютное ускорение точки  ;
;
 – переносное ускорение точки
– переносное ускорение точки  ползуна, которая в настоящий момент времени совпадает с точкой
ползуна, которая в настоящий момент времени совпадает с точкой  кулисы;
кулисы;
 – ускорение точки
– ускорение точки  относительно
относительно  , направлено по оси кулисы
, направлено по оси кулисы  ;
;
 – ускорение Кориолиса точки
– ускорение Кориолиса точки  .
.
Поскольку относительное движение происходит в плоскости, перпендикулярной оси вращения ползуна 2, то ускорения Кориолиса определим из формулы:

где  – угловая скорость вращательного переносного движения ползуна 2,
– угловая скорость вращательного переносного движения ползуна 2, 
 – относительная скорость точки
– относительная скорость точки  относительно
относительно  ,
,

Для определения направления ускорения Кориолиса необходимо вектор относительной скорости  вернуть на
вернуть на  в сторону переносного вращательного движения, то есть в направлении угловой скорости
в сторону переносного вращательного движения, то есть в направлении угловой скорости  . Направление повернутого вектора (рис.3.13,в), который будет перпендикулярен оси кулисы
. Направление повернутого вектора (рис.3.13,в), который будет перпендикулярен оси кулисы  , соответствует направлению ускорения Кориолиса.
, соответствует направлению ускорения Кориолиса.
С другой стороны, точка  принадлежит кулисе 3, которая вращается вокруг центра
принадлежит кулисе 3, которая вращается вокруг центра  . Таким образом, ускорение
. Таким образом, ускорение  будет иметь две составляющие:
будет иметь две составляющие:

где  – нормальное ускорение точки
– нормальное ускорение точки  при ее вращении вокруг точки
при ее вращении вокруг точки  направлено по оси кулисы от точки
направлено по оси кулисы от точки  к точке
к точке  (рис.3.14,а) и по модулю равно:
(рис.3.14,а) и по модулю равно: 
 – тангенциальное ускорение точки
– тангенциальное ускорение точки  при ее вращении вокруг точки
при ее вращении вокруг точки  , направлено перпендикулярно оси кулисы
, направлено перпендикулярно оси кулисы  и по модулю равно:
и по модулю равно:  .
.
Решим систему векторных уравнений (2, 3) графически, путем построения плана ускорений.
Первым построим векторное уравнение (2). Из произвольного полюса  (рис.3.14,б) отложим направленный отрезок
(рис.3.14,б) отложим направленный отрезок  , изображающий ускорение
, изображающий ускорение  и направлен параллельно линии
и направлен параллельно линии  от точки
от точки  к точке
к точке  .
.
Длину отрезка  выберем
выберем  . Тогда масштабный коэффициент плана ускорений будет равен:
. Тогда масштабный коэффициент плана ускорений будет равен:

От точки  отложим вектор
отложим вектор  , который изображает ускорение Кориолиса
, который изображает ускорение Кориолиса  . Направлен этот вектор перпендикулярно оси кулисы
. Направлен этот вектор перпендикулярно оси кулисы  по определенному ранее направлению (рис.3.13, в).
по определенному ранее направлению (рис.3.13, в).
Длина вектора  равна:
равна:

Через конец вектора  проводим линию
проводим линию  , вдоль которой будет направлен вектор
, вдоль которой будет направлен вектор  , который будет изображать относительное ускорение
, который будет изображать относительное ускорение  . Направление и длина этого вектора неизвестны.
. Направление и длина этого вектора неизвестны.
Следующим построим векторное уравнение (3). С полюса  отложим вектор
отложим вектор  , изображающий нормальное ускорение
, изображающий нормальное ускорение  . Направлен этот вектор параллельно оси кулисы
. Направлен этот вектор параллельно оси кулисы  от точки
от точки  к точке
к точке  и имеет длину:
и имеет длину:

Через конец вектора  проводим линию
проводим линию  , вдоль которой будет направлен вектор
, вдоль которой будет направлен вектор  , который будет изображать тангенциальное ускорение
, который будет изображать тангенциальное ускорение  .
.
Решением системы (2, 3) будет точка пересечения линий  и
и  , а вектор
, а вектор  будет изображать ускорение
будет изображать ускорение  .
.
Из плана ускорений определяем:

Угловое ускорение кулисы 3 и ползуна 2 определим через известное тангенциальное ускорение  :
:

Для определения направления углового ускорения  надо перенести в точку
надо перенести в точку  механизма тангенциальное ускорение
механизма тангенциальное ускорение  (рис.3.14, а). Угловое ускорение
(рис.3.14, а). Угловое ускорение  направлено против хода часовой стрелки.
направлено против хода часовой стрелки.
Ответ: 

Абсолютное, относительное и переносное движение точки
В кинематике точки, рассматривается движение точки относительно неподвижной системы координат (прямоугольной декартовой или относительно осей натурального трехгранника). Однако часто приходится исследовать движение точки в отношении двух и более систем координат (тел отсчета), из которых одна система координат осуществляет движение относительно другой, условно берется за неподвижную. Например, при изучении роботов-манипуляторов следует вводить несколько систем координат. Итак, предположим, что система координат  , неизменно связана с некоторым телом, движется относительно другой системы координат
, неизменно связана с некоторым телом, движется относительно другой системы координат  , которая условно взята за неподвижную (рис. 9.1).
, которая условно взята за неподвижную (рис. 9.1).
Движение точки М относительно неподвижной системы координат называется абсолютным, а относительно подвижной системы координат – относительным. Скорости и ускорения точки, рассматриваемые в отношении данных систем, соответственно называются абсолютными и относительными.
Движение подвижной системы координат  (или неизменно связанного с ней тела G) относительно неподвижной системы отсчета
(или неизменно связанного с ней тела G) относительно неподвижной системы отсчета  , является для подвижной точки переносным движением, то есть это движение той точки подвижной системы координат, с которой в данный момент времени совпадает подвижная точка М. Соответственно скорости и ускорения точки, неизменно связанной с подвижной системой координат, в которой в данный момент времени находится подвижная точка, называются переносными.
, является для подвижной точки переносным движением, то есть это движение той точки подвижной системы координат, с которой в данный момент времени совпадает подвижная точка М. Соответственно скорости и ускорения точки, неизменно связанной с подвижной системой координат, в которой в данный момент времени находится подвижная точка, называются переносными.
Основной задачей сложного движения точки является установление зависимости между кинематическими характеристиками абсолютного, переносного и относительного движений. Уравнениями абсолютного движения точки есть, например, зависимости координат точки М, заданных в неподвижной системе координат, как функции времени:
 (9.1)
(9.1)
Аналогично для уравнения относительного движения:
 (9.2)
(9.2)
Уравнения (9.1) и (9.2) определяют в параметрической форме в соответствии абсолютную и
относительную траектории. Если уравнение (9.1) и (9.2) известны, то проекции абсолютной и относительной скоростей определяются соответственно как первые производные по времени приведенных функций; тогда вторые производные по времени от этих функций
определяют проекции абсолютного и относительного ускорений. В дальнейшем введем такие обозначения:  – абсолютная, относительная и переносная скорости,
– абсолютная, относительная и переносная скорости,  – абсолютное, относительное и переносное ускорение.
– абсолютное, относительное и переносное ускорение.


Пример 1. Пусть стержень ОА вращается вокруг неподвижной оси  , (рис. 9.2). Вдоль
, (рис. 9.2). Вдоль
стержня движется гладкое кольцо, рассматриваемое как материальная точка М. Выясните характер относительного и переносного движений.
Решение. Выберем в точке О начало неподвижной системы координат  . Движение точки М в этой системе координат называется абсолютным. Подвижная система координат Oxyz, связана со стержнем, приведена на рис. 9.2. Абсолютное движение точки М происходит в плоскости
. Движение точки М в этой системе координат называется абсолютным. Подвижная система координат Oxyz, связана со стержнем, приведена на рис. 9.2. Абсолютное движение точки М происходит в плоскости  а относительное вдоль подвижной оси
а относительное вдоль подвижной оси  . Для установления характера переносного движения выясним, какое движение, подвижная система координат Oxyz осуществляет по отношению к неподвижной. Согласно условию задачи, ось
. Для установления характера переносного движения выясним, какое движение, подвижная система координат Oxyz осуществляет по отношению к неподвижной. Согласно условию задачи, ось  вращается вокруг оси
вращается вокруг оси  . Итак, переносным движением здесь является вращательное движение стержня вокруг оси
. Итак, переносным движением здесь является вращательное движение стержня вокруг оси  .
.
Итак, сложное движение точки М (кольца) можно рассматривать как совокупность прямолинейного относительного (вдоль стержня ОА) и вращательного переносного вокруг неподвижной оси Oz вместе со стержнем. Установив характер абсолютного, относительного и переносного движений, можно решать, например, такие задачи:
а) по заданным относительным и переносным движениями определять сложное (абсолютное) движение точки;
б) по заданным сложным движениям точки определить составляющие простых движений.
Центральная операция кинематики и динамики. Абсолютная и относительная
производные по времени от вектора функции
Пусть  – система координат, взятая
– система координат, взятая
за неподвижную, a  – подвижная система координат, орты которой
– подвижная система координат, орты которой  (рис. 9.3, а).
(рис. 9.3, а).
Рассмотрим произвольную точку М, которая движется относительно как подвижной, так и неподвижной систем координат. Пусть положение этой точки в подвижной системе координат определяется радиусом-вектором  в виде:
в виде:
 (9.3)
(9.3)
Установим связь между производными от функции, вычисленными в подвижной и неподвижной системах координат. Для этого сначала найдем производную по времени от вектора  в неподвижной системе, которая называется абсолютной производной от вектора
в неподвижной системе, которая называется абсолютной производной от вектора  . по времени и:
. по времени и:

 (9.4)
(9.4)
Первые три члена этого выражения представляют собой производную от вектора  , вычисленную по предположениям, что орты подвижной системы координат по направлению не меняются, что соответствует вычислению производной в подвижной системе координат. Это выражение называется локальной (относительной) производной и обозначается
, вычисленную по предположениям, что орты подвижной системы координат по направлению не меняются, что соответствует вычислению производной в подвижной системе координат. Это выражение называется локальной (относительной) производной и обозначается 
 (9.5)
(9.5)
Рассмотрим теперь последние три слагаемых в (9.4), которые обозначим через:
 (9.6)
(9.6)

Умножив обе части (9.6) скалярно на  получим:
получим:
 (9.7)
(9.7)
Правые части этих выражений являются проекциями вектора  на оси подвижной системы координат. Обозначим их через
на оси подвижной системы координат. Обозначим их через  Воспользуемся очевидными соотношениями (рис. 9.3, б):
Воспользуемся очевидными соотношениями (рис. 9.3, б):
 (9.8)
(9.8)
Продифференцировав их по времени, получим:
 (9.9)
(9.9)
Введем обозначения:
 (9.10)
(9.10)
Тогда выражения (9.7) с учетом соотношений (9.8)-(9.10) можно записать в форме:
 (9.11)
(9.11)
Если ввести на рассмотрение вектор:
 (9.12)
(9.12)
то выражение (9.6) можно подать в виде:
 (9.13)
(9.13)
Подставив (9.13) и (9.5) в выражение (9.4) получим формулу, которая устанавливает связь между производной не только вектора  но и произвольного вектора
но и произвольного вектора  по времени, вычисленного в неподвижной и подвижной системах координат:
по времени, вычисленного в неподвижной и подвижной системах координат:
 (9.14)
(9.14)
Отметим, что во второй формуле (9.14) указана система координат, в которой вычисляется соответствующая производная.
Здесь вектор to можно рассматривать как угловую скорость вращения подвижной системы координат Oxyz относительно неподвижной  Формулу (9.14) называют формулой
Формулу (9.14) называют формулой
Бура. Она имеет следующее содержание: абсолютная производная произвольного вектора  по времени:
по времени:
 равна сумме локальной производной и
равна сумме локальной производной и векторному произведению вектора
векторному произведению вектора  вращения подвижной системы координат на дифференцируемый вектор
вращения подвижной системы координат на дифференцируемый вектор 
Поскольку формула (9.14) может быть распространена на любой вектор, то в дальнейшем будем широко пользоваться ею не только в кинематике, но и в динамике.
Рассмотрим теперь частные случаи.
1. Если система Oxyz неподвижная, то  следовательно,
следовательно,  то есть
то есть
 (9.15)
(9.15)
2. Если вектор  неподвижный относительно неподвижных осей координат
неподвижный относительно неподвижных осей координат  то
то
 (9.16)
(9.16)
3. Если вектор  неизменно связанный с системой координат
неизменно связанный с системой координат  то
то
 (9.17)
(9.17)
Отметим, что в формуле (9.14) не раскрыто пока физического смысла вектора 
Полностью он будет установлен в кинематике в разделе “Движение свободного твердого тела”. Сейчас ограничимся рассмотрением некоторых случаев, которые частично отвечают на этот вопрос.
4. Рассмотрим движение подвижной системы координат, считая, что последняя неизменно связана с телом, которое вращается вокруг неподвижной оси, например  Тогда
Тогда  и
и 
являются скоростями точек, которые совпадают с концами векторов  и
и  и вычисленные относительно неподвижной системы координат, то есть являются скоростями точек неизменной системы, которой является система координат Oxyz. Причем эти скорости имеют направления в соответствии ортов
и вычисленные относительно неподвижной системы координат, то есть являются скоростями точек неизменной системы, которой является система координат Oxyz. Причем эти скорости имеют направления в соответствии ортов и
и  (рис. 9.3, б). Итак, выражение для скоростей
(рис. 9.3, б). Итак, выражение для скоростей
точек, которые совпадают с концами единичных векторов  и
и  , можно записать в виде:
, можно записать в виде:
 (9.18)
(9.18)
Сравнив эти выражения полученной ранее формуле Эйлера, делаем вывод, что вектор  имеет реальный физический смысл.
имеет реальный физический смысл.
А именно – это вектор угловой скорости тела, которое вращается вокруг неподвижной оси.
Этот вывод легко обобщается на случай произвольной точки М, положение которой
в подвижной системе координат определяется радиусом-вектором  Тогда вектор
Тогда вектор  в выражении (9.14) имеет смысл скорости точки, неизменно связанной с телом, которое вращается в неподвижной системе координат, то есть:
в выражении (9.14) имеет смысл скорости точки, неизменно связанной с телом, которое вращается в неподвижной системе координат, то есть:
 (9.19)
(9.19)
что соответствует формуле (8.23)
5. Если скалярно умножить обе части выражения (9.18) соответственно на  и
и  , то
, то
получим:
 (9.20)
(9.20)
Левые части этих выражений являются соответственно проекциями вектора  на орт
на орт и
и  на орт
на орт  , а правые части имеют значения соответственно
, а правые части имеют значения соответственно  и
и  , поскольку
, поскольку 
 . Итак, проекциями скоростей единичных векторов
. Итак, проекциями скоростей единичных векторов  и
и  являются
являются  и
и 
(рис. 9.3, б).
6. Рассмотрим подвижную систему координат и предположим, что она совершает вращательное движение как твердое тело вокруг неподвижной оси  , которое определяется углом поворота
, которое определяется углом поворота  , который задается относительно положения
, который задается относительно положения 
(Рис. 9.4). тогда:
 (9.21)
(9.21)
где  – орты осей
– орты осей 
Отсюда получим соотношение, с которыми уже встречались в полярной системе
координат:
 (9.22)
(9.22)
Умножив теперь скалярно обе части полученных выражений соответственно на j и
и, будем иметь:
 (9.23)
(9.23)
Как видим, производная от угла поворота является ничем иным, как угловой скоростью вращения подвижной системы координат. Таким образом, для одной из компонентов в (9.10) также установлено физический смысл.
7. Пусть подвижная система отсчета осуществляет поступательное движение. Тогда:

Следовательно,  и формула (9.14) имеет такую физическую интерпретацию: все точки тела движутся с равными по величине и направлением скоростями, что было установлено нами ранее при изучении поступательного движения тела. Таким образом, для отдельных случаев движения подвижной системы координат Oxyz установлен физический смысл вектора
и формула (9.14) имеет такую физическую интерпретацию: все точки тела движутся с равными по величине и направлением скоростями, что было установлено нами ранее при изучении поступательного движения тела. Таким образом, для отдельных случаев движения подвижной системы координат Oxyz установлен физический смысл вектора  – это вектор угловой скорости тела, или подвижной системы координат Oxyz. Далее будут приведены соответствующее обоснования и для общего случая движений подвижной системы отсчета, неизменно связанной с движением твердого тела.
– это вектор угловой скорости тела, или подвижной системы координат Oxyz. Далее будут приведены соответствующее обоснования и для общего случая движений подвижной системы отсчета, неизменно связанной с движением твердого тела.
Теорема о сложении скоростей
Теорема. Абсолютная скорость точки при сложном движении равна векторной сумме относительной
точки при сложном движении равна векторной сумме относительной  и переносной
и переносной  скоростей.
скоростей.
Доказательство. Рассмотрим движение точки М относительно некоторого тела G (рис. 9.1), с которым неизменно связана подвижная система координат Oxyz, которая, в свою очередь, движется относительно условно неподвижной системы координат. Пусть положение точки М в подвижной системе координат определяется радиусом-вектором  , в неподвижной – радиусом-вектором
, в неподвижной – радиусом-вектором  , а положение начала О подвижной системы координат относительно неподвижной
, а положение начала О подвижной системы координат относительно неподвижной  , – радиусом-вектором
, – радиусом-вектором  . Тогда:
. Тогда:
 (9.24)
(9.24)
Продифференцировав это выражение в соответствии формуле (9.14):
 (9.25)
(9.25)
Здесь индекс  отражает то, что вектор
отражает то, что вектор  характеризует переносное движение. На основании определения абсолютной, относительной и переносной скоростей получим:
характеризует переносное движение. На основании определения абсолютной, относительной и переносной скоростей получим:
 (9.26)
(9.26)
С учетом этих обозначений, выражение (9.25) будет иметь следующий вид:
 (9.27)
(9.27)
который отражает теорему о распределении скоростей точек при сложном движении. Очевидно, что формула (9.27) отражает правило параллелограмма для сложения скоростей.
Модуль абсолютной скорости  на основании теоремы косинусов определяется в виде:
на основании теоремы косинусов определяется в виде:
 (9.28)
(9.28)
Пример 2. Вдоль хорды АВ (рис. 95) вращающегося диска движется точка М от точки
А к точке В в соответствии с уравнением  . Закон вращения диска
. Закон вращения диска  . Определить абсолютную скорость точки в момент, когда она находится от оси вращения диска на расстоянии
. Определить абсолютную скорость точки в момент, когда она находится от оси вращения диска на расстоянии 

Решение. Движение точки М вдоль хорды подвижного диска относительно. Поэтому относительная скорость и направлена по хорде АВ

Диск вращается вокруг оси, перпендикулярной к его плоскости. Итак, переносное движение диска будет вращательным, поэтому переносная скорость точки М направлена перпендикулярно к ОМ в сторону вращения диска. По теореме о сложении скоростей абсолютная скорость  Поскольку
Поскольку 

В некоторых задачах кинематики сложного движения точки нужно определить относительную скорость  . С формулы (9.27) видно, что:
. С формулы (9.27) видно, что:

Итак, чтобы построить вектор относительной скорости, следует добавить вектор абсолютная скорости к вектору, направленному противоположно переносной скорости.
Теорема о сложении ускорений
Теорема Кориолиса. Абсолютное ускорение точки при сложном движении равно
векторной сумме относительного, переносного ускорений и ускорения Кориолиса.
Доказательство. По определению ускорения точки, с учетом (9.27), имеем:
 (9.29)
(9.29)
где
 (9.30)
(9.30)
С помощью формулы (9.14) для абсолютной производной, определим каждое слагаемое ускорения отдельно, учитывая, что векторы  и
и  заданные в подвижной системе
заданные в подвижной системе
координат Oxyz и поэтому именно на них распространяются формулы (9.14):
 (9.31)
(9.31)


 )9.32)
)9.32)
Введем обозначения:
 (9.33)
(9.33)
Тогда (9.32) перепишем в виде:

 (9.34)
(9.34)
где 
Введем обозначения в соответствии с определениями абсолютного, относительного и переносного ускорений:
 (9.35)
(9.35)
Подставив (9.31) и (9.34) в выражение (9.29), с учетом (9.35), получим:
 (9.36)
(9.36)
Последнее слагаемое в этой формуле, который не входит ни в относительное, ни в переносное ускорения, называется поворотным или кориолисовым ускорением  :
:
 (9.37)
(9.37)
Окончательно получим:
 (9.38)
(9.38)
Теорема доказана.
Заметим, что в ряде случаев может стать полезной формула для определения ускорения, которая непосредственно следует из (9.14):
 (9.39)
(9.39)
Отметим, что когда переносное движение подвижной системы координат Oxyz является поступательным  , ускорение Кориолиса обращается в ноль. Тогда формула (9.38)
, ускорение Кориолиса обращается в ноль. Тогда формула (9.38)
принимает вид:
 (9.40)
(9.40)
то есть при поступательном движении абсолютное ускорение точки равно геометрической
сумме относительного и переносного ускорений.
Следовательно, эта формула отражает правило параллелограмма для сложения ускорений в данном случае. В следующих разделах проанализируем выражения для каждой составляющей ускорения более детально.
Вращательное и осевое ускорение в случае вращения тела вокруг неподвижной оси
Проанализируем две составляющие переносного ускорение точки в выражении (9.35)  и
и  , обусловленные движением тела относительно полюса О.
, обусловленные движением тела относительно полюса О.

Поскольку кинематическое содержание векторов  и
и  в общем случае движения тела, а следовательно, подвижной системы координат еще до конца не раскрыто , пока ограничимся рассмотрением только частного случая вращения тела вокруг неподвижной оси
в общем случае движения тела, а следовательно, подвижной системы координат еще до конца не раскрыто , пока ограничимся рассмотрением только частного случая вращения тела вокруг неподвижной оси  (рис. 9.6), для которого физический смысл векторов
(рис. 9.6), для которого физический смысл векторов  и
и  полностью определен.
полностью определен.
Введем следующие обозначения:
 (9.41)
(9.41)
и будем называть ускорение  вращательным, а
вращательным, а  осевым.
осевым.
Рассмотрим ускорения произвольной точки М, неизменно связанной с телом, вращения вокруг неподвижной оси (рис. 9.6).
В этом случае 
 поэтому ускорения точки М согласно
поэтому ускорения точки М согласно
(9.38), запишем в виде, опустив индекс  при
при  и
и  :
:

 (9.42)
(9.42)
Кроме того, ускорение этой же точки, согласно п. 8.3, можно представить в виде векторной суммы нормального и тангенциально ускорений:
 (9.43)
(9.43)
Установим связь между составляющими ускорения точки М которые есть в выражениях (9.42) и (9.43). Прежде всего покажем, что составляющая ускорения точки  направлена вдоль перпендикуляра MN, который опущен с точки М на ось вращения
направлена вдоль перпендикуляра MN, который опущен с точки М на ось вращения  . Для того чтоб
. Для того чтоб
подчеркнуть это обстоятельство, его называют осевым ускорением. Действительно, если  (рис. 9.6) – это радиус-вектор точки М то вектор ее скорости
(рис. 9.6) – это радиус-вектор точки М то вектор ее скорости  направленный по касательной к траектории (круга) точки, перпендикулярно к плоскости треугольника OMN. Тогда вектор осевого ускорения
направленный по касательной к траектории (круга) точки, перпендикулярно к плоскости треугольника OMN. Тогда вектор осевого ускорения
 (9.44)
(9.44)
будет направлен перпендикулярно к плоскости KLM, которая содержит прямую МК, параллельную оси вращения  (рис. 9.6). Итак, вектор
(рис. 9.6). Итак, вектор  направленный вдоль MN. Учитывая, что
направленный вдоль MN. Учитывая, что

 (9.45)
(9.45)
получим:
 (9.46)
(9.46)
Сравнив последнее выражение с соответствующим выражением (8.27) для нормального ускорения точки, которое всегда направлено по главной нормали к абсолютной траектории с центром кривизны в точке N, которая лежит на оси вращения, получим:
 (9.47)
(9.47)
Рассмотрим теперь вторую составляющую ускорения  , которую называют вращательным ускорением. Поскольку выполняется равенство (9.47), то с учетом (9.42) и (9.43), получим:
, которую называют вращательным ускорением. Поскольку выполняется равенство (9.47), то с учетом (9.42) и (9.43), получим:
 (9.48)
(9.48)
Далее будет показано, что в общем случае движение твердого тела 
 Если учесть, что при вращении тела вокруг неподвижной оси направления векторов
Если учесть, что при вращении тела вокруг неподвижной оси направления векторов  и
и  всегда совпадают (и совпадают с осью вращения), то в каждой точке вектора скорости и касательного ускорения направлены вдоль одной прямой – касательной к траектории. Модуль вращательного ускорения запишем в виде:
всегда совпадают (и совпадают с осью вращения), то в каждой точке вектора скорости и касательного ускорения направлены вдоль одной прямой – касательной к траектории. Модуль вращательного ускорения запишем в виде:

 (9.49)
(9.49)
Ускорение Кориолиса
По формуле (9.37) ускорение Кориолиса появляется тогда, когда переносное движение является вращательным:
 (9.50)
(9.50)
Как видно из приведенной формулы, ускорение Кориолиса равно удвоенному векторному произведению вектора  на относительную скорость точки
на относительную скорость точки  Направление ускорения Кориолиса определяется по правилу векторного произведения. Оно направлено вдоль
Направление ускорения Кориолиса определяется по правилу векторного произведения. Оно направлено вдоль
нормали к плоскости, в которой расположены векторы  и
и  , в той части пространства, с
, в той части пространства, с
которой, если смотреть с конца вектора  , видно поворот на наименьший угол от вектора
, видно поворот на наименьший угол от вектора  к вектору
к вектору  против хода часовой стрелки (в правой системе координат).
против хода часовой стрелки (в правой системе координат).
Модуль ускорения Кориолиса находим по формуле:
 (9.51)
(9.51)
Спроектировав обе части равенства (9.50) на подвижные оси координат, получим такие выражения для проекций ускорения Кориолиса :
 (9.52)
(9.52)
где  – проекции угловой скорости на оси подвижной системы координат
– проекции угловой скорости на оси подвижной системы координат 
 – проекции относительной скорости на эти самые оси.
– проекции относительной скорости на эти самые оси.
Тогда модуль ускорения Кориолиса :
 (9.53)
(9.53)
Направление  определяется направляющими косинусами углов, которые вектор
определяется направляющими косинусами углов, которые вектор  образует соответственно с ортами
образует соответственно с ортами  подвижных осей:
подвижных осей:
 (9.54)
(9.54)
Случаи превращения в ноль ускорения Кориолиса
Как следует из (9.51), ускорение Кориолиса равно нулю в те моменты (или на тех промежутках времени), когда:
1) вектор  равен нулю, то есть переносное движение является поступательным;
равен нулю, то есть переносное движение является поступательным;
2) относительная скорость  равна нулю, то есть нет относительного движения;
равна нулю, то есть нет относительного движения;
3)  то есть вектор
то есть вектор  и
и  – коллинеарные.
– коллинеарные.
Следует отметить, что в те моменты времени, когда ускорения Кориолиса превращается в ноль, абсолютное ускорение точки определяется по правилу параллелограмма.
тогда:
 (9.55)
(9.55)
а модуль этого ускорения определяется по теореме косинусов:
 (9.56)
(9.56)
Физические причины возникновения ускорения Кориолиса
Покажем, что ускорение Кориолиса возникает вследствие таких двух причин:
1. Представим себе два прямолинейных отрезка  , и
, и  , по которым движутся
, по которым движутся
точки  и
и  (рис. 9.7). Отрезок
(рис. 9.7). Отрезок  движется поступательно, а отрезок
движется поступательно, а отрезок  вращается вокруг точки
вращается вокруг точки  Обозначим через
Обозначим через  и
и  соответственно относительную и переносную скорости точки М. Переносным движением точки (рис. 9.7, а) является поступательное движение, обусловленное движением отрезка
соответственно относительную и переносную скорости точки М. Переносным движением точки (рис. 9.7, а) является поступательное движение, обусловленное движением отрезка  . Через элементарный промежуток времени отрезок
. Через элементарный промежуток времени отрезок 

займет положение  Поскольку переносное движение – поступательное, то переносные
Поскольку переносное движение – поступательное, то переносные
скорости точки  и
и  одинаковы.
одинаковы.
Переносным движением точки  (рис. 9.7, б) является вращательное движение, вызванное вращением отрезка
(рис. 9.7, б) является вращательное движение, вызванное вращением отрезка  вокруг точки
вокруг точки  . Поэтому переносные скорости точки М2 на отрезке
. Поэтому переносные скорости точки М2 на отрезке  и
и  разные:
разные: 

Итак, переносная скорость точки  меняется в зависимости от ее относительного движения вдоль отрезка
меняется в зависимости от ее относительного движения вдоль отрезка  . При этом скорость изменения переносной скорости
. При этом скорость изменения переносной скорости  точки
точки  во времени, которая создает дополнительное ускорение, пропорциональна относительной скорости
во времени, которая создает дополнительное ускорение, пропорциональна относительной скорости  и угловой скорости переносного движения
и угловой скорости переносного движения  В этом суть первой физической причины возникновения ускорения Кориолиса.
В этом суть первой физической причины возникновения ускорения Кориолиса.
2. Вторая физическая причина возникновения ускорения Кориолиса такова:
относительная скорость точки  , то есть
, то есть  , зависит от переносного вращательного движения, поскольку при вращении отрезка
, зависит от переносного вращательного движения, поскольку при вращении отрезка  меняется направление относительной скорости
меняется направление относительной скорости  (Рис. 9.7, б).
(Рис. 9.7, б).
Следовательно, скорость изменение во времени относительной скорости точки (т.е. ускорение точки, которое зависит от приведенной выше причины) также будет пропорционально относительной скорости  и угловой скорости
и угловой скорости  переносного движения.
переносного движения.
А. И. Сомов обратил внимание на то, что ускорения Кориолиса как будто вращает вектор относительной скорости в направлении переносного вращательного движения, из-за чего назвал ускорение Кориолиса поворотным.
Подводя итог изложенного и обращаясь к формуле (9.34), видим, что изменение во времени переносной скорости при условии, что переносное движение является непоступательным, вызывается не только переносным, но и относительным движением точки. Дополнительное ускорение равно векторному произведению  . Так же из формулы (9.31) следует, что изменение относительной скорости во времени вызвано не только относительным, но и переносным движением точки. Дополнительное ускорение и в этом случае равна
. Так же из формулы (9.31) следует, что изменение относительной скорости во времени вызвано не только относительным, но и переносным движением точки. Дополнительное ускорение и в этом случае равна 
Ускорение Кориолиса  , таким образом, равно удвоенному векторному произведению
, таким образом, равно удвоенному векторному произведению
векторов  и
и  , то есть
, то есть  и характеризует изменение во времени относительной скорости через переносное непоступательное движение и переносной скорости – через относительное движение точки.
и характеризует изменение во времени относительной скорости через переносное непоступательное движение и переносной скорости – через относительное движение точки.
Пример 3. Определить абсолютное ускорение точки в примере 2, приведенном в п. 9.3.
Решение. Поскольку переносное движение является вращательным, то абсолютное ускорение точки М (Рис. 9.5) определим по теореме Кориолиса:

Поскольку  и переносная угловая скорость- постоянная
и переносная угловая скорость- постоянная  то
то  и
и  Следовательно,
Следовательно,



Относительное движение точки М происходит вдоль прямой АВ, поэтому относительное ускорение  направлено вдоль АВ, ускорение
направлено вдоль АВ, ускорение  – вдоль ОМ к центру вращения. Направление ускорения Кориолиса определяем по правилу векторного произведения
– вдоль ОМ к центру вращения. Направление ускорения Кориолиса определяем по правилу векторного произведения  . Вектор
. Вектор  направленный перпендикулярно к диску , а
направленный перпендикулярно к диску , а  -вдоль хорды. Итак, ускорения Кориолиса
-вдоль хорды. Итак, ускорения Кориолиса  также направлено по ОМ от центра О вращения диска. Вектор абсолютного ускорения направлен по диагонали прямоугольника со сторонами
также направлено по ОМ от центра О вращения диска. Вектор абсолютного ускорения направлен по диагонали прямоугольника со сторонами  (рис. 9.8), и
(рис. 9.8), и


Пример 4. На подвижных объектах (самолетах, кораблях и т.д.) используются гироскопические приборы маятникового типа для определения отклонения объектов от горизонтали. При движении относительно Земли в этих приборах возникают так называемые скоростные и баллистические девиации (погрешности), обусловленные тем, что эти объекты, двигаясь горизонтально по поверхности Земли (или по сфере радиусом  , где h – высота полета), на самом деле вращаются в инерциальном пространстве и поэтому они движутся с ускорением в инерциальной системе координат, если даже их скорость относительно Земли является постоянной. Поэтому необходимо найти
, где h – высота полета), на самом деле вращаются в инерциальном пространстве и поэтому они движутся с ускорением в инерциальной системе координат, если даже их скорость относительно Земли является постоянной. Поэтому необходимо найти
угловую скорость вращения подвижного объекта и его ускорение в географической системе координат, если составляющая относительной скорости объекта к северу  , на восток –
, на восток –  (рис. 9.9), а угловая скорость суточного вращения Земли –
(рис. 9.9), а угловая скорость суточного вращения Земли –  .
.
Решение. Движение объекта (точку О) задано в сферической системе координат:  – географическая долгота, что отсчитывается от меридиана Гринвича;
– географическая долгота, что отсчитывается от меридиана Гринвича;  – географическая широта, что отсчитывается от экватора;
– географическая широта, что отсчитывается от экватора;  – радиус сферы, по которой движется объект:
– радиус сферы, по которой движется объект:  где
где  – средний радиус Земли. Отметим, что линейная скорость точки на земной поверхности, расположенной на экваторе равна 1852 км/ч относительно неподвижной системы координат.
– средний радиус Земли. Отметим, что линейная скорость точки на земной поверхности, расположенной на экваторе равна 1852 км/ч относительно неподвижной системы координат.
Ось  направлена на север (N) по касательной к меридиану,
направлена на север (N) по касательной к меридиану,  – на восток (£) по касательной к параллели, а
– на восток (£) по касательной к параллели, а  – по вертикали вверх.
– по вертикали вверх.
Очевидно, что движение объекта с составляющей скорости  вызванной изменением угла
вызванной изменением угла  – географической широты, а движение по составляющей скорости на восток
– географической широты, а движение по составляющей скорости на восток  – географической долготы
– географической долготы  . Итак, угловая скорость
. Итак, угловая скорость  направлена перпендикулярно к плоскости параллели и параллельная угловой скорости вращения Земли
направлена перпендикулярно к плоскости параллели и параллельная угловой скорости вращения Земли  , а угловая скорость
, а угловая скорость  направлена в сторону, противоположную направлению оси
направлена в сторону, противоположную направлению оси  .
.
С учетом этого, очевидно, что:
 (1)
(1)
Если теперь учесть и угловую скорость вращения Земли  , то проекции угловой скорости на оси географической системы координат будут:
, то проекции угловой скорости на оси географической системы координат будут:



 (2)
(2)

В данном случае вращательное движение Земли является переносным, а движение объекта по поверхности относительным. С учетом этого и формул (2) приведем формулы для абсолютной скорости объекта в проекциях на оси географической системы координат:
 (3)
(3)
Используя уравнение (3) выражение (2) можно переписать в форме:


 (4)
(4)

Найдем теперь абсолютное ускорение подвижного объекта, воспользовавшись формулой
(9.39):
 (5)
(5)
тут  – угловая скорость вращения системы координат
– угловая скорость вращения системы координат  относительно неподвижной системы координат, которая определяется выражениями (2) или (4)
относительно неподвижной системы координат, которая определяется выражениями (2) или (4)

Проектируя (5) на оси  будем иметь:
будем иметь:
 (6)
(6)
Подставив в (6) выражения (3) и (4), получим:
 (7)
(7)
При горизонтальном движении объекта  то есть
то есть  поэтому формулы (7) немного упрощаются:
поэтому формулы (7) немного упрощаются:

 (8)
(8)


В выражениях (8) не видно явно ускорения Кориолиса, хотя понятно, что оно должно было иметь место, потому что переносное движение Земли является вращательным.
Для того, чтобы выделить явно ускорение Кориолиса, осевое ускорение, вращательное и относительное, нужно формулы (8) записать в развернутом виде:



 (9)
(9)


Перепишем в конечном итоге формулы (9) так, чтобы на первом месте было переносное, дальше относительное и в конце ускорения Кориолиса (таблица).
Таким образом, задача решена.
Пример 5. Точка М неравномерно движется по ободу колеса радиусом R с относительной
скоростью вращается с переменной угловой скоростью  Найти двумя методами ускорения точки:
Найти двумя методами ускорения точки:
1) задавая движение точки в натуральной системе координат;
2) используя понятие сложного движения точки.
Решение. 1. При заданном движения точки в натуральной системе координат нужно учесть, что ускорение в данном случае имеет две составляющие – тангенциальное и нормальное
и нормальное  ускорения:
ускорения:
 (1)
(1)
Следовательно, для определения ускорений по формулам (1) нужно найти  .
.
Очевидно, что  – это по сути абсолютная скорость точки, поэтому:
– это по сути абсолютная скорость точки, поэтому:
 (2)
(2)
Подставив (2) в (1), получим:
 (3)
(3)
Если спроектировать эти ускорения на оси ортогональной системы координат  то получим:
то получим:
 (4)
(4)
При  и
и  соответственно получим:
соответственно получим:
 (5)
(5)

2. Использование понятия сложного движения точки. В этом случае (рис. 9.10,б)
 (6)
(6)
Переносное ускорение имеет две составляющие  и
и  Вращающаяся составляющая ускорения
Вращающаяся составляющая ускорения  направленная в данном случае по оси
направленная в данном случае по оси  и равна:
и равна:

 (7)
(7)
Осевое ускорения будет направлено к оси вращения, проходящей через точку О (рис. 9.10, б) и равно:
 (8)
(8)
Ускорение Кориолиса в этом случае направлено по оси Оу и равно:
 (9)
(9)
Относительное ускорение в этом случае определяется по формуле (9.31), в которой нужно учесть только ту составляющую угловой скорости  , которая обусловлена только относительным движением, потому что взаимодействие вращательного переносного движения и относительной скорости учтено в ускорении Кориолиса:
, которая обусловлена только относительным движением, потому что взаимодействие вращательного переносного движения и относительной скорости учтено в ускорении Кориолиса:
 (10)
(10)
Очевидно, что
 (11)
(11)
Спроектировав выражение (10) на оси  и
и  и учитывая (11), получим:
и учитывая (11), получим:
 (12)
(12)
Найдем теперь проекции абсолютных ускорений на осях  и
и 
 (13)
(13)
Сравнивая выражения (3), (4) и (13), видим, что проекции ускорения на оси  и
и  совпадают. Причем в этом случае при любой
совпадают. Причем в этом случае при любой 
 (14)
(14)
Для сравнения найдем ускорение по формуле (9.39)
 (15)
(15)
Отметим, что в данном случае в формуле (15) нужно задать полную угловую скорость
вращения подвижной системы координат:
 (16)
(16)
В нашем случае  определяется по формуле (6),
определяется по формуле (6),  Из формулы (15) с учетом (6) и (16), получим:
Из формулы (15) с учетом (6) и (16), получим:
 (17)
(17)
или
 (18)
(18)
Нетрудно заметить, что выражения (3), (13) и (18) одинаковые, то есть приведенный способ решения задачи оказался достаточно эффективным. Задача решена.
Сложное движение материальной точки. Относительное, переносное и абсолютное движение материальной точки
Сложное движение материальной точки — это такое движение, при котором точка может одновременно участвовать в двух и более движениях.
Для представления о сложном движение приведем такой пример. Если человека принять за материальную точку, то ее движение по палубе корабля будет сложным, когда это движение рассматривать относительно палубы и относительно берега (поверхности Земли). Движение человека относительно палубы является относительным, вместе с кораблем — переносным, а относительно поверхности Земли — абсолютным.
При сложном движении можно рассматривать точку, тело переноса или подвижное переносное пространство, с которым связана подвижная система координат, и неподвижную систему координат, которая скреплена с поверхностью Земли.
Движение точки относительно тела переноса или подвижной системы отсчета называется относительным, а скорость и ускорение точки в этом движении — относительными скоростью и ускорением, они обозначаются  ,
,  (relative — относительный).
(relative — относительный).
Движение точки вместе с подвижным пространством, а точнее вместе с той точкой подвижного пространства, с которой в данный момент совпадает заданная точка, называется переносным движением, а скорость и ускорение точки в этом движении — переносными скоростью и ускорением, они обозначаются  ,
,  (exporter — захватить).
(exporter — захватить).
Движение материальной точки относительно неподвижной системы координат называется абсолютным, а скорость и ускорение — абсолютными, они обозначаются  ,
,  .
.
Теорема о сложении скоростей в сложном движении материальной точки
Сформулируем эту теорему.
Абсолютная скорость материальной точки при сложном ее движении равна геометрической сумме ее переносной и относительной скоростей:
 .
.
Докажем это. Выберем материальную точку М (рис. 2.45), что движется независимо по своему закону относительно подвижной системы отсчета Oxyz, которая жестко связана с телом S, и вместе с ним перемещается относительно неподвижной системы координат  . Начало подвижной системы координат Oxyz (центр O) выбрано в теле S произвольно, на соответствующих осях координат показаны единичные векторы (орты)
. Начало подвижной системы координат Oxyz (центр O) выбрано в теле S произвольно, на соответствующих осях координат показаны единичные векторы (орты)  ,
,  и
и  .
.
Определим положение материальной точки М относительно выбранных осей координат. Так, относительно подвижной системы координат Oxyz ее положение определяется радиус-вектором  . Положение точки М относительно неподвижной системы координат
. Положение точки М относительно неподвижной системы координат  определяется радиус-вектором
определяется радиус-вектором  .
.
Положение начала (центр O) подвижной системы координат Oxyz относительно неподвижной системы координат  будет определяться радиус-вектором
будет определяться радиус-вектором  .
.
Как видно из образованного на рис. 2.46 векторного треугольника  , всегда сохраняется векторное соотношение:
, всегда сохраняется векторное соотношение:
 ,
,
или, если представить радиус-вектор  в проекциях на оси координат Oxyz с учетом единичных векторов
в проекциях на оси координат Oxyz с учетом единичных векторов  ,
,  и
и  :
:
 .
.

Используя выражение определим абсолютную скорость  материальной точки М.
материальной точки М.
При произвольном переносном движении тела орты  ,
,  и
и  меняют свое направление и поэтому являются переменными векторами. Тогда все члены, входящие в выражение выше, считаются переменными величинами. На основании формулы искомая скорость будет равна:
меняют свое направление и поэтому являются переменными векторами. Тогда все члены, входящие в выражение выше, считаются переменными величинами. На основании формулы искомая скорость будет равна:
 .
.
Перегруппируем правую часть выражения и перепишем его:

Рассмотрим подробно выражение. Так, в последней скобке в этом выражении можно сделать следующие обозначения:
 ,
,
 ,
,
 .
.
Тогда она представляет собой
 — относительную скорость точки.
— относительную скорость точки.
Рассмотрим далее первую скобку в выражении, где
 — скорость начала подвижной системы координат Oxyz или скорость полюса O.
— скорость начала подвижной системы координат Oxyz или скорость полюса O.
По формулам Пуассона другие составляющие первой скобки выражения можно представить так:
 ,
,
 ,
,
 ,
,
где  — угловая скорость переносного движения, или скорость вращения подвижных осей координат и неизменно связанных с ними ортов
— угловая скорость переносного движения, или скорость вращения подвижных осей координат и неизменно связанных с ними ортов  ,
,  и
и  .
.
Подставим в первую скобку выражения:

 .
.
Тогда выражение окончательно будет иметь следующий вид:
 .
.
Сумма  является скоростью переносного движения, где
является скоростью переносного движения, где  0 — скорость полюса или начала отсчета подвижной системы координат.
0 — скорость полюса или начала отсчета подвижной системы координат.
Поскольку переносное движение в общем случае является сложным, то он разделяется на поступательное вместе с полюсом (точкой О) и вращательное вокруг полюса
Окончательно имеем:
 .
.
Что и необходимо было доказать.
Выражение называют параллелограммом скоростей.
Когда угол  , тогда модуль абсолютной скорости равен:
, тогда модуль абсолютной скорости равен:
 ,
,
Если  , так модуль абсолютной скорости
, так модуль абсолютной скорости  движения материальной точки определяется по теореме косинусов:
движения материальной точки определяется по теореме косинусов:
 .
.
Теорема Кориолиса
Сформулируем эту теорему.
Абсолютное ускорение материальной точки при произвольном переносном движении равно геометрической сумме трех ускорений: переносного, относительного и дополнительного ускорения, которое называется поворотным ускорением или ускорением Кориолиса.
Итак:
 ,
,
где  — абсолютное ускорение материальной точки;
— абсолютное ускорение материальной точки;  — переносное ускорение;
— переносное ускорение;  — относительное ускорение;
— относительное ускорение;  — ускорение Кориолиса.
— ускорение Кориолиса.
Предположим, что материальная точка М имеет сложное движение. Считаем, что она движется относительно подвижной системы координат Oxyz, которая сама произвольным образом перемещается относительно другой — неподвижной системы  (рис. 2.46). Покажем
(рис. 2.46). Покажем  ,
,  ,
,  — орты подвижной системы координат Oxyz. Координаты точки M в подвижной системе отсчета — x, y, z.
— орты подвижной системы координат Oxyz. Координаты точки M в подвижной системе отсчета — x, y, z.
Как и в предыдущем случае, определим положение материальной точки М. Так, положение точки М в подвижной системе координат Oxyz определяется радиус-вектором  . Ее положения относительно неподвижной системы координат
. Ее положения относительно неподвижной системы координат  определяется радиус-вектором
определяется радиус-вектором  . Положение точки О (начала отсчета подвижной системы координат Oxyz) в неподвижной системе координат
. Положение точки О (начала отсчета подвижной системы координат Oxyz) в неподвижной системе координат  определяется радиус-вектором
определяется радиус-вектором  .
.
Абсолютное ускорение материальной точки М равна производной по времени от абсолютной скорости:

 .
.
Проведем преобразование и анализ выражения. В первой скобке составляющая
 — ускорение полюса O.
— ускорение полюса O.
Превратим дальше выражение первой скобки, пользуясь формулами Пуассона:






 — ускорение точки в переносном сферическом движении тела вокруг полюса.
— ускорение точки в переносном сферическом движении тела вокруг полюса.
Во второй скобке
 — относительное ускорение точки.
— относительное ускорение точки.
В уравнении есть еще такие два выражения, которые также надо превратить:


 — ускорение Кориолиса или поворотное ускорение.
— ускорение Кориолиса или поворотное ускорение.
Учитывая сделанные преобразования, окончательно запишем:
 .
.
Что и требовалось доказать.
 ,
,
где  — ускорение начала подвижной системы координат (полюса О) и независимого сферического движения тела вокруг полюса, что выражается составляющей ускорения
— ускорение начала подвижной системы координат (полюса О) и независимого сферического движения тела вокруг полюса, что выражается составляющей ускорения  .
.
Модуль, направление и физические причины возникновения ускорения Кориолиса
Рассмотрим подробно ускорения Кориолиса и его свойства. Оно, согласно формуле, имеет следующий вид:
 .
.
Ускорение Кориолиса равна двойному векторном произведения векторов переносной угловой скорости и относительной скорости точки.
Как известно, модуль векторного произведения равен:

Из выражения видно, что модуль ускорения Кориолиса равен нулю  в следующих случаях:
в следующих случаях:
1.  переносное движение не является вращательным, поэтому ускорение Кориолиса называют также поворотным ускорением;
переносное движение не является вращательным, поэтому ускорение Кориолиса называют также поворотным ускорением;
2.  движение точки в данный момент времени не является сложным;
движение точки в данный момент времени не является сложным;
3.  ,или
,или  — векторы переносной угловой скорости и относительной скорости параллельны.
— векторы переносной угловой скорости и относительной скорости параллельны.
Модуль ускорения Кориолиса будет максимальным, если угол между векторами  и
и  составляет 90º или 270º, в этом случае:
составляет 90º или 270º, в этом случае:

Направление ускорения Кориолиса можно найти по двум методами: математическим — по определению векторного произведения двух векторов и физическим — по способу Жуковского.
Рассмотрим первый способ.
Предположим, что тело S вращается вокруг оси z против направления хода часовой стрелки.
Это тело переноса и вектор  направлен вверх вдоль оси z (рис. 2.47). Независимо по телу S по своей траектории движется точка М со скоростью
направлен вверх вдоль оси z (рис. 2.47). Независимо по телу S по своей траектории движется точка М со скоростью  (вектор АМ). Перенесем условно вектор
(вектор АМ). Перенесем условно вектор  в точку М. Вектор ускорения Кориолиса
в точку М. Вектор ускорения Кориолиса  , как итоговый вектор векторного произведения, перпендикулярный плоскости, которую образуют эти векторы (параллелограмм МАВС). Остается определить, к нам этот вектор направлен, или от нас. В данном случае (рис. 2.47) вектор
, как итоговый вектор векторного произведения, перпендикулярный плоскости, которую образуют эти векторы (параллелограмм МАВС). Остается определить, к нам этот вектор направлен, или от нас. В данном случае (рис. 2.47) вектор  направлен к нам, потому что кратчайший переход от вектора
направлен к нам, потому что кратчайший переход от вектора  к вектору
к вектору  происходит против направления хода часовой стрелки.
происходит против направления хода часовой стрелки.

Таким образом, вектор ускорения Кориолиса перпендикулярен плоскости, которую образуют векторы переносной угловой скорости и относительной скорости, и направлен в ту сторону, откуда видим, что кратчайший переход от вектора угловой скорости к вектору относительной скорости происходит против часовой стрелки.
Переходим к рассмотрению определения направления вектора ускорения Кориолиса по методу Жуковского.
Для определения направления вектора ускорения Кориолиса этим методом необходимо вектор относительной скорости  спроецировать на плоскость π, перпендикулярной оси переносного вращения
спроецировать на плоскость π, перпендикулярной оси переносного вращения  , затем вернуть проекцию
, затем вернуть проекцию  в плоскости π на угол 90º в направлении переносного вращения (рис. 2.48).
в плоскости π на угол 90º в направлении переносного вращения (рис. 2.48).
Нетрудно понять, что в плоских механизмах, которые являются объектом курсового проекта по теории механизмов и машин, вектор  всегда будет расположен в плоскости движения механизма. Поэтому для определения направления ускорения Кориолиса достаточно повернуть вектор
всегда будет расположен в плоскости движения механизма. Поэтому для определения направления ускорения Кориолиса достаточно повернуть вектор  на 90º в направлении переносного поворота ωе.
на 90º в направлении переносного поворота ωе.

Рассмотрим далее физические причины возникновения поворотного ускорения или ускорение Кориолиса.
Пусть по пластине, расположенной в плоскости рисунка и равномерно вращается вокруг вертикальной оси с постоянной угловой скоростью  (направление вращения показано стрелкой), движется прямолинейно вдоль ее радиуса материальная точка М с постоянной относительной скоростью
(направление вращения показано стрелкой), движется прямолинейно вдоль ее радиуса материальная точка М с постоянной относительной скоростью  (рис. 2.49). Через некоторое время пластина повернется на угол 𝞿 и точка М окажется в положении M1 на большем расстоянии от оси вращения А. В результате этого вернется вектор
(рис. 2.49). Через некоторое время пластина повернется на угол 𝞿 и точка М окажется в положении M1 на большем расстоянии от оси вращения А. В результате этого вернется вектор  результате переносного вращения, увеличится по модулю и вернется вектор переносной скорости
результате переносного вращения, увеличится по модулю и вернется вектор переносной скорости  .
.

Из выше приведенного можно сформулировать две физические причины возникновения ускорения Кориолиса:
— изменение направления вектора относительной скорости материальной точки в результате переносного вращения;
— изменение модуля и направления вектора переносной скорости точки в результате ее относительного движения; это видно из следующих выражений переносной скорости движения для различных ее положений M и M1 (расстояние  ):
):
 ,
,
 .
.
Следовательно, ускорение Кориолиса — это новый кинематический эффект, который возникает в результате взаимодействия, взаимовлияния векторов относительной и переносной скоростей при вращательном переносном движении.
Влияние ускорения Кориолиса наблюдается в природе и технике.
Так, за счет сил инерции масс воды, которые формируются этим ускорением, размываются правые берега рек, текущих вдоль меридиана. Поэтому правые берега в северном полушарии всегда являются крутыми. В южном полушарии – наоборот, левые берега являются крутыми.
В технике ускорения Кориолиса возникает в так называемых кулисных механизмах (кулиса — это подвижная направляющая). Относительно кулисы движется кулисный камень, а переносным движением является поворот кулисы относительно недвижимого центра.
Методика решения задач на сложное движение материальной точки
1. Выяснить, движение точки является относительным, какое является переносным, проанализировать законы движения и условие задачи.
2. Для определения характеристик относительного движения необходимо условно остановить переносное движение. Найти положение точки в заданный момент времени на траектории относительного движения.
3. Для определения характеристик переносного движения необходимо условно остановить относительное движение и рассмотреть движение точки, принадлежащей телу переноса, которая совпадает в данный момент с этой точкой.
4. Для определения параметров абсолютного движения точки необходимо выбрать систему координат с началом в самой точке, затем методом проекций определить проекции абсолютных скорости и ускорения и, наконец, полные скорости и ускорения
Пример.
Кольцевая трубка (рис. 2.50) радиуса 16 см вращается вокруг горизонтальной диаметра ОА по закону  рад. Внутри трубки движется жидкость согласно уравнению
рад. Внутри трубки движется жидкость согласно уравнению  см. Определить абсолютную скорость и абсолютное ускорение частицы М жидкости в момент времени
см. Определить абсолютную скорость и абсолютное ускорение частицы М жидкости в момент времени , если в начальный момент частица была в точке А.
, если в начальный момент частица была в точке А.
Решение
Определяем положение точки М в момент времени t1. Положение точки M удобно определить углом α. Определим его с помощью такого выражения:
 рад,
рад,
 .
.

Точка М в заданный момент времени изображена на рис. 2.50. Выберем подвижную систему координат, жестко связанную с кольцевой трубкой.
Выделяем переносное движение точки M. Для этого скрепляем точку М с подвижной системой координат. В этом случае точка M будет описывать круг в плоскости, перпендикулярной к диаметру ОА, радиус которого будет равен:
 ,
,
Вычислим переносную скорость точки М как скорость вращения данной точки вокруг оси ОА. Она равна:

Определим угловую скорость вращения трубки.

 .
.
Вектор угловой скорости направлен вдоль оси вращения.
Переносная скорость  точки M равна:
точки M равна:
 .
.
Для момента времени  имеем такое значение переносной скорости точки M:
имеем такое значение переносной скорости точки M:
 .
.
Вектор переносной скорости направлен перпендикулярно к плоскости чертежа в направлении вращения.
Относительное движение точки М — это движение жидкости относительно трубки. В этом случае точка М будет двигаться по кругу диаметром ОА.
Вычисляем относительную скорость точки М. Она равна:
 .
.
Для момента времени  находим значение относительной скорости движения
находим значение относительной скорости движения  :
:

Направляем вектор относительной скорости  по касательной к упомянутой окружности в точке M.
по касательной к упомянутой окружности в точке M.
Векторы переносной  и относительно
и относительно  скоростей изображены на рис. 2.50.
скоростей изображены на рис. 2.50.
Учитывая, что векторы  и
и  взаимно перпендикулярны, находим абсолютную скорость точки M. Она равна:
взаимно перпендикулярны, находим абсолютную скорость точки M. Она равна:
 .
.
Абсолютное ускорение точки M будет равно:
 .
.
Находим переносное нормальное ускорение точки M:
 .
.
При  значение переносного нормального ускорения равно:
значение переносного нормального ускорения равно:
 .
.
Направленный вектор переносного нормального ускорения  по перпендикуляру к оси вращения OA.
по перпендикуляру к оси вращения OA.
Переносное касательное ускорение  точки М равно:
точки М равно:
 .
.
Определим угловое ускорение трубки. Оно будет равно:
 .
.
Угловое ускорение  положительное, следовательно, вращения трубки являются ускоренными.
положительное, следовательно, вращения трубки являются ускоренными.
Вычисляем переносное касательное ускорение  точки M. Оно будет равно:
точки M. Оно будет равно:
 .
.
Для  имеем значение этого ускорения:
имеем значение этого ускорения:
 .
.
Направленное переносное касательное ускорение  точки M так же, как и переносная скорость
точки M так же, как и переносная скорость  , перпендикулярна к плоскости трубки.
, перпендикулярна к плоскости трубки.
Находим относительное касательное ускорение  точки М. Оно равно:
точки М. Оно равно:
 .
.
Вектор относительного касательного ускорения  совпадает с направлением вектора относительной скорости
совпадает с направлением вектора относительной скорости  , потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении
, потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении  .
.
Вычислим относительное нормальное ускорение  :
:
 .
.
Для момента времени  имеем такое значение этого ускорения:
имеем такое значение этого ускорения:
 .
.
Направленный вектор нормального относительного ускорения  по радиусу к центру кольца трубки.
по радиусу к центру кольца трубки.
Находим ускорение Кориолиса  . Оно будет равно:
. Оно будет равно:
 .
.
Направлено ускорение Кориолиса перпендикулярно плоскости, в которой лежат векторы
 и
и  , таким образом, что если посмотреть с положительного конца этого вектора, то поворот от
, таким образом, что если посмотреть с положительного конца этого вектора, то поворот от  к
к  на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса
на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса  направлен по одной прямой с вектором переносного касательного ускорения
направлен по одной прямой с вектором переносного касательного ускорения  , но имеет направление в противоположную сторону.
, но имеет направление в противоположную сторону.
Находим относительное касательное ускорение  точки М. Оно равно:
точки М. Оно равно:
 .
.
Вектор относительного касательного ускорения  совпадает с направлением вектора относительной скорости
совпадает с направлением вектора относительной скорости  , потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении
, потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении  .
.
Вычислим относительное нормальное ускорение  :
:
 .
.
Для момента времени  имеем такое значение этого ускорения:
имеем такое значение этого ускорения:
 .
.
Направленный вектор нормального относительного ускорения  по радиусу к центру кольца трубки.
по радиусу к центру кольца трубки.
Находим ускорение Кориолиса  . Оно будет равно:
. Оно будет равно:
 .
.
Направлено ускорение Кориолиса перпендикулярно плоскости, в которой лежат векторы  и
и  , таким образом, что если посмотреть с положительного конца этого вектора, то поворот о т
, таким образом, что если посмотреть с положительного конца этого вектора, то поворот о т  к
к  на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса
на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса  направлен по одной прямой с вектором переносного касательного ускорения
направлен по одной прямой с вектором переносного касательного ускорения  , но имеет направление в противоположную сторону.
, но имеет направление в противоположную сторону.
Векторы относительного, переносного и ускорение Кориолиса изображены на рис. 2.51.

Для нахождения абсолютного ускорения  выберем систему координат, как показано на рис. 2.51, и спроектируем векторное равенство, которое определяет абсолютное ускорение точки М, на оси данной системы координат:
выберем систему координат, как показано на рис. 2.51, и спроектируем векторное равенство, которое определяет абсолютное ускорение точки М, на оси данной системы координат:
 /
/
 /
/
 .
.
Модуль абсолютного ускорения  равен:
равен:
 .
.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Содержание:
Абсолютная и относительная производные от вектора:
При рассмотрении сложного движения точки в общем случае переносного движения приходится рассматривать изменение векторных величин с течением времени по отношению к системам отсчета, движущимся друг относительно друга. Одно изменение имеет векторная величина относительно подвижной системы отсчета, движущейся относительно другой, неподвижной, и другое — относительно неподвижной системы отсчета. Неподвижной системой отсчета считается система, движение которой относительно других систем отсчета не рассматривается.
Введем обозначения производных от векторных величин при рассмотрении их изменения относительно различных систем отсчета, движущихся друг относительно друга. Для любого вектора 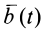
Установим зависимость между полной и относительной производными по времени вектора 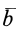 и величинами, характеризующими движение подвижной системы отсчета относительно неподвижной. Для этого разложим вектор
и величинами, характеризующими движение подвижной системы отсчета относительно неподвижной. Для этого разложим вектор 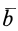 на составляющие, параллельные осям подвижной системы координат. Имеем
на составляющие, параллельные осям подвижной системы координат. Имеем
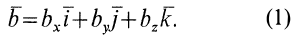
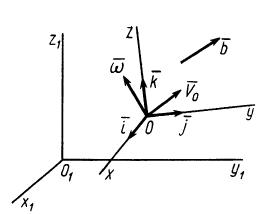
Рис. 87
Изменение вектора 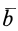 относительно неподвижной системы координат
относительно неподвижной системы координат 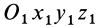 . в зависимости от времени состоит из изменения его проекций
. в зависимости от времени состоит из изменения его проекций 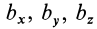 на подвижные оси координат и изменения единичных векторов
на подвижные оси координат и изменения единичных векторов 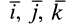 подвижных осей вследствие движения подвижной системы координат относительно неподвижной. Вычислим полную производную по времени от вектора
подвижных осей вследствие движения подвижной системы координат относительно неподвижной. Вычислим полную производную по времени от вектора 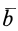 , используя формулу (1). Получим
, используя формулу (1). Получим
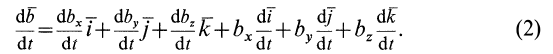
Первые три слагаемых учитывают изменение вектора 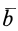 при неизменных
при неизменных 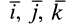 и поэтому составляют относительную производную, т. е.
и поэтому составляют относительную производную, т. е.
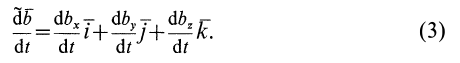
Производные по времени единичных векторов определим по формулам Пуассона
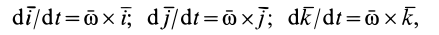
так как эти векторы не изменяются от поступательного движения со скоростью 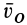 вместе с подвижной системой отсчета (рис. 87). Вектор
вместе с подвижной системой отсчета (рис. 87). Вектор 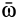 есть угловая скорость вращательной части движения вокруг точки
есть угловая скорость вращательной части движения вокруг точки  подвижной системы координат относительно неподвижной. Подставляя эти значения производных единичных векторов в (2) и вынося
подвижной системы координат относительно неподвижной. Подставляя эти значения производных единичных векторов в (2) и вынося 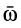 за скобки, получим
за скобки, получим
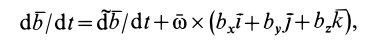
или, учитывая (1),
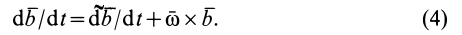
Получена формула зависимости производных векторов 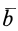 в двух системах отсчета, движущихся друг относительно друга. Формула (4) называется формулой Бура.
в двух системах отсчета, движущихся друг относительно друга. Формула (4) называется формулой Бура.
Известно, что произвольное движение системы координат как свободного твердого тела можно представить как поступательное движение вместе с полюсом, например с точкой 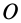 , и вращение вокруг этой точки. Из формулы Бура следует, что поступательная часть движения вместе с полюсом не влияет на зависимость между производными, а влияет только вращательная часть движения.
, и вращение вокруг этой точки. Из формулы Бура следует, что поступательная часть движения вместе с полюсом не влияет на зависимость между производными, а влияет только вращательная часть движения.
Рассмотрим частные случаи.
1. Если вектор 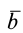 не изменяется относительно подвижной системы координат, то его относительная производная
не изменяется относительно подвижной системы координат, то его относительная производная 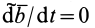 и по формуле (4) получаем
и по формуле (4) получаем
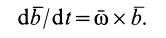
Это формула для производной от вектора постоянного модуля, доказанная ранее для радиуса-вектора при вращении вокруг неподвижной оси. Она справедлива для любого вектора при произвольном движении подвижной системы осей координат. В рассматриваемом случае 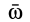 не только угловая скорость вращения подвижной системы координат, но и угловая скорость вращения вектора
не только угловая скорость вращения подвижной системы координат, но и угловая скорость вращения вектора 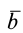 , так как вектор
, так как вектор 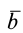 можно при этом считать скрепленным с подвижной системой координат.
можно при этом считать скрепленным с подвижной системой координат.
2. Если вектор 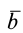 не изменяется относительно основной системы координат, то полная производная
не изменяется относительно основной системы координат, то полная производная 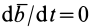 и, согласно (4), его относительная производная
и, согласно (4), его относительная производная
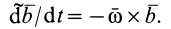
3. Если 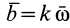 , т. е. вектор
, т. е. вектор 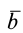 все время параллелен вектору угловой скорости
все время параллелен вектору угловой скорости 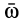 , то
, то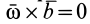 и
и
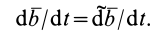
В частности, если 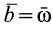 , то
, то
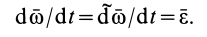
Полная и локальная производные также равны друг другу в те моменты времени, в которые вектор 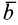 параллелен вектору угловой скорости
параллелен вектору угловой скорости 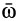 .
.
Сложение скоростей
Если 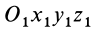 —неподвижная система осей координат, а
—неподвижная система осей координат, а  — подвижная (рис. 88), то, как известно, абсолютным движением точки называют ее движение относительно неподвижной системы осей координат, а относительным — ее движение относительно подвижной. Переносным движением точки называют ее движение в рассматриваемый момент времени вместе с подвижной системой осей относительно неподвижных. Относительные скорость и ускорение обозначают
— подвижная (рис. 88), то, как известно, абсолютным движением точки называют ее движение относительно неподвижной системы осей координат, а относительным — ее движение относительно подвижной. Переносным движением точки называют ее движение в рассматриваемый момент времени вместе с подвижной системой осей относительно неподвижных. Относительные скорость и ускорение обозначают 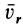 и
и 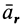 , переносные —
, переносные — 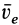 и
и 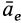 , а абсолютные —
, а абсолютные — 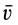 и
и 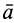 . Другие характеристики этих движений снабжаются соответствующими значками.
. Другие характеристики этих движений снабжаются соответствующими значками.
Движение подвижной системы осей координат относительно неподвижной можно охарактеризовать скоростью ее поступательного движения 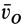 , например вместе с точкой
, например вместе с точкой 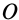 и вектором угловой скорости
и вектором угловой скорости 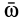 ее вращения вокруг
ее вращения вокруг 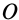 . Пусть точка
. Пусть точка 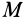 движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведем векторы
движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведем векторы 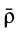 и
и 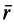 , характеризующие положение точки
, характеризующие положение точки 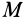 относительно неподвижной и подвижной систем осей координат, и вектор
относительно неподвижной и подвижной систем осей координат, и вектор 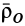 точки
точки 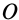 . Для любого момента времени
. Для любого момента времени
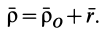
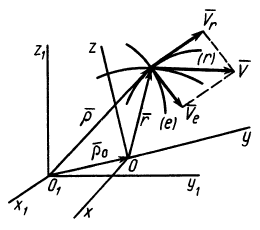
Рис. 88
Продифференцируем по времени это векторное тождество, учитывая изменения векторов относительно неподвижных осей координат, т. е. вычислим полные производные. Получим
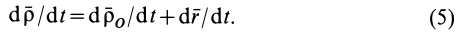
По определению, 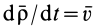 является абсолютной скоростью точки
является абсолютной скоростью точки 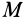 ,
, 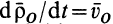 — абсолютной скоростью точки
— абсолютной скоростью точки 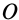 . Для вычисления
. Для вычисления 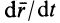 применим формулу Бура. Имеем
применим формулу Бура. Имеем
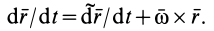
Относительная производная 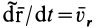 является относительной скоростью точки
является относительной скоростью точки 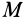 по отношению к подвижной системе отсчета, а
по отношению к подвижной системе отсчета, а 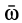 — угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора
— угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора 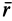 , если бы он в рассматриваемый момент времени был скреплен с подвижной системой осей координат. Таким образом, из (5) получаем
, если бы он в рассматриваемый момент времени был скреплен с подвижной системой осей координат. Таким образом, из (5) получаем

Скорость
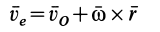
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка 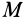 в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки
в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки 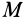 . Из (6) получаем следующую теорему сложения скоростей для точки:
. Из (6) получаем следующую теорему сложения скоростей для точки:

т. е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
Сложение ускорений точки в общем случае переносного движения
Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости (6). Имеем
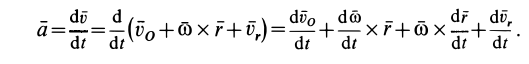
Для полных производных от векторов 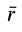 и
и 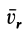 применим формулу Бура. Получим
применим формулу Бура. Получим
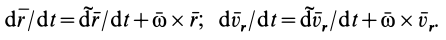
Учитывая, что
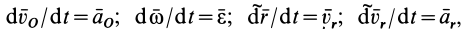
получим для абсолютного ускорения
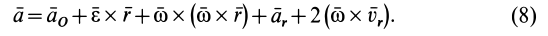
В этой формуле первые три слагаемых составляют ускорение точки свободного твердого тела в общем случае его движения вместе с подвижной системой осей координат относительно неподвижной. Первое слагаемое 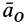 — ускорение точки
— ускорение точки 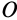 ,
, 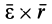 и
и 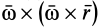 — соответственно вращательное и осестремительное ускорения точки
— соответственно вращательное и осестремительное ускорения точки 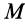 , если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемый момент времени относительного движения. После этого (8) примет вид
, если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемый момент времени относительного движения. После этого (8) примет вид

где

Ускорение 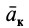 называется ускорением Кориолиса. Иногда его также называют добавочным (или поворотным) ускорением.
называется ускорением Кориолиса. Иногда его также называют добавочным (или поворотным) ускорением.
Формула (9) выражает теорему сложения ускорений точки, или кинематическую теорему Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений — переносного, относительного и Кориолиса.
Переносное ускорение рассматривалось при изучении движения свободного твердого тела. Относительное ускорение изучалось в кинематике точки. Его можно выразить в двух формах в зависимости от способа задания относительного движения. При координатном способе задания в декартовых координатах
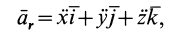
где 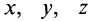 — координаты движущейся_ точки относительно подвижной системы осей координат;
— координаты движущейся_ точки относительно подвижной системы осей координат;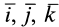 — единичные векторы этих осей. При естественном способе задания движения
— единичные векторы этих осей. При естественном способе задания движения
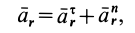
причем
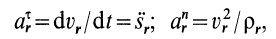
где 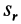 — расстояние от начала отсчета до точки по траектории относительного движения;
— расстояние от начала отсчета до точки по траектории относительного движения; 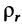 — радиус кривизны этой траектории. В частном случае, когда переносное движение есть вращение вокруг неподвижной оси, переносное ускорение
— радиус кривизны этой траектории. В частном случае, когда переносное движение есть вращение вокруг неподвижной оси, переносное ускорение
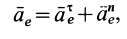
где касательное переносное ускорение
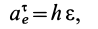
причем 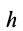 есть кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
есть кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
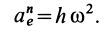
Абсолютное ускорение в этом случае
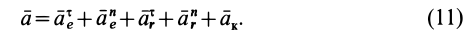
Ускорение Кориолиса
Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (10)
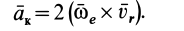
Угловую скорость вращательной части движения подвижной системы отсчета, т. е. угловую скорость переносного движения, заменили на 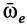 .
.
Ускорение Кориолиса является результатом взаимного влияния двух движений: переносного и относительного. Часть его 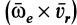 получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже
получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже 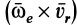 , есть результат изменения относительной скорости вследствие переносного движения. Это следует из анализа формул при выводе абсолютного ускорения.
, есть результат изменения относительной скорости вследствие переносного движения. Это следует из анализа формул при выводе абсолютного ускорения.
Модуль ускорения Кориолиса в соответствии с (10) определяется выражением
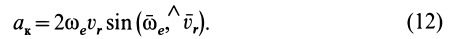
Для определения ускорения Кориолиса очень удобно правило Н. Е. Жуковского. Оно основано на формуле (10). Пусть имеем точку 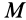 , движущуюся с относительной скоростью
, движущуюся с относительной скоростью 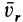 (рис. 89). Построим плоскость
(рис. 89). Построим плоскость 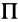 , перпендикулярную угловой скорости переносного вращения и спроецируем
, перпендикулярную угловой скорости переносного вращения и спроецируем 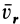 на эту плоскость. Проекцию обозначим
на эту плоскость. Проекцию обозначим 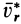 . Она является вектором; ее модуль
. Она является вектором; ее модуль
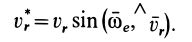
Ускорение Кориолиса выразится в форме

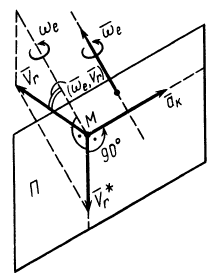
Рис. 89
Учитывая (10) и (12′), получаем правило Жуковского: модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости 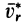 повернуть на
повернуть на 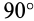 вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
Рассмотрим случаи обращения в нуль ускорения Кориолиса. Из (12) следует, что 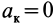 , если:
, если:
-
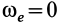 , т. е. переносное движение является поступательным;
, т. е. переносное движение является поступательным; -
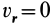 , т. е. в те моменты времени, в которые происходит изменение направления относительного движения;
, т. е. в те моменты времени, в которые происходит изменение направления относительного движения; -
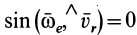 , т. е. когда скорость относительного движения
, т. е. когда скорость относительного движения 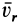 параллельна угловой скорости переносного вращения
параллельна угловой скорости переносного вращения 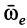 .
.
Следует отметить, что при различном разложении одного и того же абсолютного движения точки на переносное и относительное получим разные ускорения Кориолиса.
Пример №1
Шар радиусом 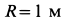 вращается вокруг вертикальной оси
вращается вокруг вертикальной оси 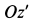 по закону
по закону 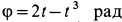 . По меридиану шара движется точка
. По меридиану шара движется точка 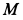 по закону
по закону 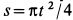 (рис. 90,а). Расстояние
(рис. 90,а). Расстояние 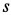 отсчитывается от точки
отсчитывается от точки 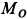 меридиана.
меридиана.
Определить абсолютные скорость и ускорение точки 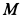 в момент времени
в момент времени 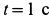 .
.
Решение. За переносное движение точки примем вращение ее вместе с шаром вокруг оси 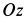 (рис. 90, б). Тогда относительным движением точки будет ее движение по меридиану шара.
(рис. 90, б). Тогда относительным движением точки будет ее движение по меридиану шара.
Определим положение точки 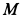 на меридиане в момент времени
на меридиане в момент времени 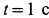 . Имеем
. Имеем 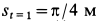 . Так как
. Так как 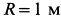 , то положение точки определяется углом широты
, то положение точки определяется углом широты 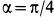 .
.
Вычислим угловые скорость и ускорение переносного движения. Получаем 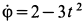 ; при
; при 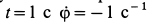 . Угловая скорость
. Угловая скорость 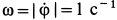 . Знак минус у
. Знак минус у 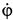 показывает, что вращение шара происходит в отрицательную сторону угла
показывает, что вращение шара происходит в отрицательную сторону угла 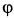 , т. е. по часовой стрелке.
, т. е. по часовой стрелке.
Так как 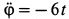 и при
и при 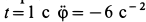 , то угловое ускорение переносного движения
, то угловое ускорение переносного движения 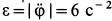 . Знак минус у
. Знак минус у 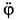 указывает, что оно направлено по часовой стрелке, против положительного направления угла ф. Так как знаки у
указывает, что оно направлено по часовой стрелке, против положительного направления угла ф. Так как знаки у 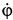 и
и 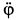 одинаковы, то вращение шара в рассматриваемый момент времени является ускоренным.
одинаковы, то вращение шара в рассматриваемый момент времени является ускоренным.
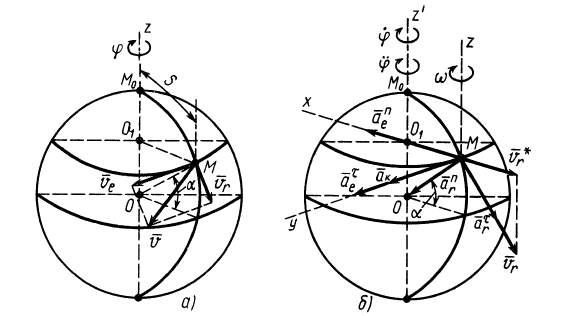
Рис. 90
Абсолютную скорость точки определяем по формуле
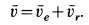
Скорость переносного движения при 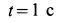
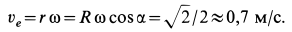
Скорость относительного движения точки 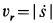 , где
, где 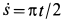 . При
. При 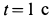
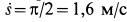 . Следовательно,
. Следовательно, 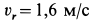 . Знак плюс у
. Знак плюс у 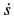 указывает, что
указывает, что 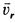 направлено в сторону возрастания
направлено в сторону возрастания 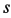 .
.
В рассматриваемом случае 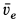 направлена по касательной к параллели шара и перпендикулярна
направлена по касательной к параллели шара и перпендикулярна 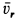 , которая направлена по касательной к меридиану. Следовательно,
, которая направлена по касательной к меридиану. Следовательно,
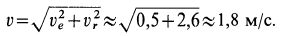
Так как переносное движение является вращением шара вокруг неподвижной оси, то абсолютное ускорение точки определяем по формуле

Переносное нормальное ускорение
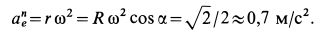
Ускорение 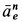 направлено по кратчайшему расстоянию от точки до оси, т. е. по
направлено по кратчайшему расстоянию от точки до оси, т. е. по 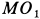 . Переносное касательное ускорение
. Переносное касательное ускорение 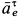 перпендикулярно
перпендикулярно 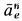 и направлено в соответствии с направлением углового ускорения по скорости
и направлено в соответствии с направлением углового ускорения по скорости 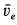 . Числовое значение этого ускорения
. Числовое значение этого ускорения
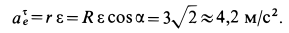
Относительное нормальное ускорение
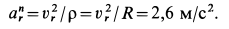
Ускорение 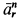 направлено к центру кривизны траектории относительною движения, т. е. к центру шара
направлено к центру кривизны траектории относительною движения, т. е. к центру шара  . Относительное касательное ускорение
. Относительное касательное ускорение 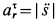 , где
, где 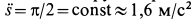 . Следовательно,
. Следовательно, 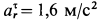 . Так как
. Так как 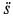 положительно, то
положительно, то 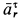 направлено в сторону возрастающих значений
направлено в сторону возрастающих значений 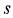 по касательной к траектории относительного движения. Относительное движение оказалось ускоренным в рассматриваемый момент времени.
по касательной к траектории относительного движения. Относительное движение оказалось ускоренным в рассматриваемый момент времени.
Ускорение Кориолиса определяем по правилу Жуковского. Его модуль 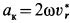 , где
, где 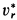 —проекция
—проекция 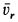 на плоскость, перпендикулярную оси переносного вращения
на плоскость, перпендикулярную оси переносного вращения 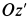 . Имеем
. Имеем
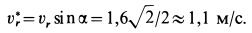
После этого находим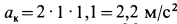 . Чтобы определить направление
. Чтобы определить направление 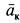 , следует
, следует 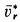 повернуть вокруг оси
повернуть вокруг оси 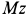 , параллельной
, параллельной 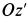 , на
, на 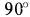 в сторону переносного вращения, т. е. в рассматриваемом случае по часовой стрелке. Получаем, что ускорение направлено по ускорению
в сторону переносного вращения, т. е. в рассматриваемом случае по часовой стрелке. Получаем, что ускорение направлено по ускорению 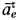 .
.
Для определения абсолютного ускорения выбираем прямоугольные оси координат 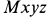 и проецируем обе части векторного равенства (а) на эти оси, учитывая направление составляющих ускорений (рис. 90, б). Получаем:
и проецируем обе части векторного равенства (а) на эти оси, учитывая направление составляющих ускорений (рис. 90, б). Получаем:
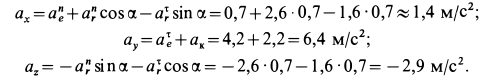
Числовое значение абсолютного значения
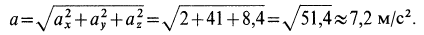
Пример №2
Колечко 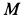 (рис. 91), надетое на стержень, движется в плоскости
(рис. 91), надетое на стержень, движется в плоскости 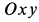 согласно уравнениям
согласно уравнениям
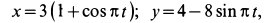
где 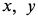 —в см;
—в см; 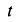 — в с. Стержень может вращаться вокруг оси
— в с. Стержень может вращаться вокруг оси 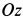 .
.
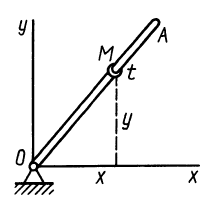
Рис.91
Определить в момент 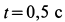 угловую скорость и угловое ускорение стержня, а также скорость и ускорение движения колечка по стержню.
угловую скорость и угловое ускорение стержня, а также скорость и ускорение движения колечка по стержню.
Решение. Положение колечка в момент времени 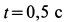 определяется координатами
определяется координатами
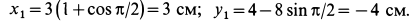
Примем движение колечка вместе с вращающимся стержнем за переносное. Тогда его движение по стержню будет относительным движением.
Вычислим проекции на оси координат абсолютных скорости и ускорения колечка для произвольного момента времени. Имеем:
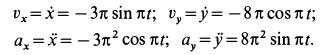
Для момента времени 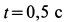 получаем:
получаем:
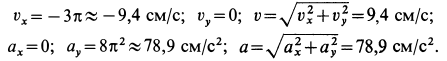
По проекциям изображаем векторы абсолютных скорости и ускорения в рассматриваемый момент времени (рис. 92). По теореме сложения скоростей для колечка,
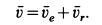
Скорость переносного движения 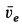 перпендикулярна стержню
перпендикулярна стержню 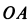 , а скорость относительного движения
, а скорость относительного движения 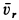 направлена по стержню. Разлагая абсолютную скорость
направлена по стержню. Разлагая абсолютную скорость 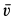 по этим двум направлениям, получаем
по этим двум направлениям, получаем
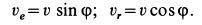
Но
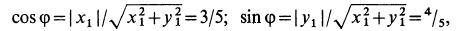
поэтому
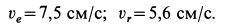
Угловая скорость вращения стержня определяется по формуле
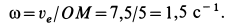
В соответствии с направлением 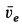 изображаем на рисунке дуговую стрелку для угловой скорости.
изображаем на рисунке дуговую стрелку для угловой скорости.
В частном случае переносного вращательного движения по теореме сложения ускорений для абсолютного ускорения имеем
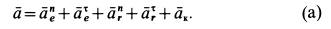
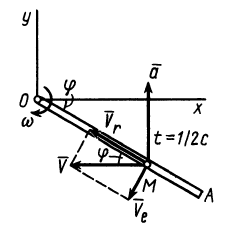
Рис. 92
Вычисляем отдельные составляющие абсолютного ускорения 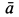 и изображаем их на рис. 93. Для модуля нормального переносного ускорения
и изображаем их на рис. 93. Для модуля нормального переносного ускорения 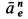 получаем
получаем
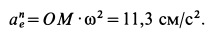
Ускорение 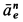 направлено к оси переносного вращения, т. е. к точке
направлено к оси переносного вращения, т. е. к точке 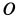 . Составляющая переносного ускорения
. Составляющая переносного ускорения 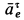 направлена перпендикулярно
направлена перпендикулярно 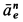 а” и по величине неизвестна. Предполагая, что дуговая стрелка для
а” и по величине неизвестна. Предполагая, что дуговая стрелка для 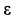 направлена против часовой стрелки, изображаем на рисунке ускорения
направлена против часовой стрелки, изображаем на рисунке ускорения 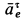 .
.
Нормальная составляющая относительного ускорения 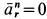 , так как относительное движение колечка по стержню является прямолинейным. Касательная составляющая относительного ускорения в этом случае равна полному относительному ускорению, т. е.
, так как относительное движение колечка по стержню является прямолинейным. Касательная составляющая относительного ускорения в этом случае равна полному относительному ускорению, т. е. 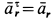 . Предположим, что
. Предположим, что 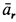 направлено от точки
направлено от точки 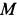 к
к 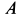 .
.
Ускорение Кориолиса 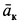 определяем по правилу Жуковского. Для его модуля имеем
определяем по правилу Жуковского. Для его модуля имеем 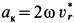 , где
, где 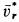 — проекция относительной скорости
— проекция относительной скорости 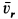 на плоскость, перпендикулярную оси переносного вращения
на плоскость, перпендикулярную оси переносного вращения 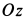 . В рассматриваемом случае
. В рассматриваемом случае 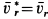 , поэтому
, поэтому 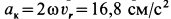 . Направление ускорения
. Направление ускорения 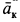 получаем поворотом на
получаем поворотом на 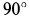 вектора
вектора 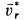 по направлению дуговой стрелки
по направлению дуговой стрелки 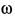 вокруг оси, проходящей через точку
вокруг оси, проходящей через точку 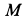 параллельно оси вращения стержня
параллельно оси вращения стержня 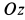 .
.
Выбираем оси координат 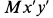 и проецируем векторы, входящие в уравнение (а) на эти оси. Имеем:
и проецируем векторы, входящие в уравнение (а) на эти оси. Имеем:
- для
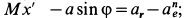
- для
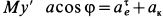 .
.
Из этих уравнений определяем неизвестные ускорения:
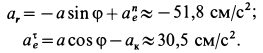
Ускорение 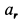 получилось отрицательным. Следовательно, предположение о направлении его оказалось неверным. В действительности
получилось отрицательным. Следовательно, предположение о направлении его оказалось неверным. В действительности 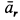 направлено против ранее принятого направления. Ускорение
направлено против ранее принятого направления. Ускорение 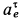 оказалось положительным. Предположение о направлении дуговой стрелки для
оказалось положительным. Предположение о направлении дуговой стрелки для 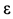 подтвердилось. Угловое ускорение стержня определяем по формуле
подтвердилось. Угловое ускорение стержня определяем по формуле
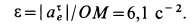
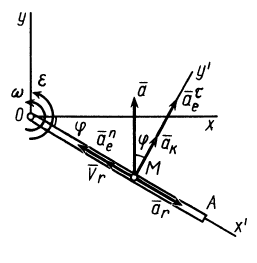
Рис. 93
Составное (сложное) движение. Относительное и переносное движения
Абсолютным движением называют движение точки или системы точек по отношению к основной системе отсчета.
Абсолютное движение
Механическое движение выражается в изменении с течением времени взаимных положений тел (или частей тела). Такое изменение можно отметить только относительно других тел. Так, река течет вдоль берегов, биллиардный шар катится по биллиардному столу, пароход пересекает экватор. Реальные или условные тела (берега, биллиардный стол, экватор), по отношению к которым мы определяем положения других движущихся тел (воды, шара, парохода) и которые мы принимаем за системы отсчета, тоже не неподвижны. Так, системы отсчета, только что приведенные нами в виде примера, находятся на поверхности нашей планеты и вместе с ней вращаются вокруг земной оси, движутся вокруг Солнца и совершают множество других движений. Но и предметы, не связанные непосредственно с Землей, тоже не неподвижны—Солнце движется относительно звезд, которые движутся относительно друг друга.
Однако для целей механики далеко не всегда нужно иметь неподвижную систему отсчета. Так, например, если мы передвигаем какой-либо груз с носа корабля на корму, то нас может интересовать движение груза по палубе независимо от движения корабля. В подобных случаях в кинематике можно условно принять за неподвижную любую систему отсчета и назвать ее основной системой отсчета. Движение же точки (или системы точек) по отношению к основной системе отсчета называют абсолютным движением.
Относительным движением называют движение точки или системы точек по отношению к подвижной системе отсчета
Относительное движение
Встречаются случаи, когда приходится изучать движение (точки или тела) по отношению к системе отсчета, которая сама передвигается относительно другой системы, принятой за основную. При рассмотрении движения точки или тела по отношению к двум системам отсчета ту из этих систем, которая движется относительно основной системы отсчета, называют подвижной системой отсчета.
Так, например, перемещение корабля в море, измеренное при помощи лага, не учитывает снос корабля морским течением. Лагом измеряют движение корабля относительно воды. Можно представить себе подвижную систему координат, плывущую вместе с водой по течению, т. е. передвигающуюся относительно другой системы отсчета, принятой за основную. Движения корабля можно рассматривать по отношению к двум системам отсчета: по отношению к подвижной системе (связанной с водой) и к основной (связанной с материками, принимаемыми за неподвижные). Движение корабля по отношению к подвижной системе координат, измеряемое лагом, будем называть относительным движением корабля. Вообще относительным движением будем называть движение (точки, тела или системы точек) по отношению к подвижной системе отсчета. Относительное движение изучают обычно в тех случаях, когда приходится учитывать не только движение данного объекта по отношению к подвижной системе отсчета, но и движение самой системы отсчета.
Переносным движением называют движение подвижной системы отсчета по отношению к основной системе отсчета
Переносное движение
Так, в данном примере, чтобы знать движение корабля относительно берегов, надо кроме движения корабля относительно воды знать также и движение самой воды, т. е. движение подвижной системы отсчета относительно основной. Движение подвижной системы отсчета по отношению к основной системе отсчета называют переносным движением.
Во многих задачах кинематики переносным бывает движение среды, в которой находится тот объект, движение которого нужно изучить. В только что рассмотренном примере течение воды действительно переносит корабль. Еще один пример: человек идет по поезду. Движение поезда является переносным движением для человека, а движение человека относительно вагонов является относительным. Поезд переносит (в буквальном смысле слова) человека. Но иногда переносное движение не является движением среды, которая увлекает с собой данный объект. Например, рассматривая движение Земли вокруг ее оси и вокруг Солнца, мы можем первое из этих движений считать относительным, а второе — переносным, хотя нет такой среды, которая вращалась бы вокруг Солнца, увлекая с собой и Землю.
Составным движением называют абсолютное движение точки или системы точек, составляемое из их относительного и переносного движений
Составное движение
В первых двух примерах движение объекта (корабля, человека) состоит из двух движений, которые мы назвали относительным и переносным. В третьем примере Земля совершает движение, которое мы искусственно разложили на относительное и переносное. Часто, чтобы упростить изучение какого-либо сложного движения, это движение искусственно раскладывают на более простые, называя одно из них относительный!, другое—переносным. Независимо от того, состоит ли движение в действительности из относительного и переносного или же мы искусственно, для упрощения расчетов, считаем его состоящим из двух движений, мы будем называть сложным или составным движением абсолютное движение точки или системы точек, состоящее (или составляемое) из относительного движения по отношению к подвижной системе отсчета и переносного движения вместе с подвижной системой отсчета.
Если в cocтавном движении мы мысленно прекратим одно из составляющих движений, то получим второе составляющее движение. При решении некоторых задач бывает удобно пользоваться таким приемом:
- чтобы определить относительное движение, мысленно остановим переносное;
- чтобы определить переносное движение, мысленно остановим относительное.
Возвращаясь к первому из только что разобранных примеров, мысленно остановим морское течение; корабль будет двигаться относительно воды, но не будет относиться течением; останется только одно движение — относительное. Остановим теперь собственный ходкорабля, но предоставим воде продолжать свое течение, и корабль поплывет по течению; останется только одно движение корабля —переносное.
Также легко выделить относительное и переносное движения во втором примере. Остановим мысленно поезд, но предоставим человеку идги по вагону, и получим относительное движение человека; остановим мысленно человека в его движении по поезду, но не будем останавливать поезд, и найдем переносное движение человека.
Движение точки, тела или системы точек часто рассматривают как составное, мысленно раскладывая его на два или несколько движений более простых
Несколько сложнее третий пример (движение Земли)
Здесь нет движения среды, переносящей Землю, подобно морскому течению, переносящему корабль. Мы лишь мысленно приняли движение Земли за составное, искусственно разложили его на переносное и относительное, чтобы упростить его, чтобы более наглядно себе его представить и легче понять. Мы можем вообразить подвижную систему координат, связанную с Землей и движущуюся относительно основной системы, связанной с Солнцем и звездами, и считать, что движение Земли состоит из переносного и относительного. Поскольку движение земного шара (движение по отношению к основной системе) мы искусственно рас: сматриваем как составное, постольку от нас самих зависит, как разложить это движение на переносное и относительное. Мы можем считать, что подвижная система отсчета движется поступательно или вращательно. В зависимости от этого, конечно, изменится и относительное движение. Земля совершает 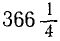 оборота в год относительно поступательно движущихся осей (рис. 114, а) и на один оборот меньше относительно осей, вращающихся вокруг Солнца (рис. 114, б) и совершающих один оборот в год.
оборота в год относительно поступательно движущихся осей (рис. 114, а) и на один оборот меньше относительно осей, вращающихся вокруг Солнца (рис. 114, б) и совершающих один оборот в год.
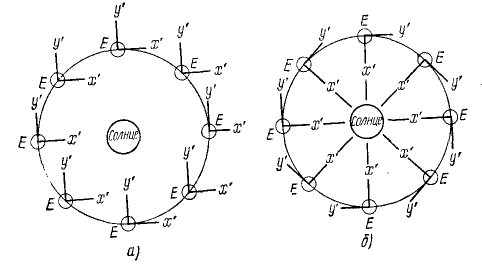
Рис. 114
Такой искусственный метод разложения движения на относительное и переносное широко применяют в различных областях механики. Л. Пуансо в предисловии ко второму изданию своей книги «Элементы статики» (1824) писал даже о невозможности представить наглядно движение тел иначе, как в виде одновременного перемещения и вращения.
Очень часто движение раскладывают не на два, а на большее число составляющих движений. Напомним, что мы уже так поступали, изучая движение точки как составное из трех прямолинейных движений, параллельных осям координат.
Теоремы параллелограмма скоростей и параллелограмма ускорений
Относительными скоростью и ускорением точки называют ее скорость и ускорение по отношению к подвижной системе отсчета
Относительные скорость и ускорение
Пусть некоторая точка M (рис. 115) движется относительно системы координат.x’Ey’z’. Если бы эту систему координат мы считали неподвижной, то движение, скорость и ускорение точки по отношению к этим координатам мы называли бы абсолютными. Но пусть система координатных осей x’Ey’z’ по условиям задачи движется относительно основной системы отсчета xОyz. В таком случае скорость и ускорение точки M относительно системы координат x’Ey’z’ называют относительными.
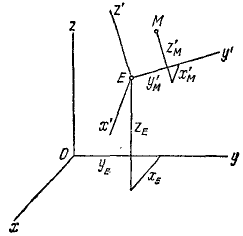
Рис. 115
Итак:
- относительной скоростью точки называют скорость точки по отношению к подвижной системе отсчета1;
- относительным ускорением точки называют ускорение точки по отношению к подвижной системе отсчета.
Мы будем обозначать относительную скорость буквой υ с индексом r (от латинского слова relativus—относительный). Относительное ускорение будем обозначать буквой а с тем же индексом r.
Для обозначения проекций относительных скорости и ускорения будем ставить рядом с индексом r второй индекс. Так, υrx есть проекция относительной скорости на ось Ox; arN—относительное нормальное ускорение.
Переносными скоростью и ускорением точки называют абсолютные скорость и ускорение той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка
Переносные скорость и ускорение
Чтобы определить переносное движение точки М, прекратим мысленно ее относительное движение, закрепив ее относительно координатных осей х’Еу’z’ в том положении, которое она занимает в данное мгновение. Таким образом, мы будем считать, что точка M неизменно скреплена с осями х’Еу’z’ , но оси продолжают двигаться относительно основной системы координат xOyz вместе с точкой М. Тогда скорость и ускорение точки M относительно основных осей координат явятся скоростью и ускорением точки M в ее переносном движении.
Итак:
- переносной скоростью точки M называют абсолютную скорость той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка М;
- переносным ускорением точки M называют абсолютное ускорение той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка М.
Мы будем обозначать переносную скорость точки буквой υ с индексом е (от французского слова entrainer—увлекать за собой), а переносное ускорение—буквой а с тем же индексом. Для обозначения проекций переносных скорости и ускорения на какую-либо ось будем ставить рядом с индексом е индекс, соответствующий оси.
Вектор абсолютной скорости равен сумме векторов относительной и переносной скоростей:
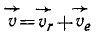
Параллелограмм скоростей
Ознакомившись с понятиями относительной и переносной скоростей точки, найдем зависимость между этими скоростями и абсолютной скоростью, т. е. скоростью точки по отношению к основной системе отсчета.
Пусть подвижная система координат x’Ey’z’ (рис. 116) движется поступательно. В таком случае оси Ex’, Ey’ и Ez’ будут оставаться параллельными своему начальному направлению. Для простоты выкладок пусть эти оси направлены параллельно осям основной системы координат. Тогда во все время движения будем иметь:
Ex’ ||Ox; Ey’||Oy; Ez’||Oz.
Рассмотрим сначала относительное движение точки M и для этого остановим мысленно движение подвижной системы отсчета.
Напишем уравнения движения точки M относительно подвижной системы отсчета:
x’ = x'(t). y’=y'(t), z’ = z'(t). (102)
Продифференцировав по времени и обозначая, как обычно, точкой производные по времени, найдем проекции относительной скорости на подвижные оси координат:
υrx’=x’; υry’=y’; υrz’ = r’.
Так как оси подвижной системы координат параллельны соответствующим осям основной системы, то проекции относительной скорости на оси Ex’, Ey’ и Ez’ соответственно равны проекциям на параллельные им оси Ox, Oy и Oz основной системы отсчета:
υrx=x’; υry = y’; υrz=z’.
Зная проекции относительной скорости, легко найдем по формулам (64) и (62) величину и направление полной относительной скорости.
Чтобы определить переносное движение, мысленно остановим движение точки относительно подвижной системы координат, но предоставим самой подвижной системе x’Ey’z’ продолжать движение.
Напишем по (77) уравнения переносного поступательного движения:
xЕ=x (t); yЕ = y(t), zЕ=z(t).
Продифференцировав равенства (77), получим проекции переносной скорости точки М, которые при поступательном движении системы равны проекциям скорости точки Е:
υex =xE; υey = yE, υez = zE.
Величину и направление вектора полной переносной скорости точки M легко найти по формулам (64) и (62).
Для определения абсолютной скорости точки M найдем сначала ее координаты х, у и г. Применив формулу преобразования начала координатных осей при сохранении направления осей, получим
х-=х’ + хE, y = y’ + yE, z = z, + zE.
Точка M находится в составном движении, следовательно, х, у и г изменяются с течением времени, причем первые члены правых частей этих равенств изменяются согласно (102), а вторые—согласно (77). Продифференцировав по времени, получим проекции абсолютной скорости точки М:
υx = x’+’xE, υy=y’ + yE, υz = z,+ zE
или
υx =υrχ+υeχ, υy =υry+ υey, υz = υrz +υez. (103)
Эти равенства показывают, что проекция абсолютной скорости на какую-либо ось равна сумме проекций относительной и переносной скоростей на ту же ось. Следовательно, вектор абсолютной скорости точки равен сумме векторов относительной скорости и переносной скорости той же точки:
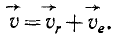 (103‘ )
(103‘ )
Поэтому доказанную теорему называют теоремой параллелограмма скоростей.
Равенства (103) и (103′) выражают связь между тремя скоростями (абсолютной, относительной и переносной) одной и той же точки и позволяют определить любую из этих скоростей, если известны две другие,Они доказаны в предположении, что переносное движение поступательное, но справедливы при всяком переносном движении, как это будет показано в § 31.
Из равенств (103) непосредственно получаем:
- проекция относительной скорости точки на какую-либо ось равна разности проекций абсолютной и переносной скоростей той же точки на ту же ось;
- проекция переносной скорости точки на какую-либо ось равна разности проекций абсолютной и относительной скоростей той же точки на ту же ось.
Из векторного равенства (103) получаем
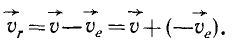
Отсюда вытекает следующее правило: чтобы найти относительную скорость точки, надо сложить вектор абсолютной скорости точки с вектором, равным по модулю, но обратным по направлению вектору ее переносной скорости. Аналогично, чтобы найти переносную скорость точки, надо сложить вектор абсолютной скорости точки с вектором, равным по модулю, но обратным по направлению вектору ее относительной скорости.
Пример №3
Вертикально падают дождевые капли со скоростью 2 м/сек. Пешеход идет справа налево со скоростью 1,5 м/сек. Найти скорость дождя по отношению к пешеходу (рис. 117, а).
Решение. В данной задаче за основную систему отсчета примем Землю. Подвижная система отсчета связана с пешеходом. Вертикальная скорость дождя является абсолютной скоростью (υ = 2 м/сек); переносной скоростью υe является скорость подвижной системы отсчета, т. е. скорость человека, направленная влево и равная 1,5 м/сек. Чтобы найти вектор относительной скорости, сложим вектор абсолютной скорости (рис. 117,6) с вектором, который по величине равен переносной скорости, а по направлению противоположен ей, т. е. направлен слева направо:
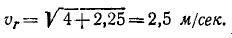
Вектор относительной скорости составляет с вертикалью угол а, тангенс которого равен
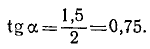
Ответ. υr = 2,5 м/сек, α = 37°.
Пример №4
Корабль плывет на юг со скоростью 42,3 км/ч. Второй корабль идет курсом на юго-восток со скоростью 30 км/ч. Найти величину и направление скорости второго корабля, определяемую наблюдателем, находящимся на палубе первого корабля. При вычислении принять 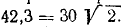 .
.
Решение. Задача аналогична предыдущей, но решать ее будем не в векторной, а в координатной форме, для чего перепишем (103) в следующем виде:
υrx=υx – υex, υry = υy– υey∙
Построим основную систему координат, связанную с Землей, направив ось Ox на юг, а ось Оу— на восток, (рис. 118). Подвижную систему отсчета свяжем с первым кораблем, так как относительно первого корабля надо определить скорость второго. Проекции абсолютной скорости второго корабля на оси основной системы таковы:
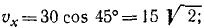
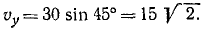
Переносным движением мы называем движение подвижной системы отсчета по отношению к основной. Поэтому в данной задаче переносной скоростью является скорость первого корабля. Ее проекции следующие:
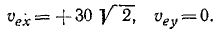
Подставляя эти значения в написанные выше уравнения, найдем проекции относительной скорости:
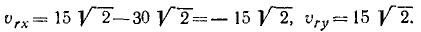
По проекциям находим модуль:
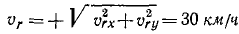
и направляющие косинусы относительной скорости:
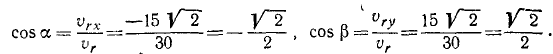
Следовательно, относительная скорость второго корабля составляет углы по 45о C положительным направлением оси Oy и с отрицательным направлением оси Ох, т. е. направлена на северо-восток.
Ответ, υr = 30 км/ч н направлена на северо-восток.
Пример №5
Ширина АВ реки (рис. 119,а) равна 900 м, и берега ее параллельны. Моторная лодка, выйдя из пункта В, держала курс перпендикулярно берегам и достигла противоположного берега через 5 мин, но не в пункте А, находящемся против В, а в пункте С, лежащем на 300 м ниже по течению. Во втором рейсе та же моторная лодка, выйдя из того же пункта В, взяла курс под углом О к BA (начальное направление на пункт D, лежащий на 300 м выше пункта А по течению) и сохраняла свое направление (угол δ), но подошла к правому берегу в пункте Е, лежащем ниже А.
Считая скорость лодки относительно воды постоянной и пренебрегая изменением течения воды у берегов, определить расстояние AE, скорость течения, скорость лодки относительно воды и скорости υ1 и υ2 лодки относительно беретов в обоих рейсах.
Решение. Возьмем начало основной системы координат в точке В, направив ось абсцисс перпендикулярно к берегу по BA, а ось ординат — вниз по течению реки (для решения задачи пользуемся формулами 103). Скорость лодки относительно этой системы является абсолютной. Подвижная система координат движется поступательно вместе с водой и скорость течения реки является переносной скоростью лодки.
Тогда, имея в виду, что АC = 300 м = DA, для первого рейса (рис. 119,6)
υ1 cos δ = υr, υ1 sin δ = υe
и для второго рейса (рис. 119, в)
υ2 cos δ’ =υr cos δ, υ2 sin δ, =υe—vr sin δ.
В первом рейсе лодка держала курс перпендикулярно берегам и в относительном движении проплыла 900 я за 5 мин = 300 сек. Следовательно, υr=3 м/сек.
За то же время ее снесло течением на 300 м, а потому υe=l м/сек.
Подставляя эти значения в уравнения, составленные для первого рейса, и деля второе из этих уравнений на первое, найдем
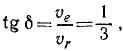 откуда
откуда 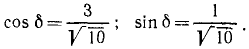
Из тех же уравнений найдем скорость лодки относительно берегов (т. е. абсолютную скорость) в первом рейсе:
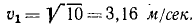
Величина относительной скорости лодки, определенная по ‘данным первого рейса, не изменится и во втором, так как по условию задачи скорость лодки относительно воды постоянна. Также не изменится и переносная скорость лодки — скорость течения реки. Подставляя найденные значения в уравнения, составленные для второго рейса, получим
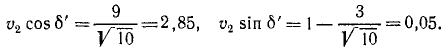
Из этих уравнении найдем: υ2 = 2,85 м/сек и sin δ’ = 0,018.
Умножая АB = 900 м на tg δ’, найдем AE.
Ответ. υe=l м/сек-, υr=3 м/сек-, υ1 = 3,16 м/сек;
v2 = 2,85 м/сек, АЕ=16 м.
Если переносное движение поступательное, то вектор абсолютного ускорения точки равен сумме векторов ее относительного и переносного ускорений
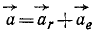
Параллелограмм ускорений
В отличие от теоремы параллелограмма скоростей, применимой при всяком переносном движении, аналогичная теорема параллелограмма ускорений справедлива только в том случае, если переносное движение поступательное.
Пусть точка совершает составное движение, причем подвижная система отсчета x’Ey’z’ движется поступательно по отношению к основной системе хОуz. Пусть соответствующие оси обеих координатных систем параллельны друг другу, это упростит доказательство.
Проекции относительной скорости точки нами уже определены. Продифференцировав эти равенства по времени, найдем проекции относительного ускорения точки:
arx = χ’; ary=y,; arz=z’.
Величину и направление полного относительного ускорения можно определить по формулам (66) и (67).
Продифференцировав по времени равенства (78), найдем проекции ускорения точки в переносном поступательном движении:
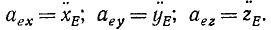
Величину и направление полного переносного ускорения можно определить по формулам (66) и (67), применимым для всякого ускорения точки, независимо от того, является это ускорение абсолютным, относительным или переносным.
Чтобы определить проекции абсолютного ускорения точки (в рассматриваемом случае переносного поступательного движения), надо продифференцировать по времени равенства (103). Получим
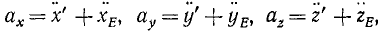
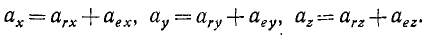 (104)
(104)
Из этих равенств видно, что если переносное движение поступательное, то проекция абсолютного ускорения точки на ось состоит из суммы проекций на ту же ось относительного и переносного ускорений точки. Следовательно, вектор абсолютного ускорения точки в этом случае равен геометрической сумме двух векторов—относительного и переносного ускорений:
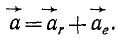 (104′)
(104′)
В этом заключается теорема параллелограмма ускорений.
Равенства (104) и (104′) выражают связь между абсолютным, относительным и переносным ускорениями точки в случае, если переносное движение поступательное, и позволяют определить какое-либо одно из этих ускорений по двум другим.
Если относительное и переносное движения заданы в естественной форме, то для определения ускорений приходится сначала определять их нормальную и касательную составляющие. Так, для определения относительного ускорения надо определить относительное касательное и относительное нормальное ускорения, а уж потом по формулам (75) и (76)—полное относительное ускорение. Аналогично для определения переносного ускорения определяют переносные касательное и нормальное ускорения, а затем полное переносное ускорение. Для получения полного абсолютного ускорения нужно взять геометрическую сумму полного относительного и полного переносного ускорений, которые составляют между собой, вообще говоря, угол, отличный от прямого.
Приводим схему разложения полного абсолютного ускорения точки для случая переносного поступательного движения. При решении задач на параллелограмм ускорений бывает полезно написать эту схему и заполнять ее справа налево:
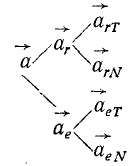
Часто определяют абсолютное ускорение по его проекциям ах, ay, az на оси основной системы координат и, получив проекции результирующего вектора 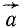 как алгебраические суммы проекций составляющих
как алгебраические суммы проекций составляющих 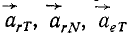 и
и 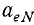 , на те же оси:
, на те же оси:
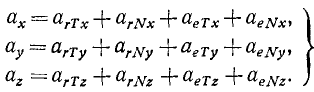 (106)
(106)
Эти равенства являются лишь некоторым видоизменением равенств (104).
Если переносное движение не поступательное, то абсолютное ускорение точки состоит из суммы трех векторов: относительного ускорения, переносного ускорения и ускорения Кориолиса. Доказательство теоремы Кориолиса дано в § 31.
Пример №6
Кривошипио-кулнсный механизм приводного молота (рис. 120, а) состоит из прямолинейной поступательно движущейся кулисы АВ, в прорези которой скользит звено C (камень), соединенный шарнирно с кривошипом ОС длины e, вращающимся с постоянной угловой скоростью ω. Найти скорость и ускорение кулисы как функции угла поворота кривошипа.
Решение. Будем рассматривать движение камня C как составное, состоящее из относительного движения по прорези кулисы и переносного движения вместе с кулисой. Для решения воспользуемся формулами (103) и (104). Примем неподвижный шарнир О за начало основной системы координат, направив ось Ox вправо и ось Oy вверх (рис. 120,6). Подвижную систему координат неизменно соединим с кулисой, взяв начало в точке E и направив ось Ex’ по прорези вправо, a Ey’- вверх. Движение подвижной системы координат, как и движение кулисы, поступательное. Ось Ex’ передвигается к неподвижной оси Ох, а ось Ey’ скользит по оси Оу.
Абсолютное движение камня есть круговое поступательное движение по отношению к основной системе координат. Для определения абсолютных скорости и ускорения обратим внимание на то, что точка C (шарнир) принадлежит не только камню, но и кривошипу, а потому абсолютная скорость точки C равна ωr. (см. рис. 120, б), а ее проекции:
υx = ωr cos ωt и υy= ωr sin ωt.
Абсолютное ускорение точки C равно ω2r, а его проекции (рис. 120, в):
ах = — ω2r sin ωt и ay = ω2r cos ωt.
Эти равенства можно было бы получить, продифференцировав предыдущие.
Относительное движение камня — это возвратно-поступательное движение по прорези вправо и влево. Такое движение камня мы видели бы, если бы сами двигались вместе с кулисой, не замечая ее движения. Камень движется по горизонтальной оси Ex’, а потому
υrx= ± υr, υry = 0.
Проекции относительного ускорения:
αrx=±ar, αry = 0.
Переносное движение камня (движение подвижной системы отсчета относительно основной) —возвратно-поступательное движение кулисы вверх и вниз. Поэтому проекции переносных скорости и ускорения на вертикальную ось Oy равны модулям скорости и ускорения со знаком «-(-» или «—», а на горизонтальную ось Ох—равны нулю. Имеем
υex = 0, υey= ± υe и αex = 0, αey=± αe.
Из трех движений камня нас интересует переносное движение (движение кулисы). Определив проекции переносной скорости
υex = υx – υrx , υey= υy – υry
и подставив найденные значения, получим переносную скорость из уравнений
0 = ωr cos ωt — υr, υe = ωr sin ωt.
Таким образом, переносная скорость камня (скорость кулисы) определена.
Для определения переносного ускорения мы могли бы продифференцировать по времени выражение, полученное для переносной скорости (так как переносное движение прямолинейно-поступательное). Но мы применим более общий метод — определим из (104) проекции переносного ускорения:
αex = ax—arx, aey=ay – ary
подставим в эти уравнения найденные нами значения проекций переносного и абсолютного ускорений камня:
0 = — ω2r sin ωt-ar, ae = ω2r cos ωt.
Таким образом, переносное ускорение ае камня равно ω2r cos ωt. Оно же является ускорением кулисы.
Ответ. υ = ωr sιnωt; a = ω2r cos ωt.
Теорема сложения ускорений точки при переносном вращательном движении (теорема Кориолиса)
При составном движении точки в случае непоступательиого переносного движения возникает добавочное ускорение, называемое ускорением Кориолиса:
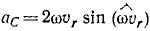
Величина ускорения Кориолиса
Теорема параллелограмма ускорений пригодна только в частном случае, если подвижная система отсчета движется поступательно. Если же переносное движение не поступательное, то у абсолютного ускорения появляется еще одна составляющая, называемая ускорением Кориолиса, или поворотным ускорением. Выведем формулы, позволяющие определить абсолютное ускорение при всяком составном движении точки.
Пусть точка M (рис. 121) движется относительно подвижной системы x’0y’z’ и это движение определяется какими-либо уравнениями
x’=x'(t), y’=y'(t), z’ = z’ (t).
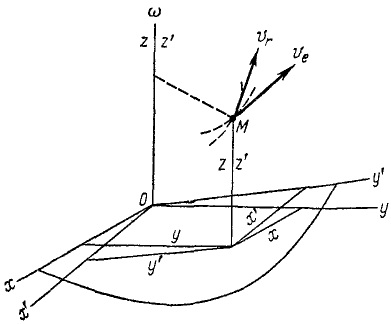
Рис. 121
Пусть подвижная система отсчета вращается вокруг оси Oz основной системы согласно уравнению T==T (О-
Сохраним и в этом параграфе расположение осей координат (см. рис. 101, стр. 165), при котором оси Oz’ и Oz подвижной и неподвижной систем совпадают между собой и с осью вращения, а плоскость х’Оу’ находится в плоскости хОу. Тогда координаты точки M в основной системе определятся соотношениями
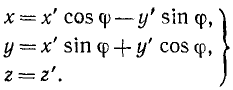 (107)
(107)
Эти равенства (107) отличаются от уже известных нам равенств (88) тем, что здесь координаты х’, у’ и z’ переменны, тогда как в равенствах (88) они были постоянны.
Если мы мысленно остановим точку M в ее относительном движении, т. е. будем считать ее координаты х’, у’ и z’ постоянными, но сохраним переносное вращение, то, дифференцируя равенства (88) по времени, найдем знакомые нам выражения (89) проекций вращательной скорости, которая в данном случае явится переносной скоростью точки М:
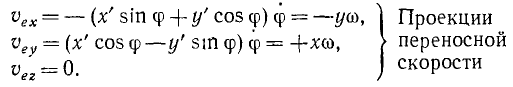
Дифференцируя вторично, найдем проекции переносного ускорения, которые выражаются также известными нам формулами (95):
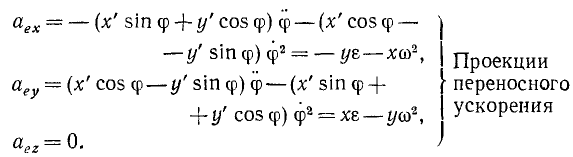
Чтобы определить относительное движение, мысленно остановим переносное, т. е. будем считать 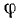 постоянной, a’, x’, у’ и z’ — переменными. Дифференцируя при таких условиях (107) по времени, определим проекции относительной скорости:
постоянной, a’, x’, у’ и z’ — переменными. Дифференцируя при таких условиях (107) по времени, определим проекции относительной скорости:
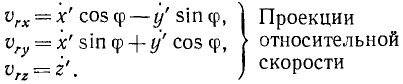
Заметим попутно, что, возводя каждое из этих равенств в квадрат, складывая и извлекая квадратный корень, мы определили бы величину относительной скорости (рис. 122). Если же мы возведем в квадрат и сложим лишь два первых равенства, то, извлекая корень, мы получим, очевидно, величину проекции относительной скорости на плоскость хОу:
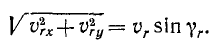
Напомним, что вектор угловой скорости  направлен по оси вращения, а потому угол γr есть угол между векторами относительной и угловой скоростей, и последнее равенство можно записать так:
направлен по оси вращения, а потому угол γr есть угол между векторами относительной и угловой скоростей, и последнее равенство можно записать так:
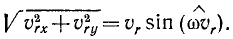
Это соотношение скоро нам понадобится.
Чтобы получить проекции относительного ускорения, надо продифференцировать по времени выражения, полученные для проекций относительной скорости, по-прежнему считая φ постоянной. Имеем
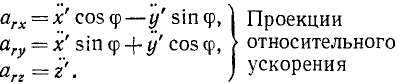
Чтобы определить проекции абсолютной скорости точки М, надо продифференцировать уравнения (107) по времени, считая все величины переменными. Имеем
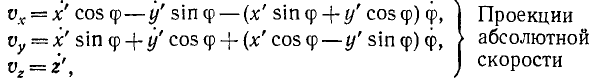
или
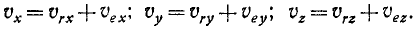 (103)
(103)
Мы получили теорему параллелограмма скоростей, которая, следовательно, остается в силе и при вращательном переносном движении.
Чтобы определить проекции абсолютного ускорения, возьмем вторые производные, опять-таки считая все величины переменными. Имеем:
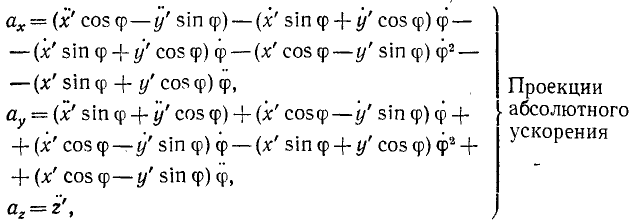
или
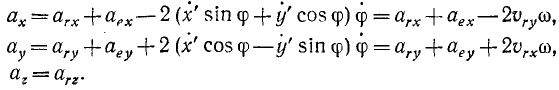
Таким образом, в выражениях проекций абсолютного ускорения, вдобавок к проекциям относительного и переносного ускорений, появляется еще одно слагаемое, выражающее проекции добавочного ускорения ac:
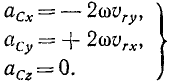 (108)
(108)
Это добавочное ускорение называют ускорением Кориолиса.
Определим величину ускорения Кориолиса:
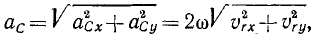
или, заменив корень полученным выше значением, находим окончательно
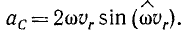 (109)
(109)
Мы вывели формулу (109) в предположении, что переносное движение вращательное. Она остается без изменений и при всяком ином непоступательном переносном движении.
Итак, если переносное движение не поступательное, то абсолютное ускорение точки равно геометрической сумме трех составляющих: относительного ускорения, переносного ускорения и ускорения Кориолиса:
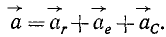 (110)
(110)
В случае, если переносное движение непоступательное, необходимо дополнить ускорением Кориолиса и схему (105), которая принимает следующий вид:
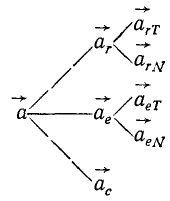 (110/)
(110/)
Пользоваться этой схемой при решении задач надо так же, как и схемой (105), заполняя ее справа и геометрически складывая составляющие.
Ускорение Кориолиса существует только при составном движении, если переносное движение непоступательное
При каком движении бывает ускорение Кориолиса
В выражение (109) ускорения Кориолиса входят множителями относительная скорость точки, угловая скорость подвижной системы отсчета и синус угла между векторами этих скоростей. Но относительная скорость бывает только при составном движении. Поэтому и ускорение Кориолиса может быть только при составном движении. Если нет относительной скорости точки, т. е. если υr = 0, то не может быть и ускорения Кориолиса. Однако ускорение Кориолиса бывает не при всяком составном движении точки. Так, если переносное движение поступательное и ω = 0, то нет и ускорения Кориолиса. Из формулы (109) видно, что и в составном движении точки, и при переносном вращательном движении ускорение Кориолиса равно нулю, если относительная скорость параллельна оси вращения. Так, например, корабль, плывущий по меридиану, имеет ускорение Кориолиса, если рассматривать его движение как составное из относительного движения корабля и переносного движения Земли. Это ускорение равно удвоенному произведению скорости корабля на угловую скорость Земли и на синус географической широты (рис. 123) и равнялось нулю в то время, когда корабль пересекал экватор и его относительная скорость была параллельна вектору угловой скорости Земли.
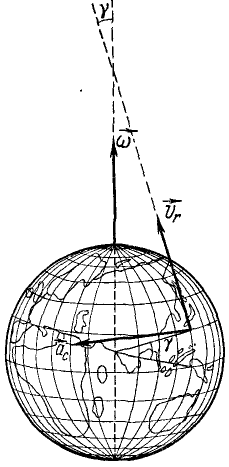
Рис. 123
Физическая причина ускорения Кориолиса заключается в изменении вектора переносной скорости от относительного движения и вектора относительной скорости от переносного движения
Физическая причина ускорения Кориолиса
Постараемся уяснить физические причины, вызывающие ускорение Кориолиса, для чего представим себе два прямолинейных отрезка O1A1 и O2A2 (рис. 124), рис. 123 по которым движутся точки B1 и B2. Штрихами отмечены положения этих отрезков и точек через промежуток времени Δ t. Первый из отрезков движется поступательно, второй вращается вокруг O2.
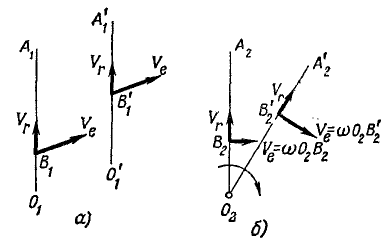
Рис. 124
Существуют две физические причины ускорения Кориолиса:
1. Переносная скорость точки B1 не зависит от положения ее на отрезке O1A1, так как, по свойству поступательного движения, скорости всех точек прямой O1X1 между собой равны. Напротив, величина переносной скорости точки B2 равна ω.O2B2 и всецело зависит от ее положения. Переносная скорость точки B2 меняется от ее относительного движения. Чем быстрее движется точка B2 по прямой O2A2 и чем быстрее вращается эта прямая, тем значительнее изменяется переносная скорость точки B2. Таким образом, изменение скорости точки в данное мгновение (т. е. ускорение точки), вызванное указанной причиной, пропорционально величине агносительной и угловой скоростей. В этом заключается один из факторов, порождающих ускорение Кориолиса.
2. Направление относительной скорости точки B1 не меняется, так как, по свойству поступательного движения, прямая O1A1 передвигается параллельно самой себе. Напротив, направление относительной скорости точки B2 непрерывно изменяется по мере вращения O2А2. Даже при прямолинейном относительном движении направление относительной скорости изменяется (вследствие переносного вращения). Изменение вектора скорости точки в данное мгновение (ускорение), вызванное этой причиной, тоже пропорционально величине относительной и угловой скоростей, В этом заключается другой фактор, порождающий ускорение Кориолиса. Ускорение Кориолиса как бы поворачивает вектор относительной скорости в направлении переносного вращения. По этой причине его иногда называют поворотным ускорением.
Вектор ускорения Кориолиса перпендикулярен векторам угловой и относительной скоростей
Направление ускорения Кориолиса
При выводе формулы ускорения Кориолиса мы убедились, что проекция этого ускорения на Oz равна нулю. Отсюда следует, что вектор ускорения Кориолиса лежит в плоскости, перпендикулярной к оси вращения, или, иными словами, к вектору угловой скорости, который направлен по оси вращения Oz.
Уточним теперь направление ускорения Кориолиса в плоскости, перпендикулярной к осп вращения, и обозначим углы, составляемые им с осью Ox и Оу, через αc и βc. Направляющими косинусами являются:
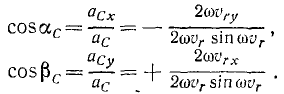
Углы, составляемые относительной скоростью точки с теми же осями, обозначим через ar и βr:
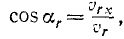
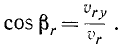
Сравнивая направляющие косинусы ускорения Кориолиса с направляющими косинусами относительной скорости, находим, что удовлетворяется известное из аналитической геометрии условие перпендикулярности двух направлений—сумма произведений соответствующих направляющих косинусов равна нулю:
cos ac cos ar + cos βc cos βr = 0,
следовательно, ускорение Кориолиса перпендикулярно не только к угловой, но и к относительной скорости точки М.
Отсюда вытекает следующее правило: для определения направления ускорения Кориолиса надо спроецировать вектор относительной скорости на плоскость, перпендикулярную Oz (оси вращения), и затем повернуть эту проекцию вокруг оси вращения на 90° в сторону переносного вращения. Следовательно, если переносное вращение происходит в положительном направлении, то проекцию υrxy относительной скорости надо повернуть на 90° против хода стрелки часов, а если переносное вращение происходит в отрицательном направлении, то по ходу стрелки. Это определяется самой сущностью поворотного ускорения, поворачивающего вектор относительной скорости в направлении переносного вращения. К тому же результату мы пришли бы, сравнивая знаки направляющих косинусов ускорения Кориолиса и относительной скорости.
Таким образом, ускорение Кориолиса по величине и направлению можно выразить удвоенным векторным произведением угловой скорости и относительной скорости:
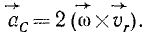 (109/)
(109/)
Если относительное движение точки происходит в плоскости, перпендикулярной оси переносного вращения, то угол между векторами угловой и относительной скоростей равен 90°, его синус равен единице и выражение ускорения Кориолиса упрощается:
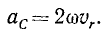 (109//)
(109//)
В этом частном, но очень распространенном в технике случае для определения направления ускорения Кориолиса не нужно проецировать вектор относительной скорости точки, а достаточно повернуть его на 90° в плоскости движения точки в сторону переносного вращения. Поясним это следующей задачей.
Пример №7
Стержень OA вращается вокруг оси, перпендикулярной к плоскости чертежа (рис. 125) в точке О. Вдоль стержня движется ползун В. Указать направление ускорения Кориолиса.
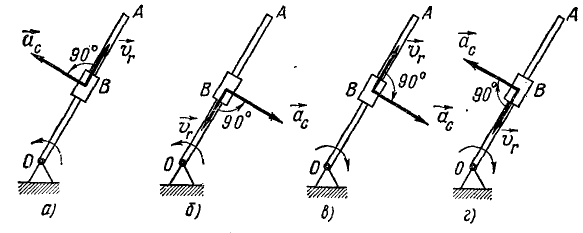
Рис. 125
Решение. Ускорение Кориолиса всегда перпендикулярно к угловой скорости к оси вращения и к относительной скорости. Следовательно, ускорение Кориолиса лежит в плоскости чертежа и перпендикулярно к стержню. Четыре возможных случая изображены на рис. 125, а, б, в, г.
Пример №8
Прямая трубка (рис. 126) равномерно вращается с угловой скоростью ω = π рад/сек вокруг осн Oz, перпендикулярной к плоскости чертежа в точке О. Шарик M совершает гармонические колебания вдоль трубки по закону x’ = ОM = A sin πt. Определить ускорение шарика при t=4 сек.
Решение. Будем рассматривать движение шарика как составное, состоящее из движения относительно трубки и движения вместе с трубкой (рис. 126, а). Для решения задачи воспользуемся схемой (110′) (см. стр. 206).
Чтобы определить относительное движение, мысленно остановим переносное вращение трубки. Уравнение относительного движения шарика есть
x’=A sin πt.
Относительная скорость
υr =x’= Aπ2 cos πt.
В относительном движении шарик имеет касательное ускорение
arT =x’=- Aπ2 sin πt.
Относительное движение в данном случае прямолинейное, поэтому относительное нормальное ускорение αrN=0.
Переносное движение обусловлено вращением трубки. Мысленно остановим шарик, предоставив трубке вращаться. Напишем уравнение равномерного вращения трубки, положив φo = 0:
φ=πt.
Переносной скоростью шарика является вращательная скорость той точки среды (трубки), в которой в это мгновение находится шарик:
υe = ωr = Aπ sin πt,
причем в этом выражении время t соответствует тому мгновению, в которое мысленно остановлен шарик, а потому t здесь нельзя рассматривать как переменную величину.
Переносное вращение равномерное, и переносное касательное ускорение равно нулю:
aeT = εr = 0.
Переносное центростремительное ускорение
aeN = ω2r — Aπ2 sin πt,
где t имеет заданное значение, соответствующее данному мгновению, в которое мысленно остановлено относительное движение.
Кроме этих составляющих абсолютного ускорения, имеется ускорение Кориолиса, так как переносное движение вращательное:
ас = 2ωυr = 2Aπ2 cos πt.
Эти составляющие абсолютного ускорения вносим в схему (110′):
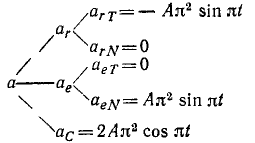
В мгновение t = 4 сек имеем:
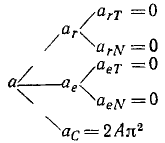
Таким образом, абсолютное ускорение в это мгновение состоит из ускорения Кориолиса a = ac = 2Aπ2.
При t = 4 сек точка M совпадала с точкой О (x’ = A sin 4π = 0) и имела относительную скорость + Аπ, направленную в положительном направлении Ox’. Чтобы определить направление ускорения Кориолиса, надо повернуть вектор относительной скорости на 90° в сторону вращения трубки, т. е. против хода часовой стрелки.
При t = 4 сек угол поворота трубки φ = 4π и ось Ox’ совпадала с осью Ох. Следовательно, в это мгновение ускорение Кориолиса направлено по положительной оси Оу.
Если мы не станем рассматривать движение шарика как составное, а изучим его непосредственно по отношению к основной системе отсчета, то получим, разумеется, тот же результат.
Составим уравнения движения шарика в основной системе координат (рис. 126, б):
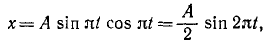
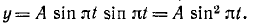
Дифференцируя эти уравнения по времени, найдем проекции скорости:
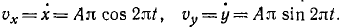
Дифференцируя по времени второй раз, найдем проекции ускорения:
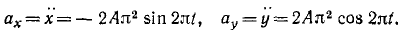
При t = 4 сек
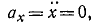
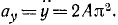
Мы получили те же значения ускорения точки, не пользуясь ускорением Кориолиса. Из этого примера видно, что ускорение Кориолиса бывает лишь при составном движении точки.
Для определения траектории шарика в основной системе отсчета исключим время из уравнений движения. Из второго уравнения находим 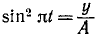 , подставляем в первое уравнение и возводим в квадрат (рис. 126, в):
, подставляем в первое уравнение и возводим в квадрат (рис. 126, в):
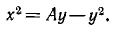
Это уравнение окружности с центром в точке x = 0, 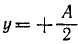 . Чтобы убедиться, достаточно перенести в эту точку начало основной системы , положив
. Чтобы убедиться, достаточно перенести в эту точку начало основной системы , положив 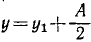 , тогда уравнение траектории примет вид:
, тогда уравнение траектории примет вид:
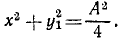
Найдем уравнение движения шарика M по этой окружности:
dx = Аπ cos 2πt dt; dy = Аπ sin 2πt dt;
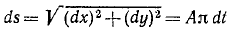
и, интегрируя,
s = Аπt + С = Аπt .
Следовательно, шарик движется по своей траектории равномерно со скоростью υ= Аπ; при t = 4 сек он находится в наинизшей точке окружности, а нормальное ускорение 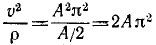 направлено вертикально вверх.
направлено вертикально вверх.
Резюмируя, убеждаемся, что движение шарика (как и движение всякого тела) можно представить различными способами и ускорение шарика в заданное мгновение (t = 4 сек) можно выразить различными формулами.
Можно представить его как составное, состоящее из колебаний шарика вдоль трубки и одновременного вращения трубки. Тогда ускорение 2Аπt2 шарика в заданное мгновение является ускорением Кориолиса.
Можно представить то же движение шарика уравнениями в декартовых координатах, а ускорение 2Аπt2— проекциями на оси координат.
Можно, наконец, это движение шарика определить как равномерное движение со скоростью υ = Аπ по окружности радиуса 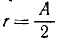 и ускорение 2Аπt2 представить как нормальное ускорение
и ускорение 2Аπt2 представить как нормальное ускорение 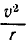 .
.
Различные способы лишь выражают объективно существующее движение и позволяют определить его характеристики.
Ответ. a = 2Аπt2.
Задача №1
Окружность радиуса г равномерно вращается по ходу стрелки часов с угловой скоростью ω вокруг оси, перпендикулярной к ней в одной из ее точек C (рис. 127, а). По окружности движется точка M со скоростью υr = ωr, обходя окружность против вращения часовой стрелки. Определить ускорение точки М.
Решение. Движение точки будем рассматривать как составное, состоящее из относительного равномерного движения по окружности и переносного равномерного вращения самой окружности.
Напишем схему (110′) и будем заполнять ее справа (см. стр. 208).
Чтобы определить относительное движение точки М, мысленно остановим вращение окружности. Относительная скорость равна υr = ωr и направлена по касательной к окружности. Относительное касательное ускорение αrT = 0, а относительное нормальное направлено к центру О окружности и равно
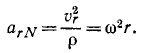
Чтобы определить переносное движение, мысленно закрепим точку M на окружности. Проведем хорду MC (рис. 127, б) и обозначим через δ угол, составляемый ею с диаметром, проходящим через С. Так как окружность вращается равномерно, то αeT = 0 и
αeN = ω2CM = ω22r cos δ
и направлено по хорде MC к точке С.
Величина ускорения Кориолиса в нашем случае равна
ac = 2ωυr-2ω2r.
Переносное вращение происходит по ходу стрелки часов, следовательно, для определения направления ускорения Кориолиса повернем вектор относительной скорости на 90° по ходу стрелки часов.
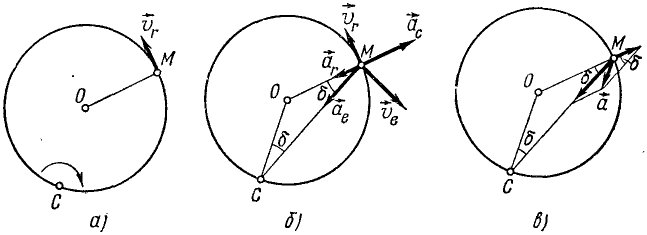
Рис. 127
Скорости и ускорения точки изображены на рис. 127, б, а ускорения записаны по схеме (110′):
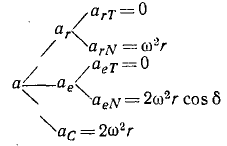
Чтобы определить абсолютное ускорение точки М, надо сложить его составляющие. Сложив ускорение Кориолиса с противоположным ему по направлению нормальным относительным ускорением, найдем, что результирующий вектор этих двух ускорений равен ω2r и направлен в сторону ускорения Кориолиса:
2ω2r-ω2r = ω2r.
Чтобы сложить этот результирующий вектор с вектором переносного ускорения, воспользуемся теоремой косинусов (рис. 127, в). Имеем
a2 = (ω2r)2+ (2ω2r cos δ)2 — 2 (ω2r) (2ω2r cos δ) cos δ = (ω2r)2.
Как видно из чертежа (рис. 127, в), абсолютное ускорение направлено параллельно ОС независимо от угла δ, т. е. независимо от положения точки M на окружности. Иными словами, независимо от положения точки M на окружности вектор ее абсолютного ускорения равен вектору ускорения центра окружности в его движении вокруг оси С.
Ответ. a = ω2r.
Задача №2
В ручке молочного сепаратора по ее длине просверлен цилиндрический канал, закрытый с одной стороны металлической пластинкой (звонком) (рис. 128). В канале помещен металлический шарик. Если вращать ручку с недостаточной скоростью (менее 45 об/мин), то шарик ударится о звонок и даст соответствующий сигнал. Определить ускорение Кориолиса сигнального шарика, если ручка сепаратора наклонена к своей оси вращения под углом 75°, рабочий вращает ручку, делая 45 об/мин, а шарик движется по каналу по закону х’= 220 sin φ + 357e-φ мм.
Решение. Вектор угловой скорости ручки направлен по оси вращения, а относительная скорость шарика —вдоль канала, составляя с ним угол 75°. Ускорение Кориолиса определяем по формуле (105). Угловая скорость 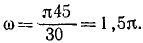 Синус 75° берем из таблиц или подсчитываем как sin (45°+30°) = 0,966.
Синус 75° берем из таблиц или подсчитываем как sin (45°+30°) = 0,966.
Чтобы определить относительную скорость, надо продифференцировать по времени уравнение движения, в котором φ=ωt=1,5πt.
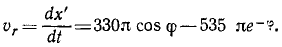
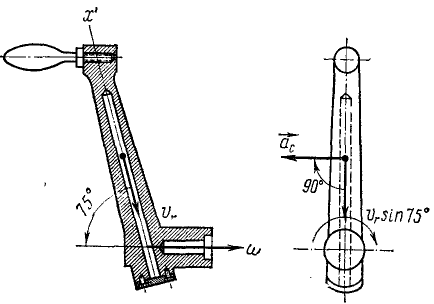
Рис. 128
Таким образом, имеем
αс = 2 • 1, 5π (330π cos φ—535πe – φ) 0,966.
Ответ. Ускорение Кориолиса равно 9420 cos φ—15300e-φ мм/сек2 и направлено перпендикулярно к ручке и к ее оси.
Сложное движение точки и тела
При решении задач, в которых рассматривается сложное движение точки или тела, необходимо уметь правильно расчленить сложное (составное), или так называемое абсолютное движение, на переносное и относительное.
При расчленении сложного движения рекомендуется учитывать следующее. Абсолютное (составное) движение происходит относительно неподвижной системы координат. Обычно эту систему координат связывают с Землей или с неподвижными относительно Земли предметами: зданием, деревом, полотном дороги и т. д.
Переносное движение точки или тела происходит вместе с некоторой материальной средой (телом), внутри или на поверхности которой находится рассматриваемое в задаче тело или рассматриваемая точка. Таким образом, переносное движение — это движение
материальной среды вместе с точкой также относительно неподвижной системы координат.
Относительное движение точки или тела — это перемещение их внутри материальной среды, или по ее поверхности, независящее от движения самой материальной среды.
В тех случаях когда заданы движения двух (или более) тел (точек) относительно неподвижной системы координат и необходимо определить движение одного из этих тел относительно другого, удобно пользоваться теми же приведенными выше соображениями.
Тело, относительно которого требуется рассмотреть движение, мысленно остановим, а неподвижную систему координат заставим двигаться по его закону, но в обратном направлении. Тогда для второго тела это движение станет переносным, а движение второго тела — относительным. После этого очень просто понять, как будет двигаться второе тело по отношению к первому.
Этот последний прием использован при решении задач 177-36 и 184-37 и обычно его используют при рассмотрении планетарных механизмов (см. ниже § 40-9).
Решение всех задач на сложное движение необходимо иллюстрировать рисунком.
Сложение движений точки, когда переносное и относительное движения направлены вдоль одной прямой
При изучении сложного движения точки будем рассматривать только перемещение и скорость.
Если переносное и относительное движения направлены вдоль одной прямой, то:
- перемещение точки в абсолютном движении равно алгебраической сумме перемещений в переносном и относительном движениях;
- скорость точки в абсолютном движении равна алгебраической сумме переносной и относительной скоростей.
Условимся направление переносного перемещения и соответственно направление переносной скорости считать положительными. Тогда относительное перемещение и соответственно относительная скорость будут также положительными, если они направлены в ту же сторону, что и переносное. Если же относительное перемещение (и скорость) имеют направление, противоположное переносному, то будем считать их отрицательными.
Таким образом, при совпадении направлений переносного и относительного движений
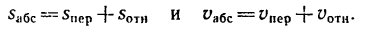
При противоположных друг другу направлениях переносного и относительного движений
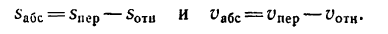
Задача №3
Вниз по течению реки равномерно плывет лодка, приводимая в движение гребным винтом от мотора. Скорость течения реки 4 км/ч, скорость лодки, сообщаемая ей гребным винтом по отношению к воде, составляет 8 км/ч. Определить скорость лодки относительно берегов и расстояние, которое проходит лодка вдоль берегов за 20 мин.
Решение иллюстрировать рисунком, считая берега реки на данном участке прямолинейными и параллельными.
Решение.
1. Лодку принимаем за материальную точку, а водную массу реки —за материальную среду.
Движение лодки относительно берегов или, иначе говоря, движение лодки, наблюдаемое с берега, — это абсолютное движение.
Переносное движение лодки—ее перемещение вместе с рекой; скорость 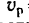 = 4 км/ч, которую сообщает лодке река, — ее переносная скорость.
= 4 км/ч, которую сообщает лодке река, — ее переносная скорость.
Относительное движение— перемещение лодки по поверхности воды, создаваемое гребным винтом; скорость относительного движения 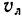 = 8 км/ч.
= 8 км/ч.
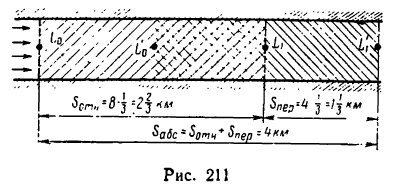
2. Так как в данном случае переносное и относительное движения направлены в одну и ту же сторону, то скорость лодки относительно берегов (абсолютная скорость)
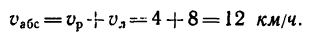
3. За время 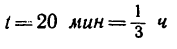 лодка вдоль берегов проходит расстояние
лодка вдоль берегов проходит расстояние
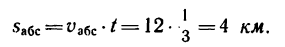
4. Иллюстрируем решение задачи следующим образом (рис. 211).
Изобразим на рисунке тот участок водного пространства, который проходит лодка независимо от того, перемещается этот участок воды или нет. За 20 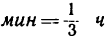 лодка успевает пройти по этому пространству из положения
лодка успевает пройти по этому пространству из положения 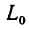 в положение
в положение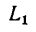 расстояние
расстояние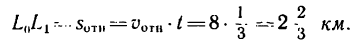
За эти же 20 мин, или
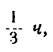 показанное водное пространство
показанное водное пространство
переместится на расстояние
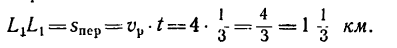
Таким образом, лодка, находившаяся в начале рассматриваемого движения относительно берегов в точке 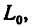 через 20 сек оказывается в точке
через 20 сек оказывается в точке 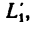 т. е. проходит расстояние
т. е. проходит расстояние
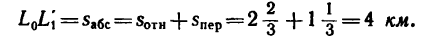
Следовательно, скорость абсолютного движения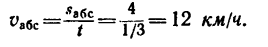
Задача №4
Два автомобиля 1 и 2 движутся параллельно друг другу в одну и ту же сторону со скоростями 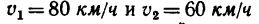 (рис. 212, а). С какой скоростью второй автомобиль двигается относительно первого? Решение.
(рис. 212, а). С какой скоростью второй автомобиль двигается относительно первого? Решение.
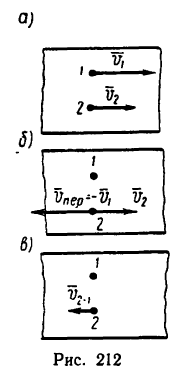
1. Ответ «по соображению» получается мгновенно: 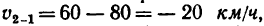 т. е. относительно первого второй автомобиль двигается со скоростью 20 км/ч, но в обратную сторону.
т. е. относительно первого второй автомобиль двигается со скоростью 20 км/ч, но в обратную сторону.
2. Объясним это решение с точки зрения теории сложного движения точки. Условно остановим первый автомобиль. Но тогда, чтобы не изменились условия движения, необходимо мысленно представить, что полотно дороги под вторым автомобилем и вместе с ним получает движение в обратную сторону со скоростью 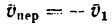 (рис. 212, б).
(рис. 212, б).
Находясь в условном переносном движении со скоростью 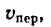 второй автомобиль относительно дороги движется со скоростью
второй автомобиль относительно дороги движется со скоростью 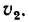
Поэтому результирующая обеих скоростей 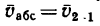 численно равна их разности:
численно равна их разности:
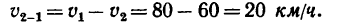
Как видно на рис. 212, а, результирующая направлена в сторону, противоположную скорости 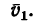
Задача №5
Расстояние s = 90 км между двумя пристанями, расположенными на роке, теплоход проходит без остановки в одном направлении (по течению) за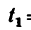 = 3 ч и в обратном направлении (против течения) за
= 3 ч и в обратном направлении (против течения) за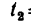 = 5 ч. Определить скорость течения реки и собственную скорость теплохода.
= 5 ч. Определить скорость течения реки и собственную скорость теплохода.
Решение.
1. Теплоход, который принимаем за материальную точку, двигаясь по течению, имеет абсолютную скорость (скорость относительно берегов):
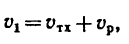
где 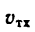 — искомая собственная скорость теплохода (относительная скорость);
— искомая собственная скорость теплохода (относительная скорость);
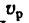 — скорость течения реки (переносная скорость).
— скорость течения реки (переносная скорость).
При движении против течения абсолютная скорость теплохода
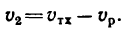
2. Движение теплохода по течению описывается уравнением (рис. 213, а)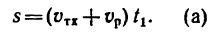
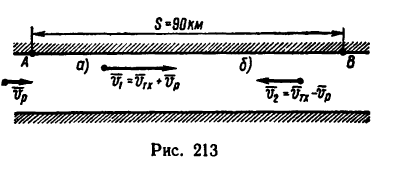
Движение теплохода против течения происходит по уравнению (рис. 213, б)
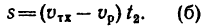
2. Решаем полученную систему уравнения. Из (а) и (б)
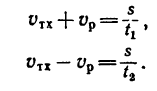
Сложим правые и левые части этих уравнений:
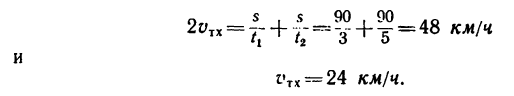
Вычитаем из верхнего равенства нижнее:
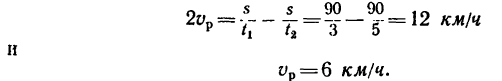
Таким образом, собственная скорость теплохода составляет 24 км/ч и скорость течения реки равна 6 км/ч.
Следующую задачу рекомендуется решить самостоятельно.
Задача №6
Расстояние между двумя пристанями, расположенными на реке, теплоход, двигаясь равномерно без остановки, проходит по течению реки за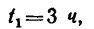 а против течения (двигаясь в обратном направлении) —
а против течения (двигаясь в обратном направлении) —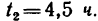 За какое время
За какое время 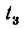 проплывает это же расстояние плот, передвигаемый только течением реки?
проплывает это же расстояние плот, передвигаемый только течением реки?
Задачу надо решить в общем виде, а потом подставить числовые значения.
Ответ.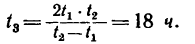
Сложение движений точки, когда переносное и относительное движения направлены под углом друг к другу
Когда переносное и относительное движения направлены под углом друг к другу, то перемещения и скорости складываются геометрически.
Таким образом, абсолютная скорость точки 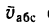 определяется как геометрическая сумма переносной
определяется как геометрическая сумма переносной 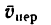 и относительной оог„ скоростей;
и относительной оог„ скоростей;

т. е. либо как диагональ параллелограмма, построенного на переносной и относительной скоростях (рис. 214, а), либо как замыкающий вектор треугольника скоростей (рис. 214, б).
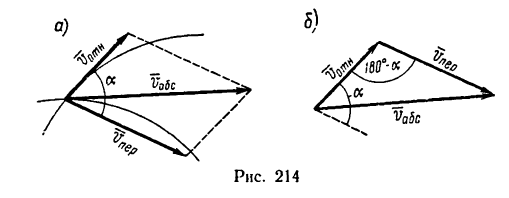
При решении задач на определение скоростей наиболее удобно применять графо-аналитический способ (см. § 3-1 настоящего пособия).
Если применяется правило параллелограмма, то модуль абсолютной скорости определяется по формуле, выведенной из теоремы косинусов
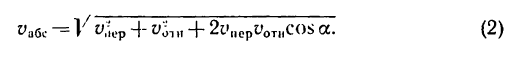
Если применяется правило треугольника, то модуль абсолютной скорости определяется по теореме синусов.
Направление абсолютной скорости по отношению к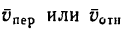 можно найти также при помощи теоремы синусов.
можно найти также при помощи теоремы синусов.
В частном случае, когда параллелограмм скоростей превра шается в прямоугольник или когда треугольник скоростей получается прямоугольным, для решения задачи используются тригонометрические функции и теорема Пифагора (см. ниже задачи 181-37, 182-37, 185-37).
Бели в частном случае 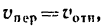 то при геометрическом сложении таких скоростей образуется ромб (рис. 215, а) или равнобедренный треугольник (рис. 215, б), тогда
то при геометрическом сложении таких скоростей образуется ромб (рис. 215, а) или равнобедренный треугольник (рис. 215, б), тогда
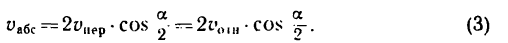
Задача №7
Вертикально падающие капли дождя оставляют на боковых стеклах автомобиля полосы под углом 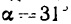 к вертикали. Скорость движения автомобиля 40 км’ч. Определить, с какой скоростью надают капли дождя.
к вертикали. Скорость движения автомобиля 40 км’ч. Определить, с какой скоростью надают капли дождя.
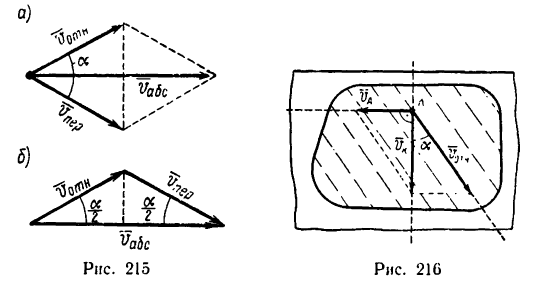
Решение.
1. Изобразим движение капли дождя на рисунке (рис. 216). Капли падают вертикально, следовательно, скорость ик какой-либо капли К относительно Земли является скоростью абсолютного (составного) движения. И эту скорость 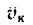 можно представить в виде геометрической суммы горизонтально направленной переносной скорости автомобиля
можно представить в виде геометрической суммы горизонтально направленной переносной скорости автомобиля 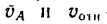 — относительно скорости капли при ее движении по стеклу автомобиля.
— относительно скорости капли при ее движении по стеклу автомобиля.
2. Получившийся параллелограмм скоростей диагональ делит на два прямоугольных треугольника. Рассмотрев любой из этих треугольников, найдем
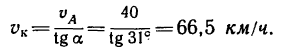
Переводим полученную скорость падения капель в м/сек:
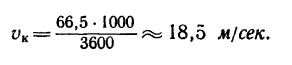
Задача №8
От одного берега реки к другому плывет лодка, держа курс перпендикулярно к берегам. Ширина реки 800 м лодка достигает противоположного берега через 12 мин после начала переправы. За это время лодку сносит вниз по течению на расстояние 600 м. Определить скорость течения реки; собственную скорость лодки: скорость лодки относительно берегов. Скорость течения у берегов и на середине реки считать одинаковой.
Решение.
1. Изобразим на рисунке движение лодки (рис. 217). Представим, что лодка отплывает из точки А на правом берегу. Если бы
не было течения, она достигла бы противоположного берега в точке В; известно, что ширина реки 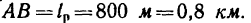 Но лодку сносит вниз по течению (переносное движение) на расстояние
Но лодку сносит вниз по течению (переносное движение) на расстояние 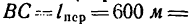 0,6 км и поэтому движение лодки относительно берегов (абсолютное движение) происходит но прямой АС.
0,6 км и поэтому движение лодки относительно берегов (абсолютное движение) происходит но прямой АС.
Обозначим точкой L положение лодки через некоторое время после начала движения. Скорость лодки относительно берегов — абсолютная скорость 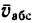 — направлена вдоль прямой АС и складывается из собственной скорости
— направлена вдоль прямой АС и складывается из собственной скорости 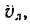 сообщаемой гребным винтом или веслами, и из переносной скорости течения реки
сообщаемой гребным винтом или веслами, и из переносной скорости течения реки 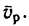
2. Допустим, что нет течения реки, тогда лодка будет перемещаться относительно берегов так же, как и относительно воды, по прямой АВ и ее движение опишется уравнением
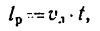
где t — время переправы (t=12 мин =0,2 ч).
Отсюда находим собственную скорость лодки (скорость лодки относительно воды — относительную скорость)
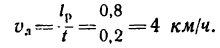
3. Если лодка будет плыть, подчиняясь только течению реки, ее движение опишется уравнением
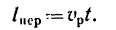
Из этого уравнения найдем скорость течения реки:
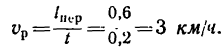
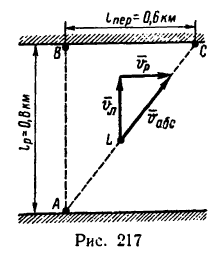
4. Теперь из прямоугольного треугольника скоростей (см. рис. 217) легко найти скорость лодки относительно берегов — абсолютную скорость:
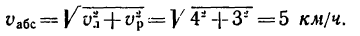
Задача №9
Трассы двух воздушных лайнеров пересекаются над поселком А. Первый лайнер летит точно на север, второй лайнер — на юго-восток. Скорости 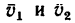 обоих лайнеров численно равны (
обоих лайнеров численно равны ( ). Определить, чему равна и как направлена в этот момент скорость второго лайнера относительно первого.
). Определить, чему равна и как направлена в этот момент скорость второго лайнера относительно первого.
Решение 1—методом «остановки» одного из тел.
1. Обозначим точкой А поселок, над которым” в определенный момент находятся оба лайнера. Покажем страны света: С —север, Ю — юг, В —восток и 3 —запад. Изобразим скорости лайнеров относительно Земли: 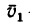 —скорость первого лайнера и
—скорость первого лайнера и 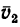 — скорость второго (рис. 218, а).
— скорость второго (рис. 218, а).
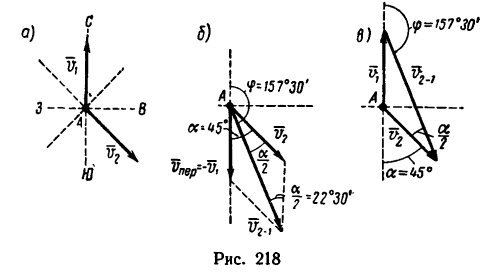
2. Так как нужно определить скорость второго лайнера относительно первого, то мысленно первый лайнер остановим над пунктом А, а воздушной среде вместе со вторым лайнером сообщим скорость 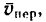 но в обратную сторону по отношению к скорости
но в обратную сторону по отношению к скорости 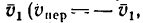 рис. 218, б). Тогда скорость
рис. 218, б). Тогда скорость 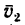 второго лайнера приобретет значение относительной скорости (скорости относительно перемещающейся воздушной среды).
второго лайнера приобретет значение относительной скорости (скорости относительно перемещающейся воздушной среды).
3. Сложив по правилу параллелограмма скорости 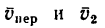 (см. рис. 218, б), получим скорость
(см. рис. 218, б), получим скорость 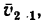 ( изображающую скорость второго лайнера по отношению к первому.
( изображающую скорость второго лайнера по отношению к первому.
4. Так как скорости лайнеров 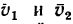 численно равны
численно равны 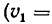
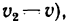 то параллелограмм скоростей на рис. 218, б — ромб и, следовательно [см. формулу (3) в начале этого параграфа], числовое значение
то параллелограмм скоростей на рис. 218, б — ромб и, следовательно [см. формулу (3) в начале этого параграфа], числовое значение 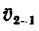 равно:
равно:
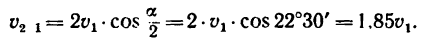
Таким образом, второй лайнер движется относительно первого со скоростью, численно равной и, как видно из рис. 218, б, удаляется от него на юго-юго-запад, т. е. под углом 157°30′ (903 + 45° + 22‘30′) к направлению скорости первого лайнера.
* Когда будет определен этот угол, его нужно сравнить с углом между векторами 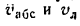 из предыдущей задачи.
из предыдущей задачи.
Решение 2 —методом разности скоростей.
1. Из выражения геометрической суммы скоростей
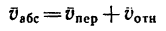
следует, что

2. Для определения скорости второго лайнера относительно первого примем за абсолютную скорость  — скорость первого лайнера и за переносную скорость
— скорость первого лайнера и за переносную скорость 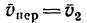 – скорость второго лайнера; тогда искомую относительную скорость
– скорость второго лайнера; тогда искомую относительную скорость 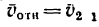 получим как разность (см. рис. 3)
получим как разность (см. рис. 3)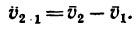
3. Чтобы произвести вычитания векторов, необходимо конец вычитаемого вектора 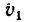 соединить с концом уменьшаемого вектора
соединить с концом уменьшаемого вектора 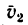 в направлении от первого ко второму искомым вектором
в направлении от первого ко второму искомым вектором 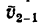 (рис. 218, в).
(рис. 218, в).
4. В результате построения имеем равнобедренный треугольник скоростей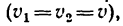 из которого легко найти, что числовое значение
из которого легко найти, что числовое значение
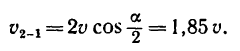
Угол 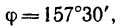 определяющий в данный момент направление вектора
определяющий в данный момент направление вектора 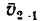 относительно
относительно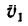 определяется непосредственно по рис. 218, в.
определяется непосредственно по рис. 218, в.
Задача №10
В кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип ОА (расположенный позади кулисы) длиной l= 400 мм вращается с постоянной угловой скоростью 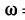 =10 рад/сек. Концом А, соединенным шарнирно с камнем, скользящим в прорези кулисы, кривошип сообщает кулисе ВС возвратно-поступательное движение. Определить скорость кулисы в момент, когда кривошип образует с осью кулисы угол
=10 рад/сек. Концом А, соединенным шарнирно с камнем, скользящим в прорези кулисы, кривошип сообщает кулисе ВС возвратно-поступательное движение. Определить скорость кулисы в момент, когда кривошип образует с осью кулисы угол 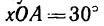 (рис. 219, а).
(рис. 219, а).
Решение.
1. В данном случае движение точки А вместе с кривошипом можно считать сложным, т. е. получающимся в результате сложения:
а) движения точки А вместе с кулисой в ее возвратно-поступательном (переносном) движении вдоль оси х;
б) относительного движения точки А вместе с камнем, движущимся возвратно-поступательно в прорези кулисы в направлении, перпендикулярном к оси х.
2. Абсолютная скорость точки А, модуль которой легко определяется по формуле 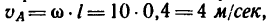 направлена перпендикулярно к кривошипу ОА. Переносная скорость точки А равна поступательной скорости кулисы
направлена перпендикулярно к кривошипу ОА. Переносная скорость точки А равна поступательной скорости кулисы 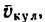 направлена по прямой АО (рис. 219, б). Относительная скорость
направлена по прямой АО (рис. 219, б). Относительная скорость 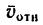 точки А, равная скорости камня в прорези кулисы, направлена по прямой Ас.
точки А, равная скорости камня в прорези кулисы, направлена по прямой Ас.
3. Изобразим скорость 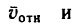
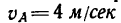 вектором, перпендикулярным к ОА. Разложим ее на составляющие уоти и
вектором, перпендикулярным к ОА. Разложим ее на составляющие уоти и 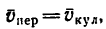 как показано на рис. 219, б. Вектор
как показано на рис. 219, б. Вектор 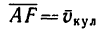 изображает искомую скорость кулисы.
изображает искомую скорость кулисы.
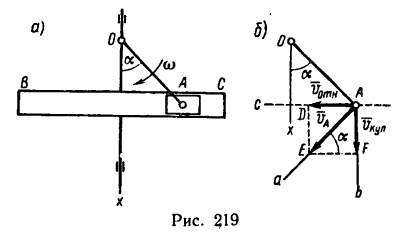
4. 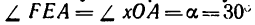 (как углы с взаимно перпендикулярными сторонами) и, следовательно,
(как углы с взаимно перпендикулярными сторонами) и, следовательно,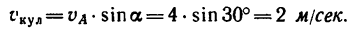
Таким образом, в данный момент кулиса перемещается вниз со скоростью 2 м,сек.
Чтобы лучше проанализировать движение кулисы, необходимо знать, когда кулиса двигается ускоренно, когда замедленно, при каких положениях кривошипа кулиса имеет максимальную скорость и чему равна эта скорость, при каких положениях кривошипа скорость кулисы равна нулю?
Следующие задачи рекомендуется решить самостоятельно.
Задача №11
Кривошип 0С=30 см вращается равномерно с угловой скоростью 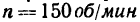 и приводит в возвратно-поступательное движение кулису АВ при помощи ползуна С, передвигающегося в прорези кулисы. Определить скорость
и приводит в возвратно-поступательное движение кулису АВ при помощи ползуна С, передвигающегося в прорези кулисы. Определить скорость 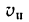 ползуна в прорези кулисы и скорость
ползуна в прорези кулисы и скорость 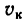 самой кулисы в тот момент, когда кривошип составляет с горизонталью угол а = 35° (рис. 220). Ответ.
самой кулисы в тот момент, когда кривошип составляет с горизонталью угол а = 35° (рис. 220). Ответ. 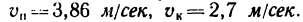
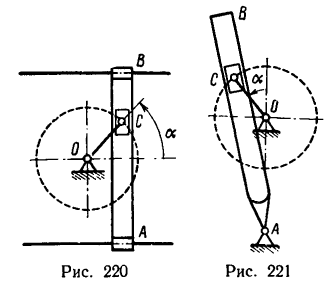
Задача 187-37. Кривошип ОС = 20 см вращается равномерно с угловой скоростью n = 180 об/мин и приводит в движение качающуюся кулису АВ при помощи ползуна С, двигающегося в прорези кулисы. Определить скорость 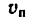 ползуна в прорези кулисы и угловую скорость
ползуна в прорези кулисы и угловую скорость  кулисы в тот момент, когда кривошип составляет с вертикалью угол а=40°. Расстояние /40 = 40 см (рис. 221).
кулисы в тот момент, когда кривошип составляет с вертикалью угол а=40°. Расстояние /40 = 40 см (рис. 221).
Ответ. 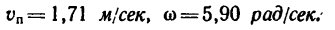
Сложное движение точки в плоскости
постановка задачи. Геометрическая фигура вращается вокруг оси, перпендикулярной ее плоскости по известному закону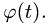 . В канале, расположенном на фигуре, движется точка М по закону
. В канале, расположенном на фигуре, движется точка М по закону 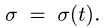 Найти абсолютную скорость и абсолютное ускорение точки в заданный момент времени
Найти абсолютную скорость и абсолютное ускорение точки в заданный момент времени 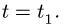
План решения:
Сложное движение точки М представляется в виде суммы относительного и переносного. Характерной особенностью этой задачи является то, что траектории относительного, переносного и абсолютного движения лежат в одной плоскости. Ось z, на которую проектируются векторы переносной угловой скорости и переносного углового ускорения, перпендикулярна этой плоскости и направлена на наблюдателя. Угол поворота считается положительным, если со стороны оси 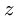 он виден против часовой стрелки.
он виден против часовой стрелки.
Искомые величины получаем из векторных равенств:
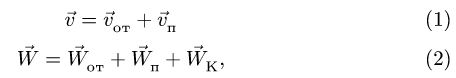
где 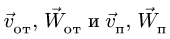 — соответственно относительные и переносные скорости и ускорения:
— соответственно относительные и переносные скорости и ускорения: 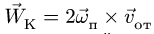 — ускорение Кориолиса .
— ускорение Кориолиса .
1. Вычисляем значение дуговой координаты 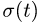 при
при 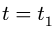 и определяем положение точки в подвижной системе координат.
и определяем положение точки в подвижной системе координат.
2. Дифференцируя 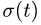 по времени, находим относительную скорость (скорость точки относительно фигуры):
по времени, находим относительную скорость (скорость точки относительно фигуры):
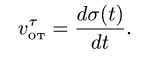
 Кориолис Гаспар Гюстав (1792-1843) французский механик и математик.
Кориолис Гаспар Гюстав (1792-1843) французский механик и математик.
Вектор 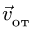 направляем по касательной к относительной траектории в сторону увеличения
направляем по касательной к относительной траектории в сторону увеличения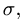 , если
, если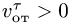 и в обратную сторону в противном случае;
и в обратную сторону в противном случае; 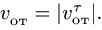
3. Вычисляем радиус траектории переносного движения 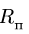 — расстояние от точки М в положении
— расстояние от точки М в положении 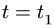 до оси переносного вращения.
до оси переносного вращения.
4. Находим переносную скорость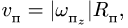 где переносная угловая скорость
где переносная угловая скорость
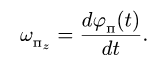
Вектор 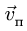 направляем перпендикулярно
направляем перпендикулярно 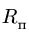 в сторону переносного вращения.
в сторону переносного вращения.
5. Определяем вектор абсолютной скорости, вычисляя компоненты 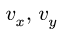 векторной суммы (1) на произвольно выбранные оси, и модуль
векторной суммы (1) на произвольно выбранные оси, и модуль
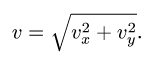
6. Вычисляем относительное ускорение. В случае криволинейной относительной траектории
где 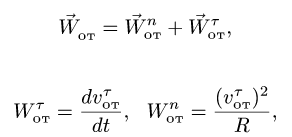
R — радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения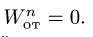 Вектор
Вектор 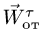 направляем по касательной к относительной траектории, вектор
направляем по касательной к относительной траектории, вектор 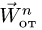 — к центру кривизны этой же кривой.
— к центру кривизны этой же кривой.
7. Вычисляем переносное ускорение:
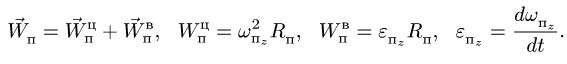
Вектор 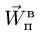 направляем перпендикулярно
направляем перпендикулярно 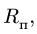 , вектор
, вектор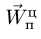 — к оси переносного вращения (вдоль
— к оси переносного вращения (вдоль 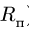 ).
).
8. Находим ускорение Кориолиса 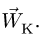 Так как в задачах этого типа вектор переносной угловой скорости перпендикулярен вектору относительной скорости, то
Так как в задачах этого типа вектор переносной угловой скорости перпендикулярен вектору относительной скорости, то 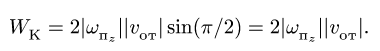
Направление вектора ускорения Кориолиса можно определить по правилу Жуковского 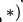 поворотом на 90° вектора относительной скорости по направлению переносного вращения. В результате вектор ускорения Кориолиса в таких задачах будет лежать на одной прямой с
поворотом на 90° вектора относительной скорости по направлению переносного вращения. В результате вектор ускорения Кориолиса в таких задачах будет лежать на одной прямой с 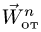 при криволинейном относительном движении, а в случае прямолинейного относительного движения
при криволинейном относительном движении, а в случае прямолинейного относительного движения 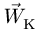 перпендикулярен относительной траектории.
перпендикулярен относительной траектории.
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат. Модуль абсолютного ускорения 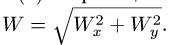
Задача №12
Прямоугольник ABCD вращается вокруг оси, проходящей через вершину А, по закон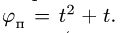 Ось вращения перпендикулярна плоскости прямоугольника (рис. 109). По круговому каналу радиуса R = 10 см с центром в точке С, расположенному на прямоугольнике, движется точка М. Дуговая координата точки меняется по закону
Ось вращения перпендикулярна плоскости прямоугольника (рис. 109). По круговому каналу радиуса R = 10 см с центром в точке С, расположенному на прямоугольнике, движется точка М. Дуговая координата точки меняется по закону 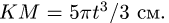 Дано: АВ = 12 см, ВС = 15
Дано: АВ = 12 см, ВС = 15 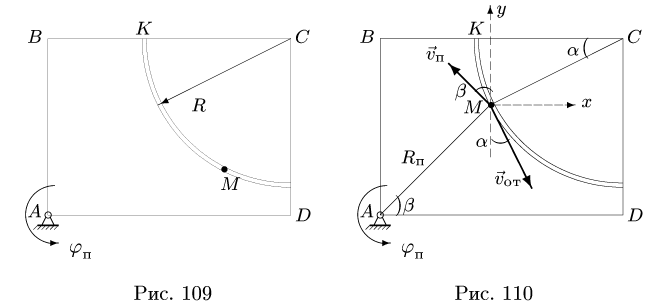
Найти абсолютную скорость и абсолютное ускорение точки М при 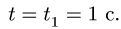
Решение
Движение точки М представим в виде относительного движения по круговому каналу и переносного движения вместе с вращающимся прямоугольником.
1. Вычисляем значение дуговой координаты 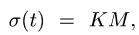 при
при
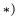 Жуковский Николай Егорович (1847-1921) русский ученый, основоположник гидроаэродинамики. Преподавал теоретическую механику в МГУ. Правило Жуковского для общего случая см. с. 204
Жуковский Николай Егорович (1847-1921) русский ученый, основоположник гидроаэродинамики. Преподавал теоретическую механику в МГУ. Правило Жуковского для общего случая см. с. 204
Гл.9.Сложное движение точки
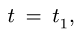 и определяем положение точки в подвижной системе координат. За время
и определяем положение точки в подвижной системе координат. За время 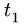 точка проходит по дуге окружности путь
точка проходит по дуге окружности путь 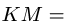
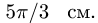 Центральный угол, соответствующий этой дуге,
Центральный угол, соответствующий этой дуге, 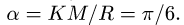 Изображаем точку в этом положении (рис.110).
Изображаем точку в этом положении (рис.110).
2. Дифференцируя 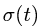 по времени, находим относительную скорость. Находим ее значение при t = 1с:
по времени, находим относительную скорость. Находим ее значение при t = 1с:
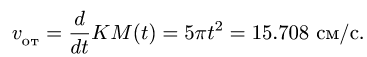
Вектор 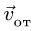 направлен по касательной к окружности.
направлен по касательной к окружности.
3. Вычисляем радиус траектории переносного движения 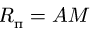
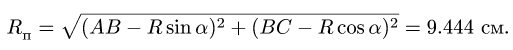
4. Находим переносную скорость 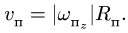 Переносной скоростью точки является скорость точки прямоугольника, совпадающей в данный момент с М
Переносной скоростью точки является скорость точки прямоугольника, совпадающей в данный момент с М  .Угловая скорость фигуры, при t =1с,
.Угловая скорость фигуры, при t =1с,
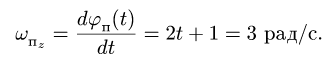
Отсюда 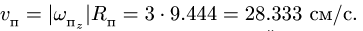
5. Определяем вектор абсолютной скорости по формуле (1). Модуль абсолютной скорости 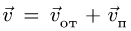 находим, проецируя
находим, проецируя
это равенство на неподвижные оси координат х, у (можно воспользоваться также теоремой косинусов):
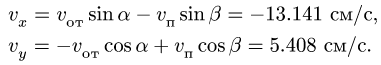
Тригонометрические функции угла 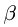 вычисляем по формулам
вычисляем по формулам
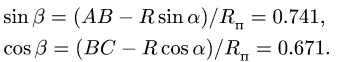
Модуль абсолютной скорости 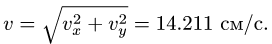
 Иногда переносная скорость обозначается
Иногда переносная скорость обозначается 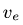 (от французского слова emporter), реже
(от французского слова emporter), реже 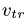 (от английского слова transport), а относительная —
(от английского слова transport), а относительная — 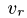 (от английского слова relativ). Эти же индексы используются и для других компонентов сложного движения.
(от английского слова relativ). Эти же индексы используются и для других компонентов сложного движения.
6. Вычисляем относительное ускорение. Ускорение точки, движущейся относительно прямоугольника по окружности, имеет нормальную и тангенциальную составляющую:
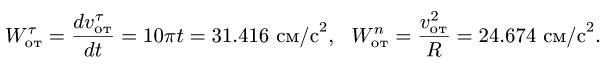
Модуль относительного ускорения
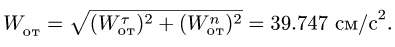
Вектор ускорения 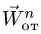 направляем по радиусу окружности к точке
направляем по радиусу окружности к точке 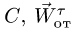 — по касательной, в сторону увеличения дуги КМ, так как
— по касательной, в сторону увеличения дуги КМ, так как 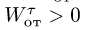 (рис.11)
(рис.11)
7. Вычисляем переносное ускорение 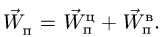 Траектория переносного движения точки — окружность радиуса
Траектория переносного движения точки — окружность радиуса  с центром А. Прямоугольник вращается с угловой скоростью
с центром А. Прямоугольник вращается с угловой скоростью 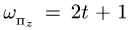 и угловым ускорением
и угловым ускорением
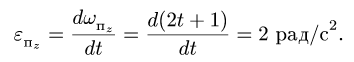
Отсюда получаем
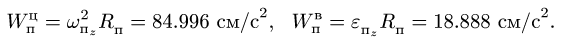
Вектор 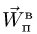 направлен против часовой стрелки перпендикулярно радиусу
направлен против часовой стрелки перпендикулярно радиусу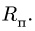 Вектор
Вектор 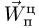 — к центру А. Модуль переносного ускорения
— к центру А. Модуль переносного ускорения
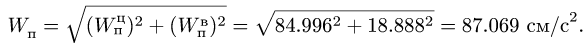
8. Находим ускорение Кориолиса 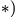 . Модуль вектора ускорения
. Модуль вектора ускорения 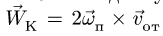 определяем по формуле
определяем по формуле где
где 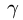 — угол между
— угол между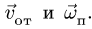 Вектор
Вектор 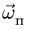 перпендикулярен плоскости чертежа, следовательно, угол
перпендикулярен плоскости чертежа, следовательно, угол 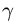 равен 90°. Имеем
равен 90°. Имеем
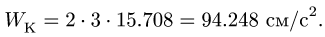
Направление вектора ускорения Кориолиса получаем по правилу Жуковского — поворотом на 90° вектора относительной скорости
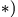 Это ускорение называют иногда поворотным, а в англоязычной литературе — supplementary (дополнительным).
Это ускорение называют иногда поворотным, а в англоязычной литературе — supplementary (дополнительным).
по направлению переносного вращения, т.е. против часовой стрелки (рис. 112).
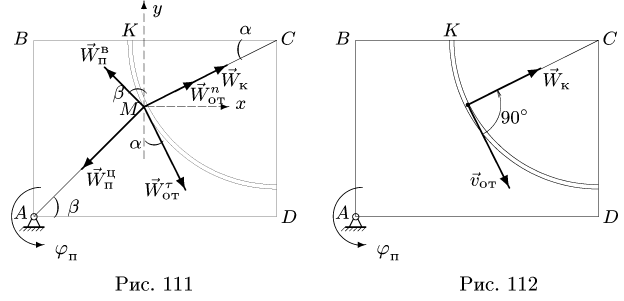
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат (рис. 111):
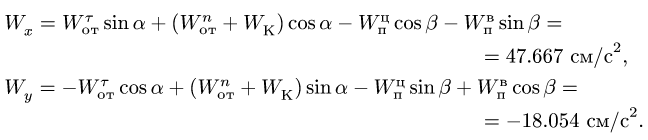
Находим модуль ускорения: 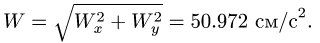
Ответы заносим в таблицу. Радиус траектории переносного движения — в см, скорости — в см/с, ускорения — в 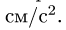

Сложное движение точки в пространстве
Постановка Задачи. Геометрическая фигура вращается по заданному закону вокруг неподвижной оси, лежащей в ее плоскости. По каналу, расположенному на фигуре, движется точка М по известному закону 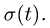 Найти абсолютную скорость и абсолютное ускорение точки.
Найти абсолютную скорость и абсолютное ускорение точки.
План решения:
Искомые величины получаем из векторных равенств
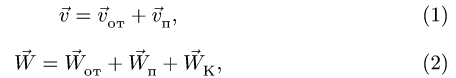
где 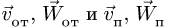 — соответственно относительные и переносные скорости и ускорения;
— соответственно относительные и переносные скорости и ускорения; 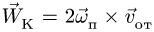 — ускорение Кориолиса. Решение задачи о сложном движении точки в пространстве отличается от аналогичной задачи, где точка движется в плоскости (с. 195) тем, что векторные суммы для абсолютных величин вычисляются по трем компонентам, а ускорение Кориолиса содержит синус угла между вектором переносной угловой скорости и относительной скоростью. Относительная скорость в этих задачах всегда перпендикулярна переносной, что упрощает вычисление модуля их суммы.
— ускорение Кориолиса. Решение задачи о сложном движении точки в пространстве отличается от аналогичной задачи, где точка движется в плоскости (с. 195) тем, что векторные суммы для абсолютных величин вычисляются по трем компонентам, а ускорение Кориолиса содержит синус угла между вектором переносной угловой скорости и относительной скоростью. Относительная скорость в этих задачах всегда перпендикулярна переносной, что упрощает вычисление модуля их суммы.
1. Вычисляем значение дуговой координаты 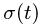 при
при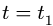 и определяем положение точки в подвижной системе координат.
и определяем положение точки в подвижной системе координат.
2. Дифференцируя 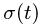 по времени, находим величину относительной скорости
по времени, находим величину относительной скорости 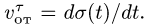 Вектор
Вектор 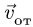 направляем по касательной к относительной траектории в сторону увеличения
направляем по касательной к относительной траектории в сторону увеличения 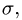 если
если 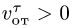 и в обратную сторону в противном случае;
и в обратную сторону в противном случае; 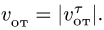
3. Вычисляем радиус траектории переносного движения 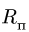 — расстояние от точки М в расчетном положении до оси переносного вращения.
— расстояние от точки М в расчетном положении до оси переносного вращения.
4. Находим модуль переносной скорости 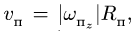 где переносная угловая скорость
где переносная угловая скорость 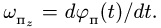 Вектор
Вектор 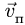 располагается в плоскости перпендикулярной оси вращения и направлен перпендикулярно
располагается в плоскости перпендикулярной оси вращения и направлен перпендикулярно 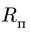 в сторону переносного вращения.
в сторону переносного вращения.
5. Определяем величину абсолютной скорости 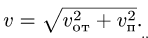
6. Вычисляем относительное ускорение. В случае криволинейной относительной траектории
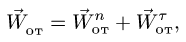
где 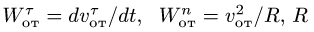 — радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения
— радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения 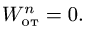 Вектор
Вектор 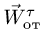 направляем по касательной к относительной траектории, вектор
направляем по касательной к относительной траектории, вектор 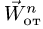 — к центру кривизны этой же кривой.
— к центру кривизны этой же кривой.
7. Вычисляем переносное ускорение:
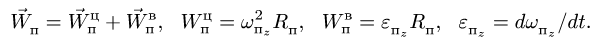
Вектор 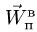 направляем перпендикулярно
направляем перпендикулярно 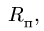 вектор
вектор 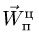 — к оси переносного вращения (вдоль
— к оси переносного вращения (вдоль 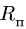 ).
).
8. Величину вектора ускорения Кориолиса определяем по формуле
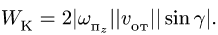
Направление вектора ускорения Кориолиса можно определить по правилу Н.Е. Жуковского поворотом на 90° проекции вектора относительной скорости на плоскость, перпендикулярную 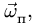 по направлению переносного вращения.
по направлению переносного вращения.
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат. Ось 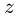 направляем по оси вращения. Модуль абсолютного ускорения
направляем по оси вращения. Модуль абсолютного ускорения
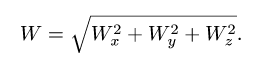
- Заказать решение задач по теоретической механике
Задача №13
Прямоугольник ABCD вращается вокруг неподвижной оси, проходящей по стороне DC (рис. 113). По круговому каналу радиуса R = 12 см с центром в точке О, расположенному на прямоугольнике, движется точка М по закону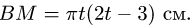 Найти абсолютную скорость и абсолютное ускорение точки при
Найти абсолютную скорость и абсолютное ускорение точки при 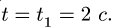
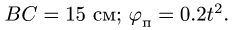
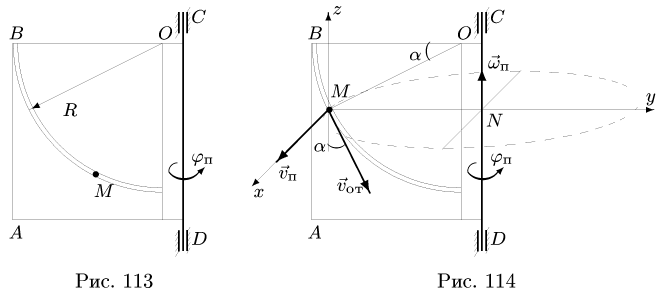
Решение
1. Вычисляем значение дуговой координаты 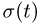 при
при 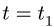 и определяем положение точки в подвижной системе координат:
и определяем положение точки в подвижной системе координат:
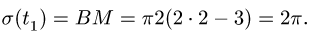
Находим центральный угол, соответствующий дуге ВМ:
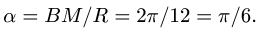
Изображаем точку в этом положении (рис. 114).
9.2.Сложное движение точки в пространстве
2. Дифференцируя 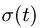 по времени, находим относительную скорость:
по времени, находим относительную скорость:
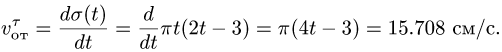
3. Траекторией переносного движения является окружность с центром N. Относительна скорость точки М направлена по касательной к этой окружности. Траектория лежит в плоскости ху, перпендикулярной к оси вращения 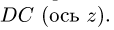 Находим радиус окружности:
Находим радиус окружности:
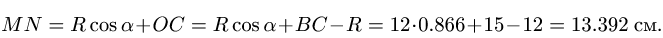
4. Находим переносную скорость. Вычисляем угловую скорость вращения прямоугольника ABCD:
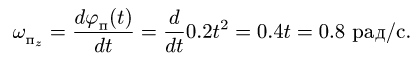
Вычисляем переносную скорость
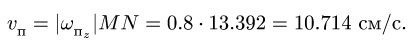
5. Определяем величину абсолютной скорости. Вектор 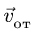 лежит в плоскости
лежит в плоскости 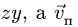 направлен по оси х, следовательно, они перпендикулярны. Модуль скорости
направлен по оси х, следовательно, они перпендикулярны. Модуль скорости
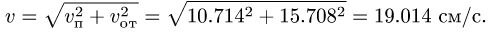
6. Вычисляем относительное ускорение. Находим нормальную составляющую ускорения точки, движущейся по окружности радиуса R:
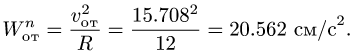
Тангенциальная составляющая
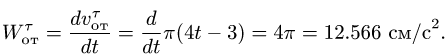
Оба вектора лежат в плоскости 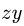 (рис.115.),
(рис.115.),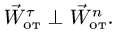
7. Вычисляем компоненты переносного ускорения. Прямоугольник вращается с угловой скоростью 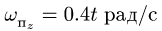 и угловым ускорением
и угловым ускорением
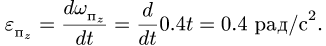
Получаем

Вектор 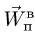 направлен по оси х, вектор
направлен по оси х, вектор 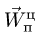 — к оси вращения вдоль оси у.
— к оси вращения вдоль оси у.
8. Величину вектора ускорения Кориолиса определяем по формуле 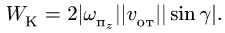 Вектор
Вектор 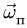 всегда направлен по оси вращения в ту сторону, откуда вращение видно против часовой стрелки. В нашем случае — вверх.
всегда направлен по оси вращения в ту сторону, откуда вращение видно против часовой стрелки. В нашем случае — вверх.
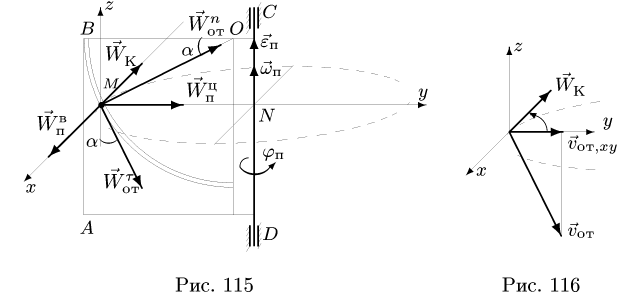
Угол 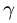 между
между 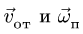 равен 150°. Определяем
равен 150°. Определяем
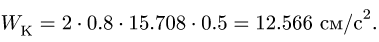
Для того, чтобы найти направление вектора ускорения Кориолиса, воспользуемся правилом Жуковского (рис. 116). Проецируем вектор относительной скорости 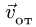 на плоскость перпендикулярную оси вращения, т.е. на плоскость ху. Повернув проекцию
на плоскость перпендикулярную оси вращения, т.е. на плоскость ху. Повернув проекцию 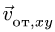 по направлению переносного вращения на 90°, получаем направление вектора ускорения Кориолиса. Вектор
по направлению переносного вращения на 90°, получаем направление вектора ускорения Кориолиса. Вектор 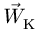 лежит на оси х и направлен в сторону отрицательных значений.
лежит на оси х и направлен в сторону отрицательных значений.
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат:
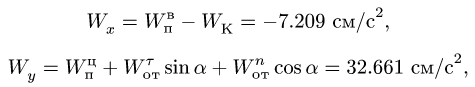
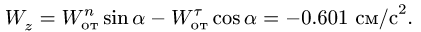
Окончательно, абсолютное ускорение точки М
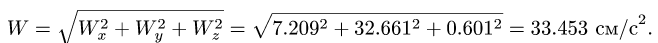
Ответы заносим в таблицу. Радиус траектории переносного движения — в см, скорости — в см/с, ускорения — в 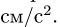

Движение точки по звену механизма
Постановка Задачи. Плоский шарнирно-стержневой механизм приводится в движение кривошипом, который вращается с заданной угловой скоростью. Вдоль одного из стержней по известному закону движется тючка М. Найти абсолютную скорость и абсолютное ускорение точки М.
План решения:
Представляем движение точки в виде суммы относительного движения по звену механизма и переносного движения вместе со звеном.
1. Вводим неподвижную систему координат ху, совмещая се начало с положением одного из шарниров механизма в заданный момент времени. Вдоль стержня, по которому движется точка, располагаем подвижную ось 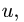 направляя ее в сторону движения точки. Зная закон относительного движения
направляя ее в сторону движения точки. Зная закон относительного движения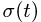 (он задан в условии), определяем положение точки относительно звена и неподвижных осей ху в расчетный момент. Определяем координаты х и у шарниров.
(он задан в условии), определяем положение точки относительно звена и неподвижных осей ху в расчетный момент. Определяем координаты х и у шарниров.
2. Дифференцируя 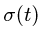 по времени, находим проекции относительной скорости и относительного ускорения на ось и:
по времени, находим проекции относительной скорости и относительного ускорения на ось и:
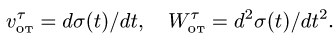
Зная угол между осями 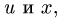 находим проекции векторов
находим проекции векторов 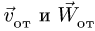 на оси ху.
на оси ху.
3. Решаем задачу о скоростях точек многозвенного механизма, используя аналитические методы (§ 8.3, с. 179, § 8.5, с. 188). Вычисляем вектор скорости той точки механизма, в которой в данный момент находится подвижная точка М. Эта скорость является переносной скоростью для точки М.
4. Определяем вектор абсолютной скорости, 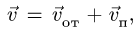 и его модуль,
и его модуль,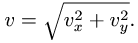
5. Решаем задачу об ускорениях точек многозвенного механизма, используя аналитические методы (§ 8.4, с. 183, § 8.5, с. 188). Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М.
6. Находим ускорение Кориолиса:
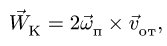
где 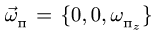 — вектор угловой скорости звена, по которому движется точка.
— вектор угловой скорости звена, по которому движется точка.
7. Находим абсолютное ускорение, 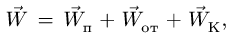 и его модуль:
и его модуль: 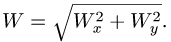
Задача №14
Плоский шарнирно-стержневой механизм ОABC приводится в движение кривошипом OA =60 см, который вращается с постоянной угловой скоростью 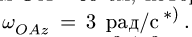 Вдоль стержня АВ движется точка М по закону
Вдоль стержня АВ движется точка М по закону 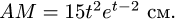
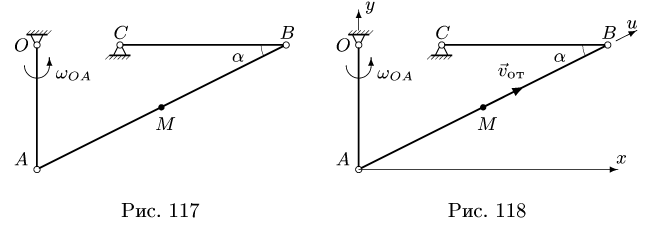
Положение механизма при 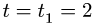 с указано на рис. 117; АВ =120 см, ВС =80 см,
с указано на рис. 117; АВ =120 см, ВС =80 см, 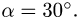 Найти абсолютную скорость и абсолютное ускорение точки М в этот момент.
Найти абсолютную скорость и абсолютное ускорение точки М в этот момент.
Решение
Абсолютное движение точки представляем в виде суммы относительного движения по звену АВ и переносного движения вместе с ним. Переносные скорость и ускорение являются соответственно скоростью и ускорением той точки звена, в которой в данный момент располагается точка М.
1. Вводим неподвижную систему координат ху, совмещая ее начало с положением шарнира А механизма в заданный момент времени. Вдоль стержня АВ, по которому движется точка, располагаем подвижную ось 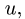 направляя ее в сторону движения точки (рис. 118). Зная закон относительного движения
направляя ее в сторону движения точки (рис. 118). Зная закон относительного движения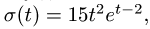 определяем положение точки относительно звена при t = 2 с:
определяем положение точки относительно звена при t = 2 с: 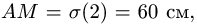 т.е. точка находится в центре звена АВ. Определяем координаты шарниров в неподвижных осях координат:
т.е. точка находится в центре звена АВ. Определяем координаты шарниров в неподвижных осях координат:
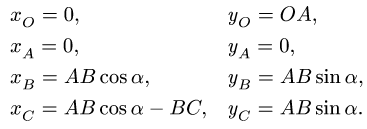
 Проекция угловой скорости на ось
Проекция угловой скорости на ось 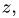 перпендикулярную плоскости чертежа,
перпендикулярную плоскости чертежа, 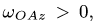 следовательно, кривошип вращается против часовой стрелки.
следовательно, кривошип вращается против часовой стрелки.
2. Дифференцируя  по времени, находим проекции относительной скорости и относительного ускорения на ось
по времени, находим проекции относительной скорости и относительного ускорения на ось 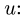
Угол между осями  равен
равен 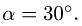 Находим проекции:
Находим проекции:
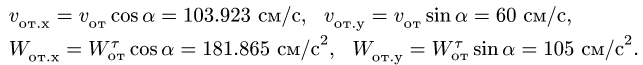
3. Решаем задачу о скоростях точек многозвенного механизма, используя уравнения трех угловых скоростей (§ 8.3, с. 179):
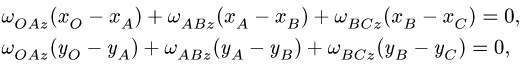
где по условию 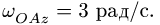 Решаем систему двух уравнений относительно
Решаем систему двух уравнений относительно 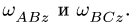 Подставляя численные значения, получаем
Подставляя численные значения, получаем 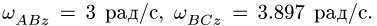 Скорость
Скорость 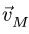 определяем из
определяем из
равенства 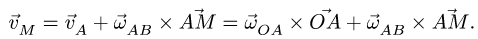
Переписываем это равенство в виде
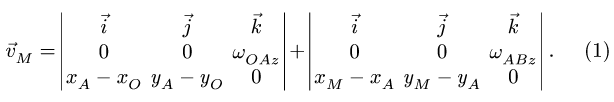
Получаем
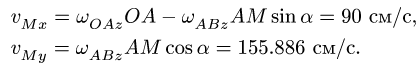
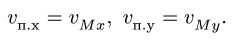
Модуль переносной скорости 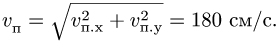
4. Определяем проекции.
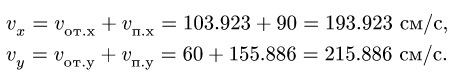
и модуль абсолютной скорости: 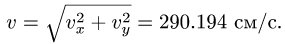
5. Решаем задачу об ускорениях точек многозвенного механизма, используя уравнения трех угловых ускорений (уравнение (2), с. 184), где 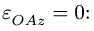
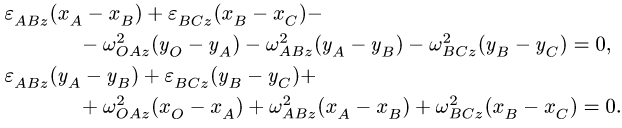
Находим 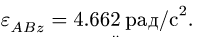 Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М. Учитывая, что
Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М. Учитывая, что 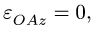 записываем векторное равенство
записываем векторное равенство
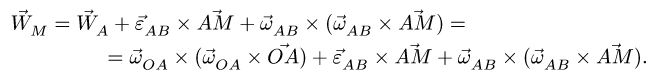
Раскрывая векторные произведения по аналогии с (1), вычисляем
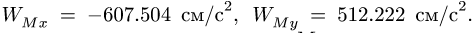 Это ускорение является переносным для точки М:
Это ускорение является переносным для точки М:
Модуль переносного ускорения 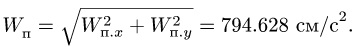
6. Находим ускорение Кориолиса 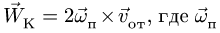 — вектор угловой скорости звена АВ, по которому движется точка:
— вектор угловой скорости звена АВ, по которому движется точка:
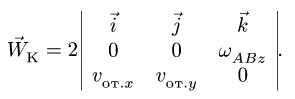
Вычисляем
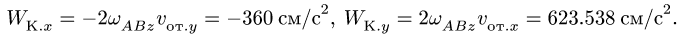
Модуль ускорения Кориолиса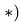
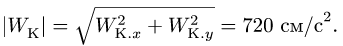
7. Вычисляем абсолютное ускорение 
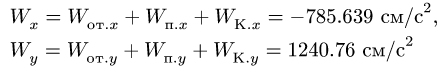
и его модуль 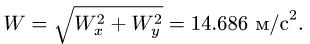
Результаты заносим в таблицу. Скорости в м/с, ускорения — в 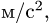 угловая скорость — в рад/с, угловое ускорение — в
угловая скорость — в рад/с, угловое ускорение — в 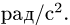

Механизм с муфтой
Постановка Задами. Плоский механизм с одной степенью свободы состоит из шарнирно соединенных стержней и муфты, скользящей по направляющему стержню и шарнирно закрепленной на другом стержне или на неподвижном шарнире. Задана угловая скорость ведущего звена механизма. Найти скорость муфты относительно направляющего стержня.
План решения:
1. Представляем движение муфты М в виде суммы относительного движения по направляющему стержню механизма и переносного движения вместе с этим стержнем. Траекторией относительного движения муфты является прямая. Задачу решаем, используя координатную запись векторных соотношений для скоростей при плоском движении. Выбираем систему координат и определяем координаты всех шарниров механизма и муфты.
2. Мысленно снимаем муфту с механизма и находим скорости шарниров и угловые скорости звеньев получившегося механизма (§ 8.1, с. 158, § 8.3, с. 179, § 8.5, с. 188).
3. Записываем уравнение сложения скоростей: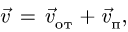 где абсолютная скорость
где абсолютная скорость 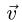 или относительная скорость
или относительная скорость 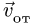 выражается через скорости шарниров механизма. Составляем уравнение
выражается через скорости шарниров механизма. Составляем уравнение
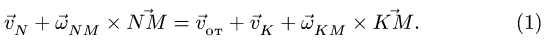
Это векторное уравнение содержит две неизвестные величины. Одна из них — искомый модуль вектора относительной скорости 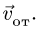 Направление этого вектора всегда известно и задается направлением стержня, по которому скользит муфта
Направление этого вектора всегда известно и задается направлением стержня, по которому скользит муфта 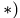 . В зависимости от варианта задачи второй неизвестной может быть угловая скорость
. В зависимости от варианта задачи второй неизвестной может быть угловая скорость 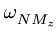 или
или 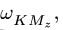 где N и К — точки механизма с известными скоростями.
где N и К — точки механизма с известными скоростями.
Если муфта скользит по стержню КМ, угловая скорость 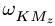 которого известна, то неизвестной величиной будет угловая скорость
которого известна, то неизвестной величиной будет угловая скорость 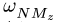 звена, шарнирно соединяющего муфту с неподвижной точкой
звена, шарнирно соединяющего муфту с неподвижной точкой 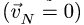 или с шарниром N механизма с известной скоростью.
или с шарниром N механизма с известной скоростью.
Если муфта шарнирно закреплена на стержне NM с известной угловой скоростью 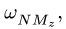 то неизвестной величиной будет угловая скорость
то неизвестной величиной будет угловая скорость 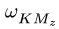 звена, по которому скользит муфта, где точка К неподвижна или является шарниром с известной скоростью.
звена, по которому скользит муфта, где точка К неподвижна или является шарниром с известной скоростью.
Если муфта закреплена на неподвижном шарнире, то абсолютная скорость равна нулю 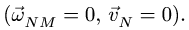
3. Решаем векторное уравнение (1). Определяем 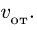
Задача №15
Плоский механизм с одной степенью свободы состоит из шарнирно соединенных стержней и муфты D, скользящей по направляющему стержню (кривошипу) OA. Муфта шарнирно закреплена на стержне BD. Кривошип вращается против часовой стрелки с постоянной угловой скоростью 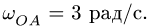 Даны длины: OA = 40 см, АВ = 111 см, ВС = 43 см, ОС = 62 см. Найти скорость муфты относительно направляющего стержня в тот момент, когда
Даны длины: OA = 40 см, АВ = 111 см, ВС = 43 см, ОС = 62 см. Найти скорость муфты относительно направляющего стержня в тот момент, когда 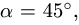 а муфта находится на середине кривошипа: OD = ОА/2 (рис. 119).
а муфта находится на середине кривошипа: OD = ОА/2 (рис. 119).
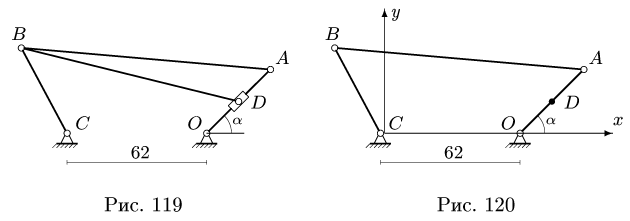
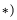 Направляющий стержень.
Направляющий стержень.
Решение
1. Представляем движение муфты М в виде суммы относительного движения по направляющему стержню OA и переносного движения вместе с .этим стержнем. Выбираем систему координат и определяем координаты всех шарниров механизма и муфты. Помещаем начато координат в точку С (рис. 120) и вычисляем координаты:
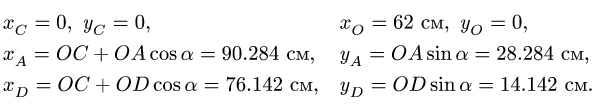
Координаты точки В найдем из системы уравнений
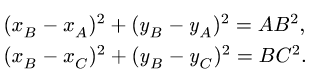
Система имеет два решения (задача о точках пересечения двух окружностей с радиусами АВ и ВС). Выбираем то решение, у которого 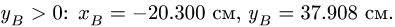
Нелинейную систему уравнений удобно решать на компьютере, например, в системе Maple V. Программа решения имеет вид

Числа заносятся в десятичной форме: АВ: =111.0 и т.д.
2. Мысленно снимаем муфту с механизма (рис. 120) и находим скорости шарниров и угловые скорости звеньев получившегося механизма. Записываем уравнения трех угловых скоростей четырехзвенника ОABC (§8.3, с. 179):
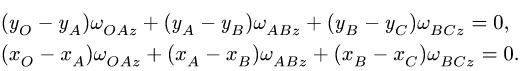
При 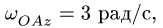
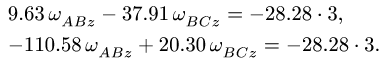
Получаем решение: 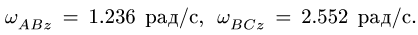 Зная
Зная 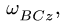 находим
находим
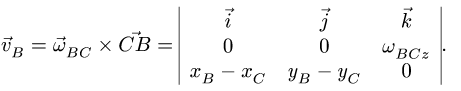
Компоненты скорости имеют следующие значения:
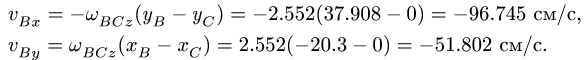
3. Записываем уравнение сложения скоростей 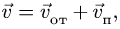 где абсолютная скорость
где абсолютная скорость 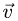 выражается через известную скорость шарнира В. Составляем векторное уравнение
выражается через известную скорость шарнира В. Составляем векторное уравнение
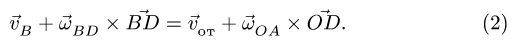
Это уравнение содержит две неизвестные величины. Одна из них — искомый модуль вектора относительной скорости 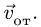 Направление этого вектора известно и задается направлением стержня OA, по которому скользит муфта. Вторая неизвестная — угловая скорость
Направление этого вектора известно и задается направлением стержня OA, по которому скользит муфта. Вторая неизвестная — угловая скорость 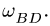 Подставляем численные значения. Уравнение (2) принимает вид
Подставляем численные значения. Уравнение (2) принимает вид

где 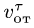 — проекция относительной скорости муфты на ось, направленную от О к А. Находим решение системы:
— проекция относительной скорости муфты на ось, направленную от О к А. Находим решение системы: 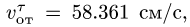
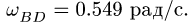 Таким образом, в указанный момент муфта движется по стержню OA вверх со скоростью
Таким образом, в указанный момент муфта движется по стержню OA вверх со скоростью 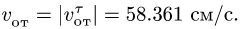
Замечание. Эту задачу можно решить по крайней мере ещё двумя способами. Во-первых, методами аналитической геометрии можно найти расстояние 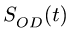 от шарнира О до муфты D как функцию времени. Дифференцируя
от шарнира О до муфты D как функцию времени. Дифференцируя 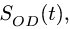 найдем относительную скорость. Во-вторых, можно найти скорость стержня OA относительно муфты. Подвижная система координат будет связана с муфтой. В этом случае абсолютная скорость точки стержня OA под муфтой — это скорость точки тела при вращательном движении с угловой скоростью
найдем относительную скорость. Во-вторых, можно найти скорость стержня OA относительно муфты. Подвижная система координат будет связана с муфтой. В этом случае абсолютная скорость точки стержня OA под муфтой — это скорость точки тела при вращательном движении с угловой скоростью 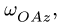 переносная — скорость муфты, выраженная через скорость шарнира В.
переносная — скорость муфты, выраженная через скорость шарнира В.
Замечание. В ответах, помимо искомой относительной скорости, даны промежуточные результаты — скорости точек А, Б и D. Причем в вариантах 1,2,7,8 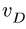 — это скорость той точки направляющего стержня, в которой в этот момент находится муфта.
— это скорость той точки направляющего стержня, в которой в этот момент находится муфта.
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
Проекция – абсолютная скорость
Cтраница 1
Проекции абсолютной скорости на меридиональное сечение и на направление переносной скорости будут соответствовать меридиональной составляющей абсолютной скорости vm, которая ка-сательна к линиям тока и определяет расход жидкости в проточной части, и окружной составляющей абсолютной скорости ии, которая определяет вращение жидкости и момент на колесах гидропередачи.
[1]
Проекция абсолютной скорости clu в формуле (11.28) представляет собой скорость закручивания потока жидкости до того, как жидкость поступила в рабочее колесо.
[2]
Проекции абсолютной скорости точки К получим, прибавляя соэтветственно к предыдущим величинам проекции Ар %, Aq %, Cr ее относительной скорости.
[3]
Чтобы иметь проекции абсолютной скорости, нужно прибавить к предыдущим величинам проекции переносной скорости, происходящей от мгновенного вращения ( р, q, r) подвижных осей.
[4]
Штрихом обозначены проекции абсолютной скорости на направление окружной треугольников скоростей при конечном числе лопаток, без штриха проекции абсолютной скорости на направление окружной треугольников скоростей при бесконечном числе лопаток.
[5]
Следовательно, проекция абсолютной скорости на любую ось равна алгебраической сумме проекций переносной и относительной скоростей на ту же ось.
[6]
Для вычисления проекций абсолютной скорости vg на подвижные оси представим ид как сумму относительной ( по отношению к осям Oxyz) скорости аот и переносной скорости – ипер.
[7]
Для вычисления проекций абсолютной скорости чВ на подвижные оси, представим ъв как сумму относительной ( по отношению к осям Oxyz) и переносной скоростей.
[8]
Для вычисления проекций абсолютной скорости vg на подвижные оси представим ид как сумму относительной ( по отношению к осям Oxyz) скорости цот и переносной скорости апер.
[9]
Для вычисления проекций абсолютной скорости VB на подвижные оси, представим VB как сумму относительной ( по отношению к осям Oxyz) и переносной скоростей.
[10]
С и – проекция абсолютной скорости газа на входе в межлопаточный канал на окружную скорость U u г) иэ – изоэнтропный КПД компрессора; k – показатель изоэнтропы; R – газовая постоянная; е – отношение давлений в компрессоре; 7 вк – температура газа на входе в компрессор.
[11]
Также используют и проекцию абсолютной скорости v2 на направление радиуса.
[13]
Эти равенства показывают, что проекция абсолютной скорости на какую-либо ось равна сумме проекций относительной и переносной скоростей на ту же ось.
[14]
Поскольку при он – 90 проекция абсолютной скорости на направление переносной скорости равна нулю ( viu 0), то условие радиального входа также означает, что жидкость подводится к рабочему колесу без предварительного закручивания.
[15]
Страницы:
1
2
3
4