Как найти проекцию диагонали на сторону

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Найти длину диагонали параллелограмма, построенного на векторах , если

Рассм. диагонали параллелограмма ;

Вычислим ;

;

Задача 3 Показать, что точки Являются вершинами параллелограмма и найти проекцию одной из диагоналей на большую сторону параллелограмма.

Рассм.

, след. – параллелограмм (так как две противоположные стороны параллельны и равны);

Рассм. Рассм. ; ,

След. – большая сторона параллелограмма ; рассм. диагональ ;

Вычислим Вычислим ;

.

Задача 4 Длина гипотенузы прямоугольного треугольника равна . Вычислить

Задача 5 Найти момент силы, приложенной в точке относительно точки, а также модуль и направляющие косинусы вектора силы

1) , где ; ;

;

2) ;

Направл. косинусы вектора : ; ; .

Задача 6 Треугольник построен на векторах Найти длину высоты , если векторы взаимно перпендикулярны и по модулю равны

Рассм. векторы рассм. ;

;

;

;

Задача 7 Найти координаты вершины тетраэдра, если известно, что она лежит на оси , объём тетраэдра равен , .

Пусть искомая вершина тетраэдра (т. к. т. );

Рассм. в-ры: ;

Рассм. смешанное произв-е:

Рассм. объём тетраэдра : ; ; ;

; ; ; след., возможные положения искомой т.: ; .

Задача 8 В треугольнике известны координаты двух вершин: И точки пересечения медиан . Составить уравнение высоты треугольника, проведённой из вершины .

1) Определим координаты точки Как середины отрезка :;

2) Определим координаты вершины , используя равенство , где ;

Рассм.

;

3) составим ур-е высоты : рассм. в-р ;

Рассм. т. И рассм. в-р ; тогда по условию задачи и и, след., ур-е прямой , проходящей через Перпендикулярно в-ру , можно записать в виде: т. е. .

Задача 9 В параллелограмме известны уравнения сторон и координаты точки пересечения диагоналей Составить уравнения двух других сторон и диагоналей параллелограмма.

1) определим координаты точки как точки пересечения прямых :

;

2) определим координаты точки из условия, что т. – середина отрезка :

;

3) составим уравнение диагонали как прямой, проходящей через точки : ;

4) составим уравнение стороны как прямой, проходящей через точку параллельно

Прямой ;

5) составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

6) определим координаты точки как точки пересечения прямых :

;

7) составим уравнение диагонали как прямой, проходящей через точки : .

Задача 10 Составить уравнение плоскости, проходящей через точки

Пусть – искомая плоскость; рассм. векторы ;

Рассм. норм. вектор ;

Рассм. произв. т. и рассм. вектор ;

, т. е. ;

Задача 11 Составить уравнение прямой , которая, проходит через точку и пересекает две прямые и .

Рассм. направл. векторы прямых ;

Рассм. т.; рассм. векторы ;

Пусть – плоскость, в которой лежат прямые ; пусть – плоскость, в которой лежат прямые ; тогда искомая прямая есть линия пересечения плоскостей ;

;

;

В качестве направл. вектора прямой можно взять вектор ; выберем ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. А параллельно

Вектору : ; параметрические ур-я прямой :

Задача 12 Составить уравнение геометрического места всех прямых, проходящих через точку перпендикулярно прямой .

Запишем канонич. уравнения прямой в виде: ; её направл. вектор ;

Рассм. произв. прямую , удовлетв. условию задачи; рассм. произв. точку и её направл. вектор ; , т. е. ;

Плоскость и есть искомое геометрическое место.

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке.

1) Непосредственное вычисление:

2) Разложение по 1-й строке:

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы:

Запишем данную систему уравнений в матричной форме: , (1) , где ; ; ;

Рассм. опред-ль матрицы : ,

След., матр. – невырожденная и можно применять формулы Крамера и вычислять обратную матр. ;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул: , , , где ;

;

;

; , , ;

реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. :

, след., матр.– невырожденная и существует обратная матр. ;

Умножим рав-во (1) слева на матрицу : , ; вычислим обратную матр. :

Находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

Транспонируем м-цу и получим «присоединённую» м-цу

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. :

Находим теперь вектор-решение :

Задача 15 Установить, являются ли векторы линейно зависимыми.

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

ранг матрицы , след. данная система векторов линейно независима.

Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса.

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

имеем ;

Так как , то по теореме Кронекера – Капелли данная система уравнений совместна, а так как , то система имеет бесконечное множество решений; объявим свободной переменной и выпишем общее решение системы в координатной форме:

общее решение системы имеет вид:

Задача 17 Найти матрицу преобразования, выражающего Через , если

Запишем данные преобразования в матричной форме: , где матрицы и

Вектор – столбцы имеют вид:

Рассм. ;

Вычислим матрицу .

Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

– собств. значения (действ.) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм.

Рассм. Пусть , тогда вектор ;

Б) рассм.

Рассм.

Пусть , тогда , вектор ;

Пусть , тогда , вектор ;

След. собств. векторы линейного преобразования суть:

; ; .

< Предыдущая

Ромб с углами 60° и 120° стоит, опираясь острым углом на плоскость. Каким должен быть угол alpha между ромбом и плоскостью (показан дугой), чтобы в проекции ромба на плоскость получился квадрат? Ответ дать в градусах. бонус за лучший ответ (выдан): 20 кредитов В принципе задача не сложная. Нужно только вспомнить определения основных тригонометрических функций. А далее рассуждаем. Малая диагональ ромба равна его стороне, а большая √3. нужно чтобы в проекции диагонали были равны. Для этого запишем cos(alpha)=1/√3. Тогда arccos(1/√3)=54.7° Для пояснения: у ромба диагонали разновеликие, у квадрата одинаковые. У исходного ромба сторона и малая диагональ это 1, а большая диагональ √3. У проекции получаются диагонали 1. автор вопроса выбрал этот ответ лучшим smog2­605 [14.6K] 3 года назад  Наверное не повториться не получится, но тем не менее. Отличие квадрата от ромба в его равных диагоналях. Обозначим: а- сторона ромба; М- малая диагональ; Б- большая диагональ. Поскольку поворот фигуры производится относительно ось перпендикулярной большой диагонали, то все линии параллельные оси поворота не изменят свой размер на проекции. В том числе и малая диагональ. Большая же диагональ с проектируется на плоскость в размер: Б*cos(альфа) и эта величина должна быть равна малой диагонали, поскольку мы хотим получить квадрат. М=Б*cos(альфа) Из ромба имеем. М=2а*sin(30) Б=2а*cos(30) Подставляем. 2а*sin(30)=2а*cos(30­)cos(альфа) cos(альфа)=sin(30)/c­os(30)=tg(30)=1/sqr(3­) альфа=arccos(1/sqr(3­))=54.7356103172 градуса ≈136839/2500 Rafai­l [136K] 3 года назад  Прежде всего условие задачи – неполное и оттого неопределённое. Представьте себе, что ромб вращается вокруг большей диагонали (в принципе на на 180°). Тот чертёж, который Вы хотели начертить, относится только к такому положению ромба, когда его малая диагональ параллельна заданной плоскости. Только тогда угол между плоскостью ромба и заданной плоскостью (или как Вы написали, между ромбом и плоскостью), который Вы обозначили alpha) будет равен углу меду большой диагональю ромба и её проекцией на плоскость ромба, и равен arccos(1/√3)=0,955 радиан или 54,7°. Но во всех других положениях он будет больше, и в пределе будет приближаться к 90°. Поэтому в той редакции, как Вы написали, задача имеет бесчисленное множество решений, вида alpha = arccos(sin(фи)/√3), где угол фи – это угол, на который повёрнут ромб повёрнут ромб вокруг своей большей диагонали. Для однозначного решения нужно указать положение ромба (например, указав угол между малой диагональю ромба и её проекцией на заданную плоскость. Евген­ий Борис­ович [2.2K] 3 года назад  Ответ уже дали. Повторять не буду. Чертеж в вопросе какой-то несуразный. Привожу более наглядный. Проекцией ромба может быть ромб, в частности квадрат, или параллелограмм. Более интересен такой вопрос: При каком угле α между ромбом, со стороной 4, и плоскостью, проекцией ромба будет параллелограмм с углами 60º и 120º, и сторонами a и b? P.S. Может задать вопрос отдельно? Георг­ий22 [403] 3 года назад  Пояснение: малая диагональ равна своей проекции, поскольку параллельна плоскости, на которую и делается проекция. А так как у квадрата диагонали равны, то проекция большой диагонали равна малой диагонали. P.S. Прошу прощения, что заново пишу ответ; не знаю, как восстановить старый. Длина отрезка AD равна (sqr(2))/2, а длина отрезка AD1 равна 1/2 Чтобы отрезок AD дал проекцию AD1, угол alpha должен быть 45 градусов, ибо sec(45) = sqr(2). Ответ: угол alpha равен 45 градусов. Знаете ответ?

Смотрите также: Что такое равновеликие фигуры (куб, квадрат, многоугольник)? Для чего нужна математика, геометрия, физика в программировании? Как найти вписанный угол ACB, если дуга BC составляет 80 градусов? Как найти длину отрезка BD, если SO = 35, SD = 37? Как найти величину угла OAB, если угол OCD равен 30 градусам? По каким учебникам изучают математику израильские школьники? Как решить: В четырехугольнике АВСD противоположные стороны не параллельны? Диагональ АС параллелограмма АВСD 21, от верш. В до диаг. 12. Чему равна S? Как найти площадь треугольника ABM (см.)? В угол с вершиной D вписана окружность с центром O, которая касается…?

Проекции треугольника, многоугольника и круга

Для примера изобразим прямоугольник ABCD без осей проекций (рис. 115, а). Расстояние горизонтальной и профильной проекций от фронтальной проекции выберем произвольно. Встает вопрос о том, можно ли теперь «восстановить» положение осей, а следовательно, и плоскостей проекций. Для построения постоянной прямой чертежа (рис. 115, б) используем горизонтальную и профильную проекции любой точки, например точки А. Через точку А₁ проведем горизонтальную линию связи, а через точку А₃ — вертикальную линию связи. Проведенные прямые пересекутся между собой в точке А₀, через которую проведем постоянную прямую k₁₂₃ под углом 45 градусов к горизонтальной линии связи. Очевидно, что постоянная прямая будет единственной. Этого нельзя сказать о системе координатных плоскостей, которых может быть много. Действительно, одну из систем можно определить, приняв горизонтально-вертикальную линию связи за направление осей проекций x₁₂ и z₂₃. Точка A₀ будет для этой системы началом координат O₁₂₃. Плоскость прямоугольника будет прикасаться своей стороной AD к фронтальной плоскости проекции П₂. Вторую систему можно получить, если провести координатные оси х’₁₃ и z’₂₃ через точку О’₁₂₃, являющуюся точкой пересечения постоянной прямой с линией D₂D₃. В новой системе прямоугольник будет стоять на горизонтальной плоскости проекций П1, пересекаясь с ней по прямой DC. В промежутке между осями первых двух систем можно провести еще большое количество осей, которые определят новые системы плоскостей. Одну из таких систем определяют оси х₂1₂ и z₂2₃, пересекающиеся между собой в точке О₁, являющейся началом координат третьей системы плоскостей. В последнем случае прямоугольник отстоит от всех трех плоскостей проекций.

Итак, найдя постоянную прямую чертежа, мы можем построить одну из возможных систем плоскостей проекций. Очевидно, что начало координат любой системы должно находиться на постоянной прямой чертежа. Отсюда следует, что постоянная прямая чертежа является геометрическим местом точек, фиксирующих начало координат всех возможных систем плоскостей проекций П₂, П₃.

При построении проекций четырехугольника общего положения нельзя взять четыре произвольные точки. Как только мы возьмем три точки, плоскость определится, и четвертую точку надо строить при условии, чтобы она принадлежала этой плоскости. Практически пользуются диагоналями проекций четырехугольника (рис. 115, в).

Фронтальную проекцию четырехугольника ABCD Рис. 116 строим произвольно; также произвольно строим горизонтальные проекции трех точек А₁, В₁ и С₁ треугольника A₁B₁C₁. Для построения горизонтальной проекции D₁ точки D проводим фронтальные проекции А₂С₂ и D₂B₂ диагоналей четырехугольника.

Проекции диагоналей пересекутся между собой в точке Е₂. Находим горизонтальную проекцию E₂ этой точки на горизонтальной проекции А₁С₁ будущей диагонали АС; соединяем точки В₁ и E₁ и на продолжении этой линии находим точку D₁ на вертикальной линии связи D₂D₁. При таком построении четырехугольник ABCD будет плоским. Пользуясь вспомогательными прямыми, пересекающимися со сторонами четырехугольника, можно построить проекции пятиугольника, шестиугольника и т. д.

Построим проекции правильного шестиугольника, вписанного в окружность, при горизонтальном их расположении (рис, 116, а). Построение начинаем с проведения окружности; затем вписываем в нее правильный шестиугольник А₁В₁C₁D₁E₁F₁.

Фронтальная проекция шестиугольника изобразится прямой горизонтально расположенной линией A₂D₂, точки B₂F₂ и С₂Е₂, принадлежащие этой линии, попарно совпадут.

В практике нередко приходится строить наклонно расположенные многоугольники, и особенно, окружности. Придадим плоскостям шестиугольника и круга наклонное положение, т. е. расположим их во фронтально-проецирующей плоскости т (рис. 116, б). При таком расположении плоскости прямые FB и ЕС шестиугольника и диаметр HG круга останутся фронтально-проецирующими прямыми и спроецируются на плоскость П₁ в истинную величину. Наоборот, прямые ВС, AD и FE спроецируются с искажением, зависящим от величины угла наклона плоскости т. В связи с этим горизонтальная проекция шестиугольника не будет являться правильным шестиугольником, а горизонтальная проекция круга будет проецироваться эллипсом, большая ось которого H₁G₁, малая — A₁D₁

Аналитический портал Ua-News Главные новости Украины: политика, интернет, шоу-BIZ, спорт, столица.

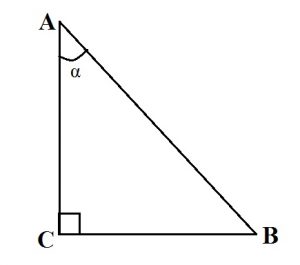
Прямоугольный треугольник формулы

Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

Прямоугольный треугольник: формулы площади и проекции

1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH 2 = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA 2 = AB·AH; CB 2 = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.

Прямоугольный треугольник: формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. ctgα = AC:BC.
5. Основное тригонометрическое тождество: cos 2 α + sin 2 α = 1.
6. Теорема косинусов: b 2 = a 2 + c 2 – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

Прямоугольный треугольник: формулы для описанной окружности

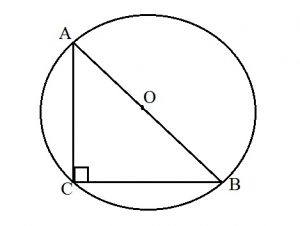
1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник: формулы для вписанной окружности

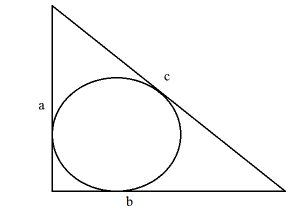
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

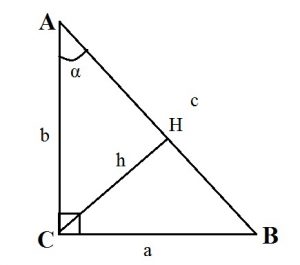
Проекции катетов на гипотенузу

Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

[spoiler title=”источники:”]

[/spoiler]

Как рассчитать диагональ прямоугольника

Замкнутая геометрическая фигура, образованная двумя парами лежащих друг напротив друга параллельных отрезков одинаковой длины, называется параллелограммом. А параллелограмм, все углы которого равны 90°, называют еще и прямоугольником. В этой фигуре можно провести два отрезка одинаковой длины, соединяющих противоположные вершины – диагонали. Длина этих диагоналей вычисляется несколькими способами.

Инструкция

Если известны длины двух смежных сторон прямоугольника (А и В), то длину диагонали (С) определить очень просто. Исходите из того, что диагональ лежит напротив прямого угла в треугольнике, образуемом ею и этими двумя сторонами. Это позволяет применить в расчетах теорему Пифагора и вычислить длину диагонали, найдя квадратный корень из суммы возведенных в квадрат длин известных сторон: С=v(А?+В?).

Если известна длина лишь одной стороны прямоугольника (А), а также величина угла (?), который с ней образует диагональ, то для вычисления длины этой диагонали (С) придется использовать одну из прямых тригонометрических функций – косинус. Разделите длину известной стороны на косинус известного угла – это и будет искомая длина диагонали: С=А/cos(?).

Если прямоугольник задан координатами своих вершин, то задача вычисления длины его диагонали сведется к нахождению расстояния между двумя точками в этой системе координат. Примените теорему Пифагора к треугольнику, который образуют проекции диагонали на каждую из координатных осей. Допустим, прямоугольник в двухмерных координатах образован вершинами A(X?;Y?), B(X?;Y?), C(X?;Y?) и D(X?;Y?). Тогда вам нужно вычислить расстояние между точками A и C. Длина проекции этого отрезка на ось X будет равна модулю разности координат |X?-X?|, а проекции на ось Y – |Y?-Y?|. Угол между осями равен 90°, из чего вытекает, что эти две проекции являются катетами, а длина диагонали (гипотенузы) равна квадратному корню из суммы квадратов их длин: AC=v((X?-X?)?+(Y?-Y?)?).

Для нахождения диагонали прямоугольника в трехмерной системе координат действуйте так же, как в предыдущем шаге, лишь добавив в формулу длину проекции на третью координатную ось: AC=v((X?-X?)?+(Y?-Y?)?+(Z?-Z?)?).

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Перпендикуляр и наклонная к прямой

Если через какую-нибудь точку, взятую вне прямой, провести прямую, перпендикулярную к ней, то отрезок от данной точки до прямой для краткости называют одним словом перпендикуляр.

Отрезок СО — перпендикуляр к прямой АВ. Точка О называется основанием перпендикуляра СО (рис).

Если прямая, проведённая через данную точку, пересекает другую прямую, но не перпендикулярна к ней, то отрезок её от данной точки до точки пересечения с другой прямой называют наклонной к этой прямой.

Отрезок ВС — наклонная к прямой АО. Точка С называется основанием наклонной (рис.).

Если из концов какого-нибудь отрезка опустим перпендикуляры на произвольную прямую, то отрезок прямой, заключённый между основаниями перпендикуляров, называется проекцией отрезка на эту прямую.

Отрезок А&#146В&#146 — проекция отрезка АВ на ЕС. Отрезок ОМ&#146 — также называется проекцией отрезка ОМ на ЕС.

Проекцией отрезка КР, перпендикулярного к ЕС, будет точка К&#146 (рис.).

2. Свойства перпендикуляра и наклонных.

Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой.

Отрезок АС (рис.) является перпендикуляром к прямой ОВ, а АМ — одна из наклонных, проведённых из точки А к прямой ОВ. Требуется доказать, что АМ > АС.

В ΔМАС отрезок АМ является гипотенузой, а гипотенуза больше каждого из катетов этого треугольника. Следовательно, АМ > АС. Так как наклонная АМ взята нами произвольно, то можно утверждать, что всякая наклонная к прямой больше перпендикуляра к этой прямой (а перпендикуляр короче всякой наклонной), если они проведены к ней из одной и той же точки.

Верно и обратное утверждение, а именно: если отрезок АС (рис.) меньше всякого другого отрезка, соединяющего точку АС любой точкой прямой ОВ, то он является перпендикуляром к ОВ. В самом деле, отрезок АС не может быть наклонной к ОВ, так как тогда он не был бы самым коротким из отрезков, соединяющих точку А с точками прямой ОВ. Значит, он может быть только перпендикуляром к ОВ.

Длина перпендикуляра, опущенного из данной точки на прямую, принимается за расстояние от данной точки до этой прямой.

Теорема 2. Если две наклонные, проведённые к прямой из одной и той же точки, равны, то равны и их проекции .

Пусть ВА и ВС — наклонные, проведённые из точки В к прямой АС (рис.), причём АВ = ВС. Нужно доказать, что равны и их проекции.

Для доказательства опустим из точки В перпендикуляр ВО на АС. Тогда АО и ОС будут проекции наклонных АВ и ВС на прямую АС. Треугольник АВС равнобедренный по условию теоремы. ВО — высота этого треугольника. Но высота в равнобедренном треугольнике, проведённая к основанию, является в то же время и медианой этого треугольника.

Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой.

Пусть АС и СВ — наклонные к прямой АВ (рис.). СО ⊥ АВ и АО = ОВ.

Требуется доказать, что АС = ВС.

В прямоугольных треугольниках АОС и ВОС катеты АО и ОВ равны. СО — общий катет этих треугольников. Следовательно, ΔAOС = ΔВОС. Из равенcтва треугольников вытекает, что АС = ВС.

Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.

Пусть АВ и ВС — наклонные к прямой АО; ВО ⊥ АО и АО>СО. Требуется доказать, что АВ > ВС.

1) Наклонные расположены по одну сторону перпендикуляра.

Угол АСЕ внешний по отношению к прямоугольному треугольнику СОВ (рис.), а поэтому ∠АСВ > ∠СОВ, т. е. он тупой. Отсюда следует, что АВ > СВ.

2) Наклонные расположены по обе стороны перпендикуляра. Для доказательства отложим на АО от точки О отрезок ОК = ОС и соединим точку К с точкой В (рис.). Тогда по теореме 3 имеем: ВК = ВС, но АВ > ВК, следовательно, АВ > ВС, т. е. теорема справедлива и в этом случае.

Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую.

Пусть КС и ВС — наклонные к прямой КВ (рис.), СО ⊥ КВ и КС > ВС. Требуется доказать, что КО > ОВ.

Между отрезками КО и ОВ может быть только одно из трёх соотношений:

КО не может быть меньше ОВ, так как тогда по теореме 4 наклонная КС была бы меньше наклонной ВС, а это противоречит условию теоремы.

Точно так же КО не может равняться ОВ, так как в этом случае по теореме 3 КС = ВС, что также противоречит условию теоремы.

Следовательно, остаётся верным только последнее соотношение, а именно, что КО > ОВ.

Как найти проекцию наклонной

Раздел ІІ. СТЕРЕОМЕТРИЯ

§8. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. ПРОЕКЦИЯ НАКЛОННОЙ НА ПЛОСКОСТЬ.

2. Свойства перпендикуляра и наклонной.

Рассмотрим свойства перпендикуляра и наклонной.

1) Перпендикуляр, опущенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к плоскости.

На рисунке 411: АН АК.

2) Если две наклонные, проведенные из данной точки к плоскости, равны, то равны их проекции.

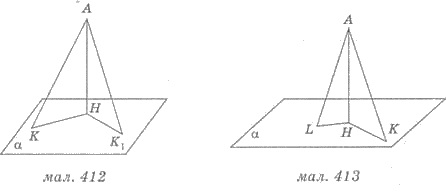
На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K ₁ и перпендикуляр АН и АК = АК ₁ . Тогда по свойству: НК = НК₁.

3) Если две наклонные, проведенные из данной точки к данной плоскости, имеют равные проекции, то они равны между собой.

На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K ₁ и перпендикуляр АН, причем КН = К ₁ Н. Тогда по свойству: АК = АК ₁ .

4) Если из данной точки проведены к плоскости две наклонные, то большая наклонная имеет большую проекцию.

На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, A К > AL . Тогда по свойству: H К > HL .

5) Если из данной точки проведены к плоскости две наклонные, то большей из них является та, которая имеет большую проекцию на данную плоскость.

На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, НК > Н L . Тогда по свойству: АК > А L .

Пример 1. Из точки к плоскости проведены две наклонные, длины которых 41 см и 50 см. Найти проекции наклонных, если они относятся, как 3 : 10, и расстояние от точки до плоскости.

Решения. 1) А L = 41 см; АК = 50 см (рис. 413). По свойством имеем Н L НК. Обозначим Н L = 3 х см, НК = 10 х см, АН = h см. АН — расстояние от точки А до плоскости α .

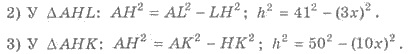
4) Приравнивая, получаем 41 2 — 9х 2 = 50 2 — 100 х 2 ; х 2 = 9; х = 3 (учитывая х > 0). Итак, Н L = 3 ∙ 3 = 9 (см), НК = 10 ∙ 3 = 30 (см).

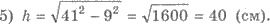
Пример 2. С данной точки к плоскости проведены две наклонные, каждая по см. Угол между наклонными равен 60°, а угол между их проекциями — прямой. Найти расстояние от точки до плоскости.

1) АС = ВС = см — наклонные, ВАС = 60°; ВНС = 90° (рис. 414). Необходимо найти АН.

2) В рівнобедреному треугольнике АВС: 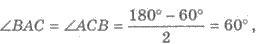поэтому ∆ АВС — равносторонний; ВС = см.

3) Так как АВ = АС, то НВ = НС ; обозначим НВ = НС = х см. Тогда в ∆ ВНС :

Как найти проекцию наклонной

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

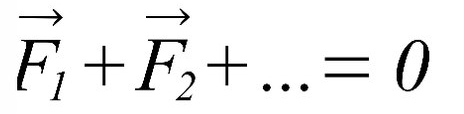
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

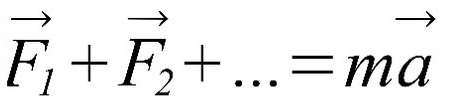
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

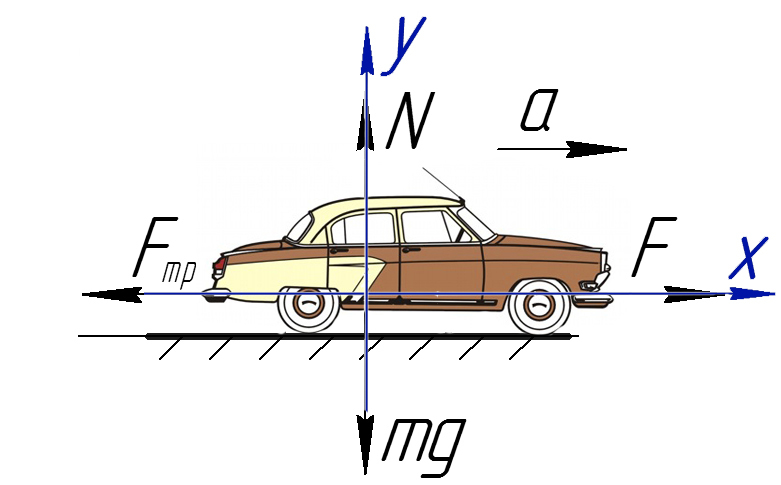
На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

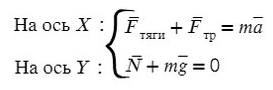
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

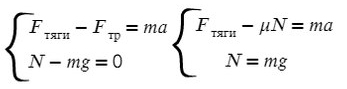
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

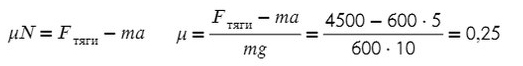
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

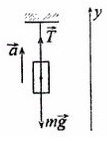
T — сила натяжения нити

На ось X: нет сил

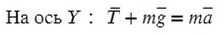
Разберемся с направлением сил на ось Y:

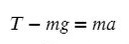
Выразим T (силу натяжения) и подставим числительные значения:

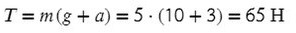
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

Простой пример: мальчик тянет санки

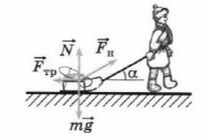
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

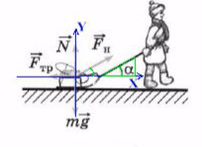Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

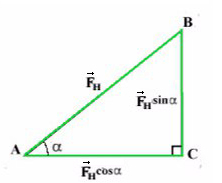
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

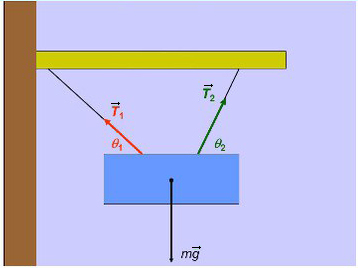
Введем оси и спроецируем силы:

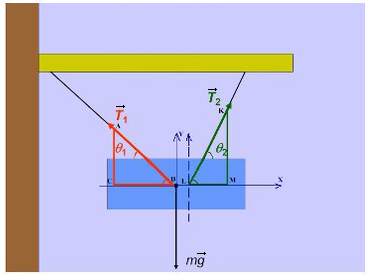
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

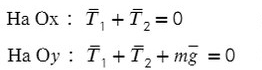
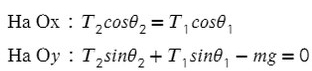
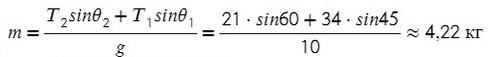
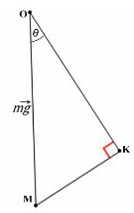
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

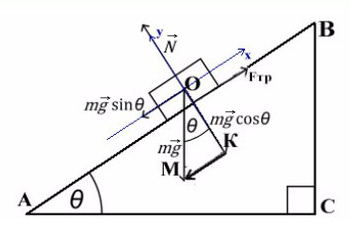
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM:

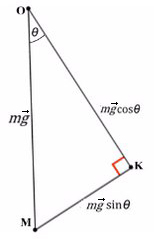
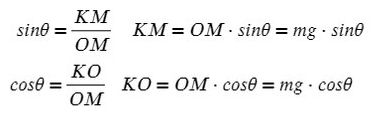Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

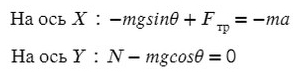
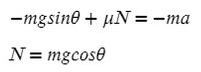
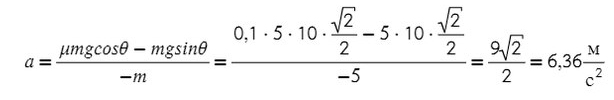
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

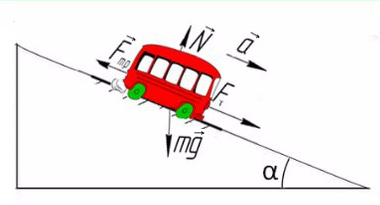
Введем оси X и Y. Спроецируем mg на оси:

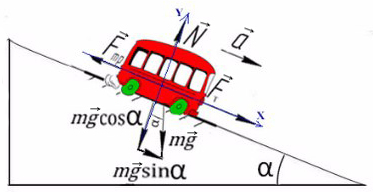
Запишем второй закон Ньютона на X и Y:

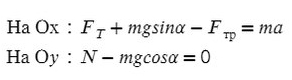
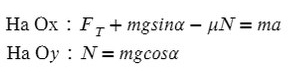
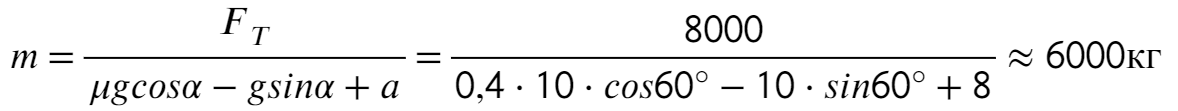
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

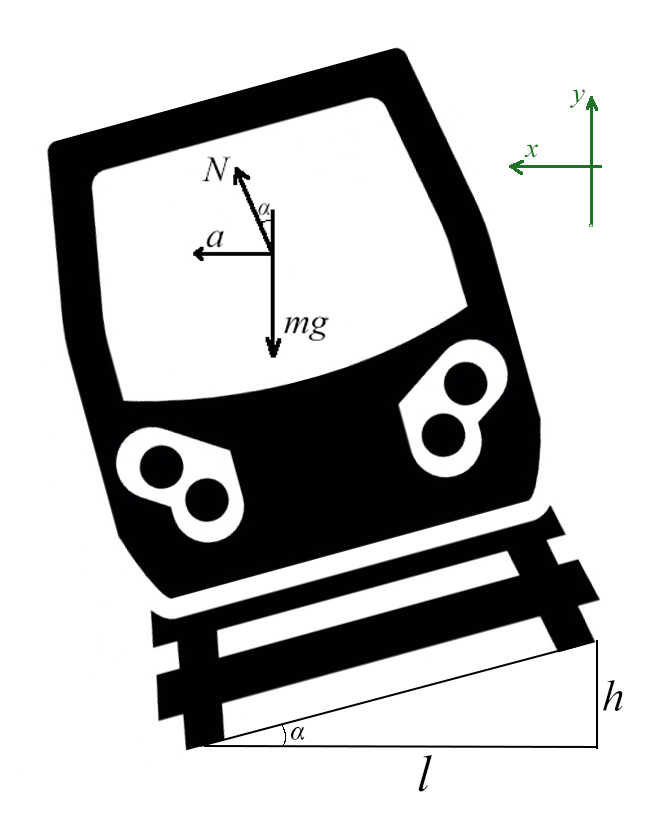
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

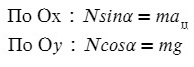
Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

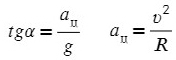
Тангенс — это отношение противолежащего катета к прилежащему:

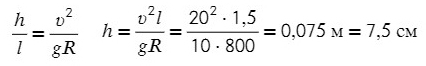
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.