Задача 1 Разложить вектор ![]() По векторам
По векторам ![]() и
и ![]() .
.
Пусть ![]() , т. е.
, т. е. ![]() ;
; ![]()
![]()
След., вектор ![]() .
.
Задача 2 Найти длину диагонали параллелограмма, построенного на векторах ![]() , если
, если ![]()
Рассм. диагонали параллелограмма ![]() ;
;
Вычислим ![]() ;
;
![]() ;
;
Задача 3 Показать, что точки ![]() Являются вершинами параллелограмма и найти проекцию одной из диагоналей на большую сторону параллелограмма.
Являются вершинами параллелограмма и найти проекцию одной из диагоналей на большую сторону параллелограмма.
Рассм. ![]()
![]() , след.
, след. ![]() – параллелограмм (так как две противоположные стороны параллельны и равны);
– параллелограмм (так как две противоположные стороны параллельны и равны);
Рассм. ![]() Рассм.
Рассм. ![]() ;
; ![]() ,
,
След. ![]() – большая сторона параллелограмма
– большая сторона параллелограмма ![]() ; рассм. диагональ
; рассм. диагональ ![]() ;
;
Вычислим  Вычислим
Вычислим ![]() ;
;
![]() .
.
Задача 4 Длина гипотенузы ![]() прямоугольного треугольника
прямоугольного треугольника ![]() равна
равна ![]() . Вычислить
. Вычислить ![]()
![]()
Задача 5 Найти момент силы![]() , приложенной в точке
, приложенной в точке ![]() относительно точки
относительно точки![]() , а также модуль и направляющие косинусы вектора силы
, а также модуль и направляющие косинусы вектора силы ![]()
1) ![]() , где
, где ![]() ;
; ![]() ;
;

![]() ;
;
2) ![]() ;
;
Направл. косинусы вектора ![]() :
: ![]() ;
; ![]() ;
; ![]() .
.
Задача 6 Треугольник ![]() построен на векторах
построен на векторах ![]() Найти длину высоты
Найти длину высоты ![]() , если векторы
, если векторы ![]() взаимно перпендикулярны и по модулю равны
взаимно перпендикулярны и по модулю равны ![]()
Рассм. векторы ![]() рассм.
рассм.  ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]()
Задача 7 Найти координаты вершины ![]() тетраэдра, если известно, что она лежит на оси
тетраэдра, если известно, что она лежит на оси ![]() , объём тетраэдра равен
, объём тетраэдра равен ![]() ,
, ![]() .
.
Пусть искомая вершина тетраэдра ![]() (т. к. т.
(т. к. т. ![]() );
);
Рассм. в-ры: ![]() ;
;
Рассм. смешанное произв-е:

Рассм. объём тетраэдра ![]() :
: ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ; след., возможные положения искомой т.
; след., возможные положения искомой т.![]() :
: ![]() ;
; ![]() .
.
Задача 8 В треугольнике ![]() известны координаты двух вершин:
известны координаты двух вершин: ![]() И точки пересечения медиан
И точки пересечения медиан ![]() . Составить уравнение высоты треугольника, проведённой из вершины
. Составить уравнение высоты треугольника, проведённой из вершины ![]() .
.

1) Определим координаты точки ![]() Как середины отрезка
Как середины отрезка ![]() :
:![]() ;
;
2) Определим координаты вершины ![]() , используя равенство
, используя равенство ![]() , где
, где ![]() ;
;
Рассм. ![]()
![]() ;
;
3) составим ур-е высоты ![]() : рассм. в-р
: рассм. в-р ![]() ;
;
Рассм. т.![]() И рассм. в-р
И рассм. в-р ![]() ; тогда по условию задачи
; тогда по условию задачи ![]() и
и ![]() и, след., ур-е прямой
и, след., ур-е прямой ![]() , проходящей через
, проходящей через ![]() Перпендикулярно в-ру
Перпендикулярно в-ру ![]() , можно записать в виде:
, можно записать в виде: ![]() т. е.
т. е. ![]() .
.
Задача 9 В параллелограмме ![]() известны уравнения сторон
известны уравнения сторон ![]() и координаты точки пересечения диагоналей
и координаты точки пересечения диагоналей ![]() Составить уравнения двух других сторон и диагоналей параллелограмма.
Составить уравнения двух других сторон и диагоналей параллелограмма.
1) определим координаты точки ![]() как точки пересечения прямых
как точки пересечения прямых ![]() :
:
![]() ;
;
2) определим координаты точки ![]() из условия, что т.
из условия, что т.![]() – середина отрезка
– середина отрезка ![]() :
:
 ;
;
3) составим уравнение диагонали ![]() как прямой, проходящей через точки
как прямой, проходящей через точки ![]() :
: ![]() ;
;

4) составим уравнение стороны ![]() как прямой, проходящей через точку
как прямой, проходящей через точку ![]() параллельно
параллельно
Прямой ![]() ;
;
5) составим уравнение стороны ![]() как прямой, проходящей через точку
как прямой, проходящей через точку ![]() Параллельно
Параллельно
Прямой ![]() ;
;
6) определим координаты точки ![]() как точки пересечения прямых
как точки пересечения прямых ![]() :
:
 ;
;
7) составим уравнение диагонали ![]() как прямой, проходящей через точки
как прямой, проходящей через точки ![]() :
: ![]() .
.
Задача 10 Составить уравнение плоскости, проходящей через точки ![]()
Пусть ![]() – искомая плоскость; рассм. векторы
– искомая плоскость; рассм. векторы ![]() ;
;
Рассм. норм. вектор  ;
;
Рассм. произв. т.![]() и рассм. вектор
и рассм. вектор ![]() ;
;
![]() , т. е.
, т. е. ![]() ;
;
Задача 11 Составить уравнение прямой ![]() , которая, проходит через точку
, которая, проходит через точку ![]() и пересекает две прямые
и пересекает две прямые ![]() и
и ![]() .
.
Рассм. направл. векторы прямых ![]() ;
;
Рассм. т.![]() ; рассм. векторы
; рассм. векторы ![]() ;
;
Пусть ![]() – плоскость, в которой лежат прямые
– плоскость, в которой лежат прямые ![]() ; пусть
; пусть ![]() – плоскость, в которой лежат прямые
– плоскость, в которой лежат прямые ![]() ; тогда искомая прямая
; тогда искомая прямая ![]() есть линия пересечения плоскостей
есть линия пересечения плоскостей ![]() ;
;
 ;
;
 ;
;
В качестве направл. вектора прямой ![]() можно взять вектор
можно взять вектор  ; выберем
; выберем ![]() ;
;
Запишем канонические ур-я прямой ![]() Как ур-я прямой, проходящей через т. А параллельно
Как ур-я прямой, проходящей через т. А параллельно
Вектору ![]() :
: ![]() ; параметрические ур-я прямой
; параметрические ур-я прямой ![]() :
: 
Задача 12 Составить уравнение геометрического места всех прямых, проходящих через точку ![]() перпендикулярно прямой
перпендикулярно прямой ![]() .
.
Запишем канонич. уравнения прямой ![]() в виде:
в виде: ![]() ; её направл. вектор
; её направл. вектор ![]() ;
;
Рассм. произв. прямую ![]() , удовлетв. условию задачи; рассм. произв. точку
, удовлетв. условию задачи; рассм. произв. точку ![]() и её направл. вектор
и её направл. вектор ![]() ;
; ![]() , т. е.
, т. е. ![]() ;
;
Плоскость ![]() и есть искомое геометрическое место.
и есть искомое геометрическое место.
Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением
Определителя по первой строке.

1) Непосредственное вычисление:
![]()
2) Разложение по 1-й строке:
![]()
Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы:
![]()
Запишем данную систему уравнений в матричной форме: ![]() , (1) , где
, (1) , где  ;
; ![]() ;
; ![]() ;
;
Рассм. опред-ль матрицы ![]() :
:  ,
,
След., матр. ![]() – невырожденная и можно применять формулы Крамера и вычислять обратную матр.
– невырожденная и можно применять формулы Крамера и вычислять обратную матр. ![]() ;
;
1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул: ![]() ,
, ![]() ,
, ![]() , где
, где ![]() ;
;
 ;
;
 ;
;
 ;
; ![]() ,
, ![]() ,
, ![]() ;
;
![]() реш–е с–мы ур–й (1) в коорд. форме:
реш–е с–мы ур–й (1) в коорд. форме: ![]() вектор–решение с-мы (1):
вектор–решение с-мы (1): ![]() ;
;
2) получим реш–е с–мы ур–й (1) с помощью обратной матр. ![]() :
:
![]() , след., матр.
, след., матр.![]() – невырожденная и существует обратная матр.
– невырожденная и существует обратная матр. ![]() ;
;
Умножим рав-во (1) слева на матрицу ![]() :
: ![]() ,
, ![]() ; вычислим обратную матр.
; вычислим обратную матр. ![]() :
:
Находим алгебр. дополнения ![]() для всех эл-тов матрицы
для всех эл-тов матрицы ![]() и составим из них м-цу
и составим из них м-цу ![]() :
:
![]()
![]()
Транспонируем м-цу ![]() и получим «присоединённую» м-цу
и получим «присоединённую» м-цу 
Разделим все эл-ты присоедин. м-цы ![]() на опр-ль
на опр-ль ![]() и получим обратную матр.
и получим обратную матр. ![]() :
:
![]()
Находим теперь вектор-решение ![]() :
: ![]()
Задача 15 Установить, являются ли векторы ![]() линейно зависимыми.
линейно зависимыми.
Вычислим ранг системы векторов ![]() методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:
методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

 ранг матрицы
ранг матрицы ![]() , след. данная система векторов линейно независима.
, след. данная система векторов линейно независима.
Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса.

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

 имеем
имеем ![]() ;
;
Так как ![]() , то по теореме Кронекера – Капелли данная система уравнений совместна, а так как
, то по теореме Кронекера – Капелли данная система уравнений совместна, а так как ![]() , то система имеет бесконечное множество решений; объявим
, то система имеет бесконечное множество решений; объявим ![]() свободной переменной и выпишем общее решение системы в координатной форме:
свободной переменной и выпишем общее решение системы в координатной форме:

![]()
![]() общее решение системы имеет вид:
общее решение системы имеет вид: 
Задача 17 Найти матрицу преобразования, выражающего ![]() Через
Через ![]() , если
, если
![]()
Запишем данные преобразования в матричной форме: ![]() , где матрицы
, где матрицы ![]() и
и
Вектор – столбцы ![]() имеют вид:
имеют вид: ![]()
Рассм. ![]() ;
;
Вычислим матрицу  .
.
Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей
![]()
1) Находим собств. значения ![]() линейного преобразования
линейного преобразования ![]() , т. е. корни характеристического уравнения
, т. е. корни характеристического уравнения ![]() :
:
Рассм. ![]()
![]()
![]() – собств. значения (действ.) лин. преобр-я
– собств. значения (действ.) лин. преобр-я ![]() ;
;
2) находим собств. векторы линейного преобразования ![]() , соотв. собств. значениям
, соотв. собств. значениям ![]() :
:
А) рассм. ![]()
Рассм. ![]()
 Пусть
Пусть ![]() , тогда вектор
, тогда вектор ![]() ;
;
Б) рассм. ![]()
Рассм. ![]()
![]()
Пусть ![]() , тогда
, тогда ![]() ,
, ![]() вектор
вектор ![]() ;
;
Пусть ![]() , тогда
, тогда ![]() ,
, ![]() вектор
вектор ![]() ;
;
След. собств. векторы линейного преобразования ![]() суть:
суть:
![]() ;
; ![]() ;
; ![]() .
.
| < Предыдущая |
|---|
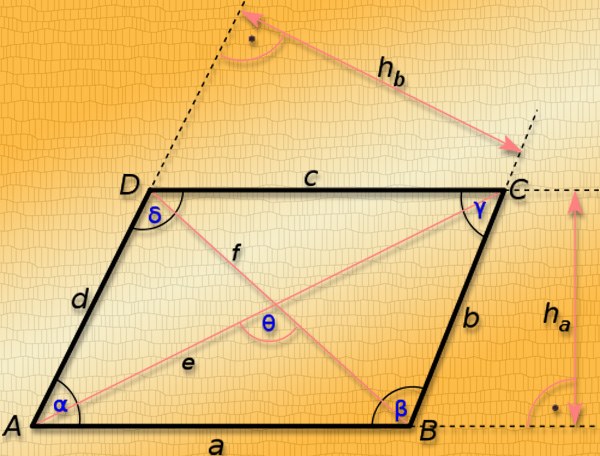
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
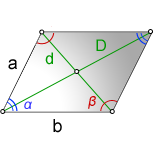
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
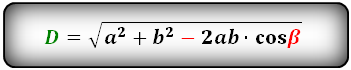
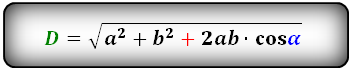
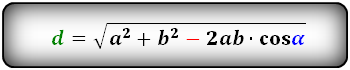

Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
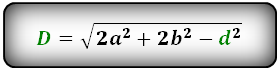
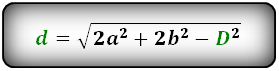
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.

D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
S – площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
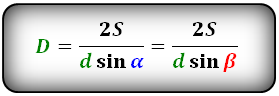
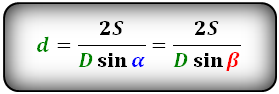
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
Плоскость а проведена через сторону AD параллелограмма ABCD.Найдите проекции сторон параллелограмма на эту плоскость, если BC=19 и проекции диагоналей параллелограмма на плоскость а равны 20 и 22.
АС1 находить нет нужды, она по условию равна 22.
Рассмотрим данный к задаче рисунок. и проекции АВ1 и В1С1 сторон АВ и ВС параллелограмма ABCD на плоскость α.
Так как
ВС
параллельна прямой АD, лежащей на плоскости α, она
параллельна
и самой
плоскости α
.
Поэтому проекция В1С1 стороны ВС на плоскость равна 19.
Проекции диагоналей на плокость равны диагоналям параллелограмма АВ1С1D со сторонами АД=В1С1=19.
Нарисуем этот параллелограмм AB1C1D.
По формуле Герона найдем площадь треугольника АОD
Полупериметр треугольника АОД=(11+10+19):2=20
S=√1800=30√2
Из площади треугольника АОД найдем его высоту ОК к основанию АД по формуле площади треугольника:
S=аh:2
2S= 60√2
ОК=60√2:19=4,4659…..≈ 4,466
Продлим АД
до пересечения с высотой С1Н, опущенной из С1,
и получим
прямоугольный треугольник АС1Н.
С1Н=2ОК= ≈ 8,93
Найдем в нем сторону АН по т. Пифагора.
АН=√(АС1²-НС1²)≈ √(22²-8,93²)=√(484-79,7449)=≈20,1
Отсюда ДН=20,1-19=1,1
Из треугольника ДНС1 найдем длину ДС1, она равна также и АВ1.
ДС1=√(НС1²+НД²)=√(79,7449+1,21)=√80,9549=8,9974≈9
Примеры решения задач

Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах
![]()
и
![]()
,
где
![]()
таковы, что
![]()
.
Решение.
Диагонали параллелограмма есть векторы
![]()
и
![]()
.
Вычислим длину вектора
:
![]()
.
Аналогично
вычисляется длина вектора
![]()
.
Задача 2.
Найдите вектор
,
коллинеарный вектору
![]()
и удовлетворяющий условию
![]()
.
Решение.
Обозначим вектор
![]()
,
тогда из условий задачи
![]()
или
![]()
,
тогда
![]()
.
Итак:
![]()
.
Задача 3.
Найти проекцию вектора
![]()
на направление вектора
![]()
.
Решение.
![]()
.
По формуле проекции вектора на ось будет
иметь место равенство
![]()
.
Задача 4.
Даны векторы:
![]()
.
П
роверить,
есть ли среди них коллинеарные. Найти
![]()
.
Решение.
Условие коллинеарности имеет вид
![]()
.
Этому условию удовлетворяют векторы
![]()
.
Следовательно, они коллинеарны. Найдем
длины
векторов
![]()
:
![]()
.
Угол между векторами
определяется по формуле
![]()
.
Т
огда
![]()
,
![]()
.
Используя формулу
![]()
,
получим
![]()
.
Задача 5.
На материальную точку действуют силы
![]()
.
Найти работу равнодействующей этих сил
при перемещении точки из положения
![]()
в положение
![]()
.
Решение.
Найдем силу
и вектор перемещения
![]()
.
![]()
,
тогда искомая работа
![]()
.
Задачи
1. Векторы
взаимно перпендикулярны, а вектор
образует с ними углы
![]()
.
Зная, что
![]()
,
найти: 1)
![]()
;
2)
![]()
.
2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах
![]()
,
если известно, что
![]()
.
3. Доказать, что
вектор
![]()
перпендикулярен к вектору
.
4. Зная, что
![]()
,
определить, при каком значении коэффициента
векторы
![]()
окажутся перпендикулярными.
5. Даны вершины
четырехугольника:
![]()
.
Доказать, что его диагонали взаимно
перпендикулярны.
6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
![]()
.
7. Даны силы
![]()
.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку
![]()
.
8. Даны вершины
треугольника:
![]()
.
Найти проекцию вектора
на вектор
.
9. Найти вектор
![]()
,
перпендикулярный векторам
![]()
,
если известно, что его проекция на вектор
![]()
равна единице.
10. Сила, определяемая
вектором
![]()
,
разложена по трем направлениям, одно
из которых задано вектором
![]()
.
Найти составляющую силы
в направлении вектора
.
11. Даны вершины
треугольника:
![]()
.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.
12. Даны три
последовательные вершины параллелограмма:
![]()
.
Найти его четвертую вершину D
и угол между векторами
![]()
.
13. На оси
![]()
найти точку, равноудаленную от точек
![]()
.
14. Доказать, что
треугольник с вершинами
![]()
![]()
прямоугольный.
Домашнее задание
1. Вычислить
скалярное произведение двух векторов
![]()
,
зная их разложение по трем единичным
взаимно перпендикулярным векторам
![]()
![]()
;
![]()
.
2. Найти длину
вектора
![]()
,
зная, что
![]()
– взаимно перпендику-
лярные орты.
3. Векторы
![]()
попарно образуют друг с другом углы,
каждый из которых равен
.
Зная, что
![]()
,
определить модуль вектора
![]()
.
4. Доказать, что
вектор
![]()
перпендикулярен к вектору
.
5. Даны векторы
![]()
,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису
![]()
.
6. Вычислить угол
между векторами
![]()
,
где
![]()
–
единичные взаимно перпендикулярные
векторы.
7. Даны силы
![]()
,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения
![]()
в положение
![]()
.
8. Даны вершины
треугольника
![]()
.
Определить его внутренний угол при
вершине В.
9. Вычислив
внутренние углы треугольника с вершинами
![]()
,
![]()
,
убедиться, что этот треугольник
равнобедренный.
10. Найти вектор
,
зная, что он перпендикулярен векторам
![]()
и
![]()
.
11. Найти вектор
,
коллинеарный вектору
![]()
и удовлетворяющий условию
![]()
,
где
![]()
.
12. Вычислить
проекцию вектора
![]()
на ось вектора
![]()
.
13. Даны векторы
![]()
.
Вычислить
![]()
.
14. Даны точки
![]()
.
Вычислить проекцию вектора
![]()
на ось вектора
![]()
.
Ответы к задачам
1) -7, 13. 2) 15,
![]()
.
4)
![]()
.
6)
![]()
.
7) 2. 8) -1/3.
9)
![]()
.
10)
![]()
.
11)
![]()
.
12)
![]()
.
13)
![]()
.
Ответы к домашнему
заданию
1) 9. 2) 5. 3) 10. 5)
![]()
.
6)
![]()
.
7) 13. 8)
.
10)
![]()
.
12) 6. 13) 5. 14) 3.
Занятие 3
Векторое
произведения векторов. Смешанное
произведение векторов
Определение1.
Тройка
некомпланарных векторов
называется правой (левой) если, находясь
внутри телесного угла, образованного
приведенными к общему началу векторами
и от него к
,
човершающимся против часовой стрелки
(по часовой стрелке)

![]()
Тройка правая
Тройка левая
Определение
2. Векторным
произведением вектора
на вектор
называется вектор
![]()
,
длина и направление которого определяются
условиями:
1.
![]()
,
где
– угол между
![]()
.
2.
![]()
.
3.
– правая тройка векторов.
Свойства
векторного произведения
1.
![]()
(свойство антиперестановочности
сомножителей);
2.
![]()
(распределительное относительно суммы
векторов);
3.
![]()
(сочетательное относиельно числового
множителя);
4.
![]()
(равенство нулю векторного произведения
означает коллинеарность векторов);
5.
![]()
,
т. е. момент сил равен векторному
произведению силы на плечо.
Если вектор
![]()
,
то
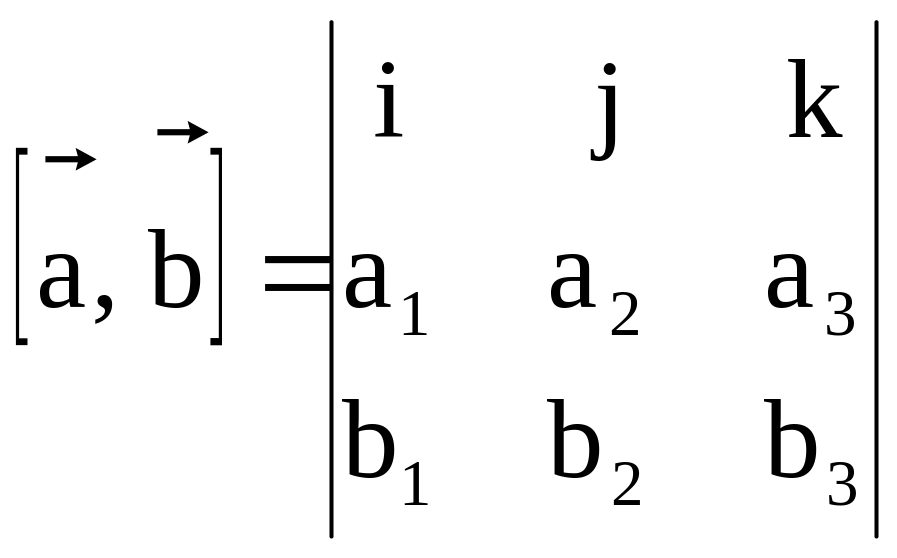
.
Определение
3. Смешанным
произведением
![]()
трех векторов называется число,
определяемое следующим образом:
![]()
.
Если векторы заданы своими координатами:
![]()
,
то
~

.
Свойства
смешанного произведения
1. Необходимым и
достаточным условием компланарности
векторов
является равенство
= 0.
2. Объем
параллелепипеда, построенного на
векторах
![]()
![]()
![]()
:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти диагональ параллелограмма, если даны стороны
Параллелограмм – это четырехугольник, противоположные стороны которого параллельны. Прямые, соединяющие его противоположные углы, называются диагоналями. Их длина зависит не только от длин сторон фигуры, но и от величин углов в вершинах этого многоугольника, поэтому без знания хотя бы одного из углов вычислить длины диагоналей можно только в исключительных случаях. Таковыми являются частные случаи параллелограмма – квадрат и прямоугольник.
Инструкция
Если длины всех сторон параллелограмма одинаковы (a), то эту фигуру можно назвать еще и квадратом. Величины всех его углов равны 90°, а длины диагоналей (L) одинаковы и могут быть рассчитаны по теореме Пифагора для прямоугольного треугольника. Умножьте длину стороны квадрата на корень из двойки – результат и будет длиной каждой из его диагоналей: L=a*√2.
Если о параллелограмме известно, что он является прямоугольником с указанными в условиях длиной (a) и шириной (b), то и в этом случае длины диагоналей (L) будут равны. И здесь тоже задействуйте теорему Пифагора для треугольника, в котором гипотенузой является диагональ, а катетами – две смежные стороны четырехугольника. Искомую величину рассчитайте извлечением корня из суммы возведенных в квадрат ширины и высоты прямоугольника: L=√(a²+b²).
Для всех остальных случаев знания одних только длин сторон хватит лишь для определения величины, включающей в себя длины сразу обеих диагоналей – сумма их квадратов по определению равна удвоенной сумме квадратов длин сторон. Если же в дополнение к длинам двух смежных сторон параллелограмма (a и b) известен еще и угол между ними (γ), то это позволит рассчитать длины каждого отрезка, соединяющего противоположные углы фигуры. Длину диагонали (L₁), лежащей напротив известного угла, найдите по теореме косинусов – сложите квадраты длин смежных сторон, от результата отнимите произведение этих же длин на косинус угла между ними, а из полученной величины извлеките квадратный корень: L₁ = √(a²+b²-2*a*b*cos(γ)). Для нахождения длины другой диагонали (L₂) можно воспользоваться свойством параллелограмма, приведенным в начале этого шага – удвойте сумму квадратов длин двух сторон, от результата отнимите квадрат уже рассчитанной диагонали, а из полученного значения извлеките корень. В общем виде эту формулу можно записать так: L₂ = √(a²+b²- L₁²) = √(a²+b²-(a²+b²-2*a*b*cos(γ))) = √(a²+b²-a²-b²+2*a*b*cos(γ)) = √(2*a*b*cos(γ)).
Источники:
- как найти длину диагонали параллелограмма
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
