Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 – 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
В данной публикации мы рассмотрим, что такое проекция вектора на ось или на другой вектор, и приведем формулу, с помощью которой можно найти значение этой проекции. Также разберем примеры решения задач по этой теме.
- Нахождение проекции вектора
- Примеры задач
Нахождение проекции вектора
Проекция вектора AB на ось l – это число, которое равняется отрезку A1B1. Точки A1 и B1 при этом являются проекциями точек A и B на ось l.
Проекция вектора a на направление вектора b – это число, которое равно проекции a на ось, проходящую через b.
Формула для нахождения проекции вектора на вектор
Рассчитать проекцию a на направление b можно следующим образом:
Примеры задач
Задание 1
Найдем проекцию вектора a = {3; 5} на b = {2; 8}.
Решение:
1. Сперва посчитаем скалярное произведение заданных векторов:
a · b = 3 · 2 + 5 · 8 = 46
2. Теперь вычислим длину (модуль) b:
3. Остается только воспользоваться формулой выше для нахождения проекции вектора:
Задание 2
Вычислим проекцию вектора a = {4; -7; 5} на b = {11; 3; 6}.
Решение:
Поочередно выполняем те же самые действия, что и в примере, разобранном выше.
a · b = 4 · 11 + (-7) · 3 + 5 · 6 = 53
Содержание:
- Формула
- Примеры нахождения проекции вектора на вектор
Формула
Чтобы найти проекцию вектора $bar{a}$ на вектор
$bar{b}$, надо
скалярное произведение указанных векторов поделить на
длину (модуль) вектора
$bar{b}$, то есть
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}$$
В случае если векторы заданы на плоскости и имеют координаты
$bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Если векторы заданы в пространстве, то есть имеют координаты bar{a}=left(a_{x} ; a_{y} ; a_{z}right) text { и } bar{b}=left(b_{x} ; b_{y} ; b_{z}right), то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Примеры нахождения проекции вектора на вектор
Пример
Задание. Найти проекцию вектора
$bar{a}$ на вектор
$bar{b}$, если
$bar{a}=(-1 ; 0)$ и $bar{b}=(3 ;-4)$
Решение. Для нахождения проекции вектора
$bar{a}$ на вектор
$bar{b}$, будем использовать формулу
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Подставляя в неё координаты заданных векторов, получим:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{-1 cdot 3+0 cdot(-4)}{sqrt{3^{2}+(-4)^{2}}}=frac{-3+0}{sqrt{9+16}}=frac{-3}{sqrt{25}}=-frac{3}{5}$$
Ответ. $Пр_{bar{b}} bar{a}=-frac{3}{5}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти проекцию вектора
$bar{a}=(-2 ; 3 ; 0)$ на вектор
$bar{b}=(-2 ; -1 ; 5)$
Решение. Подставляя координаты заданных векторов в формулу
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
получим:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|b|} =frac{-2 cdot(-2)+3 cdot(-1)+0 cdot 5}{sqrt{(-2)^{2}+(-1)^{2}+5^{2}}}=$$
$$=frac{4-3+0}{sqrt{4+1+25}}=frac{1}{sqrt{30}}$$
Ответ. $Пр_{bar{b}} bar{a}=frac{1}{sqrt{30}}$
Читать дальше: как найти длину вектора.
1.7.1. Как найти проекцию вектора на вектор?
Рассмотрим ненулевые векторы 
и 
:
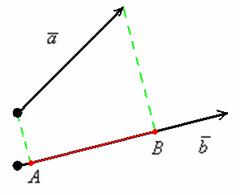
Спроецируем вектор 
на вектор 
, для этого из начала и конца вектора 
опустим перпендикуляры на вектор 
(зелёные пунктирные линии).
Представьте,
что на вектор 
перпендикулярно сверху падают
лучи света. Тогда отрезок 
будет «тенью»
вектора 
. Проекцией вектора 
на вектор 
является ДЛИНА отрезка 
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: 
, «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись 
читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами 
острый (как на рисунке выше), то 
Если векторы 
ортогональны, то 
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами 
тупой (на рисунке мысленно переставьте стрелочку вектора 
), то 
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора 
на любой ненулевой сонаправленный вектор
будет точно такой же:
– фактически это проекция вектора
на прямую 
, которая содержит сонаправленные векторы 
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно 
, то
добавится знак «минус»:
Отложим наши подопытные векторы от одной точки:
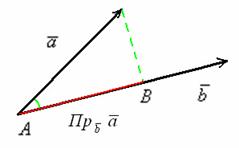
и рассмотрим прямоугольный треугольник. Косинус угла 
– есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
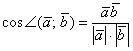
…все ли догадались, что будет дальше?
Приравниваем формулы:
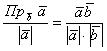
и сокращаем знаменатели обеих частей на 
,
получая формулу для вычисления проекции:
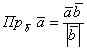
Распишем её в координатах:
Если векторы плоскости 
и 
заданы в ортонормированном базисе 
, то проекция вектора 
на вектор 
выражается формулой:
Если векторы пространства 
заданы в ортонормированном базисе 
, то проекция вектора 
на вектор 
выражается формулой:
Легко убедиться, что проекция вектора 
на
коллинеарный вектор 
может
отличаться лишь знАком, приведу выкладки для «плоского» случая 
:
, если 
, и 
, если 
Задача 34
Найти проекцию вектора 
на вектор 
Решение в одну строчку:
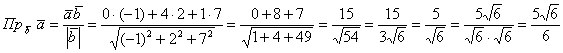, на завершающем шаге я умножил числитель и
знаменатель на 
, избавившись тем самым от
иррациональности в знаменателе.
Ответ: 
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами 
.
Найти:
а) проекцию стороны 
на сторону 
;
б) проекцию стороны 
на сторону 
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора 
на отрезок с известными концами 
? (как вариант, на продолжение этого отрезка). Находим вектор 
и используем формулу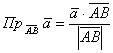 
. Либо вектор 
и формулу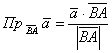 
. В
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 🙂
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:
1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
1.6.9. Как найти угол между векторами в координатах?
| Оглавление |
Автор: Aлeксaндр Eмeлин
Проекция вектора на вектор: онлайн-калькулятор
Осуществлять векторное проецирование стало проще с нашим сервисом. Студентам и школьникам, чтобы найти проекцию вектора на вектор при подготовке к занятиям, понадобится только ввести заданные координаты или точки. Дальнейшая последовательность действий определяется автоматически.
Вычисление проекции вектора а на вектор б происходит по формуле:
Пpb→a→=a→·b→b→
После отправки введенных данных на расчет вам доступно подробное решение и точный ответ.
Проекция вектора на вектор онлайн
Чтобы найти проекцию вектора на вектор онлайн по координатам, программа использует следующий алгоритм:
- Вычисляем скалярное произведение векторов.
- Рассчитываем модуль вектора.
- Подставляем данные в формулу и находим проекцию.
Для нахождения проекции по точкам необходимо предварительно вычислить векторы a и b.
На нашем сайте вы сможете не только найти проекцию вектора на вектор онлайн-калькулятором, но и произвести другие действия с векторами. Также в нашем сервисе представлены калькуляторы для решения задач на другие темы по алгебре и геометрии.
Использование сервиса не требует вносить оплату, регистрироваться, оставлять личные данные. Вы можете тренироваться без ограничений по количеству проверок. Каждый раз после отправки примера на расчет вы будете видеть подробное решение. Это позволит разобраться в теме, запомнить последовательность действий и применять их в дальнейшем для решения аналогичных задач.
Если в освоении темы даже после изучения примеров все равно возникают трудности, напишите онлайн-консультанту. Мы подберем грамотного преподавателя по вашему запросу. За минимальное количество занятий по выгодной цене вы заполните пробелы в знаниях.
