Как найти проекцию катета на прямую

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Проекции прямоугольного треугольника

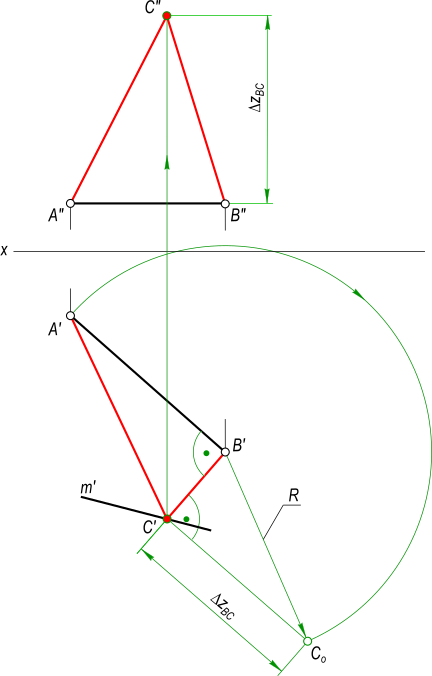
Построить Проекции прямоугольного треугольника ABC, если его катет AB(A`B`, . ) принадежит горизонтальной прямой h(h`, h”), катеты равны между собой, а вершина C принадлежит прямой m(m`, . ) и zC больше zB

AB – один из катетов прямоугольного треугольника, представляет собой прямую уровня – горизонтальную прямую так как A”B” || Ox. На горизонтальную плоскость проекции он проецируется в натуральную величину. Выполняем построение BC: – прямой угол при вершине B проецируется без искажения на горизонтальную плоскость проекции, следовательно здесь можно провести направление для катета BC; – в пересечении направления катета BC с m` получим C`. По способу прямоугольного треугольника определяем Δz = zC-zB: – из центра O описываем дугу радиусом R=|AB|=A`B` до пересечения с направлением перпендикуляра в точке C0; – определяем разницу аппликат катета BC – Δz. Откладываем Δz на фронтальной плоскости проекций от точки B” и по линии проекционной связи находим точку C”.

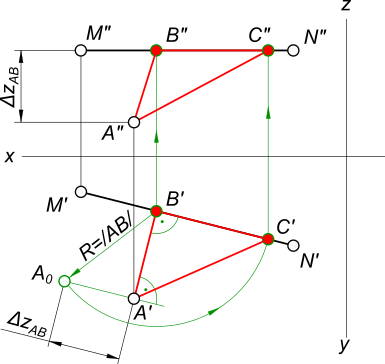
Построить проекции прямоугольного равнобедренного треугольника ABC, катет которого BC лежит на прямой MN. A(60,40,10), M(75,10,30); N(15,25,30).

Так как zM=zN делаем вывод, что отрезок MN – горизонтальная прямая и мы можем опустить из точки A перпендикуляр на него. В пересечении которого с M`N` находим B` и затем по линии проекционной связи B”. Находим натуральную величину катета AB способом прямоугольного треугольника:
– через точку A проводим перпендикуляр к AB и на нем откладываем ΔzAB и находим A0 и BA0; – откладываем на отрезке MN катет BC, описывая дугу радиуса R=/AB/ и отмечая точку C` и по линии проекционной связи C”; – вершины A`B`C` и A”B”C” соединяем прямыми линиями, получая проекции искомого треугольника.

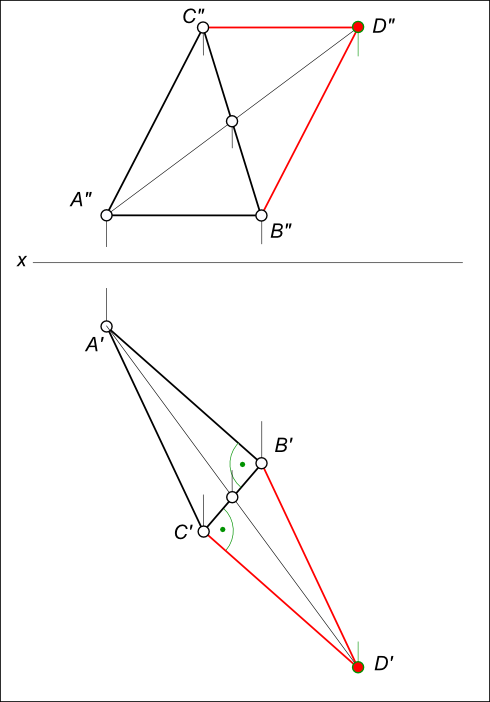
Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
Построить фронтальную и горизонтальную проекции параллелограмма ABCD

Построение параллелограмма заключается: – в проведении BD // AC; – в проведении CD // AB.

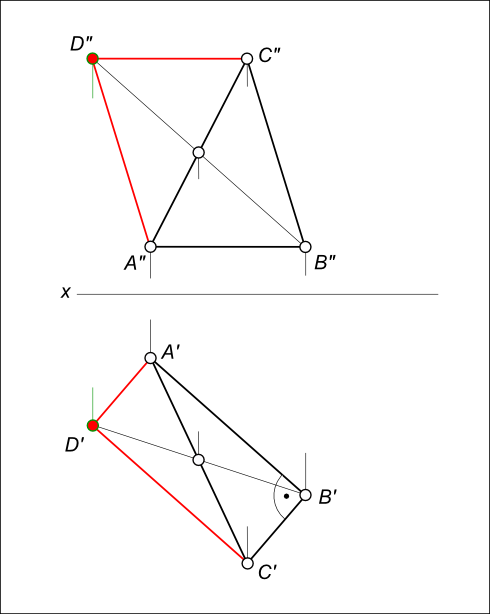
Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
Построить фронтальную и горизонтальную проекции квадрата ABCD

Построение квадрата заключается: – в проведении AD // BC; – в проведении CD // AB.

Прямоугольный треугольник формулы

Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

Прямоугольный треугольник: формулы площади и проекции

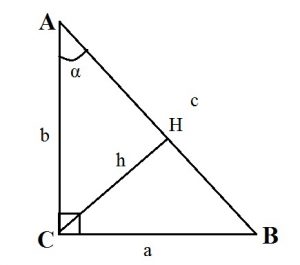
1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH 2 = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA 2 = AB·AH; CB 2 = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.

Прямоугольный треугольник: формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. ctgα = AC:BC.
5. Основное тригонометрическое тождество: cos 2 α + sin 2 α = 1.
6. Теорема косинусов: b 2 = a 2 + c 2 – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

Прямоугольный треугольник: формулы для описанной окружности

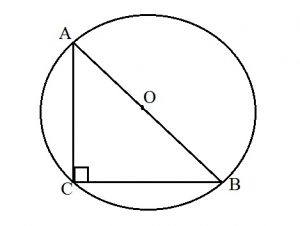
1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник: формулы для вписанной окружности

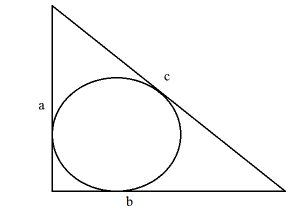
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Проекции катетов на гипотенузу

Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

[spoiler title=”источники:”]

[/spoiler]

Пусть треугольник ABC — прямоугольный с прямым углом при вершине B; AB = 30 [см], AC = 60 [см]. Опустим из вершины B высоту на AC в точку D. Требуется найти AD:

Т.к., DB — высота, то треугольники ADB и CDB — прямоугольные. Теорема Пифагора для всех трёх имеющихся треугольников позволяет записать такую систему уравнений:

30^2 + BC^2 = 60^2, (1)

CD^2 + DB^2 = BC^2, (2)

AD^2 + DB^2 = 30^2, (3)

AD + CD = 60. (4)

Из (1), BC^2 = 60^2 – 30^2. Приравниваем к (2) и получаем CD^2 + DB^2 = 60^2 – 30^2. Подставляем сюда CD из (4):

(60-AD)^2 + DB^2 = 60^2 – 30^2 =>

=> 60^2 – 2*60*AD + AD^2 + DB^2 = 60^2 – 30^2 =>

=> AD^2 – 2*60*AD + DB^2 + 30^2 = 0.

В полученное уравнение подставляем DB^2 из (3):

AD^2 – 2*60*AD + 30^2 – AD^2 + 30^2 = 0 =>

=> -2*60*AD = -2*30^2 => 60*AD = 30^2 =>

=> AD = 30^2/(2*30) = 30/2 = 15 [см].