Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Если имеем ось L и ненулевой вектор AB→, то можем построить вектор A1B1⇀, обозначив проекции его точек A1 и B1.
A1B→1 будет являться проекцией вектора AB→ на L.
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. npLAB→→ принято обозначать проекцию AB→ на L. Для построения проекции на L опускают перпендикуляры на L.
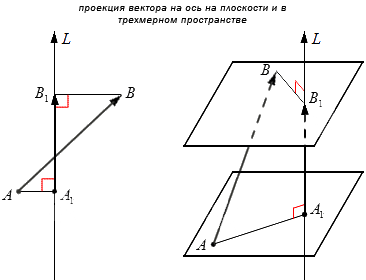
Пример проекции вектора на ось.
На координатной плоскости Оху задается точка M1 (x1, y1). Необходимо построить проекции на Ох и Оу для изображения радиус-вектора точки M1. Получим координаты векторов (x1, 0) и (0, y1).
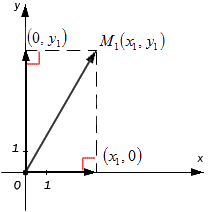
Если идет речь о проекции a→ на ненулевой b→ или проекции a→ на направление b→, то имеется в виду проекция a→на ось, с которой совпадает направление b→. Проекция a→ на прямую, определяемая b→, имеет обозначение npb→a→→. Известно, что когда угол междуa→ и b→, можно считать npb→a→→ и b→ сонаправленными. В случае, когда угол тупой, npb→a→→ и b→противоположно направлены. В ситуации перпендикулярностиa→ и b→, причем a→ – нулевой, проекция a→ по направлению b→ является нулевым вектором.
Числовая проекция вектора на ось
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.
Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.
Числовая проекция AB→ на L имеет обозначениеnp LAB→, а a→ на b→ – npb→a→.
Исходя из формулы, получим npb→a→=a→·cosa→, b→^, откуда a→ является длиной вектора a→, a⇀, b→^ – угол между векторами a→ и b→.
Получим формулу вычисления числовой проекции: npb→a→=a→·cosa→, b→^. Она применима при известных длинах a→ и b→ и угле между ними. Формула применима при известных координатах a→ и b→, но имеется ее упрощенный вид.
Узнать числовую проекцию a→ на прямую по направлению b→ при длине a→ равной 8 и углом между ними в 60 градусов. По условию имеем a⇀=8, a⇀, b→^=60°. Значит, подставляем числовые значения в формулу npb⇀a→=a→·cosa→,b→^=8·cos 60°=8·12=4.
Ответ: 4.
При известном cos(a→, b→^)=a⇀, b→a→·b→, имеем a→, b→ как скалярное произведение a→ и b→. Следуя из формулы npb→a→=a→·cosa⇀, b→^, мы можем найти числовую проекцию a→ направленную по вектору b→ и получим npb→a→=a→, b→b→. Формула эквивалента определению, указанному в начале пункта.
Числовой проекцией вектора a→ на ось , совпадающей по направлению с b→, называют отношение скалярного произведения векторовa→ иb→ к длине b→. Формула npb→a→=a→,b→b→ применима для нахождения числовой проекции a→ на прямую, совпадающую по направлению с b→, при известных a→ и b→ координатах.
Задан b→=(-3, 4). Найти числовую проекцию a→=(1, 7) на L.
Решение
На координатной плоскости npb→a→=a→, b→b→ имеет вид npb→a→=a→, b→b→=ax·bx+ay·bybx2+by2, при a→=(ax, ay) и b→=bx, by. Чтобы найти числовую проекцию вектора a→ на ось L, нужно: npLa→=npb→a→=a→,b→b→=ax·bx+ay·bybx2+by2=1·(-3)+7·4(-3)2+42=5.
Ответ: 5.
Найти проекцию a→ на L, совпадающей с направлением b→, где имеются a→=-2, 3, 1 и b→=(3, -2, 6). Задано трехмерное пространство.
Решение
По заданнымa→=ax, ay, az и b→=bx, by, bz вычислим скалярное произведение: a⇀, b→=ax·bx+ay·by+az·bz. Длину b→ найдем по формуле b→=bx2+by2+bz2. Отсюда следует, что формула определения числовой проекции a→ будет: npb→a⇀=a→, b→b→=ax·bx+ay·by+az·bzbx2+by2+bz2.
Подставляем числовые значения: npLa→=npb→a→=(-2)·3+3·(-2)+1·632+(-2)2+62=-649=-67.
Ответ: -67.
Просмотрим связь междуa→ на L и длиной проекции a→ на L. Начертим ось L, добавив a→ и b→ из точки на L, после чего проведем перпендикулярную прямую с конца a→ на L и проведем проекцию на L. Существуют 5 вариаций изображения:
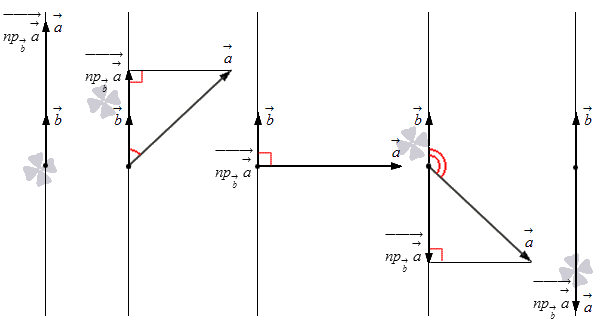
Первый случай при a→=npb→a→→ означает a→=npb→a→→, отсюда следует npb→a→=a→·cos(a,→b→^)=a→·cos0°=a→=npb→a→→.
Второй случай подразумевает применение npb→a→⇀=a→·cosa→,b→, значит, npb→a→=a→·cos(a→,b→)^=npb→a→→.
Третий случай объясняет, что при npb→a→→=0→ получаем npb⇀a→=a→·cos(a→,b→^)=a→·cos90°=0, тогда npb→a→→=0 и npb→a→=0=npb→a→→.
Четвертый случай показывает npb→a→→=a→·cos(180°-a→,b→^) = -a→·cos(a →, b→^), следует npb→a→=a→·cos(a→,b→^)=-npb→a→→.
Пятый случай показывает a→=npb→a→→, что означаетa→=npb→a→→, отсюда имеем npb→a→=a→·cosa→,b→^=a→·cos180°=-a→=-npb→a→.
Числовой проекцией вектора a→ на ось L, которая направлена как и b→, имеет значение:
- длины проекции вектора a→ на L при условии, если угол между a→ и b→ меньше 90 градусов или равен 0: npb→a→=npb→a→→ с условием 0≤(a→,b→)^<90°;
- ноля при условии перпендикулярности a→ и b→: npb→a→=0, когда (a→, b→^)=90°;
- длины проекции a→ на L, умноженной на -1, когда имеется тупой или развернутый угол векторов a→ и b→: npb→a→=-npb→a→→ с условием 90°<a→,b→^≤180°.
Дана длина проекцииa→ на L, равная 2. Найти числовую проекциюa→ при условии, что угол равен 5π6 радиан.
Решение
Из условия видно, что данный угол является тупым: π2<5π6<π. Тогда можем найти числовую проекцию a→ на L: npLa→=-npLa→→=-2.
Ответ: -2.
Дана плоскость Охyzс длиной вектора a→ равной 63,b→(-2, 1, 2) с углом в 30 градусов. Найти координаты проекции a→ на ось L.
Решение
Для начала вычисляем числовую проекцию вектораa→: npLa→=npb→a→=a→·cos(a→,b→)^=63·cos30°=63·32=9.
По условию угол острый, тогда числовая проекция a→= длине проекции вектора a→: npLa→=npLa→→=9. Данный случай показывает, что векторы npLa→→ и b→ сонаправлены, значит имеется число t, при котором верно равенство: npLa→→=t·b→. Отсюда видим, что npLa→→=t·b→, значит можем найти значение параметра t: t=npLa→→b→=9(-2)2+12+22=99=3.
Тогда npLa→→=3·b→ с координатами проекции вектора a→ на ось L равны b→=(-2,1, 2), где необходимо умножить значения на 3. Имеем npLa→→=(-6, 3, 6). Ответ: (-6, 3, 6).
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Для понятия проекции вектора на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
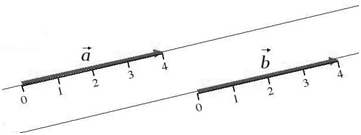
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
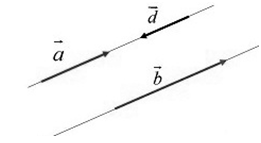
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
«Проекция вектора на ось. Как найти проекцию вектора» 👇
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A’$ – начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B’$ – конец искомого вектора. Вектор $overline{A’B’}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
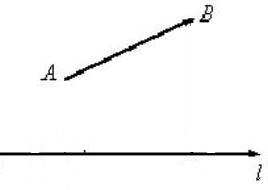
Постройте геометрическую проекцию $overline{AB}$ на ось $l$, изображенные на рисунке 6.
Решение.
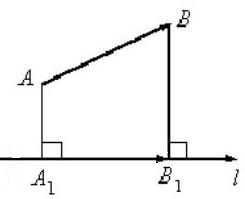
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A’$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B’$ (рис. 7).
Полученный на оси $l$ вектор $overline{A’B’}$ и будет искомой геометрической проекцией.
Замечание 1
Заметим, что если угол между вектором и осью острый, то проекция сонаправлена с осью, а если тупой, то проекция противоположно направлена с осью.
Числовая проекция
Как мы уже знаем, результатом алгебраической проекции будет неотрицательное действительное число.
Определение 9
Числовой (алгебраической) проекцией на ось будем называть неотрицательное число, равное длине вектора геометрической проекции.
Рассмотрим это понятие на примере задачи:
Пример 2
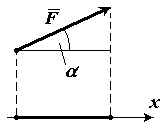
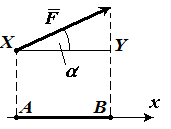
Найти числовую проекцию вектора $overline{F} на сонаправленную ему ось $x$, если угол между ними равняется $α$ (рис. 8). (рис. 8).
Решение.
Введем на рисунке следующие обозначения:
Видим, что длина вектора геометрической проекции, равняется длине $XY$. Из определения косинуса получим, что
$XY=|overline{F}|cosα$
где $|overline{F}|$ – длина вектора $overline{F}$. Это и будет искомая алгебраическая проекция на ось.
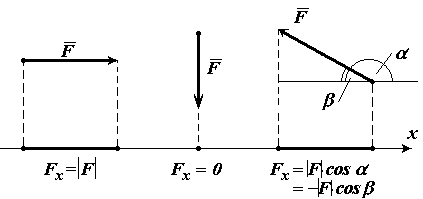
Другие случаи можете видеть на рисунке 9.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В математике существуют два определения:
1) геометрическая проекция вектора — вектор;
2) проекция вектора на ось — число.
Геометрическая проекция вектора — это вектор, который можно получить, если провести перпендикуляры от концов вектора до выбранной оси. Проекция начала вектора соответствует началу геометрической проекции, а проекция конца вектора соответствует концу геометрической проекции.

Ваш браузер не поддерживает HTML5 видео
Для вектора
v→
геометрическая проекция на оси (t) — это вектор
vt→
.
Для вектора
n→
геометрическая проекция на оси (y) — это вектор
ny→
.
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.

ax=4bx=−3
Если длина вектора
a→
равна
a→
и
α
— это острый угол, созданный вектором и осью (x), то скалярная проекция вектора вычисляется по формуле:
ax=a→⋅cosα
.
Знак проекции вектора выбирается в зависимости от направления оси.

На рисунке видно, что эту формулу можно получить из соотношения в прямоугольном треугольнике:
.
Обрати внимание!
Если вектор и ось проекций параллельны, то скалярная проекция на этой оси — число, которое равно длине вектора, если направления вектора и оси совпадают, или число, противоположное длине вектора, если направления вектора и оси — противоположные.
Если вектор и ось проекций перпендикулярны, то проекция вектора на этой оси равна (0).

at=3bt=−5ct=0dt=0
Вова Воробьёв
Профи
(726),
закрыт
11 лет назад
Как определить проекцию вектора на ось x,y?
Лучший ответ
Video
Просветленный
(28010)
13 лет назад
проекция на ось х = модуль вектора умножить на косинус угла между осью х и вектором
проекция на ось у = модуль вектора умножить на синус !
Хотя.. . да, лучше всётаки опустить перпендикуляры …
Остальные ответы
Анна Матвеева
Ученик
(175)
13 лет назад
опустить перпендикуляры от начала и конца вектора….
Владимир Токмаков
Ученик
(128)
6 лет назад
проекция на ось х = модуль вектора умножить на косинус угла между осью х и вектором
проекция на ось у = модуль вектора умножить на синус !
Похожие вопросы

|
x |
x1 x2 |
, |
y |
y1 y2 |
, |
z |
z1 z2 |
. |
(8. |
) |
||
|
2 |
2 |
2 |
||||||||||
|
3 |
Замечание. На плоскости (в двумерном пространстве) можно также задать прямоугольную систему координат Oxy. С помощью введенной системы координат любую точку или ее радиус-вектор можно представить парой чисел (x, y). Все соотношения, полученные нами ранее для координат векторов и точек трехмерного пространства, будут справедливы и на плоскости с той лишь разницей, что из них нужно всюду убрать третью координату z. Аналогичные рассуждения можно повторить и для произвольной прямой (одномерного пространства).
Определение 9.1. Осью называется прямая с лежащим на ней единичным вектором (ортом), задающим положительное направление на прямой.
На рисунке ось будем изображать в виде направленной прямой. Пусть в пространстве задана ось l и точка А, не принадлежащая оси.
Определение 9.2. Основание перпендикуляра, опущенного из точки А на пря-
мую l, точка A‘ называется проекцией (ортогональной проекцией) точки на ось.
В случае, если точка А принадлежит оси l, то проекция точки на ось совпадает с самой точкой А.
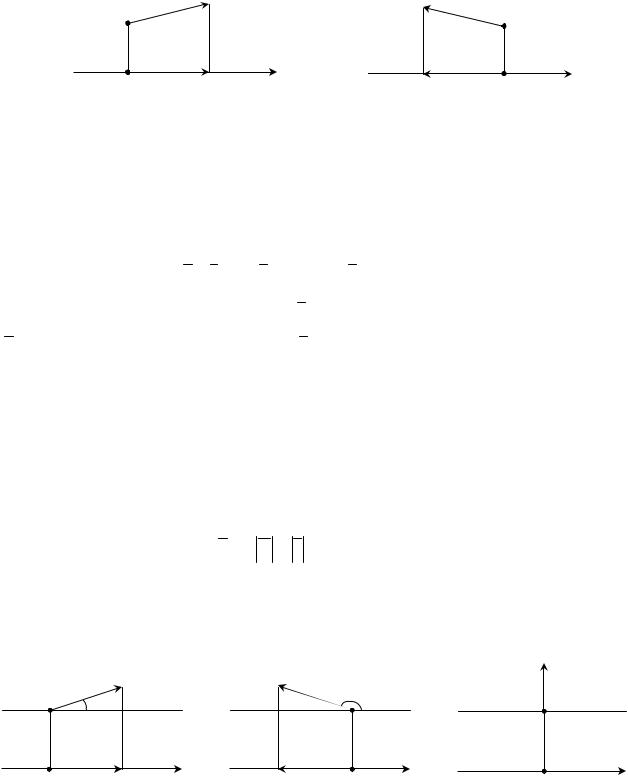
Пусть задан некоторый вектор a AB . Находя проекции начала и конца вектора a на ось l, получим вектор a‘ A‘ B‘ , где A‘, B‘ — соответственно проекции точек А, В на ось l.
Определение 9.3. Проекцией вектора a на ось l будем называть положительное число, равное a‘ , если вектор a‘ и ось l направлены одинаково (см. рис. 12) и отрица-
тельное число a‘ , если вектор a‘ и ось l направлены противоположно (см. рис. 13).
26
|
a |
В |
В |
|||||||||||||||||||||
|
a |
|||||||||||||||||||||||
|
А |
А |
||||||||||||||||||||||
|
a |
l |
a |
l |
||||||||||||||||||||
|
А’ |
В’ |
B’ |
A’ |
||||||||||||||||||||
|
Рис. 12 |
Рис. 13 |
||||||||||||||||||||||
|
Проекцию вектора |
на |
ось l |
будем обозначать прl |
. Таким образом, соглас- |
|||||||||||||||||||
|
a |
a |
||||||||||||||||||||||
|
но определению прl |
или прl |
||||||||||||||||||||||
|
a |
a |
a |
a |
. |
Замечание. Если a 0 или a l , то прl a 0 .
Теорема 9.1. Проекция вектора a на ось l равна произведению длины вектора a на косинус угла между вектором a и осью l, где под углом понимается наименьший из двух углов, образуемых вектором и осью.
Таким образом,
|
прl |
cos |
(0 ) . |
(9.1) |
||||
|
a |
a |
||||||
|
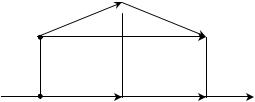
Доказательство. В зависимости от величины угла |
возможны следующие |
случаи (рис. 14):
1. Если 900 , то прl a a a cos .
|
2. Если |
900 1800 , то прl |
cos( ) |
cos . |
||||||||||||||||||||||||
|
a |
a |
a |
a |
||||||||||||||||||||||||
|
3. Если |
900 , то пр |
0 |
cos . ▲ |
||||||||||||||||||||||||
|
a |
a |
||||||||||||||||||||||||||
|
l |
|||||||||||||||||||||||||||
|
a |
a |
a |
|||||||||||||||||||||||||
|
a |
a |
||||||||||||||||||||||||||
|
l |
l |
l |
Рис. 14
27
Следствие 9.1. Проекция вектора на ось есть число положительное, если уголмежду вектором и осью острый, и отрицательное, если угол тупой. Если уголпрямой, то проекция вектора на ось равна нулю.
Следствие 9.2. Проекции равных векторов на одну и ту же ось равны между
собой.
Свойства проекций векторов на ось
|
1) прl |
прl |
прl ( |
). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
b |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) прl ( |
) прl |
, |
R. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Доказательство: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) обозначим c a b . Рассмотрим прl c |
a |
прl |
a прl b (рис.15); ▲ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
с |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
l |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
с |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рис. 15 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2) в зависимости от знака возможны следующие случаи: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прl ( |
по теореме 9.1 |
cos прl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a) 0 : |
a |
) |
a |
cos |
a |
a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прl ( |
по теореме 9.1 |
( cos ) прl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b) 0 : |
a |
) |
a |
cos( ) |
a |
a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
прl ( |
см. замечание копр.9.3 |
0 прl |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c) 0 : |
a |
) прl (0) |
a |
. ▲ |
Таким образом, линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов.
Замечание. Все рассуждения, приведенные выше, будут также справедливы, если вместо оси l рассматривать произвольный ненулевой вектор. Проекцию (ортого-
28
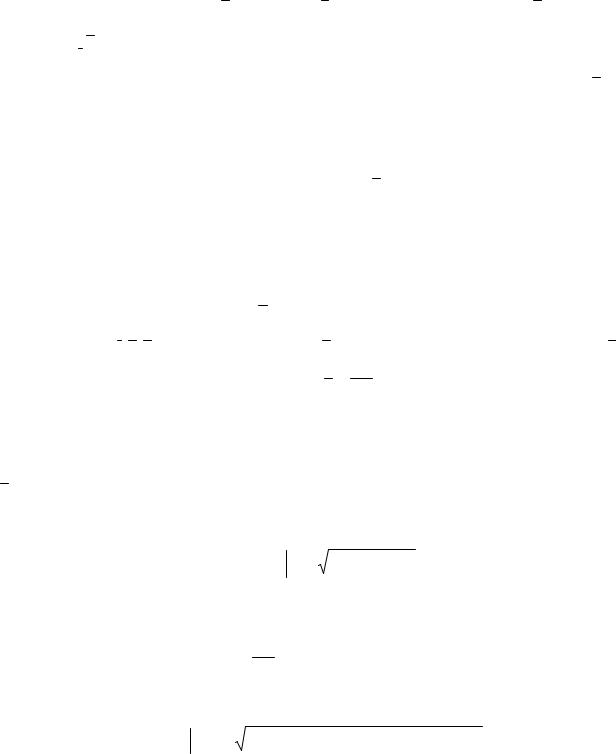
нальную проекцию) вектора a на вектор b (на направление вектора b ) будем обо-
значать прb a .
Теорема 9.2. Декартовы прямоугольные координаты a1 , a2 , a3 вектора a рав-
ны соответственно проекциям этого вектора на оси Ox, Oy и Oz.
Можно дать еще одно определение координат вектора.
Определение 9.4. Координатами вектора a в прямоугольной декартовой системе координат Oxyz называются проекции этого вектора на соответствующие координатные оси.
Рассмотрим задачу о нахождении длины вектора по его координатам.
Задача. Пусть дан вектор a , который относительно прямоугольного декар-
тового базиса {i, j, k} имеет координаты: a {a1 , a2 , a3}. Найдем длину вектора a .
Решение. Найдем проекции вектора a OA на координатные оси и обозначим их OA1,OA2 иOA3 . Согласно теореме 9.2, OA1 a1 , OA2 a2 , OA3 a3 . Построим пря-
моугольный параллелепипед так, что его три измерения равны OA1,OA2 иOA3 . Вектор
a в построенном параллелепипеде совпадает с диагональю (см. рис. 9). Так как квадрат диагонали в прямоугольном параллелепипеде равен сумме квадратов его сторон, то
|
a2 |
a2 |
a2 . |
(9.2) |
||
|
a |
|||||
|
1 |
2 |
3 |
Таким образом, длина вектора равна корню квадратному из суммы квадратов координат этого вектора.
Замечание. Длина вектора AB , где A(x1 , y1 , z1 ) , B(x2 , y2 , z2 ) , согласно формулам (8.2), (9.2), находится по формуле
|
(x |
x )2 |
( y |
y )2 |
(z |
z )2 . |
(9.3) |
||||
|
AB |
2 |
2 |
2 |
|||||||
|
1 |
1 |
1 |
29
Соседние файлы в папке Вектора
- #
- #
- #
- #
- #
- #