Как найти проекцию наклонной на плоскость альфа

Стереометрия

Глава 9. Прямые и плоскости в пространстве

9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью

Определение 1

Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.

Определение 2

Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).

Определение 3

Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.

Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.

Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.

Следствие

Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).

Определение 4

Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.

Определение 5

Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.

Теорема 5

Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.

Теорема о трёх перпендикулярах

13 декабря 2021

Сегодня в уроке:

1. Теорема о трёх перпендикулярах
2. Применение в доказательствах
3. Применение для вычислений
4. Дополнение. Перпендикулярность прямой и плоскости

На прошлом уроке мы узнали, что такое наклонная. И познакомились с несколькими её свойствами. Сегодня идём дальше и разбираем теорему о трёх перпендикулярах — одну из немногих «чисто стереометрических теорем», которые нельзя свести к привычной планиметрии.

1. Теорема о трёх перпендикулярах

Теорема о трёх перпендикулярах. Пусть $AB$ — наклонная к плоскости $alpha $, $MB$ — проекция этой наклонной на плоскость $alpha $, прямая $l$ принадлежит плоскости $alpha $. Тогда:

1. Если проекция $MBbot l$, то и наклонная $ABbot l$;

2. Верно и обратное: если наклонная $ABbot l$, то проекция $MBbot l$.

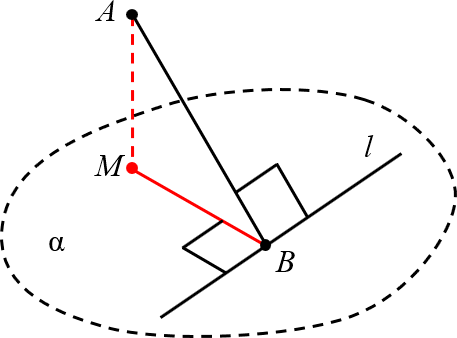
Из формулировки ясно, что теорема о трёх перпендикулярах работает при выполнении трёх обязательных условий:

1. Есть наклонная и есть проекция наклонной на плоскость $alpha $;
2. Эта проекция (либо сама наклонная) перпендикулярна некой прямой $l$;
3. Прямая $l$ находится именно в плоскости $alpha $.

Лишь в этом случае можно заявить, что наклонная (либо проекция) тоже перпендикулярна:

[left. begin{align} & 1. MB={{}_{alpha }}AB \ & 2. MBbot l \ & 3. lin alpha \ end{align} right|Rightarrow ABbot alpha ]

Убрать любое из этих трёх условий — и теорема не работает. Все дальнейшие рассуждения становятся необоснованными. Это особенно актуально на всевозможных экзаменах типа ЕГЭ и ДВИ, где недостаточно дать правильный ответ — нужно строгое обоснование каждого шага.

Многие задачи на теорему о трёх перпендикулярах сводятся к рассмотрению простой фигуры на плоскости $alpha $ (треугольник, четырёхугольник).

Идеальный чертёж для таких задач — «вид сверху» на плоскость $alpha $ и эту фигуру, а затем наклонная под любым удобным углом. Наглядность чертежа максимальна, вероятность ошибки — ноль.

Рассмотрим простой пример:

В треугольнике $ABC$ $AB=BC=20$, $AC=32$, $BM=5$ — перпендикуляр к плоскости $ABC$.

Найдите расстояние от точки $M$ до прямой $AC$.

Сравните два чертежа. Привычный для планиметрии «вид сверху»:

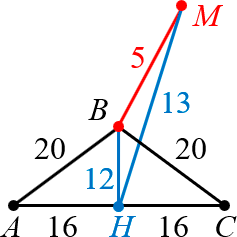
Без труда угадывается равнобедренный треугольник $ABC$ и дополнительное построение: Наклонная $MH$ и проекция $BH$.

А вот «вид сбоку», более типичный для стереометрии:

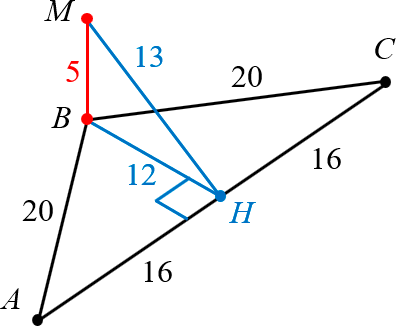
То же треугольник и те же дополнительные построения. Работать с таким чертежом большинству начинающих учеников гораздо сложнее. Поэтому смело используйте первый вариант. С опытом возьмёте на вооружение и второй.

2. Применение в доказательствах

Теорема о трёх перпендикулярах часто встречается в задачах на доказательство. Но перед тем, как мы перейдём к задачам, важное уточнение:

Прямая, перпендикулярная проекции наклонной, далеко не всегда будет проходить через основание этой наклонной.

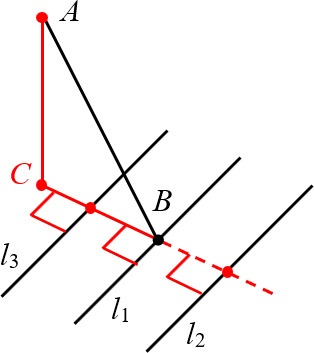
Простой пример: наклонная $AB$, её проекция $BC$ и несколько прямых, перпендикулярных этой проекции: ${{l}_{1}}$, ${{l}_{2}}$ и ${{l}_{3}}$.

Из трёх прямых лишь ${{l}_{1}}$ проходит через основание наклонной — точку $B$. Но все они равноправны с точки зрения теоремы о трёх перпендикулярах. И согласно ей, все они перпендикулярны наклонной $AB$.

Учитывая это, переходим к задачам.:)

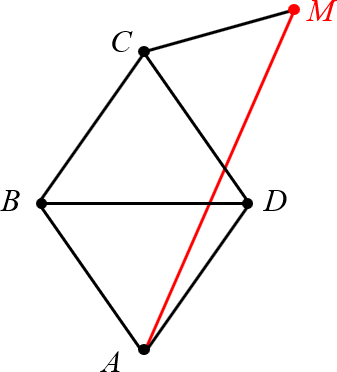
Задача. Дан ромб $ABCD$ и прямая $MC$, перпендикулярная его плоскости. Докажите, что прямые $AM$ и $BD$ перпендикулярны.

Исходный чертёж выглядит так:

1. Дополнительное построение: $AC$ — диагональ ромба:

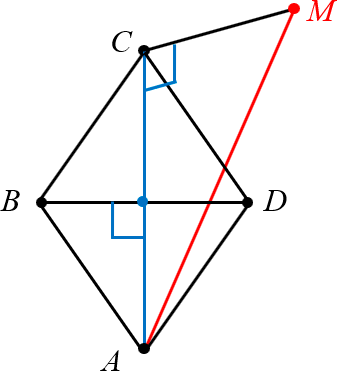
2. $MCbot ABCD$ (по условию). Следовательно, $MCbot AC$, поэтому $AC$ — проекция наклонной $AM$ на плоскость $ABCD$.

3. $ABCD$ — ромб (по условию); $BD$ и $AC$ — его диагонали (по построению). Следовательно, $ACbot BD$ (диагонали ромба перпендикулярны).

4. $AC$ — проекция наклонной $AM$ на плоскость $ABCD$ (доказано в п.2); $BDbot AC$ (доказано в п. 3); $BDin ABCD$ (по условию). Следовательно, по теореме о трёх перпендикулярах $AMbot BD$, что и требовалось доказать.

Вот именно так — по пунктам, в каждом пункте по одной теореме — и нужно решать любые геометрические задачи. К таким выкладкам никто никогда не придерётся.

3. Применение для вычислений

Переходим к вычислениям. Примечательное свойство вычислительных задач в стереометрии состоит в том, что они почти всегда сводятся к обычной планиметрии. Исключение — задачи на вычисление объёма фигуры. Просто потому что на плоскости никаких объёмов нет.:)

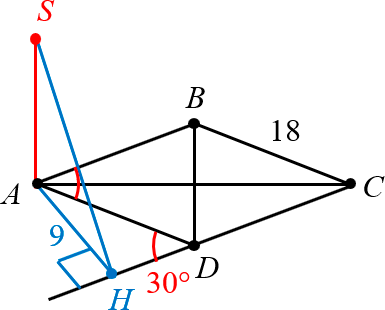
Задача. Отрезок $SA$ — перпендикуляр к плоскости ромба $ABCD$. Найдите расстояние от точки $S$ до прямой $CD$, если $angle BAD=30{}^circ $, $AD=18$, $AM=2sqrt{10}$.

1. Дополнительное построение: $AHbot CD$ — высота на продолжение $CD$; отрезок $MH$.

2. $ASbot ABCD$ (по условию). Следовательно, $AH$ — проекция наклонной $SH$ на плоскость $ABCD$.

3. $AH={{}_{ABCD}}SH$ (доказано в п. 2); $AHbot CD$ (по построению); $CDin ABCD$ (по условию). Следовательно, по теореме о трёх перпендикулярах $SHbot CD$. Поэтому длина отрезка $SH$— это искомое расстояние.

4. $ABparallel CD$ (по условию, $ABCD$ — ромб); $AD$ — секущая. Следовательно, $angle ADH=angle BAD=30{}^circ $ (внутренние накрест лежащие).

5. Треугольник $ADH$: $angle AHD=90{}^circ $ (по построению); $angle ADH=30{}^circ $ (доказано в п. 4). Следовательно

[begin{align} AH & =ADcdot sin 30{}^circ = \ & =18cdot frac{1}{2}=9 end{align}]

6. Треугольник $ASH$: $angle SAH=90{}^circ $ (по условию). Теорема Пифагора:

[begin{align} S{{H}^{2}} & =A{{S}^{2}}+A{{H}^{2}}= \ & =40+81=121 end{align}]

Получили $SH=11$ — это окончательный ответ.

Как и следовало ожидать, от стереометрии в этой задаче лишь определение прямой, перпендикулярной к плоскости, а также сама теорема о трёх перпендикулярах.

4. Дополнение. Перпендикулярность прямой и плоскости

Далеко не всегда прямая, проходящая через «свободный» конец наклонной, будет перпендикулярна плоскости прямо по условию задачи. Поэтому вспомним определение и признак перпендикулярности:

Определение. Прямая $l$ перпендикулярна плоскости $alpha $, если она перпендикулярна любой прямой $cin alpha $, лежащей в этой плоскости.

Критерий перпендикулярности. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым в этой плоскости.

Чтобы доказать, что прямая $l$ перпендикулярна плоскости $alpha $, достаточно отыскать две пересекающиеся прямые $ain alpha $ и $bin alpha $ в этой плоскости и доказать, что обе эти прямые перпендикулярны исходной прямой $l$:

[left. begin{align} & lbot ain alpha \ & lbot bin alpha \ & abigcap b=M \ end{align} right|Rightarrow lbot alpha ]

По этой теме будет отдельный урок. Сейчас просто отмечу, что большинство задач в стереометрии (особенно на доказательство) вполне решаются с помощью двух рассмотренных сегодня теорем: теорема о трёх перпендикулярах и признак перпендикулярности прямой и плоскости.

Смотрите также:

1. Следствия из аксиом стереометрии
2. 7 аксиом стереометрии
3. Локальная теорема Муавра — Лапласа
4. C2: расстояние между двумя прямыми
5. Задачи B2 на проценты: налоги и зарплата
6. Семья из трех человек (нестандартная задача)

Теорема о трех перпендикулярах

Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а₁ — проекция наклонной а на плоскость α.

Сформулируем теорему о трех перпендикулярах:

Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

На рисунке показаны все три перпендикуляра.

Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.

Вот как все это выглядит в пространстве:

На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

Теорема о трех перпендикулярах — полезный инструмент для решения задач.

Например, с ее помощью можно доказать, что диагональ куба АС₁ перпендикулярна прямой BD:

Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:

Или — что в правильной треугольной призме прямая А₁М (где М — середина ВС) перпендикулярна ребру ВС:

Читаем дальше: Параллельное проецирование.