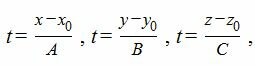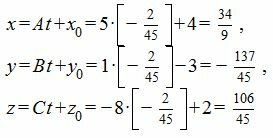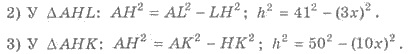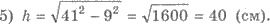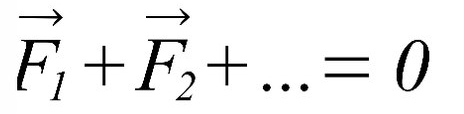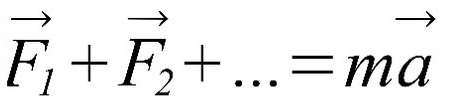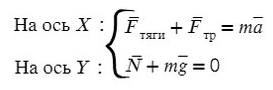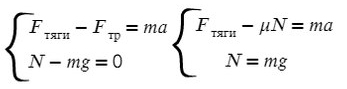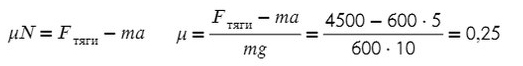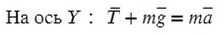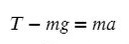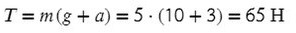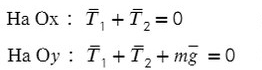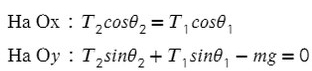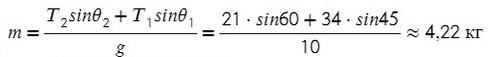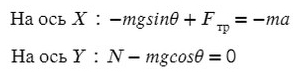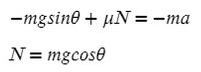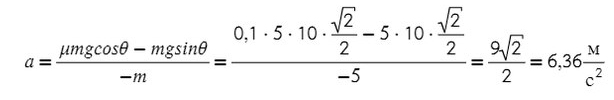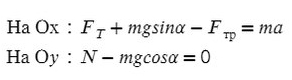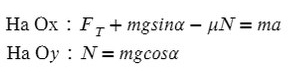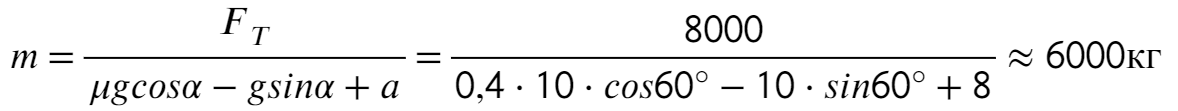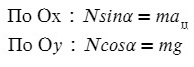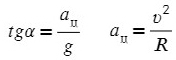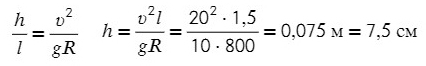На чтение 8 мин Просмотров 3.7к. Опубликовано 04.07.2019
Содержание
- Теоретические материалы
- Предупреждение
- Проекция точки на плоскость − теория, примеры и решения
- Проекция прямой на плоскость
- Угол между прямой и плоскостью
- Теорема о трех перпендикулярах
Теоретические материалы
Глава 9. Прямые и плоскости в пространстве
9.5. Наклонные и их проекции на плоскость. Угол наклонной с плоскостью
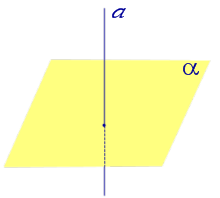
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости.
Точка пересечения перпендикуляра (наклонной) с плоскостью называется основанием перпендикуляра (наклонной).
Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных к плоскости из одной и той же точки вне ее, называется проекцией наклонной на эту плоскость.
Если из одной и той же точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и наклонные, то:
1) две наклонные, имеющие равные проекции, равны;
2) из двух наклонных та больше, проекция которой больше;
3) (обратная) равные наклонные имеют равные проекции;
4) (обратная) большей наклонной соответствует большая проекция.
Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.
Перпендикуляр к плоскости меньше всякой наклонной, проведенной к той же плоскости из той же точки вне ее (катет меньше гипотенузы).
Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на данную плоскость.
Углом между наклонной и плоскостью называется острый угол между наклонной и ее проекцией на эту плоскость.
Угол между наклонной и ее проекцией на плоскость является наименьшим из всех углов, образуемых данной наклонной с прямыми, лежащими в данной плоскости.
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
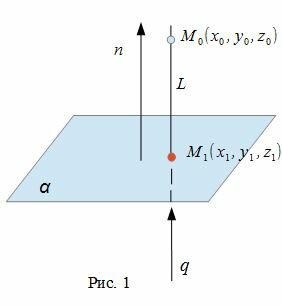
Для нахождения проекции точки M на плоскость α, необходимо:
- построить прямую L, проходящую через точку M и ортогональной плоскости α.
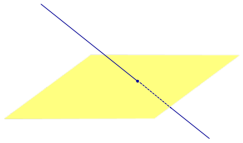
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
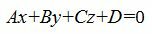 |
(1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M(x, y, z) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
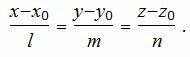 |
(2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M(x, y, z) и ортогональной плоскости (1) имеет следующий вид:
 |
(3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
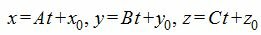 |
(4) |
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
A(At+x)+B(Bt+y)+C(At+z)+D=0,
A 2 t+Ax+B 2 t+By+C 2 t+Cz+D=0,
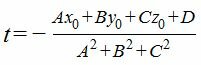 |
(5) |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M на плоскость (1).
Пример 1. Найти проекцию M1 точки M(4, -3, 2) на плоскость
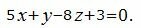 |
(6) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M и нормального вектора плоскости в (5), получим:
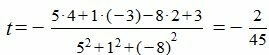 |
(7) |
Из выражений (7) находим:
Проекцией точки M(4, -3, 2) на плоскость (6) является точка:
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
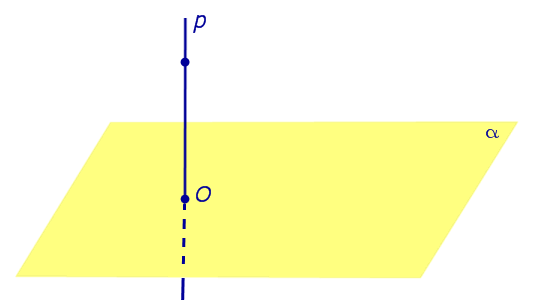
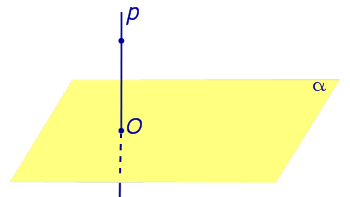
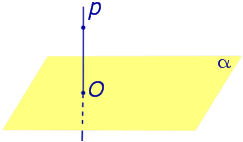
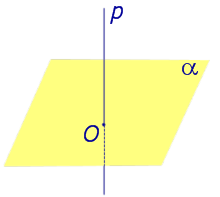
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
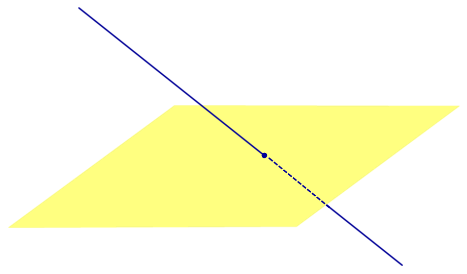
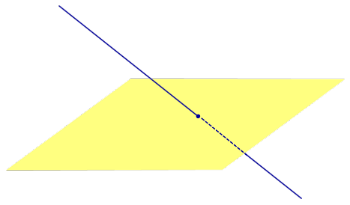
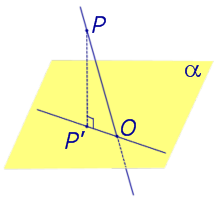
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
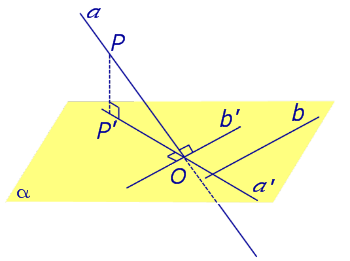
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
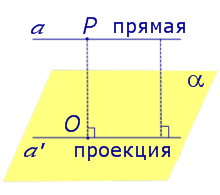
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
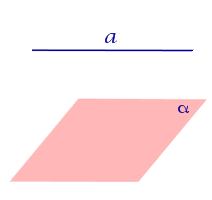
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
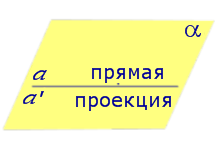
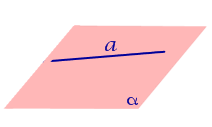
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.
| Фигура | Рисунок | Свойство проекции |
| Наклонная к плоскости α | 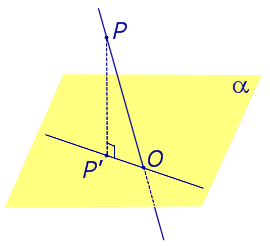 |
|
| Прямая, параллельная плоскости | 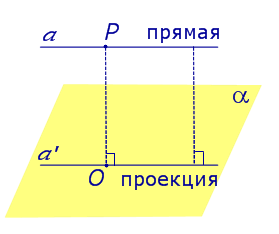 |
|
| Прямая, лежащая на плоскости | 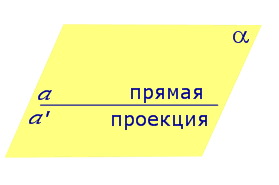 |
|
| Прямая, перпендикулярная к плоскости | 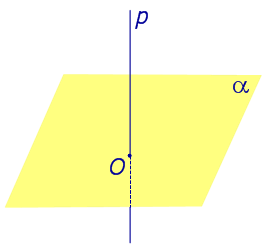 |
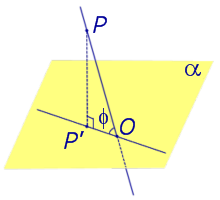
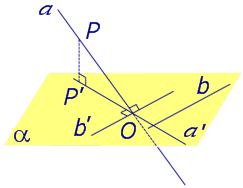
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
Теорема о трех перпендикулярах
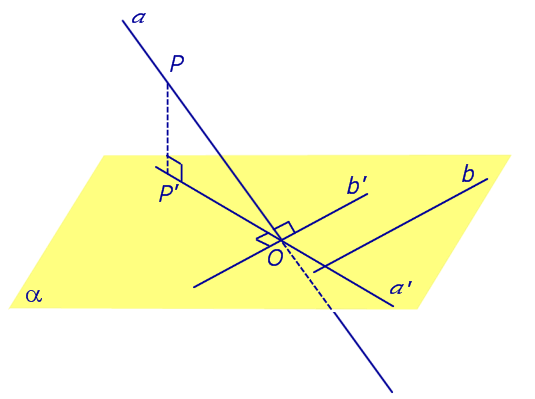
Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.
Доказательство. Рассмотрим следующий рисунок 3.
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.
Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.
Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.
Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.
Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.
| Фигура | Рисунок | Определение |
| Наклонная к плоскости α | 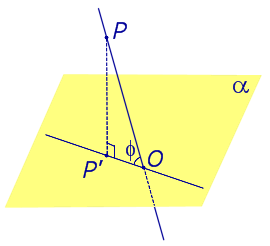 |
|
| Прямая, параллельная плоскости | 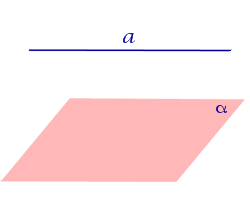 |
|
| Прямая, лежащая на плоскости |  |
|
| Прямая, перпендикулярная к плоскости | 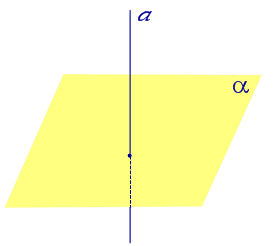 |
Перпендикуляр и наклонная к прямой
Если через какую-нибудь точку, взятую вне прямой, провести прямую, перпендикулярную к ней, то отрезок от данной точки до прямой для краткости называют одним словом перпендикуляр.
Отрезок СО — перпендикуляр к прямой АВ. Точка О называется основанием перпендикуляра СО (рис).
Если прямая, проведённая через данную точку, пересекает другую прямую, но не перпендикулярна к ней, то отрезок её от данной точки до точки пересечения с другой прямой называют наклонной к этой прямой.
Отрезок ВС — наклонная к прямой АО. Точка С называется основанием наклонной (рис.).
Если из концов какого-нибудь отрезка опустим перпендикуляры на произвольную прямую, то отрезок прямой, заключённый между основаниями перпендикуляров, называется проекцией отрезка на эту прямую.
Отрезок А’В’ — проекция отрезка АВ на ЕС. Отрезок ОМ’ — также называется проекцией отрезка ОМ на ЕС.
Проекцией отрезка КР, перпендикулярного к ЕС, будет точка К’ (рис.).
2. Свойства перпендикуляра и наклонных.
Теорема 1. Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой.
Отрезок АС (рис.) является перпендикуляром к прямой ОВ, а АМ — одна из наклонных, проведённых из точки А к прямой ОВ. Требуется доказать, что АМ > АС.
В ΔМАС отрезок АМ является гипотенузой, а гипотенуза больше каждого из катетов этого треугольника. Следовательно, АМ > АС. Так как наклонная АМ взята нами произвольно, то можно утверждать, что всякая наклонная к прямой больше перпендикуляра к этой прямой (а перпендикуляр короче всякой наклонной), если они проведены к ней из одной и той же точки.
Верно и обратное утверждение, а именно: если отрезок АС (рис.) меньше всякого другого отрезка, соединяющего точку АС любой точкой прямой ОВ, то он является перпендикуляром к ОВ. В самом деле, отрезок АС не может быть наклонной к ОВ, так как тогда он не был бы самым коротким из отрезков, соединяющих точку А с точками прямой ОВ. Значит, он может быть только перпендикуляром к ОВ.
Длина перпендикуляра, опущенного из данной точки на прямую, принимается за расстояние от данной точки до этой прямой.
Теорема 2. Если две наклонные, проведённые к прямой из одной и той же точки, равны, то равны и их проекции .
Пусть ВА и ВС — наклонные, проведённые из точки В к прямой АС (рис.), причём АВ = ВС. Нужно доказать, что равны и их проекции.
Для доказательства опустим из точки В перпендикуляр ВО на АС. Тогда АО и ОС будут проекции наклонных АВ и ВС на прямую АС. Треугольник АВС равнобедренный по условию теоремы. ВО — высота этого треугольника. Но высота в равнобедренном треугольнике, проведённая к основанию, является в то же время и медианой этого треугольника.
Теорема 3 (обратная). Если две наклонные, проведённые к прямой из одной и той же точки, имеют равные проекции, то они равны между собой.
Пусть АС и СВ — наклонные к прямой АВ (рис.). СО ⊥ АВ и АО = ОВ.
Требуется доказать, что АС = ВС.
В прямоугольных треугольниках АОС и ВОС катеты АО и ОВ равны. СО — общий катет этих треугольников. Следовательно, ΔAOС = ΔВОС. Из равенcтва треугольников вытекает, что АС = ВС.
Теорема 4. Если из одной и той же точки проведены к прямой две наклонные, то та из них больше, которая имеет большую проекцию на эту прямую.
Пусть АВ и ВС — наклонные к прямой АО; ВО ⊥ АО и АО>СО. Требуется доказать, что АВ > ВС.
1) Наклонные расположены по одну сторону перпендикуляра.
Угол АСЕ внешний по отношению к прямоугольному треугольнику СОВ (рис.), а поэтому ∠АСВ > ∠СОВ, т. е. он тупой. Отсюда следует, что АВ > СВ.
2) Наклонные расположены по обе стороны перпендикуляра. Для доказательства отложим на АО от точки О отрезок ОК = ОС и соединим точку К с точкой В (рис.). Тогда по теореме 3 имеем: ВК = ВС, но АВ > ВК, следовательно, АВ > ВС, т. е. теорема справедлива и в этом случае.
Теорема 5 (обратная). Если из одной и той же точки проведены к прямой две наклонные, то большая наклонная имеет и большую проекцию на эту прямую.
Пусть КС и ВС — наклонные к прямой КВ (рис.), СО ⊥ КВ и КС > ВС. Требуется доказать, что КО > ОВ.
Между отрезками КО и ОВ может быть только одно из трёх соотношений:
КО не может быть меньше ОВ, так как тогда по теореме 4 наклонная КС была бы меньше наклонной ВС, а это противоречит условию теоремы.
Точно так же КО не может равняться ОВ, так как в этом случае по теореме 3 КС = ВС, что также противоречит условию теоремы.
Следовательно, остаётся верным только последнее соотношение, а именно, что КО > ОВ.
Как найти проекцию наклонной
Раздел ІІ. СТЕРЕОМЕТРИЯ
§8. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. ПРОЕКЦИЯ НАКЛОННОЙ НА ПЛОСКОСТЬ.
2. Свойства перпендикуляра и наклонной.
Рассмотрим свойства перпендикуляра и наклонной.
1) Перпендикуляр, опущенный из данной точки к плоскости, меньше любой наклонной, проведенной из этой же точки к плоскости.
На рисунке 411: АН АК.
2) Если две наклонные, проведенные из данной точки к плоскости, равны, то равны их проекции.
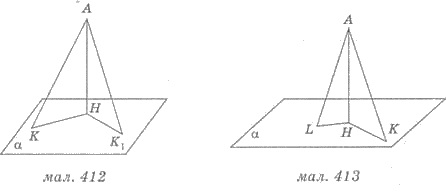
На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K 1 и перпендикуляр АН и АК = АК 1 . Тогда по свойству: НК = НК1.
3) Если две наклонные, проведенные из данной точки к данной плоскости, имеют равные проекции, то они равны между собой.
На рисунке 412 из точки А к плоскости а проведены две наклонные АК и А K 1 и перпендикуляр АН, причем КН = К 1 Н. Тогда по свойству: АК = АК 1 .
4) Если из данной точки проведены к плоскости две наклонные, то большая наклонная имеет большую проекцию.
На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, A К > AL . Тогда по свойству: H К > HL .
5) Если из данной точки проведены к плоскости две наклонные, то большей из них является та, которая имеет большую проекцию на данную плоскость.
На рисунке 413 из точки А к плоскости а проведены две наклонные АК и А L и перпендикуляр АН, НК > Н L . Тогда по свойству: АК > А L .
Пример 1. Из точки к плоскости проведены две наклонные, длины которых 41 см и 50 см. Найти проекции наклонных, если они относятся, как 3 : 10, и расстояние от точки до плоскости.
Решения. 1) А L = 41 см; АК = 50 см (рис. 413). По свойством имеем Н L НК. Обозначим Н L = 3 х см, НК = 10 х см, АН = h см. АН — расстояние от точки А до плоскости α .
4) Приравнивая, получаем 41 2 — 9х 2 = 50 2 — 100 х 2 ; х 2 = 9; х = 3 (учитывая х > 0). Итак, Н L = 3 ∙ 3 = 9 (см), НК = 10 ∙ 3 = 30 (см).
Пример 2. С данной точки к плоскости проведены две наклонные, каждая по см. Угол между наклонными равен 60°, а угол между их проекциями — прямой. Найти расстояние от точки до плоскости.
1) АС = ВС = см — наклонные, ВАС = 60°; ВНС = 90° (рис. 414). Необходимо найти АН.
2) В рівнобедреному треугольнике АВС: 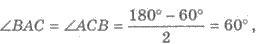
3) Так как АВ = АС, то НВ = НС ; обозначим НВ = НС = х см. Тогда в ∆ ВНС :
Как найти проекцию наклонной
Задачи по динамике.
I и II закон Ньютона.
Ввод и направление осей.
Проецирование сил на оси.
Решение систем уравнений.
Самые типовые задачи по динамике
Начнем с I и II законов Ньютона.
Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.
I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.
II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.
При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.
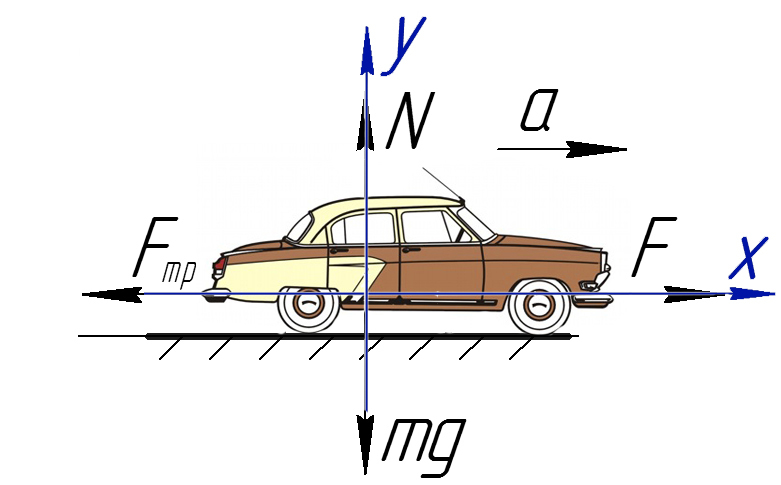
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:
На Ось Х: движение с ускорением
На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.
По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.
Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.
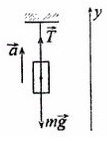
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.
Сделаем рисунок, покажем силы, которые дествуют на груз
T — сила натяжения нити
На ось X: нет сил
Разберемся с направлением сил на ось Y:
Выразим T (силу натяжения) и подставим числительные значения:
Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.
Далеко не всегда все силы, действующие на тело, направлены вдоль осей.
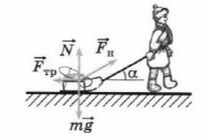
Простой пример: мальчик тянет санки
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.
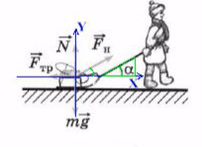
Отношение противолежащего катета к гипотенузе — это синус.
Отношение прилежащего катета к гипотенузе — это косинус.
Сила тяги на ось Y — отрезок (вектор) BC.
Сила тяги на ось X — отрезок (вектор) AC.
Если это непонятно, посмотрите задачу №4.
Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.
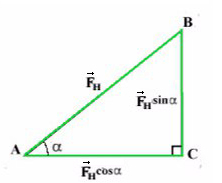
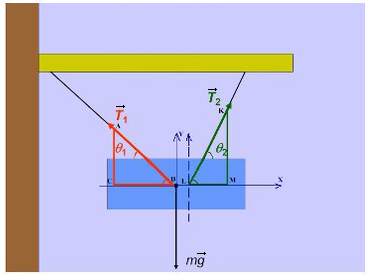
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.
Введем оси и спроецируем силы:
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.
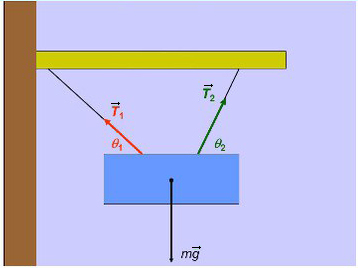
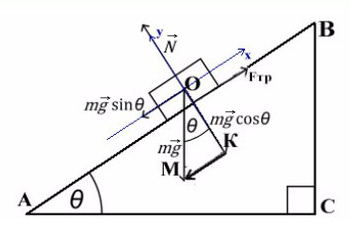
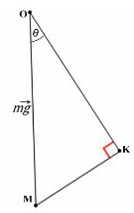
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?
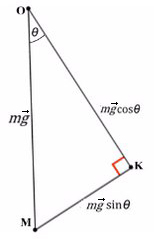
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).
Рассмотрим поподробнее ΔKOM:
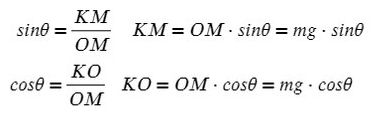
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!
Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:
Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.
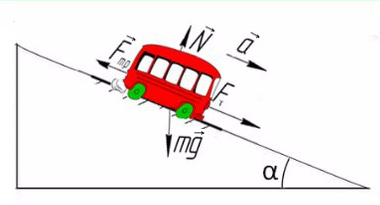
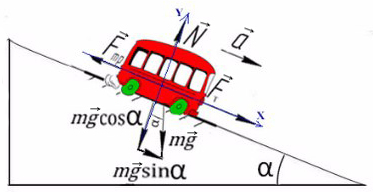
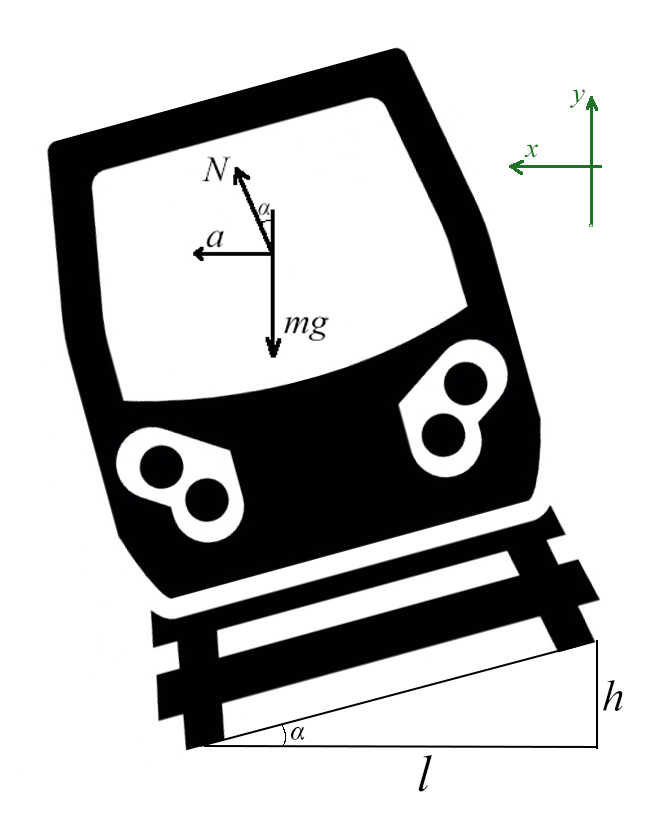
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.
Сделаем рисунок с силами:
Введем оси X и Y. Спроецируем mg на оси:
Запишем второй закон Ньютона на X и Y:
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.
Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!
Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)
Запишем какие силы действуют на оси:
Ускорение в данной задачи центростремительное!
Поделим одно уравнение на другое:
Тангенс — это отношение противолежащего катета к прилежащему:
Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.
В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.
- Главная
- Математика
- найдите проекци…
-
Предмет:
Математика
-
Автор:
khalil
-
Создано:
3 года назад
Ответы 6
спасибо большое,а можешь это решить : Найдите полную площадь поверхности цилиндра,если его осевое сочение – квадрат со стороной 20 см
-
Автор:
rodriguez
-
Оценить ответ:
0
Формула полной площади S=2*π*R*(h+R). Т.к. осевое сечение квадрат, то h=20 см, R=10 см (т.к. сторона квадрата будет диаметром окружности, а радиус это половина диаметра).Тогда S=2*π*R*(h+R)=2*π*10*(20+10)=20π*30=600π=600*3,14=1884 см^2
-
Автор:
pranavbaird
-
Оценить ответ:
0
огромное спасибо,знаю ,прошу многово ,но помоги еще вот с этим: Тело движется прямолинейно со скоростью V=9t^2+1 м в сек.Найти длину пути , пройденного телом за 10 сек от начала движения.
-
Автор:
gunner
-
Оценить ответ:
0
Пройденный путь есть первообразная от скорости, т.е. нужно проинтегрировать уравнение скорости. S=integral(9t^2+1)dt=3t^3+t. Дальше подставляем в уравнение пути время t=10c и находим путь. Т.е. S=3t^3+t=3*10^3+10=3010 м. По ходу единица измерения метры, судя по секундам. Ответ: 3010 м
-
Автор:
marcossoto
-
Оценить ответ:
0
Проекция, перпендикуляр и наклонная образуют прямоугольный треугольник с прямым углом между перпендикуляром и проекцией. Значит, проекция – это катет в прямоугольном треугольнике. По теореме Пифагора: проекция =
Ответ: 21 см
-
Автор:
stephenson
-
Оценить ответ:
0
На рисунке АВ=20 см – перпендикуляр, АС=29 см – наклонная, СВ – проекция наклонной на плоскость. Данный ΔАВС – прямоугольный.
Тогда по теореме Пифагора:
АВ²+СВ²=АС²
СВ²=АС²-АВ²=29²-20²=841-400=441
СВ=±21
Т.к. длина не может быть отрицательной, то СВ=21 см.
Ответ:21 см
-
Автор:
shane8bbc
-
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
-
Информатика42 минут назад
Помогите, пожалуйста, срочно ♥
-
Русский язык6 часов назад
Составьте 2 диалога на темы: книга, учëба, добро и т. д+схемы по русскому языку
-
Математика8 часов назад
150 центеров это сколько грамм
-
Биология13 часов назад
ХЕЛП СРОЧНО
Установи последовательность движения нервного сигнала по рефлекторной дуге.
1. Двигательный нерв
2. Чувствительный нерв
3. Рецептор
4. ЦНС
5. Орган
-
Физика15 часов назад
Нужно рассчитать энергию связи никеля 9 класс
Все полностью
Все действия!
-
Математика15 часов назад
Нужно рассчитать энергию связи никеля 9 класс
Все полностью
Все действия!
-
Математика16 часов назад
Найти амплитуду колебания и рисунок
-
Математика17 часов назад
Поле площадью 560 га засеяно огурцами, морковью и помидорами. Огурцы занимают 35% всего поля. Сколько гектаров занимают помидоры, морковь и огурцы в отдельности, если моркови засеяно в раз больше, чем помидоров? ПОМОГИТЕ СРОЧНО!!! 15 МИНУТ ОСТАЛОСЬ!
-
Математика18 часов назад
. Выполните действия: ( 3). помогите решить
-
Математика20 часов назад
Дан треугольник ABC Найти 1)длины сторон 2)углы треугольника 3)периметр треугольника 4)площадь треугольника 5)длину медианы СМ 6)длину высоты АН 7) сделать чертеж
Если кординаты вершины равны
А(-3;4;2),В(3;-4;4).С(2;-2;-3)
-
Другие предметы20 часов назад
Найти координаты вектора P.
Помогите пожалуйста очень срочно!!!
-
Химия1 день назад
Органическое вещество А содержит по массе 56,81% углерода; 6,98% водорода и кислород. Вещество А можно получить гидратацией вещества Б.
На основании данных условия задачи:
1) проведите необходимые вычисления и установите молекулярную формулу вещества А;
2) составьте структурную формулу вещества А, которая однозначно отражает порядок атомов в его молекуле;
3) напишите уравнение реакции получения вещества А гидратацией вещества Б.
-
Химия1 день назад
Через 480 г 15%-ного раствора едкого натра пропускали постоянный электрический ток до тех пор, пока на электродах не выделилось 358,4 л газов (объем приведен к нормальным условиям). Из полученного раствора отобрали пробу массой 96 г для полного осаждения ионов меди из 290 г насыщенного при 25°С раствора сульфата меди(II). Вычислите растворимость медного купороса – пентагидрата сульфата меди(II) при 25°С. В ответе запишите уравнения реакций, которые указаны в условии задачи, и произведите все необходимые вычисления (указывайте единицы измерения искомых физических величин).
-
Литература1 день назад
Художественные выразительные средства в произведении джека лондона любовь к жизни
можно пару штук хотя бы =_
-
Русский язык1 день назад
Письмён на писька содержание своей любимой книге перед началом работы составь план в последнем абзаце своего текста напиши почему это книга
твоя любимая
Из точки к плоскости проведены две равные наклонные 20 и 15 см проекция одной из них 16 см найти проекцию 2 – ой наклонной.
На этой странице находится вопрос Из точки к плоскости проведены две равные наклонные 20 и 15 см проекция одной из них 16 см найти проекцию 2 – ой наклонной?. Здесь же – ответы на него,
и похожие вопросы в категории Математика, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 10 – 11 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
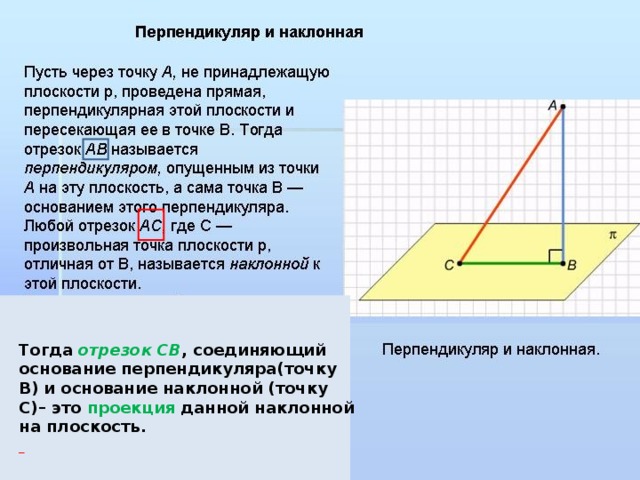
Перпендикуляр и наклонная.
Знать понятия:
Перпендикуляр к плоскости, его основание, наклонная к плоскости, ее основание, как найти проекцию наклонной, проведенной к плоскости.
Тогда отрезок СВ , соединяющий основание перпендикуляра(точку В) и основание наклонной (точку С)– это проекция данной наклонной на плоскость.
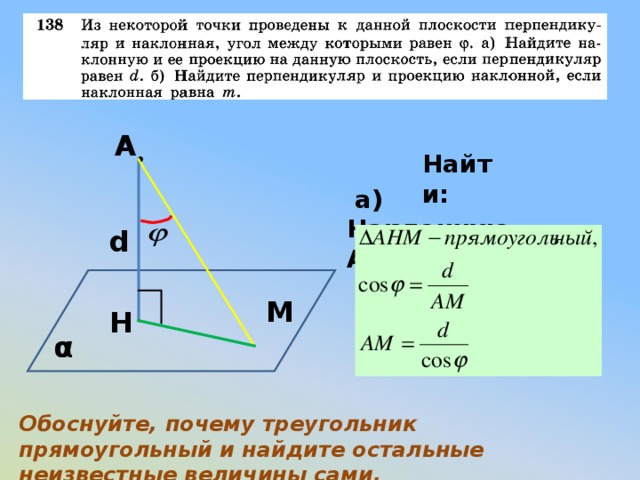
А
•
Найти:
а) Наклонную АМ
d
М
Н
α
Обоснуйте, почему треугольник прямоугольный и найдите остальные неизвестные величины сами.
Расстояние от точки до плоскости.
Знать понятия:
расстояние от точки до плоскости.
Обратите внимание как на рисунке обозначается расстояние ( величина «ро»)
плоскость.
Нетрудно догадаться, что расстоянием от точки до прямой будет длина перпендикуляра, проведенного из этой точки к данной прямой.
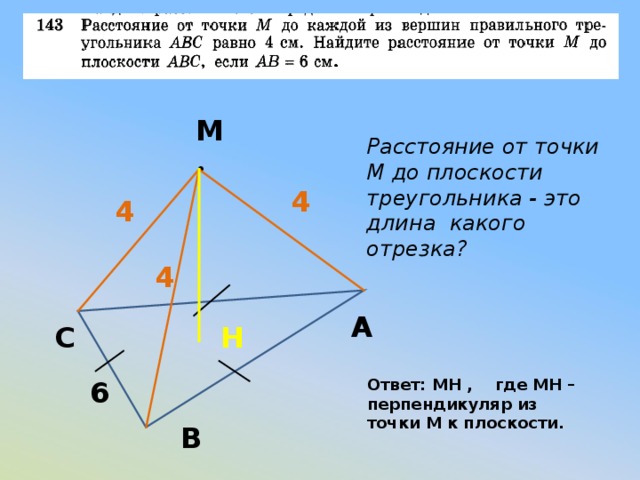
М
Расстояние от точки М до плоскости треугольника – это длина какого отрезка?
•
4
4
4
А
С
H
6
Ответ: MH , где MH – перпендикуляр из точки М к плоскости.
В
Как определить, где именно расположена внутри треугольника точка H?
М
•
4
4
Рассмотрите треугольники MHC, MHB, MHA. Докажите их равенство.
4
H
А
С
6
Сделайте вывод о равенстве отрезков HC, HB, HA.
В
Это значит, что точка Н равноудалена от вершин данного треугольника, т.е. она центр описанной около этого треугольника окружности. А т.к. этот треугольник правильный, то точка H – точка пересечения медиан(биссектрис, высот)
Найдите CH, зная сторону правильного треугольника, а затем из треугольника CHM найдите искомую высоту HM
Теорема о трех перпендикулярах.
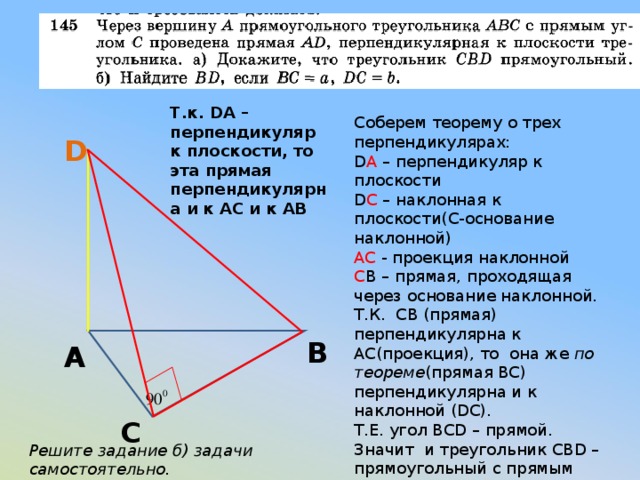
Т.к. DA – перпендикуляр к плоскости, то эта прямая перпендикулярна и к АС и к АВ
Соберем теорему о трех перпендикулярах:
D A – перпендикуляр к плоскости
D С – наклонная к плоскости(С-основание наклонной)
АС – проекция наклонной
С В – прямая, проходящая через основание наклонной.
Т.К. СВ (прямая) перпендикулярна к АС(проекция), то она же по теореме (прямая ВС) перпендикулярна и к наклонной (DC).
Т.Е. угол BCD – прямой. Значит и треугольник CBD – прямоугольный с прямым углом С.
D
В
А
С
Решите задание б) задачи самостоятельно.
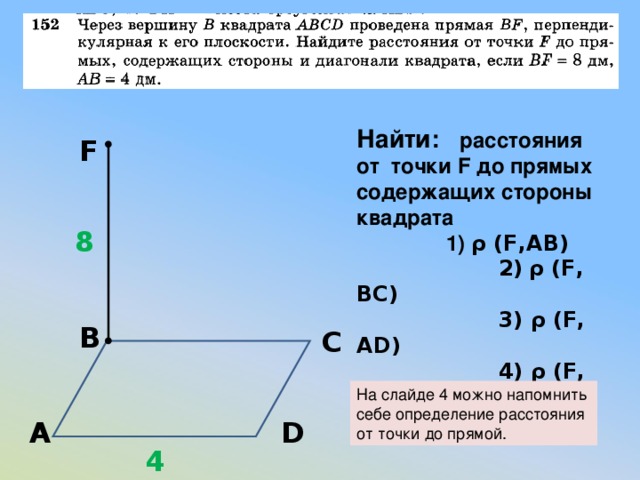
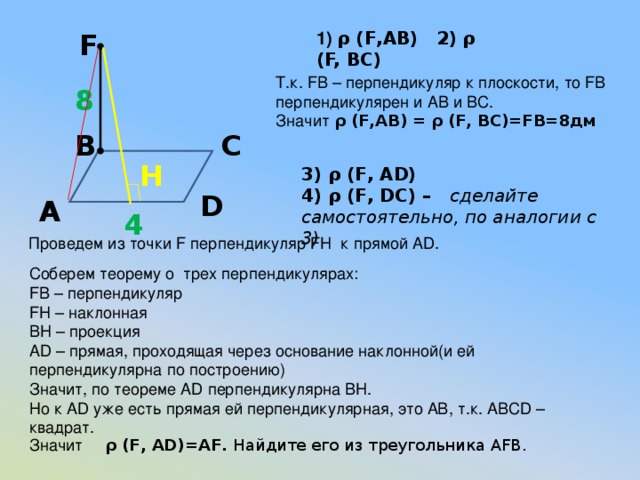
Найти: расстояния от точки F до прямых содержащих стороны квадрата
1) ρ (F,AB)
2) ρ (F, BC)
3) ρ (F, AD)
4) ρ (F, DC)
F
8
В
С
На слайде 4 можно напомнить себе определение расстояния от точки до прямой.
А
D
4
F
1) ρ (F,AB) 2) ρ (F, BC)
Т.к. FB – перпендикуляр к плоскости, то FB перпендикулярен и АВ и ВС.
Значит ρ (F,AB) = ρ (F, BC)=FB=8дм
8
С
В
H
3) ρ (F, AD)
4) ρ (F, DC) – сделайте самостоятельно, по аналогии с 3)
D
А
4
Проведем из точки F перпендикуляр FH к прямой AD.
Соберем теорему о трех перпендикулярах:
FB – перпендикуляр
FH – наклонная
BH – проекция
AD – прямая, проходящая через основание наклонной(и ей перпендикулярна по построению)
Значит, по теореме AD перпендикулярна BH.
Но к AD уже есть прямая ей перпендикулярная, это АВ, т.к. ABCD – квадрат.
Значит ρ (F, AD)=AF. Найдите его из треугольника AFB.
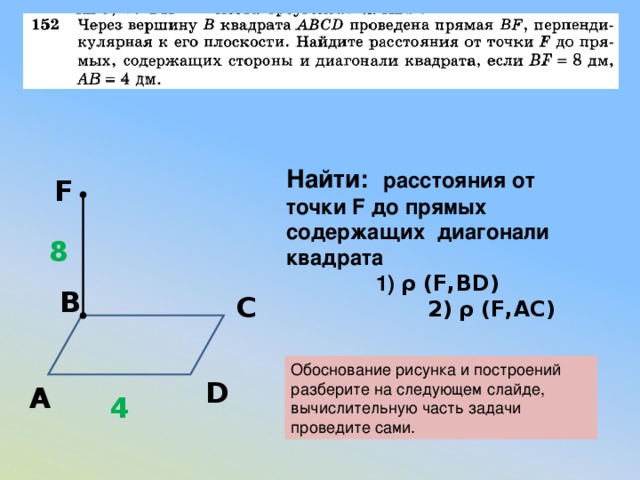
Найти: расстояния от точки F до прямых содержащих диагонали квадрата
1) ρ (F,BD)
2) ρ (F,AC)
F
8
В
С
Обоснование рисунка и построений разберите на следующем слайде, вычислительную часть задачи проведите сами.
D
А
4
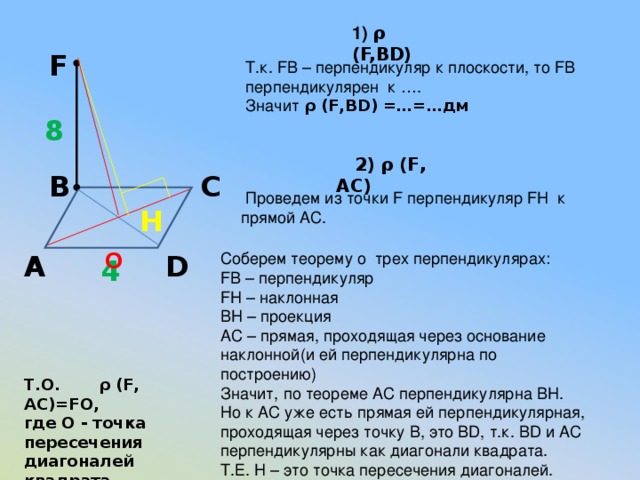
1) ρ (F,BD)
F
Т.к. FB – перпендикуляр к плоскости, то FB перпендикулярен к ….
Значит ρ (F,BD) =…=…дм
8
2) ρ (F, АC)
В
С
Проведем из точки F перпендикуляр FH к прямой AС.
H
О
Соберем теорему о трех перпендикулярах:
FB – перпендикуляр
FH – наклонная
BH – проекция
AС – прямая, проходящая через основание наклонной(и ей перпендикулярна по построению)
Значит, по теореме AС перпендикулярна BH.
Но к AС уже есть прямая ей перпендикулярная, проходящая через точку В, это ВD, т.к. BD и AC перпендикулярны как диагонали квадрата.
Т.Е. H – это точка пересечения диагоналей.
А
D
4
Т.О. ρ (F, АC)=FO,
где О – точка пересечения
диагоналей квадрата.