Как найти проекцию отрезка на ось

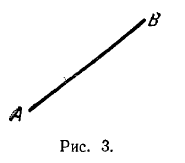
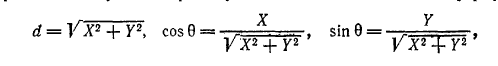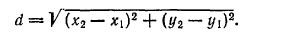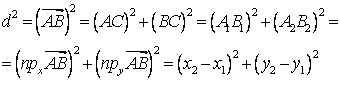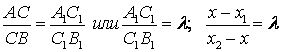Прямолинейный отрезок называется направленным, если указано, какая из ограничивающих его точек считается началом, какая – концом. Направленный отрезок, имеющий точку А своим началом и точку В концом (рис. 3), обозначается символом АB (т. е. так же, как отрезок оси; см. § 1). Длина направленного отрезка АB (при заданном масштабе) обозначается символом |АВ| (или АВ см. сноску на стр. 13).

Проекцией отрезка АB на ось u называется число, равное величине отрезка А₁B₁ оси u, где точка A₁ является проекцией на ось u точки А, а В₁ – проекцией на эту же ось точки. В.

Проекция отрезка АB на ось u обозначается символом пр_u АB. Если на плоскости задана система декартовых прямоугольных координат, то проекция отрезка на ось Ох обозначается символом X, его проекция на ось Оу – символом У.

Если известны координаты точек М₁(х₁;у₁) и М₂(х₂;у₂), то проекции X и У на оси координат направленного отрезка M₁M₂ могут быть вычислены по формулам

Х = х₂ – х₁, У = у₂ – у₁

Таким образом, чтобы найти проекции направленного отрезка на оси координат нужно от координат его конца отнять соответствующие координаты начала.

Угол Θ, на который нужно повернуть положительную полуось Ох так, чтобы ее направление совпало с направлением отрезка M₁M₂, называется полярным углом отрезка M₁M₂.

Угол Θ понимается, как в тригонометрии. Соответственно зтому Θ имеет бесконечно много возможных значений, которые отличаются друг от друга на величину вида ±2nπ (где n – целое положительное число). Главным значением полярного угла называется то из его значений, которое удовлетворяет неравенствам -π < Θ ≤ +π.

Формулы

X = d • cosΘ, У = d • sinΘ

выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Отсюда же вытекают формулы

которые выражают длину и полярный угол отрезка через его проекции на оси координат.

Если на плоскости даны две точки М₁(х₁;у₁) и М₂(х₂;у₂), то расстояние d между ними определяется формулой

44. Вычислить проекцию отрезка на ось u, если даны его длина d и угол φ наклона к оси: 1) d = 6, φ = π/3; 2) d = 6, φ = 2π/3; 3) d = 7, φ = π/2; 4) d = 5, φ = 0;
5) d = 5, φ = π; 6) d = 4, φ = -π/3.

45. Построить на чертеже отрезки, исходящие из начала координат, зная их проекции на координатные оси: 1) Х=3, У = 2; 2) Х = 2, Y = -5; 3) X = -5, У = 0; 4) X = -2, У = 3; 5) X = 0, У = 3; 6) X = -5, У = -1.

46. Построить на чертеже отрезки, имеющие началом точку М(2; -1), зная их проекции на координатные оси: 1) X = 4, У = 3; 2) X = 2, У = 0; 3) X = -3, У = 1; 4) X = -4, У = -2; 5) X = 0, У = -3; 6) Х= 1, У = -3.

47. Дацы точки M₁(l; -2), M₂(2; 1), M₃(5; 0), М₄(-1; 4) и М₅(0; -3). Найти проекции на координатные оси следующих отрезков: 1) M₁M₂, 2) M₃M₁, 3) M₄M₅ 4) M₅M₃.

48. Даны проекции отрезка M₁M₂ на оси координат X = 5, У = -4; зная, что его начало в точке М₁(-2; 3), найти координаты его конца.

49. Даны проекции отрезка АB на оси координат X = 4, Y = – 5; зная, что его конец в точке B(1; – 3), найти координаты его начала.

50. Построить на чертеже отрезки, исходящие из начала координат, зная длину d и полярный угол Θ каждого из них: 1) d = 5, Θ = π/5; 2) d = 3, Θ = 5/6π; 3) d = 4, Θ = -π/3; 4) d = 3, Θ = -4/3Θ.

51. Построить на чертеже отрезки, имеющие началом точку M(2; 3), зная длину и полярный угол каждого из них: 1) d = 2, Θ = – π/10 2) d== 1, Θ = π/9; 3) d = 5, Θ = -π/2 (координаты точки М – декартовы),

52. Вычислить проекции на координатные оси отрез-ков, зная длину d и полярный угол Θ каждого из них!
1) d = 12, Θ = 2/3π 2) d = 6, Θ = -π/6; 3) d = 2, Θ = -π/4.

53. Даны проекции отрезков на координатные оси: 1) X = 3, Y = -4; 2) Х = 12, У = 5; 3) X = -8, У = 6. Вычислить длину каждого из них.

54. Даны проекции отрезков_ на координатные оси: 1) X = 1 , Y = √3; 2) Х = З√2, Y = – 3√2 ; 3) Х = – 2√3, У = 2. Вычислить длину d и полярный угол Θ каждого из них.

55. Даны точки M₁(2; -3), M₂(1; -4), М₃(- 1; -7) и M₄(-4: 8). Вычислить длину и полярный угол следующие отрезков: 1) M₁M₂, 2) M₁M₃, 3) M₂M₄, 4) M₄M₃.

56. Длина d отрезка равна 5, его проекция на ось абсцисс равна 4. Найти проекцию этого отрезка на ось ординат при условии, что он образует с осью ординат 1) острый угол, 2) тупой угол.

57. Длида отрезка MN равна 13; его начало в точке М(3; -2), проекция на ось абсцисс равна -12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат: 1) острый угол, 2) тупой угол,

58. Длина отрезка MN равна 17, его конец в точке N{-7; 3), проекция на ось ординат равна 15. Найти ко-ординаты начала этого отрезка при условии, что он образует с осью абсцисс: 1) острый угол, 2) тупой угол.

59. Зная проекции отрезка на координатные оси X = 1, Y = – √3 , найти его проекцию на ось, которая
составляет с осью Ох угол Θ = 2/3π.

60. Даны две точки M₁(1; -5) и М₂(4; -1). Найти проекцию отрезка M₁M₂ на ось, которая составляет
с осью Ох угол Θ = -π/6 .

61. Даны две точки Р(-5; 2) и Q (3; 1). Найти проекцию отрезка PQ на ось, которая составляет с осью Ох угол Θ = arctg4/3 .

62. Даны две точки M₁(2; -2) и М₂(7; -3). Найтипроекцию отрезка M₁M₂ на ось, проходящую через точки A(5; -4), В(-7; 1) и направленную: 1) от A к В, 2) от В к A.

63. Даны точки A(0; 0), В(3; -4), С(-3; 4), D(- 2; 2) и E(10; -3). Определить расстояние d между точками: 1)A и В; 2) В и С; 3) Л и С; 4) С и D; 5) A и D; 6) D и E.

64. Даны две смежные вершины квадрата A(3; -7) и В(-1; 4). Вычислить его площадь.

65. Даны две противоположные вершины квадрата Р(3; 5) и Q(1; -3). Вычислить его площадь.

66. Вычислить площадь правильного треугольника, две вершины которого суть A(-3; 2) и B(1; 6).

67. Даны три вершины A(3; -7), B(5; -7), С(- 2; 5) параллелограмма ABCD, четвертая вершина которого D противоположна В. Определить длину диагоналей этого параллелограмма.

68. Сторона ромба равна 5√10 две его противоположные вершины суть точки Р(4; 9) и Q(-2; 1). Вычислить площадь этого ромба.

69. Сторона ромба равна 5√2, две его противоположные вершины суть точки Р(3; -4) и Q(l; 2). Вычислить длину высоты этого ромба.

70. Доказать, что точки A(3; -5), В(-2; -7) и С(18; 1) лежат на одной прямой.

71. Доказать, что треугольник с вершинами A₁(1; 1), A₂(2; 3) и A₃(5; -1) прямоугольный.

72. Доказать, что точки А (2; 2), B(- 1; 6), С(-5; 3) и D(-2; -1) являются вершинами квадрата.

73. Определить, есть ли среди внутренних углов тре-угольника с вершинами М₁(1; 1), М₂(0; 2) и М₃(2; -1) тупой угол.

74. Доказать, что все внутренние углы треугольника с вершинами М(- 1; 3), N(1; 2) и Р(0; 4) острые.

75. Вершины треугольника суть точки A(5; 0), B(0; 1) и С(3; 3). Вычислить его внутренние углы.

76. Вершины треугольника суть точки A(-√3;1) B(0; 2) и С(-2√3; 2). Вычислить его внешний угол при вершине А.

77. На оси абсцисс найти такую точку М, расстояние которой до точки N (2; -3) равнялось бы 5.

78. На оси ординат найти такую точку М, расстояние которой до точки N (-8; 13) равнялось бы 17

79. Даны две точки М{2; 2) и N(5; -2); на оси абсцисс найти такую точку Р, чтобы угол MPN был прямым.

80. Через точку А (4; 2) проведена окружность, касающаяся обеих координатных осей. Определить ее центр С и радиус R.

81. Через точку М₁(1; -2) проведена окружность радиуса 5, касающаяся оси Ох. Определить центр С окружности.

82. Определить координаты точки M₂, симметричной точке М₁(1; 2) относительно прямой, проходящей через точки A(1; 0) и B(- 1; -2).

83. Даны две противоположные вершины квадрата A(3; 0) и С(-4; 1). Найти две его другие вершины.

84. Даны две смежные вершины квадрата А(2; -1) и B(-1; 3). Определить две его другие вершины.

85. Даны вершины треугольника М₁(-3; 6), М₂(9; -10) и М₃(-5; 4). Определить центр С и радиус R описанного около этого треугольника круга.

44 Вычислить проекцию отрезка на
ось u, если даны его длина d и угол j наклона к оси: 44.1 d=6, j =p
/3; 44.2 d=6, j =2p
/3; 44.3 d=7, j =p
/2; 44.4 d=5, j =0; 44.5 d=5, j =p
; 44.6 d=4, j = –p
/3. 45 Построить на
чертеже отрезки, исходящие из начала координат,
зная их проекции на координатные оси: 45.1 X=3, Y=2; 45.2 X=2, Y=-5; 45.3 X=-5, Y=0; 45.4 X=-2, Y=3; 45.5 X=0, Y=3; 45.6 X=-5, Y=-1; 46 Построить на
чертеже отрезки, имеющие началом точку M(2; -1), зная
их проекции на координатные оси: 46.1 X=4. Y=3; 46.2 X=2, Y=0; 46.3 X=-3, Y=1; 46.4 X=-4, Y=-2; 46.5 X=0, Y=-3; 46.6 X=1, Y=-3. 47 Даны точки М₁(1; -2), М₂(2; 1), М₃(5; 0), М₄(-1;
4), М₅(0; -3). Найти проекции на координатные оси
следующих отрезков: 47.1 47.2 47.3 47.4 48 Даны проекции X=5, Y=-5
отрезка на координатные оси; зная,
что его начало в точке М₁(-2; 3), найти координаты его конца. 49 Даны проекции X=4, Y=-5
отрезка на координатные оси; зная,
что его конец в точке B(1; -3), найти координаты его
начала. 50 Построить на
чертеже отрезки, исходящие оиз начала координат,
зная длину d и полярный угол q каждого из них: 50.1 d=5, q =p /5; 50.2 d=3, q =5p
/6; 50.3 d=4, q =-p
/3; 50.4 d=3, q =-4p
/3. 51 Построить на
чертеже отрезки, имеющие началом точку М(2; 3), зная
длину и полярный угол каждого из них (координаты
точки М декартовы): 51.1 d=2, q =-p /10; 51.2 d=1, q =p
/9; 51.3 d=5, q =-p
/2ж 52 Вычислить проекции
на координатные оси отрезков, зная длину d и
полярный угол q каждого из них: 52.1 d=12, q =2p /3; 52.2 d=6, q =-p
/6; 52.3 d=2, q =-p
/4. 53 Даны проекции
отрезков на координатные оси. Вычислить длину
каждого из них. 53.1 X=3, Y=-4; 53.2 X=12, Y=5; 53.3 X=-8, Y=6. 54 Даны проекции
отрезков на координатные оси. Вычислить длину d и
полярный угол q каждого из них. 54.1 X=1, Y=; 54.2 X=,
Y=; 54.3 X=,
Y=2. 55 Даны точки М₁(2; -3), M₂(1; -4), M₃(-1; -7), M₄(-4;
8). Вычислить длину и полярный
угол слдующих отрезков: 55.1 55.2 55.3 55.4 56 Длина d отрезка
равна 5, его проекция на ось абсцисс равна 4. Найти
проекцию этого отрезка на ось ординат при
условии, что он образует с осью ординат: 56.1 Острый угол; 56.2 Тупой угол. 57 Длина отрезка равна 13; его начало в точке М(3; -2),
проекция на ось абсцисс равна –12. Найти
координаты конца этого отрезка при условии, что
он образует с осью ординат: 57.1 Острый угол; 57.2 Тупой угол. 58 Длина отрезка равна 17, его конец в точке N(-7; 3),
проекция на ось ординат равна 15. Найти координаты
начала этого отрезка при условии, что он образует
с осью абсцисс: 58.1 Острый угол; 58.2 Тупой угол. 59 Зная проекции X=1, Y= отрезка на координатные оси, найти
его проекцию на ось, которая составляет с осью Ox
угол q =2p /3. 60 Даны две точки M₁(1; -5), M₂(4; -1). Найти
проекцию отрезка на ось, которая составляет
с осью Ox угол q =-p
/6. 61 Даны две точки P(-5; 2),
Q(3; 1). Найти проекцию отрезка на
ось, которая составляет с осью Ox угол 62 Даны две точки M₁(2; -2), M₂(7; -3). Найти
проекцию отрезка на ось, проходящую через
точки A(5; -4), B(-7; 1) и направленную: 62.1 от А к В; 62.2 от В к А. 63 Даны точки A(0; 0), B(3;
-4), C(-3; 4), D(-2; 2), E(10; -3). Определить расстояние d между
точками: 63.1 А и В. 63.2 В и С. 63.3 А и С. 63.4 C и D. 63.5 A и D. 63.6 D и E. 64 Даны две смежные
вершины квадрата A(3; -7) и В(-1; 4). Вычислить его
площадь. 65 Даны две
противоположные вершины квадрата P(3; 5), Q(1; -3).
Вычислить его площадь. 66 Вычислить площадь
правильного треугольника, две вершины которого
суть A(-3; 2), B(1; 6). 67 Даны три вершины А(3;
-7), В(5; -7), С(-2; 5) параллелограмма ABCD, четвертая
вершина которого D противоположна B. Определить
длины диагоналей того параллелограмма. 68 Сторона ромба равна
, две его противоположные вершины
суть точки P(4; 9), Q(-2; 1). Вычислить площадь этого
ромба. 69 Сторона ромба равна
, две его противоположные вершины
суть точки P(3; -4), Q(1; 2). Вычислить длину высоты
этого ромба. 70 Доказать, что точки
А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой. 71 Доказать, что
треугольник с вершинами A₁(1; 1), A₂(2;
3), A₃(5; -1) прямоугольный. 72 Доказать, что точки
А(2; 2), В(-1; 6), С(-5; 3), D(-2; -1) являются вершинами
квадрата. 73 Определить, есть ли
среди внутренних углов треугольника с вершинами
M₁(1; 1), M₂(0; 2), M₃(2; -1) тупой угол. 74 Доказать, что все
внутренние углы треугольника с вершинами M(-1; 3),
N(1; 2), P(0, 4) острые. 75 Вершины
треугольника суть точки A(5; 0), B(0; 1), C(3; 3). Вычислить
его внутренние углы. 76 Вершины
треугольника суть точки А(; 1), B(0, 2), C(; 2). Вычислить
его внешний угол при вершине А. 77 На оси абсцисс
найти такую точку М, расстояние от которой до
точки N(2; -3) равнялось бы 5. 78 На оси ординат
найти такую точку М, расстояние от которой до
точки N(-8; 13 равнялось бы 17. 79 Даны две точки M(2; 2),
N(5; -2); на оси абсцисс найти такую точку Р, чтобы
угол MPN был прямым. 80 Через точку А(4; 2)
проведена окружность, касающаяся обеих
координатных осей. Определить ее центр С и радиус
R. 81 Через точку М₁(1; -2) проведена
окружность радиуса 5, касающаяся оси Ox.
Определить центр С окружности. 82 Определить
координаты точки М₂, симметричной точке М₁(1; 2) относительно прямой, проходящей
через точки А(1; 0), В(-1; -2). 83 Даны две
противоположные вершины квадрата А(3; 0) и С(-4; 1).
Найти две его другие вершины. 84 Даны две смежные
веришны квадрата А(2; -1) и В(-1; 3). Определить две его
другие вершины. 85 Даны вершины
треугольника M₁(-3; 6), M₂(9;
-10), M₃(-5; 4). Определить центр
С и радиус R круга, описанного около этого
треугольника.

Макеты страниц

или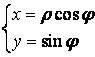 
–  формулы, выражающие декартовы координаты через полярные.

  –
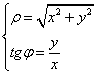
 формулы, выражающие полярные координаты через декартовы.

§ 2 Простейшие задачи аналитической геометрии на
плоскости

п 1. Проекция отрезка на оси координат

Определение. Прямая, на которой выбрано положительное
направление, называется осью
(рис. 4).

 Определение.
Отрезок АВ называется направленным, если сказано, какая из точек считается
началом отрезка, какая концом. Направлением отрезка считается направление от начала
к концу .

Рассмотрим произвольный отрезок .  (рис.
5)

Пусть А₁ и В₁ – основания
перпендикуляров, опущенных из начала и конуса отрезка АВ на ось х.

А₂ и В₂ – основания
перпендикуляров, опущенных из начала и конца от отрезка АВ на ось у. В нашем
случае направление отрезка А₁ В₁ совпадает с положительным
направлением оси ох. Направление отрезка А₂ В₂ противоположному
направлению оси оу.

Определение. Число, равное разности х₂ –  х₁
назовем проекцией отрезка АВ на ось ох и обозначим символом

Определение. Число, равное разности у₂ – у₁
назовем проекцией отрезка АВ на ось оу и обозначим символом

т.е. проекции отрезка на ох равно разности абсцисс
конца и начала отрезка, а проекции отрезка на ось оу равна разности ординат
конца и начала от резка.

В нашем случае

п 2 .Расстояние между двумя точками на координатной
плоскости

Расстояние между двумя точками обычно обозначаются
буквой d (d>0).

Пусть А (х₁, у₁) и В (х₂,
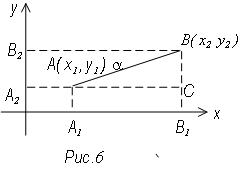
у₂) начало и конец отрезка АВ (рис. 6)

Опустим из А и В перпендикуляры на координатные оси из
Δ АВС

п 3. Деление отрезка в данном отношении

Пусть А (х₁, у₁) – начало, а В
(х₂, у₂) конец отрезка АВ. Пусть точка С делит отрезок АВ
в отношении λ. Требуется найти х_с и у_с – координаты точки
С (рис. 7)

Пусть

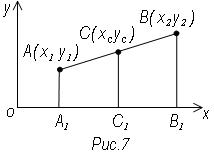
Опустим из А, В, С перпендикуляры на ось ох. АА₁,
ВВ₁, СС₁ – параллельные прямые, поэтому они отсекают на
отрезке АВ и оси х т. Пропорциональные отрезки т.е.

или  

Если точка С (х₀, у₀) – середина
отрезка АВ, то  и

§ 3 Линии и их уравнения

п 1. Понятие уравнения линии

В элементарной геометрии достаточно исследуются лишь
немногие линии: прямая, окружность, ломанная. Между тем потребности техники
ставят перед математикой общую задачу исследования многочисленных линий, многообразных
по своей форме и характеру своих свойств. Для решения этой задачи, требуется
более совершенные методы. Такие методы дают алгебры и математический анализ. В
основе применения методов алгебры и анализа лежит общий способ задания линии
при помощи ее уравнения.