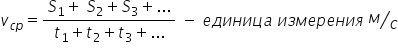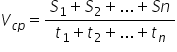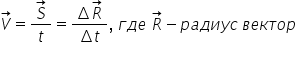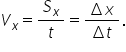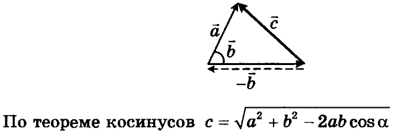Конспект по физике для 8 класса «Перемещение и описание движения». Как определить координаты тела, движущегося равномерно и прямолинейно. Что такое уравнение движения.
Конспекты по физике Учебник физики Тесты по физике
Перемещение и описание движения
Система отсчёта используется для того, чтобы определить положение тела в пространстве в некоторый момент времени. В случае когда тело движется, возникает задача вычисления его координат в некоторые моменты времени.
ПРОЕКЦИИ ПЕРЕМЕЩЕНИЯ НА КООРДИНАТНЫЕ ОСИ
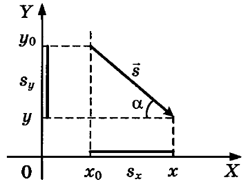
Если известен вектор перемещения тела, то при расчетах, как правило, используют не координаты вектора, как такового, а его проекции на оси координат. Если опустить перпендикуляры из начала и конца вектора перемещения s на координатную ось X, то получится отрезок sx, который называют проекцией перемещения. При этом проекция вектора на ось считается положительной, если координата конца вектора перемещения оказывается больше координаты его начала. В противном случае проекция считается отрицательной.
Если вектор и ось параллельны, то длина вектора равна его проекции на эту ось.
При решении многих задач необходимо уметь находить проекции вектора перемещения на координатные оси. Если (х0; у0) и (х; у) — координаты начала и конца вектора, то его проекции на оси абсцисс и ординат будут равны соответственно
sx = x – x0, (1)
sy = y – y0
Зная проекции вектора перемещения, можно найти его длину (модуль) по теореме Пифагора:
ОПРЕДЕЛЕНИЕ КООРДИНАТ ДВИЖУЩЕГОСЯ ТЕЛА И ЕГО ПЕРЕМЕЩЕНИЯ
Если тело движется прямолинейно, то траектория его движения совпадает с перемещением. При этом пройденный телом путь равен значению модуля вектора перемещения.
А как описать движение тела в более сложном случае? На рисунке представлен график движения самолёта. Сначала он набирал высоту, двигаясь из точки А в точку В, затем двигался на одной и той же высоте (до точки С) и, наконец, приземлился в точке D. На какой высоте проходил полёт? Высоте полёта соответствуют координаты по оси OY, значит, в точке В самолёт набрал высоту 3 км.
Теперь ответим на вопрос: какой путь проделал самолёт на этой высоте? Проекция перемещения s2x = 80 — 20 = 60 км.
Так как всё это время самолёт двигался параллельно оси ОХ, длина вектора перемещения равна его проекции на эту ось. Следовательно, модуль перемещения самолёта из точки В в точку С равен 60 км. Этому же значению равен и путь самолёта из точки В в точку С.
И наконец, определим дальность полёта самолёта. Для этого нам надо найти модуль перемещения самолёта из точки А в точку D: |s| = sx = 100 — 0 = 100 км.
Таким образом, при помощи перемещения и его проекций мы описали сложное движение самолёта.
ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ
Так как при прямолинейном движении пройденный телом путь равен значению модуля вектора перемещения, мы можем сказать, что скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела ко времени, за которое это перемещение произошло. При равномерном прямолинейном движении векторы скорости и перемещения направлены в одну сторону. Зная скорость равномерного движения, можно найти перемещение тела за любой промежуток времени:
Поскольку скорость υ является векторной величиной, её тоже можно изобразить графически. Обозначим её проекцию на координатную ось υx. Если направление координатной оси совпадает с направлением движения тела, то для расчёта перемещения тела можно использовать формулу
УРАВНЕНИЕ ДВИЖЕНИЯ
Уравнение зависимости координаты тела от времени называют уравнением движения.
Пусть тело совершило перемещение s. Направим координатную ось X по направлению перемещения тела. Обозначим начальную координату тела х0, а конечную координату тела х. Тогда по формуле (1) sx = х – х0.
Но по формуле (3) sx = υxt. Следовательно,
Таким образом, координату тела при равномерном прямолинейном движении в любой момент времени можно определить, если известны его начальная координата и проекция скорости движения на ось X.
Ранее при решении задач мы использовали формулу s = υt без стрелочек. Почему? Символом s здесь обозначался путь, пройденный телом, а символом и — модуль скорости. Теперь нам известно, что при равномерном прямолинейном движении путь равен модулю перемещения. Поэтому если нас не интересует направление движения тела, а необходимо только найти его путь, то эта формула поможет нам найти решение.
Вы смотрели Конспект по физике для 8 класса «Перемещение и описание движения».
Вернуться к Списку конспектов по физике (Оглавление).
Просмотров: 13 167
Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
На рис. 1.1:
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
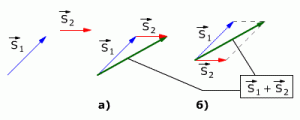
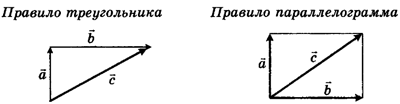
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
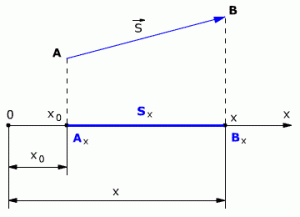
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения (см.рис. 1.3).
Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Sx = AxBx
ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть
Sx = x – x0
Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Sy = y – y0 Sz = z – z0
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
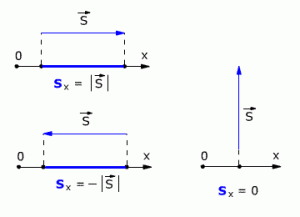
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
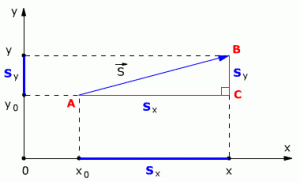
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
Sx = x – x0 Sy = y – y0
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
АС = sx CB = sy
По теореме Пифагора
S2 = Sx2 + Sy2
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.
Проекцией вектора на ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.
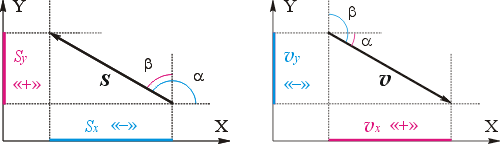
На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол 150° с направлением оси X. Пользуясь определением, найдём проекцию перемещения на ось X:
sx = s · cos(α) = 50 км · cos( 150°) = –43 км
Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:
sy = s · cos(β) = 50 км · cos( 60°) = +25 км
Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.
На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:
υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c
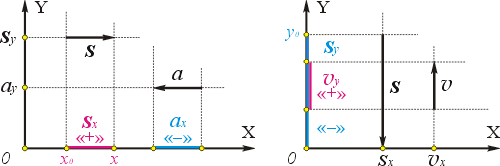
Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.
Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.
Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .
Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .
На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.
Скорость
Скорость
(v) – физическая величина, численно равна
пути (s), пройденного телом за единицу
времени (t).
Путь
Путь
(S) – длина траектории, по которой двигалось
тело, численно равен произведению
скорости (v) тела на время (t) движения.
Время
движения
Время
движения (t) равно отношению пути (S),
пройденного телом, к скорости (v) движения.
Средняя
скорость
Средняя
скорость (vср)
равна отношению суммы участков пути
(s1 s2,
s3,
…), пройденного телом, к промежутку
времени (t1+
t2+
t3+
…), за который этот путь пройден.
Средняя
скорость –
это отношение длины пути,
пройденного телом, ко времени,
за которое этот путь был пройден.
Средняя
скорость при
неравномерном движении по прямой: это
отношение всего пути ко всему времени.
Два
последовательных этапа с разными
скоростями: 
При решении
задач –
сколько этапов движения столько будет
составляющих:
Проекции
вектора перемещения на оси координат
Проекция
вектора перемещения на ось ОХ:
Проекция
вектора перемещения на ось OY:
Проекция
вектора на ось равна нулю, если вектор
перпендикулярен оси.
Знаки
проекций перемещения: проекцию считают
положительной, если движение от проекции
начала вектора к проекции конца происходит
по направлению оси, и отрицательной,
если против оси. В данном примере
Модуль
перемещения –
это длина вектора перемещения:
По
теореме Пифагора:
Проекции
перемещения и угол наклона
В
данном примере:
Уравнение
координаты (в общем виде):
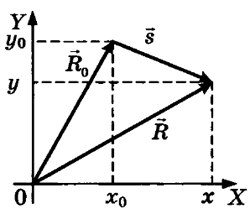
Радиус-вектор —
вектор, начало которого совпадает с
началом координат, а конец — с положением
тела в данный момент времени. Проекции
радиус-вектора на оси координат определяют
координаты тела в данный момент времени.
Радиус-вектор
позволяет задать положение материальной
точки в заданной системе
отсчета:
Равномерное
прямолинейное движение – определение
Равномерное
прямолинейное движение —
движение, при котором тело за любые
равные промежутки времени, совершает
равные перемещения.
Скорость
при равномерном прямолинейном движении.
Скорость —
векторная физическая величина, которая
показывает, какое перемещение совершает
тело за единицу времени.
В
векторном виде:
В
проекциях на ось ОХ:
Дополнительные
единицы измерения скорости:
1
км/ч = 1000 м/3600 с,
1
км/с = 1000 м/с,
1
см/с = 0,01 м/с,
1
м/мин =1 м/60 с.
Измерительный
прибор — спидометр — показывает модуль
скорости.
Знак
проекции скорости зависит от направления
вектора скорости и оси координат:
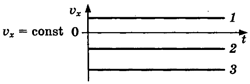
График
проекции скорости представляет собой
зависиость проекции скорости от времени:
График
скорости при равномерном прямолинейном
движении —
прямая, параллельная оси времени (1, 2,
3).
Если
график лежит над осью времени (.1), то
тело движется по направлению оси ОХ.
Если график расположен под осью времени,
то тело движется против оси ОХ (2, 3).
Чем
дальше график от оси времени, тем больше
модуль скорости (3).
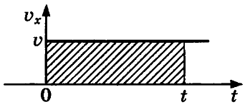
Геометрический
смысл перемещения.
При
равномерном прямолинейном движении
перемещение определяют по формуле .
Такой же результат получим, если вычислим
площадь фигуры под графиком скорости
в осях .
Значит, для определения пути и модуля
перемещения при прямолинейном движении
необходимо вычислять площадь фигуры
под графиком скорости в осях :
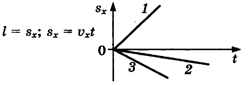
График
проекции перемещения —
зависимость проекции перемещения от
времени.
График
проекции перемещения при равномерном
прямолинейном движении —
прямая, выходящая из начала координат
(1, 2, 3).
Если
прямая (1) лежит над осью времени, то тело
движется по направлению оси ОХ, а если
под осью (2, 3), то против оси ОХ.
Чем
больше тангенс утла наклона (1) графика,
тем больше модуль скорости.
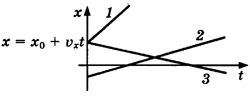
График
координаты —
зависимость координаты тела от времени:
График
координаты при равномерном прямолинейном
движении — прямые (1, 2, 3).
Если
с течением времени координата увеличивается
(1, 2), то тело движется по направлению
оси ОХ; если координата уменьшается
(3), то тело движется против направления
оси ОХ.
Чем
больше тангенс угла наклона (1), тем
больше модуль скорости.
Если
графики координат двух тел пересекаются,
то из точки пересечения следует опустить
перпендикуляры на ось времени и ось
координат.
Относительность
механического движения
Под
относительностью мы понимаем зависимость
чего-либо от выбора системы отсчета.
Например, покой относителен; движение
относительно и положение тела относительно.
Правило
сложения перемещений. Векторная
сумма перемещений
где —
перемещение тела относительно подвижной
системы отсчета (ПСО); —
перемещение ПСО относительно неподвижной
системы отсчета (НСО); —
перемещение тела относительно неподвижной
системы отсчета (НСО).
Векторное
сложение:
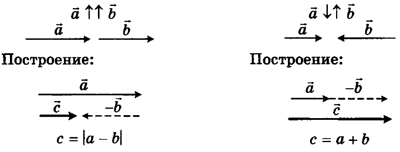
Сложение
векторов, направленных вдоль одной
прямой:
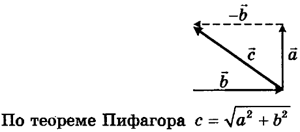
Сложение
векторов, перпендикулярных друг другу
По теореме
Пифагора
Сложение
векторов, расположенных под углом друг
к другу
Правило
сложения скоростей. Векторная
сумма скоростей:
где —
скорость тела относительно подвижной
системы отсчета (ПСО); —
скорость ПСО относительно неподвижной
системы отсчета (НСО); —
скорость тела относительно неподвижной
системы отсчета (НСО).
Относительная
скорость. Векторная
разность скоростей:
где —
скорость первого тела относительно
второго (относительная скорость); —
скорость первого тела; —
скорость второго тела.
Векторное
вычитание:
Вычитание
векторов, направленных по одной прямой:
Вычитание
векторов перпендикулярных друг другу
Вычитание
векторов, расположенных под углом друг
к другу:
6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Физика. помогите пожалуйста) Как найти модуль перемещения и проекции векторов на координатные оси?
Полина
Ученик
(166),
закрыт
12 лет назад
Валентина ???
Гений
(71098)
12 лет назад
Проекция вектора перемещения на координатную ось равна изменеию соответствующей координаты, т. е.
Sx = X – X0
Sy = Y – Y0
Модуль вектора перемещения находят через проекции его на оси по теореме Пифагора.