Две задачи на построение сечений
Здесь рассмотрено подробное решение двух наиболее сложных, на мой взгляд, задач из представленных в группе Задачи на построение сечений многогранников на этом сайте. Если Вы еще не выполняли подобных заданий, вернитесь на указанную страницу и попробуйте поработать самостоятельно.
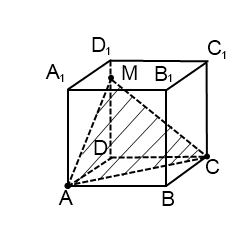
Задача 6.
Замечание: куб на чертеже может быть повёрнут к нам любой гранью, но трудно предугадать, какой удобнее для построения. Поэтому, если совсем не получается решение какой-либо задачи по стереометрии, то я рекомендую начинать заново, перерисовав исходный чертёж. А зачастую бывает достаточно просто переставить символы, обозначающие вершины основания многоугольника (естественно, не произвольно, а согласовав между собой и с условием задачи).
Для начала вспомним признак перпендикулярности прямой и плоскости.
Теорема. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости.
Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
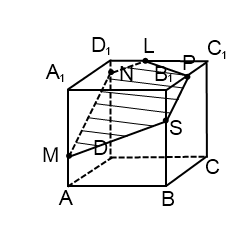
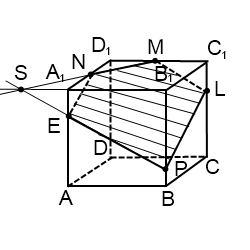
Поэтому для реализации нашей цели нужно найти две различные плоскости, содержащие прямую B1D, и построить в них нужные перпендикуляры. В качестве таковых в кубе можно взять, например, плоскости B1BDD1 и B1ADC1

Построим сечение B1BDD1. Две противоположные стороны этого четырёхугольника являются рёбрами куба, а две другие – диагоналями его граней. По свойствам куба можем сделать вывод, что B1BDD1 – прямоугольник длина которого в √2 _ раз больше ширины. Делим диагональ на 4 части и ставим точку К, удовлетворяющую условию B1K : B1D = 1 : 4. Проводим через эту точку перпендикуляр к B1D. Отрезок MN лежит на одной из искомых прямых.
При необходимости легко уточнить положение точек M и N на поверхности куба. Если задана длина ребра (или можно обозначить её, например, символом a), то длины отрезков B1M и B1N легко вычисляются из подобия прямоугольных треугольников, которое хорошо просматривается на плоском чертеже.

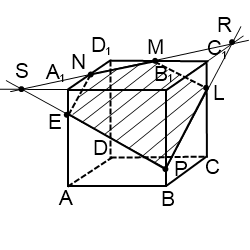
Получили четыре точки, принадлежащие искомой плоскости сечения и поверхности куба. Соединяем прямой линией точки M и F на грани BСС1B1. Соединяем точки F и N на грани A1B1С1D1 и продолжаем прямую до пересечения с ребром A1B1 в точке R. Соединяем точки R и E на грани A1B1BA и продолжаем прямую до пересечения с ребром B1B в точке. M ? Но где гарантия, что именно в точке M, а не выше или ниже по ребру?

Если были проведены вычисления отрезков B1F = B1M и B1N = B1E в процессе анализа плоских прямоугольников, то ответ становится очевидным: так как прямоугольные треугольники B1RF, B1RM и B1FM равнобедренные и равные.
Если же при построении положение точек M и F не вычислялось, а контролировался только факт их положения на рёбрах куба, то придётся произвести ряд вычислений на этапе доказательства верности построения.
Замечание I.
Возможен альтернативный подход к этой задаче. Так как куб является правильным многогранником и имеет центр симметрии, расположенный в точке пересечения диагоналей, а значит на линии B1D, с которой мы работаем, то можно предположить, что сечение также будет симметричным и будет иметь форму равностороннего треугольника. Поэтому после анализа (жёлтого) прямоугольника на первом чертеже и получения точки М, можно сразу отложить от вершины B1 на рёбрах куба равные отрезки B1R = B1F = B1M, а затем доказать, что плоскость RMF перпендикулярна прямой B1D. Для этого лучше всего воспользоваться теоремой о трёх перпендикулярах.
Теорема. Прямая, проведенная на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Замечание II.
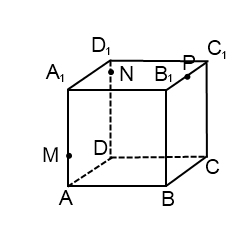
Вид сечения сильно зависит от положения точки K на диагонали куба. Попробуйте сместить точку K ближе к середине отрезка B1D и построить MN ⊥ B1D в прямоугольнике B1BDD1. На каких гранях и рёбрах куба теперь окажутся точки искомого сечения?
Ниже вы можете посмотреть маленькое видео о том, как изменяется сечение куба плоскостью, перпендикулярной его диагонали, в зависимости от положения их точки пересечения.
Задача 16.
При решении задачи предполагаем, что все операции на плоскости, в частности, построение параллельных и перпендикулярных прямых, нам известны из планиметрии и в подробном описании не нуждаются.
Решение.
Чтобы построить плоскость, параллельную заданной плоскости, нужно вспомнить признак параллельности двух плоскостей.
Теорема. Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости.
Теорема. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Кроме того, нам нужно, чтобы плоскость сечения проходила через заданную точку А2. Значит, хорошо бы сразу найти две такие пересекающиеся прямые, параллельные каким-либо прямым в плоскости PQR, чтобы хотя бы одна из них содержала точку А2. В этом и будет состоять первый этап решения задачи.
 Через точки R и Р проводим РN || CC1 и RM || CC1 . Соединяем точки M и N прямой линией. По свойствам призмы получим MN || RР и MN = RР .
Через точки R и Р проводим РN || CC1 и RM || CC1 . Соединяем точки M и N прямой линией. По свойствам призмы получим MN || RР и MN = RР .
 Терерь рассмотрим диагональное сечение призмы, проведенное через параллельные прямые AA1 и СС1. Плоскость AA1C1C содержит заданные точкии A2 и Q и пересекает заданную плоскость PQR по линии QE. (Буквой Е обозначена общая точка линии пересечения плоскостей и прямой RP.) В этой плоскости (голубой на чертеже) через точку А2 проводим прямую, параллельную QE до пересечения с верхним основанием призмы в точке F. А2F || QE по построению.
Терерь рассмотрим диагональное сечение призмы, проведенное через параллельные прямые AA1 и СС1. Плоскость AA1C1C содержит заданные точкии A2 и Q и пересекает заданную плоскость PQR по линии QE. (Буквой Е обозначена общая точка линии пересечения плоскостей и прямой RP.) В этой плоскости (голубой на чертеже) через точку А2 проводим прямую, параллельную QE до пересечения с верхним основанием призмы в точке F. А2F || QE по построению.
 На верхней грани призмы через точку F проводим прямую, параллельную линии MN, которая в нашем случае пересекает рёбра призмы A1D1 и B1C1 в точках H и G соответственно. HG || MN .
На верхней грани призмы через точку F проводим прямую, параллельную линии MN, которая в нашем случае пересекает рёбра призмы A1D1 и B1C1 в точках H и G соответственно. HG || MN .
В зависимости от положения точки А2 на ребре АА1 положение точек H и G на рёбрах призмы может изменяться. Например, если бы точка А2 располагалась ближе к вершине А1, то точка G могла бы оказаться на ребре А1В1, а если бы она находилась близко к вершине А, то точка Н могла бы оказаться на ребре D1С1. От этого зависит окончательная форма искомого сечения призмы. Т.е. поскольку в условии задачи положение точек на рёбрах не фиксировано, то ваши ответы могут отличаться от приведенного мной не только формой на чертеже, но и количеством сторон получившегося многоугольника.
Обе прямые HG и RР параллельны прямой MN по построению, следовательно HG || RР . Для прямых в плоскости это вам уже известно давно. Для прямых в пространстве это тоже доказано.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Таким образом, прямые А2F и HG и есть те самые прямые, которые мы искали. А2F параллельна QE, следовательно параллельна плоскости PQR. HG параллельна RР, следовательно параллельна плоскости PQR. А2F и HG пересекаются в точке F. Эти прямые определят секущую плоскость, параллельную заданной PQR.
Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.


Продолжим прямую HG до пересечения с ребром A1B1 в точке L. Точка L принадлежит верхней и фронтальной (на нашем чертеже) граням призмы, поскольку она принадлежит их общему ребру. Кроме того, точка L принадлежит плоскости сечения, поскольку находится на прямой HG. Следовательно, эта точка должна принадлежать и линии пересечения фронтальной грани с плоскостью сечения. Соединяем точку L с точкой А2. Эта прямая будет принадлежать плоскости грани АА1В1В на основании следующей теоремы.
Теорема. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
 Пользуясь этим же утверждением, соединяем и остальные две пары точек, принадлежащих одной грани призмы.
Пользуясь этим же утверждением, соединяем и остальные две пары точек, принадлежащих одной грани призмы.
То, что оно удовлетворяет условию проходить через точку А2 очевидно по построению. То, что плоскость A2HGK параллельна плоскости RQP мы доказали, ссылаясь на соответствующие положения теории на каждом шаге построения.
 Замечание.
Замечание.
Конечно, во время экзамена вы не будете делать несколько чертежей и так подробно описывать построение. Итоговый чертёж будет выглядеть примерно так.
Однако, не забывайте, что основное требование к заданиям второй части ЕГЭ профильного уровня это обоснованность решения. Поэтому, если вы просто выполнили все построения и представили на проверку итоговый чертёж, то к нему необходимо написать доказательство, которое содержит ссылки на теорию. При этом не обязательно цитировать теоремы полностью, можно упомянуть их названия.
Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.
Понравились материалы сайта?
Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания? Обращайтесь – mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
Узнать ещё
Знание — сила. Познавательная информация
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
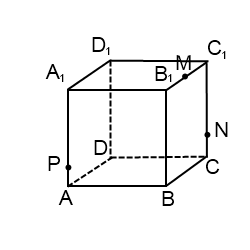
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
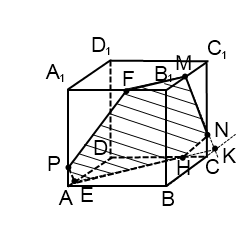
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
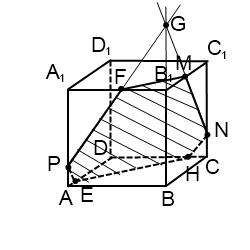
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Как построить плоскость параллельную прямой в кубе
И.М. Смирнова , В.А. Смирнов
ЛЕКЦИЯ 7: СЕЧЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР
Рассмотрим вопрос об исследовании и построении сечений многогранников плоскостью. Задачи на построение сечений многогранников, определение вида сечений или вычисление элементов этих сечений часто включаются в различные контрольные и проверочные работы, конкурсы и олимпиады по математике. Решение таких задач способствует развитию пространственных представлений, выработке практических навыков изображения пространственных фигур.
Выясним, какими могут быть сечения куба плоскостью.
Если плоскость пересекает три ребра куба, выходящих из одной вершины, то в сечении получается треугольник (рис. 1). При этом если отсекаемые плоскостью отрезки ребер равны, то в сечении получается равносторонний треугольник, если равны два отрезка из трех, то получается равнобедренный треугольник, наконец, если все три отрезка различны, то в сечении получается разносторонний треугольник.
Покажем, что в сечении куба плоскостью не могут получаться прямоугольный или тупоугольный треугольники. Для этого обозначим отрезки, выходящие из вершины куба и отсекаемые плоскостью, соответственно a , b и c . По теореме Пифагора имеем равенства: AB 2 = a 2 + b 2 , AC 2 = a 2 + c 2 , BC 2 = b 2 + c 2 . Из этих равенств следует, что AB 2 AC 2 + BC 2 и, значит, угол C – острый. Аналогично, углы A и B – также острые, т.е. треугольник ABC – остроугольный. Таким образом, в сечении куба плоскостью можно получить только остроугольный треугольник и нельзя получить прямоугольный или тупоугольный треугольники.
Выясним, какие четырехугольники могут получаться в сечении куба плоскостью.
Ясно, что если плоскость параллельна одной из граней куба, то в сечении получается квадрат (рис. 2). Если плоскость параллельна одному из ребер куба, то в сечении получается прямоугольник (рис. 3). Если плоскость пересекает четыре параллельных ребра куба, то в сечении получается параллелограмм (рис. 4).
Самостоятельно выясните, может ли в сечении куба плоскостью получиться: а) трапеция; б) равнобедренная трапеция; в) неравнобедренная трапеция; г) прямоугольная трапеция; д) тупоугольная трапеция?
Поскольку для любых четырех граней куба обязательно найдутся две из них, параллельные между собой, то в четырехугольнике, являющемся сечением куба плоскостью обязательно найдутся две параллельные стороны. Таким образом, в сечении куба плоскостью не может получиться четырехугольник, у которого нет параллельных сторон.
На рисунке 5 показано сечение куба плоскостью в форме пятиугольника ABCDE . Прямые AB и DE , CD и AE параллельны, как линии пересечения двух параллельных плоскостей третьей плоскостью.
Таким образом, в сечении куба плоскостью может получиться только тот пятиугольник, у которого имеется две пары параллельных сторон. В частности, не может получиться правильный пятиугольник.
На рисунке 6 показано сечение куба плоскостью в форме шестиугольника ABCDEF . Прямые AB и DE , BC и EF , CD и AF параллельны, как линии пересечения двух параллельных плоскостей третьей плоскостью.
Таким образом, в сечении куба плоскостью может получиться только тот шестиугольник, у которого имеется три пары параллельных сторон.
Самостоятельно докажите, что в случае, если точки A , B , C являются серединами ребер, то в сечении получается правильный шестиугольник.
Поскольку у куба имеется только шесть граней, то в сечении куба плоскостью не может получиться многоугольник с числом сторон, большим шести.
Рассмотрим теперь вопрос о построении сечений многогранников.
Пусть дано изображение куба и три точки A , B , C , принадлежащие ребрам этого куба, выходящим из одной вершины. Тогда для того чтобы построить сечение куба плоскостью, проходящей через эти точки, достаточно просто соединить их отрезками. Полученный треугольник ABC и будет искомым изображением сечения куба (рис. 1).
Для построения более сложных сечений используют метод «следов», заключающийся в нахождении точки пересечения прямой и плоскости по заданным двум точкам этой прямой и их проекциям на плоскость.
Решим несколько предварительных задач на построение.
Задача 1. Пусть прямая k проходит через точки A , B и известны параллельные проекции A ’ , B ’ этих точек на плоскость p . Требуется найти точку пересечения прямой AB с плоскостью p .
Решение. Через точки A ’ , B ’ проведем прямую k ’ . Тогда пересечение прямой k с прямой k ’ и будет искомым пересечением прямой k с плоскостью p (рис. 7).
Задача 2. Даны точки A , B , C и их параллельные проекции A ’ , B ’ , C ’ на плоскость p . Требуется построить линию пересечения плоскости ABC и плоскости p .
Решение. Используя решение предыдущей задачи, построим точки X и Y пересечения прямых AB и AC с плоскостью p . Прямая XY будет искомой линией пересечения плоскости ABC и плоскости p (рис. 8).
Задача 3. Через данную точку C ( C ’ ) провести прямую, параллельную данной прямой AB ( A ’ B ’ ), и найти ее точку пересечения с плоскостью p .
Решение. Через точку C проводим прямую, параллельную AB . Через точку C ’ проводим прямую, параллельную A ’ B ’ . Точка X пересечения этих прямых и будет искомой (рис. 9).
Используя этот метод, решим задачи на построение сечений куба, пирамиды и призмы.
Задача 4. Построить сечение куба плоскостью проходящей через три точки A , B , C , принадлежащие попарно скрещивающимся ребрам этого куба (рис. 10).
Решение. Найдем пересечение прямой AB , лежащей в плоскости сечения, с плоскостью основания куба. Для этого построим параллельные проекции A ’, B ’ точек A , B на основание куба в направлении бокового ребра куба (рис. 11). Пересечение прямых AB и A ’ B ’ будет искомой точкой P . Она принадлежит плоскости сечения и плоскости основания куба. Следовательно, плоскость сечения пересекает основание куба по прямой CP . Точка пересечения этой прямой с ребром основания куба даст еще одну точку D сечения куба. Соединим точки C и D , B и D отрезками. Через точку A проведем прямую, параллельную BD , и точку ее пересечения с ребром куба обозначим E . Соединим точки E и C отрезком. Через точку A проведем прямую, параллельную CD , и точку ее пересечения с ребром куба обозначим F . Соединим точки A и F , B и F отрезками. Многоугольник AECDBF и будет искомым изображением сечения куба плоскостью (рис. 11 ).
Задача 5. Построить сечение треугольной пирамиды плоскостью, проходящей через три точки A , B , C , принадлежащие ее ребрам (рис. 12).
Решение. Проведем прямую AB и ее точку пересечения с боковым ребром пирамиды обозначим через E . Проведем прямую EC и ее точку пересечения с ребром основания пирамиды обозначим через D . Соединим отрезками точки B и C , A и D . Четырехугольник ABCD будет искомым сечением пирамиды.
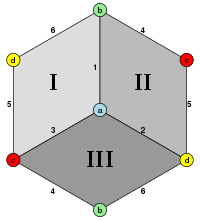
Задача 6. Построить сечение шестиугольной пирамиды плоскостью, проходящей через точки A 1 , C 1 , E 1 (рис. 13).
Решение. Проведем прямую A 1 C 1 и найдем точку P ее пересечения с прямой AC . Проведем прямую E 1 C 1 и найдем точку Q ее пересечения с прямой EC . Проведем прямую PQ , являющуюся линией пересечения плоскостей a и p . Проведем прямую AB и найдем точку V ее пересечения с прямой PQ . Проведем прямую A 1 V и найдем точку B 1 ее пересечения с SB . Аналогичным образом строятся и остальные точки D 1 , F 1 .
Задача 7. На гранях четырехугольной призмы ABCDA 1 B 1 C 1 D 1 даны точки K , L и M (рис. 14). Постройте сечение призмы плоскостью, проходящей через эти точки.
Решение. Через точки K , L и M проведем прямые, параллельные боковому ребру призмы, и найдем точки K ’ , L ’ и M ’ их пересечения со сторонами основания. Обозначим N ’ точку пересечения прямых K ’ L ’ и BM ’ . Через точку N ’ проведем прямую, параллельную боковому ребру призмы, и найдем точку N ее пересечения с прямой KL . Через точки N и M проведем прямую, и найдем точку P ее пересечения с ребром BB 1 . Точка P будет принадлежать искомому сечению. Через точку P и точки K и L проведем прямые, и найдем точки Q и R их пересечения с боковыми ребрами AA 1 и CC 1 призмы. Через точки Q и M проведем прямую, и найдем точку S ее пересечения с боковым ребром DD 1 . Четырехугольник PQSR будет искомым сечением призмы плоскостью.
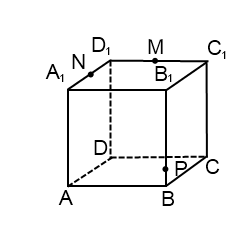
1. Какой фигурой является сечение куба A . D 1 плоскостью, проходящей через вершины B 1 , D и середину ребра CC 1 ?
2. Какой фигурой является сечение куба A . D 1 плоскостью, проходящей через середины ребер AB , BC и DD 1 ?
3. Через середину ребра куба, перпендикулярно скрещивающейся с этим ребром диагонали, проведено сечение. Определите его вид.
Ответ: Правильный шестиугольник.
4. Какой фигурой является сечение куба плоскостью, которая проходит через две противоположные вершины нижнего основания и середину одного из ребер верхнего основания? Найдите его периметр, если длина ребра куба равна 1.
Ответ: Равнобедренная трапеция периметра
5. Через вершины A , C , D 1 куба A … D 1 проведено сечение. В каком отношении оно делит диагональ DB 1 , и какой образует угол с этой диагональю?
6. Может ли в сечении куба плоскостью получиться четырехугольник, изображенный на рисунке 15?
7. Выясните, какие могут быть сечения правильного тетраэдра плоскостью.
Ответ: Правильный, равнобедренный и разносторонний треугольники; квадрат, прямоугольник и четырехугольник с непараллельными сторонами.
8. Каким является сечение тетраэдра ABCD плоскостью, проходящей через середины ребер AB , BC и CD ?
9. Какой фигурой является сечение правильного тетраэдра ABCD плоскостью, проходящей через вершину B и точки M , N – середины соответственно ребер AD , CD ?
10. Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке 16?
11. Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью?
Ответ: Треугольник, четырехугольник, пятиугольник.
12. Определите вид сечения правильной треугольной призмы плоскостью, проходящей через сторону нижнего основания и середину скрещивающейся с ней стороны верхнего основания.
Ответ: Равнобедренная трапеция.
13. Верно ли утверждение о том, что в сечении правильной шестиугольной призмы плоскостью, проходящей через середины двух соседних боковых ребер и вершину верхнего основания, принадлежащей смежной боковой грани, получается равнобедренная трапеция?
14. Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунках 17, 18.
15. Постройте сечение куба A . D 1 плоскостью, проходящей через вершины B 1 , D и точку H , принадлежащую ребру CC 1 .
16. Постройте сечение правильной четырехугольной пирамиды плоскостью, проходящей через точки, указанные на рисунке 19 .
17. Как построить сечение правильного тетраэдра ABCD плоскостью, параллельной грани BDC и проходящей через точку K – середину ребра AD ?
18. Постройте сечение правильной шестиугольной призмы плоскостью, проходящей через точки, указанные на рисунке 20.
19. Меньший куб поставлен на больший таким образом, что они имеют общую вершину и их грани попарно параллельны (рис. 21). Постройте сечение полученной фигуры плоскостью, проходящей через три точки, которые принадлежат скрещивающимся ребрам меньшего куба.
Сечения цилиндра плоскостью можно рассматривать как параллельные проекции основания цилиндра на эту плоскость. Поэтому, если плоскость параллельна плоскости основания, то в сечении получается круг, равный основанию. Здесь мы докажем, что если плоскость сечения составляет некоторый угол с плоскостью основания цилиндра и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.
Напомним, что эллипсом называется геометрическое место точек, сумма расстояний от которых до двух данных точек F 1 , F 2 есть величина постоянная, называется эллипсом. Точки F 1 , F 2 называются фокусами эллипса.
Таким образом, для точек A эллипса с фокусами F 1 и F 2 сумма AF 1 + AF 2 постоянна и равна некоторому положительному числу c (рис. 22). Из неравенства треугольника следует, что число c должно быть больше длины отрезка F 1 F 2 .
Слово “фокус” в переводе с латинского языка означает “очаг”, “огонь”, и именно это свойство эллипса послужило основанием для названия точек F 1 , F 2 фокусами.
Отрезок прямой F 1 F 2 , соединяющий две точки эллипса, называется большой осью.
Отрезок прямой, проходящей через середину большой оси и перпендикулярной этой оси, соединяющий две точки эллипса, называется малой осью эллипса.
Еще И. Кеплер обнаружил, что планеты Солнечной системы движутся вокруг Солнца не по окружностям, как думали раньше, а по эллипсам, причем Солнце находится в фокусах этих эллипсов. Точка орбиты планеты, ближайшая к Солнцу, называется перигелий, а наиболее удаленная – афелий. Однако из-за того, что орбита Земли представляет собой очень мало сжатый эллипс, похожий на окружность, такое приближение и удаление от Солнца незначительно сказывается на температуре. Гораздо большее значение для температуры на поверхности Земли имеет угол падения солнечных лучей. Например, когда Земля бывает в перигелии, в нашем полушарии зима, а когда в афелии – в нашем полушарии лето. Луна, искусственные спутники Земли также движутся вокруг Земли по эллипсам.
Для того чтобы нарисовать эллипс потребуется нить и кнопки. Прикрепим концы нити к фокусам. Карандашом натянем нить так, чтобы его острие касалось бумаги. Будем перемещать карандаш по бумаге так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге эллипс (рис. 23).
Теорема. Если плоскость сечения составляет некоторый угол с плоскостью основания цилиндра и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.
Доказательство. Рассмотрим цилиндрическую поверхность, составленную из образующих цилиндра и ее сечение плоскостью . Впишем в эту поверхность две сферы, касающиеся плоскости в некоторых точках F 1 , F 2 и цилиндрической поверхности по окружностям C 1 , С2 (рис. 24). Пусть A – произвольная точка сечения. Проведем через нее образующую и обозначим через А1, А2 точки пересечения этой образующей с окружностями C 1 , C 2 соответственно. Заметим, что прямая A 1 A 2 является касательной к обеим сферам. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF 1 = AA 1 , AF 2 = AA 2 . Поэтому AF 1 + AF2 = AA1 + AA2 = A1 A2. Но длина отрезка А1 А2 есть расстояние между плоскостями окружностей C 1 , C 2 . Поэтому оно не зависит от выбора точки А сечения, т. е. является постоянной величиной. Значит, сечением цилиндрической поверхности является эллипс с фокусами F 1 , F 2 .
На рисунке 25 показано построение точек эллипса, получающегося как сечение боковой поверхности цилиндра плоскостью.
Для этого зададим два сопряженных диаметра AB и CD . Через точку A проведем образующую и выберем на ней какую-нибудь точку A ’ , принадлежащую сечению. Прямая A ’ O пересечет образующую, проходящую через точку B в некоторой точке B ’ , также принадлежащую сечению. Возьмем теперь на отрезке CD произвольную точку и проведем через нее прямую, параллельную A ’ B ’ . Ее точки пересечения с образующими цилиндра будут принадлежать сечению.
Рассмотрим еще одно свойство сечений цилиндра плоскостью, а именно, связь этих сечений с тригонометрическими функциями.
Возьмем прямоугольный лист бумаги и нарисуем на нем оси координат Ox и Oy параллельно соответствующим сторонам (рис. 26). Затем свернем этот лист в боковую поверхность прямого кругового цилиндра, радиус основания которого примем за единицу. Ось Ox свернется в окружность радиуса 1, а ось Oy станет образующей цилиндра (рис. 27). Через диаметр OD полученной окружности проведем сечение, составляющее с плоскостью окружности угол в 45 . В этом случае сечением будет эллипс.
Развернем цилиндр обратно в прямоугольник. При этом эллипс развернется в кривую, являющуюся частью синусоиды. Для доказательства этого из произвольной точки A на эллипсе опустим перпендикуляры на плоскость окружности и диаметр окружности OD . Получим соответственно точки B и C . Треугольник ABC прямоугольный и равнобедренный, так ABC = 90 ° , ACB = 45 ° . Следовательно, AB = BC . Заметим, что BC = sin x , где x – длина дуги OB . Для этого достаточно обратиться к рисунку 28 и вспомнить определение синуса. Таким образом, AB = sin x , где x = OB , т. е. эта кривая является частью синусоиды с уравнением y = sin x (рис. 29).
1. В каком случае сечением цилиндра плоскостью является круг?
Ответ: В случае, если плоскость сечения параллельна плоскости основания цилиндра.
2. Что будет сечением цилиндра плоскостью, проходящей через ось цилиндра?
3. Какую форму принимает поверхность воды в круглом наклоненном стакане?
4. Нарисуйте цилиндр и плоскость, пересекающую его боковую поверхность по эллипсу.
5. Может ли в сечении цилиндра плоскостью получиться: а) круг; б) прямоугольник; в) параллелограмм; г) трапеция д) треугольник?
Ответ: а), б) Да; в), г), д) нет.
6. Могут ли в сечениях цилиндра плоскостью получаться фигуры, отличные от круга, прямоугольника и эллипса?
Ответ: Да, если сечение пересекает боковую поверхность и основания цилиндра.
7. Используя карандаш, бумагу, нить и кнопки, нарисуйте эллипс.
8. Радиус основания цилиндра равен R . Плоскость сечения боковой поверхности цилиндра составляет с плоскостью основания угол j . Найдите малую и большую оси эллипса.
Ответ: R , .
9. Докажите, что сумма расстояний от любой точки эллипса до фокусов равна длине большой оси эллипса.
10. Докажите, что расстояния от концов малой оси эллипса до его фокусов равны половине большой оси.
11. Нарисуйте цилиндр и постройте несколько точек эллипса, получающегося в сечении его боковой поверхности плоскостью.
12. Докажите, что площадь эллипса, у которого большая и малая полуоси равны соответственно R , r , выражается формулой S = Rr . (Воспользуйтесь тем, что площадь ортогональной проекции фигуры равна произведению площади фигуры на косинус угла, образованного плоскостью фигуры и плоскостью ортогональной проекции.)
13. В основании цилиндра круг радиуса R . Боковая поверхность цилиндра пересечена плоскостью. Найдите площадь сечения цилиндра этой плоскостью, если она образует с плоскостью основания угол: а) 30 ° ; б) 45 ° ; в) 60 ° .
Ответ: а) ; б) ; в) .
14. Докажите, что если сечение цилиндра, свернутого из бумаги, проводить не под углом 45 ° , а под углом j , то уравнение соответствующей кривой будет иметь вид y = k · sin x , где k = tg j . Нарисуйте кривые соответствующие углам: а) j = 30 ° ; б) j = 60 ° .
15. Докажите, что если исходный прямоугольник свернуть в прямой круговой цилиндр не единичного, а некоторого другого радиуса a и произвести с этим цилиндром аналогичные операции, то получится кривая, задаваемая уравнением y = a · sin ( ).
16. Нарисуйте график функции: а) y = 2 sin ( ); б) y = sin 2 x .
17. Докажите, что если плоскость сечения проходит не через точку О, а через диаметр, образующий с О D (рис. 27) угол 0, то получится кривая, задаваемая уравнением y = sin ( x – j 0 ).
18. Нарисуйте график функции: а) y = sin ( x – ); б) y = sin ( x + ).
19. Возьмем прямоугольный лист бумаги с нарисованными на нем осями координат (рис. 26). Свернем этот лист в боковую поверхность правильной четырехугольной призмы (рис. 30). Сторону основания призмы примем за 1. Через точки О и D проведем сечение плоскостью, составляющей с плоскостью основания угол 45 ° . Развернем лист бумаги. Выясните, какая при этом получится кривая? Что изменится, если сечение проводить под другими углами?
Для данного конуса рассмотрим коническую поверхность, образованную прямыми, проходящими через вершину конуса и точки окружности основания конуса (рис. 31).
Сечения конической поверхности плоскостью можно рассматривать как центральную проекцию окружности основания конуса на эту плоскость. Поэтому, если плоскость параллельна плоскости основания и не проходит через вершину конуса, то в сечении конической поверхности получается окружность.
Исследуем другие возможные случаи сечения конической поверхности плоскостью, не проходящей через вершину конуса.
Теорема. Если плоскость образует с осью конуса угол, больший, чем угол между образующей и этой осью, то в сечении конической поверхности получается эллипс.
Доказательство. Докажем, что с умма расстояний от произвольной точки сечения до двух данных точек есть величина постоянная.
Впишем в коническую поверхность две сферы, касающиеся плоскости сечения в некоторых точках F 1 , F 2 и конической поверхности по окружностям C 1 и C 2 соответственно (рис. 32).
Пусть А – произвольная точка сечения. Проведем образующую AS и обозначим через А1, А2 точки ее пересечения с окружностями C 1 , C 2 соответственно. Заметим, что прямая AS является касательной к обеим сферам. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF 1 = AA 1 , AF 2 = AA 2 . Поэтому AF 1 + AF2 = AA1 + AA2 = A1 A2. Но длина отрезка А1 А2 не зависит от выбора точки А сечения. Она равна образующей соответствующего усеченного конуса. Поэтому сумма расстояний от точки А до точек F 1 , F 2 будет постоянной.
На рисунке 33 показано построение точек эллипса, получающегося как сечение конуса плоскостью.
Для этого нужно зададим два сопряженных диаметра AB и CD . Выберем на образующих SA и SB точки A ’ и B ’ . Возьмем какую-нибудь точку O 1 на диаметре AB , проведем через нее прямую, параллельную CD и найдем ее точки пересечения C 1 и D 1 с окружностью основания конуса. Соединим точки O 1 , C 1 , D 1 с вершиной конуса. Через точку O ’ 1 пересечения O 1 S с A ’ B ’ проведем прямую, параллельную C 1 D 1 и найдем ее точки пересечения с C 1 S и D 1 S . Полученные точки будут принадлежать сечению.
Теорема. Если плоскость образует с осью конуса угол, равный углу между образующей и этой осью, то в сечении конической поверхности получается парабола.
Доказательство. Напомним, что параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F , называемой фокусом, и данной прямой d , называемой директрисой, лежащих в этой плоскости.
Впишем в коническую поверхность сферу, касающуюся плоскости a в некоторой точке F и конической поверхности по окружности C , лежащей в плоскости b , перпендикулярной оси. Плоскости a и b образуют между собой угол 90 ° – j и пересекаются по некоторой прямой d (рис. 34).
Пусть А – произвольная точка сечения. Проведем образующую AS и обозначим через А1 точку ее пересечения с окружностью C . Заметим, что прямая AS является касательной к сфере. Прямая AF также является касательной. Отрезки А F и АА1 равны как отрезки касательных, проведенных к сфере из одной точки.
Опустим из точки А перпендикуляр АВ на плоскость b и перпендикуляр А D на прямую d . Угол А1 АВ равен j . Угол А D В является углом между плоскостями a и b и поэтому равен 90 ° – j . Следовательно, угол BAD равен j .
Прямоугольные треугольники АВА1 и АВ D равны, так как имеют общий катет и соответственно равные углы. Поэтому АА1 = А D . Окончательно получаем равенство AF = AD , которое означает, что расстояние от произвольной точки сечения до точки F равно расстоянию от этой точки до прямой d , т. е. сечением конической поверхности в этом случае является парабола.
На рисунке 35 показано построение точек параболы, получающейся как сечение конуса плоскостью.
Теорема. Если плоскость образует с осью конуса угол, меньший угла между образующей и этой осью, то в сечении конической поверхности получается гипербола.
Доказательство. Напомним, что гиперболой называется геометрическое место точек на плоскости, модуль разности расстояний от которых до двух заданных точек плоскости постоянен.
Впишем в коническую поверхность сферы, касающиеся плоскости сечения в некоторых точках F 1 и F 2 и конической поверхности по окружностям C 1 и C 2 соответственно.
Пусть А – точка сечения, расположенная в той же части конической поверхности, что и точка F 1 (рис. 36). Проведем образующую AS и обозначим через А1, А2 точки ее пересечения с окружностями C1, C2 соответственно. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF1 = AA1, AF2 = AA2. Поэтому AF 2 – AF1 = AA2 – AA1 = A1 A2. Но длина отрезка А1 А2 не зависит от выбора точки А сечения. Она равна сумме образующих соответствующих конусов. Следовательно, разность AF2 – AF1 расстояний от точки А до точек F1, F2 будет постоянной. Аналогичным образом показывается, что если точка A расположена в той же части конической поверхности, что и точка F 2 , то разность AF1 – AF2 будет постоянной. Таким образом, сечением конической поверхности в этом случае является гипербола.
На рисунке 37 показано построение точек гиперболы, получающейся как сечение конуса плоскостью.
Конические сечения с древних времен привлекали к себе внимание ученых. Так древнегреческий ученый Менехм ( IV в. до н. э.) пользовался параболой и гиперболой для решения знаменитой задачи удвоения куба. Исследовали свойства конических сечений Евклид ( IV в. до н. э.) и Архимед ( III в. до н. э.). Полное и систематическое учение об этих кривых было изложено Аполлонием Пергским ( III – II вв. до н. э.) в восьмитомном труде “Конические сечения”. Там он впервые показал, как можно получить эти кривые, рассекая один и тот же конус плоскостью под разными углами. Он же ввел термины “эллипс”, “парабола” и “гипербола”, означающие в переводе с греческого соответственно “недостаток”, “приложение” и “избыток”. Происхождение этих названий связано с задачей построения прямоугольника с заданным основанием, равновеликого данному квадрату. Переводя с геометрического языка, которым пользовался Аполлоний, на современный алгебраический язык, получаем уравнение
y 2 = 2 px + lx 2 ,
где эллипсу соответствует отрицательное, гиперболе – положительное, а параболе – равное нулю значение второго члена в правой части. Таким образом, для параболы площадь квадрата, построенного на ординате y , равна площади прямоугольника со сторонами 2 p и x . Для эллипса площадь прямоугольника меньше, а для гиперболы – больше площади соответствующего квадрата.
Интерес к коническим сечениям особенно возрос после того, как Г. Галилей (1564-1642) установил, что тело, брошенное под углом к горизонту, двигается по параболе, а И. Кеплер сформулировал законы движения планет, согласно которым они описывают эллипсы. Позднее было установлено, что кометы и другие небесные тела движутся по эллипсам, параболам или гиперболам в зависимости от их начальной скорости.
Так, если скорость космического корабля при выходе на орбиту Земли составляет 7,9-11,1 км/с (первая космическая скорость), то он будет двигаться вокруг Земли по эллиптической орбите.
Если его скорость составляет 11,2-16,7 км/с (вторая космическая скорость), то он будет двигаться по параболической орбите и покинет зону земного притяжения. Однако он не сможет выйти за пределы Солнечной системы.
Если же его скорость больше 16,7 км/с (третья космическая скорость), то он будет двигаться по гиперболической орбите и уйдет за пределы Солнечной системы.
1. В каком случае сечением конуса плоскостью является круг?
Ответ: В случае, если плоскость сечения параллельна плоскости основания конуса.
2. Что будет сечением конуса плоскостью, проходящей через ось конуса?
3. Может ли в сечении конуса плоскостью получиться: а) круг; б) треугольник, в) прямоугольник?
Ответ: а), б) Да; в) нет.
4. Могут ли в сечениях боковой поверхности конуса плоскостью получаться фигуры, отличные от окружности, эллипса, параболы, гиперболы?
Ответ: Да, если сечение проходит через вершину конуса.
5. Какой фигурой является сечение конуса плоскостью, проходящей через его вершину?
Ответ: Равнобедренный треугольник.
6. Какую форму принимает поверхность воды в наклоненной конусообразной колбе?
Ответ: В зависимости от угла наклона будет эллипс, парабола или гипербола.
7. Пучок света карманного фонарика имеет форму конуса. Какую форму имеет освещенный фонариком участок ровной поверхности в зависимости от угла наклона фонарика?
Ответ: Эллипс, парабола или гипербола.
8. Может ли центральная проекция сферы быть фигурой, ограниченной: а) окружностью; б) эллипсом; в) параболой; г) гиперболой?
Ответ: а), б), в) г) Да.
9. Через центр основания конуса и середину образующей проведена плоскость. Что представляет собой сечение конуса этой плоскостью?
Ответ: Фигура, ограниченная параболой.
10. Высота конуса равна радиусу основания. Что представляет собой сечение конуса плоскостью, образующей с осью угол: а) 30 ° ; б) 45 ° ; в) 60 ° ?
Ответ: Фигура, ограниченная а) гиперболой; б) параболой; в) эллипсом.
11. Образующая конуса в два раза больше радиуса основания. Под каким углом к оси нужно провести сечение конуса плоскостью, чтобы в сечении конической поверхности получить: а) эллипс; б) параболу; в) гиперболу?
Ответ: а) Больше 60 ° ; б) 60 ° ; в) меньше 60 ° .
12. Осевое сечение конуса – равносторонний треугольник со стороной, равной единице. Через середину образующей проведено сечение конуса плоскостью, перпендикулярной этой образующей. Найдите площадь сечения.
Ответ: .
[spoiler title=”источники:”]
http://vasmirnov.ru/Art/Lecture7.htm
[/spoiler]
Параллельное проецирование. Площадь проекции фигуры
В задачах по геометрии успех зависит не только от знания теории, но и от качественного чертежа.
С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.
Как это сделать?
Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.
Возьмем объемное тело.
Выберем плоскость проекции.
Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.

Как строить проекции объемных тел?
Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:
Проекцией отрезка будет отрезок.

Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.
Проекцией круга в общем случае окажется эллипс.

Проекцией прямоугольника — параллелограмм.

Вот как выглядит проекция куба на плоскость:

Здесь передняя и задняя грани параллельны плоскости проекции
Можно сделать по-другому:

Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.
Рисуем проекции пирамиды,

цилиндра:

и шара:

Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.

Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.
Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.

В следующей статье рассказано, как выбрать наиболее удачный ракурс для построения чертежей в задачах по стереометрии, а также о распространенных ошибках, которые могут помешать решению.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Параллельное проецирование. Площадь проекции фигуры» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
 Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
 Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
 Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
 Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Содержание
- Теорема о трех перпендикулярах
- Теорема о трёх перпендикулярах
- Материалы к уроку
- 20. Теорема о трех перпендикулярах.doc
- 20. Теорема о трёх перпендикулярах.ppt
- Конспект урока
- Остались вопросы по теме? Наши репетиторы готовы помочь!
- Куб — Cube
- Содержание
- Ортогональные проекции
- Сферическая черепица
- Декартовы координаты
- Формулы
- Точка в пространстве
- Удвоение куба
- Равномерная окраска и симметрия
- Геометрические отношения
- Другие размеры
- Связанные многогранники
- В однородных сотах и полихорах
- Кубический граф
Теорема о трех перпендикулярах
Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а1 — проекция наклонной а на плоскость α.
Сформулируем теорему о трех перпендикулярах:
Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

На рисунке показаны все три перпендикуляра.
Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.
Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.
Ты нашел то, что искал? Поделись с друзьями!
Вот как все это выглядит в пространстве:

На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

Теорема о трех перпендикулярах — полезный инструмент для решения задач.
Например, с ее помощью можно доказать, что диагональ куба АС1 перпендикулярна прямой BD:

Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:

Или — что в правильной треугольной призме прямая А1М (где М — середина ВС) перпендикулярна ребру ВС.
Источник
Теорема о трёх перпендикулярах
Материалы к уроку
20. Теорема о трех перпендикулярах.doc
20. Теорема о трёх перпендикулярах.ppt
Конспект урока
Перпендикулярность прямых и плоскостей. Теорема о трёх перпендикулярах.
На прошлых занятиях вы уже познакомились с такими понятиями как: перпендикуляр к плоскости, наклонная, проекция, расстояние от точки до плоскости.

Желательно, что бы картинка была анимированной, т.е. параллельно словам «перпендикуляр к плоскости» проводился перпендикуляр АВ , так же к словам «наклонная» — АС, «проекция» — СВ и «расстояние от точки до плоскости» — тоже АВ.
А теперь попробуем провести прямую через основание наклонной перпендикулярно её проекции. Что можно сказать о данном перпендикуляре?
Если в плоскости провести прямую через основание наклонной перпендикулярно к её проекции на данную плоскость, то эта прямая будет перпендикулярна и к самой наклонной.
Докажем, что прямая ДС перпендикулярна прямой АС:
1.Известно, что прямая АВ перпендикулярна плоскости α, АС-наклонная к плоскости α, ВС-проекция наклонной АС, прямая СД принадлежит плоскости альфа, а так же прямая СД перпендикулярна прямой ВС по построению.
2.Рассмотрим плоскость АСВ: прямая ДС перпендикулярна прямой ВС по условию, а так как прямая АВ перпендикулярна плоскости альфа, значит прямая АВ будет перпендикулярна и прямой ДС, лежащей в этой плоскости (по теореме о перпендилурности прямой и плоскости).
3.Прямая СД перпендикулярна к двум пересекающимся прямым АВ и ВС, принадлежащим плоскости АВС, значит прямая будет перпендикулярна и самой плоскости АВС-по признаку перпендикулярности прямой и плоскости.
4.Из признака перпендикулярности прямой и плоскости следует, что прямая ДС перпендикулярна к любой прямой, лежащей в плоскости АВС, значит прямая ДС перпендикулярна прямой АС.
Таким мы образом мы доказали, что прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярная к самой наклонной.
Доказанное утверждение называется теоремой о трёх перпендикулярах, так как в ней говорится о связи между тремя перпендикулярами АВ, ДС и ВС.

Желательно выделять прямые и плоскости, о которых говорится в доказате льстве.
Существует так же и обратная теорема:
Если провести прямую в плоскости через основание наклонной перпендикулярно к ней, то данная прямая будет перпендикулярна и к ее проекции.
Докажите эту теорему самостоятельно.

Докажите эту теорему самостоятельно.
Рассмотрим применение теоремы о трех перпендикулярах при решении задач.
Отрезок АД перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ =АС=5 см, ВС=6 см. АД=12 см.Найти расстояние от концов отрезка АД до прямой ВС.
1.Дополнительное построение: проведем АЕ перпендикулярно ВС. Отрезок АЕ и будет расстоянием от точки А до прямой ВС.
2. Так как треугольник АВС равнобедренный, то АЕ является высотой и медианой, значит ВЕ=ЕС=3 см
3.Так как треугольник АЕС прямоугольный, то АЕ можем найти по теореме Пифагора:
АЕ=√ AC 2- EC 2 АЕ=√5 2 -3 2 , АЕ=4 см.
4.Отрезок ВС перпендикулярен АЕ, вместе с тем отрезок ВС перпендикулярен D А(по признаку перпендикулярности прямой и плоскости), тогда по теореме о трех перпендикулярах ВС перпендикулярен D Е.
5.Из прямоугольного треугольника ДАЕ найдем ДЕ по теореме Пифагора: ДЕ=√АЕ 2 +АД 2 , D Е=√4 2 +12 2 =√160=4√10 см.

АВ=АС=5 см, ВС=6 см, А D =12 см.
2.ΔАВС-равнобедренный→АЕ-высота и медиана→ ВЕ=ЕС=3 см
3. АЕ=√ AC 2- EC 2 АЕ=√5 2 -3 2 , АЕ=4 см.
5. D Е=√АЕ 2 +А D 2 , D Е=√4 2 +12 2 =√160=4√10 см.
Прямая ВД перпендикулярна к плоскости треугольника АВС. Известно, что ВД=9см, АС=10 см, ВС=ВА=13 см.Найти расстояние а)от точки Д до прямой АС
б)площадь треугольника АСД.
1.Проведём ВЕ перпендикулярно АС.
2.Так как Треугольник АВС равнобедренный, то ВЕ –высота и медиана, значит СЕ=ЕА=5 см.
3.ВД перпендикулярна АС, ВЕ перпендикулярна АС, то по теореме о трёх перпендикулярах ДЕ перпендикулярна АС.
4.Расстояние от точки Д до прямой АС это отрезок ДЕ. Так как треугольник ВЕД прямоугольный, то по теореме Пифагора
В свою очередь ВЕ можно найти из прямоугольного треугольника СВЕ:
ВЕ=√ВС 2 -ЕС 2 =√13 2 -5 2 =√169-25=12 см.
Тогда ДЕ=√12 2 +9 2 =√144+81=15 см
5.В треугольнике АСД: АС-основание, ДЕ-высота, тогда по формуле нахождения площади треугольника(половина произведения основания и высоты) найдем площадь треугольника АДС:
SACD = 1/2 АС*ДЕ= 1/2 *10*15=75см 2

2. ВЕ –высота и медиана , СЕ=ЕА=5 см.
3. В D ┴АС, ВЕ┴АС→ D Е┴АС(по т.т.п.)
D Е=√ВЕ 2 +В D 2 =√12 2 +9 2 =√144+81=15 см
ВЕ=√ВС 2 -ЕС 2 =√13 2 -5 2 =√169-25=12 см.
5. SACD = 1/2АС* D Е= 1/2 *10*15=75см 2
Ответ : DE =15см, SACD = 75см 2
Сегодня мы расширили свои знания по теме «Перпендикулярность прямых и плоскостей», познакомились с теоремой о трёх перпендикулярах, доказали ее, научились применять данную теорему при решении задач.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Источник
Куб — Cube
| Правильный шестигранник | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) |
|
| Тип | Платоново твердое тело |
| Элементы | F = 6, E = 12 V = 8 (χ = 2) |
| Лица по сторонам | 6 |
| Обозначение Конвея | C |
| Символы Шлефли | |
| t <2,4>или <4>× <> tr <2,2>или <> × <> × <> |
|
| Конфигурация лица | V3.3.3.3 |
| Символ Wythoff | 3 | 2 4 |
| Диаграмма Кокстера |      |
| Симметрия | Очас, B3, [4,3], (*432) |
| Группа вращения | О, [4,3] + , (432) |
| Рекомендации | U06, C18, W3 |
| Характеристики | обычный, выпуклыйзоноэдр |
| Двугранный угол | 90° |
 4.4.4 (Фигура вершины) |
 Октаэдр (двойственный многогранник) |
 Сеть |

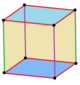
В геометрия, а куб [1] это трехмерный твердый объект, ограниченный шестью квадрат лица грани или сторон, по три встречи на каждой вершина.
Куб — единственный обычный шестигранник и является одним из пяти Платоновы тела. У него 6 граней, 12 ребер и 8 вершин.
Куб — это тоже квадрат параллелепипед, равносторонний кубовид и право ромбоэдр. Это правильный квадрат призма в трех ориентациях, а треугольный трапецоэдр в четырех направлениях.
Куб — единственный выпуклый многогранник, все грани которого равны квадраты.
Содержание
Ортогональные проекции
В куб имеет четыре специальных ортогональные проекциипо центру, на вершине, ребрах, грани и нормали к ее вершина фигуры. Первый и третий соответствуют A2 и B2 Самолеты Кокстера.
| В центре | Лицо | Вершина |
|---|---|---|
| Самолеты Кокстера | B2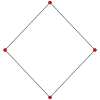 |
А2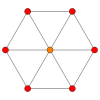 |
| Проективный симметрия |
[4] | [6] |
| Наклонные взгляды |  |
 |
Ортогональные проекции
Сферическая черепица
Куб также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются как дуги окружности на плоскость.
Декартовы координаты
Для куба с центром в начале координат, с ребрами, параллельными осям, и с длиной ребра 2, Декартовы координаты вершин
а интерьер состоит из всех точек (Икс0, Икс1, Икс2) с −1 Уравнение в р 3 ^ <3>> 
Куб также можно рассматривать как предельный случай трехмерного суперэллипсоид поскольку все три показателя стремятся к бесконечности.
Формулы
Для куба с длиной ребра а 
| площадь поверхности | 6 а 2 ,>  |
объем | а 3 ,>  |
| диагональ лица | 2 а > a>  |
диагональ пространства | 3 а > а>  |
| радиус ограниченная сфера | 3 2 а > <2>> a>  |
радиус касательной к краям сферы | а 2 >>>  |
| радиус вписанная сфера | а 2 >>  |
углы между лицами (в радианы) | π 2 <2>>>  |
Поскольку объем куба — это третья степень его сторон а × а × а 
Куб имеет самый большой объем среди кубоиды (прямоугольные коробки) с заданным площадь поверхности. Кроме того, куб имеет самый большой объем среди кубоидов с таким же общим линейным размером (длина + ширина + высота).
Точка в пространстве
Для куба, описывающая сфера которого имеет радиус р, а для данной точки в ее трехмерном пространстве с расстояниями dя из восьми вершин куба имеем: [2]
∑ я = 1 8 d я 4 8 + 16 р 4 9 = ( ∑ я = 1 8 d я 2 8 + 2 р 2 3 ) 2 . ^ <8>d_ ^ <4>> <8>> + > <9>> = left ( ^ <8>d_ ^ <2>> <8>> + > <3>> ight) ^ <2>.>
Удвоение куба
Удвоение куба, или Делианская проблема, была проблема древнегреческие математики использования только компас и линейка чтобы начать с длины ребра данного куба и построить длину ребра куба с удвоенным объемом исходного куба. Решить эту задачу им не удалось, и в 1837 г. Пьер Ванцель оказалось невозможным, потому что кубический корень из 2 не является конструктивное число.
Равномерная окраска и симметрия

Куб имеет три одинаковых раскраски, названных цветами квадратных граней вокруг каждой вершины: 111, 112, 123.
Куб имеет четыре класса симметрии, которые могут быть представлены как вершинно-транзитивный раскрашивание лиц. Высшая октаэдрическая симметрия Oчас все лица одного цвета. В двугранная симметрия D4ч происходит от куба, представляющего собой призму, все четыре стороны которой одного цвета. Призматические подмножества D2d имеет ту же раскраску, что и предыдущий, а D2ч имеет чередующиеся цвета сторон, всего три цвета, соединенные противоположными сторонами. Каждая форма симметрии имеет разные Символ Wythoff.
| Имя | Обычный шестигранник |
Квадратная призма | Прямоугольный трапеция |
Прямоугольный кубовид |
Ромбический призма |
Тригональный трапецоэдр |
|---|---|---|---|---|---|---|
| Coxeter диаграмма |
     |
     |
     |
     |
     |
     |
| Schläfli символ |
<4>×< > rr |
s2 | < >3 tr |
< >×2 | ||
| Wythoff символ |
3 | 4 2 | 4 2 | 2 | 2 2 2 | | |||
| Симметрия | Очас [4,3] (*432) |
D4ч [4,2] (*422) |
D2d [4,2 + ] (2*2) |
D2ч [2,2] (*222) |
D3D [6,2 + ] (2*3) |
|
| Симметрия порядок |
24 | 16 | 8 | 8 | 12 | |
| Изображение (униформа окраска) |
 (111) |
 (112) |
 (112) |
 (123) |
 (112) |
 (111), (112) |
Геометрические отношения

В кубе одиннадцать сети (один показан выше): то есть существует одиннадцать способов сгладить полый куб, разрезав семь граней. [3] Чтобы раскрасить куб так, чтобы никакие две смежные грани не имели одинаковый цвет, потребуется как минимум три цвета.
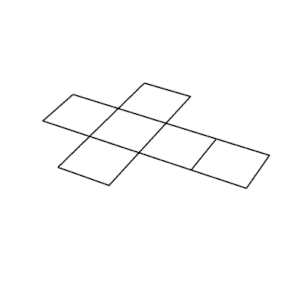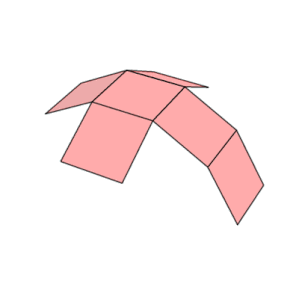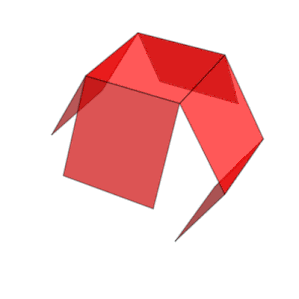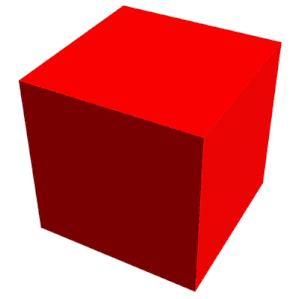
Куб — это ячейка единственная регулярная мозаика трехмерного евклидова пространства. Он также уникален среди Платоновых тел тем, что имеет грани с четным числом сторон, и, следовательно, это единственный член этой группы, который является зоноэдр (каждая грань имеет точечную симметрию).
Куб можно разрезать на шесть одинаковых квадратные пирамиды. Если эти квадратные пирамиды затем прикрепить к граням второго куба, ромбический додекаэдр получается (пары копланарных треугольников объединены в ромбические грани).
Другие размеры
Аналог куба в четырехмерном Евклидово пространство имеет особое имя — а тессеракт или же гиперкуб. Вернее, гиперкуб (или п-мерный куб или просто п-куб) является аналогом куба в п-мерное евклидово пространство и тессеракт — это гиперкуб порядка 4. Гиперкуб также называют мерный многогранник.
Есть аналоги куба и в более низких измерениях: точка в размерности 0, a отрезок в одном измерении и квадрат в двух измерениях.
Связанные многогранники

Если исходный куб имеет длину ребра 1, его двойственный многогранник (ан октаэдр) имеет длину ребра 2 / 2 > / 2> 
Куб является частным случаем в различных классах общих многогранников:
| Имя | Равные длины кромок? | Равные углы? | Прямые углы? |
|---|---|---|---|
| Куб | да | да | да |
| Ромбоэдр | да | да | Нет |
| Кубоид | Нет | да | да |
| Параллелепипед | Нет | да | Нет |
| четырехсторонний граненый шестигранник | Нет | Нет | Нет |
Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр; в более общем смысле это называется полукуб. Эти двое вместе образуют обычный сложный, то Stella Octangula. Их пересечение образует правильный октаэдр. Симметрии правильного тетраэдра соответствуют симметрии куба, который отображает каждый тетраэдр в себя; другие симметрии куба отображают их друг в друга.
Один такой правильный тетраэдр имеет объем 1 / 3 этого куба. Оставшееся пространство состоит из четырех равных неправильных тетраэдров объемом 1 / 6 куба каждый.
В исправленный куб это кубооктаэдр. Если срезать меньшие углы, получится многогранник с шестью восьмиугольный лиц и восемь треугольных. В частности, мы можем получить правильные восьмиугольники (усеченный куб). В ромбокубооктаэдр получается путем обрезания углов и краев до нужной длины.
Куб можно вписать в додекаэдр так что каждая вершина куба является вершиной додекаэдра, а каждое ребро — диагональю одной из граней додекаэдра; взятие всех таких кубиков дает правильное соединение из пяти кубиков.
Если два противоположных угла куба усечь на глубине трех вершин, непосредственно связанных с ними, получается неправильный октаэдр. Восемь из этих неправильных октаэдров могут быть присоединены к треугольным граням правильного октаэдра, чтобы получить кубооктаэдр.
Куб топологически связан с серией сферических многогранников и мозаик третьего порядка. фигуры вершин.
| *п32 изменения симметрии правильных мозаик: <п,3>
Кубооктаэдр — один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
Куб топологически связан как часть последовательности правильных мозаик, простирающейся в гиперболическая плоскость: <4, p>, p = 3,4,5 .
Как треугольный трапецоэдр, куб относится к семейству гексагональной диэдральной симметрии.
Регулярные и равномерные соединения кубиков
В однородных сотах и полихорах
Это также элемент пяти четырехмерных однородная полихора:
Кубический графВ скелет куба (вершины и ребра) образуют график, с 8 вершинами и 12 ребрами. Это частный случай граф гиперкуба. [4] Это один из 5 Платоновы графики, каждый — скелет своего Платоново твердое тело. Расширение — трехмерное k-ари Граф Хэмминга, который для k = 2 — куб-граф. Подобные графы встречаются в теории параллельная обработка в компьютерах. Источник Adblock |
|---|
22
Окт 2014
13 Задание (2022) (C2)ВИДЕОУРОКИПРЕЗЕНТАЦИИ
Построение сечения куба
Построение сечения куба с помощью вспомогательной плоскости.
Решим задачу:
Построить сечение куба 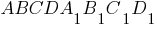 плоскостью, проходящей через точки
плоскостью, проходящей через точки :
:
Сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат ребрам, а стороны – граням многогранника.
При построения сечения для нас важно, что две соседние вершины сечения должны принадлежать одной грани многогранника. Отрезок, соединяющий вершины, не лежащие в одной грани, не является стороной сечения.
В этой задаче ни одна пара точек, через которые мы должны провести сечение, не лежит в одной грани куба, поэтому мы не можем соединить никакие две из данных точек отрезком, чтобы найти сторону сечения.
В этом случае для построения сечения мы введем вспомогательную плоскость.
Мы введем вспомогательную плоскость следующим образом.
Найдем ортогональную проекцию точки К на плоскость основания куба, получим точку  .
.
Найдем ортогональную проекцию точки L на плоскость основания куба, это точка С. Затем через параллельные прямые  и
и  проведем вспомогательную плоскость
проведем вспомогательную плоскость  (голубая плоскость). Точка N – точка пересечения прямых
(голубая плоскость). Точка N – точка пересечения прямых  и
и  и, следовательно, она лежит в плоскости искомого сечения и в плоскости основания.
и, следовательно, она лежит в плоскости искомого сечения и в плоскости основания.
Прямая  лежит и в плоскости сечения, и в плоскости основания куба, поэтому точка R -точка пересечения прямой
лежит и в плоскости сечения, и в плоскости основания куба, поэтому точка R -точка пересечения прямой  с ребром
с ребром  является вершиной сечения, лежащей в одной грани с вершиной М.
является вершиной сечения, лежащей в одной грани с вершиной М.
Мы нашли стороны сечения  и
и  :
:
Самую сложную часть решения мы прошли. Дальше проще.
Посмотрите видео с подробным решением этой задачи:

Презентация:
И.В. Фельдман, репетитор по математике.

Для вас другие записи этой рубрики:
- Решение тригонометрических уравнений с помощью введения вспомогательного угла
- Видеолекция «Метод координат. Задание 14. Углы в пространстве»
- Задание С2 из диагностической работы 13 марта 2013
- Решение Задания С5 из диагностической работы №3
- Задание С2 из досрочного ЕГЭ по математике
- Задание 14 из Тренировочной работы МИОО 27.04.2016 (вар. 509)