Как найти проекцию прямой в параллелепипеде

10 класс. Геометрия. Параллельные плоскости.

10 класс. Геометрия. Параллельные плоскости.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Поделись с друзьями

Комментарии преподавателя

1. Тема урока

На этом уроке мы дадим определение параллелепипеда, обсудим его строение, свойства и его элементы (стороны, диагонали).

2. Параллелепипед

Параллелепипед образован с помощью двух равных параллелограммов АВСD и А1B1C1D1, которые находятся в параллельных плоскостях. Обозначение: АВСDА1B1C1D1 или АD1 (рис. 1.).

Рис. 1. Параллелепипед

3. Свойства параллелепипеда

1) Все грани параллелепипеда – параллелограммы.

Так как плоскости АВС и А1B1C1 параллельны, а плоскость АА1В1 пересекает их соответственно по прямым АВ и А1В1, то из свойств параллельных плоскостей следует, что прямые АВ и А1B1 параллельны. А так как и прямые АА1 и ВВ1 параллельны по условию, то АВВ1А1 параллелограмм. Аналогично, можно рассмотреть и другие грани.

2) Ребра АА1, ВВ1, СС1, DD1 равны.

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Значит, отрезки параллельных прямых АА1, ВВ1, СС1, DD1, которые заключены между параллельными плоскостями АВС и А1B1C1, равны.

3) Имеются три четверки равных и параллельных ребер: 1 – АВ, А1В1, D1C1, DC, 2 – AD, A1D1, B1C1, BC, 3 – АА1, ВВ1, СС1, DD1.

4) Имеются равные углы (с сонаправленными сторонами). Например, углы А1АВ и D1DC.

4. Свойство 1 (Грани параллелепипеда)

Противоположные грани параллелепипеда параллельны и равны.

Например, плоскости параллелограммов АА1В1В и DD1C1C параллельны, так как пересекающиеся прямые АВ и АА1 плоскости АА1В1 соответственно параллельны двум пересекающимся прямым DC и DD1 плоскости DD1C1. Параллелограммы АА1В1В и DD1C1C равны (т. е. их можно совместить наложением), так как равны стороны АВ и DС, АА1 и DD1, и равны углы А1АВ и D1DC.

5. Свойство 2 (Ребра параллелепипеда)

Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Рис. 2. Диагонали параллелепипеда

Рассмотрим диагонали параллелепипеда А1C и D1B (рис. 2). Они также являются диагоналями четырехугольника A1D1CB. В этом четырехугольнике стороны A1D1 и BC параллельны и равны, а значит, A1D1CB – параллелограмм (по признаку параллелограмма). А в параллелограмме диагонали А1C и D1B пересекаются в одной точке О и делятся этой точкой пополам.

Рассмотрим теперь четырехугольник АВС1D1 (рис. 3). В этом четырехугольнике стороны С1D1 и АВ параллельны и равны, а значит, АВС1D1 – параллелограмм (по признаку параллелограмма). А в параллелограмме диагонали С1А и D1В пересекаются в одной точке и делятся этой точкой пополам. Эти диагонали также пересекаются в точке О, так как мы уже выяснили, что середина диагонали D1В – это точка О. Следовательно, все диагонали параллелепипеда А1C, С1А и D1В, DВ1 пересекаются в одной точке и делятся этой точкой пополам.

6. Задача 1

В параллелепипеде АВСDА1B1C1D1 постройте сечение плоскостью AD1M, где М – середина ребра ВС. Определите вид полученного сечения.

Соединим точки А и D1. Точки А и D1 лежат и в плоскости сечения и в плоскости АА1D1. Значит, АD1– линия пересечения этих плоскостей.

Проведем прямую МN параллельно прямой АD1. Плоскости АА1D1 и ВСС1 параллельны, значит, плоскость АМN рассекает их по параллельным прямым МN и АD1. Итак, АМND1 – искомое сечение.

Четырехугольник АМND1 – трапеция с основаниями АD1 и МN, так как АD1 и МN лежат на параллельных прямых.

Заметим, что средняя линия М1N1 в треугольнике АDD1 равна отрезку МN. Этот факт понадобится нам дальше для решения задач на нахождения периметра.

7. Итоги урока по теме “Параллелепипед”, “Стороны параллелепипеда, диагонали”, свойства

Итак, мы рассмотрели параллелепипед и его свойства. На следующих уроках мы продолжим рассмотрение тетраэдра и параллелепипеда.

Практическое занятие:” Построение сечений параллелепипеда”

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Практическое занятие : «Параллелепипед. Построение сечений параллелепипеда ».

1. Цель практической работы : . Закрепить знания теоретического материала о многогранниках, навыки решения задач на построение сечений, умения анализировать чертеж.

2.Дидактическое оснащение практической работы : АРМ, модели и развёртки многогранников, измерительные инструменты, ножницы, клей, плотная бумага.

Задания к работе:

Построить сечение параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ плоскостью, проходящей через точки M, N, P, лежащие, на прямых, соответственно, A ₁ B _1, А D , DC

Образец и последовательность решения задачи:

1.Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

2.Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

3.Так как точка M также принадлежит плоскости сечения и пересекает прямую АА ₁ в некоторой точке Х.

4.Точки X и N лежат в одной плоскости грани АА ₁ D ₁ D, соединим их и получим прямую XN.

5.Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A ₁ B ₁ C ₁ D ₁ , параллельную прямой NP. Эта прямая пересечет сторону В ₁ С ₁ в точке Y.

6.Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Вариант1. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, заданной следующими точками M , N и P

1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныА

2 Уровень. M лежит в грани AA1D1D, N лежит в грани АА1В1В, P лежит в грани СС1D1D.

3 Уровень. M лежит на диагонали B1D, N лежит на диагонали АС1, P лежит на ребре С1D1.

Вариант2. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей через прямую DQ, где точка Q лежит на ребре СС1 и точку Р, заданную следующим образом

1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныС

2 Уровень: М лежит на продолжении ребра А1В1, причем точка А1 находится между точками В1 и Р.

3 Уровень: Р лежит на диагонали В1D

Порядок выполнения работы:

1.Изучите теоретический материал по темам:

Противолежащие грани параллелепипеда.

Свойства диагоналей параллелепипеда.

П онятие секущей плоскости и правила её построения.

Какие виды многоугольников получаются в сечении куба и параллелепипеда.

2. Постройте параллелепипед ABCDA ₁ B ₁ C ₁ D ₁

3.Разберите решение задачи № 1

4.Последовательно постройте сечение параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ плоскостью, проходящей через точки P, Q, R задачи № 1.

5.Постройте ещё три параллелепипеда и выделите на них сечения к задачам 1, 2, и 3 уровней

Литература: Атанасян Л.С. Геометрия: Учебник для 10-11 кл. общеобразоват. учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. – М.: Просвещение, 2010г Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. – М.: Просвещение, 2010. В. Н. ЛитвиненкоЗадачи на развитие пространственных представлений. Книга для учителя. – М.: Просвещение, 2010г

Дидактический материал к заданию практического занятия

Некоторые возможные сечения:

Построить сечения параллелепипеда плоскостью, проходящей через данные точки

Методы построения сечений многогранников

Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
2. В задачах используются в основном простейшие многогранники.
3. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

• что значит построить сечение многогранника плоскостью;
• как могут располагаться относительно друг друга многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

• тремя точками;
• прямой и точкой;
• двумя параллельными прямыми;
• двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

1. Метод следов.
2. Метод вспомогательных сечений.
3. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

• построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
• построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
• построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
• построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
• построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:

• Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
• Погорелова А.В. (Геометрия, 7-11);
• Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
• Смирновой И.М. (Геометрия, 10-11);
• Шарыгина И.Ф. (Геометрия, 10-11).

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:

1. Определение сечения многогранников.
2. Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
3. Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
4. Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

[spoiler title=”источники:”]

http://infourok.ru/prakticheskoe-zanyatie-postroenie-secheniy-parallelepipeda-1401196.html

http://urok.1sept.ru/articles/212754

[/spoiler]

В
стереометрии большое значение имеет умение наглядно изображать неплоские фигуры
на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают
плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В
стереометрии же рассматриваются фигуры, у которых не все точки расположены в
одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости
пространственные фигуры.

Итак,
зачастую для изображения на плоскости (например, на листе бумаги)
геометрических фигур, расположенных в пространстве, используется параллельное
проектирование. Определяется оно следующим образом.

Пусть
 —
некоторая плоскость, а  —
некоторая прямая, пересекающая эту плоскость. Возьмём в пространстве
произвольную точку .
Если точка  не
лежит на прямой ,
то проведём через точку  прямую,
параллельную прямой ,
и обозначим через  точку
пересечения этой прямой с плоскостью .
Если же точка  лежит
на прямой ,
то обозначим через  точку
пересечения прямой  с
плоскостью .

Точка
 называется
проекцией точки  на
плоскость  при
проектировании параллельно прямой  (или
параллельной проекцией точки ).

Плоскость
 называется
плоскостью проекций, а о прямой  говорят,
что она задаёт направление проектирования.

Все
прямые, параллельные прямой ,
задают одно и то же направление проектирования, поэтому также называются проектирующими
прямыми.

Пусть
 —
плоская или пространственная фигура. Проекцией фигуры  на
плоскость  при
проектировании параллельно прямой  называется
множество  проекций
всех точек фигуры.

Заметим,
что проекция заданной фигуры зависит от выбора плоскости проекций и
проектирующей прямой.

Вспомним
основные свойства параллельного проектирования при условии, что
проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.

1.
Проекция прямой есть прямая, а проекция отрезка — отрезок.

2.
Проекции параллельных прямых параллельны или совпадают.

3.
Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных
прямых, равно отношению длин самих отрезков.

Следствие.
При параллельном проектировании середина отрезка проектируется в середину его
проекции.

При
параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно
сохраняется параллельность прямых.

Если
точка делит отрезок в отношении ,
то проекция точки будет делить проекцию отрезка также в отношении .

Центр
правильного треугольника отображается в точку пересечения медиан проекции этого
треугольника, центр квадрата — в точку пересечения диагоналей проекции
квадрата.

А
теперь давайте поговорим об изображении пространственных фигур.

Рассмотренные
свойства параллельного проектирования применяются при выполнении рисунков
(изображений фигур), иллюстрирующих теоремы и задачи стереометрии.

Изображением
фигуры  называется
любая фигура, подобная проекции этой фигуры на некоторую плоскость.

Выполняя
изображения фигур, расположенных в пространстве, необходимо учитывать свойства,
сохраняющиеся при параллельном проектировании, а в остальном изображение может
быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были
наглядными и давали верное представление о них.

При
различном выборе плоскости проекций и направления проектирования получаются
различные проекции данной фигуры, а значит, и различные её изображения.

Например,
вы видите фигуры, которые являются изображениями куба.

Причём
изображение куба, данное на первом рисунке, не даёт представления о кубе,
наглядным является изображение, которое дано на последнем рисунке.

При
построении изображений плоских фигур, расположенных в пространстве,
предполагается, что плоскости рассматриваемых фигур не параллельны направлению
проектирования.

Итак,
проекцией треугольника может быть любой треугольник.

При
этом величины углов и отношение длин непараллельных сторон не сохраняются, но
при этом медианы треугольника отображаются в медианы его проекции. В частности,
за изображение прямоугольного, равнобедренного, равностороннего треугольников
можно принять любой треугольник.

Параллелограмм
проектируется в параллелограмм, так как параллельные прямые сохраняют
параллельность.

В
частном случае за изображение прямоугольника, квадрата, ромба можно принять
любой параллелограмм.

Трапеция
проектируется в другую трапецию, но с сохранением параллельности оснований.

Правильный
шестиугольник проектируется в искажённый шестиугольник
с сохранением параллельности противолежащих сторон.

Окружность
проектируется в эллипс, большая ось которого имеет длину, равную диаметру
окружности.

При
изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую
из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно
считать изображением треугольной пирамиды при определённом выборе направления
проектирования и плоскости, на которую проектируется эта пирамида.

Например,
фигуры, изображённые на экране, являются изображениями треугольной пирамиды при
соответствующем выборе направления проектирования.

Изображение
параллелепипеда строится, исходя из того, что все его грани параллелограммы
и, следовательно, изображаются параллелограммами.

При
изображении куба плоскость изображений обычно выбирается параллельной
одной из его граней. В этом случае две грани куба, параллельные плоскости
изображений (передняя и задняя), изображаются равными квадратами. Остальные
грани куба изображаются параллелограммами.

Аналогичным
образом изображается прямоугольный параллелепипед.

Для
того чтобы построить изображение призмы, достаточно построить
многоугольник, изображающий её основание. Затем из вершин многоугольника
провести прямые, параллельные некоторой фиксированной прямой, и отложить на них
равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся
изображением второго основания призмы.

Для
того чтобы построить изображение пирамиды, достаточно построить
многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку,
которая будет изображать вершину пирамиды, и соединить её с вершинами
многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.

Для
изображения цилиндра достаточно изобразить его основания в виде двух
эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две
образующие, соединяющие соответствующие точки этих оснований.

Для
изображения конуса достаточно изобразить его основание в виде эллипса,
отметить вершину и провести через неё две образующие, являющиеся касательными к
этому эллипсу.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. Точки  и
 находятся
по одну сторону от плоскости .
Точки  и
 —
их параллельные проекции на эту плоскость, причём .
Постройте точку пересечения  прямой
 с
плоскостью .
И найдите расстояние между серединой отрезка  и
её проекцией на плоскость ,
если  и
 см.

Решение.

Задача
вторая. На диагонали  параллелепипеда
 взята
точка ,
а на прямой  –
точка  так,
что отрезки  и
 параллельны.
Найти их отношение.

Решение.

Содержание:

Перпендикулярность в пространстве

В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свой­ство ортогональной проекции многоугольника.

Угол между прямыми в пространстве

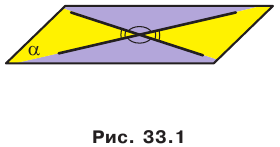
Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает (рис. 33.1).

Угол между двумя параллельными прямыми считают равным 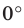Следовательно, если 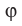— угол между двумя прямыми, лежащими в одной плоскости, то .

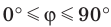Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся пря­мым.

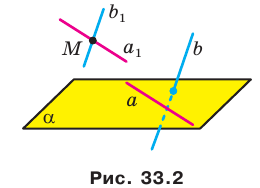
Пусть прямые 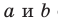скрещивающиеся. Через точку М простран­ства проведем прямые 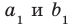так, что 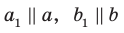(рис. 33.2). По определению угол между скрещивающимися прямыми 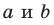равен углу между пересекающимися прямыми .

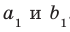Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 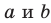от выбора точки М ? Ответить на этот вопрос помогает следующая теорема.

Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.

Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми 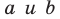равен углу между пересекающимися прямыми 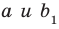, где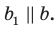

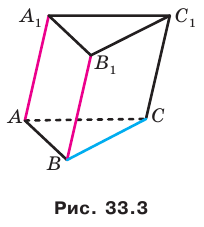
Например, на рисунке 33.3 изображена треугольная призма 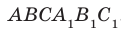. Угол между скрещивающимися прямыми 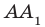и ВС равен углу между пересекающимися прямыми 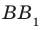и ВС.

Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.

Если прямые 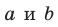перпендикулярны, то записывают: 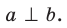Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.

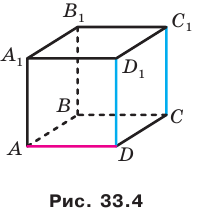
Например, ребра AD и 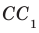куба 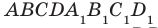перпендикулярны (рис. 33.4). Действительно, поскольку 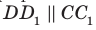то угол между прямыми AD и 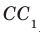равен углу между прямыми AD и 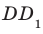. Но 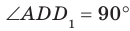, поэтому .

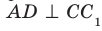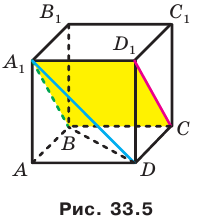
Пример:

На рисунке 33.5 изображен куб 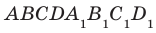. Най­дите угол между прямым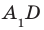и и .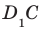

Решение:

Соединим точки 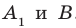. Поскольку 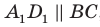, то точки 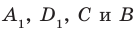лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости 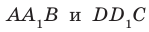по параллельным прямым 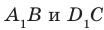. Следовательно, угол между прямыми 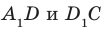равен углу 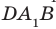. Соединим точки В и D. Отрезки 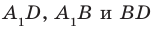равны как диагонали равных квадратов. Следовательно, треугольник 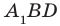равносторонний. Тогда 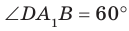. Ответ : 60°.

Перпендикулярность прямой и плоскости

В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.

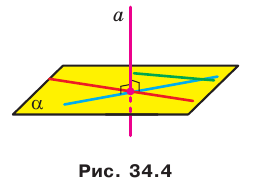
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной пло­скости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).

Если прямая 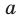перпендикулярна плоскости 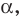то записывают: 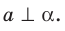Также принято говорить, что плоскость 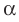перпендикулярна прямой 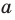или прямая 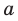и плоскость 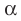перпендикулярны.

Из определения следует, что если прямая 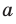перпендикулярна плоскости 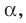то она пересекает эту плоскость.

Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.

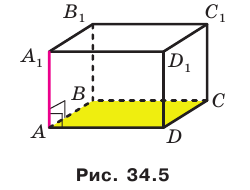
Например, интуитивно понятно, что ребро 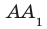прямоугольного параллелепипеда 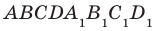перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.

Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.

На рисунке 34.5 прямая 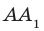перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпен­дикулярности прямой и плоскости 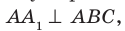а значит, и ребро 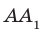также перпендикулярно плоскости АВС.

Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).

Приведем теорему, которую можно рассматривать как еще один признак перпендикуляр­ности прямой и плоскости.

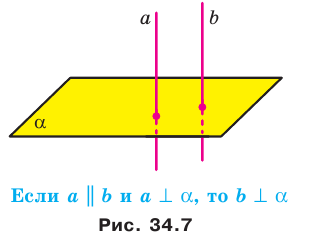
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).

Например, на рисунке 34.5 прямая 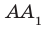перпендикулярна плоскости АВС, а прямая 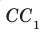параллельна прямой 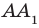. Следовательно, по теореме 34.2 прямая 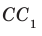также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.

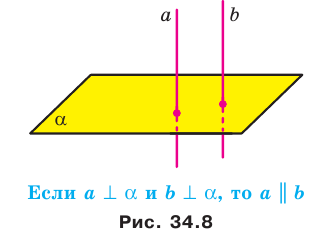
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.

Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Пример:

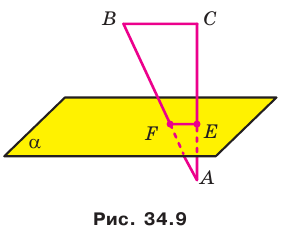
Плоскость 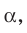перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а ги­потенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.

Решение:

Поскольку прямая АС перпендикулярна плоскости 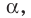то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому . Из этого следует, что треугольники AEF и 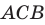подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.

Перпендикуляр и наклонная

Пусть фигура 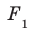— параллельная проекция фигуры F на плоскость 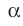в направлении прямо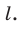й Если 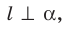, то фигуру 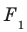называют ортогональной проекцией фигуры F на плоскость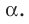

Например, основание ABCD прямоугольного параллелепипеда 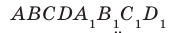является ортогональной проекцией основания 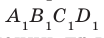на пло­скость АВС в направлении прямой 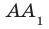(рис. 35.1).

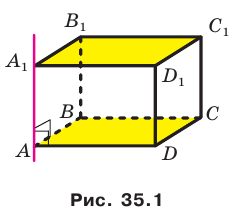
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.

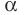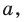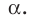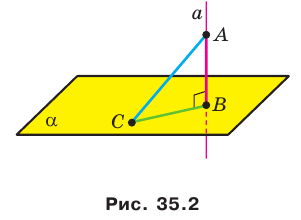
Пусть даны плоскость и не принадлежащая ей точка А . Через точку А проведем прямую перпендикулярную плоскости Пусть 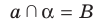(рис. 35.2).

Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость 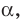точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость .

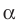Отметим на плоскости какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости 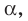точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.

Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.

Пример:

Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.

Решение:

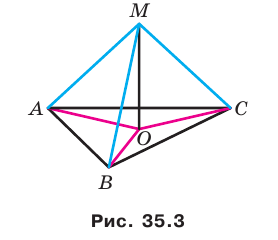
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку 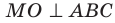, то 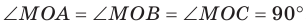. В пря­моугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.

Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.

Определение. Если точка не принадлежит плоскости, то рас­стоянием от точки до плоскости называют длину перпен­дикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Пример:

Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.

Решение:

Пусть А и В — две произвольные точки прямой 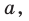параллельной плоскост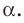и Точки 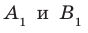— основания перпендикуляров, опущенных соответственно из точек А и В на плоскость 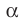(рис. 35.4). Докажем, что .

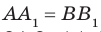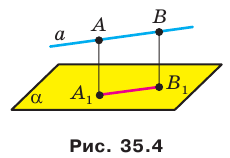
По теореме 34.3 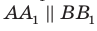. Следовательно, точки 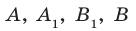лежат в одной пло­скости. Плоскость 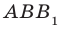проходит через прямую 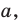параллельную плоскости 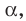и пересекает плоскость 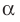по прямой 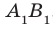. Тогда по теореме 30.2 получаем: 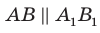. Таким образом, в четырехугольнике 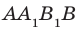каждые две противолежащие стороны параллельны. Следовательно, четырехугольник 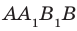— параллелограмм. Отсюда 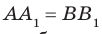Так как точки А и В выбраны на прямой 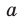произвольно, то утверждение задачи доказано.

Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллель­ной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.

Пример:

Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллель­ными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.

Результаты, полученные в ключевых задачах 2 и 3, часто ис­пользуют в практической деятельности, например в строительстве (рис. 35.5).

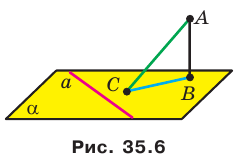
Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

Доказательство. Докажем первую часть теоремы.Пусть прямая 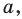принадлежащая плоскости 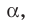перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что 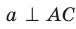. Имеем: 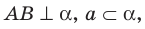следовательно, 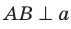. Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,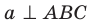. Поскольку 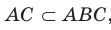то 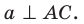Доказательство второй части теоремы аналогично доказатель­ству первой части.

Пример:

Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.

Решение:

Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.

Отрезок ON является проекцией на­клонной MN на плоскость АВС. По построению 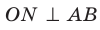. Тогда по теореме о трех перпендикулярах получаем: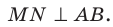

Аналогично можно доказать, что 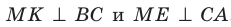. Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ.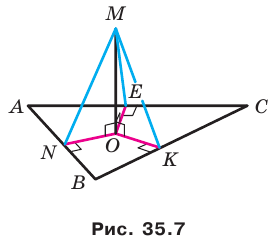

В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.

Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.

Угол между прямой и плоскостью

Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.

Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.

Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.

Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен .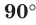

Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).

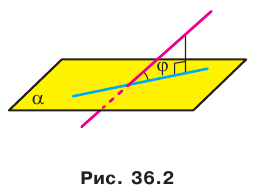
Из определения следует, что если 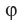— угол между прямой и плоскостью, то .

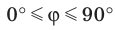Также принято говорить, что прямая образует угол 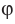с плоскостью.

Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.

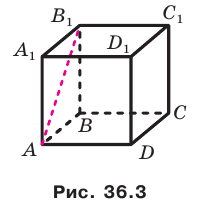
Например, рассмотрим куб 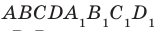(рис. 36.3). Угол между диагональю 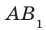грани 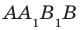и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой 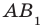на плоскость АВС. Тогда угол между прямой 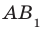и плоскостью АВС равен величине угла 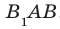. Поскольку четырехугольник 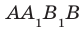— квадрат, то .

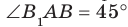Пример:

Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.

Решение:

Пусть МЛ и М В — наклонные, образующие с плоскостью 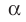равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.

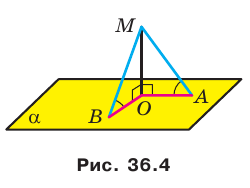
Прямая ОА является проекцией прямой МА на плоскость 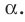Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью 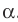. Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью 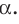По условию .

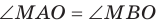Поскольку 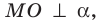то 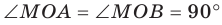. Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда .

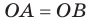• Заказать решение задач по высшей математике

Двугранный угол. Угол между плоскостями

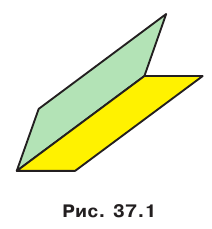
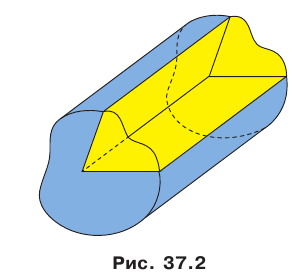
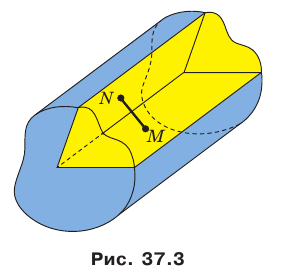
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугран­ным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).

Отрезок MN принадлежит «желтому» двугранному углу, а «сине­му» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).

Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).

Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.

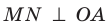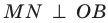Отметим на ребре MN двугранного угла произ­вольную точку О. Через точку О в гранях двугран­ного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугран­ного угла. Поскольку и , то 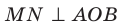. Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.

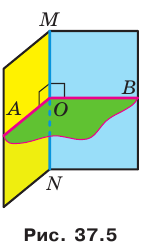
Определение. Величиной двугранного угла называют величину его линейного угла.

Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.

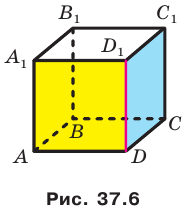
Например, рассмотрим куб 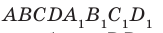(рис. 37.6). Двугранный угол с ребром 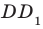, грани которого принадлежат плоскостям 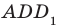и 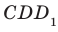является прямым. Действительно, поскольку 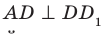и 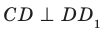, то угол ADC — линейный угол двугранного угла с ребром .

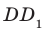Угол ADC прямой.

При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:

1. все четыре двугранных угла прямые (рис. 37.7, а);
2. из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).

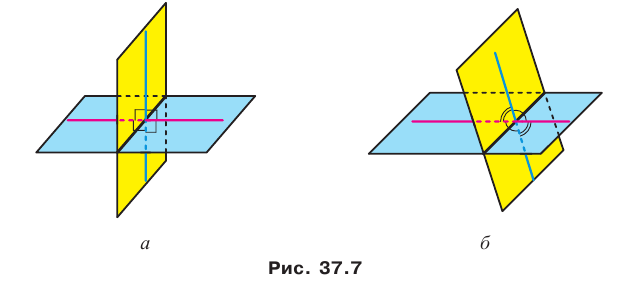
В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.

Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся дву­гранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.

Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.

Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.

Пример:

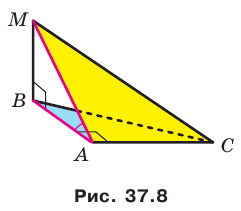
Прямоугольные треугольники 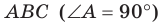и АВМ 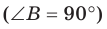имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.

Решение:

Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как 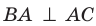, то по теореме о трех перпендикулярах 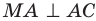. Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.

Для стороны AM прямоугольного треугольника АМС можно записать: 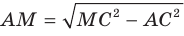. Отсюда 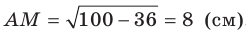. Для угла МАВ прямоугольного треугольника МАВ запишем: 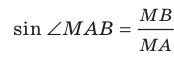. Отсюда 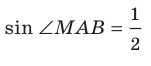и 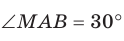. Ответ: 30°.

Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.

Теорема 37.1 (площадь ортогональной проекции мно­гоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где .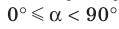

Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.

Если плоскости 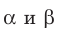перпендикулярны, то записывают: 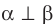. Также принято говорить, что плоскость 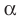перпендикулярна плоскости 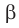или плоскость 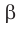перпендикулярна плоскости .

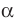Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).

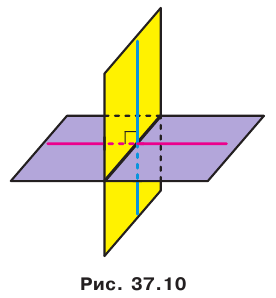
Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).

Теорема 37.2 (признак перпендикулярности плоско­стей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

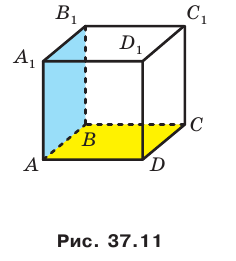
Например, плоскость грани 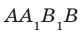прямоугольного параллелепипеда 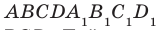, (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость 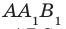проходит через прямую 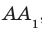, перпендикулярную плоскости АВС.

ГЛАВНОЕ В ПАРАГРАФЕ 5

Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют ве­личину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Перпендикулярность прямой и плоскости

• Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
• Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
• Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
• Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
• Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Ортогональная проекция фигуры

Пусть фигура 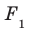— параллельная проекция фигуры F на плоскость 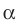в направлении прямой 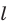. Если 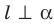, то фигуру 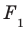называют ортогональной проекцией фигуры F на плоскость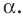

Расстояние от точки до плоскости

Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Расстояние от прямой до параллельной ей плоскости

Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.

Расстояние между двумя параллельными плоскостями

Расстоянием между двумя параллельными плоскостями назы­вают расстояние от любой точки одной плоскости до другой плоскости.

Теорема о трех перпендикулярах

Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

Угол между прямой и плоскостью

• Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
• Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
• Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.

Величина двугранного угла

Величиной двугранного угла называют величину его линейного угла.

Угол между двумя пересекающимися плоскостями

Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.

Площадь ортогональной проекции многоугольника

Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где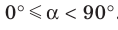

Перпендикулярные плоскости

Две плоскости называют перпендикулярными, если угол между ними равен 90°.

Признак перпендикулярности плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.