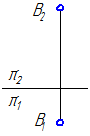Как найти проекцию прямой в треугольнике

2.1. Задание прямой на эпюре

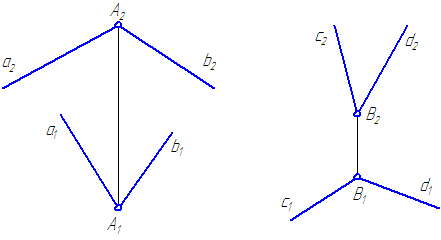
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.

а                                                                  б
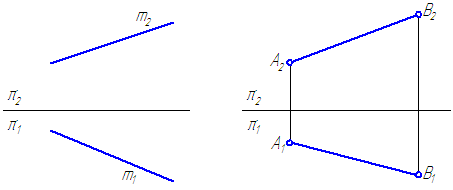
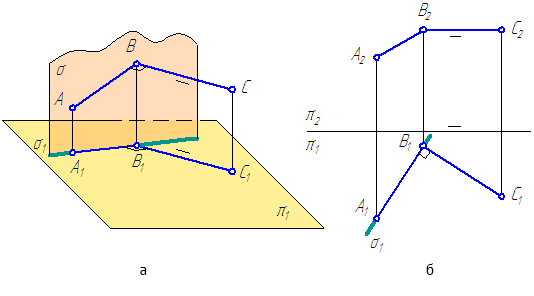
Рисунок 2.1 – Проекции прямой

Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.

Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.

Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.

2.2. Прямые частного положения

Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения.

Прямые, параллельные плоскостям проекций, называются прямыми уровня.

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).

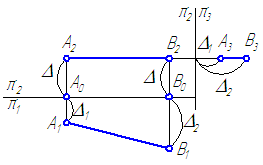
Рисунок 2.2 – Эпюр горизонтали

Если отрезок параллелен плоскости проекций π₁, то его фронтальная проекция А₂В₂ параллельна оси проекций π₁/π₂, а горизонтальная проекция отрезка А₁В₁ определяет истинную величину АВ:

А₂А₀=В₂В₀
А₂В₂ || π₂/π₁

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).

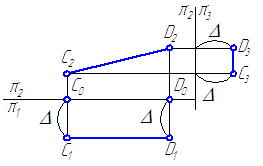
Рисунок 2.3 – Эпюр фронтали

Если отрезок параллелен плоскости проекций π₂, то его горизонтальная проекция параллельна оси проекций π₂/π₁, а фронтальная проекция отрезка C₂D₂ определяет истинную величину CD.

С₁А₀=D₁D₀

C₁D₁ || π₂/π₁

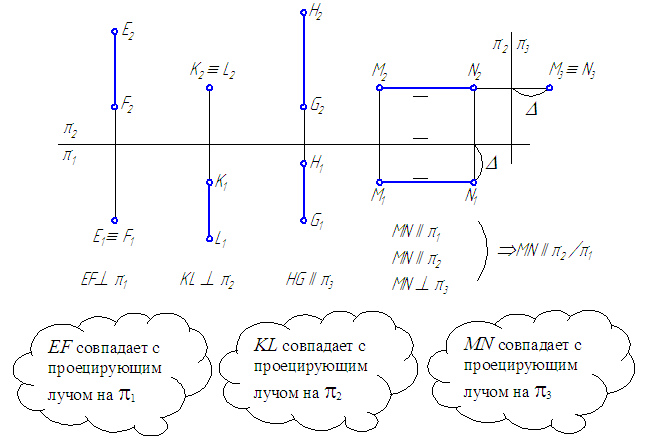
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).

Рисунок 2.4 – Эпюр профильной прямой

Прямые, перпендикулярные плоскостям проекций, называются проецирующими.

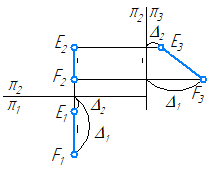
Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).

Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).

Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).

Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH

2.3. Метод прямоугольного треугольника

Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.

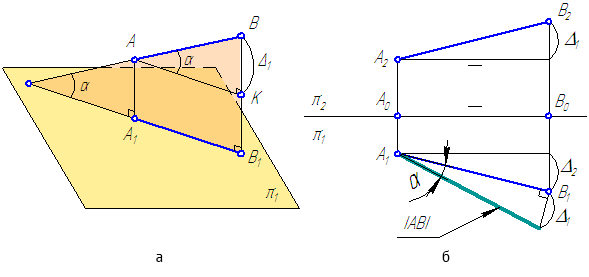
Рассмотрим положение отрезка  АВ относительно горизонтальной плоскости проекций π₁ (Рисунок 2.5).

Рисунок 2.5 – Определение истинной величины отрезка общего положения

На рисунке 2.5, а:

АА₁ – расстояние от точки А до плоскости проекций π₁;

ВВ₁ – расстояние от точки В до плоскости проекций π₁;

А₁В₁ – проекция отрезка АВ на π₁;

∠(AB; AK)=∠(AB; A₁B₁)=α – угол наклона прямой АВ к плоскости проекций π₁.

ΔАКВ – прямоугольный треугольник, в котором:

АК=А₁В₁ – катет, равный горизонтальной проекции отрезка АВ;

ВК=ВВ₁–АА₁=Δ₁ – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π₁ (то есть, разности координат Z точек А и В);

АВ – гипотенуза ΔАКВ – истинная величина.

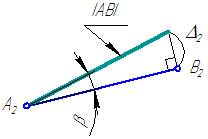
При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.

Истинная величина отрезка может быть найдена как гипотенуза прямоугольного треугольника, одним катетом которого является проекция этого отрезка на плоскость проекций (А₂В₂), а другим – разность координат концов этого отрезка до плоскости (Δ₂), в которой ведется построение. Угол между истинной величиной (АВ) и проекцией (А₂В₂) определяет угол наклона (β) прямой к той плоскости проекций, в которой ведётся построение (Рисунок 2.6).

Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π₂

2.4. Точка и прямая

Если точка принадлежит прямой, то её проекции:

1. Принадлежат одноимённым проекциям данной прямой;
2. Лежат на одной линии связи.

Рисунок 2.7 – Принадлежность точки прямой
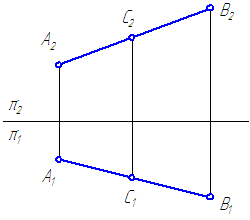
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:

• С₁∈А₁В₁;
• С₂∈А₂В₂;
• С₁С₂⊥π₂/π₁;

Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:

{frac{A_2C_2}{C_2B_2}=frac{A_1C_1}{C_1B_1}=frac{AC}{CB}}
Справедливо и обратное утверждение.

Упражнение

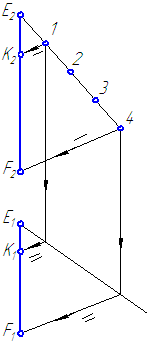
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)

Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:

• 1. Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е₂.
  2. Отложим  на этой прямой от точки Е₂ равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
  3. Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F₂.
  4. Из точки 1 проведём прямую, параллельную прямой (4—F₂) до пересечения с проекцией E₂F₂, таким образом будет найдена фронтальная проекция искомой точки К₂.
  5. Горизонтальную проекцию точки К₁ получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.

  Упражнение

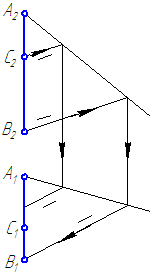
  Определить принадлежность  точки С отрезку прямой АВ (Рисунок 2.9).
  
  Рисунок 2.9а – Решение упражнения 2. Способ 1.

  
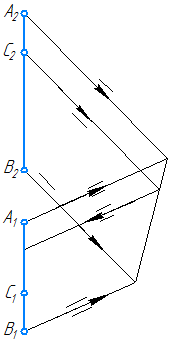
  Рисунок 2.9б – Решение упражнения 2. Способ 2.

  Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.

  2.5. Следы прямой

  След прямой – точка пересечения прямой с плоскостью проекций.

  Прямая общего положения в общем случае может быть три следа:

  • горизонтальный след M₁– точка пересечения прямой с горизонтальной плоскостью проекций π₁;
  • фронтальный след N₂– точка пересечения прямой с фронтальной плоскостью проекций π₂;
  • профильный  след L₃ – точка пересечения прямой с профильной плоскостью проекций π₃.

  След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

  • горизонтальный след совпадает со своей горизонтальной проекцией M≡M₁,
  • фронтальный – с фронтальной проекцией N≡N₂,
  • профильный – с профильной проекцией L≡L₃ (Рисунок 2.10).

  

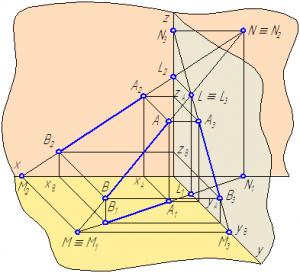
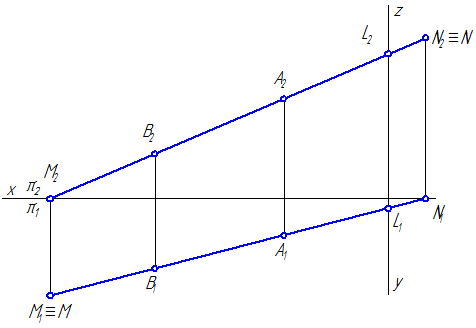
  Рисунок 2.10 – Построение следов отрезка прямой АВ

  Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

  Для построения горизонтального следа прямой АB необходимо:

  1. Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М₂ является фронтальной проекцией горизонтального следа;
  2. Из точки М₂ провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М₁ и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.

  Чтобы построить фронтальный след отрезка АB прямой, необходимо:

  1. Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N₁ является горизонтальной проекцией фронтального следа;
  2. Из точки N₁ провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB  или ее продолжением. Точка пересечения N₂ и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.

  Ниже приводим алгоритм построения следов отрезка прямой АВ:

  A₁B₁ ∩ xO =N₁;       Y_N=0;                   N ∈ xOz (π₂)      ⇒      AB ∩ xOz=N

  A₂B₂ ∩ xO =M₂;       Z_M=0;                  M ∈ xOy (π₁)     ⇒      AB ∩ xOy=M

  A₁B₁ ∩ yO =L₁;        X_L=0;                   L ∈ yOz (π₃)     ⇒      AB ∩ yOz=L

  A₂B₂ ∩ zO =L₂;

  
  Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

  Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

  2.6. Взаимное расположение прямых

  Две прямые в пространстве могут быть:

  • параллельными;
  • пересекающимися;
  • скрещивающимися.

  Параллельные прямые – прямые, пересекающиеся в несобственной точке.

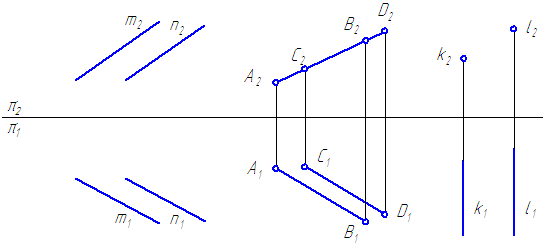
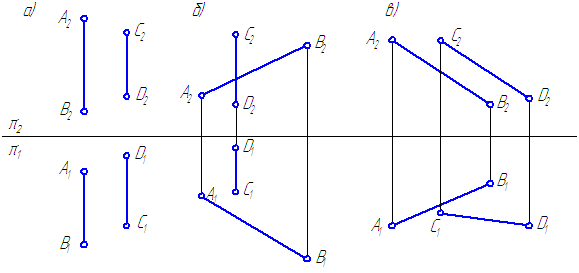
  Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).

  
  Рисунок 2.12 – Параллельные прямые
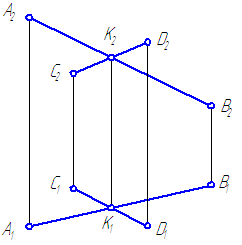
  Пересекающиеся прямые – прямые, имеющие одну общую точку.

  Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).

  {{A_2B_2}cap{C_2D_2}=K_2}

   {{A_1B_1}cap{C_1D_1}=K_1}

   {frac{A_2K_2}{K_2B_2}=frac{A_1K_1}{K_1B_1}}

   {frac{C_2K_2}{K_2D_2}=frac{C_1K_1}{K_1D_1}}

   
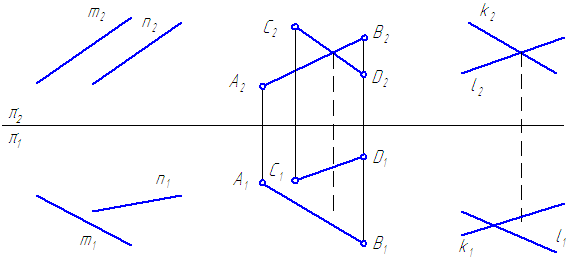
  Рисунок 2.13 – Пересекающиеся прямые

  Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок  2.14).

  
  Рисунок 2.14 — Скрещивающиеся прямые

  2.7. Проекции плоских углов

  Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.

  
  Рисунок 2.15

  По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.

  Теорема о проецировании прямого угла в частном случае

  Теорема. Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).

  Обратная теорема. Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.

  

  Рисунок 2.16 – Проецирование прямого угла

  Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,

  причём ВС // π₁ (Рисунок 2.16,б).

  Доказательство:

  1. Проведём через отрезок АВ проецирующую плоскость – σ, σ⊥π₁;
  2. Прямые АВ и ВВ₁ лежат в плоскости σ;
  3. ВС⊥ВВ₁ так как ВС//π₁, а ВВ₁⊥π₁;
  4. Следовательно, ВС⊥σ, а значит ВС перпендикулярна и любой прямой, лежащей в плоскости σ, в частности А₁В₁;
  5. Следовательно В₁С₁⊥σ;
  6. Так как В₁С₁//ВС, то В₁С₁⊥А₁В₁.

  2.8. Задачи для самостоятельного решения

  1. Построить отрезок прямой  АВ // π₁,  равный 35 мм и наклонённый к π₂ под углом 25° (Рисунок 2.17).

  
  Рисунок 2.17

  2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π₂ и π₁.

  3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π₁ и 45° — к плоскости проекций π₂.

  4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π₂/π₁ (Рисунок 2.18).

  

  Рисунок 2.18

1. Проекции прямой

При
проецировании прямой на какую-либо
плоскость проекций проецирующие лучи,
проходящие через точки прямой, образуют
проецирующую плоскость, которая
пересекает плоскость проекции по прямой
(рис. 4.18). Следовательно, проекцией
отрезка будет отрезок прямой. Чаще всего
проекция отрезка меньше самого отрезка,
так как его проекция (ab) является частью
катета прямоугольной: треугольника
(ВbМ),
а отрезок (АВ) — частью гипотенузы. Так
как Mb < MB, то и ab<AB. Отношение проекции
отрезка к его натуральной величине
называют коэффициентом искажения.

Рис.
4.17.

Коэффициент
искажения обозначают буквой К,

К=
аb/AB
≤1

Если
отрезок прямой параллелен плоскости
проекций, при проецировании образуется
прямоугольник, в котором сам отрезок и
его проекция являются противоположными
сторонами этого прямоугольника.
Следовательно ВС=bс.
В этом случае коэффициент искажения К=
аb/AB
=1, т. е. отрезок проецируется без искажения.

Положение
прямой в пространстве можно определить
двумя ее точками, поэтому, чтобы задать
прямую на эпюре, достаточно задать
проекции двух ее точек (рис. 4.18), т.е.
проекции отрезка этой прямой. Данные
проекции отрезка прямой полностью
определяют положение прямой в пространстве.

Рис.
4.18.

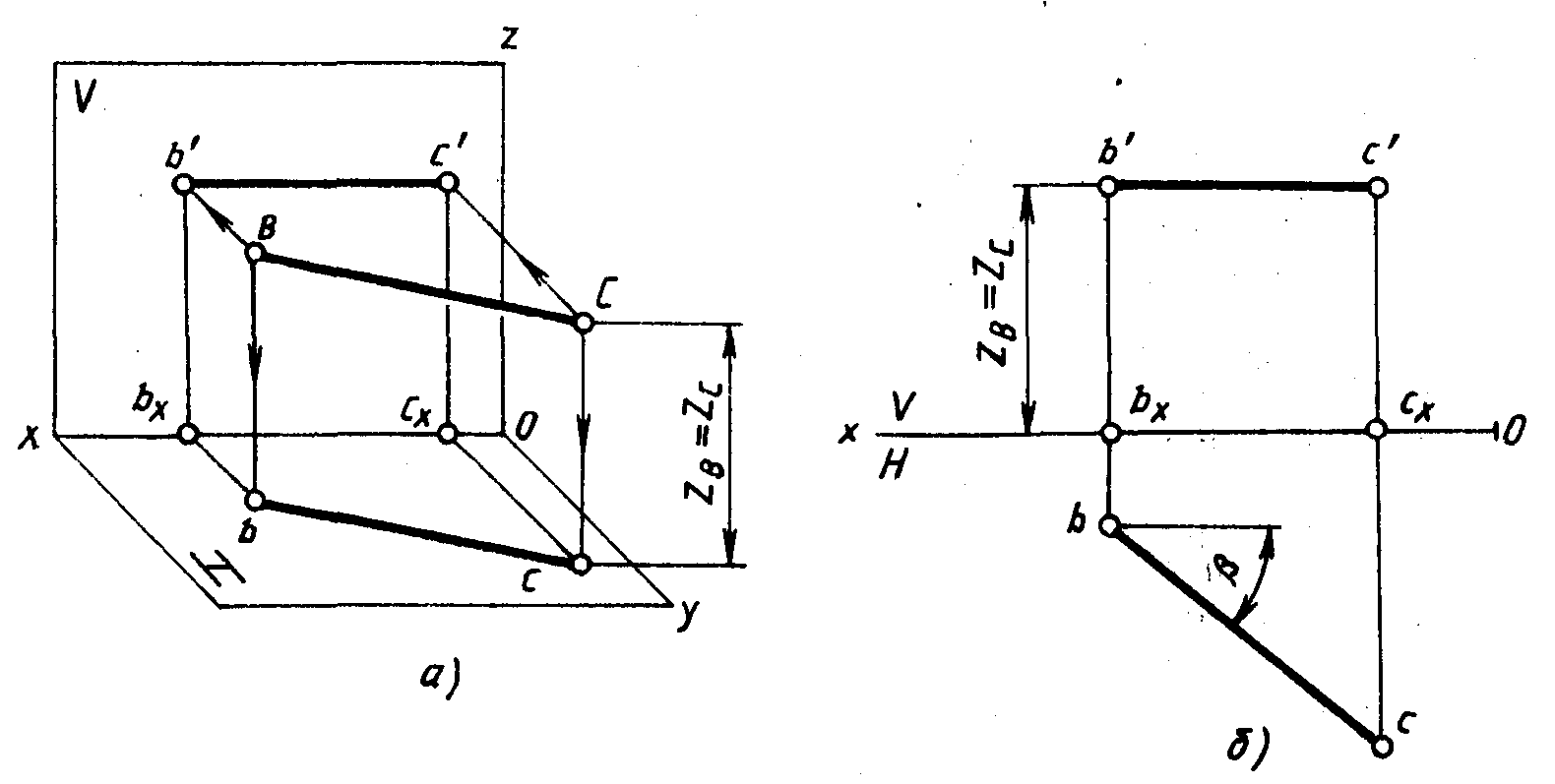
Сравнивая
координаты точек А и В, являющихся
концами отрезка, можно представить
себе, как располагается отрезок в
пространстве. Точка В находится выше
точки А относительно плоскости Н, так
как b’b_х>а’а_х,
т. е. ZB>ZA, и точка В ближе к плоскости
V, чем точка А, так как bb_x<aa_x,
т. е. YB<YA.

Различные
случаи расположения прямых относительно
плоскостей проекций

Прямая
общего положения
— прямая, не параллельная ни одной из
плоскостей проекций (рис. 4.18), т. е. ни
одна из проекций этой прямой не параллельна
какой-либо оси проекций.

Горизонтальная
прямая
— прямая, параллельная плоскости Н. Все
точки прямой находятся на одинаковом
расстоянии от плоскости Н (рис. 4.19, а),
т. е. координаты Z всех точек отрезка ВС
равны между собой, ВЬ= = Сс — b’bx—c’cx — ZH
= Zc- Фронтальная проекция горизонтальной
прямой параллельна оси Ох (рис. 4.19,б).
Положение второй проекции относительно
оси Ох определяется положением самой
прямой, Угол наклона горизонтальной
прямой к плоскости V — р. На плос­кость
Н отрезок горизонтальной прямой
проецируется в натуральную величину.

Рис.
4.19.

Фронтальная
прямая
— прямая, параллельная плоскости V. Все
точки прямой находятся на одинаковом
расстоянии от плоскости V (рис. 4.20, а), т.
е. координаты Y всех точек отрезка CD
равны между собой. Горизонтальная
проекция фронтальной прямой параллельна
оси Ох (рис. 4.20,б). Положение второй
проекции относительно оси Ох опреде­ляется
положением самой прямой. Угол наклона
фронтальной прямой к горизонтальной
плоскости H
равен α. На плоскость V отрезок фронтальной
прямой проецируется в натуральную
величину.

Рис.
4.20.

Профильная
прямая
— прямая, параллельная плоскости H.
Все точки прямой находятся на одинаковом
расстоянии от плоскости W (рис. 4.21,а), т.
е. координаты X всех точек отрезка DE
равны между собой. Фронтальная проекция
профильной прямой параллельна оси Oz, а
горизонтальная проекция — оси Оу (рис.
4.21,б). Положение профильной проекции
определяется положением самой профильной
прямой. Угол наклона профильной прямой
к плоскости Н — α, к плоскости V — β. На
плоскость W отрезок профильной прямой
проецируется в натуральную величину.

Рис.
4.21.

Прямые,
перпендикулярные одной из плоскостей
проекций, называют проецирующими
прямыми.

Горизонтально-проецирующая
прямая
перпендикулярна плоскости H.
Проекция такой прямой на плоскости Н
является точкой, а ее фронтальная
проекция перпендикулярна оси Ох и
параллельна оси Оz
(рис. 4.22). На плоскость V прямая проецируется
в натуральную величину.

Фронтально-проецирующая
прямая
перпендикулярна плоскости V. Проекция
этой прямой на плоскость V является
точкой, а ее горизонтальная проекция
перпендикулярна оси Ох и параллельна
оси Оу (рис. 4.23). На плоскость Н прямая
проецируется в натуральную величину.

Профильно-проецирующая
прямая
перпендикулярна плоскости W. Проекция
этой прямой на плоскость W является
точкой. Ее горизонтальная проекция
перпендикулярна оси Оу и параллельна
оси Ох, а фронтальная — перпендикулярна
оси Oz и параллельна оси Ох (рис. 4.24). На
плоскости Н и V прямая проецируется в
натуральную величину.

Рис.
4.22.

Рис.
4.23.

Рис.
4.24.

Точка,
принадлежащая прямой.
Если точка лежит на прямой, то ее проекции
лежат на одноименных проекциях этой
прямой и на одной линии проекционной
связи. На рис. 4.25,а точка М лежит на прямой
CD. Ее горизонтальная проекция т (рис.
4.25,б) лежит на горизонтальной проекции
прямой cd, а фронтальная проекция т’ —
на фронтальной проекции прямой c’d’.

Обычно
по двум проекциям можно определить
взаимное расположение точки и прямой.
Точка 5 принадлежит прямой CD (рис. 4.25,б),
так как ее проекции лежат на про­должении
одноименных проекций прямой и на одной
линии проекционной связи. Только одна
проекция точки F (горизонтальная) лежит
на одноименной проекции прямой ей,
поэтому точка F не принадлежит прямой
CD (рис. 4.25, а и б).

Рис.
4.25.

Если
прямая параллельна одной из плоскостей
проекций, о взаимном расположении прямой
и точки можно получить представление
на плоскости проекций, параллельной
данной прямой. Для горизонтальной прямой
— на плоскости, для фронтальной прямой
— на плоскости V, для профильной прямой
— на плоскости W.

На
рис. 4.25, в и г показаны частные случаи
расположения точки и прямой, когда
только две проекции точки F лежат на
одноименных проекциях прямой CD, и сама
точка F не принадлежит прямой CD, так как
третья проекция точки не лежит на
проекции прямой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

§ 7. Первая позиционная задача. Построение точки пересечения прямой линии с плоскостью

Задача 7.1. Построить точку пересечения прямой п с плоскостью треугольника АВС. Определить видимость прямой п. (Рисунок 101)

Решение.

Задачи данного типа решаются в три этапа:

1. Проведение через заданную прямую вспомогательной проецирующей плоскости и нахождение линии пересечения этой вспомогательной плоскости с заданной плоскостью.

2. Построение точки пересечения прямой и плоскости, опираясь на результат этапа 1..

3. Определение видимости прямой.

1. Для решения задачи применяют проецирующую плоскость, проходящую через заданную прямую. Заключим прямую п в горизонтально проецирующую плоскость. Данная плоскость перпендикулярна горизонтальной плоскости проекций, на которой она отобразится в виде прямой, совпадающей с проекцией п1 . Обозначим ее утолщенной линией и буквами ГП1 (рисунок 102).

ГП пересекает стороны ΔАВС в точках 1 и 2: в точке 1 – со стороной АВ, а в точке 2 – со стороной ВС. Покажем проекции этих точек на эпюре (см. рис. 102).

Можно утверждать, что ГП, проведенная через прямую п пересекает плоскость треугольника АВС по прямой, проходящей через точки 1 и 2. На горизонтальной проекции эта прямая совпадает с прямой п (как и все другие прямые, лежащие в плоскости ГП), а на фронтальной проекции мы получаем эту прямую, соединив точки 12 и 22.

2. На пересечении проекций прямых п2 и (12 – 22) построим точку К2, которая является фронтальной проекцией точки К – точки пересечения прямой п и прямой, проходящей через точки 1 и 2. Найдем проекцию К1, проведя линию связи с фронтальной проекции на горизонтальную до пересечения с проекцией прямой п1 (рисунок 103).

3. Чтобы определить видимость прямой п, рассмотрим конкурирующие точки (рисунок 104)

Конкурирующими называются две точки, одна из проекций которых совпадает. На горизонтальной проекции рассмотрим конкурирующие точки, лежащие на стороне АВ (проекция А1В1) и прямой п (проекция п1). Их горизонтальная проекция совпадает – это точка 11. Если мы посмотрим на фронтальную проекцию эпюра, направив взгляд по проекционной линии связи, то увидим, что Прямая АВ лежит выше, чем прямая п, а это значит, что на горизонтальной проекции сторона А1В1 перекрывает прямую п1 , которая после пересечения с А1В1 становится невидимой. Далее, в точке К1 прямая как бы «протыкает» плоскость треугольника и становится видимой.

На фронтальной проекции также рассмотрим конкурирующие точки на прямой АВ (проекция А2В2) и прямой п (проекция п2). Направляем взгляд по стрелке вниз (рис. 104) и видим, что точка, расположенная на прямой п ближе к нам (ниже на эпюре), поэтому прямая п2 в месте пересечения со стороной А2В2 видимая, а после прохождения точки К2 становится невидимой.

Окончательно решение задачи выглядит так, как показано на рисунке 105.

Задача 7. 2. Построить точку пересечения прямой а с плоскостью, заданной параллельными прямыми m и n. Определить видимость прямой а. (Рисунок 106).

Решение:

Данную задачу решаем аналогично задаче 1.Для разнообразия вместо горизонтально проецирующей плоскости проведем фронтально проецирующую – результат решения от этого не изменится. Заключим прямую а в фронтально-проецирующую плоскость ФП, обозначив ее на эпюре как ФП2.

Плоскость ФП, проведенная через прямую а пересекает заданную плоскость по прямой, проходящей через точки 1 и 2. фронтальной проекции эта прямая совпадает с прямой п, а на горизонтальной проекции мы получаем эту прямую, соединив точки 12 и 21. Получив на эпюре точку N1 от пересечения прямой (11-21) и а1, «поднимаем» от нее линию связи на фронтальную проекцию и получаем на проекции а2 точку N2.

Видимость прямой определяем методом конкурирующих точек. Решение задачи представлено на рисунке 107.

Задача 7.3. Построить точку пересечения прямой l с плоскостью α, заданной следами . Определить видимость прямой l. (Рисунок 108).

Решение.

Заключим прямую l в горизонтально-проецирующую плоскость ГП и найдем точки пересечения этой плоскости со следами заданной плоскости α. Точка 1 – это точка пересечения ГП с горизонтальным следом α1, а точка 2 – это точка пересечения ГП с фронтальным следом α2 (рисунок 109).

Поскольку следы плоскости – это прямые, принадлежащие плоскостям проекций и самой плоскости, то нахождение проекций точек пересечения их с вспомогательной плоскостью ГП не представляет затруднений (см. рис. 109).

Также как и в двух предыдущих задачах, проведем прямую (1-2), являющуюся результатом пересечения ГП и плоскости α. Фронтальная проекция этой прямой представлена отрезком [12-22], а ее горизонтальная проекция совпадает с проекцией l1. Теперь мы можем получить проекцию М2, и «опустив» ее на плоскость Н получаем проекцию М1. Точка пересечения Прямой l и плоскости α найдена.

Видимость в данном случае легко определить интуитивно, поскольку плоскость задана следами. Применение метода конкурирующих точек также дает верное решение.

Упражнение 7.

Построить точку пересечения прямой l с плоскостью, заданной пересекающимися прямыми а и b. Определить видимость прямой l. (Рисунок 110)

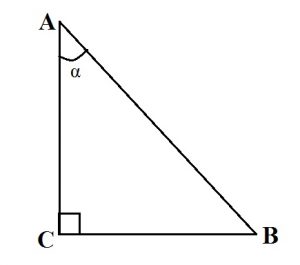
Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

1. Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
2. Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
3. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.  AB² = AC² + CB²

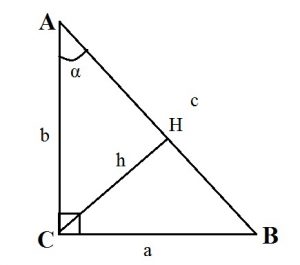
Прямоугольный треугольник:  формулы площади и проекции

1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH² = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое  между гипотенузой и проекцией этого катета на гипотенузу:  CA² = AB·AH;  CB² = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты.  S = (hc):2.

Прямоугольный треугольник:  формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.                 cosα  = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.           sinα = BC:AB.
3. Тангенс  острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.    tgα  = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.    ctgα  = AC:BC.
5. Основное тригонометрическое тождество:  cos²α + sin²α = 1.
6. Теорема косинусов: b² = a² + c² – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

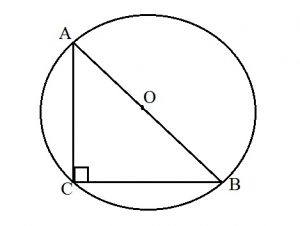
Прямоугольный треугольник:  формулы для описанной окружности

1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

Прямоугольный треугольник:  формулы для вписанной  окружности

Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b  -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из  сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

Решение:

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Ответ: AB = 28.

ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)