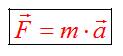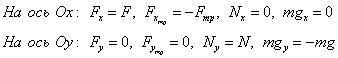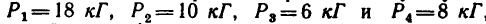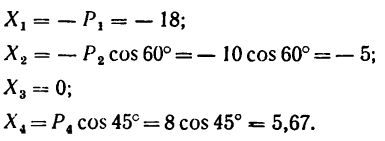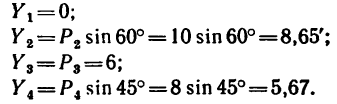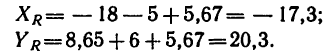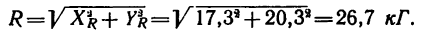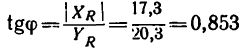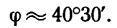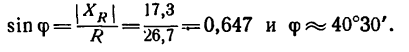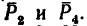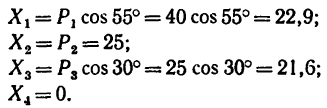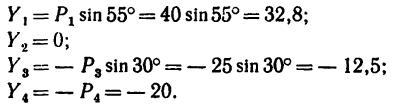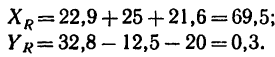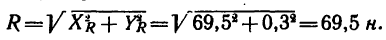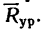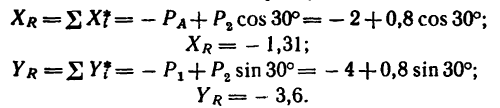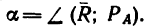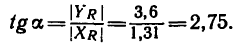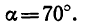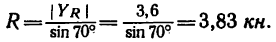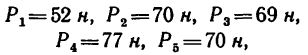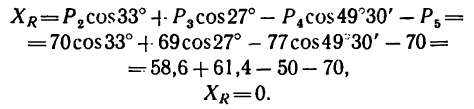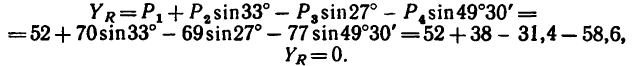Как найти проекцию равнодействующих сил на ось

I. Механика

Тестирование онлайн

Определение

Это векторная сумма всех сил, действующих на тело.

Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности

Взаимосвязь со вторым законом Ньютона

Вспомним закон Ньютона:

Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.

Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз.

Сила тяжести уравновешивается силой упругости. Книга покоится

Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.

Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.

Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх

Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее.

Нахождение равнодействующей силы

Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения.
Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.

Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.

Примеры

На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.

Обозначим силы, выберем координатные оси

Найдем проекции

Записываем уравнения

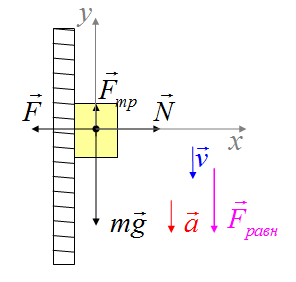
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить

1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил

Системы и блоки*

4. Определение равнодействующей аналитическим способом

Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.

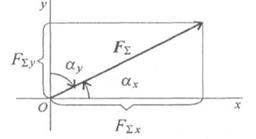
Проекция силы на две взаимно перпендикулярные оси.

F_x = Fcosα > 0

F_y = Fcosβ = Fsinα > 0

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.

F_Σx= F_1x + F_2x + F_3x + F_4x;

F_Σy= F_1y + F_2y + F_3y + F_4y.

Модуль (величину) равнодействующей можно определить по известным проекциям:

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской системы сходящихся сил:

При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

Определение равнодействующей сходящихся сил:

Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом  либо методом проекций.

Задачи, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.

Задача №1

Определить равнодействующую четырех сил:

Решение — методом проекций.

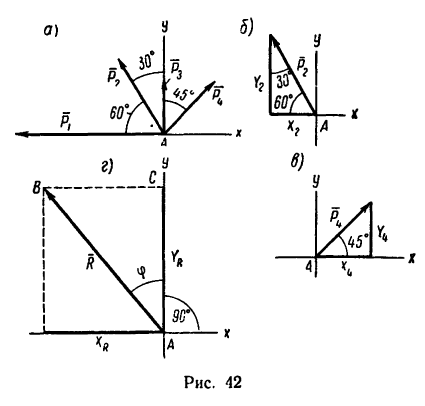
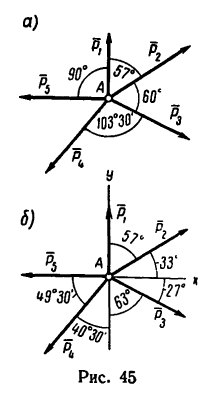
1.    Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами (рис. 42, а).

2.    Находим проекции данных сил на ось х:

3.    Находим проекции данных сил на ось у:

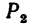
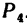
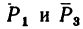
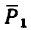
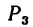
Если трудно определить знак и числовое значение проекции, то необходимо помнить, что проектируемую силу и две проекции на взаимно перпендикулярные оси всегда можно представить в виде прямоугольного треугольника. В тех случаях, когда еще нет достаточных навыков, силы и ее проекции можно изобразить отдельно, как показано на рис. 42,6 для силы и на рис. 42, в для силы . Эти рисунки облегчают правильное определение проекций.

Для сил такие рисунки не нужны, так как сила лежит на оси х и, следовательно, проектируется на эту ось в натуральную величину, но зато на ось у проекция этой силы равна нулю. Сила проектируется в натуральную величину на ось у, а ее проекция на ось х равна нулю.

4.    Находим проекции искомой равнодействующей 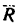на оси хну:

Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор 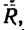заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х — влево. Положение равнодействующей R показано отдельно на рис. 42, г.

5.    Находим модуль равнодействующей (т. е. заканчиваем решение задачи первым путем, см. п. 7 в § 4-1):

6.    Находим угол ф, определяющий направление R относительно оси у (см. рис. 42, а):

и, следовательно,

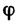
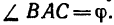
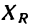
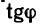
Для определения угла использован АВС (см. рис. 42, г), в котором Поэтому не имеет значения и в выражение подставлена его абсолютная величина.

Угол 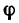можно найти при помощи синуса:

Для определения угла 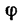можно воспользоваться и косинусом, но при работе с логарифмической счетной линейкой эта функция менее удобна.

Таким образом, равнодействующая четырех заданных сил равна 26,7 кГ направлена под углом 40°30′ к положительному направлению оси у и под углом 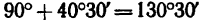к положительному направлению оси х.

Задача №2

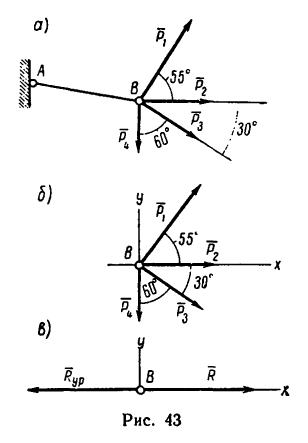
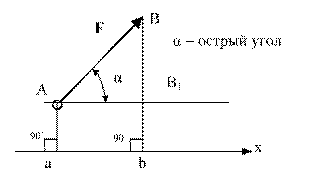
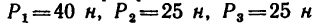
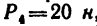
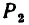
К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: , направленные, как показано на рис. 43, а (сила горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.

Решение — методом проекций.

1.    Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.

2.    Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, 6) и совместим оси проекций с силами

3.    Найдем проекции заданных сил на ось х:

4.    Найдем проекции заданных сил на ось у:

5.    Найдем проекции равнодействующей R на оси х и у:

6.    Найдем модуль равнодействующей:

Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.

Таким образом, четыре заданные силы натягивают веревку равнодействующей силой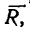 приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.

Другой конец веревки (точка А, рис. 43,а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.

На  рис. 43, в показаны равнодействующая 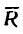и уравновешивающая

Задача №3

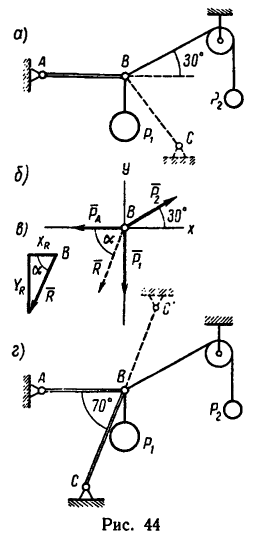
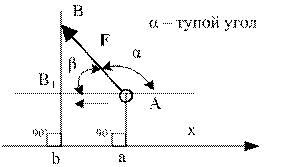
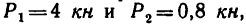
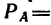
На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами , как показано на рис. 44, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой 2 кн? Какое усилие при этом будет испытывать стержень ВС?

Соединения стержней между собой и с опорами шарнирные.

Решение — методом проекций.

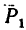
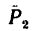
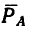
1.    На точку В действуют три силы: — вертикально вниз, — вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 44,6 и найдем их равнодействующую, вдоль направления действия которой необходимо установить стержень ВС.

2.    Оси проекций совместим с силами 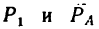и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:

3.    Обе проекции получаются отрицательными. Значит равнодействующая расположится так, как показано штриховым 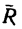на рис. 44,6, и положение стержня ВС определится углом

4.    Определим значение угла а из треугольника, образуемого 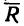и его проекциями (рис. 44,в):

Этому значению соответствует угол
5.    Стержень ВС необходимо установить под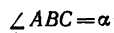= 70° к стержню АВ., и тогда он будет сжиматься силой, равной

Описанное положение стержня показано на рис. 44, г.

Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кн.

Задача №4

Определить равнодействующую пяти сил:

действующих на точку А, как показано на рис. 45,а.

Решение — методом проекций.

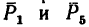
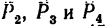
1.    Так как силы направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы будут образовывать с осями проекций углы, показанные на рис. 45.б

2. Найдем проекцию равнодействующей на ось х:

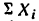
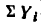
* Здесь – обозначена алгебраическая сумма проекций всех сил на ось х, а — алгебраическая сумма проекций тех же сил на ось у.

3. Найдем проекцию равнодействующей на ось у:

4.    Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.

Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.

Проекцией
силы на ось называется алгебраическая
величина, равная произведению силы на
косинус угла между направлением силы
и положительным направлением оси.

Если проекцию
силы 
 обозначить 
,
то согласно определению

.

В случае,
когда сила и ось расположены в одной
плоскости, для определения проекции
силы 
 на
ось 
 (рис.
3.1) следует из начала 
 и
конца 
 силы 
 опустить
перпендикуляры на ось 
.
Полученный отрезок 
 есть проекция 
.
Знак проекции принимается положительным,
если направление отрезка 
 совпадает
с положительным направлением оси 
 (рис.
3.1), и отрицательным,
если направления противоположны (рис.
3.2).

Рис. 3.1. Определение проекции силы  на ось (направление отрезка совпадает  с положительным направлением оси Х)	Рис. 3.2. Определение проекции  силы на ось (направления отрезка  и оси Х противоположны)

Модуль
проекции 
 или
длина отрезка 
 вычисляется
из прямоугольного треугольника 
: для рис.
3.1 имеем 
;
для рис. 3.2 – 
, 
.

9.
аналитический
способ определения равнодействующей
плоской системы сходящихся силВеличина
равнодействующей равна векторной
(геометрической) сумме векторов системы
сил. Определяем равнодействующую
геоме­трическим способом. Выберем
систему координат, определим про­екции
всех заданных векторов на эти оси (рис.
3.4а). Складываем проекции всех векторов
на оси х и у (рис. 3.46).

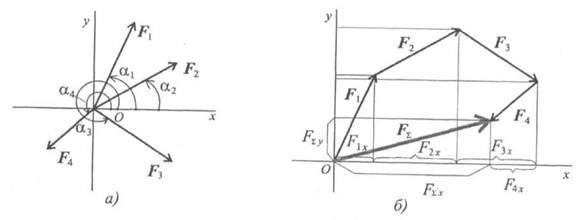
FΣч =
Flx + F2x + F3x + F4x; FΣн = Fly + F2y + F3y + F4y;

; 
.

Модуль
(величину) равнодействующей можно найти
по известным проекциям:

 
.Направление
вектора равнодействующей можно определить
по величинам и знакам косинусов углов,
образуемых равнодействую­щей с осями
координат (рис. 3.5).

;

Условия
равновесия плоской системы сходящихся
сил в аналитической форме

Исходя
из того, что равнодействующая равна
нулю, получим:

 FΣ
= 0.

Условия
равновесия в аналитической форме можно
сформулиро­вать следующим образом:
Плоская система сходящихся сил находится
в равновесии, ес­ли алгебраическая
сумма проекций всех сил системы на любую
ось равна нулю.Система уравнений
равновесия плоской сходящейся системы
сил:

.

В
задачах координатные оси выбирают так,
чтобы решение было наиболее простым.
Желательно, чтобы хотя бы одна неизвестная
сила совпадала с осью координат.

10. Момент силы относительно точки

Если
под действием приложенной силы твердое
тело может совершать вращение вокруг
некоторой точки, то для того, чтобы
охарактеризовать вращательный эффект
силы вводится понятие – момент силы
относительно точки (или центра).

Моментом
силы относительно точки (рисунок
1.1) называется векторное произведение
радиус-вектора  точки  приложения
силы на вектор силы. 

             
                   
              M_o(F)
= r ⊗ F

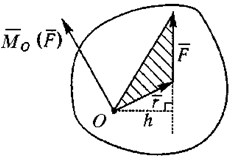
Рисунок
1.1

Вектор
момента направлен перпендикулярно
плоскости, в которой лежат сила и точка,
в ту сторону, откуда поворот от действия
силы виден происходящим против хода
часовой стрелки. Вектор момента
характеризует положение плоскости и
направление вращательного действия
силы, а также дает меру этого действия:

 |M_o(F)|
= F⋅r⋅sinα
= F⋅h,

где
 h –
плечо силы (кратчайшее
расстояние от точки  O –
центра момента – до линии действия
силы). Если сила проходит через точку,
то ее момент относительно этой точки
равен нулю.

Момент
силы относительно точки не меняется от
переноса силы вдоль линии ее действия.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R→=F1→2+F2→2+2F1→2F2→2cos α

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4-х сил: F1→, F2→, F3→, F4→. Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы. 

Рисунок 3. Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0: ∑i=1nFi→=0→. В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2-мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2-х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2-х составляющих сил.