I. Механика
Тестирование онлайн
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
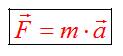
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.
Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. |
Сила тяжести уравновешивается силой упругости. Книга покоится |
Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.
Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.
Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх |
Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее. |
Нахождение равнодействующей силы
Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения.
Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.
Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Примеры
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси
Найдем проекции
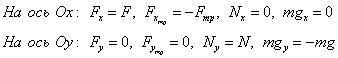
Записываем уравнения
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.
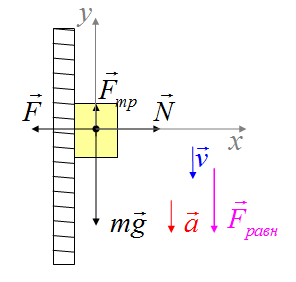
Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.
Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Системы и блоки*
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Fx = Fcosα > 0
Fy = Fcosβ = Fsinα > 0
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.
FΣx= F1x + F2x + F3x + F4x;
FΣy= F1y + F2y + F3y + F4y.
Модуль (величину) равнодействующей можно определить по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской системы сходящихся сил:
При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Определение равнодействующей сходящихся сил:
Для сложения любого числа сходящихся сил применяется правило многоугольника. Используя это правило, задачу можно решить либо графическим методом либо методом проекций.
Задачи, решены методом проекций. Графическим методом рекомендуется решить эти задачи самостоятельно.
Задача №1
Определить равнодействующую четырех сил: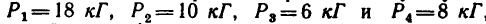 
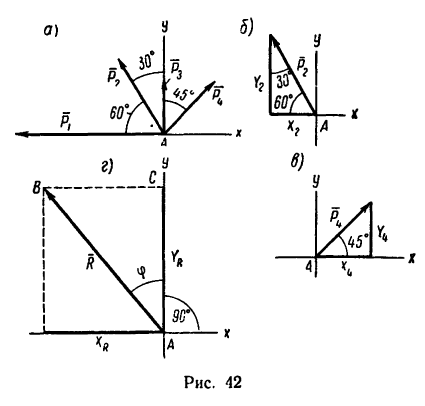
Решение — методом проекций.
1. Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами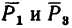 
(рис. 42, а).
2. Находим проекции данных сил на ось х:
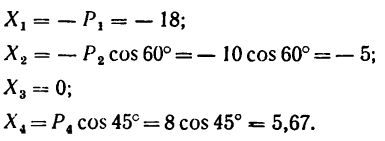
3. Находим проекции данных сил на ось у:
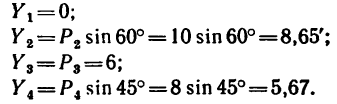
Если трудно определить знак и числовое значение проекции, то необходимо помнить, что проектируемую силу и две проекции на взаимно перпендикулярные оси всегда можно представить в виде прямоугольного треугольника. В тех случаях, когда еще нет достаточных навыков, силы и ее проекции можно изобразить отдельно, как показано на рис. 42,6 для силы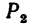 
и на рис. 42, в для силы 
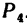. Эти рисунки облегчают правильное определение проекций.
Для сил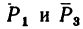 
такие рисунки не нужны, так как сила 
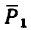лежит на оси х и, следовательно, проектируется на эту ось в натуральную величину, но зато на ось у проекция этой силы равна нулю. Сила 
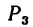проектируется в натуральную величину на ось у, а ее проекция на ось х равна нулю.
4. Находим проекции искомой равнодействующей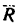 
на оси хну:
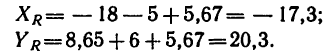
Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор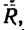 
заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х — влево. Положение равнодействующей R показано отдельно на рис. 42, г.
5. Находим модуль равнодействующей (т. е. заканчиваем решение задачи первым путем, см. п. 7 в § 4-1):
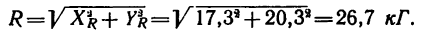
6. Находим угол ф, определяющий направление R относительно оси у (см. рис. 42, а):
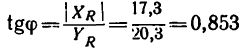
и, следовательно,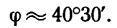 
Для определения угла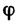 
использован 
АВС (см. рис. 42, г), в котором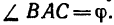 
Поэтому 
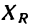не имеет значения и в выражение 
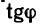подставлена его абсолютная величина.
Угол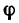 
можно найти при помощи синуса:
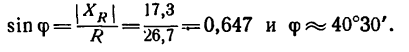
Для определения угла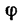 
можно воспользоваться и косинусом, но при работе с логарифмической счетной линейкой эта функция менее удобна.
Таким образом, равнодействующая четырех заданных сил равна 26,7 кГ направлена под углом 40°30′ к положительному направлению оси у и под углом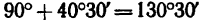 
к положительному направлению оси х.
Задача №2
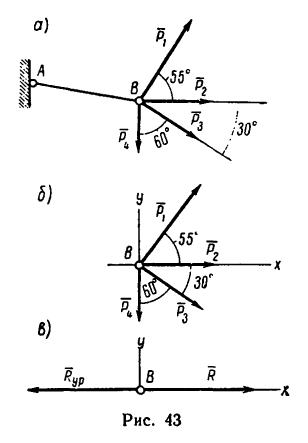
К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: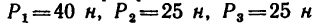 
,
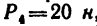направленные, как показано на рис. 43, а (сила 
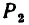горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.
Решение — методом проекций.
1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.
2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 43, 6) и совместим оси проекций с силами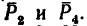
3. Найдем проекции заданных сил на ось х:
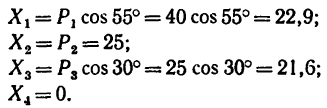
4. Найдем проекции заданных сил на ось у:
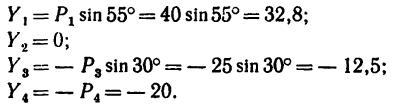
5. Найдем проекции равнодействующей R на оси х и у:
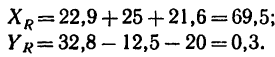
6. Найдем модуль равнодействующей:
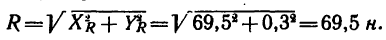
Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.
Таким образом, четыре заданные силы натягивают веревку равнодействующей силой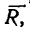
приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.
Другой конец веревки (точка А, рис. 43,а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.
На рис. 43, в показаны равнодействующая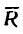 
и уравновешивающая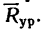 
Задача №3
На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами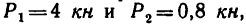 
, как показано на рис. 44, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой 
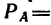2 кн? Какое усилие при этом будет испытывать стержень ВС?
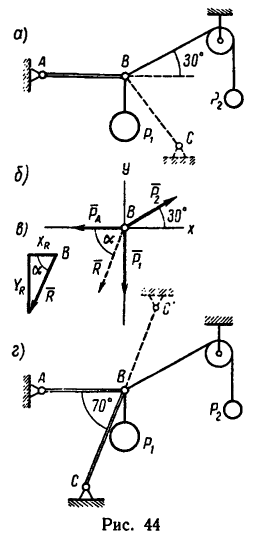
Соединения стержней между собой и с опорами шарнирные.
Решение — методом проекций.
1. На точку В действуют три силы: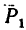 
— вертикально вниз, 
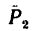— вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня 
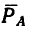тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 44,6 и найдем их равнодействующую, вдоль направления действия которой необходимо установить стержень ВС.
2. Оси проекций совместим с силами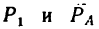 
и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:
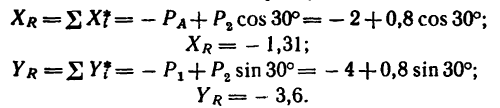
3. Обе проекции получаются отрицательными. Значит равнодействующая расположится так, как показано штриховым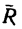 
на рис. 44,6, и положение стержня ВС определится углом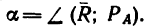 
4. Определим значение угла а из треугольника, образуемого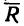 
и его проекциями (рис. 44,в):
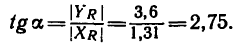
Этому значению соответствует угол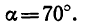
5. Стержень ВС необходимо установить под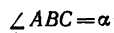
= 70° к стержню АВ., и тогда он будет сжиматься силой, равной
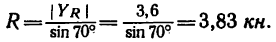
Описанное положение стержня показано на рис. 44, г.
Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кн.
Задача №4
Определить равнодействующую пяти сил:
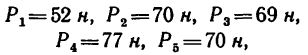
действующих на точку А, как показано на рис. 45,а.
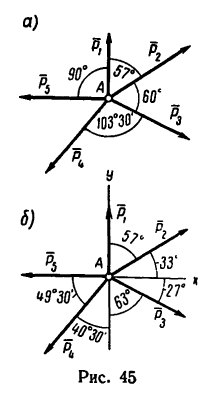
Решение — методом проекций.
1. Так как силы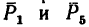 
направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы 
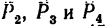будут образовывать с осями проекций углы, показанные на рис. 45.б
2. Найдем проекцию равнодействующей на ось х:
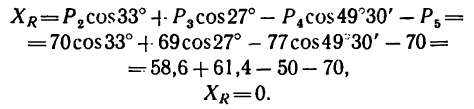
* Здесь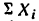 
– обозначена алгебраическая сумма проекций всех сил на ось х, а
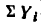— алгебраическая сумма проекций тех же сил на ось у.
3. Найдем проекцию равнодействующей на ось у:
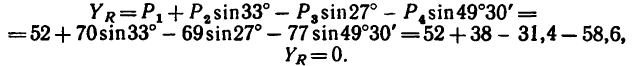
4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.
Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Потенциальная энергия
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
Проекции сил на координатные оси
Графический способ решения задач часто не дает необходимой точности. Намного проще решать задачи аналитически, оперируя не векторами сил, а скалярными величинами, к которым относятся проекции сил на оси.
Проекцией силы на ось называют длину направленного отрезка, который откладывается на оси и заключен между двумя перпендикулярами, опущенными из начала и из конца вектора силы.
Проекция вектора силы (рис. 2.10я, б) считается положительной (принимается со знаком «плюс»), если направление от точек проецирования начала и конца силы совпадает с направлением оси. Если направление проекции начала силы и ее конца не совпадает с направлением оси, проекция считается отрицательной (знак «минус»).
Рис. 2.10. Проекции сил на ось: а), б) наклонно расположенные силы по отношении к оси х; в) силы, перпендикулярные к оси х; г) силы, параллельные оси х
Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Соответственно, силы, расположенные перпендикулярно к оси, проецируются в точку – проекция равна нулю, а силы, параллельные оси, проецируются в натуральную величину, т.е. длина проекции равна модулю силы (рис. 2.10в, г).
Проекции сил, если они действуют по одной оси, можно суммировать (складывать или вычитать в зависимости от их знака).
Любую произвольно направленную силу F можно разложить на составляющие ее векторы. Если принять, что между составляющими силу векторами будет угол 90° и их направление параллельно координатным осям, получаем исходящие из точки А два вектора: Fx, Fy равные по модулям и направлению проекциям силы на соответствующие координатные оси (рис. 2.11).
Значение проекций сил можно определить алгебраически:
Рис. 2.11. Разложение силы на векторы и их проекции на координатные оси
Проекции одной и той же силы на разные координатные оси могут различаться знаками, так на рис. 2.12 проекция силы F на ось х совпадает с направлением оси, Fx и имеет знак «плюс», а проекция на ось у не совпадает с направлением оси и Fy имеет знак «минус».
Если взять систему сил и спроецировать все силы на координатные оси, то проекции сил по каждой оси можно суммировать, учитывая их значения и знаки (рис. 2.13а, б):
Результирующие значения проекций всей системы сил на оси х, у соответствуют проекциям равнодействующей на эти же
определить равнодействующую всей системы сил и затем спроецировать ее на координатные оси, то получим такой же результат, как при суммировании проекций всех сил системы на эти же оси.
Итак, проекция равнодействующей системы сходящихся сил на ось равна алгебраической сумме проекций всех векторов системы на ту же ось.
Рис. 2.13. Суммирование проекций сил: а) проекции сил на координатные оси; б) проекции сил, входящих в силовой многоугольник, и проекции равнодействующей
Как уже отмечалось, при равновесии системы сходящихся сил ее равнодействующая равна нулю, что соответствует условию (2.1). Отсюда следует, что при равновесии системы алгебраические суммы проекций всех сил системы на координатные оси равны нулю.
Условия равновесия системы сходящихся сил
Для упрощения написания, систему уравнений (2.3) часто записывают следующим образом:
где X X- алгебраическая сумма проекций всех сил на ось х; ? Y- алгебраическая сумма проекций всех сил на ось у. В дальнейшем будем применять упрощенную запись системы уравнений.
Зная проекции сил на координатные оси, значение равнодействующей всех сходящихся сил можно определить по формуле (1.7)
Направление вектора равнодействующей можно найти через косинусы углов (рис. 2.13б):
Пример 2.2. Необходимо определить проекции силы F на координатные оси, сила действует под углом а = 30° к оси х. Модуль силы F = 16 кН (рис. 2.14).
Рис. 2.14. К примеру 2.2, задаче 2.6
Решение. 1. Проецируем силу на координатные оси, проводя перпендикуляры из точек начала и конца силы к осям х, у. Направление полученных проекций совпадает с направлением осей, следовательно, они имеют положительные значения.
- 2. Устанавливаем значения косинуса и синуса угла a (cos 30° = 0,886; sin 30° = 0,5).
- 3. По формулам (2.2) определяем значения проекций силы: FX = F cos 30° = 76 • 0,886 = 67,34 кН; Fy = F sin 30° = 76 • 0,5 = 38 кН.
Рис. 2.15. К примеру 2.3: а) система сходящихся сил; б) равнодействующая системы и ее проекции на оси
Пример 2.3. Определить суммы проекций системы сходящихся сил (рис. 2.15я) на оси х, у. Установить значение и направление действия равнодействующей. Модули сил: F = 90 кН, F2 = 60 кН, F3 = 72 кН.
Решение. 1. Проецируем силы F, Fi, F3 на координатные оси и устанавливаем знаки проекций. Проекции на ось х:
Проекции на ось у:
2. Суммируем проекции сил, учитывая их знаки:
3. Модуль равнодействующей определяем по формуле (1.7)
Откладываем на координатных осях от проекций точки А суммарные значения проекций сил (?Х, ? Y) и строим на их основе равнодействующую (рис. 2.156).
Определяем косинусы углов наклона равнодействующей к
Отсюда, получаем углы наклона равнодействующей а = 59°24′; (3 = 30°36′.
Задача 2.6. Определите значения проекций силы F на оси координат, модуль силы F= 68 кН (рис. 2.14); угол наклона силы а = 45°.
Задача 2.7. Определите модуль и направление силы по ее проекциям: Fx = 35 кН; Fy = -20 кН.
Рис. 2.16. К задаче 2.8
Задача 2.8. Определите суммы проекций сходящейся системы сил на оси х, у. Установите значение и направление действия равнодействующей. Модули сил: F — 30 кН, Fi = 25 кН, Fz = 38 кН (рис. 2.16).
Как составить уравнение проекций ?
При решении задачек по статике, в теоретической механике или при решении задач по сопромату, часто, требуется определять сумму проекций сил на какую-то ось. Например, в термехе это используется при приведении какой-то системы сил к простейшему виду. В сопромате для определения реакций возникающих в опорах.
Уравнения проекций на примере
Рассмотрим, как составить уравнение проекций всех сил на какую-либо ось на примере. Возьмем прямоугольную декартову систему координат x-y и произвольную систему сил:
Проецируем все силы на координатные оси.Сила F1 дает положительную проекцию на ось X, так как ее направление совпадает с направлением этой оси. На ось Y эта сила не дает проекции, так как она перпендикулярная этой оси. Рассуждая, таким образом, можно записать следующие уравнения сумм проекций:
В выше описанном примере все силы были параллельны или перпендикулярны осям, но на практике же в задачах обычно силы расположены под некоторым углом к координатным осям. В таком случае силы раскладываются на две проекции параллельные осевым линиям:
Для нахождения этих сил удобнее вынести отдельно силовой треугольник и найти их следующим образом:
После этого можно записать уравнение проекций сил на горизонтальную и вертикальную ось:
Как составить силовые уравнения
В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.
Что такое равнодействующая
Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.
Результат сложения может дать:
- вектор, имеющий длину,
- или вектор, не имеющий длины.
Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.
Длина вектора содержит сумму квадратов всех его проекций на оси.
Где ( a_ ) и ( a_ ) — это проекции вектора (ссылка) ( vec ) на оси Ox и Oy.
Когда вектор равен нулю, равна нулю каждая его проекция на осях.
Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.
Левая часть силового уравнения
В левой части силового уравнения записываем силы, действующие на тело.
Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.
Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».
Правая часть силового уравнения
В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.
Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.
Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.
Тогда в правой части уравнения запишем:
- (ma), если ускорение направлено туда же, куда направлена ось;
- (- ma), если ускорение направлено противоположно оси;
А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.
В правой части уравнения запишем ноль (0 = ускорения нет).
Векторы сил параллельны
В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.
Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.
Проведем на рисунке ось, направим ее вверх.
Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.
Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:
Сила ( F_<text<сопр>>) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.
В правую часть уравнения поместим равнодействующую.
Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.
Математики запишут, что ускорение есть, но оно – нулевое (vec=0).
То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.
Примечания:
- На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec>). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
- На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.
Итоговое силовое уравнение имеет вид:
[large F_<text<сопр>> — m cdot g = 0 ]
Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.
Векторы сил не параллельны
Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.
Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).
Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.
Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.
Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.
Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.
Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.
Так выглядит уравнение для горизонтальной оси
Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.
Для вертикальной оси уравнение выглядит так:
[large N — m cdot g = 0 ]
Система, пригодная для решения задачи, состоит из двух уравнений
Куда направить оси
Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).
Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.
Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.
Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.
Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.
При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.
Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.
Выводы:
- Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
- Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.
Движение по наклонной плоскости
Составим систему уравнений для решения такой задачи:
Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.
Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.
Выражение для ускорения
Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)
Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.
Пользуясь осями координат, составляем теперь уравнения в проекциях.
Уравнение для проекций векторов на ось Ox:
[ large — F_<text<трен>> – m cdot g_ = — m cdot a ]
Уравнение для проекций векторов на ось Oy:
[ large N – m cdot g_ = 0 ]
Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.
[ large begin m cdot g_ = mg cdot cos left(alpha right) \ m cdot g_ = mg cdot sin left(alpha right) end ]
Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений
[ large begin — F_<text<трен>> – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end ]
Дополним эту систему выражением для силы трения.
Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.
[ large begin N = mg cdot cos left(alpha right) \ F_<text<трен>> = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end ]
Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:
[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]
Выражение для пройденного пути
Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:
[ large begin 0 = v_ <0>— a cdot t \ S = v_ <0>cdot t — a cdot frac <2>end ]
Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.
Упрощенная система для решения задачи теперь включает всего два уравнения
[ large begin mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_ <0>cdot frac> — frac> <2>cdot frac> end ]
Подставив в эту систему известные значения начальной (v_<0>) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.
[spoiler title=”источники:”]
http://ssopromat.ru/statika/kak-sostavit-uravnenie-proektsiy/
[/spoiler]
Оглавление:
- Основные теоретические сведения
- Основы динамики
- Проекции сил
- Законы Ньютона
- Сила упругости
- Вес тела
- Сила трения
- Особенности решения задач по динамике с несколькими телами
- Вращательное движение
- Закон всемирного тяготения. Спутники
Основные теоретические сведения
Основы динамики
К оглавлению…
Если в кинематике только описывается
движение тел, то в динамике изучаются причины этого движения под
действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие
– процесс, в ходе которого тела оказывают взаимное действие друг на
друга. В физике все взаимодействия обязательно парные. Это значит, что
тела взаимодействуют друг с другом парами. То есть всякое действие
обязательно порождает противодействие.
Сила – это
количественная мера интенсивности взаимодействия тел. Сила является
причиной изменения скорости тела целиком или его частей (деформации).
Сила является векторной величиной. Прямая, вдоль которой направлена
сила, называется линией действия силы. Сила характеризуется тремя
параметрами: точкой приложения, модулем (численным значением) и
направлением. В Международной системе единиц (СИ) сила измеряется в
Ньютонах (Н). Для измерения сил используют откалиброванные пружины.
Такие откалиброванные пружины называются динамометрами. Сила измеряется
по растяжению динамометра.
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
Чтобы найти векторную сумму нескольких
сил нужно выполнить чертеж, где правильно нарисовать все силы и их
векторную сумму, и по данному чертежу с использованием знаний из
геометрии (в основном это теорема Пифагора и теорема косинусов) найти
длину результирующего вектора.
Виды сил:
1. Сила тяжести.
Приложена к центру масс тела и направлена вертикально вниз (или что тоже
самое: перпендикулярно линии горизонта), и равна:
где: g – ускорение свободного падения, m
– масса тела. Не перепутайте: сила тяжести перпендикулярна именно
горизонту, а не поверхности на которой лежит тело. Таким образом, если
тело лежит на наклонной поверхности, сила тяжести по-прежнему будет
направлена строго вниз.
2. Сила трения.
Приложена к поверхности соприкосновения тела с опорой и направлена по
касательной к ней в сторону противоположную той, куда тянут, или
пытаются тянуть тело другие силы.
3. Сила вязкого трения
(сила сопротивления среды). Возникает при движении тела в жидкости или
газе и направлена против скорости движения.
4. Сила реакции опоры.
Действует на тело со стороны опоры и направлена перпендикулярно опоре от
нее. Когда тело опирается на угол, то сила реакции опоры направлена
перпендикулярно поверхности тела.
5. Сила натяжения нити. Направлена вдоль нити от тела.
6. Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.
Проекции сил
К оглавлению…
В большинстве задач по динамике на тело
действует больше чем одна сила. Для того чтобы найти равнодействующую
всех сил в этом случае можно пользоваться следующим алгоритмом:
- Найдем проекции всех сил на ось ОХ и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось ОХ.
- Найдем проекции всех сил на ось OY и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось OY.
- Результирующая всех сил будет находится по формуле (теореме Пифагора):
При этом, обратите особое внимание на то, что:
- Если сила перпендикулярна одной из осей, то проекция именно на эту ось будет равна нулю.
- Если при проецировании силы на одну из
осей «всплывает» синус угла, то при проецировании этой же силы на другую
ось всегда будет косинус (того же угла). Запомнить при проецировании на
какую ось будет синус или косинус легко. Если угол прилежит к проекции,
то при проецировании силы на эту ось будет косинус. - Если сила направлена в ту же сторону
что и ось, то ее проекция на эту ось будет положительной, а если сила
направлена в противоположную оси сторону, то ее проекция на эту ось
будет отрицательной.
Законы Ньютона
К оглавлению…
Законы динамики, описывающие влияние
различных взаимодействий на движение тел, были в одной из своих
простейших форм, впервые четко и ясно сформулированы Исааком Ньютоном в
книге «Математические начала натуральной философии» (1687 год), поэтому
эти законы также называют Законами Ньютона. Ньютоновская формулировка
законов движения справедлива только в инерциальных системах отсчета (ИСО). ИСО – система отсчета, связанная с телом, движущимся по инерции (равномерно и прямолинейно).
Есть и другие ограничения на
применимость законов Ньютона. Например, они дают точные результаты
только до тех пор, пока применяются к телам, скорости которых много
меньше скорости света, а размеры значительно превышают размеры атомов и
молекул (обобщением классической механики на тела, двигающиеся с
произвольной скоростью, является релятивистская механика, а на тела,
размеры которых сравнимы с атомными — квантовая механика).
Первый закон Ньютона (или закон инерции)
Формулировка: В ИСО,
если на тело не действуют никакие силы или действие сил скомпенсировано
(то есть равнодействующая сил равна нулю), то тело сохраняет состояние
покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при
отсутствии действия на него других тел называется инерцией. Поэтому
первый закон Ньютона называют законом инерции. Итак, причиной изменения
скорости движения тела целиком или его частей всегда является его
взаимодействие с другими телами. Для количественного описания изменения
движения тела под воздействием других тел необходимо ввести новую
величину – массу тела.
Масса – это свойство
тела, характеризующее его инертность (способность сохранять скорость
постоянной. В Международной системе единиц (СИ) масса тела измеряется в
килограммах (кг). Масса тела – скалярная величина. Масса также является
мерой количества вещества:
Второй закон Ньютона – основной закон динамики
Приступая к формулировке второго закона,
следует вспомнить, что в динамике вводятся две новые физические
величины – масса тела и сила. Первая из этих величин – масса – является
количественной характеристикой инертных свойств тела. Она показывает,
как тело реагирует на внешнее воздействие. Вторая – сила – является
количественной мерой действия одного тела на другое.
Формулировка:
Ускорение, приобретаемое телом в ИСО, прямо пропорционально
равнодействующей всех сил, действующих на тело, и обратно
пропорционально массе этого тела:
Однако при решении задач по динамике второй закон Ньютона целесообразно записывать в виде:
Если на тело одновременно действуют
несколько сил, то под силой в формуле, выражающей второй закон Ньютона,
нужно понимать равнодействующую всех сил. Если равнодействующая сила
равна нолю, то тело будет оставаться в состоянии покоя или равномерного
прямолинейного движения, т.к. ускорение будет нулевым (первый закон
Ньютона).
Третий закон Ньютона
Формулировка: В ИСО
тела действуют друг на друга с силами, равными по модулю и
противоположными по направлению, лежащими на одной прямой и имеющими
одну физическую природу:
Эти силы приложены к разным телам и
поэтому не могут уравновешивать друг друга. Обратите внимание, что
складывать можно только силы, которые одновременно действуют на одно из
тел. При взаимодействии двух тел возникают силы, равные по величине и
противоположные по направлению, но складывать их нельзя, т.к. приложены
они к разным телам.
Алгоритм решения задач по динамике
Задачи по динамике решаются с помощью законов Ньютона. Рекомендуется следующий порядок действий:
1. Проанализировав условие задачи, установить, какие силы действуют и на какие тела;
2. Показать на рисунке все силы в виде векторов, то есть направленных отрезков, приложенных к телам, на которые они действуют;
3. Выбрать систему
отсчета, при этом полезно одну координатную ось направить туда же, куда
направлено ускорение рассматриваемого тела, а другую – перпендикулярно
ускорению;
4. Записать II закон Ньютона в векторной форме:
5. Перейти к скалярной
форме уравнения, то есть записать все его члены в том же порядке в
проекциях на каждую из осей, без знаков векторов, но учитывая, что силы,
направленные против выбранных осей будут иметь отрицательные проекции,
и, таким образом, в левой части закона Ньютона они будут уже вычитаться,
а не прибавляться. В результате получатся выражения вида:
6. Составить систему
уравнений, дополнив уравнения, полученные в предыдущем пункте, в случае
необходимости, кинематическими или другими простыми уравнениями;
7. Провести далее все необходимые математические этапы решения;
8. Если в движении
участвует несколько тел, анализ сил и запись уравнений производится для
каждого из них по отдельности. Если в задаче по динамике описывается
несколько ситуаций, то подобный анализ производится для каждой ситуации.
При решении задач учитывайте также следующее: направление скорости тела и равнодействующей сил необязательно совпадают.
Сила упругости
К оглавлению…
Деформацией называют
любое изменение формы или размеров тела. Упругими называют такие
деформации, при которых тело полностью восстанавливает свою форму после
прекращения действия деформирующей силы. Например, после того, как груз
сняли с пружины, её длина в недеформированном состоянии не изменилась.
При упругой деформации тела возникает сила, которая стремится
восстановить прежние размеры и форму тела. Ее называют силой упругости.
Простейшим видом деформации является деформация одностороннего
растяжения или сжатия.
При малых деформациях сила упругости
пропорциональна деформации тела и направлена в сторону, противоположную
направлению перемещения частиц тела при деформации:
где: k – жесткость тела, х
– величина растяжения (или сжатия, деформации тела), оно равно разности
между конечной и начальной длиной деформируемого тела. И не равно ни
начальной ни конечной его длине в отдельности. Жесткость не зависит ни
от величины приложенной силы, ни от деформации тела, а определяется
только материалом, из которого изготовлено тело, его формой и размерами.
В системе СИ жесткость измеряется в Н/м.
Утверждение о пропорциональности силы упругости и деформации называют законом Гука.
В технике часто применяются спиралеобразные пружины. При растяжении или
сжатии пружин возникают упругие силы, которые также подчиняются закону
Гука. Коэффициент k называют жесткостью пружины. В пределах применимости
закона Гука пружины способны сильно изменять свою длину. Поэтому их
часто используют для измерения сил. Пружину, растяжение которой
проградуировано в единицах силы, называют динамометром.
Таким образом, у каждого конкретного
тела (а не материала) есть своя жесткость и она не изменяется для
данного тела. Таким образом, если у Вас в задаче по динамике несколько
раз растягивали одну и ту же пружину Вы должны понимать, что ее
жесткость во всех случаях была одна и та же. С другой стороны если в
задаче было несколько пружин разных габаритов, но, например, все они
были стальные, то тем не менее у них у всех будут разные жесткости. Так
как жесткость не является характеристикой материала, то ее нельзя найти
ни в каких таблицах. Жесткость каждого конкретного тела будет либо Вам
дана в задаче по динамике, либо ее значение должно стать предметом
некоторых дополнительных изысканий при решении данной задачи.
При сжатии сила упругости препятствует
сжатию, а при растяжении – препятствует растяжению. Рассмотрим также то,
как можно выразить жесткость нескольких пружин соединенных определённым
образом. При параллельном соединении пружин общий коэффициент жесткости рассчитывается по формуле:
При последовательном соединении пружин общий коэффициент жесткости может быть найден из выражения:
Вес тела
К оглавлению…
Силу тяжести, с которой тела
притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко
используется в повседневной жизни в неправильном смысле, под весом
подразумевается масса, однако это не так.
Весом тела называют силу, с которой тело действует на опору или подвес. Вес – сила, которая, как и все силы, измеряется в ньютонах (а не в килограммах), и обозначается P.
При этом предполагается, что тело неподвижно относительно опоры или
подвеса. Согласно третьему закону Ньютона вес зачастую равен либо силе
реакции опоры (если тело лежит на опоре), либо силы натяжении нити или
силе упругости пружины (если тело висит на нити или пружине). Сразу
оговоримся – вес не всегда равен силе тяжести.
Невесомость – это состояние, которое наступает, когда вес тела равен нолю. В этом состоянии тело не действует на опору, а опора на тело.
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Перегрузка рассчитывается по формуле:
где: P – вес тела, испытывающего перегрузку, P0
– вес этого же тела в состоянии покоя. Перегрузка – безразмерная
величина. Это хорошо видно из формулы. Поэтому не верьте
писателям-фантастам, которые в своих книгах измеряют ее в g.
Запомните, что вес никогда не
изображается на рисунках. Он просто вычисляется по формулам. А на
рисунках изображается сила натяжения нити либо сила реакции опоры,
которые по третьему закону Ньютона численно равны весу, но направлены в
другую сторону.
Итак, отметим еще раз три существенно важных момента в которых часто путаются:
- Несмотря на то, что вес и сила реакции
опоры равны по величине и противоположны по направлению, их сумма не
равна нулю. Эти силы вообще нельзя складывать, т.к. они приложены к
разным телам. - Нельзя путать массу и вес тела. Масса –
собственная характеристика тела, измеряется в килограммах, вес – это
сила действия на опору или подвес, измеряется в Ньютонах. - Если надо найти вес тела Р, то сначала находят силу реакции опоры N, или силу натяжения нити Т, а по третьему закону Ньютона вес равен одной из этих сил и противоположен по направлению.
Сила трения
К оглавлению…
Трение – один из видов
взаимодействия тел. Оно возникает в области соприкосновения двух тел при
их относительном движении или попытке вызвать такое движение. Трение,
как и все другие виды взаимодействия, подчиняется третьему закону
Ньютона: если на одно из тел действует сила трения, то такая же по
модулю, но направленная в противоположную сторону сила действует и на
второе тело.
Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя
всегда равна по величине внешней вызывающей силе и направлена в
противоположную ей сторону. Сила трения покоя не может превышать
некоторого максимального значения, которое определяется по формуле:
где: μ – безразмерная величина, называемая коэффициентом трения покоя, а N – сила реакции опоры.
Если внешняя сила больше максимального
значения силы трения, возникает относительное проскальзывание. Силу
трения в этом случае называют силой трения скольжения.
Она всегда направлена в сторону, противоположную направлению движения.
Силу трения скольжения можно считать равной максимальной силе трения
покоя.
Коэффициент пропорциональности μ поэтому называют также коэффициентом трения скольжения. Коэффициент трения μ
– величина безразмерная. Коэффициент трения положителен и меньше
единицы. Он зависит от материалов соприкасающихся тел и от качества
обработки их поверхностей. Таким образом коэффициент трения является
неким конкретным числом для каждой конкретной пары взаимодействующих
тел. Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо
быть дан в задаче, либо Вы сами должны найти его в ходе решения из
каких-либо формул.
Если в рамках решения задачи у Вас
получается коэффициент трения больше единицы или отрицательный – Вы
неправильно решаете эту задачу по динамике.
Если в условии задачи просят найти
минимальную силу, под действием которой начинается движение, то ищут
максимальную силу, под действием которой, движение ещё не начинается.
Это позволяет приравнять ускорение тел к нулю, а значит значительно
упростить решение задачи. При этом силу трения полагают равной ее
максимальному значению. Таким образом рассматривается момент, при
котором увеличение искомой силы на очень малую величину сразу вызовет
движение.
Особенности решения задач по динамике с несколькими телами
К оглавлению…
Связанные тела
Алгоритм решения задач по динамике в которых рассматриваются несколько тел связанных нитями:
- Сделать рисунок.
- Записать второй закон Ньютона для каждого тела в отдельности.
- Если нить нерастяжима (а так в большинстве задач и будет), то ускорения всех тел будут одинаковы по модулю.
- Если нить невесома, блок не имеет массы, трение в оси блока отсутствует, то сила натяжения одинакова в любой точке нити.
Движение тела по телу
В задачах этого типа важно учесть, что
сила трения на поверхности соприкасающихся тел действует и на верхнее
тело, и на нижнее тело, то есть силы трения возникают парами. При этом
они направлены в разные стороны и имеют равную величину, определяемую
весом верхнего тела. Если нижнее тело тоже движется, то необходимо
учитывать, что на него также действует сила трения со стороны опоры.
Вращательное движение
К оглавлению…
При движении тела по окружности
независимо от того, в какой плоскости происходит движение, тело будет
двигаться с центростремительным ускорением, которое будет направлено к
центру окружности, по которой движется тело. При этом понятие окружность
не надо воспринимать буквально. Тело может проходить только дугу
окружности (например, двигаться по мосту). Во всех задачах этого типа
одна из осей обязательно выбирается по направлению центростремительного
ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось
целесообразно направить перпендикулярно первой. В остальном алгоритм
решения этих задач совпадает с решением остальных задач по динамике:
1. Выбрав оси, записать
закон Ньютона в проекциях на каждую ось, для каждого из тел,
участвующих в задаче, или для каждой из ситуаций, описываемых в задаче.
2. Если это необходимо,
дополнить систему уравнений нужными уравнениями из других тем по
физике. Особенно хорошо нужно помнить формулу для центростремительного
ускорения:
3. Решить полученную систему уравнений математическими методами.
Так же есть ряд задач на вращение в
вертикальной плоскости на стержне или нити. На первый взгляд может
показаться, что такие задачи будут одинаковы. Это не так. Дело в том,
что стержень может испытывать деформации как растяжения, так и сжатия.
Нить же невозможно сжать, она сразу прогибается, а тело на ней просто
проваливается.
Движение на нити. Так
как нить только растягиваться, то при движении тела на нити в
вертикальной плоскости в нити будет возникать только деформация
растяжения и, как следствие, сила упругости, возникающая в нити, будет
всегда направлена к центру окружности.
Движение тела на стержне.
Стержень, в отличие от нити, может сжиматься. Поэтому в верхней точке
траектории скорость тела, прикрепленного к стержню, может быть равна
нулю, в отличии от нити, где скорость должна быть не меньше
определенного значения, чтобы нить не сложилась. Силы упругости,
возникающие в стержне, могут быть направлены как к центру окружности,
так и в противоположную сторону.
Поворот машины. Если
тело движется по твердой горизонтальной поверхности по окружности
(например, автомобиль проходит поворот), то силой, которая удерживает
тело на траектории, будет являться сила трения. При этом сила трения
направлена в сторону поворота, а не против него (наиболее частая
ошибка), она помогает машине поворачивать. Например, когда машина
поворачивает направо, сила трения направлена в сторону поворота
(направо).
Закон всемирного тяготения. Спутники
К оглавлению…
Все тела притягиваются друг к другу с
силами, прямо пропорциональными их массам и обратно пропорциональными
квадрату расстояния между ними. Таким образом закон всемирного тяготения в виде формулы выглядит следующим образом:
Такая запись закона всемирного тяготения справедлива для материальных точек, шаров, сфер, для которых r измеряется между центрами. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной. В системы СИ он равен:
Одним из проявлений силы всемирного
тяготения является сила тяжести. Так принято называть силу притяжения
тел к Земле или другой планете. Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если же удалиться от поверхности Земли на некоторое расстояние h,
то ускорение свободного падения на этой высоте станет равно (при помощи
нехитрых преобразований можно также получить соотношение между
ускорением свободного падения на поверхности планеты и ускорением
свободного падения на некоторой высоте над поверхностью планеты):
Рассмотрим теперь вопрос об
искусственных спутниках планет. Искусственные спутники движутся за
пределами атмосферы (если таковая у планеты имеется), и на них действуют
только силы тяготения со стороны планеты. В зависимости от начальной
скорости траектория космического тела может быть различной. Мы
рассмотрим здесь только случай движения искусственного спутника по
круговой орбите практически на нулевой высоте над планетой. Радиус
орбиты таких спутников (расстояние между центром планеты и точкой где
находится спутник) можно приближенно принять равным радиусу планеты Rп.
Тогда центростремительное ускорение спутника, сообщаемое ему силами
тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Движение спутника можно рассматривать
как свободное падение, подобное движению снарядов или баллистических
ракет. Различие заключается только в том, что скорость спутника
настолько велика, что радиус кривизны его траектории равен радиусу
планеты. Для спутников, движущихся по круговым траекториям на
значительном удалении от планеты, гравитационное притяжение ослабевает
обратно пропорционально квадрату радиуса r траектории. Скорость спутника в таком случае находится с помощью формулы:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Если речь идёт о планете Земля, то нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ,
период обращения спутника окажется равным 24 часам. Спутник с таким
периодом обращения, запущенный в плоскости экватора, будет неподвижно
висеть над некоторой точкой земной поверхности. Такие спутники
используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
