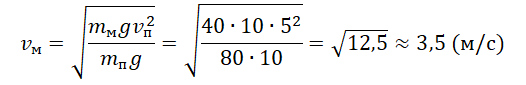Как найти проекцию силы тяжести на ось

Закрепленный вектор — упорядоченная пара точек (направленный отрезок, имеющий начало и конец).

Обозначать можем следующими способами: (overrightarrow{AB}), где (A) — начало, а (B) — конец вектора или просто (vec{a}).

Длина вектора — расстояние между началом и концом вектора.

Длина векторов обозначается следующим образом: (|vec{a}|) или (|overrightarrow{AB}|).

Если задана прямоугольная система координат, и координаты начала и конца вектора заданы в ней парами (A=(x_1,y_1)) и (B=(x_2,y_2)) соответственно, тогда координаты вектора можно задать [overrightarrow{AB}={,x_2-x_1, y_2-y_1,}]

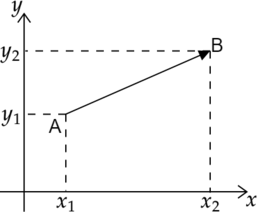
Тогда длина вектора (overrightarrow{AB}) задается формулой

[|overrightarrow{AB}|=sqrt{(x_2-x_1)^2-(y_2-y_1)^2}]

Проекцией вектора на какую-либо ось называется длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком <<(displaystyle +)>> или <<(displaystyle -)>>.

Например, проекцией вектора (overrightarrow {AB}) на ось можно считать отрезок (displaystyle A’B’), взятый со знаком <<+>>.

Рассмотрим ситуацию, когда брусок движется по наклонной плоскости:

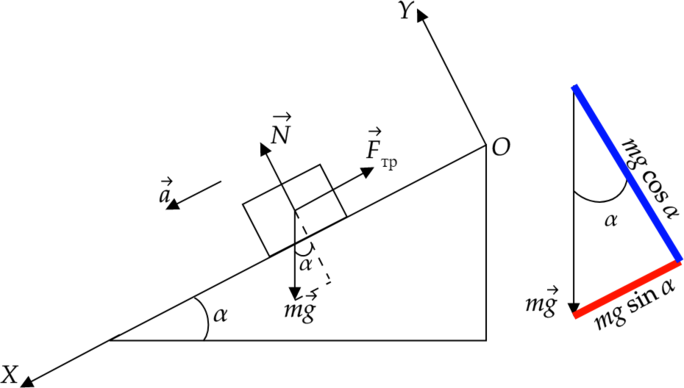
Исходя из рисунка мы можем записать II закон Ньютона в векторной форме: [vec{F}_text{тр}+mvec{g}+vec{N}=mvec{a}]

Запишем теперь проекции на оси:

[OY:-mgcosalpha+N=0] [OX:-F_text{тр}+mgsinalpha=ma]

Посмотрим, как получили два вышеприведенных равенства. Направим оси, как на рисунке, тогда по оси (OY) ускорение и сила трения на тело не действуют, так как они направлены перпендикулярно этой оси, а проекции сил, перпендикулярных оси, равны нулю.

Сила реакции опоры направлена по оси (OY), значит, возьмем ее положительную проекцию.

Также рассмотрим силу тяжести, вектор которой НЕ КОЛЛИНЕАРЕН осям координат, разложим его на два составляющие (см. рисунок сбоку) и возьмем синюю линию, являющуюся проекцией силы тяжести на ось (OY). Из простых геометрических соображений видим, что она равна (-mgcosalpha).

Аналогично действуем для оси (OX).

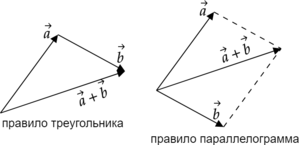
Сложение векторов можно производить по правилу треугольника или по правилу параллелограмма, рассмотрим на примере.

Даны векторы (vec{a}) и (vec{b}), по правилу треугольника мы можем получить сумму (vec{a}+vec{b}), совместив конец вектора (vec{a}) с началом вектора (vec{b}).

Даны векторы (vec{a}) и (vec{b}), по правилу параллелограмма мы можем получить сумму (vec{a}+vec{b}), совместив начало вектора (vec{a}) с началом вектора (vec{b}).

Умножение вектора на число.

Рассмотрим различные варианты произведения вектора (vec{a}) на какое-то вещественное число (lambda):

1) (lambda=0)

[vec{a}cdot0=vec{0}]

При умножении на нулевое число получается нулевой вектор (вектор нулевой длины);

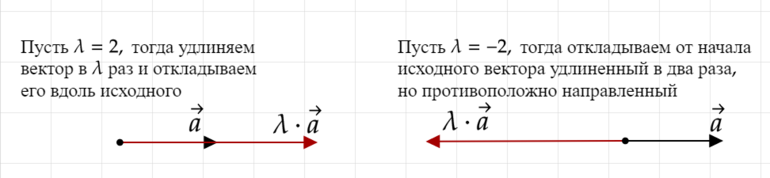
2) (lambda>0)

При умножении на положительное число получается вектор, сонапаравленный исходному вектору (происходит просто “удлинение” или “укорачивание” нашего вектора, направление не меняется);

3) (lambda<0)

При умножении на отрицательное число получается вектор, противоположно направленный исходному вектору (происходит “разворот”  вектора на 180 градусов и изменение его длины одновременно).

Скалярное произведение

Скалярным произведением векторов называют число, равное произведению длин этих векторов на косинус угла между ними.

Обозначение скалярного произведения векторов (vec{a}) и (vec{b}) имеет вид ((vec{a},vec{b})=|vec{a}|cdot|vec{b}|cdotcosBig(widehat{vec{a},vec{b}}Big))

Физический смысл скалярного произведения

Работу (A) тела, перемещаемого из точки (M) в (N) с постоянной силой (vec{F}), можно найти как произведение длин векторов (vec{F}) и (overrightarrow{MN}) с косинусом угла между ними, значит работа равна скалярному произведению векторов силы и перемещения:

[A=Big(vec{F},overrightarrow{MN}Big)]

На картинке внизу изображен кубик льда, находящийся на ледяной горке.

Давайте сразу обозначим силы, действующие на него (предположим, что трением можно пренебречь).

Обычно мы направляем ось x вправо, а ось y вертикально вверх. Но теперь нам следует нарисовать их иначе:

Так будет гораздо удобнее. Для анализа движения не нужно будет раскладывать все участвующие в процессе силы на составляющие. Единственная сила, с которой придется поработать, – это сила тяжести. В этой статье будет показано, как можно найти числовые значения ее компонентов, зная угол alpha.

Одну из составляющих силы тяжести, параллельную плоскости, по которой движется кубик, обозначим как vec{F}_parallel. А составляющую, которая перпендикулярна плоскости движения, обозначим как vec{F}_perp.

Сейчас мы выведем формулы, по которым в дальнейшем будем находить модули этих самых компонентов. Нам потребуется немного геометрии и тригонометрии.

Для начала рассмотрим треугольник, изображенный на рисунке. Он прямоугольный, значит, сумма его острых углов составляет девяносто градусов.

Теперь посмотрим на катет, лежащий напротив угла alpha, и на вектор силы тяжести.

Они параллельны. Чтобы вам было проще, я уберу все лишнее из рисунка.

Секущая проходит через две параллельные прямые, образуя накрест лежащие углы, которые будут равны между собой.

Теперь обратимся к треугольнику, который образует вектор силы тяжести со своими компонентами. Начертив его, мы увидим, что угол между вектором mvec{g} и вектором vec{F}_perp равен углу alpha.

Осталось применить определения косинуса и синуса:

sinalpha=dfrac{F_parallel}{mg}rArr,F_parallel=mgsinalpha

cosalpha=dfrac{F_perp}{mg}rArr,F_perp=mgcosalpha

Вам необязательно запоминать эти выражения. Достаточно запомнить угол, который в конце концов равен углу alpha. Тогда вы запросто сможете вновь получить написанные выше формулы.

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Неколлинеарные силы.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

---

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

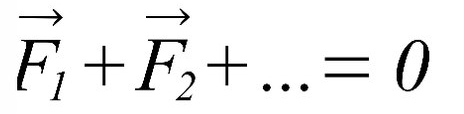
Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

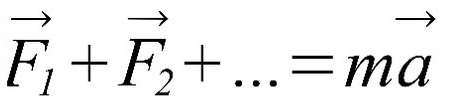
Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

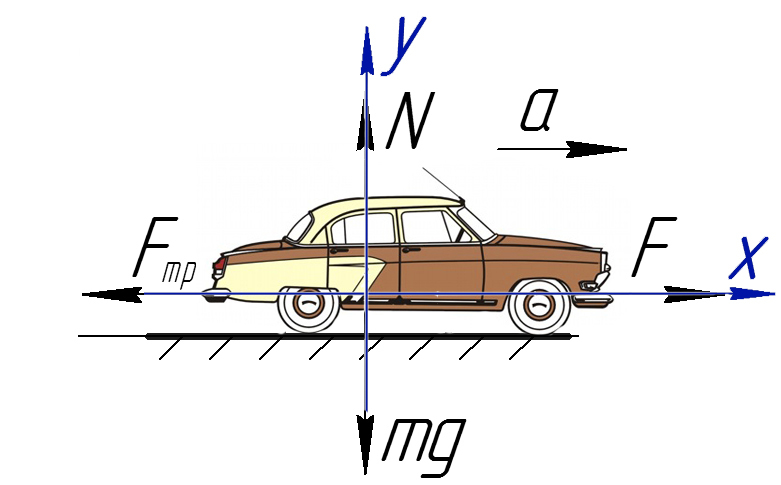
На Ось Х: движение с ускорением 

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

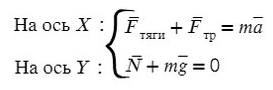
Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

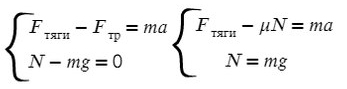
Fтр = μN, где N — сила реакции опоры. На оси Y:  N = mg, тогда в данной задаче Fтр = μmg.

Получаем, что: 

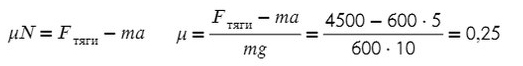
Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Ответ: 0,25

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

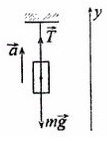
T – сила натяжения нити

На ось X: нет сил

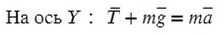
Разберемся с направлением сил на ось Y:

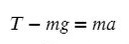
Выразим T (силу натяжения) и подставим числительные значения:

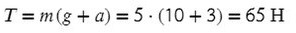
Ответ: 65 Н

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

Простой пример: мальчик тянет санки

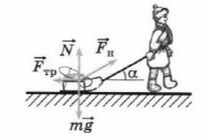
Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей. 

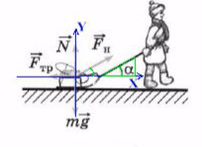Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

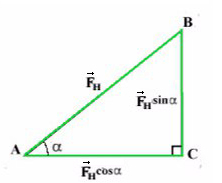
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

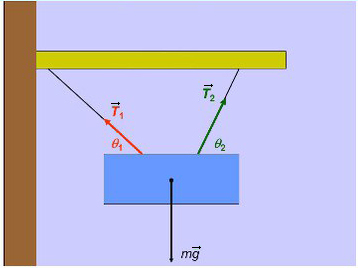
Введем оси и спроецируем силы:

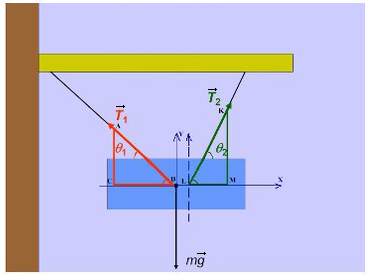
Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

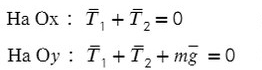
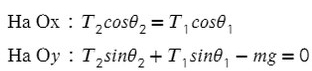
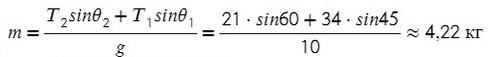
Ответ: 4,22 кг

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска? 

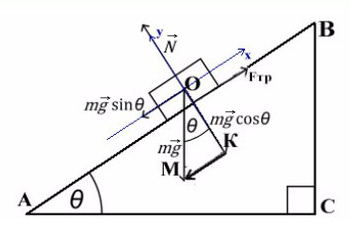
Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

Рассмотрим поподробнее ΔKOM: 

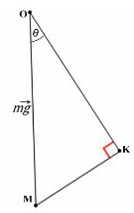
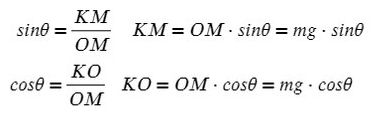Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

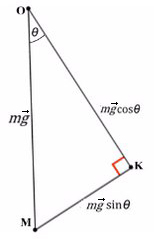
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

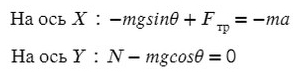
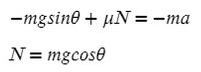
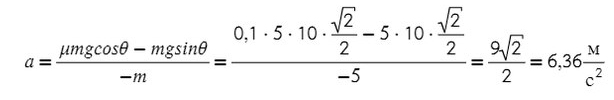
Ответ: 6,36 м/с²

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время. 

Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с²  и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

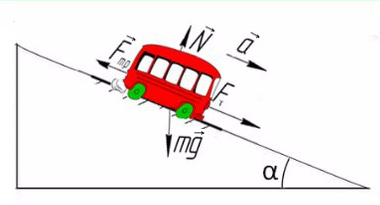
Введем оси X и Y. Спроецируем mg на оси:

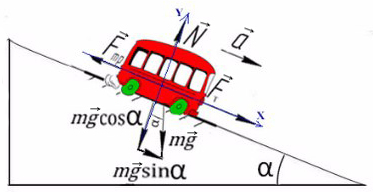
Запишем второй закон Ньютона на X и Y:

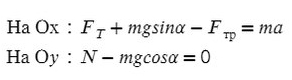
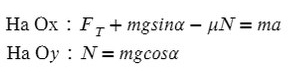
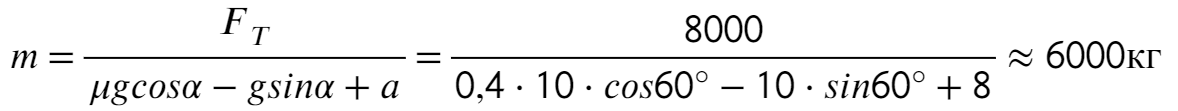
Ответ: 6000 кг

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное – понять, какие силы куда действуют, и как угол влияет на них.

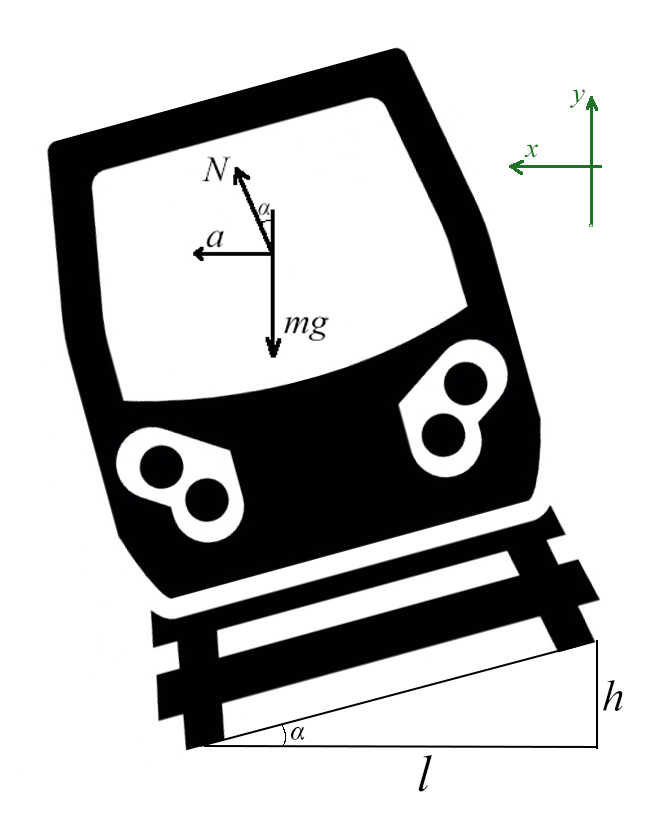
Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

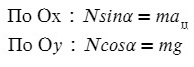
Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

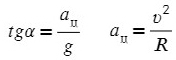
Тангенс – это отношение противолежащего катета к прилежащему:

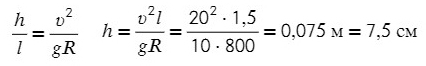
Ответ: 7,5 см

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами. 

Будь в курсе новых статеек, видео и легкого технического юмора.

Описывая движение тела с помощью законов Ньютона, нужно учитывать все силы, действующие на тело, а также их направления. Определить направления сил вам поможет таблица:

Сила	Направление
Сила тяжести	Вертикально вниз
Сила реакции опоры	Перпендикулярно опоре
Сила натяжения нити	Вдоль оси подвеса
Сила упругости	Противоположно деформации
Сила трения	Противоположно скорости или направлению возможного движения
Сила сопротивления
Выталкивающая (Архимедова) сила	Вертикально вверх

Алгоритм решения задач на законы Ньютона

1. Запись условий задачи в кратком виде.
2. Перевод известных данных в СИ.
3. Построение чертежа. На нем отображается само тело, а также направление сил, которые на него действуют. Выбирается система координат, указывается направление ускорения тела.
4. Запись второго закона Ньютона в векторном виде.
5. Запись второго закона Ньютона в проекциях на оси координат.
6. Решение задачи в общем виде (выделение из формулы искомой величины).
7. Подстановка в полученную формулу известных данных и вычисление искомой величины.
8. Проверка размерности.

Совет! Нужно выбирать такую систему координат, чтобы одна из ее осей совпадала с направлением ускорения движения тела.

Равномерное вертикальное движение (без ускорения)

Сила тяжести и сила реакции опоры
Подъем		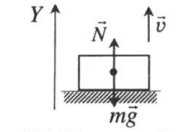Векторная запись II закона Ньютона: N + mg = ma	Проекция на ОУ: N – mg = 0
Спуск		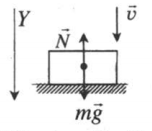Проекция на ОУ: mg – N = 0
Сила тяжести и сила натяжения нити
Подъем		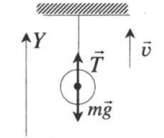Векторная запись II закона Ньютона: T + mg = ma	Проекция на ОУ: T – mg = 0
Спуск		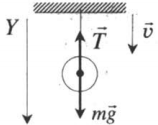Проекция на ОУ: mg – T = 0
Сила тяжести и сила сопротивления воздуха
Спуск		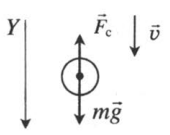Векторная запись II закона Ньютона: mg + Fc = ma	Проекция на ОУ: mg – Fc = 0
Сила тяжести, сила сопротивления и Архимедова сила
Подъем		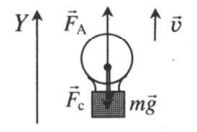Векторная запись II закона Ньютона: FA + mg + Fc = ma	Проекция на ОУ: FA – mg – Fc = 0
Спуск		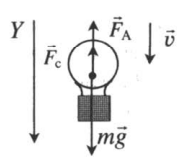Проекция на ОУ: mg – FA – Fc = 0

Пример №1. Парашютист массой 80 кг падает при открытом парашюте с установившейся скоростью 5 м/с. Какой будет установившаяся скорость, если на том же парашюте спускается мальчик массой 40 кг. Сила сопротивления воздуха пропорциональна квадрату скорости.

Согласно условию задачи сила сопротивления воздуха пропорциональна квадрату скорости:

F_c = v²

Следовательно, отношение сил сопротивления воздуха парашютиста и мальчика пропорционально отношению квадратов их скоростей:

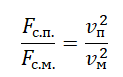
Отсюда:

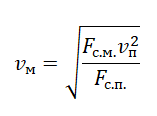
Проекция сил на ось ОУ при равномерном вертикальном движении под действием силы тяжести и силы сопротивления воздуха:

mg – F_c = 0

Силы сопротивления воздуха, действующие на парашютиста и мальчика:

F_c.п. = m_пg

F_c.м. = m_мg

Следовательно:

Равноускоренное вертикальное движение

Сила тяжести и сила реакции опоры
Подъем		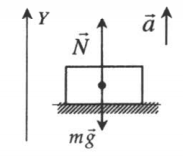Векторная запись II закона Ньютона: N + mg = ma	Проекция на ОУ: N – mg = ma
Спуск		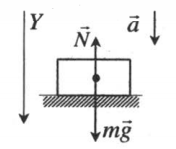Проекция на ОУ: mg – N = ma
Сила тяжести и сила натяжения нити
Подъем		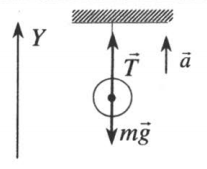Векторная запись II закона Ньютона: T + mg = ma	Проекция на ОУ: T – mg = ma
Спуск		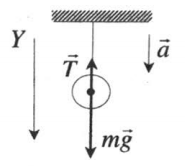Проекция на ОУ: mg – T = ma
Сила тяжести и сила сопротивления воздуха
Подъем		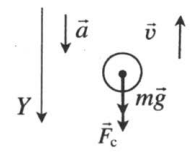Векторная запись II закона Ньютона: mg + Fc = ma	Проекция на ОУ: mg + Fc = ma
Спуск		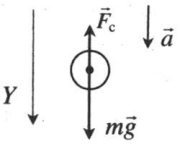Проекция на ОУ: mg – Fc = ma
Сила тяжести, сила сопротивления и выталкивающая (Архимедова) сила
Подъем		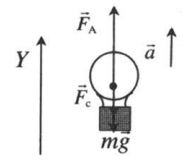Векторная запись II закона Ньютона: FA + mg + Fc = ma	Проекция на ОУ: FA – mg – Fc = ma
Спуск		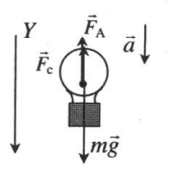Проекция на ОУ: mg – FA – Fc = ma

Пример №2. Прочность троса на разрыв составляет 1600 Н. Какой максимальной массы груз можно поднимать этим тросом с ускорением 15 м/с²?

Тело висит на подвесе (тросе) и поднимается ускоренно вверх. Значит, второй закон Ньютона принимает вид:

T – mg = ma

Выразим массу:

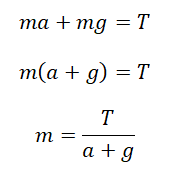
Подставляем известные данные и вычисляем максимальную массу:

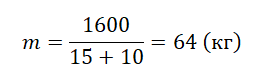
Задание EF17647

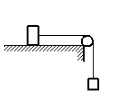По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:

а) 2,25 Н

б) 2,7 Н

в) 3 Н

г) 3,6 Н

---

Алгоритм решения

• Записать исходные данные.

• Сделать чертеж. Указать все силы, действующие на тела, и их направление. Выбрать систему отсчета.

• Записать второй закон Ньютона для бруска и подвешенного к нити груза в векторной форме.

• Записать второй закон Ньютона для обоих тел в виде проекций на оси.

• Вывести формулу для вычисления искомой величины.

• Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса первого тела (движущегося по плоскости) равна: m₁ = 0,9 кг.

• Масса второго тела (подвешенного к нити) равна: m₂ = 0,3 кг.

• Коэффициент трения первого тела о поверхность плоскости равна: μ = 0,2.

Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.

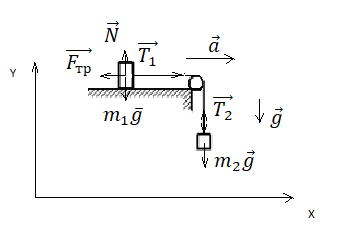
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:

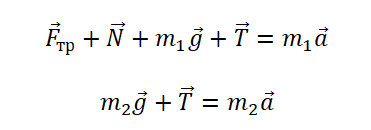
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:

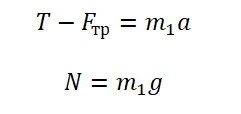
Запишем проекцию на ось ОУ для груза на нити:

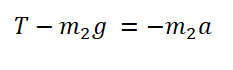
Выразим из этого выражения ускорение и получим:

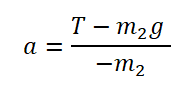
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:

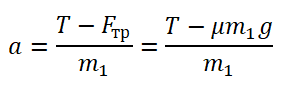
Приравняем правые части уравнений и получим:

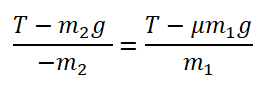
Произведем вычисления:

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17982

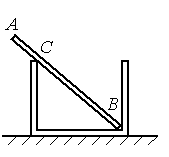Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.

Ответ:

а) 0,3 Н

б) 0,25 Н

в) 0,6 Н

г) 0,13 Н

---

Алгоритм решения

1. Записать исходные данные и перевести единицы измерения величин в СИ.
2. Выполнить чертеж. Выбрать ось вращения. Указать силы и их плечи.
3. Использовать второй и третий законы Ньютона, чтобы выполнить общее решение.
4. Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса стержня: m = 100 г.
• Модуль силы, с которой стержень давит на стенку сосуда в точке С: F_C = 0,5 Н.
• Модуль вертикальной составляющей силы, с которой стержень давит на сосуду в точке В: F_By = 0,6 Н.

Переведем единицы измерения в СИ:

100 г = 0,1 кг

Выполним чертеж:

Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы:

• сила тяжести (mg);
• сила реакции опоры в точке С (F_C);
• сила реакции опоры в точке В (F_В).

Поэтому:

m→g+→FC+→FB=0

Запишем проекции на оси Ox и Oy соответственно:

FCx=FBx

FCy+FBy=mg

Модуль горизонтальной составляющей силы в точке В можно выразить через теорему Пифагора:

FCx=√F2C−F2Cy

Но вертикальная составляющая силы в точке C равна разности силы тяжести и горизонтальной составляющей силы в точке В:

FCy=mg−FBy

Отсюда:

FBx=FCx=√F2C−F2Cy=√F2C−(mg−FBy)2

Подставим известные данные и вычислим:

FBx=√0,52−(0,1·10−0,6)2=√0,25−0,16=0,3 (Н)

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22586

Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:

а) больше 100 Н, направленной вниз

б) меньше 100 Н, направленной вверх

в) 100 Н, направленной вниз

г) 100 Н, направленной вверх

 

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж, иллюстрирующий ситуацию.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций.

5.Вычислить силу, с которой гиря действует на руку мальчика.

Решение

Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.

Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.

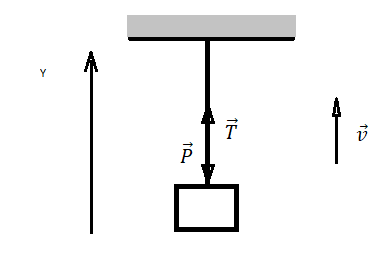
На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:

P + T = 0

Запишем этот же закон в проекции на ось ОУ:

–P + T = 0

Отсюда:

P = T

Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.

Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17555

Груз массой 4 кг подвешен к укреплённому в лифте динамометру. Лифт начинает спускаться с верхнего этажа с постоянным ускорением. Показания динамометра при этом равны 36 Н. Чему равно и куда направлено ускорение лифта?

а) 1 м/с², вниз

б) 1 м/с², вверх

в) 9 м/с², вниз

г) 9 м/с², вверх

---

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж с указанием известных сил, действующих на груз, их направлений и выбором системы координат.

3.Определить, какая сила действует на тело.

4.Записать второй закон Ньютона в векторной форме.

5.Записать второй закон Ньютона в виде проекций на оси.

6.Выразить из формулы проекцию ускорения лифта и рассчитать ее.

7.По знаку проекции ускорения лифта определить, в какую сторону оно направлено.

Решение

Запишем исходные данные:

• Масса груза равна: m = 4 кг.

• Показания динамометра во время спуска: F = 36 Н.

Сделаем чертеж:

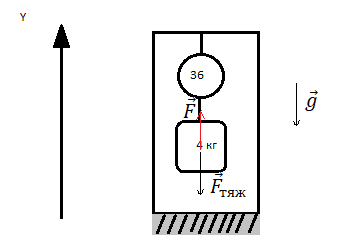
Направление силы, действующей на тело, обратно силе, которую оказывает тело на подвес в виде динамометра. Поэтому сила F равна по модулю весу тела во время спуска, но направлена противоположно ему (вверх). Направление ускорения лифта пока остается неизвестным.

Второй закон Ньютона в векторной форме:

F + mg = ma

Второй закон Ньютона в виде проекции сил на ось ОУ:

F – mg = ma

Выразим отсюда ускорение лифта и вычислим его, подставив известные данные:

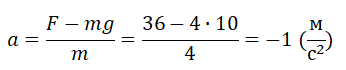
Перед проекцией ускорения стоит знак «–». Это значит, что оно направлено противопроложно оси ОУ (т.е. вниз).

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 3.7k