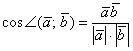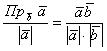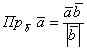Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.
Проекция точки на прямую, определение
В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.
Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.
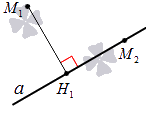
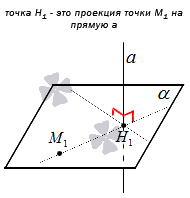
Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.
Рассмотрим рисунок ниже: точка H1 служит проекцией точки М1 на прямую a, а точка М2, принадлежащая прямой, является проекцией сама себя.
Данное определение верно для случая на плоскости и в трехмерном пространстве.
Чтобы на плоскости получить проекцию точки М1 на прямую a, проводится прямая b, проходящая через заданную точку M1 и перпендикулярная прямой a. Таким образом, точка пересечения прямых a и b будет проекцией точки М1 на прямую a.
В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой a и плоскости α, проходящей через точку М1 и перпендикулярной прямой a.
Нахождение координат проекции точки на прямую
Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.
Пусть нам заданы прямоугольная система координат Oxy, точка М1(x1, y1) и прямая a. Необходимо найти координаты проекции точки М1 на прямую a.
Проложим через заданную точку М1(x1, y1) прямую b перпендикулярно прямой a. Точку пересечения маркируем как H1. Точка Н1 будет являться точкой проекции точки М1 на прямую a.
Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки М1(x1, y1) на прямую a:
– составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;
– записываем уравнение прямой b (проходящей через точку М1 и перпендикулярной прямой a). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;
– определяем искомые координаты проекции как координаты точки пересечения прямых a и b. Для этого решаем систему уравнений, составляющие которой – уравнения прямых a и b.
На плоскости Oxy заданы точки М1(1, 0) и прямая a (общее уравнение – 3x + y + 7 = 0). Необходимо определить координаты проекции точки М1 на прямую a.
Решение
Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой b. Прямая b перпендикулярна прямой a, а значит нормальный вектор прямой a служит направляющим вектором прямой b. Тогда направляющий вектор прямой b запишем как b→=(3, 1). Запишем и каноническое уравнение прямой b, поскольку нам также заданы координаты точки М1, через которую проходит прямая b:
x-13=y1
Заключительным шагом определяем координаты точки пересечения прямых a и b. Перейдем от канонических уравнений прямой b к общему ее уравнению:
x-13=y1⇔1·(x-1)=3·y⇔x-3y-1=0
Составим систему уравнений из общих уравнений прямых a и b и решим ее:
3x+y+7=0x-3y-1=0⇔y=-3x-7x-3y-1=0⇔y=-3x-7x-3·(-3x-7)-1=0⇔⇔y=-3x-7x=-2⇔y=-3·(-2)-7x=-2⇔y=-1x=-2
В конечном итоге мы получили координаты проекции точки М1(1, 0) на прямую 3x + y + 7 = 0: (-2,-1).
Ответ: (-2, -1).
Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.
Пусть заданы координатные прямые Ox и Oy, а также точка М1(x1, y1). Понятно, что проекцией заданной точки на координатную прямую Ox вида y = 0 будет точка с координатами (x1, 0). Так и проекция заданной точки на координатную прямую Oy будет иметь координаты 0, y1.
Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением By+C=0⇔y=-CB, а прямую, параллельную оси ординат – Ax+C=0⇔x=-CA.
Тогда проекциями точки М1(x1, y1) на прямые y=-CB и x=-CAстанут точки с координатами x1, -CB и -CA, y1.
Определите координаты проекции точки М1(7, -5) на координатную прямую Oy, а также на прямую, параллельную прямой Oy 2y-3=0.
Решение
Запишем координаты проекции заданной точки на прямую Oy: (0, -5).
Запишем уравнение прямой 2y-3=0 в виде y=32. Становится видно, что проекция заданной точки на прямую y=32 будет иметь координаты 7, 32 .
Ответ: (0, -5) и 7, 32 .
Пусть в трехмерном пространстве заданы прямоугольная система координат Oxyz, точка М1(x1, y1, z1) и прямая a. Найдем координаты проекции точки М1 на прямую a.
Построим плоскость α, проходящую через точку М1 и перпендикулярную прямой a. Проекцией заданной точки на прямую a станет точка пересечения прямой a и плоскости α. Исходя из этого, приведем алгоритм для нахождения координат проекции точки М1(x1, y1, z1) на прямую a:
– запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;
– составим уравнение плоскости α, проходящей через точку М1 и перпендикулярной прямой a (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);
– найдем искомые координаты проекции точки М1(x1, y1, z1) на прямую a – это будут координаты точки пересечения прямой α и плоскости α (в помощь – статья «Координаты точки пересечения прямой и плоскости»).
Задана прямоугольная система координат Oxyz, и в ней – точка М1(0, 1, -1) и прямая a. Прямой a соответствуют канонические уравнения вида: x+23=y-6-4=z+11. Определите координаты проекции точки М1 на прямую a.
Решение
Используем указанный выше алгоритм. Уравнения прямой a известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости α. Для этого определим координаты нормального вектора плоскости α. Из заданных канонических уравнений прямой a выделим координаты направляющего вектора этой прямой: (3, -4, 1), который будет являться нормальным вектором плоскости α, перпендикулярной прямой a. Тогда n→ = (3, -4, 1) – нормальный вектор плоскости α. Таким образом, уравнение плоскости α будет иметь вид:
3·(x-0)-4·(y-1)+1·(z-(-1))=0⇔3x-4y+z+5=0
Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:
- Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую a:
x+23=y-6-4=z+11⇔-4·(x+2)=3·(y-6)1·(x+2)=3·(z+1)1·(y-6)=-4·(z+1)⇔4x+3y-10=0x-3z-1=0
Чтобы найти точки пересечения прямой 4x+3y-10=0x-3z-1=0 и плоскости 3x-4y+z+5=0 , решим систему уравнений:
4x+3y-10=0x-3z-1=03x-4y+z+5=0⇔4x+3y=10x-3z=13x-4y+z=-5
В данном случае используем метод Крамера, но возможно применить любой удобный:
∆=43010-33-41=-78∆x=103010-3-5-41=-78⇒x=∆x∆=-78-78=1∆y=410011-33-51=-156⇒y=∆y∆=-156-78=2∆z=43101013-4-5=0⇒z=∆z∆=0-78=0
Таким образом, проекцией заданной точки на прямую a является точка cкоординатами (1, 2, 0)
- На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:
x+23=y-6-4=z+11⇔x=-2+3·λy=6-4·λz=-1+λ
Подставим в уравнение плоскости, имеющее вид 3x-4y+z+5=0, вместо x, y и z их выражения через параметр:
3·(-2+3·λ)-4·(6-4·λ)+(-1+λ)+5=0⇔26·λ=0⇔λ=1
Вычислим искомые координаты точки пересечения прямой a и плоскости αпо параметрическим уравнениям прямой a при λ = 1:
x=-2+3·1y=6-4·1z=-1+1⇔x=1y=2z=0
Таким образом, проекция заданной точки на прямую a имеет координаты (1, 2, 0)
Ответ: (1, 2, 0)
Напоследок отметим, что проекциями точки М1(x1, y1, z1) на координатные прямые Ox, Oy и Oz буду являться точки с координатами (x1, 0, 0), (0, y1, 0) и (0, 0, z1) соответственно.
Проекция точки на прямую онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на прямую − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
где q=(m,p) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (1)(Рис.1).
Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
где n=(A,B) нормальный вектор прямой L1.
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
Откроем скобки
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
Подставим значения x и y в (4):
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’.
Пример 1. Найти проекцию точки M0(1, 3) на прямую
Решение.
Направляющий вектор прямой (6) имеет вид:
Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x0, y0, x’, y’ в (5′):
Подставляя значение t в (5), получим:
Ответ:
Проекцией точки M0(1, 3) на прямую (6) является точка:
2. Пусть в трехмерном пространстве задана точка M0(x0, y0, z0) и прямая L:
где q=(m, p, l) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (7)(Рис.2).
Нахождение проекцию точки на прямую L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) имеет следующий вид:
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:
Откроем скобки
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (7):
Подставим значения x и y в (9):
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’, z1=lt’+z’.
Пример 2. Найти проекцию точки M0(3, −1, −2) на прямую
Решение.
Направляющий вектор прямой (11) имеет вид:
Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (10′):
Подставляя значение t=t’ в (10), получим:
Ответ:
Проекцией точки M0(3, −1, −2) на прямую (11) является точка:
Проекция вектора на вектор
Рассмотрим
векторы
и
:
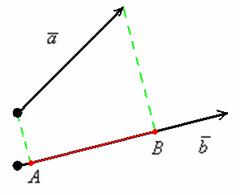
Спроецируем
вектор
на
вектор
,
для этого из начала и конца вектора
опустим
перпендикуляры на
вектор
(пунктирные
линии). В данном случае проекцией
вектора
на
вектор
является
ДЛИНА отрезка
.
То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Данное
ЧИСЛО обозначается следующим образом:
,
«большим вектором» обозначают
вектор, КОТОРЫЙ проецируют,
«маленьким подстрочным вектором»
обозначают вектор НА
который проецируют.
Сама
запись
читается
так: «проекция вектора «а» на вектор
«бэ»».
Что
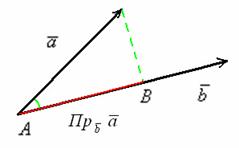
произойдёт, если вектор «бэ» будет
«слишком коротким»? Проводим прямую
линию, содержащую вектор «бэ». И вектор
«а» будет проецироваться уже на
направление вектора «бэ»,
попросту – на прямую, содержащую вектор
«бэ». То же самое произойдёт, если вектор
«а» отложить в тридесятом царстве – он
всё равно легко спроецируется на прямую,
содержащую вектор «бэ».
Если
угол между
векторами
острый (как
на рисунке), то
Если
векторы
ортогональны,
то
(проекцией
является точка, размеры которой считаются
нулевыми).
Если
угол между
векторами
тупой (на
рисунке мысленно переставьте стрелочку
вектора
),
то
(та
же длина, но взятая со знаком минус).
Отложим
данные векторы от одной точки:
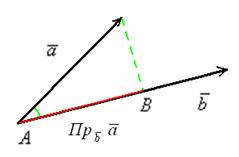
Очевидно,
что при перемещении вектора его проекция
не меняется
Рассмотрим
прямоугольный треугольник. Косинусом
острого угла называется отношение
прилежащего катета к гипотенузе. В
данном случае:
С
другой стороны, у нас уже получена
формула косинуса угла между векторами:
Таким
образом:

Сокращаем
знаменатели обеих частей на
и
получаем формулу для вычисления
проекции:

Формула
выведена, распишем её в координатах:
Если
векторы плоскости
и
,
заданы в ортонормированном базисе
,
то проекция вектора
на
вектор
выражается
формулой:
.
Если
векторы пространства
,
заданы в ортонормированном базисе
,
то проекция вектора
на
вектор
выражается
формулой:
Пример
Найти
проекцию вектора
на
вектор
Решение:
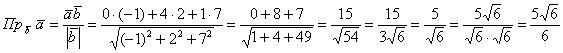
Ответ:
Проекция вектора на координатные оси. Направляющие косинусы вектора
Рассмотрим
вектор плоскости
,
заданный своими координатами в
ортонормированном базисе
.
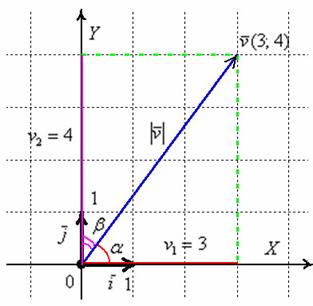
Проекцией
вектора
на
координатную ось
является
в точности его первая координата:
.
Обозначим через
угол
между вектором
и
координатным вектором
:
.
Тогда:
(определение
косинуса в прямоугольном треугольнике
недавно упоминалось).
Аналогично
со второй координатой: проекцией
вектора
на
координатную ось
является
его вторая координата:
.
Обозначим через
угол
между вектором
и
координатным вектором
:
.
Тогда:
Косинусы
называются направляющими
косинусами вектора.
Причём, для любого ненулевого вектора
справедливо равенство
.
Проверим его справедливость для
рассматриваемого вектора:
,
что и требовалось проверить.
Заметьте,
что приведённые выше выкладки не
изменятся, если вектор
отложить
от любой другой точки плоскости.
Координаты
вектора в ортонормированном базисе –
это его проекции на направления
соответствующих координатных векторов
(координатные оси).
Направляющие
косинусы ненулевого
вектора
,
заданного в ортонормированном
базисе
, выражаются
формулами
,
а сами координаты вектора можно выразить
через его длину и данные косинусы:
,
то есть:
.
С
пространственными векторами, заданными
в ортонормированном базисе
,
разборки точно такие же. Рассмотрим
произвольный ненулевой вектор
.
Его координаты представляют собой
проекции вектора на оси
соответственно.
Обозначим углы данного вектора с ортами
через:
.
Тогда направляющие
косинусы вектора выражаются формулами:
,
и справедливым является равенство
.
Пример
Найти
направляющие косинусы векторов:
а)
,
проверить, что
;
б)
,
проверить, что
.
Решение:
а)
Найдём длину вектора:
.
Направляющие
косинусы:
.
Проверка:
,
что и требовалось проверить.
б)
Найдём длину вектора:
.
Направляющие
косинусы:
.
Проверка:
,
что и требовалось проверить.
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Ronin_v 292 / 188 / 111 Регистрация: 22.07.2020 Сообщений: 538 |
||||
|
1 |
||||
Проекция точки на вектор21.07.2021, 02:02. Показов 2679. Ответов 3 Метки unity (Все метки)
Всем привет! С чем это связанно и как исправить? Сам код тут Кликните здесь для просмотра всего текста
P.S.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
21.07.2021, 02:02 |
|
Ответы с готовыми решениями: проекция точки 1) Найти сумму… Проекция точки Проекция точки Существует ли проекция точки? 3 |
|
Storm23 10377 / 5108 / 1824 Регистрация: 11.01.2015 Сообщений: 6,226 Записей в блоге: 34 |
||||
|
21.07.2021, 09:54 |
2 |
|||
|
Решение
Хочу получить проекцию точки на вектор. Ну какие гипотенузы? Какие углы? Вы же не в школе. Как можно жить без базовой линейной алгебры???
1 |
|
Данил Т 2 / 2 / 0 Регистрация: 23.07.2013 Сообщений: 13 |
||||
|
21.07.2021, 10:30 |
3 |
|||
|
Делал как-то на Unity. Не требует извлечения квадратного корня!!!
Добавлено через 8 минут
1 |
|
292 / 188 / 111 Регистрация: 22.07.2020 Сообщений: 538 |
|
|
21.07.2021, 18:31 [ТС] |
4 |
|
Storm23, Как можно жить без базовой линейной алгебры??? Зато, я красивый…
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
21.07.2021, 18:31 |
|
Помогаю со студенческими работами здесь
Проекция точки на прямую Ортогональная проекция точки на прямую (3D) Как соеденить точки, чтобы получилась проекция? Точки M и N – середины диагоналей AC и BD четырёхугольника ABCD. Докажите, что вектор MN =½( вектора AD + вектор CB) Точки M и N – середины диагоналей AC и BD… Определить вектор скорости, вектор ускорения материальной точки Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 4 |
1.7.1. Как найти проекцию вектора на вектор?
Рассмотрим ненулевые векторы и
:
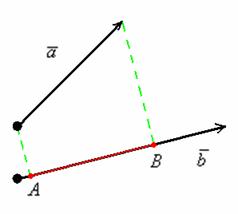
Спроецируем вектор на вектор
, для этого из начала и конца вектора
опустим перпендикуляры на вектор
(зелёные пунктирные линии).
Представьте,
что на вектор перпендикулярно сверху падают
лучи света. Тогда отрезок будет «тенью»
вектора . Проекцией вектора
на вектор
является ДЛИНА отрезка
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами острый (как на рисунке выше), то
Если векторы ортогональны, то
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой (на рисунке мысленно переставьте стрелочку вектора
), то
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора на любой ненулевой сонаправленный вектор
будет точно такой же:
– фактически это проекция вектора
на прямую
, которая содержит сонаправленные векторы
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно , то
добавится знак «минус»:
Отложим наши подопытные векторы от одной точки:
и рассмотрим прямоугольный треугольник. Косинус угла – есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
…все ли догадались, что будет дальше?
Приравниваем формулы:
и сокращаем знаменатели обеих частей на ,
получая формулу для вычисления проекции:
Распишем её в координатах:
Если векторы плоскости и
заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Если векторы пространства заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Легко убедиться, что проекция вектора на
коллинеарный вектор может
отличаться лишь знАком, приведу выкладки для «плоского» случая :
, если
, и
, если
Задача 34
Найти проекцию вектора на вектор
Решение в одну строчку:
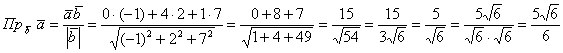
знаменатель на , избавившись тем самым от
иррациональности в знаменателе.
Ответ:
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами .
Найти:
а) проекцию стороны на сторону
;
б) проекцию стороны на сторону
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора на отрезок с известными концами
? (как вариант, на продолжение этого отрезка). Находим вектор
и используем формулу
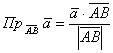
и формулу
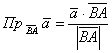
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 🙂
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:


| Оглавление |
Автор: Aлeксaндр Eмeлин




 Сообщение было отмечено Ronin_v как решение
Сообщение было отмечено Ronin_v как решение