В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.
Проецирование, виды проецирования
Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.
Проекция фигуры на плоскость – чертеж пространственной фигуры.
Очевидно, что для построения проекции существует ряд используемых правил.
Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.
Плоскость проекции – это плоскость, в которой строится изображение.
Использование тех или иных правил определяет тип проецирования: центральное или параллельное.
Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.
Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.
Проекция точки на плоскость
Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.
Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.
Допустим, задано трехмерное пространство, а в нем – плоскость α и точка М1, не принадлежащая плоскости α. Начертим через заданную точку М1 прямую а перпендикулярно заданной плоскости α. Точку пересечения прямой a и плоскости α обозначим как H1, она по построению будет служить основанием перпендикуляра, опущенного из точки М1 на плоскость α. 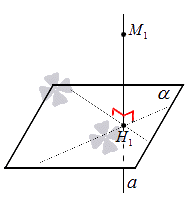
В случае, если задана точка М2, принадлежащая заданной плоскости α, то М2 будет служить проекцией самой себя на плоскость α.
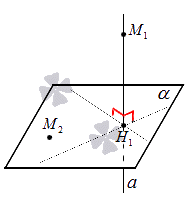
Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.
Нахождение координат проекции точки на плоскость, примеры
Пускай в трехмерном пространстве заданы: прямоугольная система координат Oxyz, плоскость α, точка М1(x1, y1, z1). Необходимо найти координаты проекции точки М1 на заданную плоскость.
Решение очевидным образом следует из данного выше определения проекции точки на плоскость.
Обозначим проекцию точки М1 на плоскость α как Н1. Согласно определению, H1 является точкой пересечения данной плоскости α и прямой a, проведенной через точку М1 (перпендикулярной плоскости). Т.е. необходимые нам координаты проекции точки М1 – это координаты точки пересечения прямой a и плоскости α.
Таким образом, для нахождения координат проекции точки на плоскость необходимо:
– получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;
– определить уравнение прямой a, проходящей через точку М1 и перпендикулярной плоскости α (изучите тему об уравнении прямой, проходящей через заданную точку перпендикулярно к заданной плоскости);
– найти координаты точки пересечения прямой a и плоскости α (статья – нахождение координат точки пересечения плоскости и прямой). Полученные данные и будут являться нужными нам координатами проекции точки М1 на плоскость α.
Рассмотрим теорию на практических примерах.
Определите координаты проекции точки М1 (-2, 4, 4) на плоскость 2х – 3y + z – 2 = 0.
Решение
Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.
Запишем канонические уравнения прямой a, проходящей через точку М1 и перпендикулярной заданной плоскости. В этих целях определим координаты направляющего вектора прямой a. Поскольку прямая а перпендикулярна заданной плоскости, то направляющий вектор прямой a – это нормальный вектор плоскости 2х – 3y + z – 2 = 0. Таким образом, a→ = (2, -3, 1) – направляющий вектор прямой a.
Теперь составим канонические уравнения прямой в пространстве, проходящей через точку М1 (-2, 4, 4) и имеющей направляющий вектор a→ = (2, -3, 1):
x+22=y-4-3=z-41
Для нахождения искомых координат следующим шагом определим координаты точки пересечения прямой x+22=y-4-3=z-41 и плоскости 2х-3y + z – 2 = 0. В этих целях переходим от канонических уравнений к уравнениям двух пересекающихся плоскостей:
x+22=y-4-3=z-41⇔-3·(x+2)=2·(y-4)1·(x+2)=2·(z-4)1·(y-4)=-3·(z+4)⇔3x+2y-2=0x-2z+10=0
Составим систему уравнений:
3x+2y-2=0x-2z+10=02x-3y+z-2=0⇔3x+2y=2x-2z=-102x-3y+z=2
И решим ее, используя метод Крамера:
∆=32010-22-31=-28∆x=220-100-22-31=0⇒x=∆x∆=0-28=0∆y=3201-10-2221=-28⇒y=∆y∆=-28-28=1∆z=32210-102-32=-140⇒z=∆z∆=-140-28=5
Таким образом, искомые координаты заданной точки М1 на заданную плоскость α будут: (0, 1, 5).
Ответ: (0, 1, 5).
В прямоугольной системе координат Oxyz трехмерного пространства даны точки А(0, 0, 2); В(2, -1, 0); С (4, 1, 1) и М1(-1, -2, 5). Необходимо найти координаты проекции М1 на плоскость АВС
Решение
В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:
x-0y-0z-02-0-1-00-24-01-01-2=0⇔xyz-22-1-241-1=0⇔⇔3x-6y+6z-12=0⇔x-2y+2z-4=0
Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.
Запишем параметрические уравнения прямой a, которая будет проходить через точку М1 перпендикулярно плоскости АВС. Плоскость х – 2y + 2z – 4 = 0 имеет нормальный вектор с координатами (1, -2, 2), т.е. вектор a→= (1, -2, 2) – направляющий вектор прямой a.
Теперь, имея координаты точки прямой М1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:
x=-1+λy=-2-2·λz=5+2·λ
Затем определим координаты точки пересечения плоскости х – 2y + 2z – 4 = 0 и прямой
x=-1+λy=-2-2·λz=5+2·λ
Для этого в уравнение плоскости подставим:
x=-1+λ, y=-2-2·λ, z=5+2·λ
Теперь по параметрическим уравнениям x=-1+λy=-2-2·λz=5+2·λ найдем значения переменных x, y и z при λ=-1: x=-1+(-1)y=-2-2·(-1)z=5+2·(-1)⇔x=-2y=0z=3
Таким образом, проекция точки М1 на плоскость АВС будет иметь координаты (-2, 0, 3).
Ответ: (-2, 0, 3).
Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.
Пусть задана точки М1(x1, y1, z1) и координатные плоскости Oxy, Оxz и Oyz. Координатами проекции этой точки на данные плоскости будут соответственно: (x1, y1, 0), (x1, 0, z1) и (0, y1, z1). Рассмотрим также плоскости, параллельные заданным координатным плоскостям:
Cz+D=0⇔z=-DC, By+D=0⇔y=-DB
И проекциями заданной точки М1 на эти плоскости будут точки с координатами x1,y1, -DC, x1, -DB, z1 и -DA, y1, z1.
Продемонстрируем, как был получен этот результат.
В качестве примера определим проекцию точки М1(x1, y1, z1) на плоскость Ax+D=0 . Остальные случаи – по аналогии.
Заданная плоскость параллельна координатной плоскости Oyz и i→= (1, 0, 0) является ее нормальным вектором. Этот же вектор служит направляющим вектором прямой, перпендикулярной к плоскости Oyz. Тогда параметрические уравнения прямой, проведенной через точку M1 и перпендикулярной заданной плоскости, будут иметь вид:
x=x1+λy=y1z=z1
Найдем координаты точки пересечения этой прямой и заданной плоскости. Подставим сначала в уравнение Аx+ D = 0 равенства: x=x1+λ, y=y1, z=z1 и получим: A·(x1+λ)+D=0⇒λ=-DA-x1
Затем вычислим искомые координаты, используя параметрические уравнения прямой при λ=-DA-x1:
x=x1+-DA-x1y=y1z=z1⇔x=-DAy=y1z=z1
Т.е., проекцией точки М1(x1, y1, z1) на плоскость будет являться точка с координатами -DA, y1, z1.
Необходимо определить координаты проекции точки М1(-6, 0, 12) на координатную плоскость Oxy и на плоскость 2y-3=0 .
Решение
Координатной плоскости Oxy будет соответствовать неполное общее уравнение плоскости z = 0. Проекция точки М1 на плоскость z = 0 будет иметь координаты (-6, 0, 0).
Уравнение плоскости 2y-3=0 возможно записать как y=322 . Теперь просто записать координаты проекции точки M1(-6, 0, 12) на плоскость y=322 :
-6, 322, 12
Ответ: (-6, 0, 0) и -6, 322, 12
Проекция точки на плоскость онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1.Найти проекцию M1 точки M0(4, -3, 2) на плоскость
Решение.
Нормальный вектор плоскости имеет вид:
т.е. A=5, B=1, C=−8.
Координаты точки M0: x0=4, y0=−3, z0=2.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (7) находим:
Ответ:
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Уравнение для описания плоскости
Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее – ниже.
Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
A*x + B*y + C*z + D = 0.
Первые три коэффициента – это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.
Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.
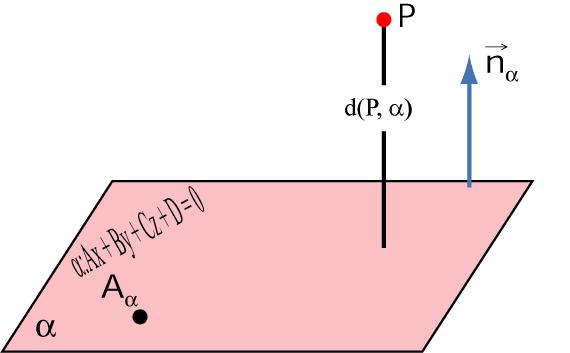
Понятие о проекции точки и ее вычисление
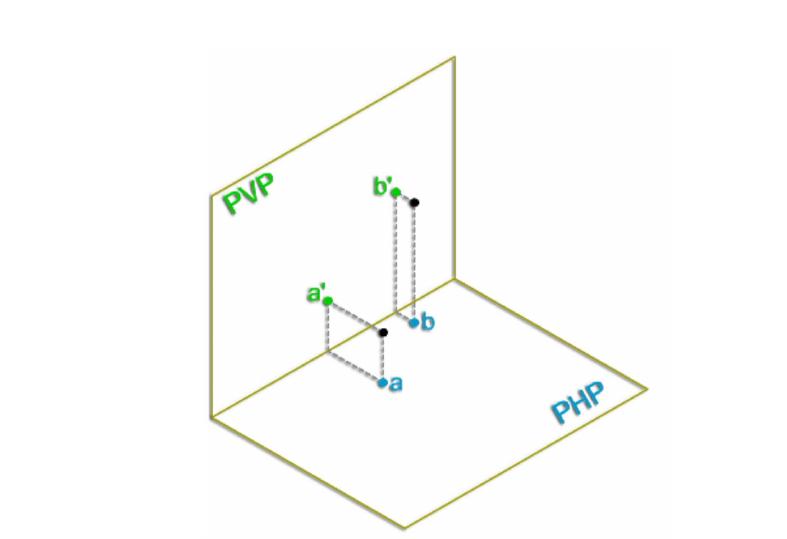
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
(x; y; z) = (x1; y1; z1) + λ*(A; B; C).
Где λ – действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
d = |PQ¯| = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2).
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Пример задачи
Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:
2*x – y + z + 4 = 0.
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90o. Имеем:
(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
x = 2*λ;
y = -2 – λ;
z = λ + 3;
2*x – y + z + 4 = 0.
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
2*(2*λ) – (-2 – λ) + λ + 3 + 4 = 0 =>
6*λ + 9 = 0 =>
λ = 9/6 = 3/2 = 1,5.
Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:
(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
d = √((3 – 0 )2 + (-3,5 + 2 )2 + (4,5 – 3 )2) = 3,674.
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.
Проекция точки на плоскость
-
Определите
координаты проекции точки М1(-1,-2.5) на
плоскость
x-2y+2z-4=0
Нормальный
вектор плоскости x-2y+2z-4=0
имеет
координаты (1.-2.2), следовательно,
вектор является направляющим вектором
прямой a. Теперь мы можем написать
параметрические
уравнения прямой в пространстве, так
как знаем координаты точки прямой
М1(-1,-2.5) и координаты ее направляющего
вектора (1.-):
X=1t-1
Y=-2t-2
Z=2t+5
Осталось
определить координаты точки пересечения
прямой и плоскости.
Для этого в уравнение плоскости ![]() подставим
подставим ![]() :
:
![]() .
.
Теперь
по параметрическим уравнениям 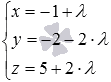 вычислим
вычислим
значения переменныхx, y и z при ![]() :
:
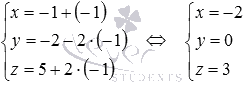 .
.
Таким
образом, проекция точки М1 на
плоскость АВС имеет
координаты ![]() .
.
Проекция
прямой на плоскость
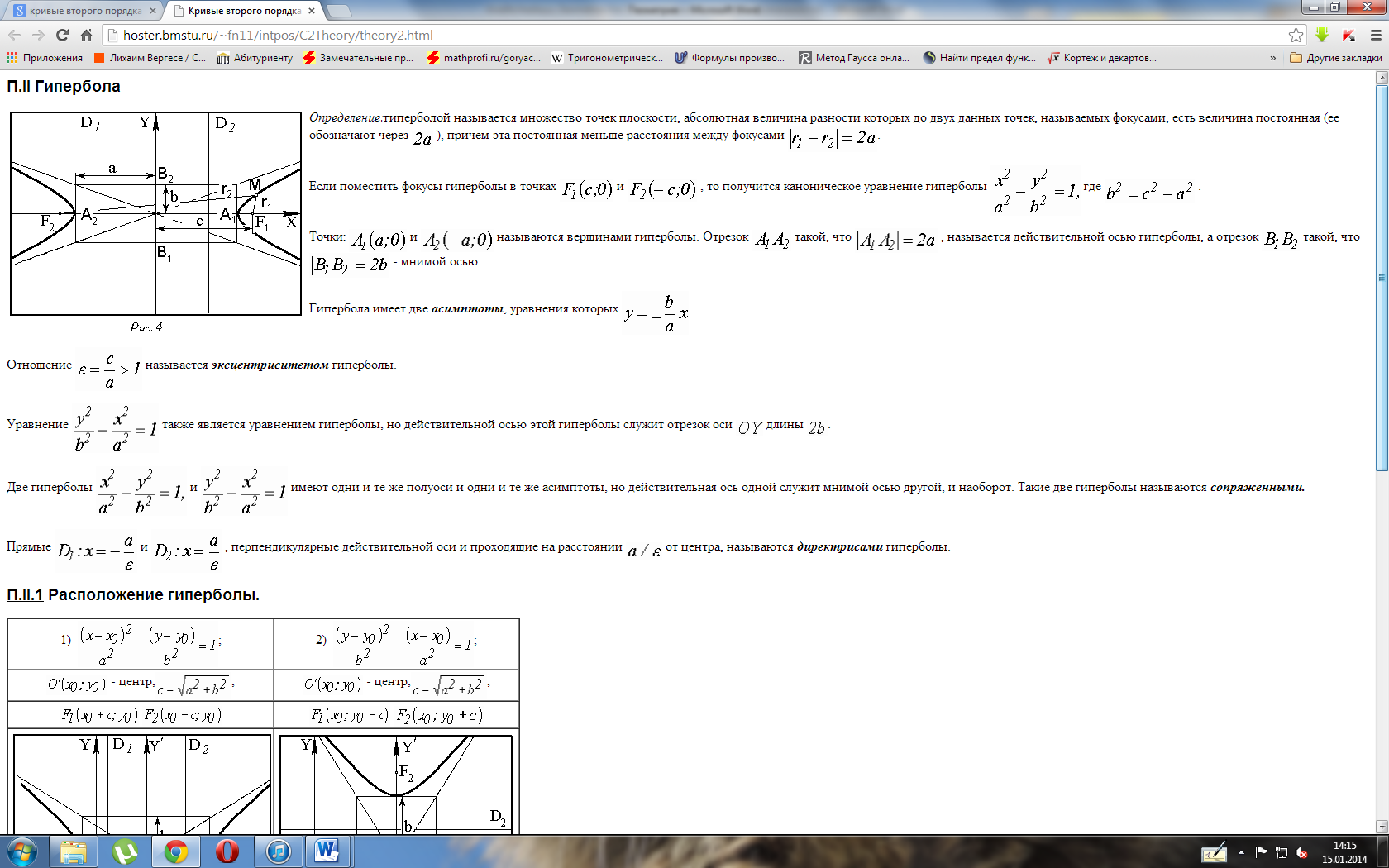
Эллипс
Эллипсом
называется множество точек плоскости,
сумма расстояний которых до двух данных
точек, называемых фокусами ![]() и
и ![]() есть
есть
величина постоянная (ее обозначают
через 2*а ). Причем эта постоянная больше
расстояния между фокусами.
Для
вывода уравнения эллипса выберем систему
координат ![]() так,
так,
чтобы фокусыF1 и F2
лежали на оси ![]() ,
,
а начало координат совпадало с серединой
отрезкаF1F2.
Тогда фокусы будут иметь следующие
координаты: ![]() и
и![]() .
.
Пусть ![]() —
—
произвольная точка эллипса. Тогда,
согласно определению эллипса,![]() ,
,
т. е.
![]() (11.5)
(11.5)
Это,
по сути, и есть уравнение эллипса.
Преобразуем
уравнение (11.5) к более простому
виду следующим образом:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Так
как a>с,
то ![]() .
.
Положим
![]() (11.6)
(11.6)
Тогда
последнее уравнение примет вид ![]() или
или
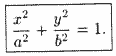
(11.7)
Эксцентрисите́т —
числовая характеристика конического
сечения,
показывающая степень его отклонения
от окружности.
Обычно обозначается “![]() ”
”
или “![]() ”.
”.
Форма
эллипса (мера его “сжатия”)
характеризуется его эксцентриситетом.
 (так
(так
как ![]() ,
,
то![]() )
)
Прямые: 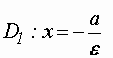 и
и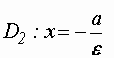 перпендикулярные
перпендикулярные
главной оси и проходящие на расстоянии![]() от
от
центра, называютсядиректрисами эллипса.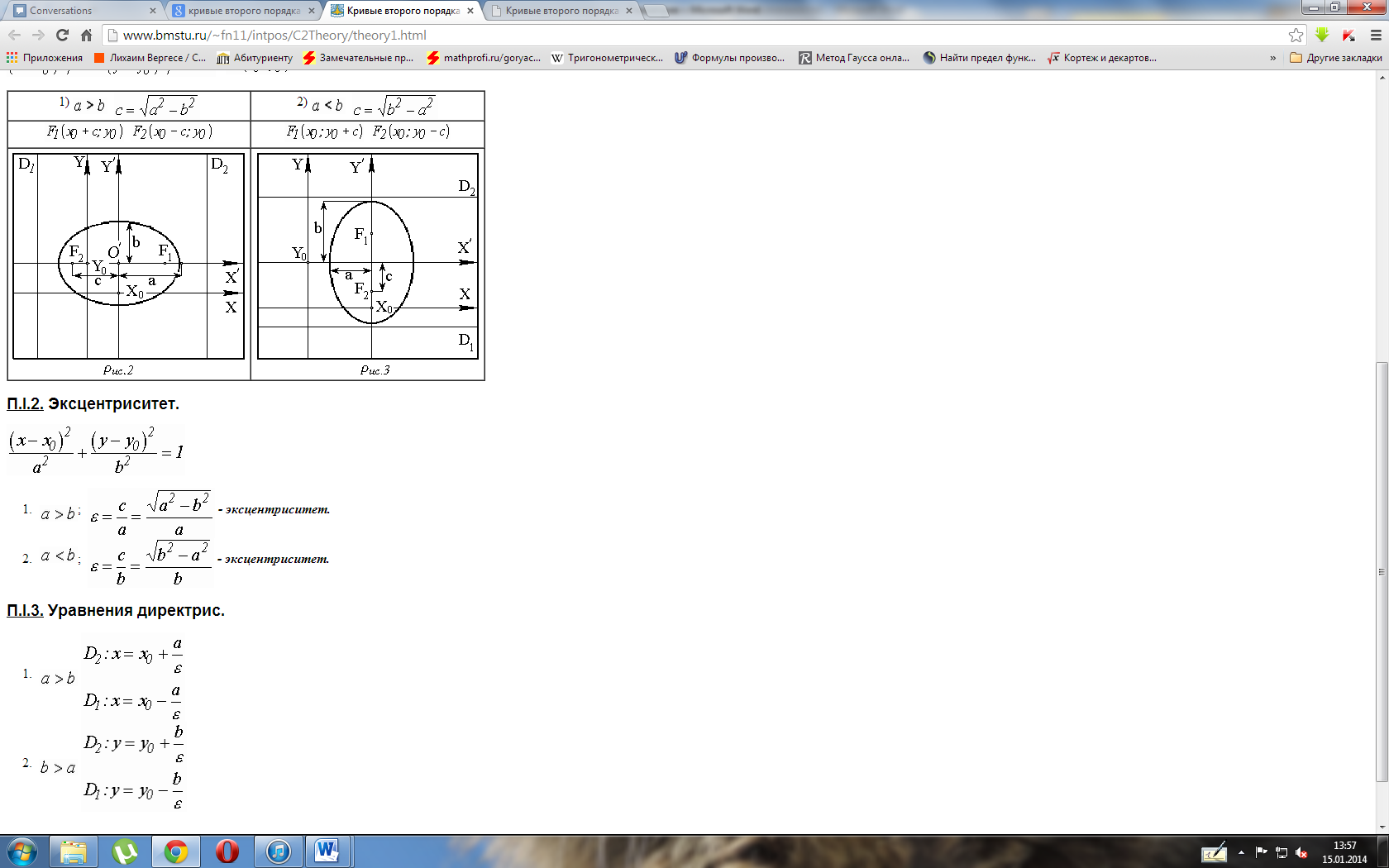
Параметрические уравнения эллипса
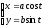
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решать можно в зависимости от уровня знаний и проходимого материала.
Изначально понимаем, что проекция точки, это точка, лежащая в плоскости и прямая проходящая через точку и проекцию точки будет перпендикулярна любой прямой (достаточно двум пресекающимся) из этой плоскости.
А дальше:
Решение 1
Пусть проекция точки P₀ (x₀;y₀;z₀)
Берем любые 2 точки плоскости (удовлетворяют уравнению): Например (0;0;7) и (0;-7;0)
Они образуют вектор a (0-0; 0-(-7); 7-0) = a (0;7;7)
Тогда вектор p = PP₀ (x₀-2;y₀-2;z₀+5) будет перпендикулярен вектору a
А значит скалярное произведение ap = 0
то есть 0•(x₀-2) + 7•(y₀-2) + 7•(z₀+5) = 0
или y₀ + z₀ + 3 = 0
Точно так же нужна вторая прямая, то есть другой вектор плоскости, но неколлинеарный. возьмем еще точку плоскости, например (-4;-1;0) и получим вектор b (0-(-4); -7-(-1); 0-0) = b (4;-6;0) – не коллинеарный a
Так же, скалярное произведение bp = 0
то есть 4•(x₀-2) – 6•(y₀-2) + 0•(z₀+5) = 0
или 2x₀ – 3y₀ + 2 = 0
При этом точка P₀ (x₀;y₀;z₀) лежит в плоскости, а значит удовлетворяет уравнению
3x₀ + 2y₀ – 2z₀ + 14 = 0
Получаем систему из 3 уравнений:
{0x₀ + 1y₀ + 1z₀ = -3
{2x₀ – 3y₀ + 0z₀ = -2
{3x₀ + 2y₀ – 2z₀ = -14
Можно составить матрицу и решить методом Крамера или методом Гаусса. Если эти темы не знаем, то тут простая система в первом уравнении выражаем z₀ = -y₀-3; во втором уравнении выражаем х₀ = 3y₀/2 – 1
И подставив в 3-е
9y₀/2 – 3 + 2y₀ + 2y₀ + 6 = -14
17y₀ = -34
y₀ = -2
тогда х₀ = -2•3/2 – 1 = -4
z₀ = 2 – 3 = -1
Ответ: точка P₀ (-4; -2; -1)
Если нигде арифметически не ошибся. (Все же ошибся (знак перед 14 вначале потерял), но уже исправил)
Решение 2
Состоит в том, что сразу знаем координаты ортогонального (нормаль) вектора к плоскости с уравнением 3x+2y-2z+14=0. Это вектор p (3;2;-2)
Тогда уравнение прямой проходящей через точку P в направлении вектора p:
(x-2)/3 = (y-2)/2 = (z+5)/-2
Отсюда получим несколько равенств
2(x-2) = 3(y-2)
-2(y-2) = 2(z+5)
-2(x-2) = 3(z+5)
Пересечение этой прямой с плоскостью и будет искомой точкой. Значит она удовлетворяет уравнению. 3x+2y-2z+14=0
Можно снова составить систему уравнений и решить её каким либо методом.
Я снова выражу х из (1): 2х-4 = 3y-6 или х = 3y/2 – 1
И выражу z из (2): -2y + 4 = 2z + 10 или z = -y – 3
И теперь это можно подставить в уравнение плоскости.
Но все это я проделал в решении 1 (повторятся не буду)
Ответ: точка P₀ (-4; -2; -1)
