Как найти проекцию точки на плоскость oxy

Проекция точки на плоскость онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку “Решить”.

Проекция точки на плоскость − теория, примеры и решения

Для нахождения проекции точки M₀ на плоскость α, необходимо:

• построить прямую L, проходящую через точку M₀ и ортогональной плоскости α.
• найти пересечение данной плоскости α с прямой L(Рис.1).

Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

Подставляя значение параметра t в выражения (4), находим проекцию M₁ точки M₀ на плоскость (1).

Пример 1.Найти проекцию M₁ точки M₀(4, -3, 2) на плоскость

Решение.

Нормальный вектор плоскости имеет вид:

т.е. A=5, B=1, C=−8.

Координаты точки M₀: x₀=4, y₀=−3, z₀=2.

Подставляя координаты точки M₀ и нормального вектора плоскости в (5), получим:

Из выражений (7) находим:

Ответ:

Проекцией точки M₀(4, -3, 2) на плоскость (6) является точка:

При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.

Уравнение для описания плоскости

Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее – ниже.

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:

A*x + B*y + C*z + D = 0.

Первые три коэффициента – это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.

Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.

Понятие о проекции точки и ее вычисление

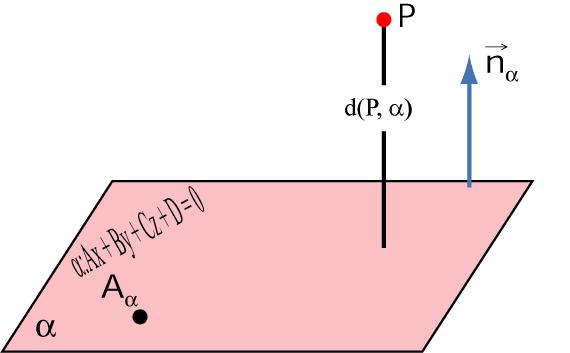
Предположим, что задана некоторая точка P(x₁; y₁; z₁) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x₂; y₂; z₂). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.

Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:

(x; y; z) = (x₁; y₁; z₁) + λ*(A; B; C).

Где λ – действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.

После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.

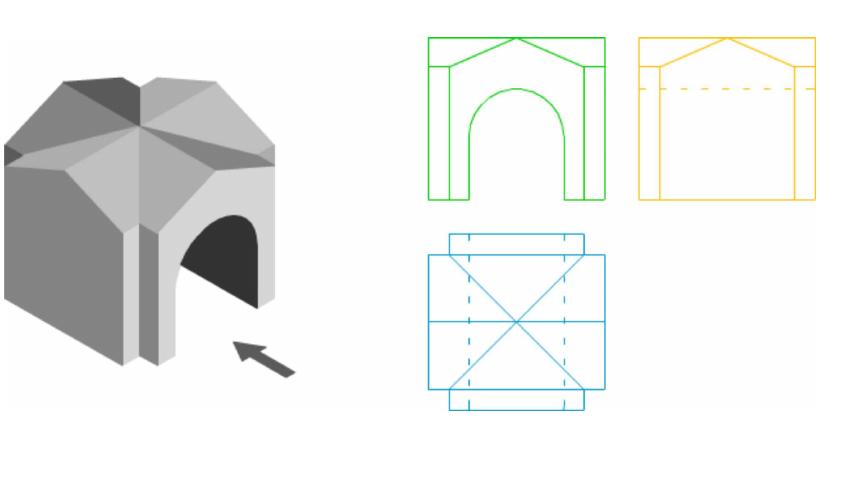
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.

Вычисление расстояния от плоскости до точки

Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:

d = |PQ¯| = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²).

Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.

Пример задачи

Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:

2*x – y + z + 4 = 0.

Следует найти точки проекцию на плоскость и вычислить между ними расстояние.

В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90^o. Имеем:

(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).

Записывая это равенство в явном виде, приходим к следующей системе уравнений:

x = 2*λ;

y = -2 – λ;

z = λ + 3;

2*x – y + z + 4 = 0.

Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:

2*(2*λ) – (-2 – λ) + λ + 3 + 4 = 0 =>

6*λ + 9 = 0 =>

λ = 9/6 = 3/2 = 1,5.

Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:

(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).

Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:

d = √((3 – 0 )² + (-3,5 + 2 )² + (4,5 – 3 )²) = 3,674.

В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.

Комментарии преподавателя

 1. Введение

Если через точку О в про­стран­стве мы про­ве­дем три пер­пен­ди­ку­ляр­ные пря­мые, на­зо­вем их, вы­бе­рем на­прав­ле­ние, обо­зна­чим еди­нич­ные от­рез­ки, то мы по­лу­чим пря­мо­уголь­ную си­сте­му ко­ор­ди­нат в про­стран­стве. Оси ко­ор­ди­нат на­зы­ва­ют­ся так: Ох – ось абс­цисс, Оy – ось ор­ди­нат и Оz – ось ап­пли­кат. Вся си­сте­ма ко­ор­ди­нат обо­зна­ча­ет­ся – Oxyz. Таким об­ра­зом, по­яв­ля­ют­ся три ко­ор­ди­нат­ные плос­ко­сти: Оxy, Оxz, Оyz.

При­ве­дем при­мер по­стро­е­ния точки В(4;3;5) в пря­мо­уголь­ной си­сте­ме ко­ор­ди­нат (см. Рис. 1).

Рис. 1. По­стро­е­ние точки B в про­стран­стве

Пер­вая ко­ор­ди­на­та точки B – 4, по­это­му от­кла­ды­ва­ем на Ox 4, про­во­дим пря­мую па­рал­лель­но оси Oy до пе­ре­се­че­ния с пря­мой, про­хо­дя­щей через у=3. Таким об­ра­зом, мы по­лу­ча­ем точку K. Эта точка лежит в плос­ко­сти Oxy и имеет ко­ор­ди­на­ты K(4;3;0). Те­перь нужно про­ве­сти пря­мую па­рал­лель­но оси Oz. И пря­мую, ко­то­рая про­хо­дит через точку с ап­пли­ка­той 5 и па­рал­лель­на диа­го­на­ли па­рал­ле­ло­грам­ма в плос­ко­сти Oxy. На их пе­ре­се­че­нии мы по­лу­чим ис­ко­мую точку B.

Рас­смот­рим рас­по­ло­же­ние точек, у ко­то­рых одна или две ко­ор­ди­на­ты равны 0 (см. Рис. 2).

Рис. 2.

На­при­мер, точка A(3;-1;0). Нужно про­дол­жить ось Oy влево до зна­че­ния -1, найти точку 3 на оси Ox, и на пе­ре­се­че­нии линий, про­хо­дя­щих через эти зна­че­ния, по­лу­ча­ем точку А. Эта точка имеет ап­пли­ка­ту 0, а зна­чит, она лежит в плос­ко­сти Oxy.

Точка C(0;2;0) имеет абс­цис­су и ап­пли­ка­ту 0 – не от­ме­ча­ем. Ор­ди­на­та равна 2, зна­чит точка C лежит толь­ко на оси Oy, ко­то­рая яв­ля­ет­ся пе­ре­се­че­ни­ем плос­ко­стей Oxy и Oyz.

Чтобы от­ло­жить точку D(-4;0;3) про­дол­жа­ем ось Ox назад за на­ча­ло ко­ор­ди­нат до точки -4. Те­перь вос­ста­нав­ли­ва­ем из этой точки пер­пен­ди­ку­ляр – пря­мую, па­рал­лель­ную оси Oz до пе­ре­се­че­ния с пря­мой, па­рал­лель­ной оси Ox и про­хо­дя­щей через зна­че­ние 3 на оси Oz. По­лу­ча­ем току D(-4;0;3). Так как ор­ди­на­та точки равна 0, зна­чит точка D лежит в плос­ко­сти Oxz.

Сле­ду­ю­щая точка E(0;5;-3). Ор­ди­на­та точки 5, ап­пли­ка­та -3, про­во­дим пря­мые про­хо­дя­щие через эти зна­че­ния на со­от­вет­ству­ю­щих осях, и на их пе­ре­се­че­нии по­лу­ча­ем точку E(0;5;-3). Эта точка имеет первую ко­ор­ди­на­ту 0, зна­чит она лежит в плос­ко­сти Oyz.

 2. Координаты вектора 

На­чер­тим пря­мо­уголь­ную си­сте­му ко­ор­ди­нат в про­стран­стве Oxyz. За­да­дим в про­стран­стве пря­мо­уголь­ную си­сте­му ко­ор­ди­нат Oxyz. На каж­дой из по­ло­жи­тель­ных по­лу­осей от­ло­жим от на­ча­ла ко­ор­ди­нат еди­нич­ный век­тор, т. е. век­тор, длина ко­то­ро­го равна еди­ни­це. Обо­зна­чим еди­нич­ный век­тор оси абс­цисс, еди­нич­ный век­тор оси ор­ди­нат , и еди­нич­ный век­тор оси ап­пли­кат  (см. рис. 1). Эти век­то­ры со­на­прав­ле­ны с на­прав­ле­ни­я­ми осей, имеют еди­нич­ную длину и ор­то­го­наль­ны – по­пар­но пер­пен­ди­ку­ляр­ны. Такие век­то­ра на­зы­ва­ют ко­ор­ди­нат­ны­ми век­то­ра­ми или ба­зи­сом.

Рис. 1. Раз­ло­же­ние век­то­ра по трем ко­ор­ди­нат­ным век­то­рам

Возь­мем век­тор , по­ме­стим его в на­ча­ло ко­ор­ди­нат, и раз­ло­жим этот век­тор по трем неком­пла­нар­ным – ле­жа­щим в раз­ных плос­ко­стях –  век­то­рам. Для этого опу­стим про­ек­цию точки M на плос­кость Oxy, и най­дем ко­ор­ди­на­ты век­то­ров ,  и . По­лу­ча­ем: . Рас­смот­рим по от­дель­но­сти каж­дый из этих век­то­ров. Век­тор  лежит на оси Ox, зна­чит, со­глас­но свой­ству умно­же­ния век­то­ра на число, его можно пред­ста­вить как ка­кое-то число x умно­жен­ное на ко­ор­ди­нат­ный век­тор . , а длина век­то­ра ровно в x раз боль­ше длины . Так же по­сту­пим и с век­то­ра­ми  и , и по­лу­ча­ем раз­ло­же­ние век­то­ра по трем ко­ор­ди­нат­ным век­то­рам:

Ко­эф­фи­ци­ен­ты этого раз­ло­же­ния x, y и z на­зы­ва­ют­ся ко­ор­ди­на­та­ми век­то­ра в про­стран­стве.

Рас­смот­рим пра­ви­ла, ко­то­рые поз­во­ля­ют по ко­ор­ди­на­там дан­ных век­то­ров найти ко­ор­ди­на­ты их суммы и раз­но­сти, а также ко­ор­ди­на­ты про­из­ве­де­ния дан­но­го век­то­ра на дан­ное число.

;  

1) Сло­же­ние: 

2) Вы­чи­та­ние:  

3) Умно­же­ние на число: , 

Век­тор, на­ча­ло ко­то­ро­го сов­па­да­ет с на­ча­лом ко­ор­ди­нат, на­зы­ва­ет­ся ра­ди­ус–век­то­ром. (Рис. 2). Век­тор – ра­ди­ус-век­тор, где x, y и z – это ко­эф­фи­ци­ен­ты раз­ло­же­ния этого век­то­ра  по ко­ор­ди­нат­ным век­то­рам , , . В дан­ном слу­чае x – это пер­вая ко­ор­ди­на­та точки A на оси Ox, y – ко­ор­ди­на­та точки B на оси Oy, z – ко­ор­ди­на­та точки C на оси Oz. По ри­сун­ку видно, что ко­ор­ди­на­ты ра­ди­ус-век­то­ра од­но­вре­мен­но яв­ля­ют­ся ко­ор­ди­на­та­ми точки М.

Рис. 2.

Возь­мем точку A(x1;y1;z1) и точку B(x2;y2;z2) (см. рис. 3). Пред­ста­вим век­тор как раз­ность век­то­ров  и по свой­ству век­то­ров. При­чем,  и – ра­ди­ус-век­то­ры, и их ко­ор­ди­на­ты сов­па­да­ют с ко­ор­ди­на­та­ми кон­цов этих век­то­ров. Тогда мы можем пред­ста­вить ко­ор­ди­на­ты век­то­ра  как раз­ность со­от­вет­ству­ю­щих ко­ор­ди­нат век­то­ров  и : . Таким об­ра­зом, ко­ор­ди­на­ты век­то­ра мы можем вы­ра­зить через ко­ор­ди­на­ты конца и на­ча­ла век­то­ра.

Рис. 3.

Рас­смот­рим при­ме­ры, ил­лю­стри­ру­ю­щие свой­ства век­то­ров и их вы­ра­же­ние через ко­ор­ди­на­ты. Возь­мем век­то­ры , , . Нас спра­ши­ва­ют век­тор . В дан­ном слу­чае найти  это зна­чит найти ко­ор­ди­на­ты век­то­ра , ко­то­рые пол­но­стью его опре­де­ля­ют. Под­став­ля­ем в вы­ра­же­ние вме­сто век­то­ров со­от­вет­ствен­но их ко­ор­ди­на­ты. По­лу­ча­ем:

Те­перь умно­жа­ем число 3 на каж­дую ко­ор­ди­на­ту в скоб­ках, и то же самое де­ла­ем с 2:

У нас по­лу­чи­лась сумма трех век­то­ров, скла­ды­ва­ем их по изу­чен­но­му выше свой­ству:

Ответ: 

При­мер №2.

Дано: Тре­уголь­ная пи­ра­ми­да AOBC (см. рис. 4). Плос­ко­сти AOB, AOC и OCB – по­пар­но пер­пен­ди­ку­ляр­ны. OA=3, OB=7, OC=4; M – сер.AC; N – сер.OC; P – сер. CB.

Найти: ,,,,,,,.

Рис. 4.

Ре­ше­ние: Вве­дем пря­мо­уголь­ную си­сте­му ко­ор­ди­нат Oxyz с на­ча­лом от­сче­та в точке O. По усло­вию обо­зна­ча­ем точки A, B и C на осях и се­ре­ди­ны ребер пи­ра­ми­ды – M, P и N. По ри­сун­ку на­хо­дим ко­ор­ди­на­ты вер­шин пи­ра­ми­ды: A(3;0;0), B(0;7;0), C(0;0;4).

Так как ко­ор­ди­на­ты век­то­ра  –  это раз­ность ко­ор­ди­нат его конца и на­ча­ла, по­лу­ча­ем:. Таким же об­ра­зом на­хо­дим ко­ор­ди­на­ты век­то­ров и . ; .

Чтобы найти ко­ор­ди­на­ты век­то­ра , нужно сна­ча­ла найти ко­ор­ди­на­ты точек M и N. По ри­сун­ку видно, что точка N имеет ко­ор­ди­на­ты, так как она лежит на оси ап­пли­кат. Рас­смот­рим . MN – сред­няя линия, . Зна­чит ко­ор­ди­на­та точки M по оси Oz 2. Те­перь про­ве­дем из точки M пер­пен­ди­ку­ляр к оси Ox, ко­ор­ди­на­та 1,5. Точка M лежит в плос­ко­сти Oxz, зна­чит по оси Oy ко­ор­ди­на­та 0. По­лу­ча­ем M(1,5;0;2). Те­перь зная ко­ор­ди­на­ты точек M и N, счи­та­ем их раз­ность: .

Те­перь най­дем ко­ор­ди­на­ты точки P. Опу­стим пер­пен­ди­ку­ляр на плос­кость Oxy, по­лу­ча­ем зна­че­ние 3,5 по оси ор­ди­нат. И про­ве­дя пер­пен­ди­ку­ляр к оси Oz, по­лу­ча­ем зна­че­ние 2 по оси ап­пли­кат. Точка P имеет ко­ор­ди­на­ты (0;3,5;2). Зная ко­ор­ди­на­ты нуж­ных точек, най­дем ко­ор­ди­на­ты остав­ших­ся век­то­ров.

;

.

Век­то­ра  и  – ра­ди­ус-век­то­ры, зна­чит, их ко­ор­ди­на­ты равны ко­ор­ди­на­там кон­цов этих век­то­ров: , .

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/pryamougolnaya-sistema-koordinat-v-prostranstve?seconds=0&chapter_id=218

http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/koordinaty-vektora-2

http://www.youtube.com/watch?v=I1ls2_8OC7o

http://900igr.net/fotografii/geometrija/Prjamougolnaja-sistema-koordinat/006-Nachalo-koordinat.html

http://www.yaklass.ru/materiali?mode=lsntheme&themeid=101

http://900igr.net/fotografii/geometrija/Prjamougolnaja-sistema-koordinat-v-prostranstve/Prjamougolnaja-sistema-koordinat-v-prostranstve.html

1


Сферические координаты Пусть A – точка в пространстве с заданной системой координат. Ортогональную проекцию точки A на плоскость Oxy обозначим A’, а длину вектора ОA – через r. Угол наклона вектора к плоскости Оxy обозначим ψ, причем будем считать его изменяющимся от -90 o до +90 o. Если точка A расположена в верхнем полупространстве, то угол ψ считается положительным, а если в нижнем, то отрицательным. Угол между вектором и осью Ox обозначим φ. Тройка (r, ψ, φ) называется сферическими координатами точки A в пространстве.

2


Сферические координаты Декартовы координаты (x,y,z) точки в пространстве выражаются через ее сферические координаты по формулам и, наоборот, если заданы декартовы координаты, то по ним можно найти сферические координаты по формулам

3


Сферические координаты Точки на сфере, имеющие одинаковый угол ψ, образуют окружность, которая называется параллелью. Точки, имеющие одинаковый угол φ, образуют полуокружность, называемую меридианом. Дуга большой окружности, соединяющая две точки сферы, является кратчайшим путем на сфере между этими двумя точками. Такой путь называют ортодромией, что в переводе с греческого означает “прямой бег”. Кривая, образующая равные углы с разными меридианами, называется локсодромия, что в переводе с греческого означает “косой бег”.

4


Упражнение 1 Найдите декартовы координаты следующих точек пространства, заданных своими сферическими координатами: (1, 45°, 120°), (2, -30°, -90°), (1, 90°, 60°). Ответ:

5


Упражнение 2 Найдите сферические координаты следующих точек пространства, заданных своими декартовыми координатами: а) A(1, 1, 1); б) B(-1, 0, 1); в) C(0, 0, 2). Ответ: A: B(, 45 о, 180 о ); C(2, 90 о, 0 о ).

6


Упражнение 3 Найдите сферические координаты вершин куба, задаваемого в декартовых координатах системой неравенств Ответ: (0, 0 о, 0 о ); (1, 0 о, 0 о ); (,0 о, 45 о ); (1, 0 о, 90 о ); (1, 90 о, 0 о ); (, 45 о, 0 о ); (,, ), sin =, sin = ; (, 45 о, 90 о ).

7


Упражнение 4 Точка A имеет сферические координаты (r,, ). Найдите сферические координаты точки, симметричной данной, относительно: а) координатных плоскостей; б) осей координат; в) начала координат. Ответ: а) (r, -, ), (r,, 180 о – ), (r,, – ); б) (r, -, – ), (r, -, 180 о – ), (r,, 180 о + ); в) (r, -, 180 о + ).

8


Упражнение 5 Найдите геометрическое место точек пространства, сферические координаты которых удовлетворяют условиям: а) r постоянно; б) постоянно; в) постоянно. Ответ: а) Сфера; б) коническая поверхность; в) полуплоскость.

9


Упражнение 6 Какая фигура в пространстве задается неравенствами: а) 0 r 1, 0 ; б) 0 r 1, 0 ; в) 0 r 1, 0, 0 ? Ответ: а) Полушар; б) полушар; в) четверть шара.

10


Упражнение 7 Найдите расстояние между точками, заданными своими сферическими координатами: A(, 0°, 45°), B(2, 60°, 0°). Ответ: 2.

11


Упражнение 8 Где закончится локсодромия, образующая острый угол с меридианами, при ее продолжении в обе стороны? Ответ: На полюсах.

12


Упражнение 9 Напишите уравнение сферы в сферических координатах Ответ: r = 1.

13


Упражнение 10 Найдите длины дуг локсодромии и ортодромии, соединяющих точки A 1 (R, 45°, 0°), A 2 (R, 45°, 180°) на сфере. Ответ: