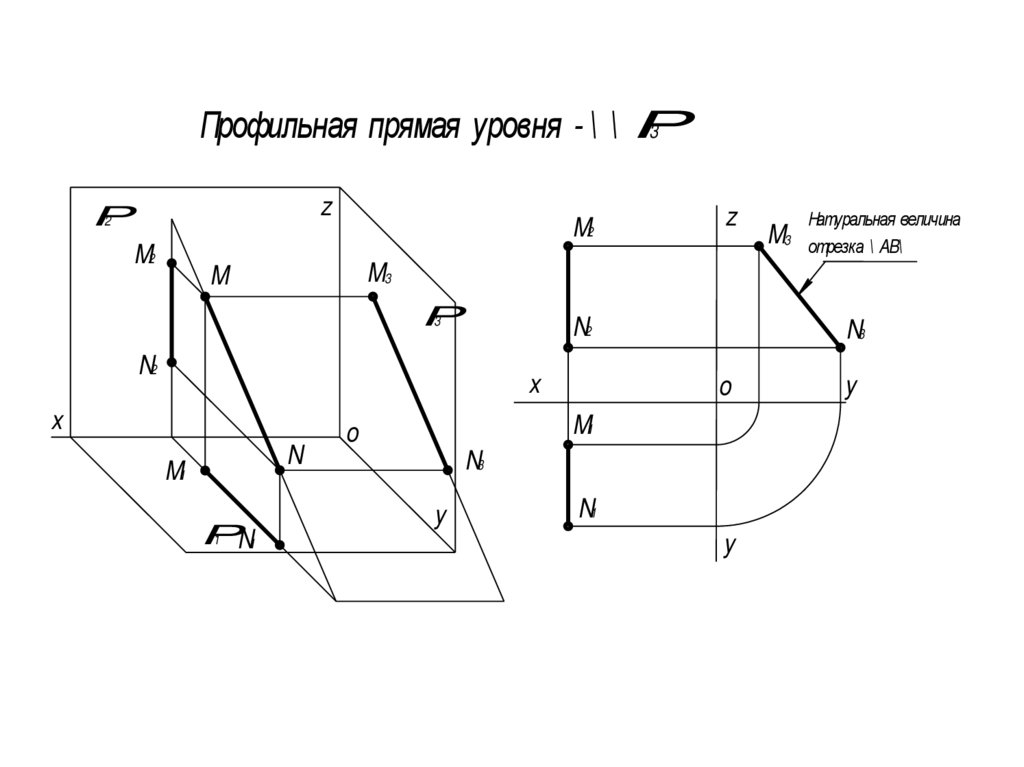
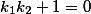Проекция точки на прямую онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку “Решить”.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на прямую − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1. Пусть в двухмерном пространстве задана точка M0(x0, y0) и прямая L:
где q=(m,p) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (1)(Рис.1).
Алгоритм нахождения проекции точки на прямую L содержит следующие шаги:
- построить прямую L1, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение прямых L и L1(точка M1)
Уравнение прямой, проходящей через точку M0(x0, y0) имеет следующий вид:
где n=(A,B) нормальный вектор прямой L1.
Как видно из рисунка Рис.1, для того, чтобы прямая L1 была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L1, поэтому в качестве нормального вектора прямой L1 достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L1, представленной уравнением (2) можно записать так:
Откроем скобки
Для нахождения точки пересечения прямых L и L1, которая и будет проекцией точки M0 на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M1(x1, y1).
Найдем точку пересечения прямых L и L1 другим методом.
Выведем параметрическое уравнение прямой (1):
Подставим значения x и y в (4):
Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L1(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’.
Пример 1. Найти проекцию точки M0(1, 3) на прямую
Решение.
Направляющий вектор прямой (6) имеет вид:
Т.е. m=4, p=5. Из уравнения прямой (6) видно, что она проходит через точку M’ (x’, y’)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x’=2, y’=-3. Подставим значения m, p, x0, y0, x’, y’ в (5′):
Подставляя значение t в (5), получим:
Ответ:
Проекцией точки M0(1, 3) на прямую (6) является точка:
2. Пусть в трехмерном пространстве задана точка M0(x0, y0, z0) и прямая L:
где q=(m, p, l) направляющий вектор прямой L.
Найдем проекцию точки M0 на прямую (7)(Рис.2).
Нахождение проекцию точки на прямую L содержит следующие шаги:
- построить плоскость α, проходящую через точку M0 и перпендикулярную прямой L,
- найти пересечение плоскости α и прямой L(точка M1)
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) имеет следующий вид:
где n=(A,B,C) нормальный вектор плоскости α.
Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (8) можно записать так:
Откроем скобки
Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M0 на прямую L, выведем параметрическое уравнение прямой (7):
Подставим значения x и y в (9):
Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (9). Следовательно, подставляя значение t’ в (10) получим координаты проекции точки M0 на прямую L:
где x1=mt’+x’, y1=pt’+y’, z1=lt’+z’.
Пример 2. Найти проекцию точки M0(3, −1, −2) на прямую
Решение.
Направляющий вектор прямой (11) имеет вид:
Т.е. m=2, p=3, l=−4. Из уравнения прямой (11) видно, что она проходит через точку M’ (x’, y’, z’)=(2, 1, 1)(в этом легко убедится − подставляя эти значения в (11) получим тождество 0=0=0), т.е. x’=2, y’=1, z’=1. Подставим значения m, p, l x0, y0, z0 x’, y’, z’ в (10′):
Подставляя значение t=t’ в (10), получим:
Ответ:
Проекцией точки M0(3, −1, −2) на прямую (11) является точка:
Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.
Проекция точки на прямую, определение
В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.
Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.
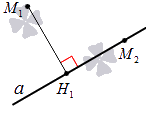
Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.
Рассмотрим рисунок ниже: точка H1 служит проекцией точки М1 на прямую a, а точка М2, принадлежащая прямой, является проекцией сама себя.
Данное определение верно для случая на плоскости и в трехмерном пространстве.
Чтобы на плоскости получить проекцию точки М1 на прямую a, проводится прямая b, проходящая через заданную точку M1 и перпендикулярная прямой a. Таким образом, точка пересечения прямых a и b будет проекцией точки М1 на прямую a.
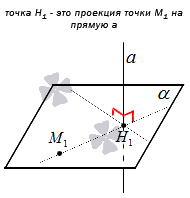
В трехмерном пространстве проекцией точки на прямую будет служить точка пересечения прямой a и плоскости α, проходящей через точку М1 и перпендикулярной прямой a.
Нахождение координат проекции точки на прямую
Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.
Пусть нам заданы прямоугольная система координат Oxy, точка М1(x1, y1) и прямая a. Необходимо найти координаты проекции точки М1 на прямую a.
Проложим через заданную точку М1(x1, y1) прямую b перпендикулярно прямой a. Точку пересечения маркируем как H1. Точка Н1 будет являться точкой проекции точки М1 на прямую a.
Из описанного построения можно сформулировать алгоритм, который позволяет находить координаты проекции точки М1(x1, y1) на прямую a:
– составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;
– записываем уравнение прямой b (проходящей через точку М1 и перпендикулярной прямой a). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;
– определяем искомые координаты проекции как координаты точки пересечения прямых a и b. Для этого решаем систему уравнений, составляющие которой – уравнения прямых a и b.
На плоскости Oxy заданы точки М1(1, 0) и прямая a (общее уравнение – 3x + y + 7 = 0). Необходимо определить координаты проекции точки М1 на прямую a.
Решение
Уравнение заданной прямой известно, поэтому, согласно алгоритму, переходим к шагу записи уравнения прямой b. Прямая b перпендикулярна прямой a, а значит нормальный вектор прямой a служит направляющим вектором прямой b. Тогда направляющий вектор прямой b запишем как b→=(3, 1). Запишем и каноническое уравнение прямой b, поскольку нам также заданы координаты точки М1, через которую проходит прямая b:
x-13=y1
Заключительным шагом определяем координаты точки пересечения прямых a и b. Перейдем от канонических уравнений прямой b к общему ее уравнению:
x-13=y1⇔1·(x-1)=3·y⇔x-3y-1=0
Составим систему уравнений из общих уравнений прямых a и b и решим ее:
3x+y+7=0x-3y-1=0⇔y=-3x-7x-3y-1=0⇔y=-3x-7x-3·(-3x-7)-1=0⇔⇔y=-3x-7x=-2⇔y=-3·(-2)-7x=-2⇔y=-1x=-2
В конечном итоге мы получили координаты проекции точки М1(1, 0) на прямую 3x + y + 7 = 0: (-2,-1).
Ответ: (-2, -1).
Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.
Пусть заданы координатные прямые Ox и Oy, а также точка М1(x1, y1). Понятно, что проекцией заданной точки на координатную прямую Ox вида y = 0 будет точка с координатами (x1, 0). Так и проекция заданной точки на координатную прямую Oy будет иметь координаты 0, y1.
Любую произвольную прямую, параллельную оси абсцисс, возможно задать неполным общим уравнением By+C=0⇔y=-CB, а прямую, параллельную оси ординат – Ax+C=0⇔x=-CA.
Тогда проекциями точки М1(x1, y1) на прямые y=-CB и x=-CAстанут точки с координатами x1, -CB и -CA, y1.
Определите координаты проекции точки М1(7, -5) на координатную прямую Oy, а также на прямую, параллельную прямой Oy 2y-3=0.
Решение
Запишем координаты проекции заданной точки на прямую Oy: (0, -5).
Запишем уравнение прямой 2y-3=0 в виде y=32. Становится видно, что проекция заданной точки на прямую y=32 будет иметь координаты 7, 32 .
Ответ: (0, -5) и 7, 32 .
Пусть в трехмерном пространстве заданы прямоугольная система координат Oxyz, точка М1(x1, y1, z1) и прямая a. Найдем координаты проекции точки М1 на прямую a.
Построим плоскость α, проходящую через точку М1 и перпендикулярную прямой a. Проекцией заданной точки на прямую a станет точка пересечения прямой a и плоскости α. Исходя из этого, приведем алгоритм для нахождения координат проекции точки М1(x1, y1, z1) на прямую a:
– запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;
– составим уравнение плоскости α, проходящей через точку М1 и перпендикулярной прямой a (см. статью «Уравнение плоскости, проходящей через заданную точку перпендикулярно заданной прямой»);
– найдем искомые координаты проекции точки М1(x1, y1, z1) на прямую a – это будут координаты точки пересечения прямой α и плоскости α (в помощь – статья «Координаты точки пересечения прямой и плоскости»).
Задана прямоугольная система координат Oxyz, и в ней – точка М1(0, 1, -1) и прямая a. Прямой a соответствуют канонические уравнения вида: x+23=y-6-4=z+11. Определите координаты проекции точки М1 на прямую a.
Решение
Используем указанный выше алгоритм. Уравнения прямой a известны, поэтому первый шаг алгоритма пропускаем. Запишем уравнение плоскости α. Для этого определим координаты нормального вектора плоскости α. Из заданных канонических уравнений прямой a выделим координаты направляющего вектора этой прямой: (3, -4, 1), который будет являться нормальным вектором плоскости α, перпендикулярной прямой a. Тогда n→ = (3, -4, 1) – нормальный вектор плоскости α. Таким образом, уравнение плоскости α будет иметь вид:
3·(x-0)-4·(y-1)+1·(z-(-1))=0⇔3x-4y+z+5=0
Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:
- Заданные канонические уравнения позволяют получить уравнения двух пересекающихся плоскостей, определяющих прямую a:
x+23=y-6-4=z+11⇔-4·(x+2)=3·(y-6)1·(x+2)=3·(z+1)1·(y-6)=-4·(z+1)⇔4x+3y-10=0x-3z-1=0
Чтобы найти точки пересечения прямой 4x+3y-10=0x-3z-1=0 и плоскости 3x-4y+z+5=0 , решим систему уравнений:
4x+3y-10=0x-3z-1=03x-4y+z+5=0⇔4x+3y=10x-3z=13x-4y+z=-5
В данном случае используем метод Крамера, но возможно применить любой удобный:
∆=43010-33-41=-78∆x=103010-3-5-41=-78⇒x=∆x∆=-78-78=1∆y=410011-33-51=-156⇒y=∆y∆=-156-78=2∆z=43101013-4-5=0⇒z=∆z∆=0-78=0
Таким образом, проекцией заданной точки на прямую a является точка cкоординатами (1, 2, 0)
- На основе заданных канонических уравнений легко записать параметрические уравнения прямой в пространстве:
x+23=y-6-4=z+11⇔x=-2+3·λy=6-4·λz=-1+λ
Подставим в уравнение плоскости, имеющее вид 3x-4y+z+5=0, вместо x, y и z их выражения через параметр:
3·(-2+3·λ)-4·(6-4·λ)+(-1+λ)+5=0⇔26·λ=0⇔λ=1
Вычислим искомые координаты точки пересечения прямой a и плоскости αпо параметрическим уравнениям прямой a при λ = 1:
x=-2+3·1y=6-4·1z=-1+1⇔x=1y=2z=0
Таким образом, проекция заданной точки на прямую a имеет координаты (1, 2, 0)
Ответ: (1, 2, 0)
Напоследок отметим, что проекциями точки М1(x1, y1, z1) на координатные прямые Ox, Oy и Oz буду являться точки с координатами (x1, 0, 0), (0, y1, 0) и (0, 0, z1) соответственно.
Проекция точки на прямую
| Координаты проекции точки на прямую |
Он лайн решение нахождения проекциии точки на прямую.
Проеция заданной точки А на прямую, это такая точка Б на прямой, что новая прямая, проходящая через точки А и Б, пересекает заданную под прямым углом.
Такое определение, непохоже, на стандартное, но тем не менее дает понимание как эту точку находить.
Для этого Вам надо знать всего одно правило.
Прямая y1=k1x+a1 которая пересекает другую прямую y2=k2x+a2 под прямым углом имеет соответствие
Таким образом зная уравнение одной прямой, находим k1 после чего находим k2 и уравнение второй прямой.
Точка пересечения этих двух прямых и будет является точкой проеции.
Как находить точку пересечения двух прямых? ну хотя бы как решение системы линейных уравнений.
Кто то скажет, есть другой путь, и проще и лучше.
Возможно. Я лишь пытаюсь рассказать что обладая отнюдь не энциклопедическими знаниями, и не запоминая “еще одну” формулу, вполне решать самые разнообразные задачи.
Онлайн калькулятор: Системы координат в пространстве
УчебаМатематикаГеометрия
Преобразование координат из / в декартову, цилиндрическую и сферическую систему координат.
Этот калькулятор предназначен для преобразования координат в пространстве, заданных в трех системах:
- Прямоугольной (декартовой)
- Цилиндрической
- Сферической
Прямоугольная, цилиндрическая и сферическая системы координат
Прямоугольная система координат
Определяет точку в пространстве при помощи трех чисел : x, y, z. Каждое число соответствует длине кратчайшего отрезка, проложенного параллельно одноименной оси координат до плоскости, образованной другими осями координат. Длина берется со знаком минус, если точка находится со стороны отрицательных значений шкалы координат.
Цилндрическая система координат
Определяет точку в пространстве при помощи радиуса r, угла азимута φ, и высоты z. Высота z соответствует координате z в прямоугольной системе координат. Радиус r — всегда неотрицательное число, задающее минимальное расстояние от точки в пространстве до оси z. Азимутальный угол φ — значение в диапазоне 0 ..360 градусов — определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.
Сферическая система координат
Определяет точку в пространстве при помощи радиуса ρ, азимута φ, и полярного угла θ. Азимут φ совпадает со значением азимута в цилиндрических координатах. Радиус ρ — расстояние от центра координат, до точки. Полярный угол образован положительной полуосью z и радиусом из центра координат до точки в пространстве.
Прямоугольные координаты в пространстве
Точность вычисления
Знаков после запятой: 2
Цилиндрические координаты
Радиус (r)
Азимут (φ), градусы
Высота (z)
Сферические координаты
Радиус (ρ)
Азимут (φ), градусы
Полярный угол (θ), градусы
Формулы преобразования декартовых координат
Радиус в цилиндрической системе:
Радиус в сферической системе:
Азимут:
, см Арктангенс с двумя аргументами
Полярный угол:
Цилиндрические координаты
Радиус (r)
Азимут (φ), градусы
Высота (z)
Точность вычисления
Знаков после запятой: 2
Прямоугольные координаты
Сферические координаты
Радиус (ρ)
Азимут (φ), градусы
Полярный угол (θ), градусы
Формулы преобразования цилиндрических координат
Декартовы координаты:
,
Радиус в сферической системе:
Полярный угол:
, см Арктангенс с двумя аргументами
Сферические координаты
Радиус (ρ)
Азимут (φ), градусы
Полярный угол (θ), градусы
Точность вычисления
Знаков после запятой: 2
Прямоугольные координаты
Цилиндрические координаты
Радиус (r)
Азимут (φ), градусы
Высота (z)
Формулы преобразования сферических координат
Декартовы координаты:
,
,
Радиус в цилиндрической системе:
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Переход между плоскими прямоугольными координатами Гаусса и географическими координатами и обратно
- • Прямоугольная и полярная система координат на плоскости
- • Площадь треугольника по координатам вершин
- • Расстояние между двумя координатами
- • Расчет длины отрезка и координат середины отрезка по двум точкам
- • Раздел: Геометрия ( 95 калькуляторов )
#геометрия #координаты 3d Геометрия декартовы координаты конверторы координаты Математика система координат Системы координат сферические координаты цилиндрические координаты
PLANETCALC, Системы координат в пространстве
Anton2020-11-03 14:19:36
Ортогональная проекция точки м на прямую.
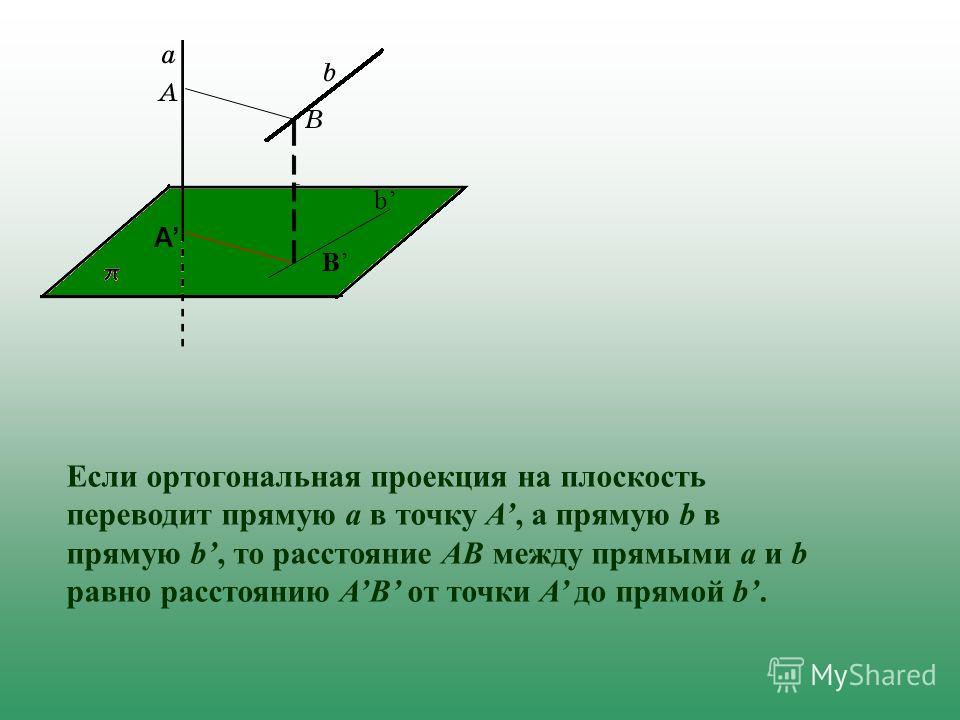
С помощю этого онлайн калькулятора можно найти проекцию точки на прямую. Дается подробное решение с пояснениями. Для вычисления проекции точки на прямую, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точки и элементы уравнения в ячейки и нажимайте на кнопку «Решить».
×
Предупреждение
Очистить все ячейки?
Закрыть
Очистить
Инструкция ввода данных.
Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на прямую − теория, примеры и решения
Рассмотрим эту задачу в двухмерном и трехмерном пространствах.
1.
Пусть в двухмерном пространстве задана точка M
0 (x
0 , y
0) и прямая L
:
Алгоритм нахождения проекции точки на прямую L
содержит следующие шаги:
- построить прямую L
1 , проходящую через точку M
0 и перпендикулярную прямой L
, - найти пересечение прямых L
и L
1 (точка M
1)
Уравнение прямой, проходящей через точку M
0 (x
0 , y
0) имеет следующий вид:
Откроем скобки
Подставим значения x
и y
в (4):
где x
1 =mt»
+x»
, y
1 =pt»
+y»
.
Пример 1.
Найти проекцию точки M
0 (1, 3) на прямую
Т.е. m
=4, p
=5. Из уравнения прямой (6) видно, что она проходит через точку M»
(x»
, y»
)=(2, −3)(в этом легко убедится − подставляя эти значения в (6) получим тождество 0=0), т.е. x»
=2, y»
=-3. Подставим значения m, p, x
0 , y
0 , x», y»
в (5″):
2.
Пусть в трехмерном пространстве задана точка M
0 (x
0 , y
0 , z
0) и прямая L
:
Нахождение проекцию точки на прямую L
содержит следующие шаги:
- построить плоскость α
, проходящую через точку M
0 и перпендикулярную прямой L
, - найти пересечение плоскости α
и прямой L
(точка M
1)
Уравнение плоскости, проходящей через точку M
0 (x
0 , y
0 , z
0) имеет следующий вид:
Откроем скобки
Подставим значения x
и y
в (9):
| m (mt +x» )+p (pt +y» )+l (lt +z» )−m x 0 −p y 0 −l z 0 =0 |
| m 2 t +mx» +p 2 t +py» +l 2 t +ly» −m x 0 −p y 0 −l z 0 =0 |
Проекция точки на прямую линию находится достаточно просто и при выполнении некоторых операций нулевое приближение вычисляется как проекция точки на касательную прямую.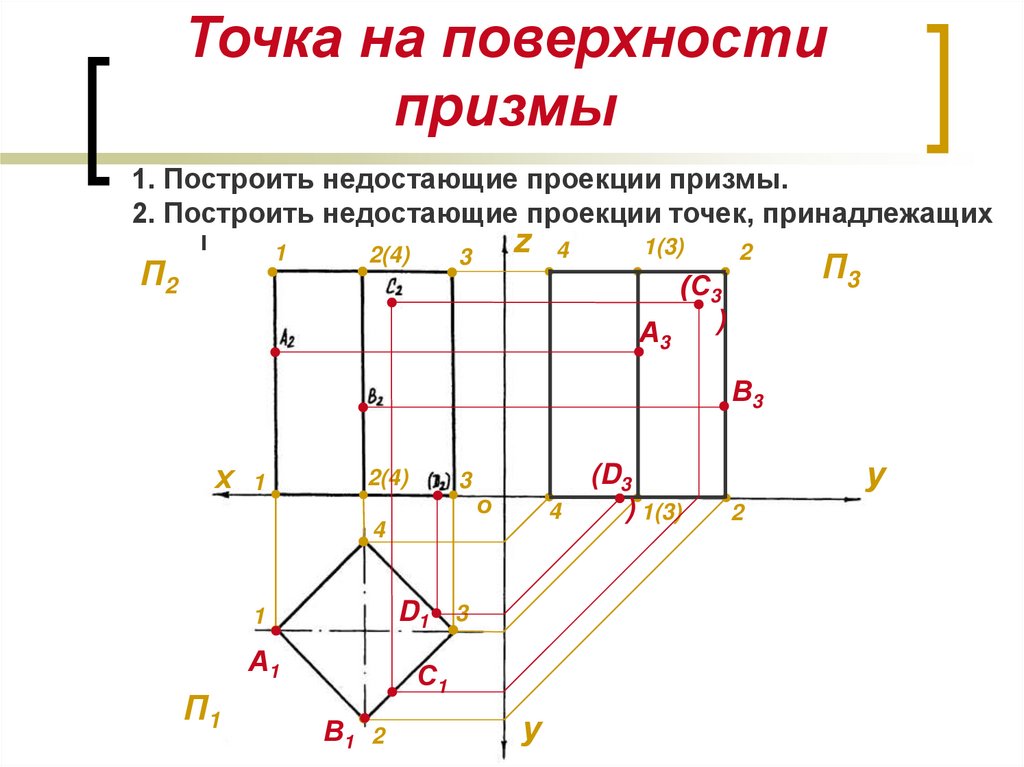
Пусть дана прямая
и точка . Будем считать, что вектор прямой w имеет произвольную длину. Прямая линия проходит через точку , в которой параметр t равен нулю, и имеет направление вектора w. Требуется найти проекцию точки на прямую линию . Эта задача имеет единственное решение. Построим вектор из точки прямой в точку и вычислим скалярное произведение этого вектора и вектора прямой w. На рис. 4.5.1 показаны направляющий вектор прямой w, ее начальная точка Со и проекция ; заданной точки. Если разделим это скалярное произведение на длину вектора w, то получим длину проекции вектора на прямую линию.
Рис. 4.5.1. Проекция точки на прямую линию
Если же разделим это скалярное произведение на квадрат длины вектора w, то получим длину проекции вектора на прямую в единицах длины вектора w, т. е. получим параметр t для проекции точки на прямую линию.
Таким образом, параметр проекции точки на прямую линию и радиус-вектор проекции ; вычисляются по формулам
(4.
Если длина вектора w равна единице, то в (4.5.2) не требуется выполнять деление на Расстояние от точки до ее проекции на кривую в общем случае вычисляется как длина вектора . Расстояние от точки до ее проекции на прямую линию можно определить, не вычисляя проекцию точки, а воспользовавшись формулой
Частные случаи.
Проекция точки на аналитические кривые также может быть найдена без привлечения численных методов. Например, чтобы найти проекцию точки на коническое сечение, нужно перевести проецируемую точку в местную систему координат конического сечения, спроецировать эту точку на плоскость конического сечения и найти параметр двухмерной проекции заданной точки.
Общий случай.
Пусть требуется найти все проекции точки на кривую линию Каждая искомая точка кривой удовлетворяет уравнению
(4.5.5)
Это уравнение содержит одну неизвестную величину — параметр t. Как было уже сказано, решение этой задачи разобьем на два этапа. На первом этапе определим нулевые приближения параметров проекций точки на кривую, а на втором этапе найдем точные значения параметров кривой, определяющие проекции заданной точки на кривую линию с
В этой статье сначала дано определение проекции точки на прямую (на ось) и приведен поясняющий рисунок.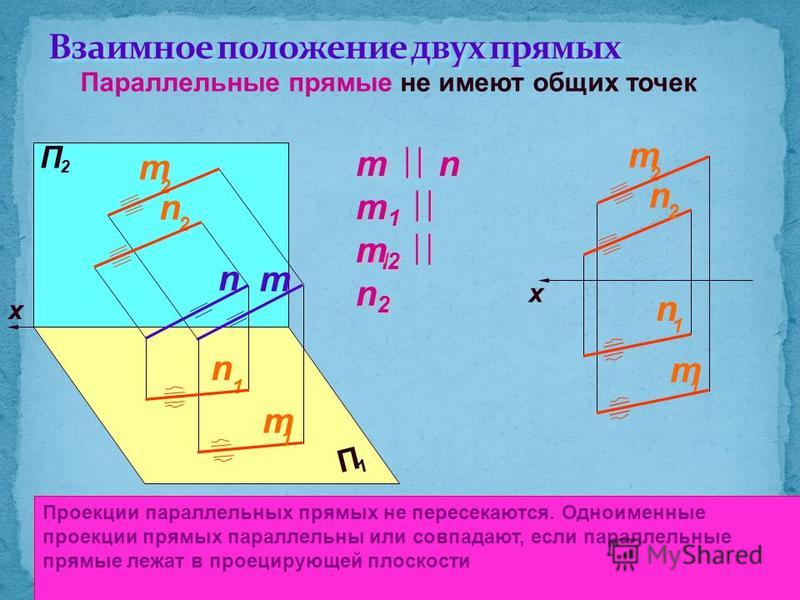
Навигация по странице.
Проекция точки на прямую – определение.
Так как все геометрические фигуры состоят из точек, а проекция фигуры представляет собой множество проекций всех точек этой фигуры, то для проецирования фигуры на прямую необходимо уметь проецировать точки этой фигуры на данную прямую.
Так что же называют проекцией точки на прямую?
Определение.
Проекция точки на прямую
– это либо сама точка, если она лежит на данной прямой, либо основание перпендикуляра, опущенного из этой точки на заданную прямую.
На приведенном ниже рисунке точка H 1
является проекцией точки M 1
на прямую a
, а точка M 2
есть проекция самой точки М 2
на прямую a
, так как М 2
лежит на прямой a
.
Это определение проекции точки на прямую справедливо как для случая на плоскости, так и для случая в трехмерном пространстве.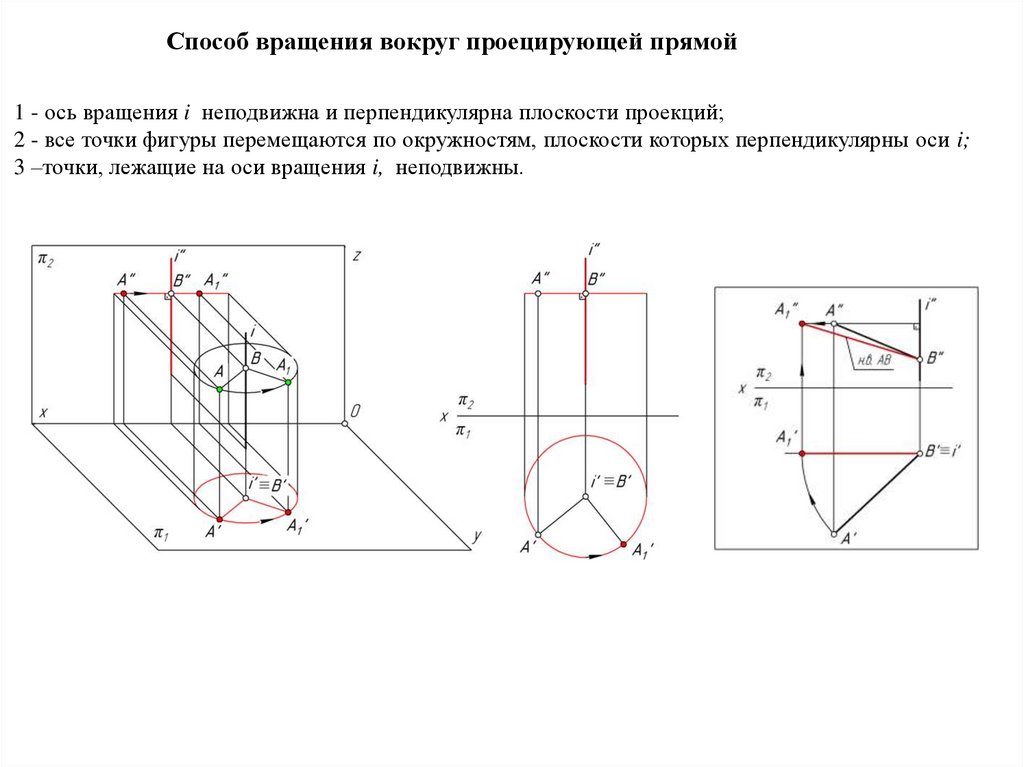
На плоскости, чтобы построить проекцию точки М 1
на прямую a
нужно провести прямую b
, которая проходит через точку М 1
и перпендикулярна прямой a
. Тогда точка пересечения прямых a
и b
является проекцией точки М 1
на прямую a
.
В трехмерном пространстве проекцией точки М 1
на прямую a
является точка пересечения прямой a
и плоскости , проходящей через точку М 1
перпендикулярно к прямой a
.
Нахождение координат проекции точки на прямую – теория и примеры.
Начнем с нахождения координат проекции точки на прямую, когда проецируемая точка и прямая заданы в прямоугольной системе координат Oxy на плоскости. После этого покажем, как находятся координаты проекции точки на прямую в прямоугольной системе координат Oxyz
в трехмерном пространстве.
Координаты проекции точки на прямую на плоскости.
Пусть на плоскости зафиксирована Oxy
, задана точка , прямая a
и требуется определить координаты проекции точки М 1
на прямую a
.
Решим эту задачу.
Проведем через точку М 1
прямую b
, перпендикулярную прямой a
, и обозначим точку пересечения прямых a
и b
как H 1
. Тогда H 1
– проекция точки М 1
на прямую a
.
Из проведенного построения логически следует алгоритм, позволяющий найти координаты проекции точки на прямую a
:
Разберемся с нахождением координат проекции точки на прямую при решении примера.
Пример.
На плоскости относительно прямоугольной системы координат Oxy
заданы точка и прямая a
, которой соответствует общее уравнение прямой вида
Решение.
Уравнение прямой a
нам известно из условия, так что можно переходить ко второму шагу алгоритма.
Получим уравнение прямой b
, которая проходит через точку М 1
и перпендикулярна прямой a
. Для этого нам потребуются координаты направляющего вектора прямой b
.Так как прямая b
перпендикулярна прямой a
, то нормальный вектор прямой a
является направляющим вектором прямой b
. Очевидно, нормальным вектором прямой является вектор с координатами , следовательно, направляющим вектором прямой b
является вектор .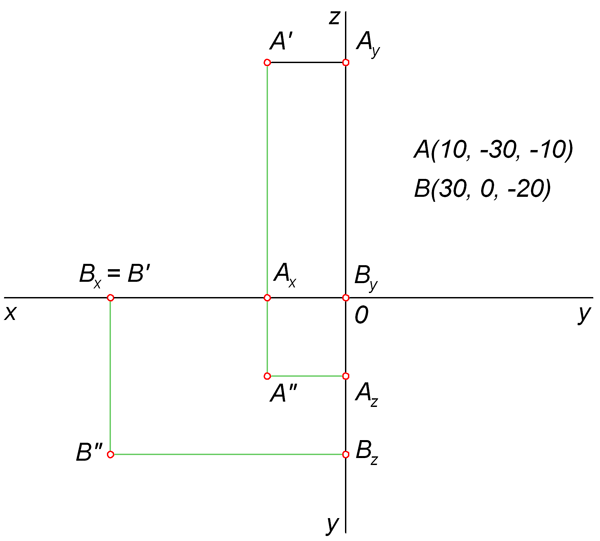
, так как знаем координаты точки , через которую она проходит, и координаты ее направляющего вектора: .
Осталось найти координаты точки пересечения прямых a
и b
, которые дадут искомые координаты проекции точки М 1
на прямую a
. Для этого сначала перейдем от канонических уравнений прямой b
к ее общему уравнению: . Теперь составим систему уравнений из общих уравнений прямых a
и b
, после чего найдем ее решение (при необходимости обращайтесь к статье ):
Таким образом, проекция точки на прямую имеет координаты .
Ответ:
Пример.
На плоскости в прямоугольной системе координат Oxy
заданы три точки . Найдите координаты проекции точки М 1
на прямую АВ
.
Решение.
Для нахождения координат проекции точки М 1
на прямую АВ
будем действовать по полученному алгоритму.
Напишем уравнение прямой, проходящей через две заданные точки и :
.
Теперь можно от полученного канонического уравнения прямой АВ
перейти к общему уравнению прямой АВ
и продолжить решение по аналогии с предыдущим примером.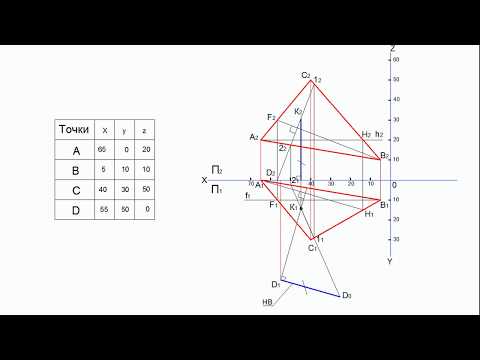
, проходящей через точку М 1
перпендикулярно прямой АВ
.
Из канонического уравнения прямой АВ
получим уравнение прямой с угловым коэффициентом : . Угловой коэффициент прямой АВ
равен , а угловой коэффициент прямой b
, которая перпендикулярна прямой АВ
, равен (смотрите условие перпендикулярности прямых). Тогда уравнение прямой b
, проходящей через точку и имеющей угловой коэффициент , имеет вид .
Чтобы определить координаты проекции точки на прямую АВ
осталось решить систему уравнений :
Ответ:
Давайте еще отдельно остановимся на нахождении координат проекции точки на координатные прямые Ox
и Oy
, а также на прямые, им параллельные.
Очевидно, что проекцией точки на координатную прямую Ox
, которой соответствует неполное общее уравнение прямой вида , является точка с координатами . Аналогично, проекция точки на координатную прямую Oy
имеет координаты .
Любая прямая, параллельная оси абсцисс, может быть задана неполным общим уравнением вида , а прямая, параллельная оси ординат, — уравнением вида .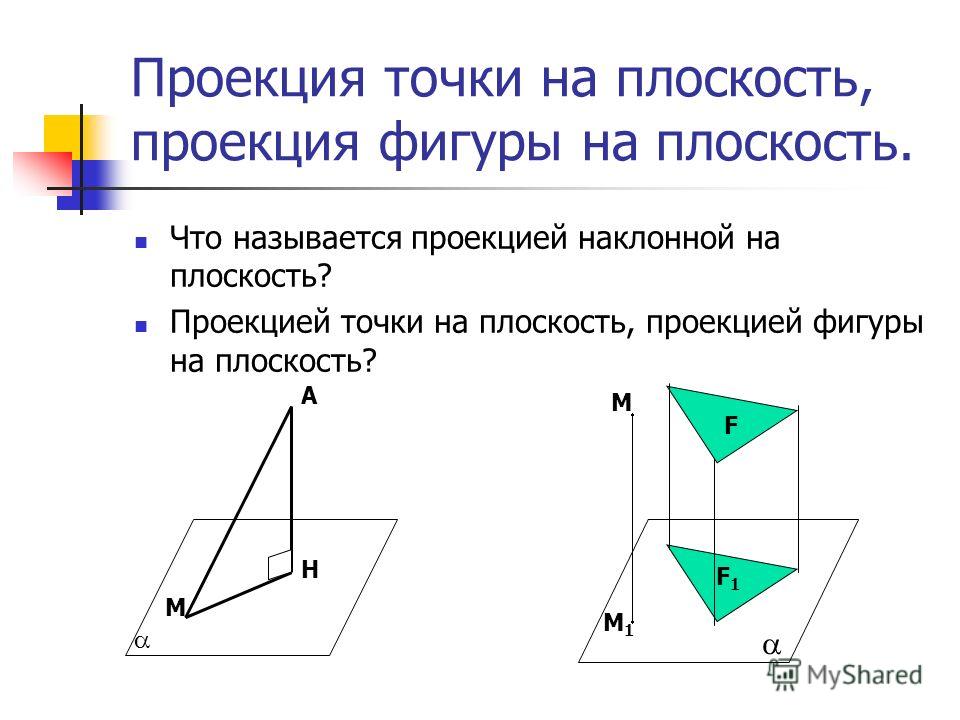
Пример.
Какие координаты имеют проекции точки на координатную прямую Oy
и на прямую .
Решение.
Проекцией точки на прямую Oy
является точка с координатами .
Перепишем уравнение прямой как . Теперь хорошо видно, что проекция точки на прямую имеет координаты .
Ответ:
И .
Координаты проекции точки на прямую в трехмерном пространстве.
Теперь переходим к нахождению координат проекции точки на прямую относительно прямоугольной системы координат Oxyz
, введенной в трехмерном пространстве.
Пусть в пространстве зафиксирована прямоугольная система координат Oxyz
, задана точка , прямая a
и требуется найти координаты проекции точки М 1
на прямую a
.
Решим эту задачу.
Построим плоскость , которая проходит через точку М 1
перпендикулярно к прямой a
. Проекцией точки М 1
на прямую a
является точка пересечения прямой a
и плоскости .
:
Рассмотрим решение примера.
Пример.
В прямоугольной системе координат Oxyz
задана точка и прямая a
, причем прямую a
определяют канонические уравнения прямой в пространстве вида . Найдите координаты проекции точки М 1
на прямую a
.
Решение.
Для определения координат проекции точки М 1
на прямую a
воспользуемся полученным алгоритмом.
Уравнения прямой a
нам сразу известны из условия, так что переходим ко второму шагу.
Получим уравнение плоскости , которая перпендикулярна к прямой a
и проходит через точку . Для этого нам нужно знать координаты нормального вектора плоскости . Найдем их. Из канонических уравнений прямой a
видны координаты направляющего вектора этой прямой: . Направляющий вектор прямой a
является нормальным вектором плоскости, которая перпендикулярна к прямой a
. То есть, — нормальный вектор плоскости . Тогда уравнение плоскости , проходящей через точку и имеющей нормальный вектор , имеет вид .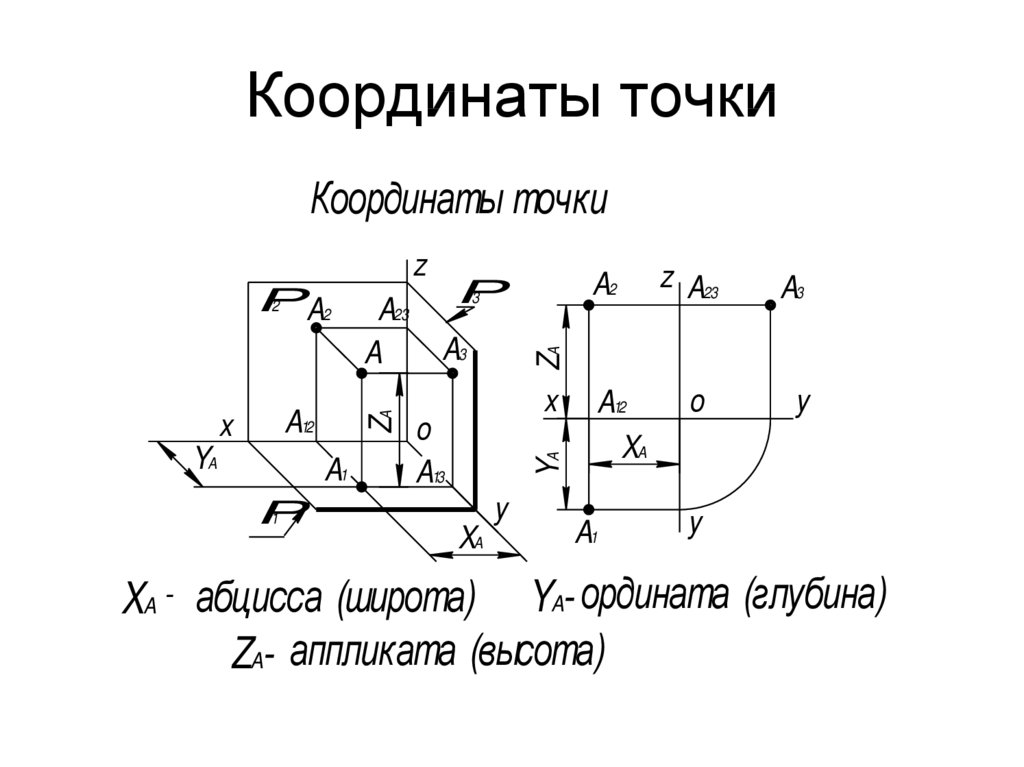
Осталось найти координаты точки пересечения прямой a
и плоскости — они являются искомыми координатами проекции точки на прямую a
. Покажем два способа их нахождения.
Первый способ.
Из канонических уравнений прямой a получим уравнения двух пересекающихся плоскостей , которые определяют прямую a:
Координаты точки пересечения прямой и плоскости мы получим, решив систему линейных уравнений вида . Применим (если Вам больше нравиться или какой-нибудь другой метод решения систем линейных уравнений, то применяйте его):
Таким образом, точка с координатами является проекцией точки М 1
на прямую a
.
Второй способ.
Зная канонические уравнения прямой a
, легко записать ее параметрические уравнения прямой в пространстве : . Подставим в уравнение плоскости вида вместо x
, y
и z
их выражения через параметр:
Теперь мы можем вычислить искомые координаты точки пересечения прямой a
и плоскости по параметрическим уравнениям прямой a
при :
1-12.
Р».
ЗАМЕЧАНИЕ.
Аналогично решается задача о нахождении коорди нат проекции точки на прямую.
ПРИМЕР.
Найти координаты проекции Р » точки Р(1,2,-1) на плоскость Зж — 2/4-22: — 4 = 0.
1. Составляем уравнения прямой, проходящей через точку Р
пер пендикулярно данной плоскости. Для этого в качестве направляю щего вектора прямой берем нормальный вектор плоскости: а = п =
|
Гл. 1. Ансиитическая геометрия |
||||
|
= {3, -1,2}. Тогда канонические уравнения прямой имеют вид |
||||
|
У-2 _ z-hl |
||||
|
2. Найдем координаты ТОЧЮЙ |
||||
|
ной плоскостью. Положим |
||||
|
х-~1 __ у-2 |
||||
|
Тогда параметрические уравнения прямой имеют вид |
||||
3.
на плос-
4х + бу -f 4z —
2х + 6у»-2г–11
4 х — 5 2 / — г — 7
ж-f-42/+ З2: 4-5 = 0.
2х -h Юу + lOz —
2х -МО2/ -f- lOz —
Ответы. 1.(2,3/2,2). 2. (-3/2,-3/2,-1/2). 3.(2,-1/2,-3/2). 4. (-1/2,1,1). 5.(1,-1/2,-1/2).
в уравнение плоскости и решая его относительно t, находим значение параметра t = to, при котором происходит пересе чение прямой и плоскости;
в) найденное значение to подставляем в параметрические уравне ния прямой и получаем искомые координаты точки Р».
2. Координаты точки Q, симметричной точке Р относительно дан ной прямой, определяем из условий (1). Получаем
XQ
= 2хр/ — Хр, yq = 2ур» — ур,
ZQ
= 22;р/ — zp.
ЗАМЕЧАНИЕ.
Аналогично решается задача о нахождении коорди нат точки, симметричной данной, относительно плоскости.
ПРИМЕР.
Найти координаты точки Q, симметричной точке Р(2, -1,2) относительно прямой
X — 1 _ у __ Z –1
Р
ЕШЕНИЕ.
1.
Найдем проекцию точки
Р
на данную прямую, т.е. точку Р». Для этого:
а) составим уравнение плоскости, проходящей через точку Р
пер пендикулярно данной прямой. В качестве нормального вектора п
этой плоскости можно взять направляющий вектор данной прямой: n = a = {1,0,-2}. Тогда
Подставляя эти выражения для х, у и z в
уравнение плоскости, на ходим значение параметра t, при котором происходит пересечение прямой и плоскости: to = -1;
в) подставляя в параметрические уравнения прямой найденное значение to = -1, получаем
жр/ = О, г/р/ = О, zpr
= 1.
геометрия — Как найти проекцию точки на плоскость
спросил
10 лет, 10 месяцев назад
Изменено
1 год, 4 месяца назад
Просмотрено
67 тысяч раз
$begingroup$
Допустим, у меня есть точка $(x, y, z)$ и плоскость с нормалью $(a, b, c)$ с точкой $(d, e, f)$. Я пытаюсь использовать это в программировании $3D$. Благодарю вас! 92}.$$
Подставьте это в $(x+ta,y+tb,z+tc)$ и получите результат.
$endgroup$
$begingroup$
Возьмем вектор смещения из точки на плоскости в заданную точку:
$$
{ bf v} = (xd, ye, zf)
$$
и пусть ${bf w}$ — вектор нормали к плоскости.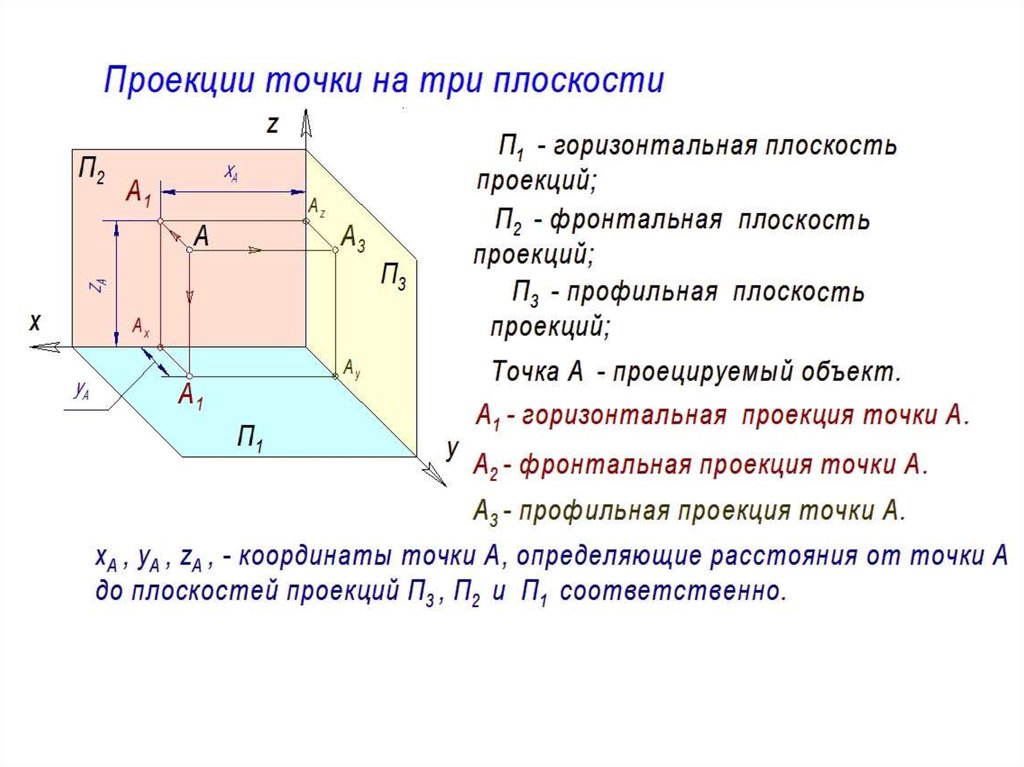
Мы можем описать ${bf v}$ как сумму двух векторов; один перпендикулярен вектору нормали ${bf w}$ (обозначается ${bf v}_perp$), а другой параллелен вектору нормали ${bf w}$ (обозначается $ {bf v}_parallel$). 92} { бф ш}
$$
Отсюда искомая точка равна $(d,e,f)+{bf v}_perp$.
$endgroup$
1
$begingroup$
Обозначим вашу точку как $(x_0,y_0,z_0)$ вместо $(x,y,z)$ и проекцию как $(x’_0,y’_0,z’_0)$
Параметрическое уравнение линии, проходящей через точку, и ее проекция определяется как:
$x’_0=x_0+acdot t$
$y’_0=y_0+bcdot t$
$z’_0=z_0+ccdot t$
Уравнение плоскости:
$a cdot(x-d)+bcdot(y-e )+ccdot(z-f)=0$
Теперь , так как точка $(x’_0,y’_0,z’_0)$ принадлежит плоскости, то в уравнение плоскости вместо $ нужно подставить ее координаты x,y,z$ и вычислить параметр $t$ .
$endgroup$
$begingroup$
Вы должны провести параллельную прямую вектору нормали в точке $(x,y,z)$, и проекция будет пересечением этой прямой с плоскостью.
$endgroup$
линейная алгебра — Ортогональная проекция точки на плоскость
спросил
4 года, 4 месяца назад
Изменено
4 года, 4 месяца назад
Просмотрено
10 тысяч раз
$begingroup$
Даны точка и плоскость: точка $P(-4, -9, -5)$ и плоскость, заданная тремя точками: $A(0, 1, 3)$, $B(-3, 2, 4)$ и $C(4, 1, -2)$. Пока мне удалось вычислить уравнение этой плоскости $5x + 11y + 4z = 23$.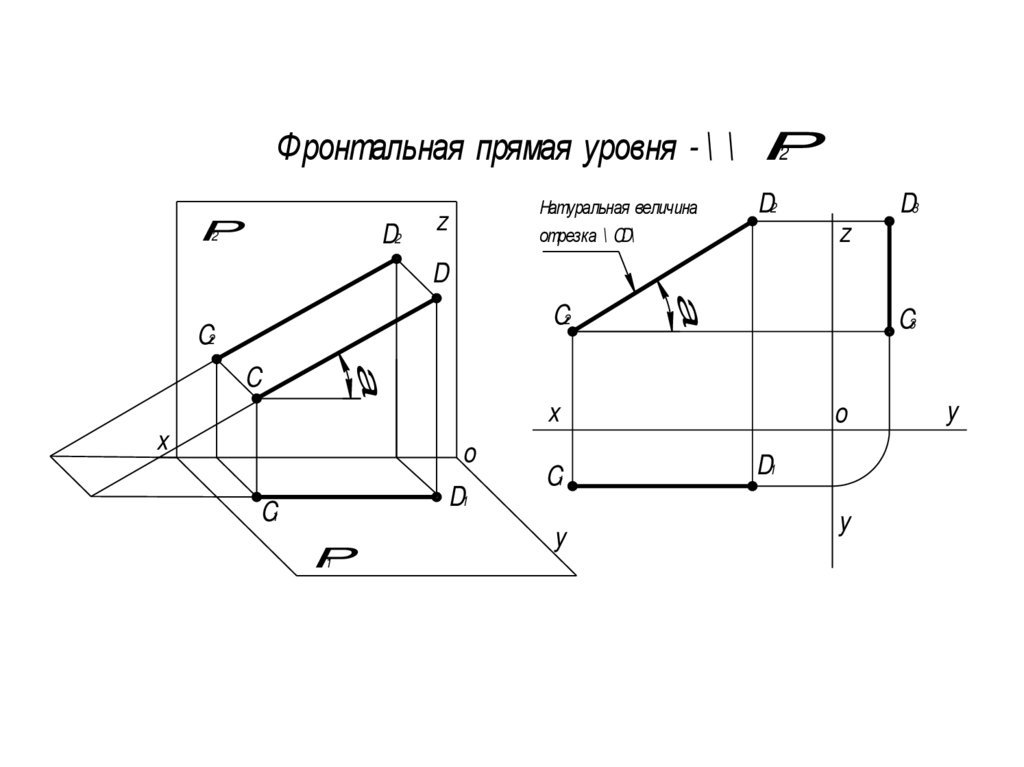
- линейная алгебра
- векторные пространства
$endgroup$
$begingroup$
Вы просили другой способ сделать это, так что вот парочка. Проекция $P$ — это пересечение плоскости, определяемой тремя точками, и прямой, проходящей через $P$, ортогональной плоскости — параллельной нормали к плоскости. Поскольку вы уже нашли уравнение плоскости, вы можете использовать его для прямого вычисления этой точки несколькими способами. 9Т$. Подставляя эти значения в приведенное выше выражение, мы получаем $$left([5,11,4,-23]cdot[5,11,4,0]right)[-4,-9,-5,1 ]-влево([5,11,4,-23]cdot[-4,-9,-5,1]вправо)[5,11,4,0] = 162[-4,-9, -5,1]+162[5,11,4,0] = [162,324,-162,162].$$ Дегомогенизируйте это, разделив на последнюю координату, чтобы получить точку $(1,2,-1)$. Конечно, вы могли бы создать систему параметрических или неявных декартовых уравнений и решить их для пересечения прямой и плоскости, но этот метод позволяет вычислить ее напрямую.
Содержание
- – Что такое ортогональная проекция точки на прямую?
- – Что такое проекция точки на ось?
- – Что такое ортогональная проекция точки на плоскость?
- – Как найти точку на прямой?
- – Как строится центральная проекция точки?
- – Какие виды проекции существуют?
- – Как найти проекцию в геометрии?
- – Как найти наклонную и ее проекцию?
- – Как обозначить проекцию точки?
Что такое ортогональная проекция точки на прямую?
Ортогональная проекция точки P на прямую (или плоскость) – это основание P’ перпендикуляра, опущенного из точки P на эту прямую (плоскость). Отображение, сопоставляющее точке P точку P’, также называется ортогональной проекцией.
Что такое проекция точки на ось?
Проекция точки на ось – это основание перпендикуляра, опущенного из этой точки на данную ось (рис. … 8). То есть, проекцией точки на ось является точка.
Что такое ортогональная проекция точки на плоскость?
Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Как найти точку на прямой?
Для поиска точки на прямой достаточно взять одну из координат, и подставить в уравнение, а затем выразить из полученного уравнение вторую. Таким образом найдется точка с заданной одной из координат.
Как строится центральная проекция точки?
Для получения центральных проекций надо задаться плоскостью проекций и центром проекций – точкой, не лежащей в этой плоскости (плоскость п0 и точка S). Взяв некоторую точку А и проведя через S и А прямую линию до пересечения ее с пл. … п0: они получаются в пересечении проецирующих прямых SA, SB, SC с плоскостью проекций.
Какие виды проекции существуют?
По характеру искажений проекции разделяются на равноугольные (или конформные), равновеликие (или эквивалентные) и произвольные.
- Равноугольные проекции. …
- Равновеликие проекции. …
- Произвольные проекции. …
- Конические проекции. …
- Цилиндрические проекции. …
- Азимутальные проекции. …
- Перспективные проекции. …
- Условные проекции.
Как найти проекцию в геометрии?
Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой О (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета.
Как найти наклонную и ее проекцию?
Повернув прямоугольные треугольники вокруг общего их катета (перпендикуляра к плоскости) до совмещения их плоскостей, получим все наклонные (гипотенузы) и их проекции (другие катеты) в одной плоскости, где эти теоремы верны.
Как обозначить проекцию точки?
Точки обозначают прописными буквами латинского алфавита или арабскими цифрами: A, B, C, D, …. 1, 2, 3, 4, …. 2. Линии, произвольно расположенные по отношению к плоскости проекций, обозначают строчными буквами латинского алфавита: a, b, c, d, ….
Интересные материалы:
Nfc в фитнес браслете что это?
Nfc в наушниках что это?
Ниссан кашкай сборка где?
Ниссан кашкай СЕ где производство?
Ниссан х трейл где собирают для России?
Ниссан х трейл сборка где?
Ниссан мурано где производят?
Ниссан террано что это?
Ниссан террано где производится сборка авто?
Ночной паралич что это такое?