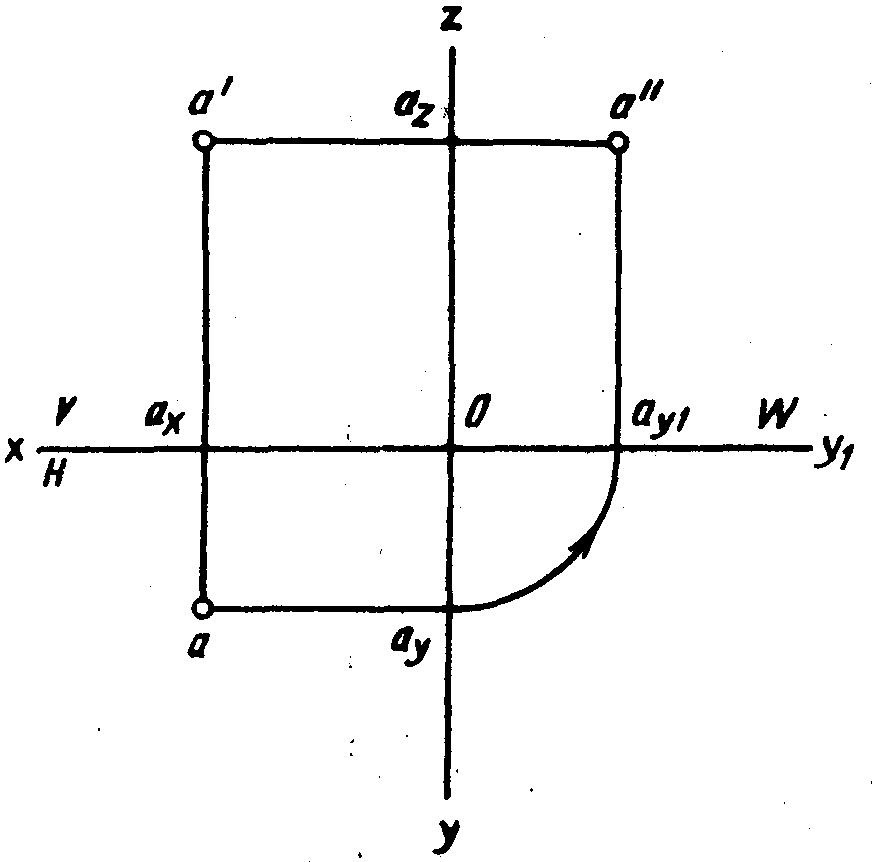Проецирование точки
- Подробности
- Категория: Основы начертательной геометрии
ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ПЛОСКОСТИ ПРОЕКЦИЙ
Образование отрезка прямой линии АА1 можно представить как результат перемещения точки А в какой-либо плоскости Н (рис. 84, а), а образование плоскости — как перемещение отрезка прямой линии АВ (рис. 84, б).
Точка — основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается с построения прямоугольных проекций точки.
В пространство двугранного угла, образованного двумя перпендикулярными плоскостями — фронтальной (вертикальной) плоскостью проекций V и горизонтальной плоскостью проекций Н, поместим точку А (рис. 85, а).
Линия пересечения плоскостей проекций — прямая, которая называется осью проекций и обозначается буквой х.
Плоскость V здесь изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 45° к его горизонтальной стороне. Длина наклонной стороны берется равной 0,5 ее действительной длины.
Из точки А опускают перпендикуляры на плоскости V и Н. Точки а’и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура Аааха’ в пространстве — прямоугольник. Сторона аах этого прямоугольника на наглядном изображении уменьшается в 2 раза.
Совместим плоскости Н с плоскостью V ,вращая V вокруг линии пересечения плоскостей х. В результате получается комплексный чертеж точки А (рис. 85, б)
Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис. 85, в).
Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий — точки а и а’ — называются проекциями точки А: а’ — фронтальная проекция точки А, а — горизонтальная проекция точки А.
Линия а’ а называется вертикальной линией проекционной связи.
Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.
Если точка А лежит на горизонтальной плоскости проекций Н (рис. 86, а), то ее горизонтальная проекция а совпадает с заданной точкой, а фронтальная проекция а’ располагается на оси При расположении точки В на фронтальной плоскости проекций V ее фронтальная проекция совпадает с этой точкой , а горизонтальная проекция лежит на оси х. Горизонтальная и фронтальная проекции заданной точки С, лежащей на оси х, совпадают с этой точкой. Комплексный чертеж точек А, В и С показан на рис. 86, б.
ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ
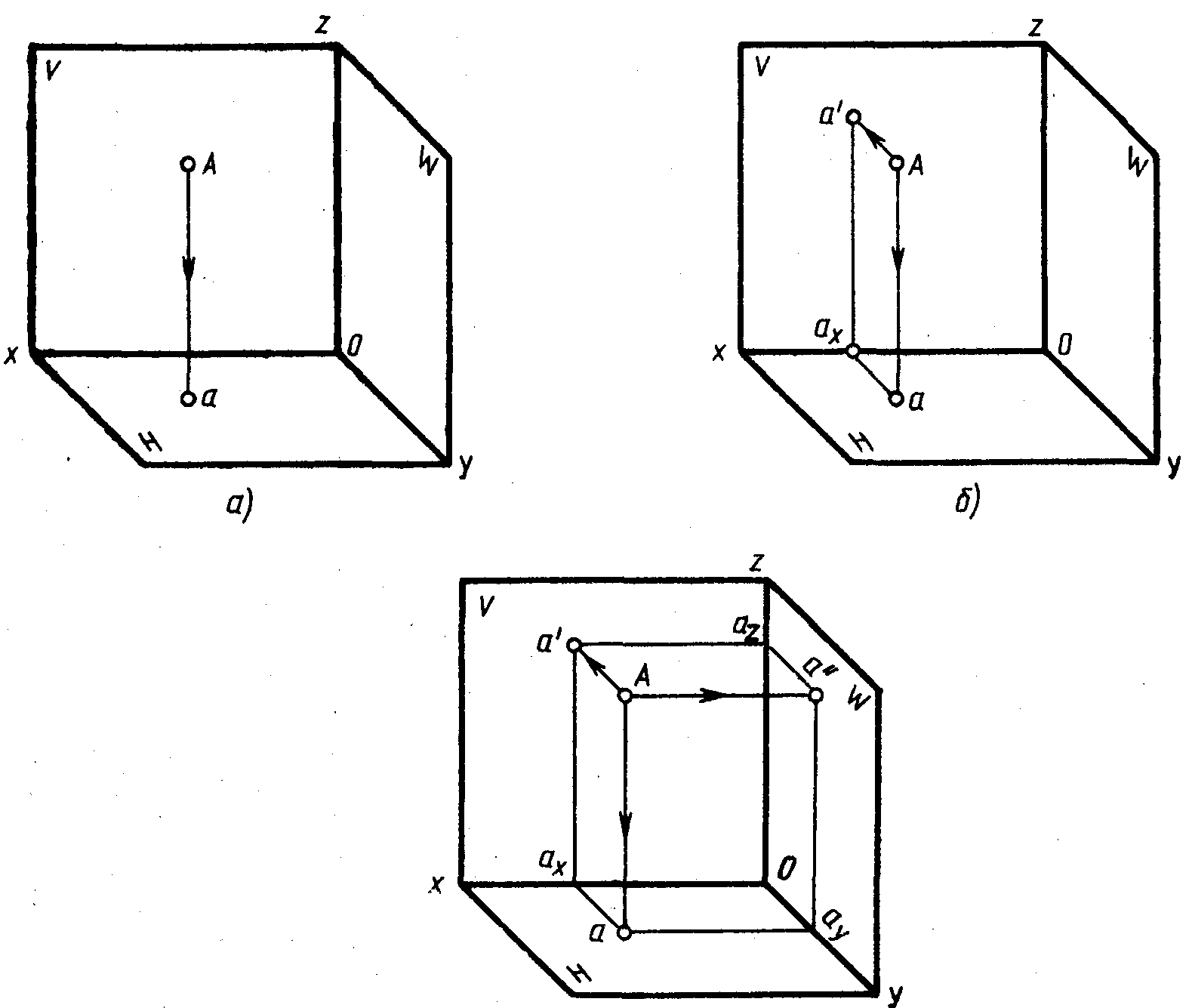
В тех случаях, когда по двум проекциям нельзя представить себе форму предмета, его проецируют на три плоскости проекций. В этом случае вводится профильная плоскость проекций W, перпендикулярная плоскостям V и Н. Наглядное изображение системы из трех плоскостей проекций дано на рис. 87, а.
Ребра трехгранного угла (пересечение плоскостей проекций) называются осями проекций и обозначаются x, у и z. Пересечение осей проекций называется началом осей проекций и обозначается буквой О. Опустим из точки А перпендикуляр на плоскость проекций W и, отметив основание перпендикуляра буквой а”, получим профильную проекцию точки А.
Для получения комплексного чертежа точки А плоскости Н и W совмещают с плоскостью V, вращая их вокруг осей Ох и Oz. Комплексный чертеж точки А показан на рис. 87, б и в.
Отрезки проецирующих линий от точки А до плоскостей проекций называются координатами точки А и обозначаются: хА, уА и zA.
Например, координата zA точки А, равная отрезку а’ах (рис. 88, а и б), есть расстояние от точки А до горизонтальной плоскости проекций Н. Координата у точки А, равная отрезку аах, есть расстояние от точки А до фронтальной плоскости проекций V. Координата хА, равная отрезку аау — расстояние от точки А до профильной плоскости проекций W.
Таким образом, расстояние между проекцией точки и осью проекции определяют координаты точки и являются ключом к чтению ее комплексного чертежа. По двум проекциям точки можно определить все три координаты точки.
Если заданы координаты точки А (например, хА=20 мм, уА=22мм и zA= 25 мм), то можно построить три проекции этой точки.
Для этого от начала координат О по направлению оси Oz откладывают вверх координату zA и вниз координату уА.Из концов отложенных отрезков — точек az и ау (рис. 88, а) — проводят прямые, параллельные оси Ох, и на них откладывают отрезки, равные координате хА. Полученные точки а’ и а — фронтальная и горизонтальная проекции точки А.
По двум проекциям а’ и а точки А построить ее профильную проекцию можно тремя способами:
1) из начала координат О проводят вспомогательную дугу радиусом Оау, равным координате (рис. 87, б и в), из полученной точки ау1 проводят прямую, параллельную оси Oz, и откладывают отрезок, равный zA;
2) из точки ау проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, а), получают точку ау1 и т. д.;
3) из начала координат О проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, б), получают точку ау1 и т. д.
Вы здесь
Проецирование точки
СОДЕРЖАНИЕ
- Проецирование точки
- Пример проецирования точки
- Литература
Проецирование точки
Точка относится к основным, неопределяемым понятиям геометрии. Она не может быть определена другими более элементарными понятиями. Точка не имеет размеров.
Положение точки А в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций.
Чтобы определить эти расстояния достаточно через точку А провести прямые, перпендикулярные к плоскостям, определить точки А′, А″, А′″ пересечения этих прямых с плоскостями проекций и измерить величины отрезков [АA′], [АA″], [АA′″], которые равны значениям аппликаты z, ординаты y и абсциссы x точки А (рис.1).
Рис.1. Проецирование точки
Точки А′, А″, А′″ называют ортогональными проекциями точки А:
Принятые обозначения:
| А1 или А′ | — | горизонтальная проекция точки А; |
| А2 или А″ | — | фронтальная проекция точки А; |
| А3 или А′″ | — | профильная проекция точки А. |
Отрезки:
| [АA′]=[ОАx] | — | абсцисса точки А (определяет расстояние точки от плоскости П3); |
| [АA″]=[ОАy] | — | ордината точки А (определяет расстояние точки от плоскости П2); |
| [АA′″]=[ОАz] | — | аппликата точки А (определяет расстояние точки от плоскости П1). |
Прямые АA′, АA″, АA′″ называют проецирующими прямыми или проецирующими лучами.
| АA′ | — | горизонтально проецирующая прямая; |
| АA″ | — | фронтально проецирующая прямая; |
| АA′″ | — | профильно проецирующая прямая. |
При построении проекций точки А необходимо знать, что горизонтальная проекция определяется абсциссой x и ординатой y, фронтальная проекция – абсциссой x и аппликатой z, а профильная – ординатой y и аппликатой z, т.е.
А′ (x, y)
А″ (x, z)
А′″ (y, z)
Если даны две проекции точки, то по ним можно найти третью проекцию, так как все проекции связаны между собой линиями связи.
Пример проецирования точки
Пример: Даны две проекции точки А (рис.2), необходимо найти третью проекцию точки.
Рис.2. Проецирование точки
Для начала найдем проекции точки А на оси координат, т.е. Аx, АyП1 и Аz (рис.3).
Рис.3. Проецирование точки
При помощи циркуля получаем проекцию точки АyП3 (рис.4).
Рис.4. Проецирование точки
Зная, что проекция точки А′″ имеет координаты (y, z), проводим проецирующие лучи из точки АyП3 и Аz. Точкой пересечения этих лучей будет точка А′″ (рис.5).
Рис.5. Проецирование точки
ЛИТЕРАТУРА
- Начертательная геометрия / С.А. Фролов. – М.: Машиностроение, 1987 – 240 с.
- Черчение / Н.С. Брилинг. – М.: Стройиздат, 1989. – 420 с.
- Краткий справочник по начертательной геометрии и машиностроительному черчению / Н.П. Сберегаев, М.А. Герб. М. – Л., Машиностроение, 1965, 264 с.
- 12443 просмотра
Лекция № 2. Точка
1. Проекции точки на две плоскости проекций
Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.
Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а́ на фронтальную плоскость называют фронтальной проекцией.
Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху а́, b́, с́…
Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций — арабскими цифрами 1, 2… и 1́, 2́…
При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.
Через перпендикулярные прямые Аа и Аа́ проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аах, а фронтальную плоскость — по прямой а́ах. Прямые аах и а́ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха́ является прямоугольником.
При совмещении горизонтальной и фронтальной плоскостей проекции а и а́ будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аах и а́ах не нарушится.
Получаем, что на эпюре проекции а и а́ некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.
Две проекции а и а́ некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а́ к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.
Рассмотрим прямоугольник Aaaха́ (рис. 5), для которого справедливы следующие утверждения:
1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.
Аа́ = аах;
2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а́ от оси пересечения плоскостей, т. е.
Аа = а́ах.
Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).
Ось пересечения плоскостей делит горизонтальную плоскость на две четверти — переднюю и заднюю, а фронтальную плоскость — на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.
При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости — с верхней частью фронтальной плоскости.
На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В — во второй, точка С — в третьей и точка D — в четвертой.
При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.
Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция — ниже оси пересечения плоскостей.
Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.
В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.
В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная ḱ показывает фактическое местонахождение этой точки.
Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.
Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.
Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.
2. Отсутствие оси проекций
Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.
Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.
При построениях на эпюре всегда следует располагать проекции а и а́ точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа́.
Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа́ ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а́ до их пересечения, можно получить точку А. При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.
3. Проекции точки на три плоскости проекций
Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.
Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной.
В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х, общую прямую горизонтальной и профильной плоскостей — осью у, а общую прямую фронтальной и профильной плоскостей — осью z. Точка О, которая принадлежит всем трем плоскостям, называется точкой начала координат.
На рисунке 15а показана точка А
Конец ознакомительного фрагмента.
Проекции точек на поверхностях геометрических тел
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
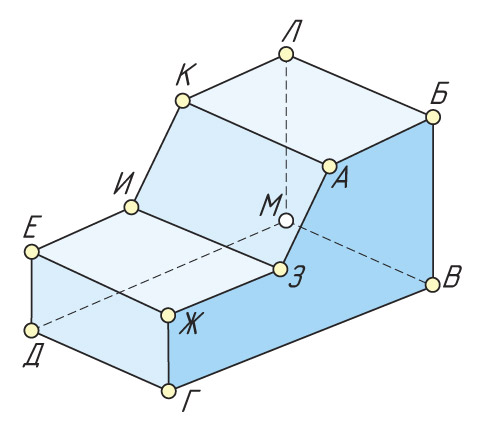
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
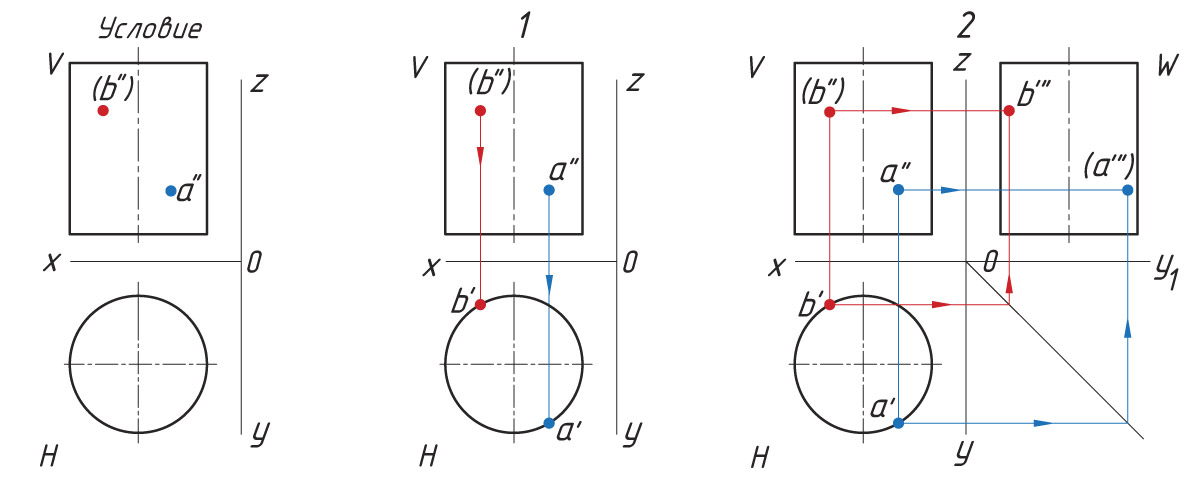
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
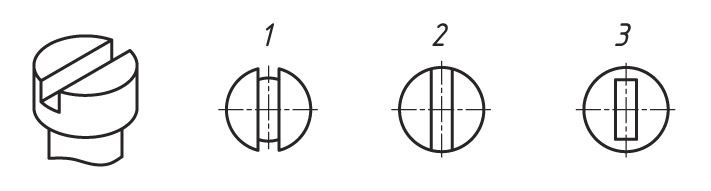
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
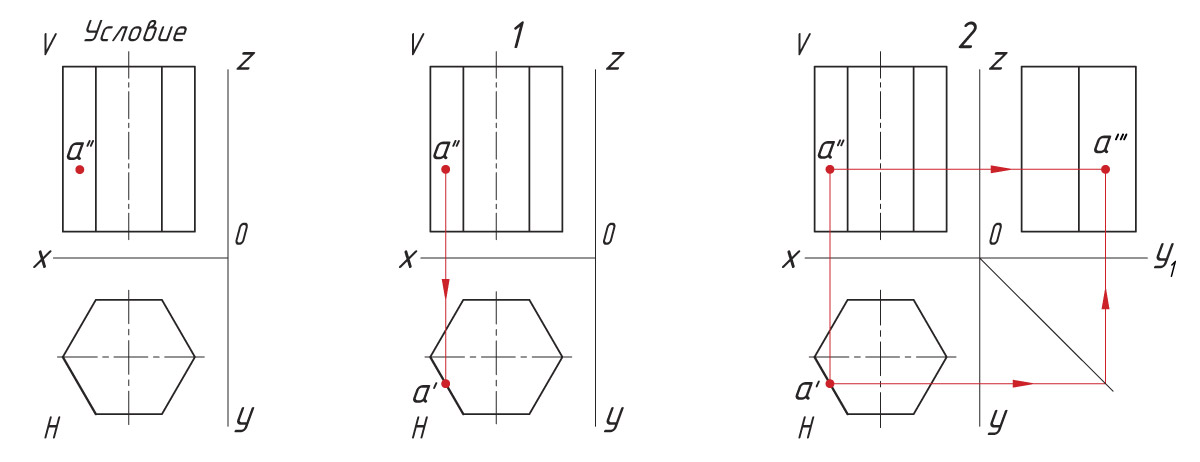
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
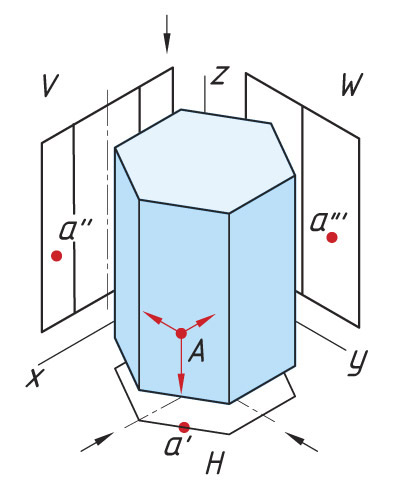 |
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
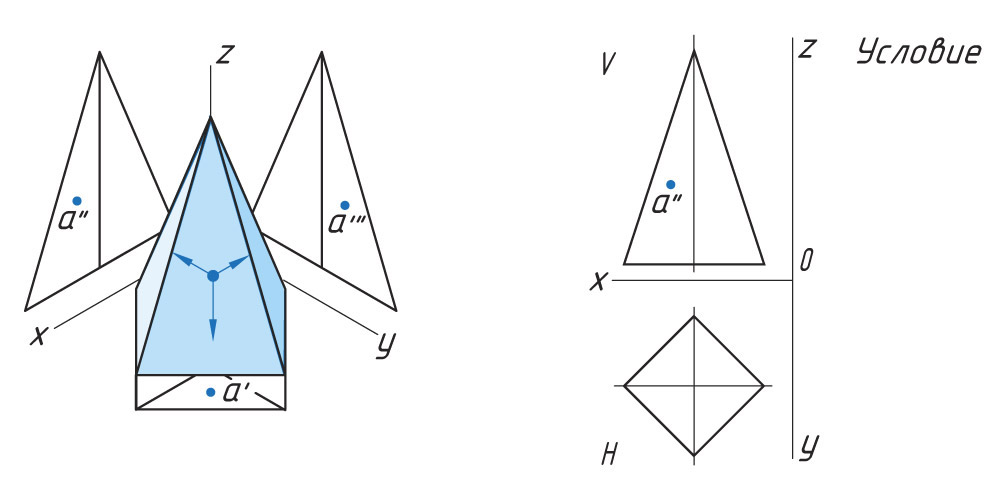
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
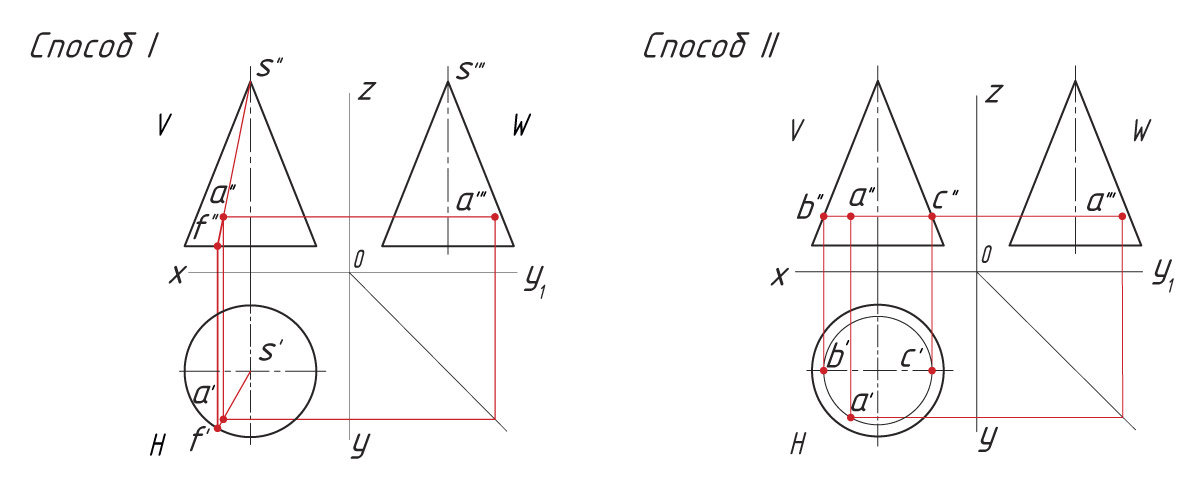
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
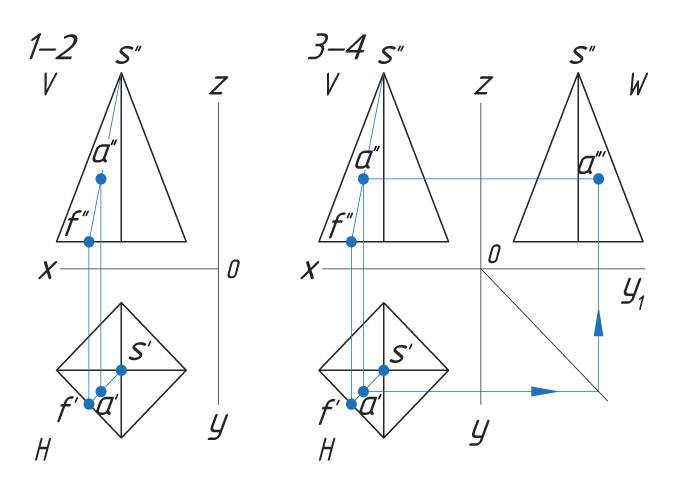
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
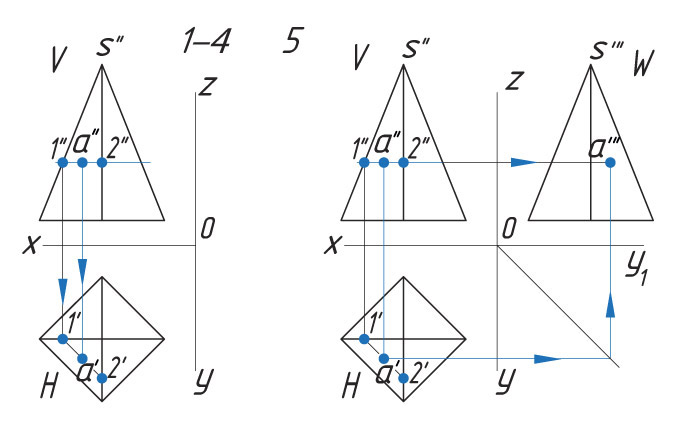 |
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
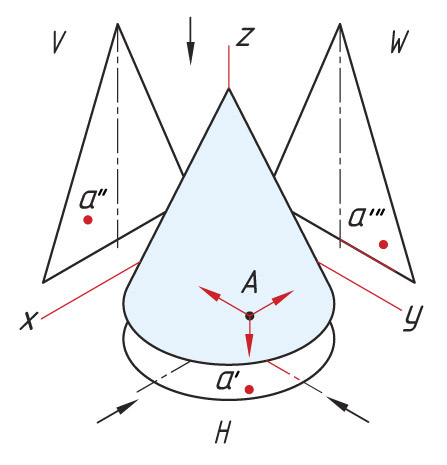
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
 |
-
Проекции точки
Проецирование
точки на три плоскости проекций
координатного угла начинают с получения
ее изображения на плоскости H
– горизонтальной плоскости проекций.
Для этого через точку А (рис. 4.12, а)
проводят проецирующий луч перпендикулярно
плоскости H.
На
рисунке перпендикуляр к плоскости Н
параллелен оси Oz. Точку пересечения
луча с плоскостью Н (точку а) выбирают
произвольно. Отрезок Аа определяет,
на каком расстоянии находится точка А
от плоскости Н, указывая тем самым
однозначно положение точки А на рисунке
по отношению к плоскостям проекций.
Точка а является прямоугольной проекцией
точки А на плоскость Н и называется
горизонтальной проекцией точки А (рис.
4.12, а).
в)
Рис.
4.12.
Для
получения изображения точки А на
плоскости V (рис. 4.12,б) через точку А
проводят проецирующий луч перпендикулярно
фронтальной плоскости проекций V. На
рисунке перпендикуляр к плоскости V
параллелен оси Оу. На плоскости Н
расстояние от точки А до плоскости V
изобразится отрезком аах,
параллельным оси Оу и перпендикулярным
оси Ох. Если представить себе, что
проецирующий луч и его изображение
проводят одновременно в направлении
плоскости V, то когда изображение луча
пересечет ось Ох в точке ах,
луч пересечет плоскость V в точке а’.
Проведя из точки ах
в плоскости V перпендикуляр к оси Ох,
который является изображением
проецирующего луча Аа на плоскости V, в
пересечении с проецирующим лучом
получают точку а’. Точка а’ является
фронтальной проекцией точки А, т. е. ее
изображением на плоскости V.
Изображение
точки А на профильной плоскости проекций
(рис. 4.12, в) строят с помощью проецирующего
луча, перпендикулярного плоскости W. На
рисунке перпендикуляр к плоскости W
параллелен оси Ох. Проецирующий луч от
точки А до плоскости W на плоскости Н
изобразится отрезком аау,
параллельным оси Ох и перпендикулярным
оси Оу. Из точки Оу параллельно оси Oz и
перпендикулярно оси Оу строят изображение
проецирующего луча аА и в пересечении
с проецирующим лучом получают точку
а”. Точка а” является профильной
проекцией точки А, т. е. изображением
точки А на плоскости W.
Точку
а” можно построить, проведя от точки
а’ отрезок а’аz
(изображение проецирующего луча Аа”
на плоскости V) параллельно оси Ох, а от
точки аz
— отрезок а”аz
параллельно оси Оу до пересечения с
проецирующим лучом.
Получив
три проекции точки А на плоскостях
проекций, координатный угол развертывают
в одну плоскость, как показано на рис.
4.11,б, вместе с проекциями точки А и
проецирующих лучей, а точку А и проецирующие
лучи Аа, Аа’ и Аа” убирают. Края
совмещенных плоскостей проекций не
проводят, а проводят только оси проекций
Oz, Оу и Ох, Оу1
(рис. 4.13).
Анализ
ортогонального чертежа точки показывает,
что три расстояния — Аа’, Аа и Аа”
(рис. 4.12, в), характеризующие положение
точки А в пространстве, можно определить,
отбросив сам объект проецирования —
точку А, на развернутом в одну плоскость
координатном угле (рис. 4.13). Отрезки
а’аz,
ааy
и Оах
равны Аа” как противоположные стороны
соответствующих прямоугольников (рис.
4.12,в и 4.13). Они определяют расстояние,
на котором находится точка А от профильной
плоскости проекций. Отрезки а’ах,
а”ау1
и Оау
равны отрезку Аа, определяют расстояние
от точки А до горизонтальной плоскости
проекций, отрезки аах,
а”аz
и Оаy1
равны отрезку Аа’, определяющему
расстояние от точки А до фронтальной
плоскости проекций.
Рис.
4.13.
Отрезки
Оах,
Оау
и Оаz,
расположенные на осях проекций, являются
графическим выражением размеров
координат X, Y и Z точки А. Координаты
точки обозначают с индексом соответствующей
буквы. Измерив величину этих отрезков,
можно определить положение точки в
пространстве, т. е. задать координаты
точки.
На
эпюре отрезки а’ах
и аах
располагаются как одна линия,
перпендикулярная к оси Ох а отрезки
а’аz
и a”az
— к оси Оz.
Эти лини называются линиями проекционной
связи. Они пересекают оси проекций в
точках ах
и аz
соответственно. Линия проекционной
связи, соединяющая горизонтальную
проекцию точки А с профильной, оказалась
«разрезанной» в точке ау.
Две
проекции одной и той же точки всегда
располагаются на одной линии проекционной
связи, перпендикулярной к оси проекций.
Для
представления положения точки в
пространстве достаточно двух ее проекций
и заданного начала координат (точка О)
На рис. 4.14, б две проекции точки полностью
определяют ее положение в пространстве
По этим двум проекциям можно построит
профильную проекцию точки А. Поэтому в
дальнейшем, если не будет необходимости
в профильной проекции, эпюры будут
построены на двух плоскостях проекций:
V и Н.
Рис.
4.14. Рис. 4.15.
Рассмотрим
несколько примеров построения и чтения
чертежа точки.
Пример
1.
Определение координат точки J заданной
на эпюре двумя проекциях (рис. 4.14).
Измеряются три отрезка: отрезок ОвХ
(координата X), отрезок bХb
(координата Y) и отрезок bХb’
(координата Z). Координаты записывают в
следующем п рядке: X, Y и Z, после буквенного
обозначения точки, например, В20; 30; 15.
Пример
2.
Построение точки по заданным координатам.
Точка С задана координатами С30; 10; 40. На
оси Ох (рис. 4.15) находят точку сх,
в которой линия проекционной связи
пересекает ось проекций. Для этого по
оси Ох от начала координат (точка О)
откладывают координату X (размер 30) и
получают точку сх.
Через эту точку перпендикулярно оси Ох
проводят линию проекционной связи и от
точки вниз откладывают координату У
(размер 10), получают точку с — горизонтальную
проекцию точки С. Вверх от точки сх
по линии проекционной связи откладывают
координату Z (размер 40), получают точку
с’ — фронтальную проекцию точки С.
Рис.
4.16.
Пример
3.
Построение профильной проекции точки
по заданным проекциям. Заданы проекции
точки D — d и d’. Через точку О проводят
оси проекций Oz, Oy и Оу1
(рис. 4.16, а). Для построения профильной
проекции точки D отточки d’ проводят
линию проекционной связи, перпендикулярную
оси Oz, и продолжают ее вправо за ось Oz.
На этой линии будет располагаться
профильная проекция точки D. Она будет
находиться на таком расстоянии от оси
Oz, на каком горизонтальная проекция
точки d располагается: от оси Ох, т. е. на
расстоянии ddx.
Отрезки dzd”
и ddx
одинаковы, так как определяют одно и то
же расстояние — расстояние от точки D
до фронтальной плоскости проекций. Это
расстояние является координатой У точки
D.
Графически
отрезок dzd”
строят перенесением отрезка ddx
с горизонтальной плоскости проекций
на профильную. Для этого проводят линию
проекционной связи параллельно оси Ох,
получают на оси Оу точку dy
(рис. 4.16,б). Затем переносят размер отрезка
Ody
на ось Оу1,
проведя из точки О дугу радиусом, равным
отрезку Ody,
до пересечения с осью Оу1
(рис. 4.16,б), получают точку dy1.
Эту точку можно построить и как показано
на рис. 4.16, в, проведя прямую под углом
45° к оси Оу из точки dy.
Из точки dy1
проводят линию проекционной связи
параллельно оси Oz и на ней откладывают
отрезок, равный отрезку d’dx,
получают точку d”.
Перенос
величины отрезка dxd
на профильную плоскость проекций можно
осуществить с помощью постоянной прямой
чертежа (рис. 4.16, г). В этом случае линию
проекционной связи ddy
проводят через горизонтальную проекцию
точки параллельно оси Оу1
до пересечения с постоянной прямой, а
затем параллельно оси Оу до пересечения
с продолжением линии проекционной связи
d’dz.
Частные
случаи расположения точек относительно
плоскостей проекций
Положение
точки относительно плоскости проекций
определяется соответствующей координатой,
т. е. величиной отрезка линии проекционной
связи от оси Ох до соответствующей
проекции. На рис. 4.17 координата У точки
А определяется отрезком аах
— расстояние от точки А до плоскости
V. Координата Z точки А определяется
отрезком а’ах
— расстояние от точки А до плоскости
Н. Если одна из координат равна нулю, то
точка расположена на плоскости проекций.
На рис. 4.17 приведены примеры различного
расположения точек относительно
плоскостей проекций. Координата Z точки
В равна нулю, точка находится в плоскости
Н. Ее фронтальная проекция находится
на оси Ох и совпадает с точкой bх.
Координата У точки С равна нулю, точка
располагается на плоскости V, ее
горизонтальная проекция с находится
на оси Ох и совпадает с точкой сх.
Следовательно,
если точка находится на плоскости
проекций, то одна из проекций этой точки
лежит на оси проекций.
Рис.
4.17.
На
рис. 4.17 координаты Z и Y точки D равны
нулю, следовательно, точка D находится
на оси проекций Ох и две ее проекции
совпадают.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #