Как найти проекцию треугольника на плоскость формула – Сайт, где вы сможете решить свои вопросы

Преподаватель который помогает студентам и школьникам в учёбе.

Ортогональное проецирование – определение и вычисление с примерами решения

Ортогональное проецирование:

Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.

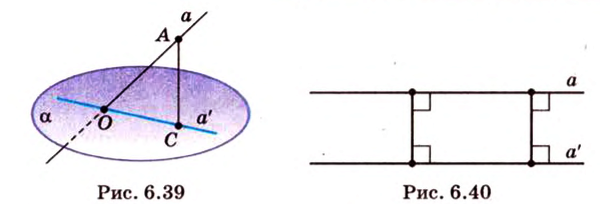
Ортогональное проецирование - определение и вычисление с примерами решения

Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой 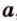Ортогональное проецирование - определение и вычисление с примерами решения

Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.

Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.

Площадь ортогональной проекции

Теорема 5

Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

Доказательство:

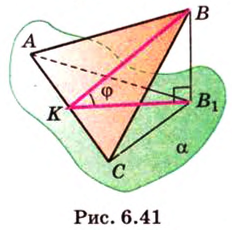
Ортогональное проецирование - определение и вычисление с примерами решения

Как пример многоугольника возьмем 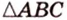Ортогональное проецирование - определение и вычисление с примерами решения (рис. 6.41). Проекцией 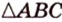на плоскость 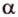является 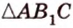. Проведем высоту 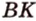треугольника 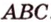. По теореме
о трех перпендикулярах 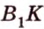Ортогональное проецирование - определение и вычисление с примерами решения – высота 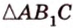. Угол 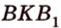– угол между плоскостью 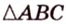и плоскостью проекции. Пусть 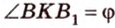. Тогда

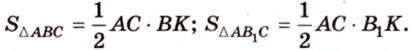
Ортогональное проецирование - определение и вычисление с примерами решения

Учитывая, что 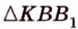Ортогональное проецирование - определение и вычисление с примерами решения прямоугольный 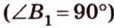, имеем: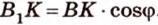. Поэтому

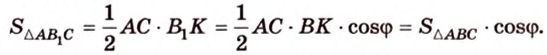
Ортогональное проецирование - определение и вычисление с примерами решения

Итак, Ортогональное проецирование - определение и вычисление с примерами решения . Теорема доказана.

Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство

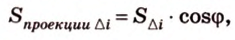
Ортогональное проецирование - определение и вычисление с примерами решения

где 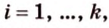Ортогональное проецирование - определение и вычисление с примерами решения поскольку угол между плоскостями этих треугольников и плоскостью их проекций будет один и тот же. Все эти равенства сложим почленно:

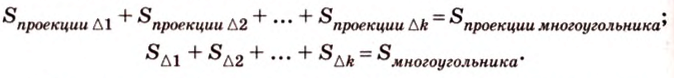
Ортогональное проецирование - определение и вычисление с примерами решения

Получим в левой части равенства площадь проекции многоугольника, а в правой – площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда

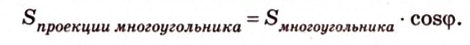
Ортогональное проецирование - определение и вычисление с примерами решения

Т.е. и для этого случая теорема истинна.

Пример:

Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.

Решение:

Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:

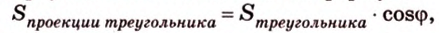
Ортогональное проецирование - определение и вычисление с примерами решения

где 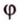Ортогональное проецирование - определение и вычисление с примерами решения – угол между плоскостью треугольника и плоскостью проекции.
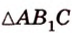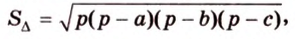
По формуле Герона найдем площадь Ортогональное проецирование - определение и вычисление с примерами решения :

Ортогональное проецирование - определение и вычисление с примерами решения

где 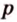Ортогональное проецирование - определение и вычисление с примерами решения – полупериметр треугольника, 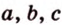– его стороны.

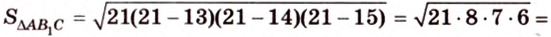
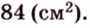
Тогда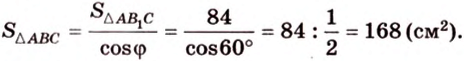

Ответ: 168 см².

Декартовы координаты на плоскости
Декартовы координаты в пространстве
Геометрические преобразования в геометрии
Планиметрия – формулы, определение и вычисление
Параллельность прямых и плоскостей
Перпендикулярность прямой и плоскости
Взаимное расположение прямых в пространстве, прямой и плоскости
Перпендикулярность прямых и плоскостей в пространстве

Источник

Материал будет полезен для учащихся 10 классов при прохождении темы” Перпендикулярность прямых и плоскостей”

Площадь ортогональной проекции.pptx

Площадь ортогональной проекции

Геометрия 10 класс

Лапшина И.И.
« Средняя школа №80 с углубленным изучением английского языка»
г. Ярославль

Понятие ортогональной проекции

Чтобы найти ортогональную проекцию
точки на плоскость, надо из этой точки
опустить на плоскость перпендикуляр

АО⊥α

Основание перпендикуляра О
ортогональная проекция
точки А на плоскость α

Ортогональная проекция треугольника на плоскость

А 𝟏 А А 𝟏 𝟏𝟏 А 𝟏

В 𝟏 В В 𝟏 𝟏𝟏 В 𝟏

С 𝟏 С С 𝟏 𝟏𝟏 С 𝟏

Если треугольник АВС
параллелен плоскости α,
то его ортогональной
проекцией на плоскость
является треугольник А 1 А А 1 1 А 1 В 1 В В 1 1 В 1 С 1 С С 1 1 С 1
равный данному

Ортогональная проекция треугольника на плоскость

Пусть сторона АВ треугольника
АВС лежит в плоскости α

Тогда ортогональной
проекцией точки С на
плоскость α является точка О.

Т.к. точки А и В лежат в
плоскости α, то их
ортогональной проекцией на
плоскость есть точки А и В

Тогда ⊿АВО-проекция ⊿ АВС на α

Площадь ортогональной проекции многоугольника

Площадь ортогональной
проекции⊿АВО равна
произведению площади ⊿ АВС
на косинус угла между
плоскостью ⊿АВО и плоскостью
⊿АВС

𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠( АВС АВС АВС ; АВО АВО АВО )

Доказательство формулы В С О 𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠(

Доказательство формулы

Проведем СК ⊥АВ и КО

АВ⊥КО ТТП

СК⊂(АВС)

СО-перпендикуляр

СК-наклонная

КО-проекция

АВ⊂α

Итак: СК⊥АВ

КО⊥АВ

СК⊂(АВС)

КО⊂(АВО)

∠СКО-линейный угол

Доказательство формулы В С О 𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠(

Доказательство формулы

⊿АВО

𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 1 2 1 1 2 2 1 2 АВ∙КО

⊿КСО

КО СК КО КО СК СК КО СК = cos α cos cos α α cos α

КО=СК∙cos⁡α

𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 1 2 1 1 2 2 1 2 АВ∙КО= 1 2 1 1 2 2 1 2 АВ∙СКcos⁡α

= 𝑆 АВС 𝑆𝑆 𝑆 АВС АВС 𝑆 АВС ∙cos⁡α

Решить №213

Домашнее задание №214

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Введите ваш emailВаш email

Источник

19
Фев 2014

Категория: Справочные материалы

Площадь ортогональной проекции многоугольника

2014-02-19
2014-02-19

Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.

Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.

Доказательство:

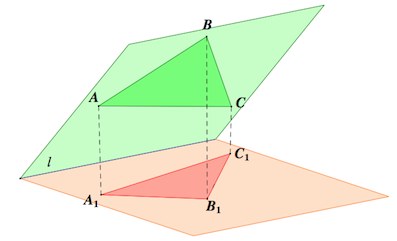
Пусть треугольник – проекция треугольника на проецируемую плоскость.

Докажем, что

$S_{A_1B_1C_1}=S_{ABC}cdot cosalpha$ ,

где – угол между плоскостями

Для этого разобьем треугольник на два треугольника c общей стороной , параллельной прямой пересечения плоскостей . (Частный случай, когда одна из сторон треугольника параллельна линии пересечения плоскостей , можно рассмотреть отдельно (самостоятельно)).

Проекция треугольника – треугольник . Причем .

Пусть – перпендикуляр к . Тогда по т. о трех перпендикулярах и – перпендикуляр к . Стало быть, – угол между плоскостями треугольников (проецируемого и проекции).

Пусть – точка пересечения и , – проекция т. на плоскость . Очевидно, – высота треугольника ( – высота треугольника ).

Из треугольника

$cosalpha =frac{B_1H}{BH}$

Но и

$frac{HT_1}{HT}=cosalpha$

Тогда $BT=BH-HT=frac{1}{cosalpha }(BH_1-HT_1)=frac{B_1T_1}{cosalpha}.$

Имеем: $S_{ABM}=frac{1}{2}BTcdot AM=frac{1}{2}cdot frac{B_1T_1}{cosalpha}cdot AM=frac{S_{A_1B_1M_1}}{{cosalpha}}.$

Аналогичные рассуждения – для пары треугольников и :

$S_{AMC}=frac{1}{2}CRcdot AM=frac{1}{2}cdot frac{C_1R_1}{cosalpha}cdot AM=frac{S_{A_1M_1C_1}}{{cosalpha}}$

(где – высота треугольника , – ее проекция)

Итак, суммируя площади треугольников и соответственно, получаем

$S_{ABC}=frac{S_{A_1B_1C_1}}{cosalpha}$

или

$S_{A_1B_1C_1}=S_{ABC}cdot cosalpha$

Что и требовалось доказать.

Пример.

Ребро куба равно 2 см. Через диагональ основания под углом $45^{circ}$ к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.

Решение:

площадь ортогональной проекции

Пусть плоскость сечения проведена через диагональ и пересекает боковое ребро () в точке .

По вышеуказанной теореме

$S_{BDT}=frac{S_{BCD}}{cosalpha},$

где треугольник – проекция треугольника на плоскость основания, – угол между плоскостями

$S_{BDT}=frac{2}{frac{sqrt2}{2}}=2sqrt2.$

Ответ:

Применение теоремы можно также посмотреть, например, в этой задаче.

Автор: egeMax |

Нет комментариев

Печать страницы

Источник

Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Площадь ортогональной проекции многоугольника

Площадь ортогональной проекции многоугольника

Теорема 18.1. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

Доказательство. Рассмотрим сначала треугольник и его проекцию на плоскость, проходящую через одну из его сторон (рис. 394). Проекцией треугольника ABC является треугольник АВС₁в плоскости . Проведем высоту CD треугольника ABC. По теореме о трех перпендикулярах отрезок CD — высота треугольника АВС₁. Угол CDC₁ равен углу между плоскостью треугольника ABC и плоскостью проекции . Имеем:

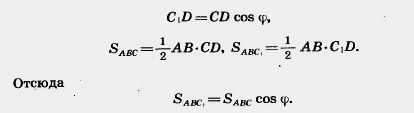
Теорема

Таким образом, в рассматриваемом случае теорема верна. Теорема верна и в случае, когда вместо плоскости а взята любая параллельная ей плоскость.

Действительно, при проектировании фигуры на параллельные плоскости ее проекции совмещаются параллельным переносом в направлении проектирования. А совмещаемые параллельным переносом фигуры равны.

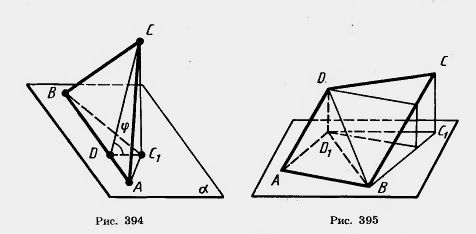
Фигуры на параллельной плоскости

Рассмотрим теперь общий случай. Разобьем данный многоугольник на треугольники. Каждый треугольник, у которого нет стороны, параллельной плоскости проекции, мы разобьем на два треугольника с общей стороной, параллельной плоскости проекции, как это показано для четырехугольника ABCD на рисунке 395.

Теперь для каждого треугольника нашего разбиения и его проекции ‘ запишем равенство . Сложим все эти равенства почленно. Тогда получим слева площадь проекции многоугольника, а справа площадь самого многоугольника, умноженную на cos . Теорема доказана.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_Видео _{по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.

Разработка – Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

Источник

2.1. Задача по построению линии пересечения плоскостей

Для решения этой задачи преобразуем
плоскость параллелограмма в проецирующую.
Для этого проведем в параллелограмме
главную линию – горизонталь или фронталь.
Выбор линии определяется заданным
чертежом и наличием вокруг него свободного
пространства. В примере удобно построить
горизонталь.

Выбираем ось проекций Х перпендикулярно
главной линии параллелограмма ( в примере
– горизонтали). Получили новую систему
плоскостей проекций П1-П4.

Строим в системе П1-П4 параллелограмм и
треугольник, используя для этого
координаты Z точек. Если
построения проведены верно, то
параллелограмм спроецируется в прямую
на плоскость П4. Далее проводим решение
задачи в частном виде в системе плоскостей
проекций П1-П4.

Для того чтобы вернуться к исходному
чертежу, надо найти проекции точек по
принадлежности их сторонам треугольника.
Пример решения задачи показан на рисунке
6.

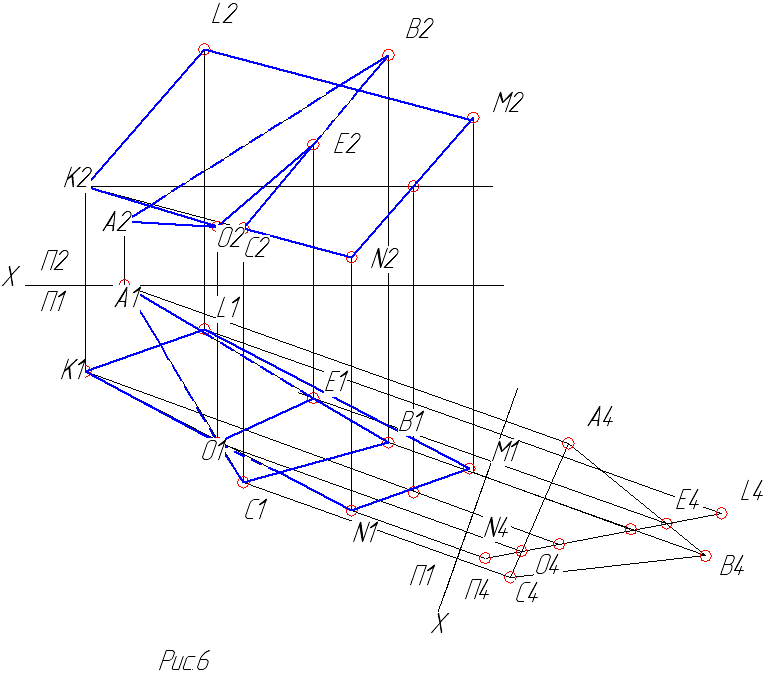
2.2 Построение ортогональной проекции треугольника на плоскость параллелограмма

Для решения этой задачи преобразуем
плоскость параллелограмма в проецирующую,
т.е. выполним построение, проведенное
в предыдущей задаче. Следовательно,
решение этой задачи можно рассматривать,
как продолжение предыдущей (смотри
рис.6).

Продолжим решение на рис.6. Для нахождения
ортогональной проекции треугольника
на плоскость параллелограмма найдем
ортогональную проекцию каждой вершины
треугольника на параллелограмм. Для
этого проведем из вершин треугольника
перпендикуляры на плоскость параллелограмма
в системе плоскостей проекций П1-П4.
Точка пересечения перпендикуляров с
прямой, в которую проецируется
параллелограмм, и есть ортогональная
проекция вершин на плоскость
параллелограмма.

Эти перпендикуляры являются прямыми
уровня, следовательно на плоскость
проекций П1 они проецируются в прямые,
параллельные оси Х (П1-П4). Из этого условия
находим горизонтальную проекцию
ортогональных проекций.

Фронтальную проекцию найдем по линиям
связи, откладывая от оси Х (П1-П2) расстояние
от соответствующих проекций до оси Х
(П1-П4).

Все построения приведены на рисунке 7.

2.3. Построение плоскости, параллельной плоскости параллелограмма

В задаче №3 надо построить плоскость
треугольника, параллельную плоскости
параллелограмма на расстоянии 40 мм.

Для решения задачи преобразуем плоскость
параллелограмма в проецирующую. Для
этого выберем новую ось проекций ( П1-П4)
перпендикулярно горизонтали
параллелограмма, как это было сделано
в предыдущих задачах. В этой задаче
работаем только с параллелограммом.

Сначала найдем точку, удаленную от
параллелограмма на расстоянии 40 мм. Для
этого восстановим перпендикуляр длиною
40 мм из одной из вершин параллелограмма,
например из К ( построение проведем в
системе плоскостей проекции П1-П4).
Получим проекцию точки, расположенной
от параллелограмма на расстоянии 40 мм
– R4.

Так как перпендикуляр есть отрезок
уровня, то на плоскость проекций П1 он
спроецируется параллельно оси Х (П1-П4).
Из этого условия найдем проекцию точки
R (R1).

Затем найдем проекцию R2
из условия, что она отстоит от оси Х
(П1-П2) на том же расстоянии, что R4
от оси Х (П1-П4).

Все эти построения приведены на рисунке
8.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Ортогональное проецирование – определение и вычисление с примерами решения

Площадь ортогональной проекции

Понятие ортогональной проекции

Ортогональная проекция треугольника на плоскость

Ортогональная проекция треугольника на плоскость

Площадь ортогональной проекции многоугольника

Доказательство формулы В С О 𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠(

Доказательство формулы В С О 𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠(

Решить №213

Домашнее задание №214

Площадь ортогональной проекции многоугольника

Пример.

2.1. Задача по построению линии пересечения плоскостей

2.2 Построение ортогональной проекции треугольника на плоскость параллелограмма

2.3. Построение плоскости, параллельной плоскости параллелограмма

Вам также может понравиться

Как найти область объединения

Как составить интерьер для своей комнаты

Как найти всю историю скайпа

Добавить комментарий Отменить ответ