Как найти проекцию ускорения движущегося тела

Как найти проекцию ускорения движущегося тела

  • Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
  • Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
  • Единица измерения ускорения — метр в секунду в квадрате (м/с2).
  • Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

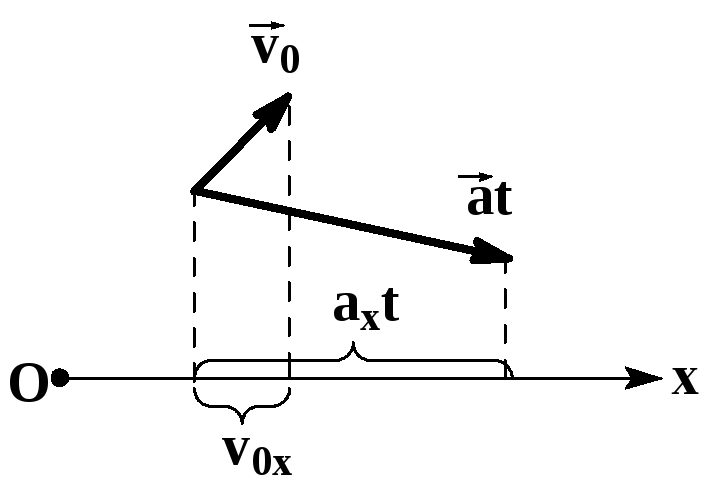
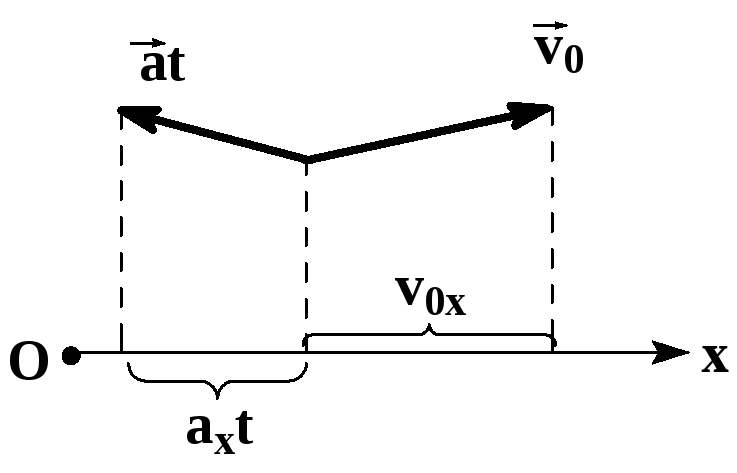
Проекция ускорения на ось ОХ

vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

  • Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
  • Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

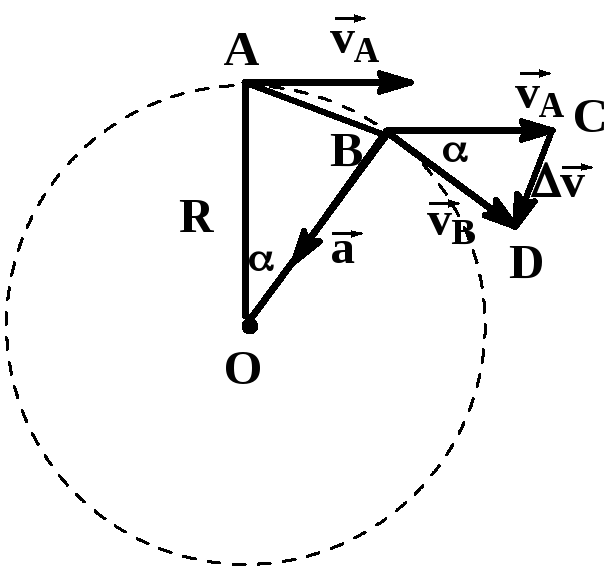
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

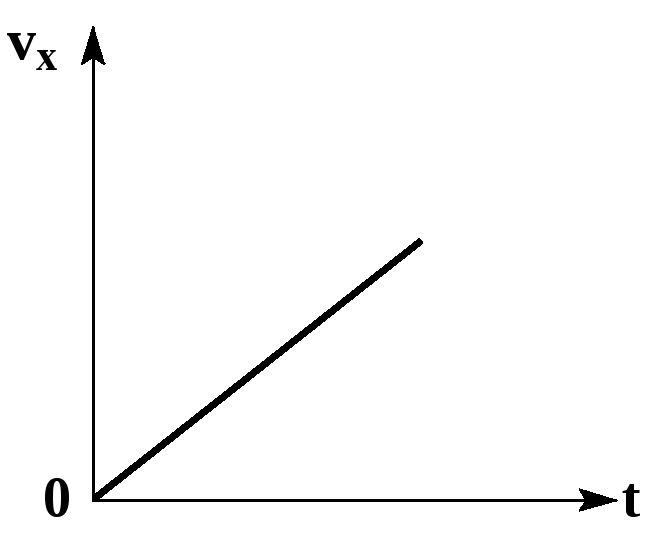
График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

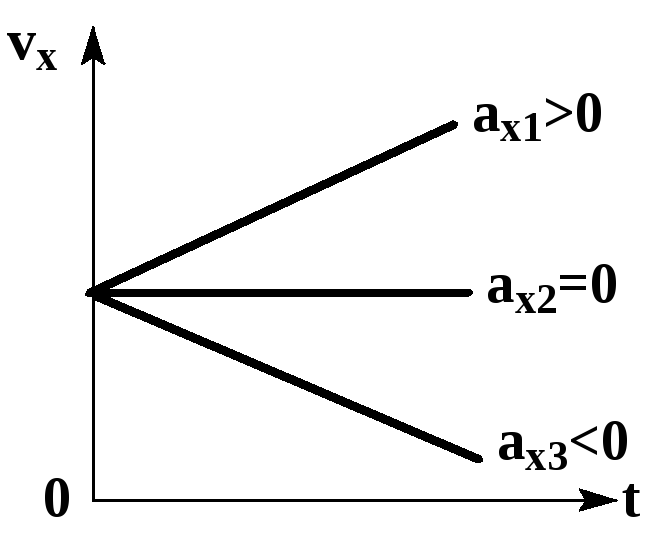
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

  • Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
  • Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

  1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
  2. Определить величины, которые характеризуют такое движение.
  3. Определить характер изменения величин, характеризующих это движение.
  4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

  • перемещение и путь;
  • скорость;
  • ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17992

Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?

Алгоритм решения

  1. Записать исходные данные.
  2. Записать формулу, связывающую известные из условия задачи величины.
  3. Выразить из формулы искомую величину.
  4. Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

  • Начальная скорость v0 = 5 м/с.
  • Конечная скорость v = 15 м/с.
  • Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18202

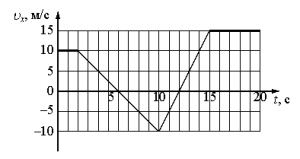
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.

Какой из указанных ниже графиков  совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?

Алгоритм решения

  1. Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
  2. Вычислить ускорение движение тела на этом участке.
  3. Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

  • t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
  • t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18027

На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.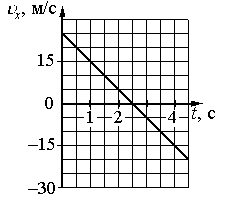

Алгоритм решения

  1. Записать формулу ускорения.
  2. Записать формулу для вычисления модуля ускорения.
  3. Выбрать любые 2 точки графика.
  4. Определить для этих точек значения времени и проекции скорости (получить исходные данные).
  5. Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

  • t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
  • t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 13.7k

Источник

Как найти ускорение — определение и формулы расчета в физике

Содержание:

  • Что такое ускорение

    • Единица измерения
  • Как рассчитать ускорение: формулы

    • Для прямолинейного движения
    • Для равноускоренного движения
    • Для равнозамедленного движения
    • Нахождение ускорения через массу и силу
  • Мгновенное ускорение
  • Максимальное ускорение
  • Среднее ускорение
  • Проекция ускорения

Что такое ускорение

Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.

Единица измерения

В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

(a;=;frac{mathrm V}t)

(a;=;frac{2S}{t^2})

(a;=;frac{V^2}{2S})

Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

(overrightarrow a=frac{overrightarrow F}m)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})

Максимальное ускорение

(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось (х):

(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.

Насколько полезной была для вас статья?

Рейтинг: 1.94 (Голосов: 35)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Проекции скорости и ускорения

Для выполнения
расчетов скоростей и ускорений необходимо
переходить от записи уравнений в
векторной форме к записи уравнений в
алгебраической форме.

Векторы начальной
скорости
и ускорениямогут иметь различные направления,
поэтому переход от векторной записи
уравнений к алгебраической может
оказаться весьма трудоемким.

Известно, что
проекция суммы двух векторов на какую-либо
координатную ось равна сумме проекций
слагаемых векторов на ту же ось.

Поэтому для
нахождения проекции
вектора скоростина произвольную ось OX нужно найти
алгебраическую сумму проекций векторовина ту же ось.

Проекцию
вектора на ось считают положительной,
если от проекции начала к проекции
конца вектора нужно идти по направлению
оси, и отрицательной в противоположном
случае.

График скорости

Из уравнения
следует, что графиком зависимости
проекции скорости равноускоренного
движения от времени является прямая.
Если проекция начальной скорости на
ось OX равна нулю, то прямая проходит
через начало координат.

Основные
виды движения

  1. аn
    = 0, a
    = 0     –
    прямолинейное равномерное движение;

  2. аn
    = 0, a
    =     const
    – прямолинейное равнопеременное
    движение;

  3. аn
    = 0, a

    0 –     прямолинейное
    с переменным ускорением;

  4. аn
    = const,
    a
    = 0 –     равномерное
    по окружности

  5. аn
    = const,
    a
    =     const
    – равнопеременное по окружности

  6. аn

    const,
    a

    const
    – криволинейное с переменным ускорением.

Вращательное движение твердого тела.

Вращательное
движение твердого тела относительно
неподвижной оси
– движение, при котором все точки
твердого тела описывают окружности,
центры которых лежат на одной прямой,
называемой осью
вращения.

Равномерное движение по окружности

Рассмотрим наиболее
простой вид вращательного движения, и
уделим особое внимание центростремительному
ускорению.

При равномерном
движении по окружности значение скорости
остается постоянным, а направление
вектора скорости
изменяется в процессе движения.

За
интервал времени ∆t
тело проходит путь
.
Этот путь равен длине дугиAB.
Векторы скоростей
ив точкахA
и B направлены
по касательным к окружности в этих
точках, а угол
между векторами
иравен углу между радиусамиOA
и OB.
Найдем разность векторов
и определим отношение изменения
скорости к∆t:

Из подобия
треугольников OAB и BCD следует

Если интервал
времени ∆t
мал, то мал и угол .
При малых значениях угла 
длина хорды AB примерно равна длине дуги
AB, т.е.
.
Т.к.,,
то получаем

.

Поскольку
,
то получаем

Период и частота

Промежуток времени,
за который тело совершает полный оборот
при движении по окружности, называется
периодам
обращения
(Т).
Т.к. длина окружности равна 2R,
период обращения при равномерном
движении тела со скоростью v
по окружности радиусом R
равняется:

Величина, обратная
периоду обращения, называется частотой.
Частота показывает, сколько оборотов
по окружности совершает тело в единицу
времени:

(с-1)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #

    01.06.2015304.13 Кб31KP.doc

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

im35.gif

Рис. (1). Изменение скорости при прямолинейном равноускоренном движении

Частным (простым) видом неравномерного движения является прямолинейное равноускоренное движение, когда траектория движения тела — прямая линия. Для характеристики изменения скорости вводят новую физическую величину — ускорение.

Ускорение — физическая величина, характеризующая изменение скорости за единицу времени:

([a]=1frac{м}{с^2}).

Равноускоренное движение — это движение с постоянным ускорением: (a=const).

Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: 

a→=v→−v0→t

.

движение_ускорение.svg

Рис. (2). Ускорение тела

Вычислить ускорение тела, движущегося прямолинейно и равноускоренно, можно с помощью уравнения, в которое входят проекции векторов ускорения и скорости:

ax=vx−v0xt

.

Единица ускорения в СИ:

1м/с2

.

Применяются и другие единицы ускорения, например:

1см/с2

.

Скорость прямолинейного равноускоренного движения:

vx=v0x+axt

, где

v0x

 — проекция начальной скорости,

ax

 — проекция ускорения, 

t

 — время.

Если в начальный момент тело покоилось, то 

v0→=0

. Для этого случая формула принимает следующий вид:

vx=axt

.

Обрати внимание!

Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость; если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону.

Источники:

Рис. 1. http://fizmat.by/kursy/kinematika/ravnouskorennoe
Рис. 2. Ускорение тела. © ЯКласс.

Источник

Содержание материала

  1. Как найти ускорение по графику формула?
  2. Видео
  3. Равноускоренное движение в направлении оси, скорость увеличивается
  4. Равноускоренное движение против оси
  5. Как составить уравнение скорости по графику?
  6. График отрицательной скорости для отрицательного ускорения
  7. Графики равноускоренного движения

Как найти ускорение по графику формула?

График ускорения — графическое представление уравнения ускорения тела а = а(t). График а(t) служит для описания движение тела. На этом графике представлено равноУскоренное движение. Как будут выглядеть графики, придуманные вами, можно увидеть здесь.

Видео

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Рис.4. Тело движется равноускорено – рис. а) по на

Рис.4. Тело движется равноускорено – рис. а) по направлению оси Ox. Изменение координаты от времени x(t) описывается правой ветвью параболы – рис. б), график v(t) скорости изображен наклонной возрастающей прямой – рис. в), а график неизменного ускорения a(t) – рис. г) изображается горизонтальной прямой, лежащей выше оси времени

Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.

Уравнение, которое описывает квадратичное изменение координаты, выглядит так:

[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

[ v  = v_{0} + a cdot t ]

Ускорение есть (рис. 4г) и оно не меняется:

[ a = const ]

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

  • по линейному закону, когда скорость не меняется — остается одной и той же.
  • по квадратичному закону, когда скорость будет изменяться (расти, или убывать).

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Рис.5. Тело движется равноускорено противоположно

Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Как составить уравнение скорости по графику?

График скорости График скорости — графическое представление уравнения скорости тела v = v(t). График v(t) служит для описания движение тела. На этом графике представлено равноУскоренное движение.

График отрицательной скорости для отрицательного ускорения

Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.

Отрицательная скорость В/с График времени

Отрицательная скорость В/с График времени

Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном д

Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.

Пусть начальная координата тела , скорость движе

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Уск

Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном д

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.

График движения при . График движения при График движения при . График движения при

График движения при . График движения при

График движения при . График движения при График движения при . График движения при

График движения при Теги. График движения при Теги

Теги

Источник

Добавить комментарий