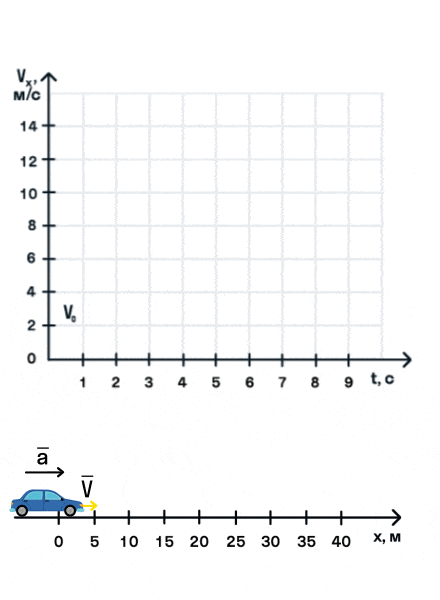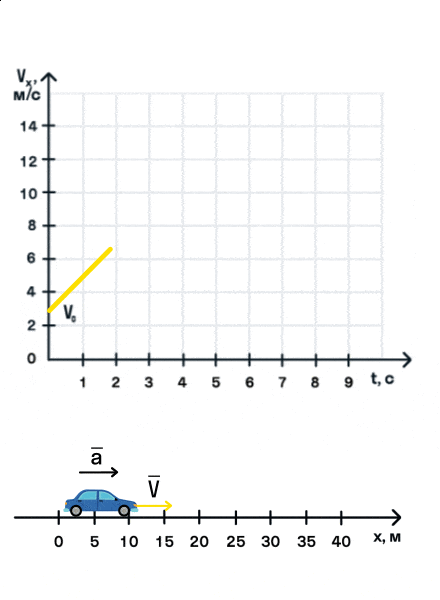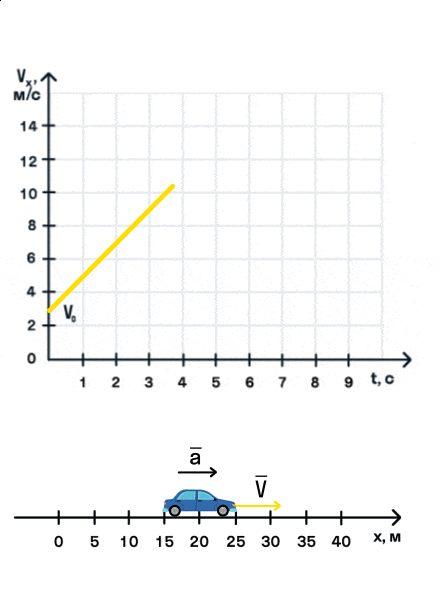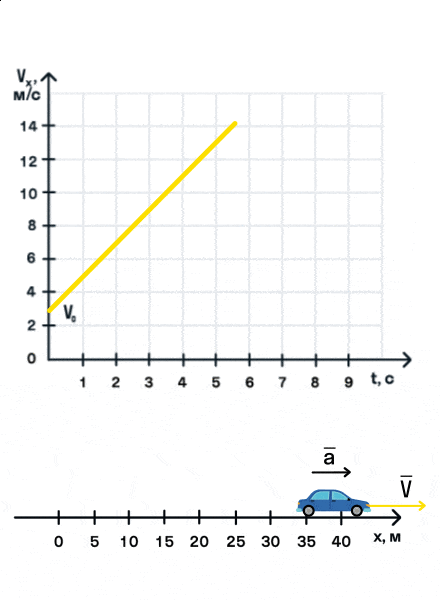
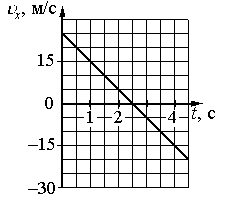- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХ
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
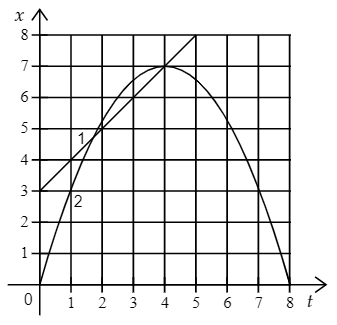
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
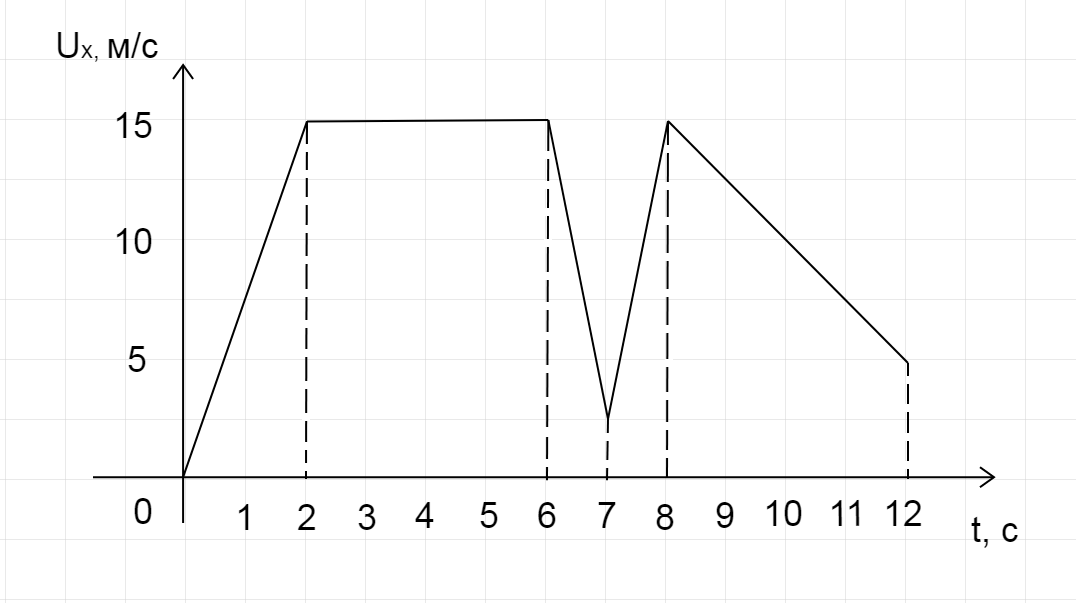
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
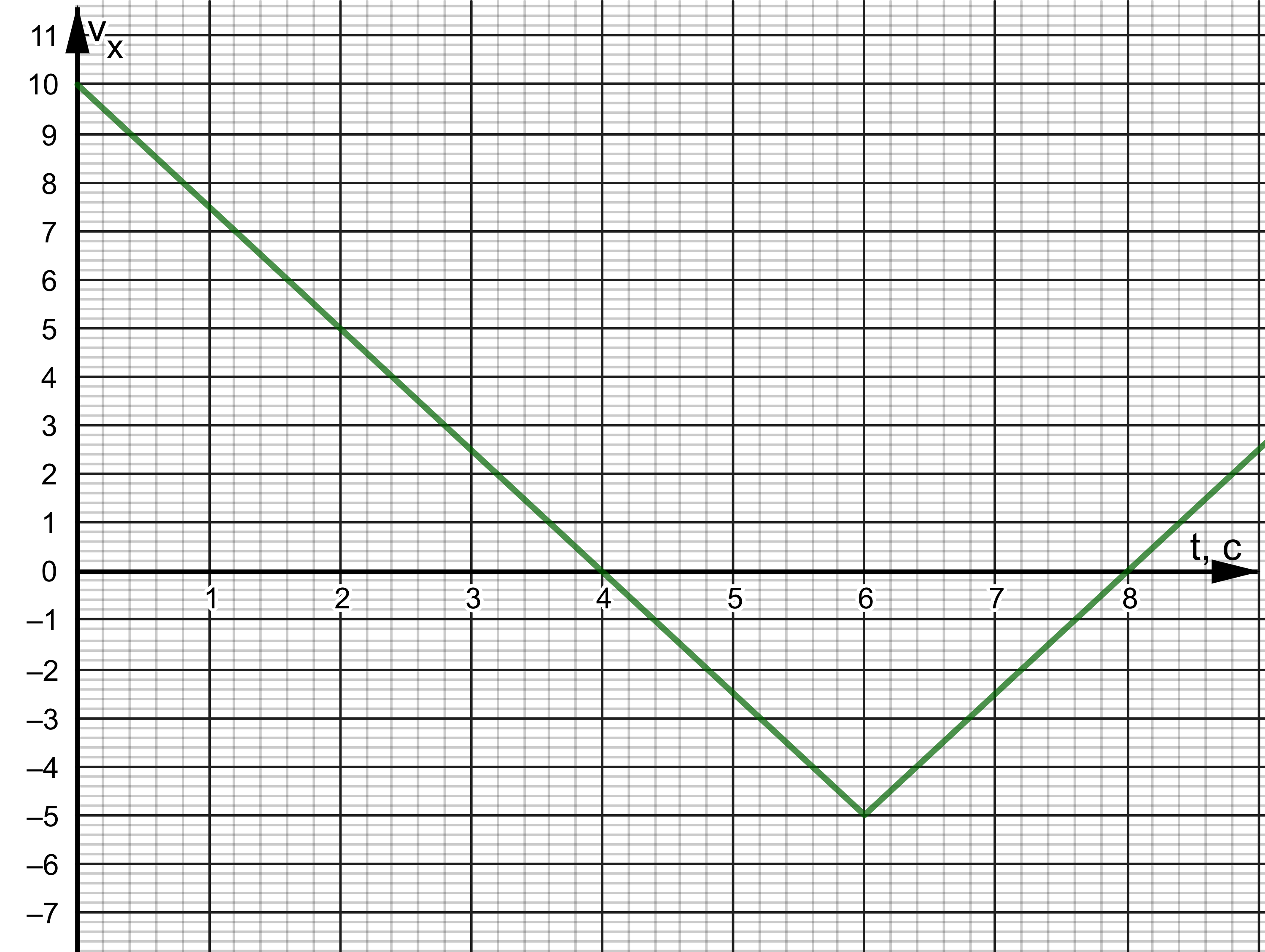
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.7k
Задание №1. Первое задание ЕГЭ по физике проверяет знания по разделу «Кинематика». Это задание относится к заданию базового уровня. В нём отсутствует возможность выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.
Определение кинематических величин по графику
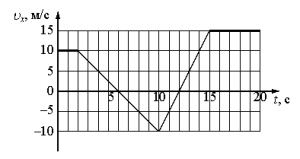
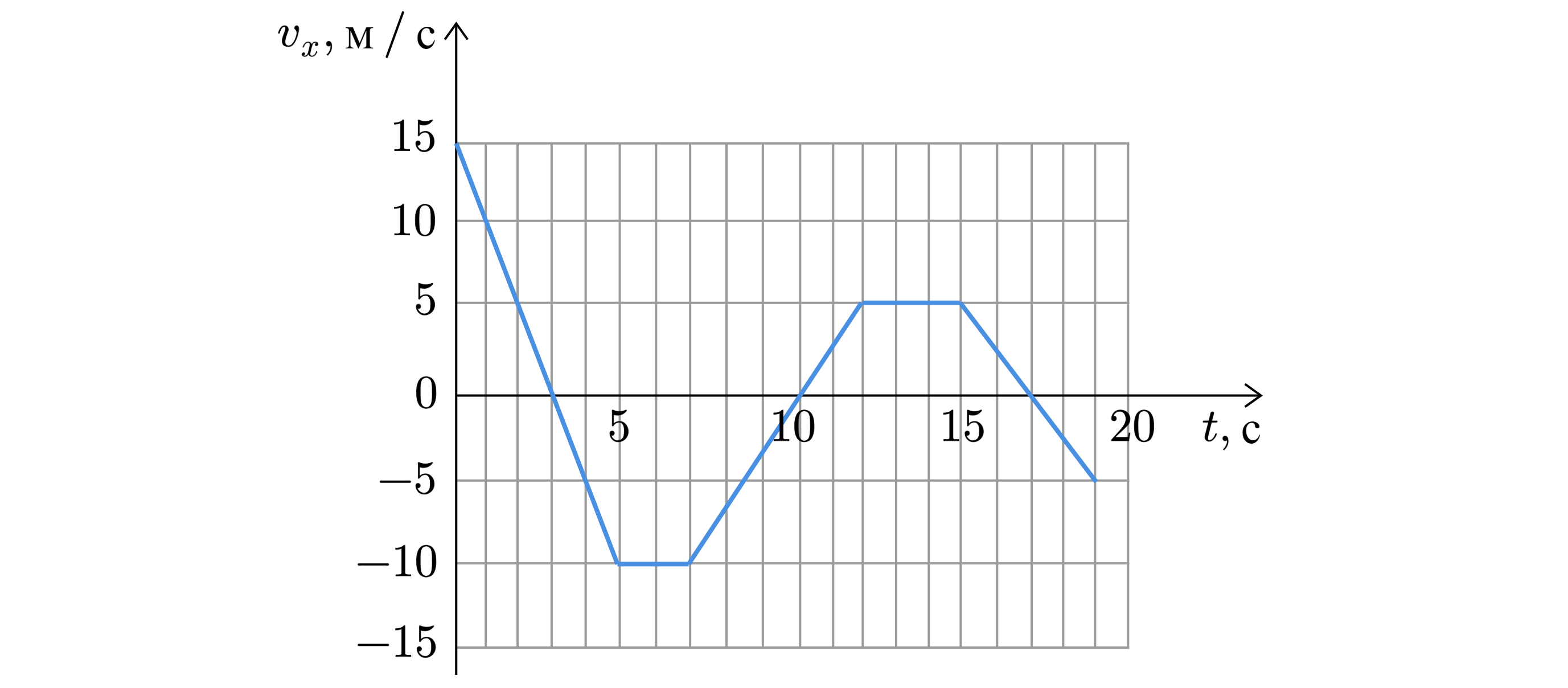
1. На рисунке приведён график зависимости проекции скорости тела vx от времени t.
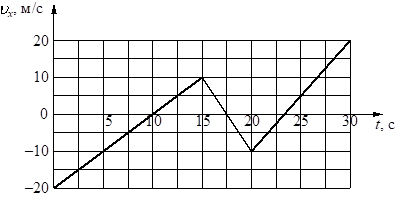
Определите проекцию ускорения тела ax в промежутке времени от 15 до 20 с.
Ответ: ___________ м/с2.
На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, при котором проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:
. Проведем расчет:
(м/с2). Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.
Ответ: -4 м/с2.
Пояснение. Долгое время движение с переменной скоростью делилось на равноускоренное (ax > 0) и равнозамедленное (ax < 0) Но в последнее время говорят, в основном, только о равноускоренном движении, подразумевая постоянство ускорения. И только лишь знак проекции ускорения определяет возрастание или убывание скорости движения тела.
2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.
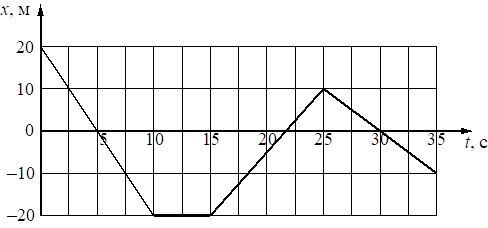
Определите проекцию скорости тела vx в промежутке времени от 25 до 30 с.
Ответ: _____________ м/с.
Согласно представленному графику зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Для решения задачи необходимо воспользоваться формулой для определения скорости при равномерном движении:
. Проведем расчет:
Ответ: -2 м/с.
Пояснение. Проекция скорости получилась отрицательной, это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.
3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.
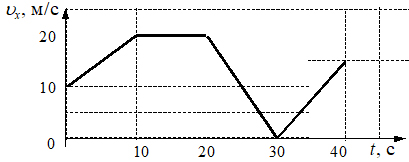
Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.
Ответ: ___________ м.
Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.)
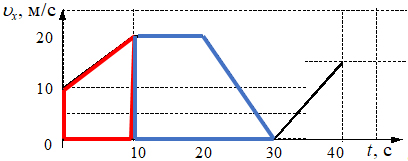
Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).
;
S = 150 + 300 = 450 (м)
Ответ: 450 м.
Пояснение. Полученный пятиугольник можно разбить не только на две трапеции, здесь можно выделить трапецию, прямоугольник, треугольник. Тогда необходимо рассчитывать площади трех фигур и также их суммировать.
4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох от времени.
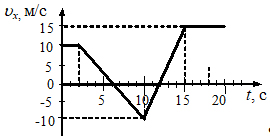
Определите проекцию перемещения пройденного телом, за 10 с от начала наблюдения.
Ответ: _________ м.
Так же как в задаче №3 модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.
;
S = 40 + (-20) = 20 (м)
Ответ: 20 м.
Пояснение. При расчете S2x можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с, тело движется в направлении противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.
Относительность движения
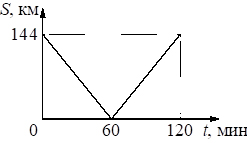
5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?
Формула для нахождения относительной скорости в векторной форме имеет вид:
Если два тела движутся навстречу друг другу, то в проекциях на ось OХ это уравнение преобразуется в следующий вид:

С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.
, отсюда скорость первого автомобиля v1 = 40 – 25 = 15 (м/c)
Ответ: 15 м/с.
Пояснение. В курсе математики при изучении движения двух тел вводятся понятия скорость сближения и скорость удаления. В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.
6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?
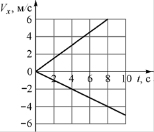
Ответ: _________ м.
Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.
Знак «минус» для S2x показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.
Ответ: 40 м.
Пояснение. Самое главное в этой задаче – выяснить в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.
7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?
Ответ: ________ км/ч
Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо, тогда для движения перпендикулярно береговой линии, катеру необходимо держать курс немного левее.
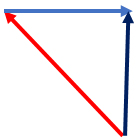
Скорость катера, скорость реки и скорость катера относительно береговой линии можно связать по теореме Пифагора:
; отсюда
;
(км/ч).
Ответ: 7,5 км/ч.
Пояснение. Подобные задачи необходимо для себя представлять в виде чертежа или рисунка. Тогда указанные в условии параметры будут наглядно изображены и это поможет геометрически решить задачу.
Равномерное движение тел по окружности
8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.
Ответ: ___________ м/с2
Так как тело движется равномерно по окружности, то в этой задаче требуется найти центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением Подставляя это выражение в первое уравнение и проводя сокращения, получим . При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.
Проведем расчет: .
Ответ:
Пояснение. В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.
9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?
Ответ: _________ Гц.
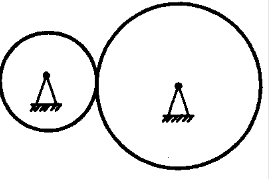
Так шетерни касаются друг друга, то это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.
Приравняем скорости и проведем сокращения.
;
;
с учетом того, что период и частота величины обратные, запишем следующее равенство:
Проведем расчет:
Ответ: 4 Гц.
Пояснение. В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В этой задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.
10. Волчок, вращаясь с частотой 20 с-1, свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?
Ответ: _________ оборотов
Определим вначале время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость надо принять равной 0. Тогда высота и время падения будут связаны формулой отсюда
Проведем расчет времени падения
=1 (с). Так как волчок вращается с частотой 20 с-1, то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.
Ответ: 20.
Пояснение. Эта задача является комбинированной. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное – не ошибиться со знаками проекций для скорости и ускорения.
См. продолжение статьи
.
02
Равноускоренное движение
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
№1 кинематика
Решаем задачи
Координата тела меняется с течением времени согласно закону , где все величины выражены в СИ. Определите проекцию
скорости этого тела. Ответ дайте в м/c.
Показать ответ и решение
При равномерном движении координата меняется
где – начальная скорость. Тогда
м/с.
На рисунке представлен график зависимости проекции скорости тела от времени
.
Определите проекцию ускорения этого тела в интервале времени от 0 до 10 с. Ответ дайте в
м/с
Показать ответ и решение
Найдем проекцию ускорения тела по формуле:
Найдем :
Подставим исходные данные:
Найдем :
Подставим исходные данные:
Подставим полученные данные в формулу проекции ускорения тела:
Показать ответ и решение
Ускорение можно найти по формуле:
где м/c,
м/c, а
c.
Подставив данные значения, получим:
На рисунке представлен график зависимости модуля скорости прямолинейно движущегося тела от
времени . Определите по графику проекцию перемещения тела (в м) в интервале времени от 1 до 5 с.
Показать ответ и решение
Путь можно найти как площадь под графиком. В данном случае площадь прямоугольной
трапеции:
На рисунке приведен график зависимости проекции скорости тела от времени
Определите путь, пройденный телом в интервале времени от 5 до 10 с. Ответ дайте в
м.
Основная волна 2020
Показать ответ и решение
Путь в данном случае можно найти, как площадь трапеции:
На рисунке приведён график зависимости проекции скорости тела от времени
.
Определите путь, пройденный телом в интервале времени от 0 до 5 с. Ответ дайте в м.
Досрочная волна 2020
Показать ответ и решение
Путь можно найти как площадь под графиком. Путь будет складываться из двух слагаемых. Первое –
при положительной скорости (до 3 с)
Второе – отрицательная скорость (от 3 с до 5 с)
В
сумме 32,5 м
На рисунке приведён график зависимости проекции скорости тела от времени. Чему равна
проекция ускорения этого тела в интервале времени от 5 до 10 с? Ответ выразите в
м/с.
Досрочная волна 2019
Показать ответ и решение
Ускорение:
Определите по графику зависимости проекции скорости от времени t модуль перемещения тела за
время от c до
c. Ответ дайте в м.
Досрочная волна 2019
Показать ответ и решение
Перемещение будет равно разности пройденных путей от 2 до 4 и от 4 до 6 секунд. В общей формуле это
запишется как:
Материальная точка движется прямолинейно с постоянным ускорением вдоль оси . График
зависимости её координаты от времени изображён на рисунке. Определите проекцию
ускорения этого тела. Ответ дайте в м/с
Демоверсия 2021
На рисунке показан график зависимости от времени для проекции скорости тела. Какова проекция
ускорения этого тела в интервале времени от 5 до 6 c? Ответ дайте в м/с
Демоверсия 2019
Показать ответ и решение
Ускорение:
На рисунке показан график зависимости от времени для проекции скорости тела. Какова проекция
ускорения этого тела в интервале времени от 4 до 8 c? Ответ дайте в м/с
Демоверсия 2018
Показать ответ и решение
Ускорение тела равно:
Тело движется равнозамедленно с ускорением м/с
не изменяя направления движения. За
время t модуль скорости тела уменьшился от 4 м/с до 3 м/с. Какой путь прошло тело за это время?
(Ответ дайте в метрах)
Показать ответ и решение
1 способ:
Примем, что начальная скорость тела равна м/с, а скорость, которую тело приобрело спустя
время , равна
м/с. Перемещение при равноускоренном движении можно выразить
формулой:
2 способ:
Примем, что начальная скорость тела равна м/с, а скорость, которую тело приобрело спустя
время , равна
м/с. По формуле скорости при равнозамедленном движении:
Отсюда выразим :
t =
По формуле перемещения при равнозамедленном движении:
S = υ0t −
Подставив , получим:
Подставим значения:
На рисунке приведён график зависимости проекции скорости тела от времени. Чему равна
проекция ускорения этого тела в интервале времени от 8 до 12 с? Ответ выразите в
м/с
Показать ответ и решение
Уравнение для координаты при равноускоренном движении имеет вид:
Согласно условию задачи тело двигалось без начальной скорости (). Тогда уравнение для
координаты имеет следующий вид:
Определим ускорение тела, используя точку в момент времени :
Скорость зависит от времени по формуле:
В
момент времени с она равна
м/с.
Показать ответ и решение
Общий вид закона изменения со временем координаты тела при движении с постоянным ускорением
имеет вид:
Приведенная в условии зависимость координаты тела от времени описывается этой
квадратичной зависимостью. Приравнивая коэффициенты при t находим, что величина постоянного
ускорения м/c
На рисунке представлен график зависимости модуля скорости Человека – паука от времени
.
Определите по графику путь, который пролетел Человек – паук за первые 10 секунд. (Ответ дайте в
метрах)
Показать ответ и решение
Путь можно найти двумя способами:
1 способ:
Путь — величина строго положительная, это длина пройденного телом участка траектории. Под
перемещением же тела понимается изменение его координаты, перемещение может быть
отрицательным. Путь можно найти как площадь под графиком зависимости скорости от времени
без учета знаков, а перемещение с их учетом. В данном случае необходимо найти площадь
трапеции.
2 способ:
Рассмотрим участок движения от 0 до 10 с, где м/с ,
м/с.
При равноускоренном движении автомобиля на пути 50 м его скорость увеличилась от 10 до 20 м/с.
Чему равно ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Показать ответ и решение
По формулам кинематики равноускоренного движения:
где S
– расстояние, м/с,
м/с
Выражая из (2) время и подставляя его в (1) находим, что
Человек съезжает с горки на мопеде, двигаясь прямолинейно и равноускоренно. За время спуска
скорость человека увеличилась на м/с. Ускорение равно 2 м/с
Сколько секунд длился
спуск?
Показать ответ и решение
Ускорение мопеда по определению:
Выразим из уравнения и подставим данные из условия:
Мяч подброшен вертикально вверх. Через 2 с после броска его скорость стала равна 5 м/с. Какова
начальная скорость мяча? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в
секунду.)
Показать ответ и решение
По условию задачи, сопротивлением воздуха пренебрегаем, тогда на мяч действует только сила тяжести,
она же и создает ускорение свободного падения, направленное против движения тела. Тогда скорость в
момент времени определяется по формуле:
Выражаем отсюда начальную скорость , которую нам и необходимо найти, подставляем значения
из условия:
Два точечных тела 1 и 2 движутся вдоль оси . Зависимости координат
этих тел от времени
изображены на рисунке. В какой момент времени проекции скоростей этих тел будут приблизительно
одинаковыми? Ответ дайте в секундах и округлите до целых.
Показать ответ и решение
1 способ:
Скорость — это производная по времени от координаты . Геометрический смысл производной —
тангенс угла наклона касательной, следовательно, чтобы проекции скоростей этих тел были
приблизительно одинаковыми, ко второму графику надо провести касательную, параллельную первой
прямой. Эта касательная примерно пройдет через точку с.
2 способ:
Напишем уравнения движения данных тел. Изменение координаты первого тела линейное,
следовательно первое тело движется равномерно:
Так
как зависимость координаты второго тела квадратичная, графиком её является парабола, то второе тело
движется равноускоренно:
Так
как первое тело движется равномерно, его скорость остается неизменной. Выразим скорость из
уравнения (1):
По
условию задачи:
Запишем уравнение (2) другим способом. Зависимость координат второго тела — парабола с вершиной
при и
с корнями (т.е. точками пересечений с осью
)
и
. Тогда
получим:
Выразим из уравнения (3) и подставим координаты вершины параболы:
Тогда уравнение (3) преобразуется в:
Заметим, что скорость — производная пути. Найдем производную пути из уравнения (4).
Получим:
Выразим отсюда время , которое и необходимо нам найти по условию задачи:
Перейти к содержанию
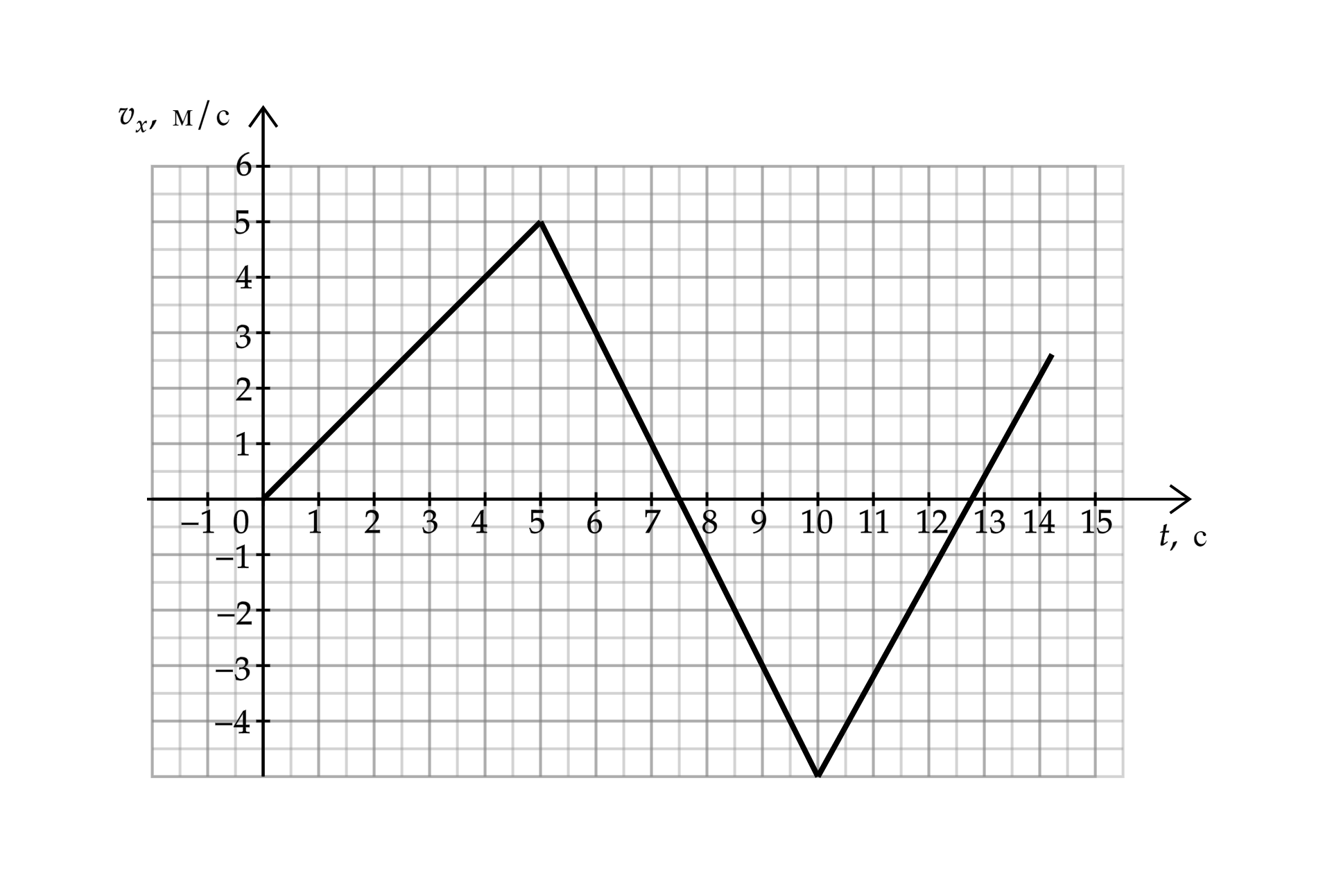
Задание 1. На рисунке приведён график зависимости проекции скорости тела от времени. Чему равна проекция ускорения в промежуток времени от 10 до 15 с?
Решение задачи
Рассмотрим по графику промежуток времени от 10 до 15 с. По формуле ускорения материальной точки найдём проекцию искомого ускорения:
Подставим числовые значения в формулу.
a = 15 -(-10) / 5 = 5 м/с2.
Ответ к задаче
Ответ: 5 м/с2.
Просмотров: 11 915
Добавить комментарий
Основные определения
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.
Несколько примеров равноускоренного движения:
-
разгон самолета перед взлетом;
-
торможение лыжника на горном склоне;
-
свободное падение в результате прыжка с парашютом;
-
велосипедист, спускающийся с горки;
-
мальчишки, играющие в догонялки.
Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Формула ускорения при равноускоренном движении
,
где a — ускорение тела [м/с2],
V — мгновенная скорость [м/с],
V0 — начальная скорость [м/с],
t — время [с].
Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:
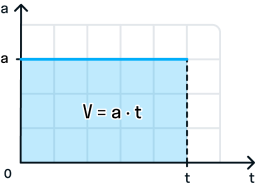
При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.
Если из формулы ускорения выразить мгновенную скорость, т. е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:
V(t) = V0 + at,
где V(t) — скорость в момент времени t [м/с],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Задача 1
Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с2?
Решение.
По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:
V(10) = 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10 с Арсений разгонится до скорости 11 м/с.
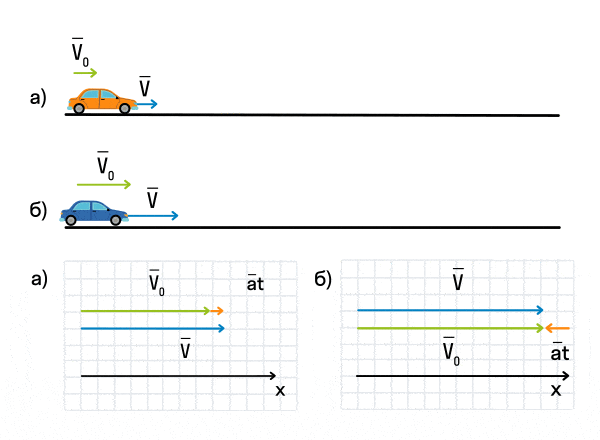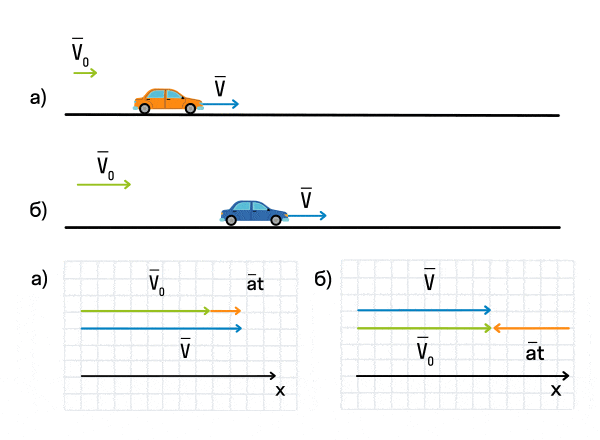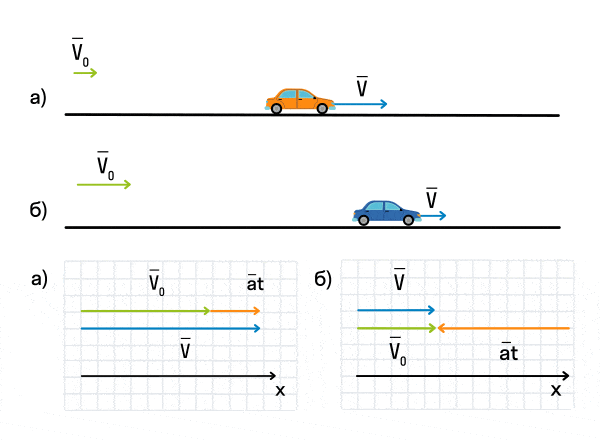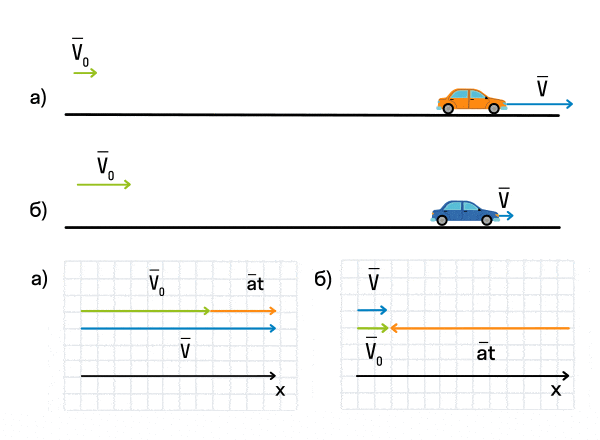
Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.
Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
График зависимости скорости от времени при равноускоренном движении
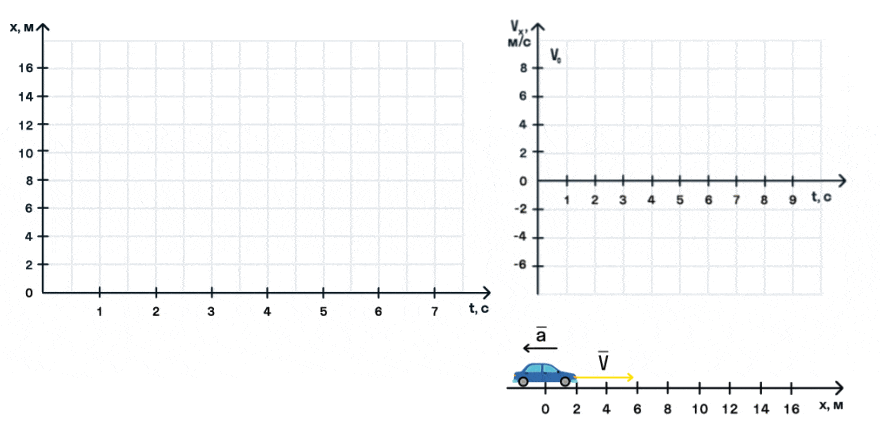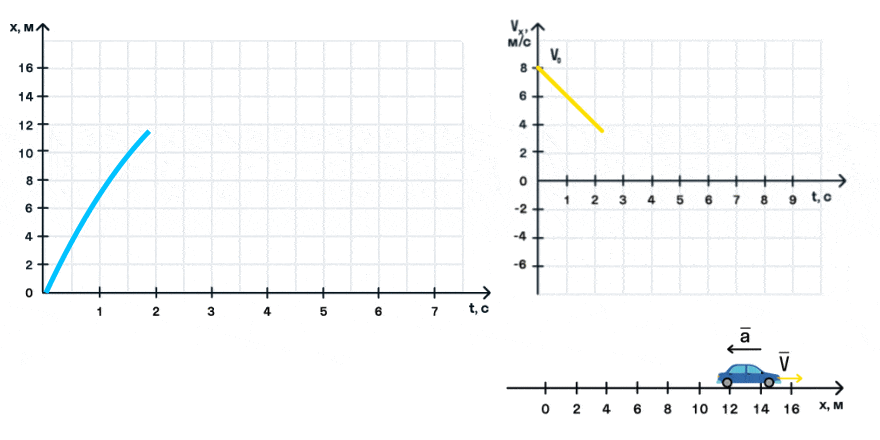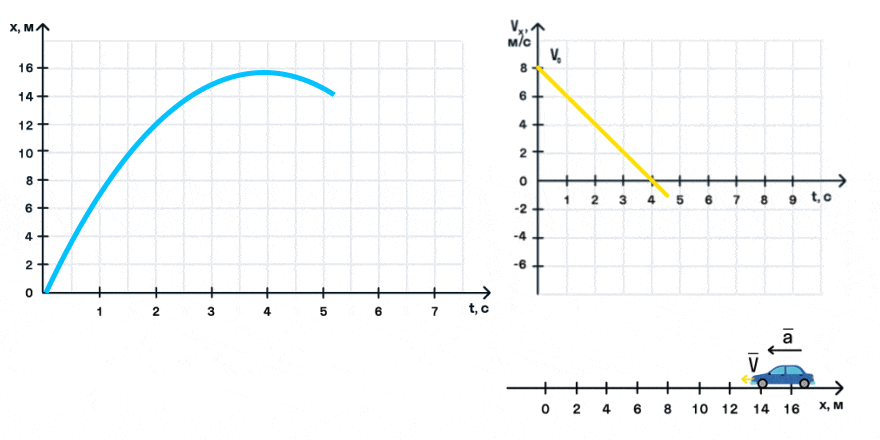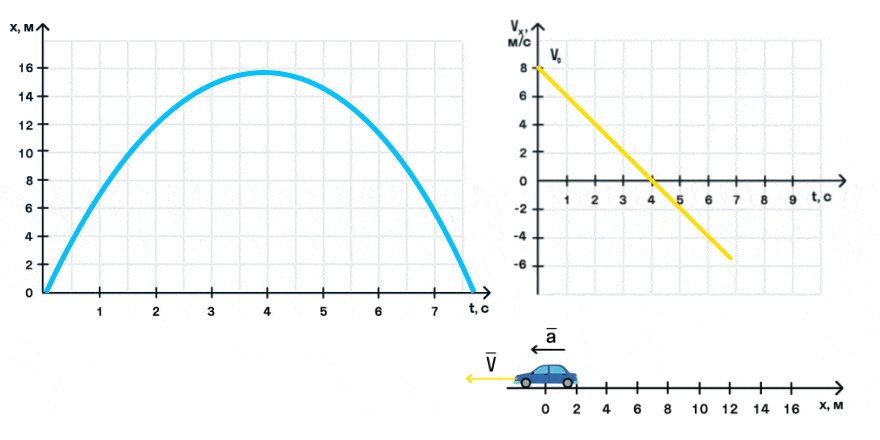
Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.
На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V0).
При равнозамедленном движении прямая на графике будет убывать.
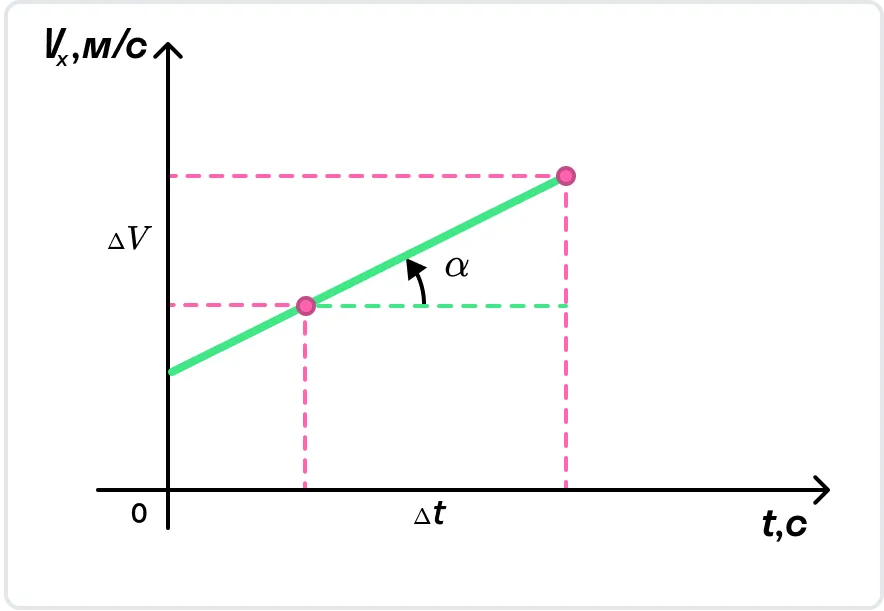
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:
.
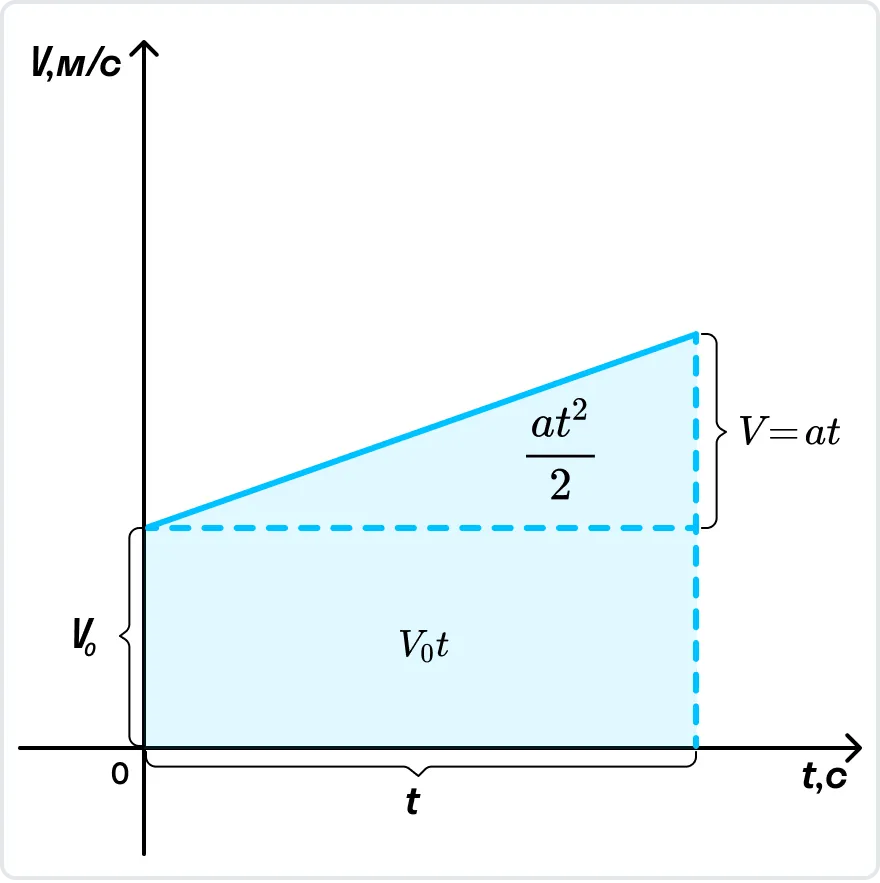
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V0t и треугольника
.
Формула пути при равноускоренном движении
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
V — скорость в момент времени t [м/с],
a — ускорение тела [м/с2].
Задача 2
Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с2 после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?
Решение.
-
По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
-
Поскольку время движения неизвестно, то определим путь по второй формуле:
-
Подставим числа и выполним расчет:
м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
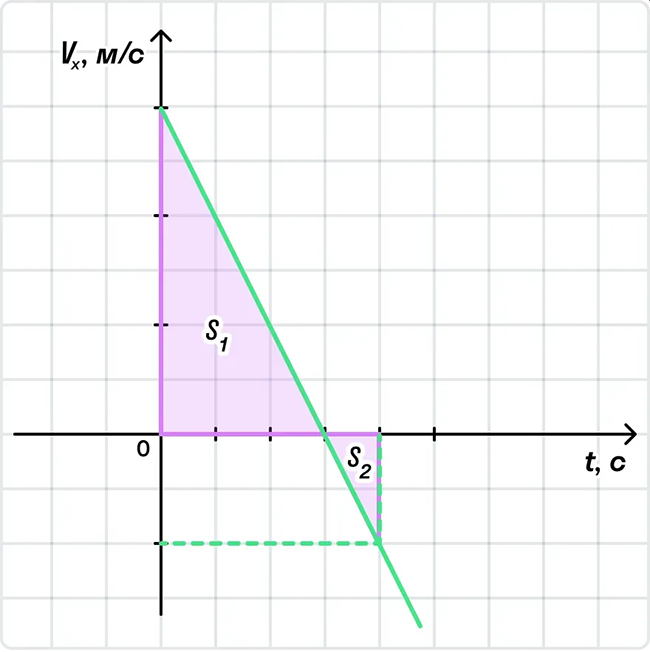
Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.
Например, на этом графике путь тела равен S1 + S2, а перемещение — S1 − S2.
Уравнение перемещения при равноускоренном движении
,
где S — перемещение за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.
Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени. Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).
Уравнение равноускоренного движения
,
где x(t) — координата в момент времени t [м],
x0 — начальная координата [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.
Решение.
-
Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V0 = 3 м/с. Начальная координата равна нулю.
-
Найдем ускорение из формулы пути при равноускоренном движении:
м/с2.
-
Составим уравнение движения лыжника:
.
-
По уравнению определим координату лыжника в момент времени t = 2 с:
м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Графики равноускоренного движения
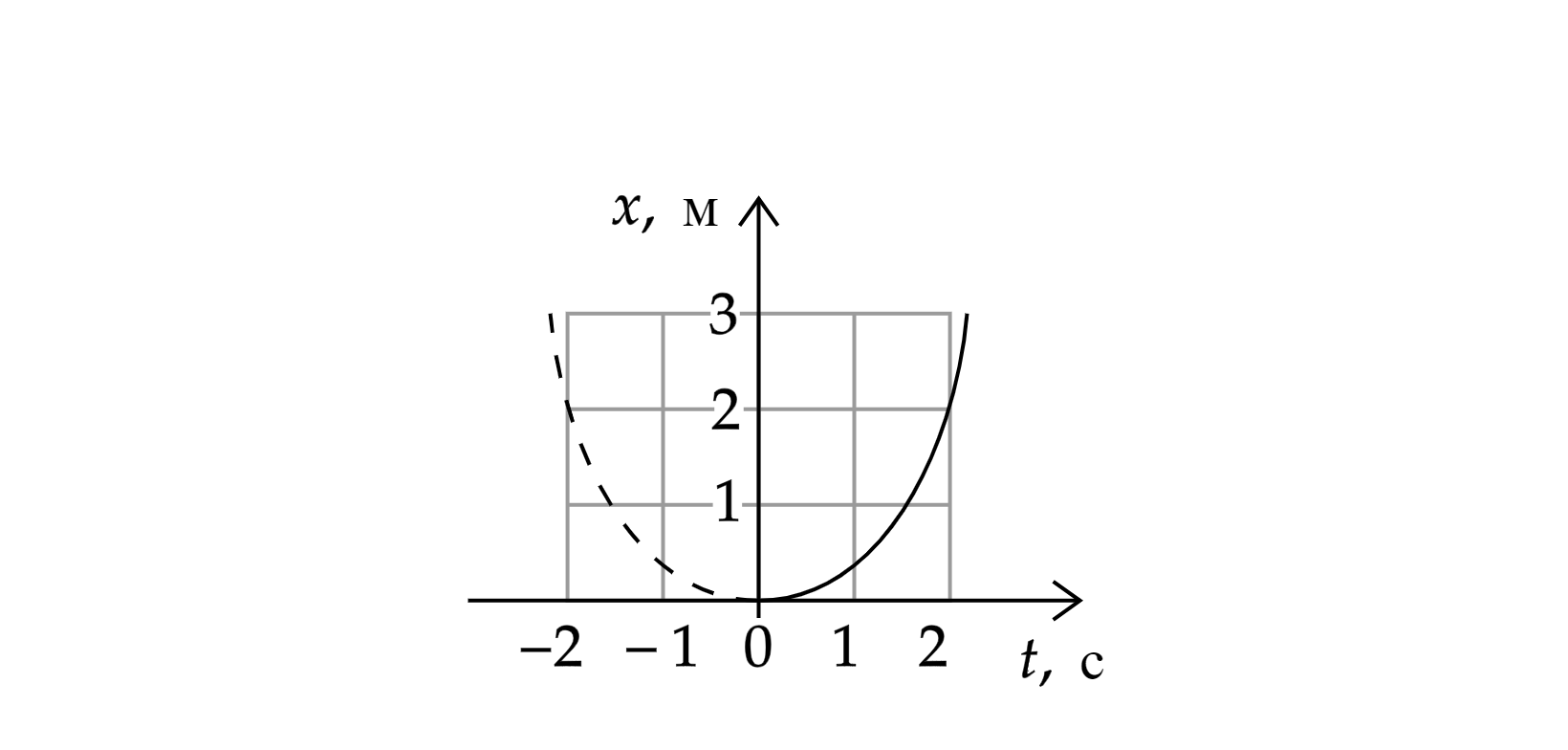
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.
Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!