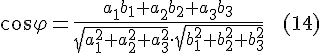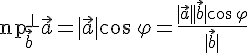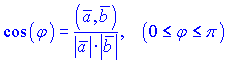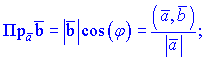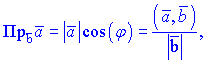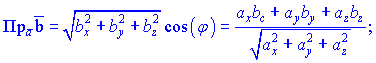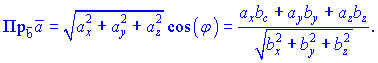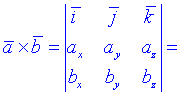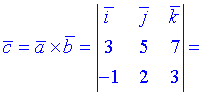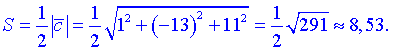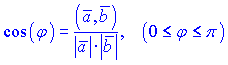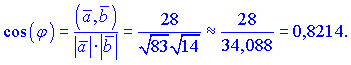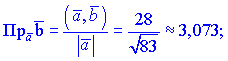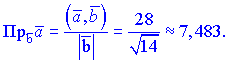Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 – 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
ТЕОРЕМА
16.1. Пусть
в пространстве выбран ортонормированный
базис , в
котором . Тогда
Доказательство. По
определению координат вектора в базисе
имеем
и
,
поэтому
Используя
доказанные свойства скалярного
произведения, получаем
Поскольку
базис ортонормированный,
то и
,
значит, окончательно получим
Теорема
доказана.
Замечание
16.1. Если
рассматривается множество векторов,
параллельных некоторой плоскости (т.е.
двумерное векторное подпространство
пространства ),
то формула принимает
вид
где в
ортонормированном базисе двумерного
подпространства .
17 Задачи, решаемые с помощью скалярного произведения
Задача
17.1. Пусть
даны координаты вектора в
ортонормированном базисе. Найти длину
вектора .
Решение. Согласно
свойству 4. скалярного произведения
длина вектора находится по формуле ,
т.е. .
Но скалярное произведение векторов в
ортонормированном базисе
вычисляется
по формуле .
Поэтому получаем следующую формулу для
нахождения длины вектора, заданного
своими координатами в ортонормированном
базисе
Задача
17.2. Пусть
даны координаты векторов и
в
ортонормированном базисе.
Найти угол между векторами и
.
Решение. Из
определения скалярного произведения
получаем следующую формулу для нахождения
косинуса угла между векторами:
С
учетом формул и
приходим
к следующей формуле для нахождения угла
между векторами, заданных своими
координатами в ортонормированном базисе
Ортогональная проекция вектора на ось.
Задача
17.3. Пусть
даны два вектора и
. Найти
ортогональную проекцию вектора на
ось вектора .
Решение. По
формуле имеем
Следовательно,
получаем формулу для нахождения
ортогональной проекции вектора на
ось вектора
Ортогональная проекция вектора на плоскость.
Определение
17.1. Пусть
дан вектор и
некоторая плоскость .
Обозначим через ортогональные
проекции точек на
плоскость .
Вектор называется
ортогональной проекцией вектора на
плоскость и
обозначается .
Задача
17.3. Найти
ортогональную проекцию данного
вектора на
плоскость ,
перпендикулярную данному
вектору .
Решение. Пусть
данный вектор .
По определению ортогональной проекции
вектора на плоскость имеем (см
рисунок).
По правилу
многоугольника для сложения векторов,
получаем равенство
Заметим,
что и
,
поэтому .
По признаку коллинеарности векторов
получаем равенство .
Кроме того, ,
поэтому
Умножим
обе части этого равенства скалярно на
вектор .
Имеем числовое равенство
Учитывая,
что
Из
последнего равенства находим,
что
Поэтому
для нахождения ортогональной проекции
вектора на плоскость, перпендикулярную
заданному вектору имеем
18 Геометрический смысл координат вектора в ортонормированном базисе
Пусть
в пространстве выбран ортонормированный
базис ,
в котором .
Тогда .
Умножим обе части этого
равенства
скалярно сначала на вектор ,
потом на и
.
Получаем
Поскольку
базис ортонормированный, то ,
а поэтому имеем равенства
С
учетом формулы имеем
Из
равенств получаем
геометрический смысл координат вектора
в ортонормированном базисе:
координаты
вектора в ортонормированном базисе
равны ортогональным проекциям данного
вектора на оси
соответствующих базисных векторов.
Обозначим
через .
Тогда, используя формулу ,
равенства примут
вид
Числа называются
направляющими косинусами вектора в
ОНБ .
Подставим в
получаем
или
Таким
образом, сумма квадратов направляющих
косинусов любого ненулевого вектора
равна единице.
Заметим,
что если —
единичный, то его координаты в ОНБ равны
направляющим косинусам этого вектора
или, иначе, направляющие косинусы данного
вектора равны
координатам единичного вектора того
же направления.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
30.03.201527.55 Mб32Административное право России Конин Н.М..pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Формула
- Примеры нахождения проекции вектора на вектор
Формула
Чтобы найти проекцию вектора $bar{a}$ на вектор
$bar{b}$, надо
скалярное произведение указанных векторов поделить на
длину (модуль) вектора
$bar{b}$, то есть
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}$$
В случае если векторы заданы на плоскости и имеют координаты
$bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Если векторы заданы в пространстве, то есть имеют координаты bar{a}=left(a_{x} ; a_{y} ; a_{z}right) text { и } bar{b}=left(b_{x} ; b_{y} ; b_{z}right), то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
Примеры нахождения проекции вектора на вектор
Пример
Задание. Найти проекцию вектора
$bar{a}$ на вектор
$bar{b}$, если
$bar{a}=(-1 ; 0)$ и $bar{b}=(3 ;-4)$
Решение. Для нахождения проекции вектора
$bar{a}$ на вектор
$bar{b}$, будем использовать формулу
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$
Подставляя в неё координаты заданных векторов, получим:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{-1 cdot 3+0 cdot(-4)}{sqrt{3^{2}+(-4)^{2}}}=frac{-3+0}{sqrt{9+16}}=frac{-3}{sqrt{25}}=-frac{3}{5}$$
Ответ. $Пр_{bar{b}} bar{a}=-frac{3}{5}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти проекцию вектора
$bar{a}=(-2 ; 3 ; 0)$ на вектор
$bar{b}=(-2 ; -1 ; 5)$
Решение. Подставляя координаты заданных векторов в формулу
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$
получим:
$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|b|} =frac{-2 cdot(-2)+3 cdot(-1)+0 cdot 5}{sqrt{(-2)^{2}+(-1)^{2}+5^{2}}}=$$
$$=frac{4-3+0}{sqrt{4+1+25}}=frac{1}{sqrt{30}}$$
Ответ. $Пр_{bar{b}} bar{a}=frac{1}{sqrt{30}}$
Читать дальше: как найти длину вектора.
В данной статье будут изложены основные инструкции, относительно векторов. С их помощью Вы будете знать что с ними можно делать, а что нет. Поэтому переходим к изучению операций над векторами.
І. Суммой двух -мерных векторов
и
называют
-мерный вектор
, координаты которого равны сумме соответствующих координат векторов – слагаемых:
Например, если ,
то
Из этого правила следует, что разностью двух векторов будет вектор, координаты которого является разницей соответствующих координат векторов
ІІ. Произведением числа (скаляра) на
-мерный вектор
называется
-мерный вектор
, координаты которого равны произведению числа
на соответствующие координаты вектора
Например
Операции сложения векторов и умножения числа на вектор ( – некоторые числа) обладают свойствами:
1)
2)
3)
4)
5)
6)
7) Для произвольного вектора существует противоположный вектор
такой, что
ІІІ. Скалярным произведением двух
-мерных векторов
и
называют число, равное сумме произведений соответствующих координат векторов:
Например,
если, то
Согласно другому определению, скалярное произведение двух векторов это число, равное произведению длин векторов (их модулей) на косинус угла между ними
Из приведенного выше определения можно получить формулу для вычисления угла между векторами
или в координатной форме
Также есть формулировка согласно которой скалярное произведение двух векторов равен модулю одного из них умноженному на проекцию второй вектор на направление первого
Из последнего определения вытекают формулы для нахождения проекции вектора на вектор
или в координатной форме
Примеры нахождения скалярного произведения, угла между векторами и проекции одного вектора на другой будут рассмотрены ниже.
Алгебраические свойства скалярного произведения векторов:
1)
2)
3)
4)Равенство
имеет место при условии
Геометрические свойства скалярного произведения
1)векторы перпендикулярны между собой, если
2) угол между векторами острый в случаях, когда
3) угол между векторами тупой в случаях, когда
ІV. Векторным произведением или
двух векторов называется вектор
, который отвечает следующим условиям:
1) модуль вектора равен произведению модулей векторов
и
на синус угла между ними
2) вектор нормальный к плоскости, построенной на векторах
и
;
3) вектор направлен так, что с его конца кратчайший поворот от вектора
к
происходит против часовой стрелки. Иными словами, векторы
образуют правую тройку.
Векторное произведение имеет следующие геометрические свойства:
Его модуль равен площади параллелограмма построенного на векторах и
Поэтому площадь треугольника построенного на векторах и
равна модулю половины векторного произведения этих векторов
Алгебраические свойства векторного произведения
1) векторное произведение равно нулю в случае коллинеарности векторов или когда один из них нулевой;
2) от перестановки векторов векторное произведение меняет знак на противоположный
3)
4)
На практике важно иметь под рукой формулу для вычисления векторного произведения в координатной форме, поэтому запишем и ее
Рассмотрим конкретные примеры для усвоения пройденного материала.
——————————————–
Задача 1.
Заданы векторы и
Найти следующие величины
1) сумму векторов
2) скалярное произведение векторов
3) ) векторное произведение площадь треугольника построенного на векторах
4) угол между векторами
5) проекцию каждого из векторов на другой
Решение
1) Проведем вычисления
2) Скалярное произведение будет равно
3) Векторное произведение вычисляем по формуле
Площадь треугольника будет равна
4) Найдем угол между векторами по формуле
В ней скалярное произведение уже найдено поэтому находим длины векторов
Подставляем нужные значения в формулу
Находим значение угла
5) Найдем проекции векторов
Проекции векторов можно искать через косинус угла между векторами, результат от этого не изменится
На этом урок окончен. Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.
—————————————————–
Посмотреть материалы:
- Длина вектора. Угол между векторами
- Скалярное произведение векторов
- Разложение вектора по базису
- Смешанное произведение векторов
- Деление отрезка в заданном отношении
- Треугольная пирамида
По этой ссылке вы найдёте полный курс лекций по математике:
Рассмотрим на оси / ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси I называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси и со знаком «-», если эти направления противоположны. Рассмотрим теперь произвольный вектор , определяемый связанным вектором АВ.
Опуская из его начала и конца перпендикуляры на заданную ось I, построим на ней направленный отрезок CD (рис. 24). Определение. Проекцией вектора АВ на ось I называется величина направленного отрезка CD, построенного указанным выше способом. Основные свойства проекций 1. Проекция вектора АВ на какую-либо ось I равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25) 2.
Проекция суммы векторов на какую-либо ось J равна сумме проекций векторов на ту же ось. Например, (рис.26). §5. Скалярное произведение векторов Пусть имеем два вектора а и I». Определение. Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а,Ь) и определяемое равенством где <р> или в иной записи (а, !>), есть угол между векторами а и b (рис. 27 а).
Заметив, что (b| cosy> есть проекция вектора b на направление вектора а, можем написать (рис. 27 6) и,аналогично, (рис.27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или Ь — нулевой, будем считать, что Проекция вектора на ось.
Скалярное произведение векторов 5.1.
Свойства скалярного произведения 1. Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и Ь ортогональны, a J.h. Это следует из формулы (1), определяющей скалярное произведение. Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так: 2.
Скалярное произведение коммутативно: Справедливость утверждении вытекает из формулы (I), если учесть четность функции 3. Скалярное произведение обладает распределительным свойством относительно сложения: 4 Действительно, 4. Числовой множитель Л можно выносить за знак скалярного произведения « Действительно, пусть А > 0. Тогда поскольку при A > 0 углы (aj>) и (Аа, h) равны (рис.28). Аналогично рассматривается случай . При 0 свойство 4 очевидно. Замечание. В обшем случае ). 5.2.
Возможно вам будут полезны данные страницы:
Скалярное произведение векторов, заданных координатами Пусть векторы а и Ь заданы своими координатами в ортонор миро ванном базисе Рассмотрим скалярное произведение векторов и и Ь: Проекция вектора на ось. Скалярное произведение векторов Пользуясь распределительным свойством скалярного произведения, находим Учитывая, что Тоесть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат. Пример.
Найти скалярное произведение векторов
Скалярное произведение вектора на себя называется скалярным квадратом: Применяя формулу (4) при b =а, найдем С другой стороны, так что из (5) следует, что — в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат. 5.3. Косинус угла между векторами. Направляющие косинусы Согласно определению где —угол между векторами а и Ь. Из этой формулы получаем (предполагается, что векторы а и b — ненулевые). Пусть .
Тогда формула (7) примет следующий вид cos Пример. Найти угол между векторами Пользуясь формулой (8), находом Пусть b = i, т.е. b = {1,0, 0}. Тогда для всякого вектора О имеем Проекция вектора на ось. Скалярное произведение векторов или, в координатной записи, где q есть угол, образованный вектором а с осью Ох.
Аналогично получаем формулы Формулы (9)-(l 1) определяют направляющие косинусы вектора а, т.е. косинусы углов, образуемых вектором а с осями координат (рис. 29). Пример. Найти координаты единичного вектора . По условию |п°| = I. Пусть Тогда (n°,k)=sz = cos 7. Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат: Проекция вектора на ось. Скалярное произведение векторов Отсюда получаем Пример. Пусть единичный вектор п° ортогонален оси г: (рис.30). Тогда его координаты х и у соответственно равны Тем самым.