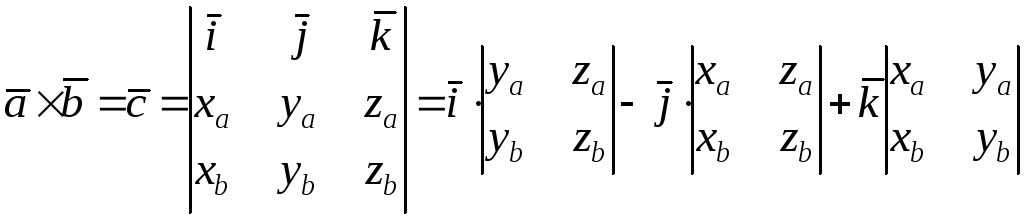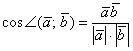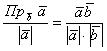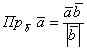Проекция вектора на ось. Проекция вектора на вектор
Навигация по странице:
- Определение проекции вектора на ось
- Определение проекции вектора на вектор
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- плоские задачи
- пространственные задачи
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l. (рис. 1).
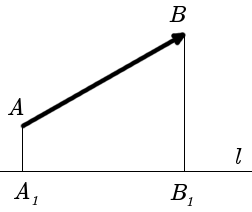 |
| рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачи
Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 12 | = 2 |
| |b| | 6 |
Ответ: Пр ba = 2.
Рассмотрим
два вектора
и
.
О
К
Отрезок
ОК
является проекцией вектора
на направление вектора
.
Из полученного прямоугольного треугольника
очевидно, что:
.
Из формулы (4.1)
следует:

следовательно,
можем записать:

Окончательно,
проекция вектора на направление другого
вектора вычисляется по формуле:
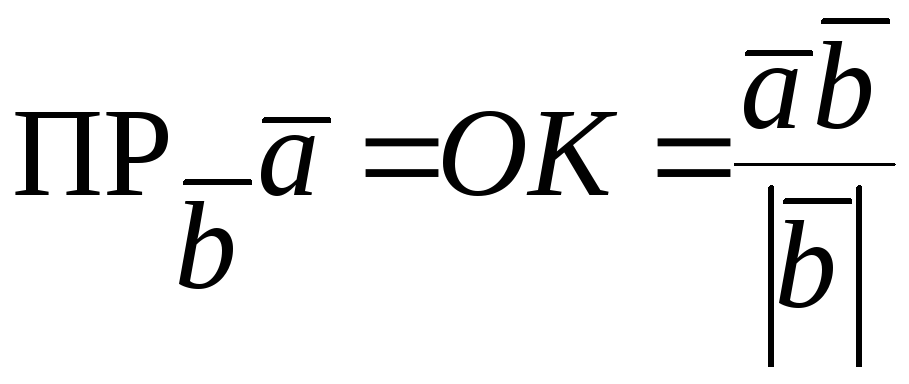
ЛЕКЦИЯ 5
ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
5.1 Определение векторного произведения
Векторным
произведением двух
векторов
и
называется третийвектор
,
обладающий свойствами:
1.
Вектор
перпендикулярен плоскости, в которой
расположены векторыи
.
.
2.
Длина
вектора
равна площади параллелограмма,
построенного на векторахи
,
как на сторонах.
(5.1)
3.
Векторы
,
,
,
в том порядке, как они записаны, образуютправую
тройку векторов.
Обозначения:
.
5.2 Вычисление векторного произведения двух векторов
Рассмотрим
векторы:
и
.
Векторное произведение этих векторов
равноопределителю
третьего порядка,
элементами первой строки которого
являются единичные орты
, элементами второй и третьей строк –
координаты векторови
соответственно.

Запишем
разложение определителя в формуле (5.2)
по элементам первой строки:
Таким
образом, координаты векторного
произведения векторов
и
,
т.е. вектораесть:
Т.е.
Из
определения векторного произведения
следует, что длина вектора
равна площади параллелограмма,
построенного на векторах
и
,
значит,
(5.3)
Равенство
(5.3) является геометрическим
смыслом векторного
произведения.
5.3 Свойства векторного произведения
1.
2.
3.
Векторное
произведение коллинеарных
векторов равно нулю.
Это следует из определения векторного
произведения.
5.4
Векторные
произведения единичных орт
Рассмотрим
векторы
.
Из определения векторного произведения
следует, что:
(5.4)
Очевидны равенства:
(5.5)
Чтобы
определить другие векторные произведения
векторов
,
пользуются схемой:
Из схемы видно,
что
5.5
Условия
коллинеарности и перпендикулярности
векторов
Исходя
из определения скалярного и векторного
произведения векторов, учитывая свойства
и приложение этих операций, делаем
выводы:
(5.6)
Т.е.
скалярное
перпендикулярных векторов равно нулю.
Если
векторы коллинеарны,
то их координаты
пропорциональны,
т.е. выполняются равенства:

ЛЕКЦИЯ 6
СМЕШАННОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
6.1
Определение
смешанного произведения векторов
Смешанным
произведением
трёх
векторов называется число,
равное скалярному
произведению векторного
произведения
первых двух векторов на третий.
(6.1)
Обозначение
.
6.2
Смешанное
произведение векторов в координатной
форме

6.3
Свойства
смешанного произведения
1.
2.
6.4
Геометрический
смысл смешанного произведения
Смешанное
произведение трёх векторов по
абсолютной величине
равно объему
параллелепипеда, построенного на этих
векторах.
ЛЕКЦИЯ 7
Элементы
аналитической геометрии
7.1
Прямая на плоскости
Уравнение
прямой линии, проходящей через точку
перпендикулярно вектору
:
(7.1)
Уравнение
пучка прямых, проходящих через заданную
точу
:
(7.2)
Уравнение прямой
линии, проходящей через
Две
заданные точки
и
:

Уравнение
прямой линии с заданным угловым
коэффициентом:
(7.4)
Уравнение
прямой линии в отрезках на осях:

Общее уравнение
прямой линии на плоскости:
(7.6)
В
уравнении (7.6) вектором-нормалью
прямой является вектор:
.
Уравнение
прямой, проходящей через точку
,
параллельно вектору(каноническое уравнение прямой на
плоскости):

Параметрические
уравнения прямой линии на плоскости:

Расстояние
от точки
до прямой
:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 – 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
В данной публикации мы рассмотрим, что такое проекция вектора на ось или на другой вектор, и приведем формулу, с помощью которой можно найти значение этой проекции. Также разберем примеры решения задач по этой теме.
- Нахождение проекции вектора
-
Примеры задач
Нахождение проекции вектора
Проекция вектора AB на ось l – это число, которое равняется отрезку A1B1. Точки A1 и B1 при этом являются проекциями точек A и B на ось l.
Проекция вектора a на направление вектора b – это число, которое равно проекции a на ось, проходящую через b.
Формула для нахождения проекции вектора на вектор
Рассчитать проекцию a на направление b можно следующим образом:
Примеры задач
Задание 1
Найдем проекцию вектора a = {3; 5} на b = {2; 8}.
Решение:
1. Сперва посчитаем скалярное произведение заданных векторов:
a · b = 3 · 2 + 5 · 8 = 46
2. Теперь вычислим длину (модуль) b:
3. Остается только воспользоваться формулой выше для нахождения проекции вектора:
Задание 2
Вычислим проекцию вектора a = {4; -7; 5} на b = {11; 3; 6}.
Решение:
Поочередно выполняем те же самые действия, что и в примере, разобранном выше.
a · b = 4 · 11 + (-7) · 3 + 5 · 6 = 53
1.7.1. Как найти проекцию вектора на вектор?
Рассмотрим ненулевые векторы и
:
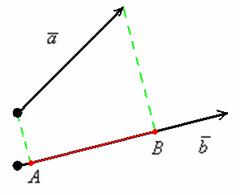
Спроецируем вектор на вектор
, для этого из начала и конца вектора
опустим перпендикуляры на вектор
(зелёные пунктирные линии).
Представьте,
что на вектор перпендикулярно сверху падают
лучи света. Тогда отрезок будет «тенью»
вектора . Проекцией вектора
на вектор
является ДЛИНА отрезка
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Это ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют,
«маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись читается так: «проекция
вектора «а» на вектор «бэ»».
Если угол между векторами острый (как на рисунке выше), то
Если векторы ортогональны, то
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой (на рисунке мысленно переставьте стрелочку вектора
), то
(та же длина с добавленным знаком «минус»).
Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую
вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую
вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на
прямую, содержащую вектор «бэ».
Из вышесказанного следует, что проекция вектора на любой ненулевой сонаправленный вектор
будет точно такой же:
– фактически это проекция вектора
на прямую
, которая содержит сонаправленные векторы
(и поскольку векторы свободны, то таких прямых будет
бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно , то
добавится знак «минус»:
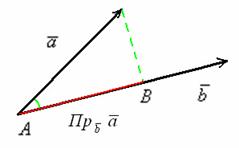
Отложим наши подопытные векторы от одной точки:
и рассмотрим прямоугольный треугольник. Косинус угла – есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена
формула косинуса угла между векторами:
…все ли догадались, что будет дальше?
Приравниваем формулы:
и сокращаем знаменатели обеих частей на ,
получая формулу для вычисления проекции:
Распишем её в координатах:
Если векторы плоскости и
заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Если векторы пространства заданы в ортонормированном базисе
, то проекция вектора
на вектор
выражается формулой:
Легко убедиться, что проекция вектора на
коллинеарный вектор может
отличаться лишь знАком, приведу выкладки для «плоского» случая :
, если
, и
, если
Задача 34
Найти проекцию вектора на вектор
Решение в одну строчку:
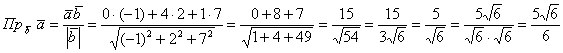
знаменатель на , избавившись тем самым от
иррациональности в знаменателе.
Ответ:
Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это
будет своеобразно.
Задача 35
Треугольник задан своими вершинами .
Найти:
а) проекцию стороны на сторону
;
б) проекцию стороны на сторону
.
Это задача для самостоятельного решения.
Итак, как найти проекцию вектора на отрезок с известными концами
? (как вариант, на продолжение этого отрезка). Находим вектор
и используем формулу
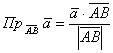
и формулу
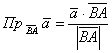
одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 🙂
О проекции же вектора на прямую поговорим в следующей главе, а пока
выясним геометрический смысл координат векторов в ортонормированном базисе:


| Оглавление |
Автор: Aлeксaндр Eмeлин