Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.
Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.
Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.
Виды балок
При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.
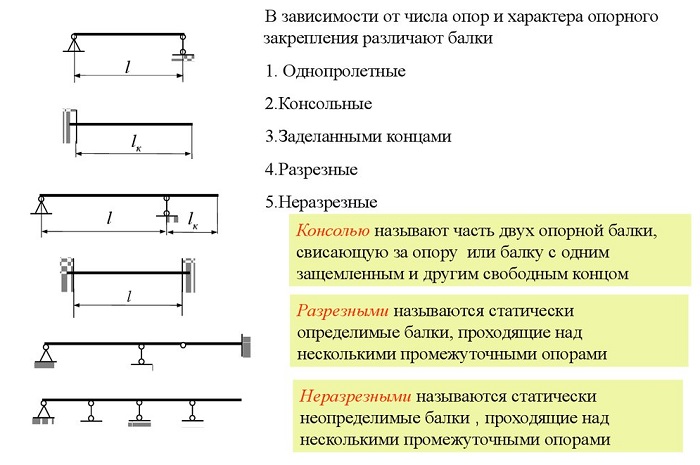
Виды балок:
-
Деревянные – их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.
-
Металлические – такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.
Прочность и жесткость балки
При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.
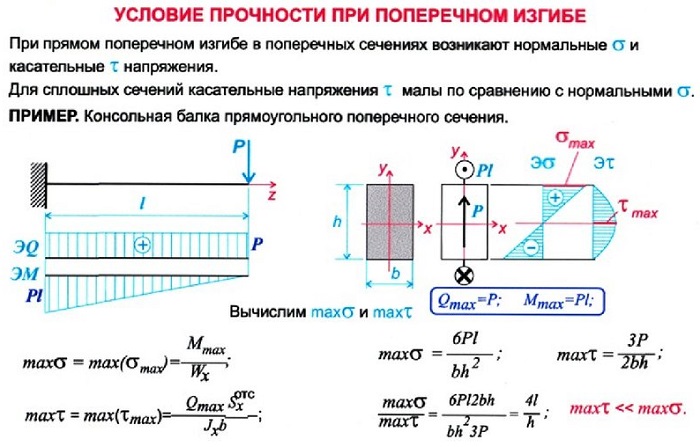
На эти параметры влияют следующие факторы:
-
величина наружных нагрузок, их положение;
-
параметры, характер, нахождение поперечного сечения;
-
продольные величины;
-
материал;
-
число опор, метод их закрепления.
Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.
Построение эпюр балки
Эпюра распределения величины нагрузки на объект:
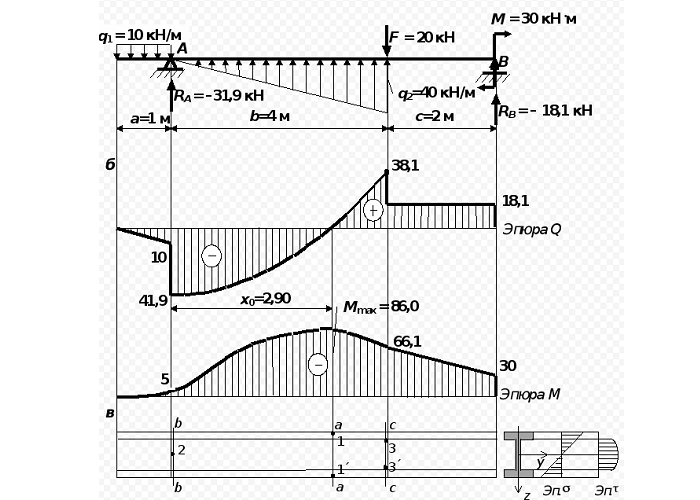
Расчет на жесткость
Алгоритм исчисления:
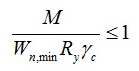
В формуле обозначены:
-
M – max момент, возникающий в брусе;
-
Wn,min – момент сопротивления сечения (табличный показатель);
-
Ry – сопротивление на изгиб (расчётный показатель);
-
γc – показатель условий труда (табличный показатель).
Такой расчет не трудоемок, но для более верного значения требуется следующее:
-
рабочий план объекта;
-
определение характеристик балки, характер сечения;
-
определение max нагрузки, воздействующей на брус;
-
оценка точки max прогиба;
-
проверка прочности max изгибающего момента.
Расчет моментов инерции и сопротивления сечения
Алгоритм исчисления:
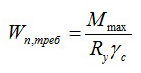
Где:
-
J – момент инерции сечения;
-
W – момент сопротивления.
Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.
Нахождение максимальной нагрузки и прогиба
Формула для вычисления:
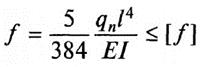
Здесь обозначены:
-
q – нагрузка равномерно-распределенная;
-
E – гибкость (табличный показатель);
-
l – длина;
-
I – момент инерции сечения.
Нагрузки учитываются статические и периодические.
Расчет на прогиб и его особенности
Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.

При применении соответствующих коэффициентов, придерживаются следующего:
-
балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;
-
балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;
-
нагрузка консольного типа;
-
воздействие комплексной нагрузки.
Пример расчет балки на прогиб
Рассмотрим задачу из курса сопромата.
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм.
Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.
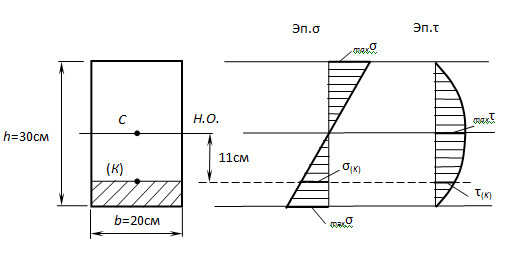
Решение.
Чтобы узнать σ(К), τ(К), σmax, τmax
определяем значение осевого момента инерции общего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсеченного ряда и статического момента середины сечения Smax:
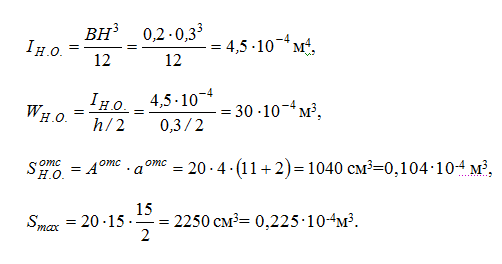
Из этого следует:
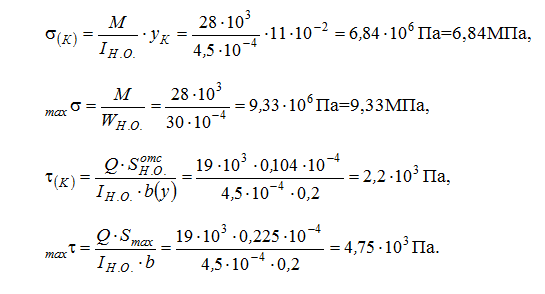
Определение прочности по нормальному напряжению:
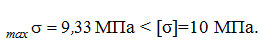
Определение прочности по касательному напряжению:
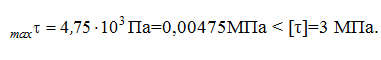
Задача решена.
При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки.
Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
![]()
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
В прошлой части мы обсудили, как может изменяться момент стержня и как выяснить, не разрушится ли он под действием нормальных и касательных сил. Однако под воздействием момента стержни могут изгибаться и изменять форму, что может приводить к неправильной работе конструкций или даже их разрушению в процессе эксплуатации. Сегодняшняя статья посвящена вопросу нахождения прогибов и углов наклона при изгибе.
Уравнение кривой
В прошлой части мы выяснили, что для нахождения момента нам необходимо знать какой у дуги изгиба радиус кривизны, какой у сечения статический момент и какой модуль Юнга у материала балки:
Затем мы устранили из уравнения такое значение как радиус кривизны, из наших уравнений, так как нас не столько волновало, как под воздействием изменится балка, сколько не сломается ли она.
Однако сейчас нас интересует именно то, как будет деталь изгибаться под воздействием моментов, как будет меняться геометрия .
В прошлый раз мы не заостряли внимание на вопросе «что такое радиус кривизны», да и просто «что такое кривизна». В этой части мы данную проблему решим, а также объясним как это значение поможет нам в сопромате вычислить деформации изгиба.
Фактически, до этого момента мы оперировали не столько радиусом, сколько кривизной, которая обратно пропорциональна радиусу:
А сейчас мы поговорим о том, какое значение она имеет с точки зрения геометрии.
Если нет желания смотреть, как с точки зрения математики выводятся геометрические характеристики, можно промотать до следующего жирного шрифта и принять за данность выводы.
Кривизна – это то, насколько сильно изменяется угол наклона касательной к нашей кривой за единицу длины дуги.

Так как любую кривую можно представить как сумму бесконечно малых дуг, принадлежащих разным окружностям, стоит посмотреть, на сколько будет изменяться угол в двух точках ее дуги.

Углы будем измерять в радианах (180°=π, 360°=2π). Длина окружности равна удвоенному произведению радиуса на π: l=2πR. Круг — фигура симметричная, и поэтому в любой точке кривизна будет одинакова и равна:
χ=frac{2π}{2π*R}=frac{1}{R}
Вот так и находилась формула кривизны балки. И теперь мы хотим поставить её на службу поиска формы балки.
Нам нужно найти изменение угла за бесконечно малый пройденный путь, и мы имеем некоторую функцию. При этом её первая производная будет равна тангенсу угла с осью x, которую мы обозначим греческой тета θ:

Нам же для вычисления кривизны необходимо найти изменение угла θ:
Гуглим таблицу дифференциалов, находим, что дифференциал от тангенса равен следующему выражению:
d(arctg (x))=frac{dx}{1+x^2}
Так как функция сложная (y’ — тоже какая-то функция, пусть нам и не известная), получившееся значение надо будет домножить на производную от аргумента:
dθ=frac{dx}{(1+(y’)²)}*y’’
Кривизна же — это изменение угла за пренебрежительно малый отрезок длины:
Уравнение угла наклона нам известно. Теперь нам нужно вычислить длину малой дуги. Достаточно малой, чтобы можно было пренебречь кривизной и считать её прямой. Тогда мы сможем воспользоваться теоремой Пифагора:
Где dx – пройденный путь по оси x, а dy – по оси y.
Нам для красоты уравнения хотелось бы избавиться побыстрее от дифференциалов, чтобы в формуле остались только производные. Для этого мы делим все, что было под корнем на (dx)^2:
frac{(dx)^2}{(dx)^2}+frac{(dy)^2}{(dx)^2}=1+(y')^2
Так как (dx)^2/(dx)^2=1, а (dy)/(dx) – это производная y по x.
Чтобы уравновесить данное вмешательство, мы должны домножить все выражение на dx (т.к. √(dx)^2=dx):
Теперь у нас есть все для нахождения кривизны:
χ=frac{dθ}{dl}=frac{dx}{(1+(y’)^2)}*y’’*frac{1}{dxsqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^2}
*frac{1}{sqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^{{3}}}
Отсюда стоит читать всем, даже тем, кому математика вывода кривизны не очень интересна.
Итак, мы смогли вычислить чему равна функция кривизны:
χ=frac{1}{R}=frac{y’’}{(sqrt{1+(y’)^2})^{3}}
Где y – прогиб (т.е. расстояние на которое выше или ниже окажется определенная точка балки, по сравнению с недоформированным состоянием), y’ – первая производная от неё, а y» – вторая (или кривизна).
Перед нами же стоит задача вычислить форму. Так как в сопротивлении материалов прогибы достаточно небольшие, изменением длины можно пренебречь. Следовательно, нам остается лишь вычислить изменение координаты y в зависимости от x. И в полученной формуле нам мешает это сделать очень объемный знаменатель (√(1+(y’)²)³.
Если подумать логически, то так как прогибы в сопромате достаточно небольшие, можно было бы не учитывать производную y’, так как она является отношением катетов треугольника, который бы получился опусти мы к оси x перпендикуляр.
Дело в том, что даже если прогиб (координата y) будет составлять 1/10 от x, производная в самом крайнем углу будет чуть больше 0,2x. А ее квадрат 0,04x. А (√(1+(y’)²)³ около 1,06.
Это не назвать пренебрежительно малым значением, однако его проще компенсировать коэффициентами запаса прочности. Да и прогиб этот слишком большой для основ сопротивления материалов (большими деформациями занимается отдельная дисциплина). Вот демонстрация прогиба в натуральном соотношении:
В результате, если мы проигнорируем знаменатель, получим формулу, которую уже можно будет использовать в дальнейших расчетах:
χ=θ’=y’’
Угол поворота и прогиб
Мы уже выяснили, что кривизна балки в каждой части зависит от момента, возникающего в этом сечении, статического момента и модуля Юнга материала, из которого это балка сделана:
Сегодня же мы будем решать обратную задачу и находить изгиб балки. В первой части статьи мы выяснили, что для малых изгибов радиус кривизны (он равен единице деленной на радиус кривизны) практически равен второй производной от прогиба (насколько по оси z поднимется или опустится балка в конкретной точке). В итоге мы, зная как распределяется момент, сможем посчитать вторую производную прогиба для каждой точки балки:
y’’=χ=frac{1}{R}=frac{M_z}{I_z×E}
Нам же интересна форма балки: углы её наклона и на сколько сантиметров выше или ниже она окажется.
Начнём с наклона. Как мы уже выяснили, первая производная будет равна тангенсу наклона. Тангенс равен отношению противолежащего катета к прилежащему:

Углы наклона у нас будут маленькими, поэтому прилежащий катет будет практически равен радиусу. Отношение противолежащей стороны к радиусу является синусом:

А синус малого угла, как мы уже выяснили вначале статьи, численно равен углу в радианах.
Примечание: мы выяснили, что для малых углов тангенс, синус и угол численно равны. Эта закономерность важна не только в сопромате, но и в большинстве других инженерных наук. Например, в геодезии, при определении величины малых скатов.

Как следствие, для того, чтобы найти угол наклона, нам необходимо проинтегрировать кривизну:
θ=∫y''dx=∫frac{M_z*dx}{J_z*E}=frac{1}{J_z*E}∫M_z*dx=y'+C
Углы и прогибы балки под воздействием момента
В простейшем случае к балке приложен только момент:

В таком случае значение момента является константой. Обозначим ее как M. Тогда найти прогиб можно по формуле:
θ=∫y''dx=frac{1}{I_z*E}∫M_z*dx=frac{M_z*x}{I_z*E}+C
Остается найти константу интегрирования. Так как в начале координат балка жестко закреплена, угол в месте закрепления будет равен нулю, как следствие, константа тоже будет равна нулю. Эпюра угла наклона будет выглядеть вот так:

Для того, чтобы найти прогибы надо, соответственно, проинтегрировать получившееся выражение еще раз:
y=∫θdx=∫frac{M_z*x*dx}{I_z*E}+∫Cdx=frac{M_z*x^2*dx}{2*I_z*E}+Cx+D
Константу C мы уже знаем, а константу D можно найти по той же логике: балка жестко закреплена в начальной точке, а значит прогиб y в ней будет равен 0. А полученная нами формула приводит к нулю в начале координат только при нулевой константе:
(M*0)2/2+C*0+D=0, только если D=0
Ну а эпюра прогибов будет выглядеть следующим образом:

Углы и прогибы балки под воздействием силы
В случае же, если момент появляется под воздействием силы, эпюры как бы сдвигаются на одну вперед:

Линейной станет функция момента, а угол будет постепенно увеличиваться (вначале быстро, потом медленнее, так как момент будет меньше).
Mz=P(l-x), где Mz— момент возникающий в балке в точке, которая расположена на расстоянии x от места закрепления балки, а l – длина балки.
Получили мы это уравнение следующим образом: мы знаем что в месте закрепления возникает момент который компенсирует момент от воздействия силы на конце балки:
Также в месте закрепления будет возникать сила, которая будет компенсировать силу внешнюю:
Когда мы будет отдаляться от точки закрепления на величину x, сила реакции опоры будет создавать для нашего сечения момент MRa=Ra*x. Он будет складываться с моментом передавшимся с начала балки:
M_z=M_{z_{0}}-M_{R_{a}}=\=p*l+R_a*x=P*l-P*x=\=P(l-x)
Зная функцию распределения момента мы можем найти функции наклона и прогиба.
Наклон будет увеличиваться по параболе:
θ=∫frac{(P*(l-x))*dx}{I_z*E}=frac{P*(l-x)^2}{2*I_z*E}+C

Ну а прогиб будет изменяться уже по кубическому закону:
y=∫frac{P*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{P*(l-x)^3*dx}{6*I_z*E}+C*x+D
Примечание: если проще, то l-x потому, что в нулевой координате момент равен расстоянию до силы, а затем уменьшается на то расстояние, которое мы до нее прошли

Углы и прогибы балки под воздействием равномерно-распределенной нагрузки
В случае с равномерно-распределенной нагрузкой ситуация абсолютно аналогична: эпюры «сдвигаются» на одну относительно воздействия силы. Поперечная сила изменяется по линейному закону Qy=Ra-qx=ql-qx=q(l-x), момент по параболе Mz=q(l-x)2/2:

Угол наклона, соответственно, будет определяться кубической функцией:
θ=∫frac{q*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{q*(l-x)^3*dx}{6*I_z*E}+C

А прогиб уже функцией четвёртой степени:
y=∫frac{q*(l-x)^3*dx}{6*I_z*E}=\=frac{q*(l-x)^4*dx}{24*I_z*E}+Cx+D

Расчет балки на прогибы и углы наклона. Метод начальных параметров. Пример
На практике достаточно редко случается ситуация, при которой на конструкцию действует только одна сила, а сама конструкция состоит из одной балки, закрепленной только в одном месте. Разберем как пример расчёт балки, в которой есть все виды воздействий:

Примечание: среди внешних воздействий отсутствует сила. Мы сделали это для того, чтобы не загружать статью лишними расчётами: сила реакции опоры в расчетах ничем не отличается от силы внешней.
Первым делом, нужно заменить места закрепления на силы, которые они создают для поддержания равновесия балки. В данном случае это две вертикальные силы (моментов шарнирные опоры не создают):
Теперь наша задача найти эти силы. Сделать это довольно просто: составляем уравнение сил по оси y и момента для точки закрепления балки.
Уравнение равновесия сил по оси Y:
R_a-ql+R_b=R_a-30+R_b=0, R_a+R_b=30
Уравнение равновесия момента в левой точке закрепления:
M_a=ql*a+frac{15l^2}{2}+M-d*R_b=30+30-10-5R_b=0
Где a — расстояние до начала действия равномерно-распределенной нагрузки, d — расстояние до опоры b.
Из уравнения момента мы можем найти, чему равна сила реакции правой опоры:
Подставляем это значение в уравнение равновесия сил и получаем силу реакции первой опоры:
R_a+R_b=R_a+14=30, R_a=16

Для того, чтобы найти прогибы, нам надо составить уравнения момента для каждого участка. В нашем случае удобнее всего Теперь найдём функцию распределения момента для первого участия. Так как в точке a балка закреплена не жестко, момент в ней по условию равен нулю. В ней возникает только сила реакции опоры Ra=16.
Момент на первом участке будет зависеть от удаления от этой силы:

Для нахождения угла наклона это выражение надо проинтегрировать:
θ_{(I)}=frac{1}{I_zE}∫R_axdx=frac{R_ax^2}{2I_zE}+C
И ещё раз для получения прогиба:
y_{(I)}=frac{1}{I_zE}∫frac{R_ax^2dx}{2}+∫Cdx=frac{R_ax^3}{6I_zE}+Cx+D
Затем нам нужно найти геометрию балки на участке с равномерно-распределенной нагрузкой.

При этом, момент на этом участке будет зависеть от двух составляющих: от силы реакции Ra с первого участка и от нагрузки q.
M_{z_{(II)}}=f(R_a,x)+f(q,x)
Функция момента (Mz(I)=Ra*x=12x) возникающего от силы на первом участке будет справедлива и для нашего участка: момент по-прежнему будет равен произведению плеча на силу.
По мере того, как мы будем отступать от начала действия равномерно-распределенной нагрузки, момент будет увеличиваться по квадратичному закону (почему, можно прочитать в статье посвященной теореме Журавского) M(q)=qx’^2/2, где x’ — расстояние от начала приложения нагрузки.
Нам удобнее все расчёты проводить из одной точки, поэтому для второго участка x’=x-a, где a координата начала приложения нагрузки. Таким образом, уравнение момента на втором участке будет выглядеть так:
Mz_{(II)}=Ra*x-frac{q(x-a)^2}2=16x-frac{15(x-1)^2}2
Интегрируем чтобы найти наклон:
θ_{(II)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6)+C
И ещё раз, чтобы найти прогиб:
y_{(II)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32})
На следующем участке действие равномерно-распределенной нагрузки заканчивается. При этом, мы хотим чтобы q(x-a)2/2 в формуле осталась: всё-таки она вносит вклад в момент и геометрию стержня.
Чтобы эту небольшую проблему исправить, мысленно продолжим распределенную силу до конца конструкции, но приложим в противовес ей точно такую же, направленную в другую сторону:

Таким образом на следующий участок стержня (который начинается в точке b) дополнительно будет приложена распределенная нагрузка q, которая будет создавать момент M=q(b-x)2/2.
Суммарный момент для третьего участка будет равен:
Mz_{(III)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2
Ну и, соответственно, найти наклон и прогибы не составляет трудности:
θ_{(III)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6)+C
y_{(III)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32})+Cx+D
Четвёртый участок начинается в месте приложения момента и заканчивается на второй опоре.
Составляем уравнение момента:
Mz_{(IV)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2+10
Где c — расстояние от начала координат до места приложения момента, а x-c, расстояние между точкой, которую мы рассматриваем и местом приложения момента. В нулевой степени это выражение всегда равно единице, поэтому для уравнения момента это константа. Но после интегрирования это выражение становится важной частью уравнения наклона:
θ_{(IV)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))+C
А затем и уравнения прогиба:
y_{(IV)}=\frac{1}{Iz*E}∫(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32}+frac{M(x-c)^2}{2})+Cx+D

Остается вычислить константы интегрирования. На первой и последней опоре прогибы (т.е. вертикальные перемещения) будут равны нулю. Подставляем x=0 в уравнение первого отрезка:
y_{(I)}=frac{R_a0^3}{6I_zE}+C*0+D
И выясняем, что константа интегрирования D равна нулю.
Подставляя константу интегрирования D в уравнение последнего участка для закрепленного конца балки (т.е. x=l=5) мы получим следующее уравнение:
0=frac{1}{Iz*E}*(frac{16*5^3}6-frac{15(5-1)^4}{32}+frac{15(5-3)^4}{32}+frac{10(5-4)^2}{2})+С*5+0
Выражение равно нулю по причине того, что прогибы в месте закрепления образовываться никак не могут.
Решив уравнение мы получим значение второй константы интегрирования:
С=frac{225,83}{5*Iz*E}=frac{45,17}{Iz*E}
Дальше остается лишь подставить эти константы в уравнения и мы получим уравнения наклонов и прогибов.

Итак, мы выяснили по каким законам будет прогибаться каждый участок балки.
Если резюмировать, то для получения уклона и прогиба на некотором участке, нам нужно просуммировать все воздействия и их проинтегрировать.
Метод начальных параметров
В общем виде углы наклона будут считаться так:
А прогибы так:
Примечание: не забывайте компенсировать равномерно-распределенную нагрузку в точке, где она заканчиваться!
На практике гораздо целесообразнее считать момент, наклон и прогиб сразу для всей балки, с помощью трех систем уравнений: системы моментов, наклонов и прогибов.
Уравнения моментов для каждого участка
Так их удобнее составлять, так как достаточно просто для каждого нового участка добавлять воздействия:
Уравнения наклонов
Как можно заметить, для того, чтобы из системы уравнений моментов получить систему уравнений наклонов достаточно проинтегрировать каждый член и добавить константу интегрирования C:
Уравнения прогибов
Как ни странно, для того, чтобы их получить, достаточно проинтегрировать каждый из членов уравнения наклона, добавить ещё одну константу интегрирования D, а первую константу C умножить на x.
Итак, подошёл к концу разговор о том, как материалы противодействуют изгибам. В прошлых частях мы уже выяснили, какие нормальные напряжения возникают в материале при попытке его согнуть. Обсудили и как с распределением момента связаны поперечные силы и касательные напряжения. А сейчас выяснили и как будет материал менять свою форму под воздействием изгиба.
Это имеет далекоидущие последствия для всех инженерных дисциплин и опирающихся на них специальностей. Например, ротор турбин, являющийся по своей сути длинным стержнем на опорах, под силой тяжести достаточно сильно изгибается. По этой причине для всех турбин большой мощности противопоказан быстрый старт. Перед тем, как соединять статор и ротор, стержень турбины необходимо повращать, чтобы он избавился от изгибающих деформаций. Иначе лопатки будут цепляться и в лучшем случае деформироваться, а в худшем ломаться. Но это уже совсем другая история.
В следующей части мы поговорим о другом виде воздействия момента на стержень: о кручении.
Автор: К.А.Овчинников
Редактор: Сабуров Даниил
Эксперт: Ершов Марк
За консультативную поддержку по математической части огромная благодарность Гришиной Ольге Андреевне, старшему преподавателю кафедры высшей математики БГТУ ВОЕНМЕХ.
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники:
- Горбатовский Александр Александрович Дифференциальное уравнение изогнутой оси балки // Курс лекций по сопротивлению материалов МГТУ ИМ. Н.Э.БАУМАНА
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Лекции по сопротивлению материалов в БГТУ «ВОЕНМЕХ» им. Устинова
- http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi
- https://spravochnick.ru/matematika/krivizna_krivoy/krivizna_i_ee_vychislenie/
- iSopromat Метод начальных параметров. Расчет перемещений сечений балки // https://youtu.be/xRp-ViFUl7Y
4 131
Расчет балок на момент и прогиб
вернуться в раздел РАСЧЕТЫ КМ И КЖ
РАСЧЕТЫ БАЛОК
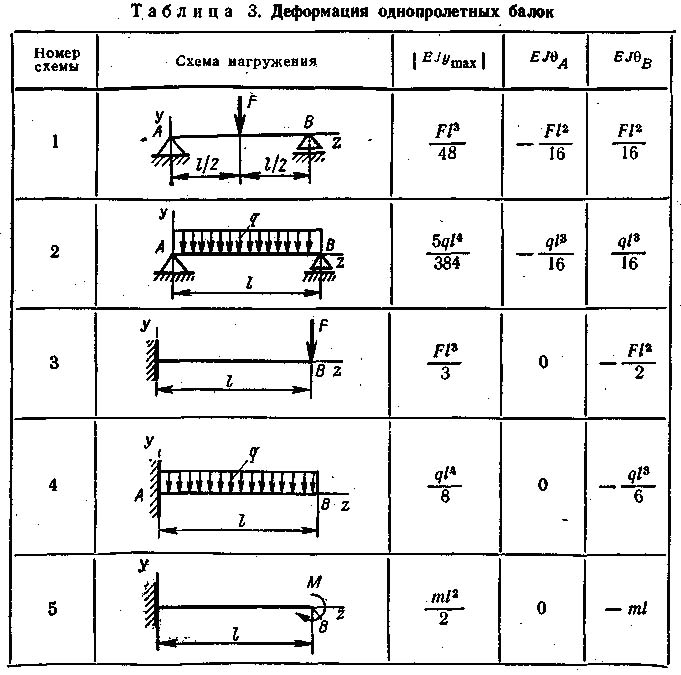
Здесь представлены формулы расчета для нахождения значений изгибающих моментов и прогибов для различных балок.
| Однопролетные балки на двух шарнирных опорах | ||
| 1 | Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 2 | Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 3 | Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 4 | Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 5 | Расчет балки на двух шарнирных опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на двух опорах | ||
| 6 | Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 7 | Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 8 | Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 9 | Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 10 | Расчет балки с жестким защемлением на опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на одной опоре (консольные) | ||
| 11 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке | Смотреть расчет |
| 12 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 13 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 14 | Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента | Смотреть расчет |
| Балки двухпролетные | ||
| 15 | Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке | Смотреть |
| 16 | Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках | Смотреть |
| 17 | Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке | Смотреть |
| 18 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
| 19 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
Расчет балки на прогиб
Содержание
- 1
Способы выполнить расчет и проверку на прогиб - 2
Методика выполнения расчета на прогиб- 2.1
Вычисляем моменты инерции и сил - 2.2
Формулы для практического использования
- 2.1
- 3
Заключение
Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
- Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.
Методика выполнения расчета на прогиб
Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.
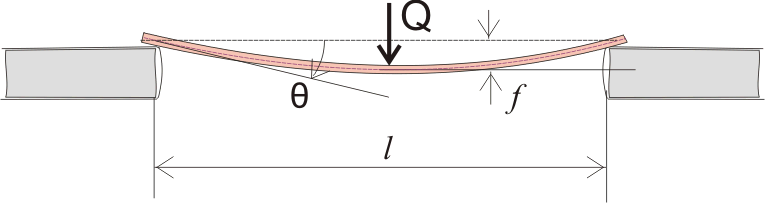
Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.
В нашем случае балка:
- Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
- Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
- Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.
Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.
Вычисляем моменты инерции и сил
Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).
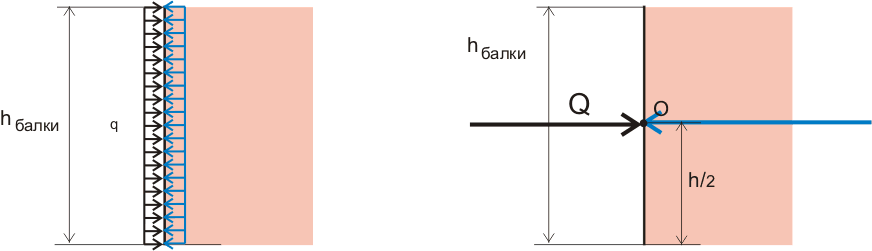
Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.
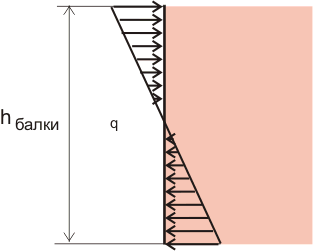
Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).
Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h2/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.
Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.
Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h3/12, где b и h – размеры сечения балки.
Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.
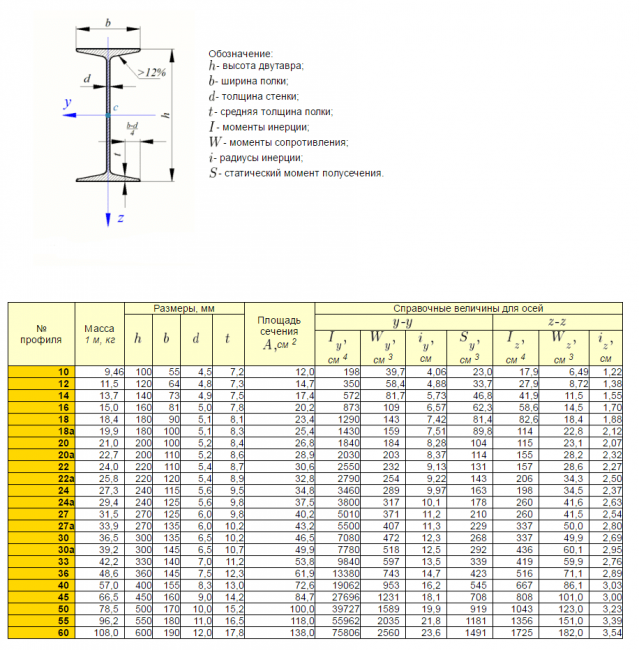
Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.
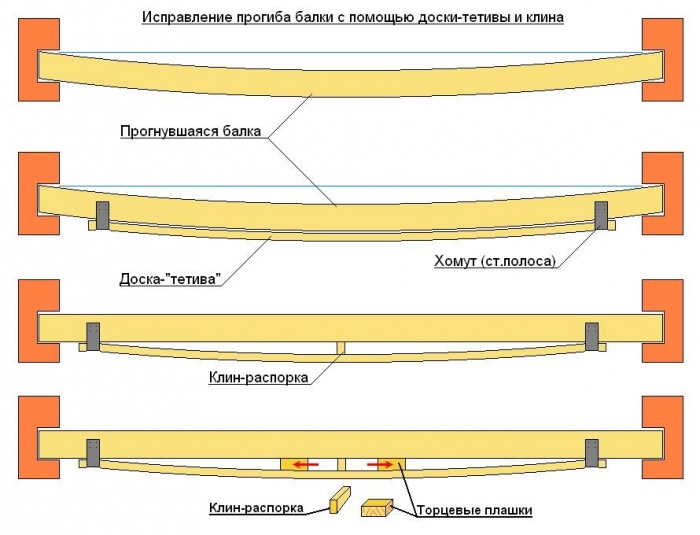
Формулы для практического использования
На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.
Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.
Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.
Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:
- Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
- По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
- По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.
Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.
Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.
Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.
Заключение
Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.
Что еще почитать по теме?

Автор статьи:
Сергей Новожилов – эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.
Оцените статью:
![]() Загрузка…
Загрузка…
