Можно выделить
два метода разработки прогнозов,
основанных на методах математической
статистики: экстраполяцию и моделирование.
В первом случае в
качестве базы прогнозирования используется
прошлый опыт, который пролонгируется
на будущее. Делается предположение,
что система развивается эволюционно в
достаточно стабильных условиях. Чем
крупнее система, тем более вероятно
сохранение ее параметров без изменения
— конечно, на срок, не слишком большой.
Обычно рекомендуется, чтобы срок
прогноза не превышал одной трети
длительности расчетной временной
базы.
Во втором случае
строится прогнозная модель, характеризующая
зависимость изучаемого параметра от
ряда факторов, на него влияющих. Она
связывает условия, которые, как ожидается,
будут иметь место, и характер их влияния
на изучаемый параметр.
Данные модели не
используют функциональные зависимости;
они основаны только на статистических
взаимосвязях.
Здесь опять же
возникает вопрос: как еще до наступления
будущего оценить точность прогнозных
оценок? Для этого обычно расчеты по
выбранной прогнозной модели сравнивают
с данными, полученными в прошлом, и для
каждого момента времени определяют
различие оценок. Затем определяется
средняя разность оценок, скажем, среднее
квадратическое отклонение. По его
величине определяется прогнозная
точность модели.
При построении
прогнозных моделей чаще всего используется
парный и множественный регрессионный
анализ
Парный регрессионный
анализ
основан на использовании уравнения
прямой линии. При использовании уравнения
регрессии в целях прогнозирования надо
иметь в виду, что перенос закономерности
связи на динамику не является, строго
говоря, корректным и требует проверки
условий допустимости такого переноса
(экстраполяции), что выходит за рамки
статистики и может быть сделано только
специалистом, хорошо знающим объект
исследования и возможности его
развития в будущем.
Ограничением
прогнозирования на основе регрессионного
уравнения, тем более парного, служит
условие стабильности или, по крайней
мере, малой изменчивости других факторов
и условий изучаемого процесса, не
связанных с ними. Если резко изменится
«внешняя среда» протекающего процесса,
прежнее уравнение потеряет свое значение.
Следует соблюдать
еще одно ограничение: нельзя подставлять
значения факторного признака,
существенно отличающиеся от входящих
в базисную информацию, по которой
вычислено уравнение регрессии. При
качественно иных уровнях фактора, если
они даже возможны в принципе, были
бы иными параметры уравнения. Можно
рекомендовать при определении значений
факторов не выходить за пределы трети
размаха вариации как за минимальное,
так и за максимальное значения
признака-фактора, имеющиеся в исходной
информации.
Анализ на основе
множественной регрессии
основан на использовании более чем
одной независимой переменной в уравнении
регрессии. Это усложняет анализ, делая
его многомерным. Однако регрессионная
модель более полно отражает действительность,
так как в реальности исследуемый
параметр, как правило, зависит от
множества факторов.
Так, например, при
прогнозировании спроса идентифицируются
факторы, определяющие спрос, определяются
взаимосвязи, существующие между
ними, и прогнозируются их вероятные
будущие значения; из них при условии
реализации условий, для которых уравнение
множественной регрессии остается
справедливым, выводится прогнозное
значение спроса.
Многофакторное
уравнение множественной регрессии
имеет следующий вид:

Термин «коэффициент
условно-чистой регрессии» означает,
что каждая из величин b
измеряет среднее по совокупности
отклонение зависимой переменной
(результативного признака) от ее средней
величины при отклонении зависимой
переменной (фактора) х от своей средней
величины на единицу ее измерения. При
этом все прочие факторы, входящие в
уравнение регрессии, закреплены на
средних значениях и не изменяются.
Помимо целей
прогнозирования множественная регрессия
может использоваться для отбора
статистически значимых независимых
факторов, которые следует использовать
при исследовании результативного
признака. В частности, при поиске
критериев сегментации исследователь
может использовать регрессионный анализ
для выделения демографических
факторов, которые оказывают наиболее
сильное влияние на какой-то результирующий
показатель, характеризующий поведение
покупателей, например выбор товара
определенной марки.
Кроме того,
множественная регрессия может
использоваться для определения
относительной важности независимых
переменных.
Поскольку независимые
переменные имеют различные размерности,
проводить их сравнение прямым образом
нельзя. Например, нельзя прямым образом
сравнивать коэффициенты b
для размера семьи и величины среднего
для семьи дохода.
Обычно в данном
случае поступают следующим образом.
Делят каждую разницу между независимой
переменной и ее средней на среднее
квадратическое отклонение для этой
независимой переменной. Далее возможно
прямое сравнение полученных величин
(коэффициентов).
Многие данные
маркетинговых исследований представляются
для различных интервалов времени,
например на ежегодной, ежемесячной и
другой основе. Такие данные называются
временными
рядами.
Анализ временных рядов направлен на
выявление трех видов закономерностей
изменения данных: трендов, цикличности
и сезонности.
Тренд
характеризует общую тенденцию в
изменениях показателей ряда.
В таблице 5
приводятся данные объема продаж коньков
определенной компании за 15 лет.
Таблица
5 – Объем продаж коньков
|
Год |
Годовой |
|
1 |
1300 |
|
2 |
1250 |
|
3 |
1005 |
|
4 |
1437 |
|
5 |
908 |
|
6 |
1170 |
|
7 |
1380 |
|
8 |
1245 |
|
9 |
1111 |
|
10 |
1508 |
|
11 |
1970 |
|
12 |
2115 |
|
13 |
2460 |
|
14 |
3040 |
|
15 |
3520 |
|
16 |
???? |
Необходимо
определить прогнозную оценку объема
продаж на шестнадцатый год. Представив
в графическом виде данные табл. 2, можно
с помощью метода наименьших квадратов
подобрать прямую линию, в наибольшей
степени соответствующую полученным
данным (рис. 1), и определить прогнозную
величину объема продаж.
Сущность метода
наименьших квадратов состоит в отыскании
параметров модели тренда, минимизирующих
ее отклонение от точек исходного
временного ряда, т. е.
 (1)
(1)
где
 – расчетные значения исходного ряда;
– расчетные значения исходного ряда;
уi
– фактические значения исходного ряда;
n – число наблюдений. Если модель тренда
представить в виде
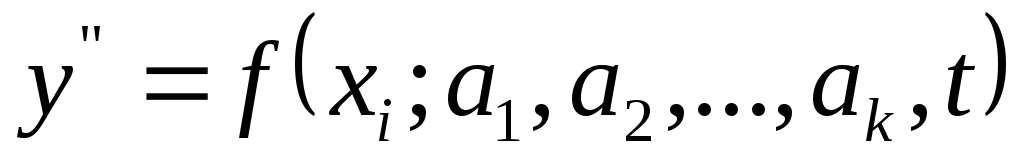 (2)
(2)
где a1
,a2
,…, ak
– параметры модели;
t – время;
xi
– независимые переменные, то для того,
чтобы найти параметры модели,
удовлетворяющие условию (1), необходимо
приравнять нулю первые производные
величины S по каждому из коэффициентов
a . Решая полученную систему уравнений
с k неизвестными, находим значения
коэффициентов a .
В то же время более
внимательное рассмотрение рис. 1 позволяет
сделать вывод о том, что не все точки
близко расположены к прямой. Особенно
эти расхождения велики для последних
лет, а верить последним данным, видимо,
следует с достаточным основанием.
В данном случае
можно применить метод экспоненциального
сглаживания, назначая разные весовые
коэффициенты (большие для последних
лет) данным для разных лет. В последнем
случае прогнозная оценка в большей
степени соответствует тенденциям
последних лет.
Алгоритм расчета
экспоненциально сглаженных значений
в любой точке ряда i основан на трех
величинах:
– фактическое
значение Ai в данной точке ряда i;
– прогноз в точке
ряда Fi;
– некоторый заранее
заданный коэффициент сглаживания W,
постоянный по всему ряду.
Новый прогноз
можно записать формулой:
![]() (3)
(3)
Коэффициент
сглаживания W может принимать любые
значения из диапазона 0 < W < 1.Однако,
аналитики большинства фирм при обработке
рядов используют свои традиционные
значения W. Так, по опубликованным данным
в аналитическом отделе Kodak, традиционно
используют значение 0,38, а на фирме Ford
Motors – 0,28 или 0,3.

Рисунок 3 –
Прогнозирование объема продаж коньков
Циклический
характер колебаний статистических
показателей характеризуется длительным
периодом (солнечная активность,
урожайность отдельных культур,
экономическая активность). Такие явления,
как правило, не являются предметом
исследования маркетологов, которых
обычно интересует динамика проблемы
на относительно коротком интервале
времени.
Сезонные колебания
показателей имеют регулярный характер
и наблюдаются в течение каждого года.
Они и являются предметом изучения
маркетологов (спрос на газонокосилки,
на отдых в курортных местах в течение
года, на телефонные услуги в течение
суток и т.д.). Поскольку выявленные
закономерности носят регулярный
характер, то их вполне обоснованно можно
использовать в прогнозных целях.
Как и любые прогнозы,
оценки, полученные при помощи статистических
методов нужно уметь правильно использовать.
Предположим, что была получена прогнозная
оценка величины спроса на какой-то
товар. Она говорит о том, что при тех
же условиях внешней среды, структуре
и силе действия исходных факторов
величина спроса к определенному
моменту времени достигнет такой-то
величины. Менеджерам, которые
используют результаты данного прогноза,
следует ответить на вопрос: «А
устраивает ли нас данная величина
спроса?» Если «да», то надо приложить
максимум усилий, чтобы все сохранить
без изменения. Если «нет», то необходимо
использовать внутренние возможности
(например, провести дополнительную
рекламную компанию) и постараться
повлиять на определенные факторы внешней
среды, поддающиеся косвенному воздействию
(например, повлиять на деятельность
посредников, пролоббироавть изменение
определенных тарифов, импортных пошлин).
Вся эта деятельность направлена на
обеспечение получения желаемой величины
спроса.
-
.
Внутренний анализ и анализ конкуренции
Для полноты
информации проводиться исследования
не только потребителей, но внутренний
анализ и анализ конкуренции.
Внутренняя среда
организации –
та часть общей среды, которая находится
в ее пределах. Она оказывает постоянное
и самое непосредственное воздействие
на функционирование организации.
Внутренняя среда имеет несколько срезов,
состояние которых в совокупности
определяет тот потенциал и те возможности,
которыми располагает организация.
Изучение внутренней среды направлено
на уяснение того, какими сильными и
слабыми сторонами обладает организация.
Сильные стороны служат базой, на которую
организация опирается в конкурентной
борьбе и которую она должна стремиться
расширять и укреплять. Слабые стороны
— это предмет пристального внимания
со стороны руководства, которое должно
делать все возможное, чтобы избавиться
от них.
Анализ внутренней
среды организации обычно
проводится для сравнения положения
компании с положением ближайших
конкурентов (для оценки конкурентной
стратегической позиции организации).
Внутренний анализ
— это большое количество взаимосвязанных
переменных, которые могут быть объединены
в несколько групп, где важнейшими будут:
ресурсы и организация корпорации; рынки
и сбыт; финансирование; производство,
операции и технические аспекты; персонал.
Рассмотрим
последовательно компоненты каждой
группы.
·
Образ
и престиж корпорации.
• Размеры корпорации.
• Гибкие и
подстраивающиеся структуры.
• Эффективные
исследования и разработки.
• Эффективные
системы управленческойинформации;
• Уровень подготовки
высшего руководства.
• Стандартные
процедуры деятельности.
• Система контроля
и планирования
Целью внутреннего
анализа является устранение разногласий
между системными и стратегическими
задачами организации
Обратимся к анализу
конкуренции. Конкуренция –
это, как известно, механизм формирования
новых рыночных ниш и наиболее
эффективное использование существующих.
Поэтому освоение таких ниш компанией
должно сопровождаться изучением
конкурентных механизмов на данном
рынке. Причем такой анализ должен
предшествовать работе маркетологов
и разработчиков продуктов.
Первоочередность
анализа конкуренции гарантирует от
возможных просчетов в будущем,
поскольку определяет реалистичную
модель поведения на рынке.
Анализ проводиться
по следующим направлениям:
-
Определение
конкурентов; -
Сбор
сведений о конкуренте; -
Анализ
конкурентов; -
Анализ
конкурентоспособности предприятия.
На основе
маркетинговых исследований делаются
прогнозные оценки маркетинговой
информации.
Прогнозная
информация есть результат ряда основных
этапов поиска: предпрогнозная
ситуация
(проблемы, цели, рабочие гипотезы и др.),
прогнозный
фон (сбор и
анализ данных, влияющих на производство
продукта, товара и т.д.), исходная
модель
(совокупность признаков, показателей,
отражающих содержание объекта); поисковый
прогноз
(выявление текущего развития предполагаемой
модели); нормативный
прогноз
(ожидаемое будущего состояния с заданными
нормами и целями); оценка
степени точности
прогнозов (например с помощью экспертов);
Прогноз должен
учитывать следующие потребности:
1)
психологические,
2) этнокультурные,
3) социальные,
4)
трудовые,
5)
экономические
Однако
прогнозная информация может оказаться
недостаточной (ущербной), если не
учитывать интересы потребителей при
личных встречах. Данное партнерство
позволяет фирме оценить продукт в
реальных условиях, а покупатель получает
изделие с учетом его требований. Без
учета мнения покупателей можно
“промахнуться”, имея в виду тот
факт, когда изделие не найдет своего
потребителя. Выявление мнения покупателя –
один из важных источников получения
прогнозной информации в маркетинге.
Лекция № 23 МОДЕЛИ СТАТИСТИЧЕСКОГО
ПРОГНОЗИРОВАНИЯ
ПЛАН
1.
О
статистике и статистических данных.
2.
Метод
наименьших квадратов.
3.
Прогнозирование
по регрессионной модели.
1
О статистике и статистических данных
Рассмотрим способ нахождения
зависимости частоты заболеваемости жителей города бронхиальной астмой от
качества возду ха (третий пример из сформулированных в начале предыдущего
параграфа). Любому человеку понятно, что такая зависимость существует.
Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное
заключение. Его недостаточно для того, чтобы управлять уровнем загрязненности
воздуха. Для управления требуются более конкретные знания. Нужно установить,
какие именно примеси сильнее всего влияют на здоровье людей, как связана
концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость
можно установить только экспериментальным путем: посредством сбора
многочисленных данных, их анализа и обобщения.
При решении таких проблем
на помощь приходит статистика.
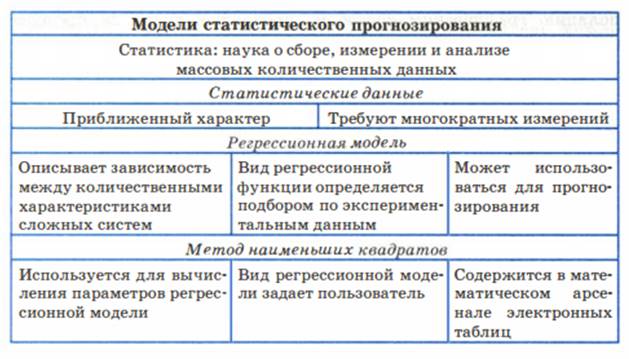
Статистика –
наука о сборе, измерении и анализе массовых количественных данных.
Существуют медицинская статистика,
экономическая статистика, социальная статистика и другие. Математический
аппарат статистики разрабатывает наука под названием математическая статистика.
Рассмотрим пример из
области медицинской статистики.
Известно, что наиболее
сильное влияние на бронхиально-легочные заболевания оказывает угарный газ –
монооксид углерода. Поставив цель определить эту зависимость, специалисты по
медицинской статистике проводят сбор данных. Они собирают сведения из разных
городов о средней концентрации угарного газа в атмосфере и о заболеваемости
астмой (число хронических больных на 1000 жителей). Полученные данные можно
свести в таблицу, а также представить в виде точечной диаграммы (рис .3.31
) .
1 Приведенные
в примере данные не являются официальной статистикой, однако правдоподобны.
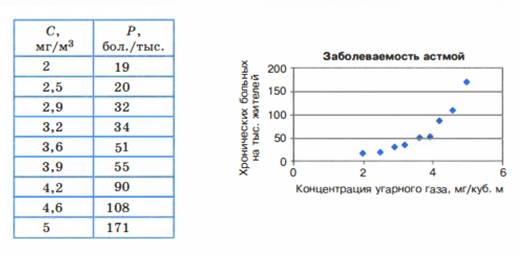
Рис. 3.3.
Табличное и графическое представление статистических данных
Статистические данные
всегда являются приближенными, усредненными. Поэтому они носят оценочный
характер, но верно отражают характер зависимости величин. И еще одно важное замечание:
для достоверности результатов, полученных путем анализа статистических данных,
этих данных должно быть много.
Из полученных данных можно
сделать вывод, что при концентрации угарного газа до 3 мг /м3 его
влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации
на ступает резкий рост заболеваемости.
А как построить
математическую модель данного явления? Очевидно, нужно получить формулу,
отражающую зависимость количества хронических больных Р от концентрации
угарного газа С. На языке математики это называется функцией зависимости Р от
С: Р(С). Вид такой функции неизвестен, ее следует искать методом подбора по
экспериментальным данным.
Понятно, что график
искомой функции должен проходить близко к точкам диаграммы экспериментальных
данных. Строить функцию так, чтобы ее график точно проходил через все данные
точки (рис.3.4,а), не имеет смысла. Во-первых, математический вид такой функции
может оказаться слишком сложным. Во-вторых, уже говорилось о том, что
экспериментальные значения являются приближенными. Отсюда следуют основные
требования к искомой функции:
• она должна быть
достаточно простой для использования ее в дальнейших вычислениях;
• график этой функции должен
проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от
графика были минимальны и равномерны (рис.3.4,6).
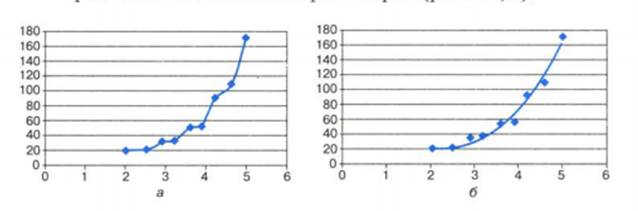
Рис. 3.4. Два
варианта построения графической зависимости по экспериментальным данным
Полученную функцию, график
которой приведен на рис.3.4,б, в статистике принято называть регрессионной
моделью.
2
Метод наименьших квадратов
Получение регрессионной
модели происходит в два этапа:
1) подбор вида функции;
2) вычисление параметров
функции.
Первая задача не имеет строгого
решения. Здесь может помочь опыт и интуиция исследователя, а возможен и
«слепой» перебор из конечного числа функций и выбор лучшей из них.
Чаще всего выбор производится
среди следующих функций:
у = ах + b –
линейная функция;
у = ах2 + bх +
с
– квадратичная функция;
у = а ln
(x) + b – логарифмическая функция;
у = а е bх –
экспоненциальная функция;
у = ахb
– степенная функция.
Квадратичная функция
называется в математике полиномом второй степени. Иногда используются
полиномы и более высоких степеней, например полином третьей степени имеет вид:
у= ах3 + bх2 + сх + d.
Во всех этих формулах:
х – аргумент,
у
– значение функции,
а, b, с, d –
параметры функции,
ln(x) – натуральный
логарифм,
е
– константа, основание натурального логарифма.
Если вы выбрали
(сознательно или наугад) одну из предлагаемых функций, то далее нужно
подобрать параметры (а, b, с и пр.) так, чтобы функция располагалась как
можно ближе к экспериментальным точкам. Что значит «располагалась как можно
ближе»? Ответить на этот вопрос значит предложить метод вычисления
параметров. Такой метод был предложен в XVIII веке немецким математиком К. Гауссом
и называется методом наименьших квадратов (МНК). Суть его заключается в
следующем: искомая функция должна быть построена так, чтобы сумма квадратов
отклонений у-координат всех экспериментальных точек от у-координат
графика функции была минимальной.
Мы не будем здесь
производить подробное математическое описание метода наименьших квадратов.
Достаточно того, что вы теперь знаете о существовании такого метода. Он очень
широко используется в статистической обработке данных и встроен во многие
математические пакеты программ. Важно понимать следующее: методом наименьших
квадратов по данному набору экспериментальных точек можно построить любую (в
том числе и из рассмотренных выше) функцию. А вот будет ли она нас удовлетворять,
это уже другой вопрос – вопрос критерия соответствия. На рис.3.5 изображены три
функции, построенные методом наименьших квадратов по приведенным
экспериментальным данным.
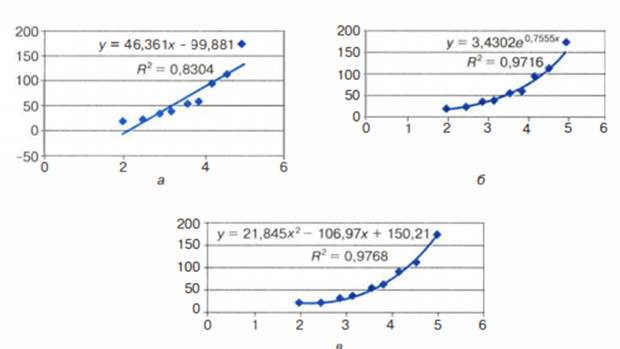
Рис. 3.5. Три функции, построенные по
МНК
Эти рисунки получены с
помощью табличного процессора Microsoft Excel . График регрессионной модели
называется трен дом. Английское слово trend можно перевести как « общее
на правление » или « тенденция») .
Уже с первого взгляда
хочется отбраковать вариант линейного тренда. График линейной функции – это
прямая. Полученная по МНК прямая отражает факт роста заболеваемости от
концентрации угарного газа, но по этому графику трудно что-либо сказать о
характере этого роста. А вот квадратичный и экспоненциальный тренды
правдоподобны. Теперь пора обратить внимание на надписи, присутствующие на
графиках. Во-первых, это записанные в явном виде искомые функции –
регрессионные модели:
линейная функция: у
= 46,361х – 99,881;
экспоненциальная функция:
у = 3,4302 е 0,7555х;
квадратичная функция: у
= 21,845х2 – 106,97х + 150,21.
На графиках присутствует
еще одна величина, полученная в результате построения трендов. Она обозначена
как R2. В статистике эта величина называется коэффициентом
детерминированности. Именно она определяет, насколько удачной является
по лученная регрессионная модель. Коэффициент детерминированности всегда
заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через
табличные значения, если О, то выбранный вид регрессионной модели предельно
неудачен. Чем R2 ближе к 1, тем удачнее регрессионная модель.
Из трех выбранных моделей
значение R2 наименьшее у линейной. Значит, она самая неудачная
(нам и так это было понятно). Значения же R2 у двух других моделей достаточно
близки (разница меньше 0,01). Если определить погрешность решения данной
задачи как 0,01, по критерию R2 эти модели нельзя разделить. Они
одинаково удачны. Здесь могут вступить в силу качественные соображения.
Например, если считать, что наиболее существенно влияние концентрации угарного
газа проявляется при больших величинах, то, глядя на графики, предпочтение
следует отдать квадратичной модели. Она лучше отражает резкий рост
заболеваемости при больших концентрациях примеси.
Интересный факт: опыт
показывает, что если человеку предложить на данной точечной диаграмме провести
«на глаз» прямую так, чтобы точки были равномерно разбросаны вокруг нее, то он
проведет линию, достаточно близкую к той, что дает МНК.
3 Прогнозирование по
регрессионной модели
Мы получили регрессионную
математическую модель и можем прогнозировать процесс путем вычислений. Теперь
можно оценить уровень заболеваемости астмой не только для тех значений
концентрации угарного газа, которые были получены путем измерений, но и для
других значений. Это очень важно с практической точки зрения. Например, если в
городе планируется построить завод, который будет выбрасывать в атмосферу
угарный газ, то, рассчитав его возможную концентрацию, можно предсказать, как
это отразится на заболеваемости астмой жителей города.
Существует два способа
прогнозирования по регрессионной модели. Если прогноз производится в пределах
экспериментальных значений независимой переменной (в нашем случае это концентрация
угарного газа С), то это называется восстановлением значения.
Прогнозирование за
пределами экспериментальных данных называется экстраполяцией.
Имея регрессионную
модель, легко прогнозировать, производя расчеты с помощью электронных таблиц.
Выберем для нашего примера в качестве наиболее подходящей квадратичную зависимость.
Построим следующую электронную таблицу:

Подставляя в ячейку А2
значение концентрации угарного газа, в ячейке В2 будем получать прогноз
заболеваемости. Вот пример восстановления значения:
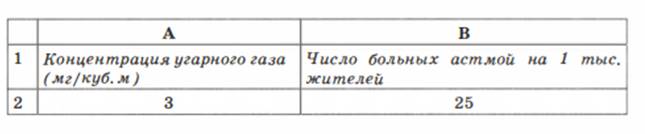
Заметим, что число, получаемое
по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла
считать число людей, даже среднее, в дробных величинах. Дробная часть удалена –
в формате вывода числа указано 0 цифр после запятой.
Экстраполяционный прогноз
выполняется аналогично.
Табличный процессор дает возможность
производить экстраполяцию графическим способом, продолжая тренд за пределы
экспериментальных данных. Как это выглядит при использовании квадратичного
тренда для
С= 7, показано на рис . 3.6.
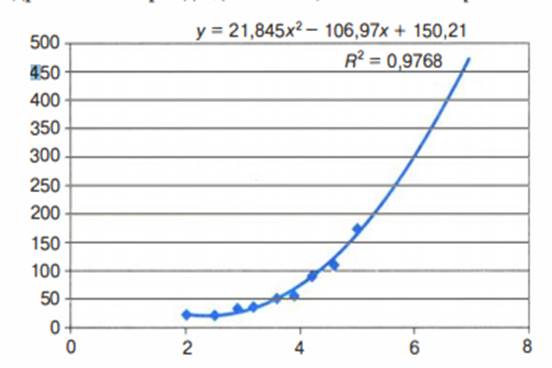
Рис. 3.6. Квадратичный тренд с
экстраполяцией
В ряде случаев с
экстраполяцией надо быть осторожным. Применимость всякой регрессионной модели
ограничена, особенно за пределами экспериментальной области. В нашем примере
при экстраполяции не следует далеко уходить от величины 5 мг/м3.
Вполне возможно, что далее характер зависимости существенно меняется. Слишком
сложной является система « экология – здоровье человека», в ней много
различных факторов, которые связаны друг с другом. Полученная регрессионная функция
является всего лишь моделью, экспериментально подтвержденной в диапазоне концентраций
от 2 до 5 мг/м3 . Что будет вдали от этой области, мы не знаем.
Всякая экстраполяция держится на гипотезе: «предположим, что за пределами
экспериментальной области закономерность сохраняется». А если не сохраняется?
Квадратичная модель в
данном примере в области малых значений концентрации, близких к 0, вообще не
годится. Экстраполируя ее на С= 0 мг/м3, получим 150
человек больных, т. е. больше, чем при 4 мг /м3. Очевидно, это
нелепость. В области малых значений С лучше работает экспоненциальная модель.
Кстати, это довольно типичная ситуация: разным областям данных могут лучше
соответствовать разные модели.
Система основных понятий
ВОПРОСЫ
И ЗАДАНИЯ
1. а) Что такое статистика?
б) Являются ли результаты
статистических расчетов точными?
в) Что такое
регрессионная модель?
2. Какие из следующих величин можно назвать
статистическими: температура вашего тела в данный момент; средняя температура в
вашем регионе за последний месяц; максимальная скорость, развиваемая дан ной
моделью автомобиля; среднее число осадков, выпадающих в вашем регионе в течение
года?
3. а) Для чего используется метод
наименьших квадратов?
б) Что такое тренд?
в) Как располагается
линия тренда, построенная по МНК, относительно экспериментальных точек?
г) Может ли тренд, построенный по МНК,
пройти выше всех экспериментальных точек?
4. а) В чем смысл параметра R 2
? Какие значения он принимает?
б) Какое значение примет
параметр R 2 , если тренд точно проходит через экспериментальные
точки?
5. По данным из следующей таблицы постройте
с помощью Excel линейную, квадратичную, экспоненциальную и логарифмическую
регрессионные модели. Определите параметры, выберите лучшую модель.

6. а) Что подразумевается под
восстановлением значения по регрессионной модели?
б) Что такое экстраполяция?
7. Соберите данные о средней дневной температуре
в вашем городе за последнюю неделю (10 дней, 20 дней). Оцените (хотя бы на
глаз), годится ли использование линейного тренда для описания характера изменения
температуры со временем. Попробуйте путем графической экстраполяции предсказать
температуру через 2-5 дней.
8. Придумайте свои примеры практических
задач, для которых имело бы смысл выполнение восстановления значений и
экстраполяционных расчетов.
Имеются данные о рейтинге авиакомпании и ее пассажирообороте. Сделайте точечный прогноз значения рейтинга авиакомпании при пассажирообороте, равном 15 млн. пасс/км (линейная регрессия).
| № п/п | х | y |
|---|---|---|
| 1 | 67,12 | 3,9 |
| 2 | 47,07 | 3,9 |
| 3 | 1,42 | 3,8 |
| 4 | 15,58 | 3,7 |
| 5 | 8,47 | 3,6 |
| 6 | 2,87 | 3,3 |
| 7 | 10,15 | 3,3 |
| 8 | 13,33 | 3,3 |
| 9 | 3,31 | 3,2 |
| 10 | 0,29 | 3,2 |
| 11 | 5,56 | 3,2 |
| 12 | 2,45 | 3,2 |
| 13 | 2,04 | 3,2 |
| 14 | 0,33 | 3,1 |
| 15 | 0,97 | 3,1 |
| 16 | 0,57 | 3,1 |
| 17 | 13,4 | 3,1 |
| 18 | 20,2 | 3,1 |
| 19 | 0,57 | 3,1 |
| 20 | 1,75 | 3 |
| 21 | 0,43 | 3 |
| 22 | 6,06 | 3 |
| 23 | 2,51 | 3 |
| 24 | 0,62 | 2,9 |
| 25 | 2,9 | 2,9 |
| 26 | 3,39 | 2,8 |
| 27 | 0,6 | 2,7 |
| 28 | 0,66 | 2,6 |
| 29 | 4,04 | 2,3 |
| 30 | 0,44 | 2,1 |
Решение:
Для расчёта параметров линейной регрессии
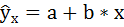
необходимо решить систему нормальных уравнений относительно a и b:
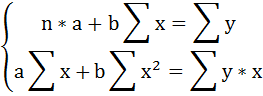
Построим таблицу исходных и расчётных данных.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | y | x2 | x×y | 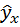 |
|---|---|---|---|---|---|
| 1 | 67,12 | 3,9 | 4505,094 | 261,768 | 4,085272 |
| 2 | 47,07 | 3,9 | 2215,585 | 183,573 | 3,759205 |
| 3 | 1,42 | 3,8 | 2,0164 | 5,396 | 3,016813 |
| 4 | 15,58 | 3,7 | 242,7364 | 57,646 | 3,247093 |
| 5 | 8,47 | 3,6 | 71,7409 | 30,492 | 3,131465 |
| 6 | 2,87 | 3,3 | 8,2369 | 9,471 | 3,040394 |
| 7 | 10,15 | 3,3 | 103,0225 | 33,495 | 3,158786 |
| 8 | 13,33 | 3,3 | 177,6889 | 43,989 | 3,210501 |
| 9 | 3,31 | 3,2 | 10,9561 | 10,592 | 3,047549 |
| 10 | 0,29 | 3,2 | 0,0841 | 0,928 | 2,998436 |
| 11 | 5,56 | 3,2 | 30,9136 | 17,792 | 3,08414 |
| 12 | 2,45 | 3,2 | 6,0025 | 7,84 | 3,033563 |
| 13 | 2,04 | 3,2 | 4,1616 | 6,528 | 3,026896 |
| 14 | 0,33 | 3,1 | 0,1089 | 1,023 | 2,999086 |
| 15 | 0,97 | 3,1 | 0,9409 | 3,007 | 3,009494 |
| 16 | 0,57 | 3,1 | 0,3249 | 1,767 | 3,002989 |
| 17 | 13,4 | 3,1 | 179,56 | 41,54 | 3,21164 |
| 18 | 20,2 | 3,1 | 408,04 | 62,62 | 3,322226 |
| 19 | 0,57 | 3,1 | 0,3249 | 1,767 | 3,002989 |
| 20 | 1,75 | 3 | 3,0625 | 5,25 | 3,022179 |
| 21 | 0,43 | 3 | 0,1849 | 1,29 | 3,000713 |
| 22 | 6,06 | 3 | 36,7236 | 18,18 | 3,092272 |
| 23 | 2,51 | 3 | 6,3001 | 7,53 | 3,034539 |
| 24 | 0,62 | 2,9 | 0,3844 | 1,798 | 3,003802 |
| 25 | 2,9 | 2,9 | 8,41 | 8,41 | 3,040881 |
| 26 | 3,39 | 2,8 | 11,4921 | 9,492 | 3,04885 |
| 27 | 0,6 | 2,7 | 0,36 | 1,62 | 3,003477 |
| 28 | 0,66 | 2,6 | 0,4356 | 1,716 | 3,004453 |
| 29 | 4,04 | 2,3 | 16,3216 | 9,292 | 3,059421 |
| 30 | 0,44 | 2,1 | 0,1936 | 0,924 | 3,000875 |
| Итого | 239,1 | 93,7 | 8051,407 | 846,736 | 93,7 |
Подставив в систему уравнений рассчитанные величины, определим параметры линейного уравнения:
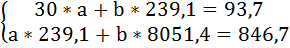
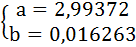
Таким образом, уравнение регрессии имеет вид:
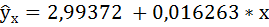
Это значит, что с увеличением пассажирооборота на 1 млн. пасс/км рейтинг авиакомпании увеличится на 0,016263.
Подставим в данное уравнение исходные значения х и найдём сумму расчётных значений у (последняя графа таблицы).
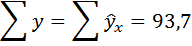
Так как суммы исходных и расчётных значений у совпадают, следовательно, параметры уравнения рассчитаны верно.
Если прогнозное значение пассажирооборота, составит 15 млн. пасс/км, то рейтинг авиакомпании будет равен:
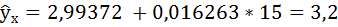
Ответ: значение рейтинга авиакомпании при пассажирообороте, равном 15 млн. пасс/км будет равно 3,2.
