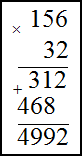Содержание:
- Определение произведения чисел
- Свойства произведения чисел
Определение произведения чисел
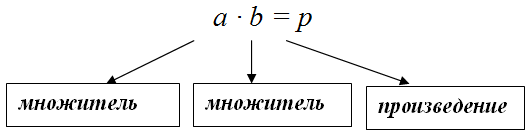
Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
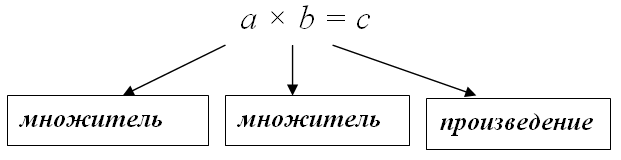
В частности, если умножаются два числа $a$ и $b$, то
Пример
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$1,2 cdot 3=3,6$
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
-
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
- Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.
Пример
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик
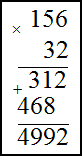
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:
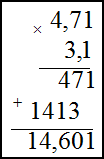
Ответ.
$156 cdot 32=4992$
$4,71 cdot 3,1=14,601$
Читать дальше: что такое простое число.
Определение
Произведением чисел в математике называется результат их умножения.
Пример: Найдите произведение чисел.
14×15=210
Здесь 14 и 15 называются — множители.
Свойства
1. Коммутативность.
Пример: Вычислить произведение чисел.
17×12=204 и 12×17=204
Переместительный закон: При перестановке множителей результат не меняется.
2. Ассоциативность.
Пример:
11×19×32=6688
(11×19)×32=6688
11×(19×32)=6688
Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.
3. Дистрибутивность.
Пример:
(15+12)×9=243 и 15×9+12×9=243
Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.
Большие числа, а также десятичные дроби умножают в столбик.
Нет времени решать самому?
Наши эксперты помогут!
Произведение цифр числа
Пример: найти произведение цифр числа 428
4×2×8=64
Произведение суммы и разности чисел
(23+14)×(23-14)=37×9=333
Наименьшее произведение чисел
При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.
Сумма двух произведений чисел
(7×8)+(9×3)=56+27=83
Ответ: 83
Пример: Найди сумму и произведение чисел 14 и 72
Решение:
14+72=86 — сумма
14×72=1008 — произведение
 Одна из важных математических операций это произведение чисел. Что же скрыто за этими словами как произведение, умножение…? Именно об этом в нашей статье.
Одна из важных математических операций это произведение чисел. Что же скрыто за этими словами как произведение, умножение…? Именно об этом в нашей статье.
Давайте наверное начнем с банальных вещей. Когда у нас появляется много чего-то, то довольно сложно это хранить даже в виде информации. Нам каким-то образом это приходится компактно сокращать. Вот скажем у нас появилось более чем две пары носков в шкафу, а точнее пусть их будет 15… Как нам из записать на бумаге. Да, конечно, мы можем взять и записать 2+2+2… и так далее, пока не перечислим цифру два, с которой ассоциируется одна из пар носков на их количество, то есть на 15. Но это ведь право не удобно, особенно если представить, что речь идет не только о наших носках в шкафу, но и о случае их хранения в магазине! И здесь проще записать словами так. У нас две пары носков взято какое-то количество раз!
Вот, здесь где-то и образуется эта самая магия перехода от обычной суммы к произведению, когда мы подразумеваем, что берем какое-то число какое-то количество раз. Самое время дать определение.
Определение произведения чисел
Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.
Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так
С=а1+а2+а3+а4…+аb где 1,2,3,4…b будут индексом указывающим на то, какое это число а по порядку и не более того!
Пример Найти произведение чисел:
1) 1.2⋅3 ;
Ответ.1,2⋅3=3,6
2) 4⋅5⋅13
Ответ: 4⋅5⋅13=260
Свойства произведения чисел
Коммутативность: n⋅m=m⋅n
Ассоциативность: (n⋅m)⋅k=n⋅(m⋅k)
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Дистрибутивность: (n+m)⋅k=n⋅k+m⋅k
Пример Найти произведение чисел удобным способом:
1) 5⋅17⋅2 ; 2) 7⋅2⋅15⋅5
Решение. По свойства умножения имеем:
5⋅17⋅2=(5⋅2)⋅17=10⋅17=170
7⋅2⋅15⋅5=(7⋅(2⋅15))⋅5=(7⋅30)⋅5=210⋅5=1050
Ответ.5⋅17⋅2=170
7⋅2⋅15⋅5=1050
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Пример Найти произведение чисел
1) 156⋅32 ; 2) 4,71⋅3,1
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе нужно отделить справа три знака:
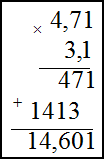
Ответ.
156⋅32=4992
4,71⋅3,1=14,601
Побалуемся с произведением!?
|
Вводим циферки Цифра которую будем брать N раз (множитель) |
|
А чему равно это самое N раз?(множитель) |
|
|
Здравствуйте, ребята!
Целую вечность вас не видел! И сегодня нашу
встречу я хочу посвятить устному умножению и делению трёхзначных чисел,
которые оканчиваются нулями.
Вот, к примеру, надо нам умножить число двести на
четыре. Трудно? А если представить число двести как две сотни? Умножаем на
четыре, получится восемь сотен. А восемь сотен это число восемьсот. Значит,
произведение чисел двести и четыре равно восьмистам. Вычисление очень простое,
а всего-то надо было представить число двести как две сотни.
А если нам надо будет, допустим, двести сорок
умножить на четыре? Число двести сорок не заменишь сотнями. А вот десятками
вполне даже можно. Двести сорок это двадцать четыре десятка. Умножаем на
четыре. Двадцать четыре это двадцать и четыре. Двадцать умножить на четыре –
восемьдесят. Четырежды четыре – шестнадцать, восемьдесят и шестнадцать –
девяносто шесть. Девяносто шесть десятков – это число девятьсот шестьдесят.
А знаете, ребята, я сейчас вот о чём подумал. При
умножении двадцати четырёх десятков я раскладывал его на сумму разрядных
слагаемых – двадцать и четыре. А может быть можно умножить подобным
способом и трёхзначное число?
Если представим число двести сорок в виде суммы
чисел двести и сорок. Каждое из них умножим на четыре – это восемьсот и сто
шестьдесят. Складываем их. Ответ: девятьсот шестьдесят.
Великолепно! Значит, можно выполнять умножение
трёхзначных чисел с нулём на конце представив их в виде десятков. А можно и
разложив на сумму разрядных слагаемых.
А сейчас я хочу немного отступить от нашей темы.
Дело в том, что устно умножать можно не только числа, которые
оканчиваются нулями, но и трёхзначные числа с нулём в разряде десятков.
Допустим, надо найти произведение чисел двести девять и четыре. Что делать
будем? Да то же самое, что и в предыдущем примере. Двести девять — это сумма
чисел двести и девять. Умножаем каждое из них на четыре. Восемьсот и тридцать
шесть. Складываем. Ответ: восемьсот тридцать шесть. …
Ну, вроде бы с устными приёмами умножения трёхзначных
чисел разобрались. Пора переходить к делению.
Хотим мы, например, шестьсот разделить на три.
Ха! Легче лёгкого! Шестьсот – это шесть сотен. Делим их на три, получается две
сотни, или число двести.
А шестьсот девяносто разделить на три? Шестьсот девяносто –
это шестьдесят девять десятков. Делим на три. Шестьдесят на три – двадцать,
девять на три – три. Двадцать три десятка, или число двести
тридцать!
А
теперь просто разложим делимое шестьсот девяносто на сумму разрядных
слагаемых и каждое из них разделим на три.
Ну
и, конечно, делить можно, разложив число на сумму только не разрядных, а
удобных для деления слагаемых. Возьмём, к примеру, такое числовое выражение:
найти частное чисел семьсот двадцать и три.
Разложим семьсот двадцать на сумму таких чисел: шестьсот и сто двадцать. Первое
слагаемое, шестьсот – это наибольшее из круглых сотен число
(конечно, в пределах нашего числа семьсот двадцать), которое легко можно
разделить на три. Поэтому берём именно его. Делим на три – двести. Сто двадцать
делим на три. Да это же двенадцать десятков. Разделили, получилось четыре
десятка или сорок. Двести и сорок – двести сорок.
А теперь я предлагаю вам разделить девятьсот на
триста. Вы думаете это будет триста? Конечно нет! Ведь вы должны помнить: деление
– это действие, обратное умножению. Значит в ответе должно получиться такое
число, на которое можно умножить делитель и получить в итоге делимое. И чтобы
получить девятьсот, надо триста умножить на три. Значит, девятьсот разделив на
триста, получим число три.
А помните ли вы мой маленький секрет, которым я
поделился с вами, когда знакомил с делением двузначного круглого числа на
двузначное круглое? Например, шестьдесят разделить на тридцать, или сто
разделить на пятьдесят?
При
делении круглого числа на круглое мы мысленно прикрываем
в делимом и делителе равное количество нулей и выполняем деление
полученных чисел.
При
делении круглых трёхзначных чисел мы тоже можем тоже
воспользоваться этим правилом. Надо, например, разделить восемьсот на
четыреста. Прикрыли в делимом и делителе равное количество нулей, по два.
Оп-ля! Делим восемь на четыре, и получаем ответ два! То есть, восемьсот
разделить на четыреста, получится два. Хотите проверить? Пожалуйста! Четыреста
умножаем на два – восемьсот. Всё верно. Даже если придётся четырёхзначное
число, тысячу, разделить, например, на пятьсот, можно воспользоваться моим
секретом! Раз, и прикрыли нули! Но не все, а только по два. Ведь в правиле
сказано: При делении круглого числа на круглое мы мысленно
прикрываем в делимом и делителе РАВНОЕ количество нулей и выполняем
деление полученных чисел.
А,
самое главное, нули убрали – да и забыли о них. В частном эти нули уже не
нужны.
Десять
делим на пять, получается два. Значит, частное чисел тысяча и пятьсот равно
двум.
Ну,
вот, пожалуй, и всё, о чём я хотел вам сегодня рассказать: как можно устно
умножать и делить трёхзначные числа. Осталось только быстро всё повторить.
Умножать
трёхзначные числа можно, переведя их в сотни или десятки.
Или
можно трёхзначное число разложить на сумму разрядных слагаемых,
каждое из которых умножить на второй множитель, и эти произведения сложить.
Делить
трёхзначные числа можно, заменив их сотнями или десятками.
Можно
трёхзначное число разложить на сумму удобных для деления
слагаемых, каждое из которых разделить на делитель, и полученные частные
сложить.
При
делении круглого числа на круглое можно мысленно прикрыть в делимом и делителе равное
количество нулей и выполнить деление полученных чисел.
Ну а теперь пришло время нам попрощаться. Успехов
вам, ребята!
Главная » Разное » Произведение чисел что это такое в математике 3 класс
Произведение (математика) – это… Что такое Произведение (математика)?
-
Произведение — (математика) результат умножения. Произведение искусства. Музыкальное произведение. Аудиовизуальное произведение. Служебное произведение … Википедия
-
Произведение (теория категорий) — Произведение двух или более объектов это обобщение в теории категорий таких понятий, как декартово произведение множеств, прямое произведение групп и произведение топологических пространств. Произведение семейства объектов это в… … Википедия
-
Произведение Кронекера — Произведение Кронекера бинарная операция над матрицами произвольного размера, обозначается . Результатом является блочная матрица. Произведение Кронекера не следует путать с обычным умножением матриц. Операция названа в честь немецкого… … Википедия
-
Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия
-
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
-
Категория (математика) — Теория категорий раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Некоторые математики[кто?] считают теорию категорий слишком абстрактной и непригодной для… … Википедия
-
Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия
-
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
-
Операция (математика) — У этого термина существуют и другие значения, см. Операция. Операция отображение, ставящее в соответствие одному или нескольким элементам множества (аргументам) другой элемент (значение). Термин «операция» как правило применяется к… … Википедия
-
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
Что такое произведение чисел
Произведением некоторых чисел называется результат умножения данных чисел. При этом компоненты умножения называются множителями Например, 2•7•13=182. Здесь 2, 7 и 13 — множители, а 182 — произведение.
Рассмотрим простейший пример.
Пример. Найдем произведение чисел 11, 13 и 19.
Решение. 11•13•19=2717.
Ответ. 11•13•19=2717.
Можно находить произведение не только натуральных чисел, но и целых, дробных, рациональных, иррациональных. Произведение любых чисел имеет свойства:
- Коммутативность — при перестановке множителей произведение не меняется.
Пример. Найдем произведение чисел 20•13•5 удобным способом.
Решение. Воспользуемся свойством коммутативности произведения чисел:
20•13•5=(20•5)•13=100•13=1300.
Ответ. 20•13•5=1300.
- Ассоциативность — при нахождении произведения порядок выполнения умножения не важен.
Пример. Найдем произведение чисел 11•2•19•5.
Решение. Воспользуемся свойствами коммутативности и ассоциативности произведения:
11•2•19•5=(11•(2•5))•19=(11•10)•19=110•19=2090.
Ответ. 11•2•19•5=2090.
- Дистрибутивность — чтобы найти произведение суммы на число можно это число умножить на каждое слагаемое данной суммы и сложить результат. Другими словами это правило о раскрытии скобок.
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
В математике существует знак для умножения – это точка посередине строки между числами, которые нужно перемножить.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
6 – первый множитель
4 – второй множитель
24 – произведение
Числа при умножении
Первый множитель
Второй множитель
Результат умножения, или Произведение
Чтение числовых выражений
6 • 4 = 24
Этот пример можно прочитать по-разному.
- 6 умножить на 4 равняется 24.
- 6 увеличить в 4 раза – получится 24.
- Первый множитель – 6, второй множитель – 4, произведение – 24.
- Произведение 6 и 4 равно 24.
Свойство умножения
3 • 4 = 12
4 • 3 = 12
Значит, 3 • 4 = 4 • 3
От перестановки мест сомножителей произведение не изменится.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
2 + 2 + 2 + 2 = 4 (к.)
Заменяем сложение умножением и получаем:
2 • 4 = 8 (к.)
Вывод: Если в задаче есть слова «в … раз больше», то задача решается умножением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Правило встречается в следующих упражнениях:
2 класс
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 43, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 47, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 55, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 33, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 10, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 72, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 39, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 75, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 12, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 29, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 4, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 8, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 10, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 13. Вариант 2. Тест, Моро, Волкова, Проверочные работы
5 класс
Упражнение 36, Мерзляк, Полонский, Якир, Учебник
© budu5.com, 2019
Пользовательское соглашение
Copyright
Нашли ошибку?
Связаться с нами
произведение чисел – это… Что такое произведение чисел?
-
ПРОИЗВЕДЕНИЕ — (product) Результат умножения. Произведение чисел, алгебраических выражений, векторов или матриц; может быть показано точкой, косой крестик или же просто написанием их последовательно один за другим, т.е. f(x).g(y), f(x) x g(y), f(x)g(y)… … Экономический словарь
-
Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел…, 3 … Большая советская энциклопедия
-
произведение — сущ., с., употр. часто Морфология: (нет) чего? произведения, чему? произведению, (вижу) что? произведение, чем? произведением, о чём? о произведении; мн. что? произведения, (нет) чего? произведений, чему? произведениям, (вижу) что? произведения,… … Толковый словарь Дмитриева
-
Произведение матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
-
Произведение матрицы на число — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
-
Произведение (математика) — В арифметике под умножением понимают краткую запись суммы одинаковых слагаемых. Например, запись 5*3 обозначает «5 сложить с собой 3 раза», то есть является просто краткой записью для 5+5+5. Результат умножения называется произведением, а… … Википедия
-
АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, основной задачей к рого является изучение свойств целых чисел полей алгебраических чисел конечной степени над полем рациональных чисел. Все целые числа поля расширения К поля степени п могут быть получены с помощью… … Математическая энциклопедия
-
Теория чисел — Теория чисел, или высшая арифметика раздел математики, изучающий целые числа и сходные объекты. В теории чисел в широком смысле рассматриваются как алгебраические, так и трансцендентные числа, а также функции различного происхождения, которые… … Википедия
-
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ — раздел теории чисел, в к ром изучаются закономерности распределения простых чисел (п. ч.) среди натуральных чисел. Центральной является проблема наилучшего асимптотич. выражения при функции p(х), обозначающей число п. ч., не превосходящих х, а… … Математическая энциклопедия
-
Скалярное произведение — (в зарубежной литературе scalar product, dot product, inner product ) операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов сомножителей и угол между… … Википедия
-
Внутреннее произведение — определённая на векторном пространстве L над полем K симметричная эрмитова форма, рассматриваемая обычно в качестве составной части определения этого пространства[1], делающей пространство (в зависимости от типа пространства и свойств внутреннего … Википедия
компоненты математических действий
Названия компонентов при сложении:
1 слагаемое, 2 слагаемое, сумма.
Суммой называют не только результат, но и само выражение .
2 + 3 = 5
2 – первое слагаемое
3 – второе слагаемое
5 – сумма
2 + 3 – сумма
Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое.
Названия компонентов при вычитании:
уменьшаемое, вычитаемое, разность.
Разностью называют не только результат действия, но и само выражение.
8 – 3 = 5
8 – уменьшаемое
3 – вычитаемое
5 – разность
8 – 3 – разность
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
Названия компонентов при умножении:
множитель, множитель, произведение.
Произведением называют не только результат действия, но и само выражение.
8 х 3 = 24
8 – множитель
3 – множитель
24 – произведение
8 х 3 – произведение
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель (24:8=3)
Названия компонентов при делении:
делимое, делитель, частное.
Частным называют не только результат действия, но и само выражение.
8 : 2 = 4
8 – делимое
2 – делитель
4 – частное
8 : 4 – частное
Чтобы найти делимое, надо частное умножить на делитель (4х2=8)
Чтобы найти делитель, надо делимое разделить на частное (8:4=2)
Математика.
Что такое частное чисел
Задание. Найти частное чисел:
1) ; 2)
Решение. Для нахождения частного в первом примере выполним деление в столбик. Для этого запишем делимое и делитель следующим образом
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком. Возьмем по . Записываем 48 под 56 и находим остаток: . Восьмерку записываем под чертой и сносим к ней следующее число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
Таким образом,
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число. Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее запишем полученные числа в столбик, как и в первом примере:
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем , можно взять по 2. Двойку записываем в частное. И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем , записываем 42 под 56 и вычитаем: . Остаток 14 списываем к нему следующую незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное, и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.
Таким образом
Ответ.
Десятичные дроби Деления чисел столбиком онлайн
Смотрите также
-

Флекс что это такое
-

Лоза что это такое
-

Миндальный пилинг что это такое
-

Дроссель клапан что это такое
-

Матовая кракле что это такое
-

Гиперпластический гайморит что это такое
-

Гомеопат что это такое
-

Диспареуния что это такое
-

Личка в контакте что это такое
-

Пишмание что это такое
-

Прополис что это такое с чего делается